Abstract
Polyanion phosphate based Li3V2(PO4)3 material has attracted considerable attention as a novel cathode material for potential use in rechargeable lithium ion batteries. The defect chemistry and dopant properties of this material are studied using well-established atomistic scale simulation techniques. The most favourable intrinsic defect process is the Li Frenkel (0.45 eV/defect) ensuring the formation of Li vacancies required for Li diffusion via the vacancy mechanism. Long range lithium paths via the vacancy mechanism were constructed and it is confirmed that the lowest activation energy of migration (0.60 eV) path is three dimensional with curved trajectory. The second most stable defect energy process is calculated to be the anti-site defect, in which Li and V ions exchange their positions (0.91 eV/defect). Tetravalent dopants were considered on both V and P sites in order to form Li vacancies needed for Li diffusion and the Li interstitials to increase the capacity respectively. Doping by Zr on the V site and Si on the P site are calculated to be energetically favourable.
Similar content being viewed by others
Introduction
The increased need for electrical energy storage for static and mobile applications in conjunction with the demand for higher capacity, better safety, increased cycle performance, and durability made the solid-state lithium batteries technologically important1,2. The research is focusing mainly on the electrolyte and cathode trying to identify more efficient materials3,4,5,6,7,8,9,10,11,12,13,14,15,16,17. In particular, electrode materials require should satisfy safety requirements, be low cost, and critically have a higher energy density (i.e. large density of Li+ ions).
State of the art cathodes for solid-state lithium batteries include polyanion-type oxides, layered lithiated transition metal oxides and Mn-based spinels18. Monoclinic Li3V2(PO4)3 has gained the interest of the community as a cathode material for solid-state lithium batteries due to its low cost, safety, low environmental impact, appropriate cycling stability, and high theoretical capacity (197 mAhg−1)18,19,20,21,22,23,24,25. Fu et al.26 synthesized this material using mixed lithium precursors with particles high surface area leading to good electrochemical performance. Solid state7 Li NMR together with two-dimensional exchange study of Lithium was used to determine the temperature dependent Li hoping process to understand the Li dynamics on the microscopic scale suggesting that their methodology can be applied to the cycled materials and other lithium metal phosphates27. Lee and Park22 employed molecular dynamics simulation to calculate the vacancy migration energy of Li at different temperatures and confirmed the mobility of Li+ ions is anisotropic. Though these separate studies show different properties in this material, fundamental understating of this material is needed to optimize its performance.
Electrochemical behaviour of an electrode material is important to assess its applicabilty in batteries. This behavour can be studied theoretically by perfoming defect calculations and we note that such studies are absent in the literature. Atomistic modelling based on the classical pair potentials is a poweful method and can provide useful information about the defect processes, cation doping behavior and ion migration mechanism. This methodology has been applied to a variety of oxides including Li containing materials and excellent agreement in trends and energetics of defect processes was observed between calculation and the experiment7,28,29. Here, we extend our recent modelling of electrode materials30,31,32,33,34 where we examined the defects, ion diffusion and dopants. In the present study, we employ established atomistic modeling techniques to investigate the intrinsic defect chemistry, the impact of doping on the formation of lithium interstitials and lithium ion diffusion pathways in Li3V2(PO4)3. We consider the solution of a range of oxides in Li3V2(PO4)3 including aliovalent dopants (e.g. Si, Ge and Ti) and isovalent dopants (e.g. Al, Ga and Sc).
Results and Discussion
Li3V2(PO4)3 structure
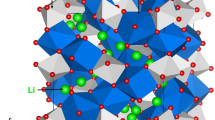
The crystal structure of Li3V2(PO4)3 exhibits a monoclinic crystallographic structure with space group P21/n (lattice parameters a = 8.5978 Å, b = 8.5933 Å, c = 12.0327 Å, α = 90.0°, β = 90.496° and γ = 90.0°) as reported by Fu et al.26 Fig. 1 shows this structure and the chemical environment of P (forming tetrahedral unit with four O atoms) and V (forming octahedral unit with six O atoms). The starting point for the present study was to reproduce the experimentally observed monoclinic crystal structure to enable an assessment of the quality and efficacy of the classical pair potentials (refer to Table S1 in the supplementary information for the potentials parameters used and method section for the detailed description of the methodology) used here. The calculated equilibrium lattice constants (refer to Table 1) are in excellent agreement with experiment.
Intrinsic defect processes
To understand the electrochemical behavior of an electrode material, intrinsic defect processes are crucial. A series of isolated point defect (vacancy and interstitial) energies were calculated, which were combined to determine the formation energies for Frenkel and Schottky-type defects in Li3V2(PO4)3. The following equations represent the reactions involving these defects as written using Kröger-Vink notation35.
The reaction energies for these intrinsic defect processes are reported in Fig. 2 and Table S2. The most favourable intrinsic disorder is Li Frenkel and the formation of other Frenkel and Schottky defects is less energetically favourable. The second most favourable defect process is calculated to be Li-V anti-site. This indicates that there will be a small percentage of Li on V sites \(({{\rm{L}}}_{{\rm{V}}}^{{\prime\prime} })\) and P on Li sites \(({{\rm{V}}}_{{\rm{Li}}}^{\cdot \cdot })\) particularly at higher temperatures. In the relaxed configuration, there is insignificant changes observed in the cation-oxygen bond distances. Antisite defects have been observed experimentally and theoretically in a variety of Li ion cathode battery materials30,31,32,33,36,37,38,39,40,41. In the experimental study of as-prepared Li2MnSiO4, a small amount of Li-Mn anti-site defect was observed41. During cycling of Li2FeSiO4, Nyten et al.36 observed structural rearrangement in the crystal structure responsible for the Li-Fe anti-site. The difference between the isolated and cluster defect energies is calculated to be ‒1.06 eV suggesting that the anti-site cluster is stable compared tom its isolated form. The formation enthalpy of Li2O via the Li2O Schottky-like reaction (relation 6) is a processes that requires an energy of 3.07 eV per defect (refer to Table S2, supplementary information). This is a process that can lead to further \(\,{V{\prime} }_{{\rm{Li}}}\) and \({V}_{O}^{\bullet \bullet }\), however, at elevated temperatures. The trend calculated for Li and V Frenkel and Li-V antisite defects is in agreement with the theoretical calculations performed by Lee et al.22, though there is a difference in defect energetics. Such difference is dependent on the choice of classical pair potentials used.
Lithium ion-diffusion
As the intrinsic lithium ion diffusion of Li3V2(PO4)3 material is of crucial importance when assessing its use as a possible high-rate cathode material in lithium batteries, we used the present static atomistic simulation to examine various possible diffusion paths responsible for Li ion conduction, which are often difficult to explore on the atomic scale by experiment alone. For the Li vacancy migration, we identified four lower activation energy local hops (A, B, C and D) and constructed long range paths connecting local Li hops (refer to Fig. 3). There are many long range three dimensional paths present. The lowest overall migration energy (0.60 eV) was calculated for the D → A → B → A path. Other possible long range paths were considered. However, the overall activation energy was calculated to be 0.87 eV due to the local hop C involved in the long range path. Here the activation energy of migration is defined as the position of the highest potential energy along the migration path. Migration energies are reported in Table 2 together with the Li-Li separation, whereas energy profile diagrams are shown in Fig. 4. Lee et al.22 calculated the one dimensional lithium ion diffusion mechanism in Li3V2(PO4)3 and their values deviates with our study. This is because in the present study we calculated three dimensional Li migation paths, which are the lowest energy migration paths (refer to Fig. 3 for detailed migration path). Migration paths calculated in this study exhibit curved trajecteries while in other studies, the paths are linear. Cahill et al.27 performed Li NMR measurements to estimate the activation energy for Li ion migration. The reported range of activation energies (0.73–0.83 eV) agrees reasonably with our calculated vlaues of 0.46–0.87 eV.
Four different energy profiles (as shown in Fig. 3) of Li vacancy hopping between two adjacent Li sites in Li3V2(PO4)3.
Tetravalent doping
The Li Frenkel is calculated to be only 0.45 eV/defect; however, an increase in the concentration of Li will further increase the applicability of Li3V2(PO4)3 as a cathode material for rechargeable lithium batteries. A way to increase the content of intrinsic defects in oxides is by the solution of aliovalent dopants as it was previously demonstrated in CeO2 (for example ref.42 and references therein). Here we considered the solution of RO2 (R = Ce, Zr, Ti, Si and Ge) via the following process (in Kröger-Vink notation):
Figure 5 reports the solution energies of RO2 and it can be observed that ZrO2 has the lowest solution energy of 2.18 eV. Solution energies of CeO2 and GeO2 are 2.31 eV and 2.35 eV respectively meaning that Ce and Ge are also promising candidate dopants. As these solution energies are higher compared to the Li Frenkel process, the solution of ZrO2, GeO2 and CeO2 during synthesis should be examined experimentally as they can increase the Li vacancy concentration (via relation (9)).
Incorporation of additional lithium into the as-prepared material will enhance the capacity and further increase the applicability of Li3V2(PO4)3 as a viable cathode material for rechargeable sodium batteries. A defect engineering way to increase the amount of lithium is by doping tetravalent cations on P site through creating Li interstitials. The efficacy of the approach has been previously demonstrated experimentally and theoretically in Li battery cathode materials18. In a theoretical study of polymorphs of Li2MnSiO4, it was suggested that Al doping on the Si site is a possible way of introducing addition Li interstitial in Li2MnSiO440. Here we considered the solution of RO2(R = Si, Ge, Ti, Zr and Ce) via the following process (in Kröger-Vink notation):
Figure 5 reports the solution energies of RO2 and it can be observed that the most favorable dopant solution energy is found for Si4+. This suggests that a possible synthesis-doping strategy of introducing additional lithium into Li3V2(PO4)3, although the exact amount of Si incorporation cannot be predicted. The second most favorable dopant is Ge4+. The solution energy increases further with the dopant size.
Concentration of Li ions will be dominated by tetravalent doping via two processes as shown in equations 9 and 10. The formation Li interstitials will be favored by Si and Ge dopants (eqn 10) on the P site whereas Ti, Zr and Ce on the V site will favor the formation of Li vacancies (eqn 9). Solution of these tetravalent dopants will create the corresponding Li defects.
Trivalent doping
A wide range of isovalent substitutions on V sites were considered. The dopant incorporation mechanism does not require the creation of vacancies or interstitials for charge-compensation. Here we considered the solution of R2O3 (R = Al, Ga, Sc, In, Y, Gd and La) via the following process (in Kröger-Vink notation):
In Fig. 6 the solution energies as a function of the dopant ionic radius are reported. The results reveal that the formation enthalpies for the dopants Sc3+, In3+, Y3+, Gd3+ and La3+ are exoergic suggesting that they are ideal candidates for substitution at the isovalent V site. The solution enthalpy for La3+ is highly negative meaning that it is worth investigating the formation of Li3(V,La)2(PO4)3 experimentally and its electrochemical performance.
Summary
In the present study, the atomistic simulation techniques have been used to provide detailed insights into intrinsic defects, lithium ion mobility and trivalent doping, which are relevant to the general electrochemical behavior of Li3V2(PO4)3. The dominant energy defect process is Li Frenkel. The Li-V anti-site defect is calculated to be the second most stable defect process suggesting that there would be small intrinsic concentration of Li on V sites at operating temperatures. The long range Li ion diffusion path with lowest migration energy was calculated to be three dimensional with the migration energy of 0.60 eV. Solution energies of RO2 (R = Al, Ga, Sc, In, Y, Gd and La) were calculated to increase Li vacancies and extra Li ions in Li3V2(PO4)3. Zr on V site and Si on P site were found to be the efficient stratergies to increase Li vacancies and extra Li ions repectively. Promising candidates for isovalent substitution on V site are Sc, In, Y, Gd and La. The present study aims to inspire further experimental work on doped Li3V2(PO4)3.
Methods
To calculate the energetics for the formation of intrinsic defects and the Li ion diffusion pathways, the classical pair potential method as implemented in the GULP package43 was employed. This method is based on the classical Born model description of the ionic crystal lattice. All systems were treated as crystalline solids with interactions between ions consisting of the long-range attractions and short-range repulsive forces representing electron-electron repulsion and van der Waals interactions. The short-range interactions were modelled using Buckingham potentials (refer to Table S1, supplementary information)30,31,44,45,46,47,48. Simulation boxes and the corresponding atom positions were relaxed using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm49. The Mott-Littleton method50 was used to investigate the lattice relaxation about point defects and the migrating ions. It divides the crystal lattice into two concentric spherical regions, where the ions within the inner spherical region (on the order of >700 ions) immediately surrounding the defect relaxed explicitly. Li ion diffusion was calculated considering two adjacent vacancy sites as initial and final configurations. Seven interstitial Li ions were considered in a direct linear route and they were fixed while all other ions were free to relax. The local maximum energy along this diffusion path is calculated and reported as activation energy of migration. As the present model assumes a full charge ionic model with the calculations corresponding to the dilute limit the defect enthalpies will be overestimated, however, relative energies and trends will be consistent.
References
Tarascon, J.-M. & Armand, M. Issues and changes facing rechargeable lithium batteries. Nature 414, 359–367 (2001).
Armand, M. & Tarascon, J.-M. Building better batteries. Nature 451, 652–657 (2001).
Kamaya, N. et al. A lithium superionic conductor. Nat. Mater. 10, 682–686 (2011).
Bruce, P. G., Freunberger, S. A., Hardwick, L. J. & Tarascon, J.-M. Li-O2 and Li-S batteries with high energy storage. Nat. Mater. 11, 19–29 (2012).
Zhao, Y. & Daemen, L. L. Superionic conductivity in lithium-rich anti-perovskites. J. Am. Chem. Soc. 134, 15042–15047 (2012).
Fisher, C. A. J., Kuganathan, N. & Islam, M. S. Defect chemistry and lithium-ion migration in polymorphs of the cathode material Li2MnSiO4. J. Mater. Chem. A 1, 4207–4214 (2013).
Jay, E. E., Rushton, M. J. D., Chroneos, A., Grimes, R. W. & Kilner, J. A. Genetics of superionic conductivity in lithium lanthanum titanates. Phys. Chem. Chem. Phys. 17, 178–183 (2015).
Klenk, M. & Lai, W. Local structure and dynamics of lithium garnet ionic conductors: tetragonal and cubic Li7La3Zr2O12. Phys. Chem. Chem. Phys. 17, 8758–8768 (2015).
Shin, D. O. et al. Synergistic multi-doping effects on the Li7La3Zr2O12 solid electrolyte for fast lithium ion conduction. Sci. Rep. 5, 18053 (2015).
Kato, Y. et al. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 1, 16030 (2016).
Chen, C., Lu, Z. & Ciucci, F. Data mining of molecular dynamics data reveals Li diffusion characteristics in garnet Li7La3Zr2O12. Sci. Rep. 7, 40769 (2017).
He, X., Zhu, Y. & Mo, Y. Origin of fast ion diffusion in super-ionic conductors. Nat. Commun. 8, 15893 (2017).
Mizushima, K., Jones, P. C., Wiseman, P. J. & Goodenough, J. B. LixCoO2 (0 < x < −1): A new cathode material for batteries of high energy density. Mater. Res. Bull. 15, 783–789 (1980).
Kang, B. & Ceder, G. Battery materials for ultrafast charging and discharging. Nature 458, 190 (2009).
Recham, N. et al. A 3.6 V lithium-based fluorosulphate insertion positive electrode for lithium-ion batteries. Nat. Mater. 9, 68 (2009).
Armstrong, A. R., Kuganathan, N., Islam, M. S. & Bruce, P. G. Structure and lithium transport pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 133, 13031–13035 (2011).
Okumura, T., Shikano, M. & Kobayashi, H. Effect of bulk and surface structural changes in Li5FeO4 positive electrodes during first charging on subsequent lithium-ion battery performance. J. Mater. Chem. A 2, 11847–11856 (2014).
Rui, X. H. et al. L3V2(PO4)3 cathode materials for lithium ion batteries: A review. J. Power Sources 258, 19–38 (2014).
Huang, H., Yin, S. C., Kerr, T., Taylor, N. & Nazar, L. F. Nanostructured composites: A high capacity, fast rate Li3V2(PO4)3/carbon cathode for rechargeable lithium batteries. Adv. Mater. 14, 1525–1528 (2002).
Pan, A. Q. et al. Nano-structured Li3V2(PO4)3/carbon composite for high-rate lithium ion batteries. Electrochem. Commun. 12, 1674–1677 (2010).
Kuang, Q. et al. Synthesis and electrochemical properties of co-doped L3V2(PO4)3 cathode materials for lithium ion batteries. Electrochimica Acta 55, 1575–1581 (2010).
Lee, S. & Park, S. S. Atomistic simulation study of monoclinic L3V2(PO4)3 as a cathode material for lithium ion battery: Structure, defect chemistry, lithium ion transport pathway, and dynamics. J. Phys. Chem. C 116, 25190–25197 (2012).
Ivanishhchev, A. V., Churikov, A. V., Ivanishcheva, I. A. & Ushakov, A. V. Lithium diffusion in Li3V2(PO4)3-based electrodes: a joint analysis of electrochemical impedance, cyclic voltammetry, pulse chronoamperometry and chronopotentiometry data. Ionics 22, 483–501 (2016).
Chen, R. J. et al. Gadolinium/chloride co-doping of lithium vanadium phosphate cathodes for lithium-ion batteries. Solid State Ionics 304, 65–70 (2017).
Wu, J. et al. F-doping effects on carbon coated Li3V2(PO4)3 as a cathode for high performance lithium rechargeable batteries: Combined experimental and DFT studies. Phys. Chem. Chem. Phys. 20, 15192–15202 (2018).
Fu, P., Zhao, Y., Dong, Y. & Hou, X. Synthesis of high tap density Li3V2(PO4)3 cathode materials using mixed lithium precursors. J. Phys. Chem. Solids 71, 394–399 (2010).
Cahill, L. S., Chapman, R. P., Britten, J. F. & Goward, G. R. 7Li NMR and Two-Dimensional Exchange Study of Lithium Dynamics in Monoclinic Li3V2(PO4)3. J. Phys. Chem. B 110, 7171–7177 (2006).
Parfitt, D., Chroneos, A., Tarancón, A. & Kilner, J. A. Oxygen ion diffusion in cation ordered/disordered GdBaCo2 O 5+δ. J. Mater. Chem 21, 2183–2186 (2011).
Islam, M. S., Driscoll, D. J., Fisher, C. A. J. & Slater, P. R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater 17, 5085–5092 (2005).
Kuganathan, N., Ganeshalingam, S. & Chroneos, A. Defects, Dopants and Lithium Mobility in Li9V3(P2O7)3(PO4)2. Sci. Rep 8, 8140 (2018).
Kuganathan, N., Iyngaran, P. & Chroneos, A. Lithium diffusion in Li5FeO4. Sci. Rep. 8, 5832 (2018).
Kordatos, A., Kuganathan, N., Kelaidis, N., Iyngaran, P. & Chroneos, A. Defects and lithium migration in Li2CuO2. Sci. Rep 8, 6754 (2018).30.
Kuganathan, N., Kordatos, A. & Chroneos, A. Li2SnO3 as a Cathode Material for Lithium-ionBatteries: Defects, Lithium Ion Diffusion and Dopants. Sci. Rep 8, 12621 (2018).
Kuganathan, N. & Chroneos, A. Defects, Dopants and Sodium Mobility in Na2MnSiO4. Sci. Rep 8, 14669 (2018).
Kröger, F. A. & Vink, H. J. In Solid State Physics Vol. 3 (eds Frederick Seitz & David Turnbull) 307–435 (Academic Press, 1956).
Nyten, A., Kamali, S., Haggstrom, L., Gustafsson, T. & Thomas, J. O. The lithium extraction/insertion mechanism in Li2FeSiO4. J. Mater. Chem. 16, 2266–2272 (2006).
Ensling, D., Stjerndahl, M., Nyten, A., Gustafsson, T. & Thomas, J. O. A comparative XPS surface study of Li2FeSiO4/C cycled with LiTFSI- and LiPF6-based electrolytes. J. Mater. Chem. 19, 82–88 (2009).
Liu, H. et al. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem C 121, 12025–12036 (2017).
Kempaiah Devaraju, M., Duc Truong, Q., Hyodo, H., Sasaki, Y. & Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 5, 11041 (2015).
Kuganathan, N. & Islam, M. S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 21, 5196–5202 (2009).
Politaev, V. V., Petrenko, A. A., Nalbandyan, V. B., Medvedev, B. S. & Shvetsova, E. S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 180, 1045–1050 (2007).
Rushton, M. J. D. & Chroneos, A. Impact of uniaxial strain and doping on oxygen diffusion in CeO2. Sci. Rep 4, 6068 (2014).
Gale, J. D. & Rohl, A. L. The General Utility Lattice Program (GULP). Molec. Simul. 29, 291–341 (2003).
Lewis, G. V. & Catlow, C. R. A. Potential models for ionic oxides. J. Phys C: Solid State Phys. 18, 1149 (1985).
McCoy, M. A., Grimes, R. W. & Lee, W. E. Planar intergrowth structures in the ZnO-In2O3 system. Philos. Mag A 76, 1187–1201 (1997).
Busker, G., Chroneos, A., Grimes, R. W. & Chen, I.-W. Solution mechanisms for dopant oxides in yttria. J. Am. Ceram. Soc. 82, 1553–1559 (1999).
Minervini, L., Zacate, M. O. & Grimes, R. W. Defect cluster formation in M2O3-doped CeO2. Solid State Ionics 116, 339–349 (1999).
Fisher, C. A. J., Hart Prieto, V. M. & Islam, M. S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 20, 5907–5915 (2008).
Gale, J. D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 93, 629–637 (1997).
Mott, N. F. & Littleton, M. J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 34, 485–499 (1938).
Acknowledgements
Computational facilities and support were provided by High Performance Computing Centre at Imperial College London.
Author information
Authors and Affiliations
Contributions
N.K. performed the calculations. A.C. contributed to the writing of the paper.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kuganathan, N., Chroneos, A. Defects and dopant properties of Li3V2(PO4)3. Sci Rep 9, 333 (2019). https://doi.org/10.1038/s41598-018-36398-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-36398-w
This article is cited by
-
Structural and electrochemical characterization of vanadium-excess Li3V2(PO4)3-LiVOPO4/C composite cathode material synthesized by sol–gel method
Journal of Solid State Electrochemistry (2021)
-
Raising the capacity of lithium vanadium phosphate via anion and cation co-substitution
Science China Chemistry (2020)
-
Defects, dopants and Mg diffusion in MgTiO3
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.