Abstract
The metal-insulator transition temperature Tc in VO2 is experimentally shown to be almost the same as a magnetic transition temperature Tm characterized by an abrupt decrease in susceptibility, suggesting the evidence of the same underlying origin for both transitions. The measurement of susceptibility shows that it weakly increases on cooling for temperature range of T > Tm, sharply decreases near Tm and then unusually increases on further cooling. A theoretical approach for such unusual observations in susceptibility near Tm or below is performed by modeling electrons from each two adjacent V4+ ions distributed along V-chains as a two-electron system, which indicates that the spin exchange between electrons could cause a level splitting into a singlet (S = 0) level of lower energy and a triplet (S = 1) level of higher energy. The observed abrupt decrease in susceptibility near Tm is explained to be due to that the sample enters the singlet state in which two electrons from adjacent V4+ ions are paired into dimers in spin antiparallel. By considering paramagnetic contribution of unpaired electrons created by the thermal activation from singlet to triplet levels, an expression for susceptibility is proposed to quantitatively explain the unusual temperature-dependent susceptibility observed at low temperatures. Based on the approach to magnetic features, the observed metal-insulator transition is explained to be due to a transition from high-temperature Pauli paramagnetic metallic state of V4+ions to low-temperature dimerized state of strong electronic localization.
Similar content being viewed by others
Introduction
Vanadium dioxide (VO2) is generally shown to undergo a metal-to-insulator (M-I) transition at a temperature Tc ~ 340 K1,2, which is accompanied by a simultaneous structural distortion from a high-temperature (T) rutile-type tetragonal (R) phase to a low-T monoclinic (M) phase2,3,4,5. This structural distortion as an important focus in M-I transition has also been verified by recent studies6,7,8. Since its discovery more than forty years ago, this transition has been attracting considerable interest for fundamental reasons9,10,11,12,13,14,15,16, and for possible applications7,17,18,19,20,21,22,23. Although various approaches have been proposed2,9,10,11,12,13,14,15,16,24, a complete and generally accepted picture of the transition has not yet been developed. It is generally believed that the transition to the insulating state is due to the formation of dimers, each being formed by two electrons from adjacent V4+ ions distributed along V-chain direction in spin antiparallel. However, a basic question is still unclear, that is-, whether does the formation of dimers cause a structural distortion to the M phase or does the structural distortion lead to the formation of dimers? This question is studied in the present work by investigations of magnetic features in VO2 based on measurements for the temperature dependence of susceptibility and a theoretical approach to electronic state by modeling electrons from each two adjacent V4+ ions distributed along V-chain direction as a two-electron system. Magnetic measurements demonstrate that the VO2 undergoes a magnetic transition characterized by an abrupt decrease in susceptibility near the M-I transition temperature, and shows Pauli and unusual paramagnetic (PM) behaviors above and below the transition temperature, respectively. Despite structural, electronic, magnetic properties and even multi degrees of freedom coupling involved have been proposed, a generally consensus on unusual behaviors of VO2 has not been developed so far25,26,27. The observed different magnetic behaviors are discussed by considering whether the spin exchange exists between electrons from adjacent V4+ ions along V-chain direction or not.
Results
A bulk VO2 polycrystalline sample is used in the present experimental investigation, which was prepared by hydrothermal method. Stoichiometric quantities of vanadium pentoxide (V2O5, 99.9%) and oxalic acid (99.5%) with a substance ratio of 1:1.5 were mixed and dissolved in pure water. The mixed liquid was put into high pressure proportion and heated at 180 °C for 48 h. The reacted intermediate VO2 (B) powders were annealed at 550 °C for 2 h in vacuum, then pressed into pellets and sintered at 900 °C for 4 h in vacuum to get the final product VO2 (M) bulks. Shown in Fig. 1 is a refinement of X-ray diffraction pattern measured at room temperature by using Fullprof 2.0. All the diffraction peaks can be indexed to a M phase of β = 122.6° with P21/c space group, and no secondary phase can be detected. The lattice parameters are calculated to be a = 0.575048 nm, b = 0.452436 nm and c = 0.538120 nm, respectively.
The zero-field resistivity (\(\rho \)) and susceptibility \((\chi )\) for an applied magnetic field of 1000 Oe as functions of T are measured in a commercial physical property measurement system (PPMS, Quantum Design). Because the sample resistance at low temperatures is over range of PPMS, the \(\rho -T\) dependence was measured only for the temperature range of T > 250 K. In Fig. 2 we display \(\rho (T)\) and \(\chi (T)\) data measured during cooling process, and corresponding differential curves. A sharp increase in \(\rho \) can be found in the \(\rho -T\) curve, which is generally explained to be a result of M-I transition. From the differential curve, we determine the M-I transition temperature Tc to be ~334 K at which \(-d\rho /dT\) reaches its maximum, and the onset temperature \({T}_{c,\mathrm{onset}}\) for the occurrence of M-I transition to be ~338 K from which \(-d\rho /dT\) starts to increase sharply. On the other hand, an evidence for the occurrence of magnetic transition can be found in the \(\chi -T\) curve, which displays an abrupt decrease in χ. From the \(d\chi /dT\) vs. T curve, we determine the magnetic transition temperature Tm to be ~333.5 K at which \(d\chi /dT\) reaches its maximum, and the onset temperature Tm,onset for the occurrence of magnetic transition to be ~338 K from which \(d\chi /dT\) sharply increases. It is essential to note that both the Tc and Tm, or Tc,onset and Tm,onset, are experimentally confirmed to be almost the same, suggesting the evidence of same origin for both the M-I and magnetic transitions. Therefore, understanding the magnetic feature involving in VO2 is helpful to find a clue to reveal the nature of M-I transition. It should be mentioned that the susceptibility as a function of temperature was also measured at various constant applied magnetic fields up to 9 T, no effect of magnetic field to magnetic transition was found. Because of this fact, in Fig. 2 we only display the \(d\chi /dT\) vs. T curve measured at the 1000 Oe field.
The VO2 is of paramagnetism for the whole range of temperature covering from high-T metallic to low-T insulating states, which can be confirmed through the measurement of hysteresis loop in which no magnetic hysteresis becomes visible at various fixed temperatures from 370 K to 10 K28. Nevertheless, the experimental fact of magnetic transition displayed in Fig. 2 proposes that the PM behavior at T > Tm should be different from that at T < Tm. In Fig. 3 we display the χ vs. T curve measured in the field of 1000 Oe during cooling process for a wide range of temperature from 390 K to 10 K. It can be seen that the susceptibility increases weakly on cooling for the range of T > Tm,onset, passing through the transition region, it no longer decreases but unusually increases on cooling from a temperature denoted by Tm,offset ~ 330 K.
Discussion
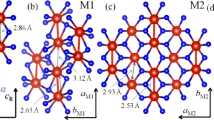
In order to explain observed different PM behaviors, here we perform a theoretical approach to electronic states in VO2. As well known, a striking feature in crystalline structure of VO2 illustrated in Fig. 4(a) is the existence of parallel chains consisting of V4+ ions. In the high-T R phase, the periodical distribution of V4+ ions forms parallel straight chains along the \({c}_{R}\) axis, while in the low-T M phase, the V4+ ions distribute periodically in zigzags along the \({c}_{M}\) axis29, as illustrated in Fig. 4(b). As a general case, we can view each chain as a chain consisting of ion pairs periodically distributed along the chain direction, where each ion pair contains two V4+ ions. Note that each V4+ ion only has a d-electron, therefore, one ion pair has two electrons so that it can be viewed as a two-electron system. According to Heisenberg model30, the Hamiltonian of the two-electron system can be written in the form
where\(\,{\hat{h}}_{i}=\,-\frac{{\hslash }^{2}}{2m}{\nabla }_{i}^{2}+V({\mathop{r}\limits^{\rightharpoonup }}_{i})\) is one-electron Hamiltonian of electron i,\(\,V({\mathop{r}\limits^{\rightharpoonup }}_{i})\,\)is a potential experiencing by electron i, and \(\hat{H}^{\prime} (1,\,{\rm{2}})=-\,2J{\hat{S}}_{1}\cdot {\hat{S}}_{2}\). is the spin exchange between electrons 1 and 2 with exchange constant J.
As shown in appendix, if no spin exchange exists between electrons, the two-electron system is of four-fold degenerate with a same energy \({E}_{0}\), while once the spin exchange appears between electrons, the energy level of four-fold degenerate would become splitting into a singlet (S = 0) level and a triplet (S = 1) levels. The theoretical approach presents the energy
for the singlet state, and
for triplet states. Since the spin exchange term in Eq. (1) is the scalar product of two vector spin operators, it should favor parallel spins if J is positive and antiparallel if J is negative. For the present system, the antiparallel (S = 0) spin alignment of two electrons is more favorable than the parallel (S = 1), meaning that J should be negative. The present approach therefore indicates that the spin exchange between electrons can cause a splitting of the four-fold degenerate level into a singlet (S = 0) state of lower energy and triplet (S = 1) states of higher energy with energy separation \({\rm{\Delta }}E={E}^{T}-{E}^{S}=2|J|\), as sketchy illustrated in Fig. 5(a). In Fig. 5(b) we also display illustration of change of electronic states with temperature as discussed below.
Based on the above theoretical approach, we can discuss on magnetic features and present interpretations of experimental observations in VO2. In the high-T R phase, electrons from two adjacent V4+ ions are separated in a larger distance so that the spin exchange between electrons can be neglected. In this case, electrons should show behavior similar to near-free electrons. This should be the reason why the VO2 shows metallic behavior at T > Tc,onset. Because of the near-free behavior of electrons, the magnetic behavior should be described to the Pauli PM theory similar to that seen commonly in simple metals. According to Pauli PM theory31, the temperature dependence of susceptibility can be expressed in the form
where \({\chi }_{P}^{0}=Na\), \(a=\frac{3}{2}\frac{{\mu }_{B}^{2}}{{E}_{F}^{0}}\), N is the number of “free” electrons,\({E}_{F}^{0}\) the Fermi energy at \(T\to 0{\rm{K}}\), and \({\mu }_{B}\) the Bohr magneton. In Fig. 3 and its inset, we present a comparison between data measured at high temperatures and curve calculated in terms of Eq. (4) by using parameters of \({\chi }_{P}^{0}=8.6\times {10}^{-6}\) (emu·g−1·Oe−1) and \({E}_{F}^{0}=105.6\) (meV). It can be seen that the Pauli PM theory yields an excellent agreement with susceptibility data measured at T > Tm,onset. The experimental facts of Pauli paramagnetism at T > Tm,onset and same values in both Tc,onset and Tm,onset provide strong support to high-T phase above Tm,onset as a near-free electron system.
On cooling to Tm,onset or below, the spin exchange appears between electrons from two adjacent V4+ ions. According to the above approach, this exchange causes the level splitting into the singlet and triplet levels. From the viewpoint of energy, the singlet level is more favorable for the occupation of electrons. Therefore, if two electrons from adjacent V4+ ions along the chain direction stay on the singlet level, the two electrons must be paired in spin antiparallel. It means that the singlet state is a state in which the dimers are formed by pairing V4+ ions in spin antiparallel. We, therefore, propose the spin exchange between electrons to be the reason for the formation of dimers in spin antiparallel. On the other hand, associated with the formation of dimers, the straight chain consisting of “free” V4+ ions would be distorted into a zigzag chain. It implies that the spin exchange between electrons is the reason causing a structural distortion from high-T R phase characterized by straight chains consisting of V4+ ions to low-T M phase characterized by zigzag chains consisting of dimers.
Owing to that each dimer contains two electrons, associated with the formation of dimers, the number of “free” electrons would change from N at T > \((N-2{N}_{d})\) at T < Tm,onset, where Nd is the number of dimers. Clearly, Nd should be zero at T > Tm,onset, but increases substantially on cooling from Tm,onset. On the other hand, each dimer has zero spin and cannot contribute to susceptibility. Therefore, the Pauli PM susceptibility would change approximately from Na at T > Tm,onset to \((N-2{N}_{d})a\) at T < Tm,onset. Because of the substantial increase in Nd on cooling from Tm,onset, the susceptibility would show an abrupt decrease as seen in experiments. It means that the observed magnetic transition is due to a transition from Pauli PM state of “free” V4+ ions at T > Tm,onset to a singlet state at T < Tm,onset in which V4+ ions along the chain direction are paired into dimers in spin antiparallel, a result predicted by the above approach. One can also notice that the abrupt decrease in χ only maintains to a temperature denoted by Tm,offset ~ 330 K, meaning that the formation of dimers occurs mainly in a narrow range of Tm,offset < T < Tm,onset and the number of dimers tends to be a T-independent constant Nd0 on further cooling from Tm,offset.
The above approach can be further confirmed by analyzing the χ vs. T dependence observed below Tm,offset. As indicated in Fig. 3, the susceptibility is no longer decreased but unusually increased on cooling from Tm,offset. The observed unusual increase in χ cannot be explained by Pauli PM theory which predicts an almost T-independent susceptibility at low temperatures. Although Curie’s law predicts a variation of χ inversely with T, the question is what kind of PM entities with magnetic moments responsible for the observed low-T paramagnetism. Below Tm,offset the dimers are formed by spin pairing of adjacent V4+ ions in antiparallel, so that each dimer has no magnetic moment. Therefore, the dimers cannot contribute to the observed low-T paramagnetism, unless that each dimer is phenomenologically assumed to be formed by spin pairing of two V4+ ions at a T-dependent angle28.
Here, we demonstrate that the observed variation of χ inversely with T can be explained by considering the contribution to Curie PM susceptibility from unpaired electrons created due to the thermal activation from singlet to triplet levels. According to the above approach, the spin exchange causes the level splitting into the singlet and triplet levels. At finite temperatures, it is likely that electrons in the singlet level could be thermally excited to the level of the triplet states, resulting in the appearance of unpaired electrons with number \(\propto {N}_{d0}{e}^{-2|J|/{k}_{B}T}\), as sketchy illustrated in Fig. 5. These unpaired electrons with magnetic moments can contribute to Curie-like PM susceptibility. In the Curie’s law, the Curie parameter C is proportional to the number of PM ions, therefore, one has \(C\propto {N}_{d0}{e}^{-2|J|/{k}_{B}T}\) for the present case. We then write the susceptibility caused by unpaired electrons created due to thermal activation in the form:
where \(B\propto {N}_{d0}\) is a T-independent constant. Besides those thermally activated electrons, it is likely for the presence of “free” electrons from residual V4+ ions which don’t participate in the formation of dimers. As seen at T > Tm,onset, these “free” electrons should show Pauli PM behavior with susceptibility approximately expressed by \({\chi }_{P}^{0}=(N-2{N}_{d0})a\). The total susceptibility is then expressed by a sum of co-contributions from two kinds of electrons, that is-
To support this approach, here we calculate the χ vs. T curve in terms of Eq. (6) by using \({\chi }_{P}^{0}={\rm{1}}\,{\rm{.}}\,{\rm{32}}\times {\rm{1}}{0}^{-{\rm{6}}}\)\(({\rm{emu}}\cdot {{\rm{g}}}^{-{\rm{1}}}\cdot {{\rm{Oe}}}^{-{\rm{1}}})\), \(B=6.8\times {\rm{1}}{0}^{-5}({\rm{emu}}\cdot K\cdot {{\rm{g}}}^{-{\rm{1}}}\cdot {{\rm{Oe}}}^{-{\rm{1}}})\) and \(2|J|/{k}_{B}=7.5\)(K). The calculated curve is displayed by red solid line in Fig. 3. It can be found that Eq. (6) yields excellent agreement with the experimental data for the whole low-T range below Tm,offset. Note that \({\chi }_{P}^{0}={\rm{1}}.{\rm{32}}\times {\rm{1}}{0}^{-{\rm{6}}}({\rm{emu}}\cdot {{\rm{g}}}^{-{\rm{1}}}\cdot {{\rm{Oe}}}^{-{\rm{1}}})\propto N-2{N}_{d0}\) below Tm,offset and \({\chi }_{P}^{0}=8.6\times {\rm{1}}{0}^{-{\rm{6}}}({\rm{emu}}\cdot {{\rm{g}}}^{-{\rm{1}}}\cdot {{\rm{Oe}}}^{-{\rm{1}}})\propto N\) above Tm,onset, respectively, their ratio gives an estimation of \(2{N}_{d0}/N\) to be ~85%. It means that in the low-T M phase ~85% V4+ ions are paired into dimers, while the remainder ~15% V4+ ions as “free” ions are still resided in the system.
Once the above magnetic features are accepted, it is reasonable to explain the electronic transport behavior observed in VO2. In the high-T R phase, because of no spin exchange existing between electrons, electrons would be of near-free behavior and hence the system shows metallic behavior. On cooling to Tm,onset or below, the spin exchange between electrons from two adjacent V4+ ions leads to the formation of V-V dimers, where each two adjacent V4+ ions become one V-V dimer by pairing in spin antiparallel. Because of the antiparallel pairing, electrons would be strongly localized, leading to low-T insulating behavior. The observed M-I transition is therefore explained to be due to a transition from high-T Pauli PM state of V4+ ions to low-T dimerized state. On the other hand, because both the M-I and magnetic transitions are all related to the formation of V-V dimers, this is the reason why the system undergoes simultaneous M-I and magnetic transitions at almost the same temperature.
Conclusions
In summary, we have shown that the metal-insulator transition in VO2 in origin is closely related to the magnetic transition characterized by an abrupt decrease in susceptibility. Based on experimental investigations of susceptibility and the theoretical approach by modeling electrons from two adjacent V4+ ions distributed along V-chains as a two-electron system, it is concluded that there is a feature temperature Tm to distinguish between high-T and low-T phases. At temperatures slightly higher than Tm, no spin exchange exists between electrons from adjacent V4+ ions, as a result, the system shows metallic and Pauli PM behavior. Near Tm, because of the spin exchange, the system enters into the singlet state in which electrons from adjacent V4+ ions along the chain direction are paired into dimers in spin antiparallel, resulting in a transition to insulating state and an abrupt decrease in χ. At temperatures slightly lower than Tm, the contribution to PM behavior from some unpaired electrons created by the thermal activation from singlet to triplet levels lead to unusual temperature-dependent susceptibility at low temperatures. These main conclusions are summarized in Fig. 6.
References
Morin, F. J. Oxides which show a metal-to-insulator transition at the Neel temperature. Phys. Rev. Lett. 3, 34–36 (1959).
Goodenough, J. B. The two components of the crystallographic transition in VO2. J. Solid State Chem. 3, 490–500 (1971).
Adler, D., Feinleib, J., Brooks, H. & Paul, W. Semiconductor-to-metal transitions in transition-metal compounds. Phys. Rev. 155, 851–860 (1967).
Kim, H. T. et al. Monoclinic and correlated metal phase in VO2 as evidence of the mott transition: Coherent phonon analysis. Phys. Rev. Lett. 97, 266401 (2006).
Bai, L. et al. Pressure-induced phase transitions and metallization in VO2. Phys. Rev. B 91, 7 (2015).
Budai, J. D. et al. In situ X-ray microdiffraction studies inside individual VO2 microcrystals. Acta Mater. 61, 2751–2762 (2013).
Gao, Y. et al. Nanoceramic VO2 thermochromic smart glass: A review on progress in solution processing. Nano Energy 1, 221–246 (2012).
Tselev, A. et al. Symmetry relationship and strain-induced transitions between insulating M1 and M2 and metallic R phases of vanadium dioxide. Nano Lett 10, 4409–4416 (2010).
Eyert, V. The metal-insulator transitions of VO2: A band theoretical approach. Ann. Phys. (Leipzig) 11, 650–702 (2002).
Eyert, V. VO2: A novel view from band theory. Phys. Rev. Lett. 107, 016401 (2011).
Wentzcovitch, R. M., Schulz, W. W. & Allen, P. B. VO2 Peierls or Mott-Hubbard? A view from band theory. Phys. Rev. Lett. 72, 3389–3392 (1994).
Biermann, S., Poteryaev, A., Lichtenstein, A. I. & Georges, A. Dynamical singlets and correlation-assisted peierls transition in VO2. Phys. Rev. Lett. 94, 026404 (2005).
Tomczak, J. M. & Biermann, S. Effective band structure of correlated materials: the case of VO2. J. Phys: Condens. Matter 19, 365206 (2007).
Strelcov, E. et al. Doping-based stabilization of the M2 phase in free-standing VO2 nanostructures at room temperature. Nano Lett. 12, 6198–6205 (2012).
Rice, T. M., Launois, H. & Pouget, J. P. Comment on VO2 Peierls or Mott-Hubbard? A view from band theory. Phys. Rev. Lett. 73, 3042 (1994).
Eguchi, R. et al. Photoemission evidence for a Mott-Hubbard metal-insulator transition in VO2. Phys. Rev. B 78, 075115 (2008).
Cueff, S. et al. Dynamic control of light emission faster than the lifetime limit using VO2 phase-change. Nat. Commun. 6, 8636 (2015).
Kivaisi, R. T. & Samiji, M. Optical and electrical properties of vanadium dioxide films prepared under optimized RF sputtering conditions. Sol. Energy Mater. Sol. C. 57, 141–152 (1999).
Strelcov, E., Lilach, Y. & Kolmakov, A. Gas sensor based on metal-insulator transition in VO2 nanowire thermistor. Nano Lett. 9, 2322–2326 (2009).
Hu, B. et al. External-strain induced insulating phase transition in VO2 nanobeam and its application as flexible strain sensor. Adv. Mater. 22, 5134–5139 (2010).
Liu, M. et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348 (2012).
Seo, M. et al. Active terahertz nanoantennas based on VO2 phase transition. Nano Lett. 10, 2064–2068 (2010).
Gea, L. A. & Boatner, L. A. Optical switching of coherent VO2 precipitates formed in sapphire by ion implantation and annealing. Appl. Phys. Lett. 68, 3081–3083 (1996).
Liechtenstein, A. I., Anisimov, V. I. & Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, R5467–R5470 (1995).
Yuan, X., Zhang, Y., Abtew, T. A., Zhang, P. & Zhang, W. VO2: Orbital competition, magnetism, and phase stability. Phys. Rev. B 86, 235103 (2012).
Zheng, H. & Wagner, L. K. Computation of the correlated metal-insulator transition in vanadium dioxide from first principles. Phys Rev Lett 114, 176401 (2015).
Xu, S., Shen, X., Hallman, K. A., Haglund, R. F. & Pantelides, S. T. Unified band-theoretic description of structural, electronic, and magnetic properties of vanadium dioxide phases. Phys. Rev. B 95, 125105 (2017).
Yin, C. Y. et al. Unusual magnetic transition near metal-insulator transition and paramagnetic anomaly in VO2. Appl. Phys. Lett. 110, 172404 (2017).
Park, J. H. et al. Measurement of a solid-state triple point at the metal-insulator transition in VO2. Nature 500, 431–434 (2013).
Heisenberg, W. Zur Theorie des Ferromagnetismus. Z. Phys. 49, 619 (1928).
Wilson, A. H. The Theory of Metals 2nd edition, pp. 155–168 (Cambridge University Press, Cambridge, 1953).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos 11474111 and 51461135004).
Author information
Authors and Affiliations
Contributions
R. Zhang, Q.S. Fu and S.L. Yuan conceived the idea, designed the experiments and analyzed the data. R. Zhang, Q.S. Fu and C.Y. Yin contributed to the bulk preparation and its structural characterization. C.L. Li, X.H. Chen and G.Y. Qian provided support in the maintenance of measurement system and performed X-ray diffraction pattern refinement. C.L. Lu, X.J. Zhao and H.Z. Tao contributed to results discussions and assisted in the writing. R. Zhang and Q.S. Fu drafted the main manuscript text and prepared all figures. S.L. Yuan serve as the academic supervisor to the graduate students supervised the project. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, R., Fu, Q.S., Yin, C.Y. et al. Understanding of metal-insulator transition in VO2 based on experimental and theoretical investigations of magnetic features. Sci Rep 8, 17093 (2018). https://doi.org/10.1038/s41598-018-35490-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-35490-5
Keywords
This article is cited by
-
Electronic structure of superconducting VN(111) films
Discover Nano (2024)
-
Hidden magnetism and split off flat bands in the insulator metal transition in VO2
npj Computational Materials (2024)
-
New Amendment of VO2 Nanoparticles with Enhanced Photocatalytic and Antibacterial Activities
BioNanoScience (2024)
-
Thermally Induced Switching of Electrical and Optical Characteristics of VO2 Thin Nanostructured Films Fabricated by Radio Frequency Magnetron Sputtering
Arabian Journal for Science and Engineering (2024)
-
Investigation of the influence of VO2 formation on the structural morphology and magnetic properties in hydrothermally synthesized V6O13
Journal of Materials Science: Materials in Electronics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.