Abstract
The lateral motion of a magnetic skyrmion, arising because of the skyrmion Hall effect, imposes a number of restrictions on the use of this spin state in the racetrack memory. A skyrmionium is a more promising spin texture for memory applications, since it has zero total topological charge and propagates strictly along a nanotrack. Here, the stability of the skyrmionium, as well as the dependence of its size on the magnetic parameters, such as the Dzyaloshinskii–Moriya interaction and perpendicular magnetic anisotropy, are studied by means of micromagnetic simulations. We propose an advanced method for the skyrmionium nucleation due to a local enhancement of the spin Hall effect. The stability of the skyrmionium being in motion under the action of the spin polarized current is analyzed.
Similar content being viewed by others
Introduction
A skyrmion is a stable magnetic configuration having a small size (10–100 nm)1,2,3, as well as a high propagation velocity (~100 m/s) under the action of low-density currents (~1 × 109 А/м2)4,5,6,7. Due to these features, the skyrmion can be used for a new type of magnetic memory called the racetrack memory8,9. However, the presence of the skyrmion Hall effect (SkHE)10,11,12, arising due to the topological properties of the skyrmion, limits its use in narrow tracks. Under the influence of the transverse Magnus force, the skyrmion deviates from the longitudinal motion along a nanotrack, which can lead to annihilation of the skyrmion at a track’s edge13. To solve this problem, several methods have been proposed that can prevent touching the edges and keep the skyrmion inside the track: changing the track’s profile through the creation of additional borders (kerbed track)14, local modification of magnetic properties of a nanotrack, such as perpendicular magnetic anisotropy (PMA)6,15, the interfacial Dzyaloshinskii–Moriya interaction (iDMI)16 or damping constant17,18. All these approaches allow creating a potential barrier that prevents the skyrmion’s deviation. Another method is based on the topological compensation of the Magnus effect. Since the direction of the skyrmion’s deflection depends on the sign of the topological charge (Q), then spin states that have a compensated total topological charge (Q = 0) must not deviate. Magnetic configurations consisting of two antiferromagnetically coupled skyrmions with opposite topological charges have been theoretically investigated in ferrimagnets19,20,21, antiferromagnets22,23,24,25,26,27, and synthetic antiferromagnets28,29,30. However, these configurations are difficult to realize and to investigate experimentally, because of the complexity of visualization of the antiferromagnetic domain structure. In ferromagnetic media, a skyrmion-like state with zero topological charge, which is called skyrmionium31,32,33,34,35, can be stabilized. For the first time a skyrmionium was described in a theoretical work and it was named as “2π-vortex”36. In the later papers the skyrmionium state was found by modeling or experimentally and called as “donut skyrmion”37, “2π-skyrmion”38 and “target skyrmion”39. A skyrmionium is a skyrmion surrounded by an annular domain wall with the opposite Q. This spin structure is elastically coupled due to magnetostatic repulsion between the skyrmion and the surrounding domain wall.
In this paper, we explore the possibility of using the skyrmionium to implement the racetrack memory. We propose a new method for the nucleation of the skyrmionium based on a locally enhanced spin-orbit torque (SOT) effect. Conditions for the formation of the skyrmionium are determined by means of micromagnetic simulations. The influence of the magnetic parameters on the size and stability of the skyrmionium is analyzed. The skyrmionium motion under the action of the spin currents is studied.
Skyrmionium Nucleation
To apply a skyrmionium in the racetrack memory, it is necessary to be able to control the nucleation and annihilation processes of this quasi-particle inside nanotracks. A magnetic skyrmionium is a composite structure consisting of a skyrmion (skyrmionium core) surrounded by an annular domain wall with an opposite topological charge (skyrmionium shell). The scheme of the skyrmionium is shown in Fig. 1(a). For nucleation of skyrmions and skyrmioniums, the optical means can be used40,41,42,43,44. However, the current-induced nucleation is technically simple for realization and compatible with the CMOS technology. In previous studies it was demonstrated that the skyrmionium can be generated inside a nanodisk using the spin-transfer torque (STT) by locally passing the spin polarized current (\(\overrightarrow{p}||-\,\overrightarrow{z}\)) perpendicularly to the nanodisk plane33. However, the experimental implementation of this method is quite problematic, because of the fabricating complexity of a circular shape nanocontact. In this case, the magnetostatic interaction between the skyrmionium and the polarizing spin filter will prevent the displacement of the skyrmionium from the contact. This will lead to an increase in the critical current required for the skyrmionium movement.
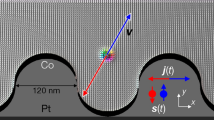
Nucleation of the skyrmionium with the help of the spin-orbit torque. (a) Spin configuration of the skyrmionium. (b) Scheme of the spin Hall effect in the HM1/FM/HM2 structure. (c) Distribution map of the spin current density (js) injected into the ferromagnetic layer. (d) The time dependence of the integral density of the spin current js = f(t) passed through the ferromagnetic layer (blue curve), the corresponding changes in the perpendicular magnetization component mz = f(t) (red curve) and the magnitude of the total topological charge Q = f(t) (black line). (e) Visualization of the processes of changing the magnetization distribution in the ferromagnetic layer for the selected time instants (1–5), indicated on the mz = f(t) graph.
We propose to use the SOT for the skyrmionium nucleation45,46,47. To realize the possibility of nucleation of domains of a given shape, for example, annular, it is necessary to locally change the SOT magnitude. In a “ferromagnet/heavy metal” system (FM/HM) the SOT magnitude depends on parameters of HM (thickness, crystal structure) being in contact with FM48,49,50. To strengthen the SOT, one can deposit a heavy metal with an opposite spin Hall angle (θSH1 > 0, θSH2 < 0) on the second interface to realize the HM1/FM/HM2 structure51. As shown in51, the total value of θSH increases from 0.1 for a Pt/Co bilayer to 0.34 for a Pt/Co/Ta system. Through the patterning of HM2, one can specify regions of a given geometry with the large value of θSH. To generate the skyrmionium, we need to switch the magnetization of the skyrmionium shell in the opposite direction relatively to the skyrmionium core. For this purpose we used a nanostructure consisting of a nanoring made of HM2 located on the top of a HM1/FM film, Fig. 1(b).
In the proposed Pt/Co/Ta structure the bottom Pt/Co interface has the main contribution to the net iDMI value, because it has been experimentally shown that Ta does not induce a significant iDMI (it is about 20 times smaller compare to Pt/Co interface)52. We have done preliminary numerical simulations considering the local enhancement of iDMI in the area under the Ta circle, Fig. S1(a) in the Supplementary file. Using this iDMI distribution we have modelled the skyrmionium nucleation processes. The calculated results are in a good agreement with the result for a case of the uniform iDMI, Fig. S1(b) in the Supplementary file. Thus, the assumption on the uniformity of iDMI in the proposed structure is correct. The larger variations of iDMI (higher than 10%) will affect on the skyrmionium stability and the critical current of its nucleation.
We calculated the distribution of the charge current density \({j}_{x}^{ijk}\), where ijk – coordinates of an elemental cell, passing through the film and nanoring, taking into account the resistivity of metals and the nanostructure’s size. The thickness of the buffer layer HM1(Pt) and the nanoring HM2(Ta) was 4 nm. The nanoring HM2(Ta) had the external and internal diameters of 100 and 50 nm, correspondingly. Using the distribution of \({j}_{x}^{ijk}\) and the spin Hall effect (SHE) in the Pt film (\({\theta }_{SH}^{film}=0.1\)) and in the Ta nanoring (\({\theta }_{SH}^{ring}=0.24\)), for each elemental cell we computed the spin current (\({\overrightarrow{j}}_{s}||-\,z\)) with the polarization \(\overrightarrow{p}||\overrightarrow{y}\), which was generated perpendicularly to the plane of the FM layer accordingly to the equation \({j}_{s}^{ij}={j}_{x}^{ijk}\cdot {\theta }_{SH}^{film}+{j}_{x}^{ijk}\cdot {\theta }_{SH}^{ring}\). The derived distribution map of \({j}_{x}^{ijk}\) is shown in Fig. 1(c).
Using the spin current distribution map, we carried out simulations of the skyrmionium nucleation processes in a nanotrack with the size of 1000 × 400 nm2. These calculations were done in the micromagnetic modeling program MuMax3 53. The thickness of the ferromagnetic layer was 0.6 nm, the size of the elemental cell was 1.0 × 1.0 × 0.6 nm3. Magnetic parameters of Co were chosen accordingly to the literature data8,51,54: saturation magnetization Ms = 580 kA/m; the exchange interaction constant A = 15 pJ/m; the PMA energy K = 1.5 MJ/m3; the iDMI energy D = 5 mJ/m2; the Gilbert damping constant α = 0.3. In order to avoid the formation of magnetostatic charges at the edges of the simulated area, the simulation was performed taking into account the periodic boundary conditions along the coordinate axes Ox and Oy.
Let us consider the nucleation processes of the skyrmionium under the action of a current pulse. Initially, the ferromagnetic layer was in a saturation state along the Oz axis. To realize the local magnetization reversal with the help of the SOT, we have to pass through the structure a charge current pulse with the amplitude jx = −8.6 × 1012 A/m2 and duration of 20 ps. Due to the SHE the spin current pulse with a maximum amplitude passes under the nanoring through the FM layer, Fig. 1(c). The average value of the spin-current amplitude under the nanoring is js = 9.1 × 1011A/m2 (see the blue curve in Fig. 1(d)). Simultaneously, a pulse of a uniform external magnetic field Bx = 0.6 T was applied to the structure along the Ox axis. Under the influence of the current and magnetic field, a decrease in mz magnetization component is observed and an annular shape domain is formed (Fig. 1(e), instants 1 and 2). In this case, the spin current torque acting on the domain walls displaces the nucleated domain. To prevent further growth and displacement of the nanoring domain, the external excitation was stopped on 40 ps (js = 0 A/m2 and Bx = 0 T).
Initially, the domain wall is not homochiral (Fig. 1(e), instant 2), because the magnetization in the domain wall was directed mainly along the effective field. After switching off the external excitation, self-organization of the magnetization configuration takes place. In thin FM layers with the high PMA and positive iDMI, Néel’s domain walls with left-handed chirality are stabilized55,56. Moreover, a full magnetization turn inside the domain wall occurs more rapidly in the central domain, while there is an area with right-handed chirality in the outer domain wall, marked in the instant 3 of Fig. 1(e) by a dashed line. Thus, the skyrmion is stabilized at 50 ps. The moment of the skyrmion’s formation is reflected by an abrupt jump in the topological charge from 0 to 1 as seen in the graph Q = f(t), Fig. 1(d).
After this, the area with right-handed chirality in the outer domain wall annihilates, the wall acquires left-handed chirality. Then the topological charge of the external domain wall will be −1, and the total topological charge will be zero again. The resulting skyrmionium has an asymmetric shape and a large size, Fig. 1(e), instant 4. Within 500 ps, a decrease in the size of the skyrmionium occurs with the following transition to the equilibrium state, Fig. 1(e), instant 5. As the size of the skyrmionium decreases, the value of mz in the considered region increases, Fig. 1(d). The complete process of the skyrmionium’s nucleation and stabilization for these magnetic parameters lasts about 700 ps. The skyrmionium spin dynamics corresponding to Fig. 1(e) is demonstrated in the Supplementary Movie.
In order to analyze the effect of the Gilbert damping on the nucleation process of a skyrmionium, the micromagnetic simulations with different values of α were performed. Since the pulsed excitation by the external magnet field and spin current of 20-ps duration is used for the skyrmionium nucleation, then with the increasing α the current density required for the nucleation of a domain of the circular shape (nanoring domain) also increases, Fig. S2(b) in the Supplementary file. If α changes from 0.2 to 1.0 the nucleation process keeps constant. Practically the same shape of the mz = f(t) curves supports this suggestion, Fig. S2(a) in the Supplementary file. The only change is the rising time required for stabilization of the homochiral domain walls and relaxation of a domain to the equilibrium size. At α = 0.1 during the excitation time of 20 ps in spite of a nanoring domain the magnetic bubbles are also nucleated. Because of the small size of these bubbles (less than 10 nm), they are unstable and annihilate inducing the excitation of spin waves affecting on the shape of domain walls and on the transfer time of the skyrmionium into the stable state. To prevent any parasitic effects at small values of α, time of the pulsed excitation has to be decreased in this case. These results demonstrate that magnetic materials with the small Gilbert damping constant (α ≤ 0.1) are not good candidates for skyrmionium media.
Topological Stability of Skyrmionium
To implement the skyrmionium-driven racetrack memory, it is necessary to know a range of magnetic parameters under which this topological state will remain stable. In the HM1/FM/HM2 systems, a replacement of heavy metals contacting with FM or a change in the thickness of the layers will primarily affect such parameters of the ferromagnetic layer as the PMA energy and iDMI57,58,59. Changing of these magnetic parameters will influence the skyrmionium size and, consequently, the density of information recording in magnetic memory.
To find the skyrmionium stability range, the anisotropy energy K and the interfacial Dzyaloshinsky-Moriya interaction constant D were varied in the range from 0.3 to 2.0 MJ/m3 and from 1.5 to 5.0 mJ/m2, correspondingly. For comparison, the stability region of a free skyrmion was also found. It is known that as the PMA energy increases, the skyrmion radius decreases2, (blue curve in Fig. 2(a)). In this case, the magnetostatic interaction between the homochiral walls in the skyrmionium core and shell leads to compression of the skyrmionium core in comparison with the free skyrmion (red curve with empty symbols in Fig. 2(a)).
With an increase in the iDMI energy density for the fixed PMA, the skyrmionium radius or its shell width increases also as in the case of the free skyrmion60, Fig. 2(b). Thus, the magnetic parameters K and D allow changing the skyrmionium size in a wide range. An increase in the recording density by decreasing the skyrmionium size is possible due to an increase in the PMA energy and a decrease in the iDMI constant. In this case, there is a certain range of magnetic parameters for which the skyrmionium is stable. The region of the stable skyrmionium depending on the K and D values is shown in Fig. 2(d), the color in this diagram corresponds to the equilibrium radius of the skyrmionium at these parameters. For comparison, Fig. 2(c) shows a similar diagram for a stable skyrmion. It was found that the stability region for the skyrmionium is smaller than for the skyrmion. If in the case of the skyrmion the stability region is bounded from above by a single-domain state, then at a high K or a weak D the structure will be in the saturation state. At a low K and a high D, a strip domain structure will be formed. The decrease of the skyrmionium stability region is due to the fact that the skyrmionium core contracts and annihilates at a lower anisotropy than the free skyrmion, because of its magnetostatic interaction with the outer shell.
Thus, magnetic parameters at which it is possible to implement a stable skyrmionium in the trilayer structure were found. In the range of magnetic parameters considered, the skyrmionium radius can be varied from 12 to 120 nm by varying the PMA energy and iDMI constant. Below we consider the stability of the skyrmionium being in motion under the action of the spin polarized current.
Spin Current Driven Motion Of Skyrmionium
Skyrmionium can be moved inside a nanotrack by spin waves61,62, magnetic field gradient31,33 and spin-polarized current32,34,63. In this section, we demonstrate the spin current-dependent dynamics of a skyrmionium in comparison with a skyrmion and analyze the skyrmionium stability under the current action.
As it was shown above, to nucleate a skyrmionium the spin current density and the applied magnetic field have to be ~2 × 1012 A/m2 and 0.6 T, correspondingly. The significantly smaller current density (~1 × 1010 A/m2) is needed for the skyrmionium movement without any external magnetic field. To move the skyrmionium towards the direction \(+\overrightarrow{x}\) the spin current has to be applied perpendicularly to the FM layer (along \(-\overrightarrow{z}\)) with the polarization along \(+\overrightarrow{y}\). Under the action of the same current, a skyrmion has non-zero components of velocity −Vx and Vy forcing it to move to the nanotrack edge, Fig. 3(a). The reason for that is the skyrmionic Hall effect resulting in the appearance of two mutually perpendicular forces acting on the skyrmion: the drag force is causing in the skyrmion motion along \(+\overrightarrow{x}\) and the deflecting Magnus force is directed along \(-\overrightarrow{y}\) at Q = +1 (see the inset of Fig. 3(a)). The skyrmionium core and shell have opposite topological charges +1 and −1, correspondingly. Thus, in addition to the drag force also directed along the nanotrack, there will be two Magnus forces acting on the skyrmionium, which are oriented down for the core and up for the shell as shown in the inset of Fig. 3(b). If the core and the shell are elastically coupled, then the Magnus forces will cancel each other allowing the skyrmionium to move strictly along the nanotrack.
To simulate the motion of both spin textures under the current action, we used the same magnetic parameters as for the modelling of the skyrmionium nucleation: Ms = 580 kA/m; A = 15 pJ/m; K = 1.5 MJ/m3; D = 5 mJ/m2; α = 0.3. At these parameters the free skyrmion moves at angle θSkH = tan−1(Vy/Vx) = 65° relatively to the nanotrack’s main axis. This angle is called the skyrmion Hall effect angle. Results of the micromagnetic simulations are in a good agreement with the analytical calculations using the formula θSkH ≈ tan−1(2Δ/αR) = 68°, where \({\rm{\Delta }}=\sqrt{\frac{A}{{K}_{eff}}}=3.4\,nm\) is the domain wall width, Keff = K-2πMs2 is the effective anisotropy energy, R = 9 nm is the skyrmion radius (Fig. 2(a))5.
As it was defined from the simulations, with the increase of the applied current from 1 to 10 × 1010 A/m2 the velocity’s components Vx and Vy grow linearly (Fig. 4(a)) resulting in the constant value of θSkH. In the case of the skyrmionium motion, there are two transverse forces applied to different points: one force drags the core down, while the second one drags the shell up. These transverse forces will try to stretch the skyrmionium shell. At the current magnitude js ≤ 5 × 1010 A/m2 the skyrmionium shell does not deform and the core does not shift relatively to the nanotrack’s main axis. In other words, we observe the straightforward motion of the skyrmionium towards the nanotrack as shown in Fig. 3(b). At that θSkH = 0 and the longitudinal velocity Vx is in 5.5 times larger than for the skyrmion, Fig. 4(a).
(a) Dependences of Vx and Vy on the spin current density for the skyrmion and the skyrmionium. (b) Skyrmionium’s deformation in motion under the action of the spin current js = 7 × 1010 A/m2. Diagrams of the absolute velocity V of the skyrmionium in coordinates D and K for various current densities: (c) 1 × 1010 A/m2, (d) 2 × 1010 A/m2, (e) 3 × 1010 A/m2.
The increase of the current density up to js > 5 × 1010 A/m2 leads to the stretching of the skyrmionium shell and the core moves in the transverse direction, Fig. 4(b). Even in this case the coupling between the core and the shell is significantly slowing down the transverse velocity Vy if to compare with the free skyrmion. At js = 7 × 1010 A/m2 the transverse velocity of the skyrmionium core is just 10 m/s (θSkH ≈ 4°), while for the free skyrmion Vy = 64 m/s (θSkH ≈ 65°), Fig. 4(a). Besides the stretching and deformation of the skyrmionium shell, under the action of the large current the skyrmionium core is compressed. At the certain critical current this compression can lead to the core’s annihilation resulting in the transformation of the skyrmionium into the skyrmion33. Thus, there is the certain range of the working currents at which the skyrmionium is stable.
In the previous section, we showed the range of the magnetic parameters K and D, at which a stable skyrmionium can be realized. Now it is necessary to investigate the stability of the skyrmionium under the action of the spin current. For the found stability parameters K and D in accordance with Fig. 2(d), simulations of the skyrmionium motion under the action of the spin current for 5 ns were carried out. As a result, parameters at which the skyrmionium remains stable were found and the velocity of its motion was determined. The obtained diagrams in the coordinates K and D are shown in Fig. 4(c–e), where the color denotes the velocity of the skyrmionium motion (V). Comparing the data from the diagrams depicted in Figs 2(d) and 4(c–e), we can conclude that a skyrmionium of a larger radius will have the maximum velocity under the action of the same current. In this case, the small-radius skyrmioniums will annihilate under the action of the spin current resulting in the stability region narrowing. With the rising current density, the velocity increases linearly, but this also leads to a decrease in the stability region.
Conclusion
The processes of nucleation and motion of the skyrmionium under the action of the spin polarized current in nanotracks, as well as the influence of magnetic parameters on the stability of this quasi-particle, were studied by means of micromagnetic simulations. We have determined values of the PMA energy and iDMI constant, at which the stable skyrmionium can be observed. The dependence of the skyrmionium size on these parameters was found. Zero total topological charge of the skyrmionium makes it possible to completely compensate the skyrmion Hall effect and to realize a rectilinear motion along the nanotracks under the action of the spin current. In this case, the longitudinal velocity of the skyrmionium’s motion is higher than that of the free skyrmion. The influence of the magnitude of the spin current density on the skyrmionium stability region was also investigated. The obtained results will make it possible to select the magnetic parameters and operating modes for the experimental implementation of the fast racetrack memory based on skyrmioniums.
The advanced method for the skyrmionium nucleation in a nanotrack composed a heavy metal nanoring with the help of a local enhancement of the spin Hall effect has been proposed. The results of modeling the Pt/Co/Ta system confirm the feasibility of this proof of concept. The generation of a skyrmionium occurs due to a local increase of the amplitude of the spin current and does not require the presence of a third electrical contact. This greatly simplifies the fabrication process, and also makes the proposed method more promising for a practical application and designing the skyrmionium-based memory. The creation of logic devices operating by topological charges of spin textures is also promising, but it requires additional studies to deeply understand the skyrmionium motion depending on the complex geometry of logical elements.
References
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Zhang, X. et al. Skyrmion-skyrmion and skyrmion-edge repulsions in skyrmion-based racetrack memory. Scientific Reports 5, 7643 (2015).
Romming, N. et al. Field-Dependent Size and Shape of Single Magnetic Skyrmions. PRL 114, 177203 (2015).
Tomasello, R. et al. A strategy for the design of skyrmion racetrack memories. Scientific Reports 4, 6784 (2014).
Litzius, K. et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nature Physics 13, 170–175 (2017).
Lai, P. et al. An Improved Racetrack Structure for Transporting a Skyrmion. Scientific Reports 7, 45330 (2017).
Liang, D. et al. Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect, Nature. Communications 6, 8217 (2015).
Sampaio, J. et al. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nature Nanotechnology 8, 839–844 (2013).
Parkin, S., Hayashi, M. & Thomas, L. Magnetic Domain-Wall Racetrack Memory. Science 320(5873), 190–194 (2008).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Universal current-velocity relation of skyrmion motion in chiral magnets, Nature. Communications 4, 1463 (2013).
Jiang, W. et al. Direct observation of the skyrmion Hall effect. Nature Physics 13, 162–169 (2017).
Litzius, K. et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nature Physics 13, 170–175 (2017).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nature Nanotechnology 8, 742–747 (2013).
Purnama, I. et al. Guided current-induced skyrmion motion in 1D potential well. Scientific Reports 5, 10620 (2015).
Zhang, Y., Luo, S. & Yan, B. Magnetic skyrmions without the skyrmion Hall effect in a magnetic nanotrack with perpendicular anisotropy. Nanoscale 29 (2017).
Mulkers, J., Waeyenberge, B. V. & Milošević, M. V. Effects of spatially engineered Dzyaloshinskii-Moriya interaction in ferromagnetic films. Phys. Rev. B 95, 144401 (2017).
Liu, J. P., Zhang, Z. D. & Zhao, G. P. Skyrmions: Topological Structures, Properties, and Applications (eds Liu, J. P., Zhang, Z. D. & Zhao, G. P.) 409–435 (CRC Press, 2016).
Zhang, X. et al. Magnetic Skyrmion Transport in a Nanotrack With Spatially Varying Damping and Non-Adiabatic Torque. IEEE Transactions on Magnetics 53, 1500206 (2017).
Kim, S. K., Lee, K.-J. & Tserkovnyak, Y. Self-focusing skyrmion racetracks in ferrimagnets. Phys. Rev. B 95, 140404(R) (2017).
Woo, S. et al. Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films, Nature. Communications 9, 959 (2018).
Woo, S. et al. Deterministic creation and deletion of a single magnetic skyrmion observed by direct time-resolved X-ray microscopy, Nature. Electronics 1, 288–296 (2018).
Barker, J. & Tretiakov, O. A. Static and Dynamical Properties of Antiferromagnetic Skyrmions in the Presence of Applied Current and Temperature. Phys. Rev. Lett. 116, 147203 (2016).
Zhang, X., Zhou, Y. & Ezawa, M. Antiferromagnetic Skyrmion: Stability, Creation and Manipulation. Scientific Reports 6, 24795 (2016).
Göbel, B., Mook, A., Henk, J. & Mertig, I. Antiferromagnetic skyrmion crystals: Generation, topological Hall, and topological spin Hall effect. Phys. Rev. B 96, 060406(R) (2017).
Keesman, R. et al. Skyrmions in square-lattice antiferromagnets. Phys. Rev. B 94, 054402 (2016).
Jin, C., Song, C., Wang, J. & Liu, Q. Dynamics of antiferromagnetic skyrmion driven by the spin Hall effect. Appl. Phys. Lett. 109, 182404 (2016).
Buhl, P. M., Freimuth, F., Blügel, S. & Mokrousov, Y. Topological spin Hall effect in antiferromagnetic skyrmions. Phys. Status Solidi RRL 11, 4 (2017).
Zhang, X., Zhou, Y. & Ezawa, M. Magnetic bilayer-skyrmions without skyrmion Hall effect, Nature. Communications 7, 10293 (2016).
Tomasello, R. et al. Performance of synthetic antiferromagnetic racetrack memory: domain wall versus skyrmion. J. Phys. D: Appl. Phys. 50 (2017).
Koshibae, W. & Nagaosa, N. Theory of skyrmions in bilayer systems. Scientific reports 7, 42645 (2017).
Komineas, S. & Papanicolaou, N. Skyrmion dynamics in chiral ferromagnets. Phys. Rev. B 92, 064412 (2015).
Komineas, S. & Papanicolaou, N. Skyrmion dynamics in chiral ferromagnets under spin-transfer torque. Phys. Rev. B 92, 174405 (2015).
Zhang, X. et al. Control and manipulation of a magnetic skyrmionium in nanostructures. Phys. Rev. B 94, 094420 (2016).
Loreto, R. P. et al. Creation, transport and detection of imprinted magnetic solitons stabilized by spin-polarized current. JMMM 455, 25–31 (2018).
Zhang, S., Kronast, F., van der Laan, G. & Hesjedal Real-Space, T. Observation of Skyrmionium in a Ferromagnet-Magnetic Topological Insulator Heterostructure. Nano Lett. 18, 1057–1063 (2018).
Bogdanov, A. & Hubert, A. The stability of vortex-like structures in uniaxial ferromagnets. Journal of Magnetism and Magnetic Materials 195(1), 182–192 (1999).
Streubel, R. et al. Manipulating Topological States by Imprinting Non-Collinear Spin Textures. Scientific Reports 5, 8787 (2015).
Hagemeister, J. et al. Controlled creation and stability of k-π skyrmions on a discrete lattice. Phys. Rev. B 97, 174436 (2018).
Zheng, F. et al. Direct Imaging of a Zero-Field Target Skyrmion and Its Polarity Switch in a Chiral Magnetic Nanodisk. Phys. Rev. Lett. 119, 197205 (2017).
Fujita, H. & Sato Encoding, M. orbital angular momentum of light in magnets. Phys. Rev. B 96, 060407(R) (2017).
Fujita, H. & Sato, M. Ultrafast generation of skyrmionic defects with vortex beams: Printing laser profiles on magnets. Phys. Rev. B 95, 054421 (2017).
Berruto, G. et al. Laser-Induced Skyrmion Writing and Erasing in an Ultrafast Cryo-Lorentz Transmission Electron Microscope. Phys. Rev. Lett. 120, 117201 (2018).
Koshibae, W. & Nagaosa, N. Creation of skyrmions and antiskyrmions by local heating. Nature Communications 5, 5148 (2014).
Finazzi, M. et al. Laser-Induced Magnetic Nanostructures with Tunable Topological Properties. Phys. Rev. Lett. 110, 177205 (2013).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Cubukcu, M. et al. Spin-orbit torque magnetization switching of a three-terminal perpendicular magnetic tunnel junction. Appl. Phys. Lett. 104, 042406 (2014).
Liu, L. et al. Current-Induced Switching of Perpendicularly Magnetized Magnetic Layers Using Spin Torque from the Spin Hall Effect. Phys. Rev. Lett. 109, 096602 (2012).
Wang, H. L. et al. Scaling of spin Hall angle in 3d, 4d, and 5d metals from Y3Fe5O12/metal spin pumping. Phys. Rev. Letters 112(19), 197201 (2014).
Akyol, M. et al. Effect of heavy metal layer thickness on spin-orbit torque and current-induced switching in Hf|CoFeB|MgO structures. Appl. Phys. Lett. 109, 022403 (2016).
Sethi, P. et al. Modulation of spin-orbit torque efficiency by thickness control of heavy metal layers in Co/Pt multilayers. JMMM 426, P. 497–503 (2017).
Woo, S. et al. Enhanced spin-orbit torques in Pt/Co/Ta heterostructures. Phys. Rev. Lett. 105, 212404 (2014).
Ma, X. et al. Interfacial Dzyaloshinskii-Moriya Interaction: Effect of 5d Band Filling and Correlation with Spin Mixing Conductance. Phys. Rev. Lett. 12, 157204 (2018).
Vansteenkiste, A. et al. The design and verifiation of MuMax3. AIP Adv. 4, 107133 (2014).
Metaxas, P. J. et al. Creep and Flow Regimes of Magnetic Domain-Wall Motion in Ultrathin Pt/Co/Pt Films with Perpendicular Anisotropy. Phys. Rev. Lett. 99, 217208 (2007).
Heide, M., Bihlmayer, G. & Blügel, S. Dzyaloshinskii-Moriya interaction accounting for the orientation of magnetic domain in ultrathin films: Fe/W(110). Phys. Rev. B 78, 140403(R) (2008).
Chen, G. et al. Tailoring the chirality of magnetic domain walls by interface engineering. Nature Communications 4, 2671 (2013).
Cho, J. et al. Thickness dependence of the interfacial Dzyaloshinskii–Moriya interaction in inversion symmetry broken systems. Nature communications 6, 7635 (2015).
Kim, N.-H. et al. Interfacial Dzyaloshinskii-Moriya interaction, surface anisotropy energy, and spin pumping at spin orbit coupled Ir/Co interface. Appl. Phys. Letters 108, 142406 (2016).
Kim, N.-H. et al. Dependence of interfacial Dzyaloshinskii–Moriya interaction and perpendicular magnetic anisotropy on the thickness of the heavy-metal layer. Applied Physics Express 10, 10 (2017).
Moreau-Luchaire, C. et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nature Nanotechnology 11, 444–448 (2016).
Shen, M. et al. Motion of a skyrmionium driven by spin wave. Appl. Phys. Lett. 112, 062403 (2018).
Li, S. et al. Dynamics of a magnetic skyrmionium driven by spin waves. Appl. Phys. Lett. 112, 142404 (2018).
Yoon, J. et al. Control and manipulation of voltage-induced skyrmion and skyrmionium motion. International Symposium on Magnetism and Magnetic Materials 3, 21–22 (2018).
Acknowledgements
This work was supported by the Russian Foundation for Basic Research (grants 18-52-53038, 18-32-00867), by the Russian Ministry of Education and Science under the state tasks 3.5178.2017/8.9 and 3.4956.2017, by Act 211 of the Government of the Russian Federation (contract No. 02.A03.21.0011), by the Grant program of the Russian President (MK-2643.2017.2).
Author information
Authors and Affiliations
Contributions
A.G.K. and A.V.O. conceived the idea. A.S.S. and A.V.O. coordinated the project. A.G.K. and M.E.S. performed the numerical simulations. All authors discussed the results and contributed to the manuscript preparation.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kolesnikov, A.G., Stebliy, M.E., Samardak, A.S. et al. Skyrmionium – high velocity without the skyrmion Hall effect. Sci Rep 8, 16966 (2018). https://doi.org/10.1038/s41598-018-34934-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-34934-2
Keywords
This article is cited by
-
Above-room-temperature chiral skyrmion lattice and Dzyaloshinskii–Moriya interaction in a van der Waals ferromagnet Fe3−xGaTe2
Nature Communications (2024)
-
Optical skyrmions and other topological quasiparticles of light
Nature Photonics (2024)
-
Stable skyrmion bundles at room temperature and zero magnetic field in a chiral magnet
Nature Communications (2024)
-
Dynamics of skyrmion textures in thin ferrimagnetic films
Indian Journal of Physics (2024)
-
Reversible conversion between skyrmions and skyrmioniums
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.