Abstract
Biologists have long sought a way to explain how statistical properties of genetic sequences emerged and are maintained through evolution. On the one hand, non-random structures at different scales indicate a complex genome organisation. On the other hand, single-strand symmetry has been scrutinised using neutral models in which correlations are not considered or irrelevant, contrary to empirical evidence. Different studies investigated these two statistical features separately, reaching minimal consensus despite sustained efforts. Here we unravel previously unknown symmetries in genetic sequences, which are organized hierarchically through scales in which non-random structures are known to be present. These observations are confirmed through the statistical analysis of the human genome and explained through a simple domain model. These results suggest that domain models which account for the cumulative action of mobile elements can explain simultaneously non-random structures and symmetries in genetic sequences.
Similar content being viewed by others
Introduction
Compositional inhomogeneity at different scales has been observed in DNA since the early discoveries of long-range spatial correlations, pointing to a complex organisation of genome sequences1,2,3. While the mechanisms responsible for these observations have been intensively debated4,5,6,7,8,9, several investigations indicate the patchiness and mosaic-type domains of DNA as playing a key role in the existence of large-scale structures4,10,11. Another well-established statistical observation is the symmetry known as “Second Chargaff Parity Rule”12, which appears universally over almost all extant genomes13,14,15. In its simplest form, it states that on a single strand the frequency of a nucleotide is approximately equal to the frequency of its complement16,17,18,19,20. This original formulation has been later extended to the frequency of short (n ≃ 10) oligonucleotides and their reverse-complement20,21,22. While the first Chargaff parity rule23 (valid in the double strand) was instrumental for the discovery of the double-helix structure of the DNA, of which it is now a trivial consequence, the second Chargaff parity rule remains of mysterious origin and of uncertain functional role. Different mechanisms that attempt to explain its origin have been proposed during the last decades19,24,25,26,27. Among them, an elegant explanation27,28 proposes that strand symmetry arises from the repetitive action of transposable elements.
Structure and symmetry are in essence two independent observations: Chargaff symmetry in the frequency of short oligonucleotides (n ≃ 10) does not rely on the actual positions of the oligonucleotides in the DNA, while correlations depend on the ordering and are reported to be statistically significant even at large distances (thousands of bases). Therefore, the mechanism shaping the complex organization of genome sequences could be, in principle, different and independent from the mechanism enforcing symmetry. However, the proposal of transposable elements29,30 as being a key biological processes in both cases suggests that these elements could be the vector of a deeper connection.
In this paper we start with a review of known results on statistical symmetries of genetic sequences and proceed to a detailed analysis of the set of chromosomes of Homo Sapiens. Our main empirical findings are: (i) Chargaff parity rule extends beyond the frequencies of short oligonucleotides (remaining valid on scales where non-trivial structure is present); and (ii) Chargaff is not the only symmetry present in genetic sequences as a whole and there exists a hierarchy of symmetries nested at different structural scales. We then propose a model to explain these observations. The key ingredient of our model is the reverse-complement symmetry for domain types, a property that can be related to the action of transposable elements indiscriminately on both DNA strands. Domain models have been used to explain structures (e.g., the patchiness and long-range correlations in DNA), the significance of our results is that it indicates that the same biological processes leading to domains can explain also the origin of symmetries observed in the DNA sequence.
Results
Statistical Analysis of Genetic Sequences
We explore statistical properties of genetic sequences s = α1α2 … αN, with αi ∈ {A, C, T, G}, by quantifying the frequency of appearance in s of a given pattern of symbols (an observable X). For instance, we may be interest in the frequency of the codon ACT in a given chromosome. More generally, we count the number of times a given symbol α0 is separated from another symbol α1 by a distance τ1, and this from α2 by a distance τ2, and so on. The case of ACT corresponds to α0 = A, α1 = C, α2 = T, τ1 = 1, τ2 = 1. We denote\(\underline{\alpha }\,:\,=({\alpha }_{0},{\alpha }_{1},\,\cdots ,\,{\alpha }_{k})\) a selected finite sequence of symbols, and by \(\underline{\tau }:=({\tau }_{1},\,\cdots ,\,{\tau }_{k})\) a sequence of gaps. For shortness, we denote this couple by \(X:=(\underline{\alpha },\,\underline{\tau })\) and the size of the observable X by \({\ell }_{X}={\sum }_{i}{\tau }_{i}+1\). The frequency of occurrence of an observable X in the sequences s is obtained counting how often it appears varying the starting point i in the sequence:
where \(N^{\prime} =N-{\ell }_{X}+1\). As a simple example, for the choice of X = ((A, C, G), (1, 2)) in the sequence s = GGACCGGCCACAGGAA we have N = 16, N′ = 13, and P(X) = 2/13. All major statistical quantities numerically investigated in literature can be expressed in this form, as we will recall momentarily.
The main advantage of the more general formulation presented above is that it allows to inspect both the role of symmetry (varying \(\underline{\alpha }\)) and structure (varying scale separations \(\underline{\tau }\)) and it thus permits a systematic exploration of their interplay. We say that a sequence has the symmetry S at the scale \(\ell \) if for any observable X with length \({\ell }_{X}=\ell \) we have, in the limit of infinitely long s,
where S(X) is the observable symmetric to X.
We start our exploration of different symmetries S with a natural extension to observables X of the reverse-complement symmetry considered by Chargaff. The reverse complement of an oligonucleotide α1α2, …, αn of size n is \({\hat{\alpha }}_{n}{\hat{\alpha }}_{n-1}\,\ldots \,{\hat{\alpha }}_{1}\), where \(\hat{A}=T,\,\hat{T}=A,\,\hat{C}=G,\,\hat{G}=C\) (e.g., the reverse-complement of CGT is ACG). For our more general case it is thus natural to consider that the observable symmetric to
is
This motivates us to conjecture the validity of an extended Chargaff symmetry
This is an extension of Chargaff’s second parity rule because X may in principle be an observable involving (a large number of) distant nucleotides and thus equation (4) symmetrically connects structures even at large scales. One of the goals of our manuscript is to investigate the validity of Eq. (4) at different scales, which will be done by choosing observables X of size \({\ell }_{X}\) of up to millions of base pairs.
By combining P(X) of different observables X this extended Chargaff symmetry applies to the main statistical analyses already investigated in literature, unifying numerous previously unrelated observations of symmetries. As paradigmatic examples we have:
-
the frequency of a given oligonucleotide \(\underline{\omega }={\omega }_{1}{\omega }_{2}\,\cdots \,{\omega }_{k}\) can be computed as P(X) with the choice \(\underline{\alpha }=({\omega }_{1},\,{\omega }_{2},\,\cdots ,\,{\omega }_{k})\) and τ = (1, 1, … 1). Equation (4) implies that the frequency of an oligonucleotide is equal to the frequency of its reverse-complement symmetric and thus implies the second Chargaff parity rule, a feature that has been extensively confirmed20,21,22 to be valid for short oligonucleotides \({\ell }_{X}\le 10\). We report few examples of frequencies of dinucleotides (\({\ell }_{X}=2\)) in human chromosome 1: P(AG) = 7.14% ≈ P(CT) = 7.13% ≠ P(GA) = 6.01% ≈ P(TC) = 6.01%, in agreement with symmetry (4). Note that, the validity of Second Chargaff Parity rule at small scales (\({\ell }_{X}=2\) for dinucleotides) is not enough to enforce equation (4) for generic observables X (e.g., of size \({\ell }_{X}\gg 100\));
-
the autocorrelation function Cω(t) of nucleotide ω at delay t is the central quantity in the study of long-range correlations in the DNA. It corresponds to the choice \(\underline{\alpha }=(\omega ,\,\omega )\) and \(\underline{\tau }=(t)\). Equation (4) predicts the symmetry \({C}_{\omega }(t)={C}_{\hat{\omega }}(t)\). In the specific case of dinucleotides, such relation has been remarked in ref.31. Our result holds for any oligonucleotide ω;
-
the recurrence-time distribution Rω(t) of the first return-time between two consecutive appearances of the oligonucleotide ω is studied in refs32,33. By using elementary arithmetic and common combinatorial techniques, it is easy to see that Rω(t) can be in fact written as a sum of different P(X). Equation (4) hence predicts \({R}_{\omega }(t)={R}_{\hat{\omega }}(t)\). This symmetry was observed for oligonucleotides in ref.34.
This brief review of previous results shows the benefits of our more general view of Chargaff’s second parity rule and motivates a more careful investigation of the validity of different symmetries at different scales \(\ell \).
Symmetry and structure in Homo Sapiens
We now investigate the existence of new symmetries in the human genome. In order to disentangle the role of different symmetries at different scales \(\ell \) we construct a family of observables \(X=(\underline{\alpha },\,\underline{\tau })\) for which we can scan different length scales by varying the gaps vector \(\underline{\tau }\). Particularly useful is to fix all gaps in \(\underline{\tau }\) but a chosen one τj, and let it vary through different scales. To be more specific consider the following construction: given two patterns \({X}_{A}=({\underline{\alpha }}_{A},\,{\underline{\tau }}_{A})\) and \({X}_{B}=({\underline{\alpha }}_{B},\,{\underline{\tau }}_{B})\) we look for their appearance in a sequence, separated by a distance \(\ell \). This is equivalent to look for composite observable \(Y=(({\underline{\alpha }}_{A},\,{\underline{\alpha }}_{B}),\,({\underline{\tau }}_{A}\ell {\underline{\tau }}_{B}))\) or, for simplicity, \(Y=\,:({X}_{A},\,{X}_{B};\,\ell )\). We consider two patterns XA, XB of small (fixed) size \({\ell }_{{X}_{A}},\,{\ell }_{{X}_{B}}\) and we vary their separation \(\ell \) to investigate the change in the role of different symmetries.
To keep the analysis feasible, we scrutinize the case where XA and XB are dinucleotides separated by a distance \(\ell \) from each other. This goes much beyond the analysis of the frequencies of short oligonucleotides mentioned above because with \(\ell \) ranging from 1 to 107 we span ranges of interests for structure and long-range correlations. This choice has two advantages: by keeping the number of nucleotides in each X small we improve statistics, but at the same time we still differentiate \(\hat{X}\) from the simpler complement transformation.
In order to compare results for pairs XA, XB with different abundance, we normalise our observable by the expectation of independence appearance of XA, XB obtaining
Deviations from z = 1 are signatures of structure (correlations). Table 1 shows the results for chromosome 1 of Homo Sapiens, using a representative set of eight symmetrically related pairs of dinucleotides at a small scale \(\ell =4\). The results show that z is significantly different from one and that Chargaff symmetric observables \((Y,\,\hat{Y})\) appear with similar frequency, in agreement with conjecture (4). Figure 1 shows the same results of the Table varying logarithmically the scale \(\ell \) from \(\ell =1\) up to \(\ell \simeq {10}^{7}\) (more precisely we use \(\ell ={2}^{i}\) with i ∈ {0, 1, 2, .., 24}). At different scales \(\ell \) we see that a number of lines (observables XA, XB) coincide with each other, reflecting the existence of different types of symmetries.
Symmetrically related cross-correlations in Homo Sapiens - Chromosome 1. The normalized cross-correlations \({z}_{[CC,TC]}(\ell )\) as a function of the scale \(\ell \), together with that of its symmetrical related companions. Symmetries are significant also at scales where non trivial correlations are present z ≠ 1.
In order to understand the observations reported above it is necessary to formalize the symmetries that arise as composition of basic transformations. Starting from a reference observable \(Y=({X}_{A},\,{X}_{B};\ell )\), these symmetries are defined as compositions of the following two transformations:
-
(R) reverses the order in the pair: \(({X}_{A},\,{X}_{B};\ell )\,\mathop{\longrightarrow }\limits^{R}\,({X}_{B},\,{X}_{A};\ell )\);
-
(C) applies our extended symmetry equation (3) to the first of the two observable in the pair: \(({X}_{A},\,{X}_{B};\ell )\,\mathop{\longrightarrow }\limits^{C}\,({\hat{X}}_{A},\,{X}_{B};\ell )\).
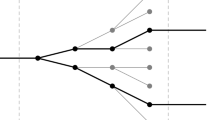
Note that RC ≠ CR (i.e. R and C do not commute), RR = CC = Id (i.e. R, C are involutions), and CRC is the symmetry equivalent to equation (3). A symmetry S is defined by a set of different compositions of C and R. We denote by \({{\mathscr{S}}}_{S}(Y)\) the set of observables obtained applying to observable Y all combinations of transformations in S. For example if S1 = {CRC} then \({{\mathscr{S}}}_{S1}({X}_{A},\,{X}_{B};\ell )=\{({X}_{A},\,{X}_{B};\ell ),\,({\hat{X}}_{B},\,{\hat{X}}_{A},\,\ell )\}\); if S2 = {CRC, R} then in addition to the set \({{\mathscr{S}}}_{S1}\) obtained from CRC we should add the observables obtained by applying R to every element of \({{\mathscr{S}}}_{S1}\), that are \(R(({X}_{A},\,{X}_{B};\ell ))=({X}_{B},\,{X}_{A};\ell )\) and \(R(({\hat{X}}_{B},\,{\hat{X}}_{A},\,\ell ))=({\hat{X}}_{A},\,{\hat{X}}_{B},\ell )\) thus obtaining \({{\mathscr{S}}}_{S2}({X}_{A},\,{X}_{B};\ell )=\)\(\{({X}_{A},\,{X}_{B};\ell ),\,({\hat{X}}_{B},\,{\hat{X}}_{A},\,\ell ),\,({X}_{B},\,{X}_{A};\ell ),\,({\hat{X}}_{A},\,{\hat{X}}_{B},\,\ell )\}\). The four symmetries we consider here are shown in Fig. 2 and correspond to: S1 (blue, obtained from {CRC} and corresponding to the extended Chargaff (4)), S2 (green, obtained from {CRC, R}), S3 (red, obtained from {R, C}), and S4 (black, obtained from {RCR, C}). We can now come back to Fig. 1 and interpret the observations as follows: at scales \(\ell < {L}_{D}\) curves are significantly different from z = 1 and appear in pairs (same symbol, symmetry S1) which almost coincide even in the seemingly random fluctuations; around \(\ell \simeq {L}_{D}\approx 2\,{10}^{2}\) two pairs merge forming two groups of four curves each (symmetry S2). At larger scales \(\ell \ge {L}_{S}\approx {10}^{3}\) all curves coincide (symmetry S3) at z ≈ 1 (no structure). At very large scales \(\ell > {L}_{M}\approx {10}^{6}\) two groups of four observables separate (symmetry S4). Similar results are obtained for all choice of dinucleotides and for all chromosomes (see SI: Supplementary data)35. These results suggest that: (i) the extended Chargaff symmetry we conjectured in Eq. (4) is valid up to a critical scale \({L}_{M}\simeq {10}^{6}\); (ii) there are other characteristic scales connected to the other symmetries.
Sets of symmetrically related observables. Starting from a reference observable \(Y=({X}_{A},\,{X}_{B},\,\ell )\), the different colors illustrate the nested sets related by symmetries S1–S4. The symmetries shown in the figure correspond to: S1 (blue, obtained from {CRC}), S2 (green, obtained from {CRC, R}), S3 (red, obtained from {R, C}), and S4 (black, obtained from {RCR, C}).
The scale-dependent results discussed above motivate us to quantify the strength of validity of symmetries at different scale \(\ell \). This is done computing for each symmetry S an indicator \({I}_{S}(\ell )\) that measures the distance between the curves \(z(\ell )\) of symmetry-related pairs (XA, XB) and compares this distance to the ones that are not related by S. More precisely, for a given reference pair Yref = (XA, XB) and symmetry S ∈ {S1, S2, S3, S4}, we consider the following distance of Yref to the set \({{\mathscr{S}}}_{S}\) of observables obtained from symmetry S:
where \(\sigma (\ell )\) denotes the standard deviation of \(z(\ell )\) over all Y. We then average over the set \({\mathscr{A}}\) of all Yref (all possible pairs XA, XB) to obtain a measure of the strength of symmetry S at scale \(\ell \) given by
Note that \({I}_{S}(\ell )=0\) indicates full validity of the symmetry S at the scale \(\ell \) (z is the same for all Y in \({\mathscr{S}}\)) and \({I}_{S}(\ell )=1\) indicate that S is not valid at scale \(\ell \) (z varies in \({\mathscr{S}}\) as much as it varies in the full set).
Figure 3 shows the results for chromosome 1 and confirms the existence of a hierarchy of symmetries at different structural scales. The estimated relevant scales in chromosome 1 (of total length N ≈ 2 × 108) are LD ≈ 102, LS ≈ 103, and LM ≈ 106. Note that LD and LM are compatible with the known average-size of transposable elements and isochores respectively36,37. Moreover, the results for all Homo-Sapiens chromosomes, summarised in Fig. 4, show that not only the hierarchy is present, but also that the scales LD, LS, and LM are comparable across chromosomes. This remarkable similarity (see also38,39,40) suggests that some of the mechanisms shaping simultaneously structure and symmetry work similarly in every chromosomes and/or act across them (e.g. chromosome rearrangements mediated by transposable elements). This, and the scales of LD, LS, and LM, provide a hint on the origin of our observations, which we explore below through the proposal of a minimal model.
Hierarchy of symmetries in Homo Sapiens - Chromosome 1. [Upper panel] The symmetry index \({I}_{S}(\ell )\) as a function of the scale \(\ell \), the smaller the value the larger the importance of the symmetry. [Bottom panel] The color bars helps visualise the onset of the different symmetries: symmetry is considered present if 0 ≤ IS ≤ 0.025 and bar is (linearly interpolated) from full color to white, correspondingly.
Hierarchy of symmetries in Homo Sapiens - All chromosomes. The symmetry index \({I}_{S}(\ell )\) as a function of the scale \(\ell \) for the full set of chromosomes in Homo Sapiens. The brighter the color, the larger is the relevance of the symmetry S1, S2, S3, or S4 (more precisely, if Imin is the minimum IS in each chromosome, IS ≤ 1.05Imin is set to full color, IS ≥ 6.5Imin is set to white, with intermediate values interpolated between these extremes).
A minimal model
We construct a minimal domain model for DNA sequences s that aims to explain the observations reported above. The key ingredient of our model is the reverse-complement symmetry of domain-types, suggested by the fact that transposable elements act on both strands. Mobile elements are recognised to play a central role in shaping domains and other structures up to the scale of a full chromosome, as well as being considered responsible for the appearance of Chargaff symmetry27. Our model accounts for structures (e.g., the patchiness and long-range correlations in DNA) in a similar way as other domain models do, the novelty is that it shows the consequences to the symmetries of the full DNA sequence.
Motivated by our finding of the three scales LD, LS, and LM, our model contains three key ingredients at different length scales \(\ell \) (see Fig. 5 for an illustration):
-
(1)
at small scales, a genetic sequence \({\bf{d}}={\alpha }_{1}{\alpha }_{2}\,\cdots \,{\alpha }_{n}\) (of average size 〈n〉 ≈ LD) is generated as a realization of a given process p. We do not impose a priori restrictions or symmetries on this process. We consider that one realization of this process builds a domain of type p. For a given domain type, the symmetrically related type is defined by the process \(\hat{p}\) as follows: take a realization (α1α2 … αn) of the process p, revert its order (αnαn−1 … α1), and complement each base \(({\hat{\alpha }}_{n}{\hat{\alpha }}_{n-1}\,\ldots ,\,{\hat{\alpha }}_{1})\), where \(\hat{A}=T\), \(\hat{T}=A\), \(\hat{C}=G\), \(\hat{G}=C\);
-
(2)
at intermediate scales, a macro-structure is composed as a concatenation of domains d1d2 … dm (of average size 〈m〉 ≈ LM), each domain belonging to one of a few types. We assume that symmetrical related domains (generated by p and \(\hat{p}\)) appear with the same relative abundance and size-distribution in a given macro-structure. The concatenation process is done so that domains of the same type tend to form clusters of average size LS such that \({L}_{D} < {L}_{S}\ll {L}_{M}\);
-
(3)
at large scales \((\,\gg \,{L}_{M})\), the full genetic sequence is composed by concatenations of macro-structures, each of them governed by different processes and statistics (e.g. different CG content)10,11.
Structure and symmetry at different scales: domain model. Structure and symmetry at different scales \(\ell \) of genetic sequences can be explained using a simple domain model. Our model considers that the full sequence is composed of macro-structures (of size LM) made by the concatenation of domains (of average size LD < LM), which are themselves correlated with neighbouring domains (up to a scale LD < LS < LM). The biological processes that shapes domains imposes that, in each macrostructure, the types of domains comes in symmetric pairs. As a consequence, we show that four different symmetries S1–S4 are relevant at different scales \(\ell \) (see text for details).
Statistical properties of the model and predictions
We now show how the model proposed above accounts for our empirical observation of a nested hierarchy of four symmetries S1-S4 at different scales. We start generating a synthetic sequence for a particular choice of parameters of the model described above (see section Methods for details). Figure 6 shows that such synthetic sequence reproduces the same hierarchy of symmetries we detected in Homo Sapiens.
Hierarchy of symmetries in a synthetic sequence generated by the domain model. The analysis of a synthetic genetic sequence generated by our model reproduces the hierarchy of symmetries observed in the human genome (compare the two panels to Figs 1 and 3). The synthetic sequence is obtained following steps (1)–(3) of the main text. As main stochastic processes p we use Markov chains with invariant probabilities μ such that μ(A) ≠ μ(T) and μ(C) ≠ μ(G) (no symmetries) (see Materials for details).
We now argue analytically why these results are expected. The key idea is to note that for different separations \(\ell \) (between the two observables XA and XB) different scales of the model above dominate the counts used to compute \(P({X}_{A},\,{X}_{B};\ell )\) through Eq. (1) (see Supplementary Information for a more rigorous derivation):
-
\((\ell \ll {L}_{D})\): \(P({X}_{A},\,{X}_{B},\,\ell )\) is dominated by XA and XB in the same domain. As domain-types appear symmetrically in each macro-structure, \(P({X}_{A},\,{X}_{B};\ell )=P({\hat{X}}_{B},\,{\hat{X}}_{A};\ell )\). This is compatible with the conjecture (4).
$$\begin{array}{rcl}S1 & = & \{CRC\}\\ {{\mathscr{S}}}_{S1} & = & \{({X}_{A},\,{X}_{B};\ell ),({\hat{X}}_{B},\,{\hat{X}}_{A};\ell \mathrm{)\}.}\end{array}$$ -
\(({L}_{D}\ll \ell \ll {L}_{S})\): \(P({X}_{A},\,{X}_{B},\,\ell )\) is dominated by XA and XB in different domains. As domains are independent realizations, the order of XA and XB becomes irrelevant and therefore R becomes a relevant symmetry (in addition to CRC). If domains of the same type tend to cluster, then for \({L}_{D} < \ell \ll {L}_{S}\) the main contribution to \(P({X}_{A},\,{X}_{B},\,\ell )\) comes from XA and XB in different domains of the same type (i.e., on different realizations of the same process p).
$$\begin{array}{rcl}S2 & = & \{CRC,\,R\}\\ {{\mathscr{S}}}_{S2} & = & \{({X}_{A},\,{X}_{B};\ell ),({\hat{X}}_{B},\,{\hat{X}}_{A};\ell ),\,({X}_{B},\,{X}_{A};\ell ),({\hat{X}}_{A},\,{\hat{X}}_{B};\ell \mathrm{)\}.}\end{array}$$Note that \({{\mathscr{S}}}_{S1}\subset {{\mathscr{S}}}_{S2}\).
-
\(({L}_{S}\ll \ell \ll {L}_{M})\): \(P({X}_{A},\,{X}_{B},\,\ell )\) is dominated by XA and XB in different domains inside the same macro-structure. For \(\ell > {L}_{S}\) the domains of XA and XB of different types can be considered independent form each other. Therefore, in addition to the previous symmetries, C is valid.
$$\begin{array}{rcl}S3 & = & \{R,\,C\}\\ {{\mathscr{S}}}_{S3} & = & \{({X}_{A},\,{X}_{B};\ell ),({\hat{X}}_{B},\,{\hat{X}}_{A};\ell ),({X}_{B},{X}_{A};\ell ),({\hat{X}}_{A},\,{\hat{X}}_{B};\ell ),\\ & & ({X}_{A},\,{\hat{X}}_{B};\ell ),({\hat{X}}_{A},\,{X}_{B};\ell ),\,({X}_{B},\,{\hat{X}}_{B};\ell ),({\hat{X}}_{B},\,{X}_{A};\ell \mathrm{)\}.}\end{array}$$Note that \({{\mathscr{S}}}_{S1}\subset {{\mathscr{S}}}_{S2}\subset {{\mathscr{S}}}_{S3}\).
-
\((\ell \gg {L}_{M})\): \(P({X}_{A},\,{X}_{B},\,\ell )\) is dominated by XA and XB in different macro-structures. Note that the frequency of XA in one macro-structure and \({\hat{X}}_{A}\) in a different macro-structure are, in general, different. Therefore, for generic XA, XB we have \(P({X}_{A},\,{X}_{B};\ell )\ne P({\hat{X}}_{B},\,{\hat{X}}_{A};\ell )\), meaning that S1 (and thus S2 and S3) is no longer valid. On the other hand, our conjectured Chargaff symmetry, Eq. (4), is valid for both XA and XB separately (because they are small scale observables). Therefore XA and XB can be interchanged in the composite observable Y.
Note that \({{\mathscr{S}}}_{S4}\subset {{\mathscr{S}}}_{S3}\).
Discussion
The complement symmetry in double-strand genetic sequences, known as the First Chargaff Parity Rule, is nowadays a trivial consequence of the double-helix assembly of DNA. However, from a historical point of view, the symmetry was one of the key ingredients leading to the double-helix solution of the complicated genetic structure puzzle, demonstrating the fruitfulness of a unified study of symmetry and structure in genetic sequences. In a similar fashion, here we show empirical evidence for the existence of new symmetries in the DNA (Figs 1–4) and we explain these observations using a simple domain model whose key features are dictated by the role of transposable elements in shaping DNA. In view of our model, our empirical results can be interpreted as a consequence of the action of transposable elements that generate a skeleton of symmetric domains in DNA sequences. Since domain models are known to explain also much of the structure observed in genetic sequences, our results show that structural complex organisation of single-strand genetic sequences and their nested hierarchy of symmetries are manifestations of the same biological processes. We expect that future unified investigations of these two features will shed light into their (up to now not completely clarified) evolutionary and functional role. For this aim, it is crucial to extend the analyses presented here to organisms of different complexity21. In parallel, we speculate that the unraveled hierarchy of symmetry at different scales could play a role in understanding how chromatin is spatially organised, related to the puzzling functional role of long-range correlations41,42.
Methods
Algorithm used to generate the synthetic sequence
We create synthetic genetic sequences through the following implementation of the three steps of the model we proposed above:
-
(1)
The processes p we use to generate genetic sequences are Markov processes of order one such that the nucleotide si at position i is drawn from a probability \(P({s}_{i}|{s}_{i-1})={M}_{{s}_{i-1},{s}_{i}}\), where M is a 4 by 4 stochastic matrix. The matrices M are chosen such that the processes’ invariant measures μ do not satisfy the Chargaff property: μ(A) ≠ μ(T) and μ(C) ≠ μ(G). The exponential decay of correlations of the Markov chains determines the domain sizes LD (in our case \({L}_{D}\simeq 10\)).
-
(2)
We use the processes p to generate chunks of average size 150 (the length of each chunck was drawn uniformly in the range [130, 170]. With probability 1/2, we applied the reverse-complement (CRC) operation to the chunck before concatenating it to the previous chunck (process \(\hat{p}\)). This choice implies that the typical cluster size is \({L}_{S}\simeq 2\ast 150=300\). The process of concatenating chunks together is repeated to form a macrostructure of length \({L}_{M}\simeq {10}^{6}\).
-
(3)
We concatenate two different macrostructures, obtained from steps (1) and (2) with two different matrices MI and MII:
where columns (and rows) corresponds to the following order: [A, C, G, T].
Data handling
Genetic sequences of Homo Sapiens were downloaded from the National Center for Biotechnology Information (ftp://ftp.ncbi.nih.gov/genomes/H_sapiens). We used reference assembly build 38.2. The sequences were processed to remove all letters different from A, C, G, T (they account for ≈1.66% of the full genome and thus their removal has no significant impact on our results).
Codes
Reference35 contains data and codes that reproduce the figures of the manuscript for different choices of observables and chromosomes.
References
Peng, C.-K. et al. Long-range correlation in nucleotide sequences. Nature 356, 168–170 (1992).
Li, W. & Kaneko, K. Long-Range Correlation and Partial 1/f α Spectrum in a Noncoding DNA Sequence. EPL 17, 655–660 (1992).
Voss, R. Evolution of Long-Range Fractal Correlations and 1/f Noise in DNA Base Sequences. Phys. Rev. Lett. 68, 3805–3808 (1992).
Karlin, S. & Brendel, V. Patchiness and correlations in DNA sequences. Science 259, 677–680 (1993).
Amato, I. DNA shows unexplained patterns writ large. Science 257, 747 (1992).
Nee, S. Uncorrelated DNA walks. Nature 357, 450 (1992).
Yam, P. Noisy nucleotides: DNA sequences show fractal correlations. Sci. Am. 267(23–24), 27 (1992).
Li, W., Marr, T. G. & Kaneko, K. Understanding long-range correlations in DNA sequences. Physica D 75, 392–416 (1994).
Bryce, R. M. & Sprague, K. B. Revisiting detrended fluctuation analysis. Sci. Rep. 2, 315 (2012).
Peng, C.-K. et al. Mosaic organization of DNA nucleotides. Phys. Rev. E 49, 1685–1689 (1993).
Bernaola-Galván, P., Román-Roldán, R. & Oliver, J. L. Compositional segmentation and long-range fractal correlations in DNA sequences. Phys. Rev. E 53, 5181–5189 (1996).
Rudner, R., Karkas, J. D. & Chargaff, E. Separation of B. subtilis DNA into complementary strands I. Biological properties, II. Template functions and composition as determined, III Direct analysis. Proc. Natl. Acad. Sci. USA 60(630–635), 915–922 (1968).
Rogerson, A. C. There appear to be conserved constraints on the distribution of nucleotide sequences in cellular genomes. J. Mol. Evol 32, 24–30 (1991).
Mitchell, D. & Bridge, R. A test of Chargaff’s second rule. Biochem. Biophys. Res. Commun. 340, 90–94 (2006).
Nikolaou, C. & Almirantis, Y. Deviations from Chargaff’s second parity rule in organellar DNA Insights into the evolution of organellar genomes. Gene 381, 34–41 (2006).
Qi, D. & Cuticchia, A. J. Compositional symmetries in complete genomes. Bioinformatics 17, 557–559 (2001).
Fickett, J. W., Torney, D. C. & Wolf, D. R. Base compositional structure of genomes. Genomics 13, 1056–1064 (1992).
Prabhu, V. V. Symmetry observations in long nucleotide sequences. Nucleic Acids Res. 21, 2797–2800 (1993).
Bell, S. J. & Forsdyke, D. R. Accounting units in DNA. J. Theor. Biol. 197, 51–61 (1999).
Baisnée, P. F., Hampson, S. & Baldi, P. Why are complementary DNA strands symmetric? Bioinformatics 18, 1021–1033 (2002).
Kong, S.-G. et al. Inverse Symmetry in Complete Genomes and Whole-Genome Inverse Duplication. PLOS one 4, e7553 (2009).
Afreixo, V. et al. The breakdown of the word symmetry in the human genome. J. Theor. Biol. 335, 153–1599 (2013).
Chargaff, E. Structure and functions of nucleic acids as cell constituents. Fed. Proc. 10, 654–659 (1951).
Bell, S. J. & Forsdyke, D. R. Deviations from Chargaff’s Second Parity Rule Correlate with Direction of Transcription. J. Theor. Biol. 197, 63–76 (1999).
Lobry, J. R. & Lobry, C. Evolution of DNA base composition under no-strand-bias condition when the substitution rates are not constant. Mol. Biol. Evol. 16, 719–723 (1999).
Zhang, S. H. & Huang, Y. Z. Limited contribution of stem-loop potential to symmetry of single-stranded genomic DNA. Bioinformatics 26, 478–485 (2010).
Albrecht-Buehler, G. Asymptotically increasing compliance of genomes with Chargaff’s second parity rules through inversions and inverted transpositions. Proc. Natl. Acad. Sci. USA 103, 17828–17833 (2006).
Shporer, S., Chor, B., Rosset, S. & Horn, D. Inversion symmetry of DNA k-mer counts: validity and deviations. BMC Genomics 17, 696 (2016).
McClintock, B. The significance of responses of the genome to challenge. Science 226, 792–801 (1984).
Fedoroff, N. V. Transposable Elements, Epigenetics, and Genome Evolution. Science 338, 758–767 (2012).
Li, W. The Study of Correlation Structures of DNA Sequences: A Critical Review. Comput. Chem. 21, 257–71 (1987).
Afreixo, V., Bastos, C. A., Pinho, A. J., Garcia, S. P. & Ferreira, P. J. Genome analysis with inter-nucleotide distances. Bioinformatics 25, 3064–3070 (2009).
Frahm, K. M. & Shepelyansky, D. L. Poincaré recurrences of DNA sequence. Phys. Rev. E 85, 016214 (2012).
Tavares, A. H. M. P. et al. DNA word analysis based on the distribution of the distances between symmetric words. Sci. Rep. 7, 728 (2017).
Altmann E. G., Cristadoro, G., Degli Esposti, M. Cross-correlations and symmetries in genetic sequences [Data set]. Zenodo 1001805, https://doi.org/10.5281/zenodo.1001805 (2017).
Bernardi, G. et al. The mosaic genome of warm-blooded vertebrates. Science 228, 953–958 (1985).
Carpena, P., Bernaola-Galván, P., Coronado, A. V., Hackenberg, M. & Oliver, J. L. Identifying characteristic scales in the human genome. Phys. Rev. E 75, 032903 (2007).
Li, W., Stolovitzky, G., Bernaola-Galván, P. & Oliver, J. L. Compositional Heterogeneity within, and Uniformity between, DNA Sequences of Yeast Chromosomes. Genome Res. 8, 916–928 (1998).
Forsdyke, D. R., Zhang, C. & Wei, J.-F. Chromosomes as interdependent accounting units: the assigned orientation of C. Elegans chromosomes minimize the total W-base Chargaff difference. J. Biol. Syst. 18, 1–16 (2010).
Bogachev, M. I., Kayumov, A. R. & Bunde, A. Universal Internucleotide Statistics in Full Genomes: A Footprint of the DNA Structure and Packaging? PLoS ONE 9, e112534 (2014).
Bechtel, J. M. et al. Genomic mid-range inhomogeneity correlates with an abundance of RNA secondary structures. BMC Genomics 9, 284 (2008).
Arneodo, A. et al. Multi-scale coding of genomic information: From DNA sequence to genome structure and function. Phys. Rep. 498, 45–188 (2011).
Acknowledgements
E.G.A. and G.C. thank the Max Planck Institute for the Physics of Complex Systems in Dresden (Germany) for hospitality and support at the early stages of this project.
Author information
Authors and Affiliations
Contributions
G.C. initiated and designed the study. E.G.A. and G.C. contributed to the development of the study, carried out statistical analysis and wrote the manuscript. E.G.A., G.C. and M.D.E. discussed and interpreted the results. E.G.A., G.C. and M.D.E. reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cristadoro, G., Degli Esposti, M. & Altmann, E.G. The common origin of symmetry and structure in genetic sequences. Sci Rep 8, 15817 (2018). https://doi.org/10.1038/s41598-018-34136-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-34136-w
Keywords
This article is cited by
-
Recurrence times, waiting times and universal entropy production estimators
Letters in Mathematical Physics (2023)
-
A role for circular code properties in translation
Scientific Reports (2021)
-
Driven progressive evolution of genome sequence complexity in Cyanobacteria
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.