Abstract
The ability of using integrated photonics to scale multiple optical components on a single monolithic chip offers key advantages to create miniature light-controlling chips. Numerous scaled optical components have been already demonstrated. However, present integrated photonic circuits are still rudimentary compared to the complexity of today’s electronic circuits. Slow light propagation in nanostructured materials is a key component for realizing chip-integrated photonic devices controlling the relative phase of light and enhancing optical nonlinearities. We present an experimental record high group-index-bandwidth product (GBP) of 0.47 over a 17.7 nm bandwidth in genetically optimized coupled-cavity-waveguides (CCWs) formed by L3 photonic crystal cavities. Our structures were realized in silicon-on-insulator slabs integrating up to 800 coupled cavities, and characterized by transmission, Fourier-space imaging of mode dispersion, and Mach-Zehnder interferometry.
Similar content being viewed by others
Introduction
The engineering of frequency dispersion in light-guiding photonic crystal (PC) structures is one of the most promising research avenues in the field of slow-light1,2,3,4. The primary goal of such device-research is to achieve structural slow-light operation over the largest possible bandwidth, with large group index, minimal index dispersion, and constant transmission spectrum. Such features are required to enable multimode or pulsed operation as they suppress pulse distortion and the onset of echoes. A commonly adopted figure of merit for this set of features is the group-index-bandwidth product (GBP). Significant progress in recent years has led to the creation of photonic structures with increasingly high GBP values5. Here, we report on the experimental demonstration of a record high GBP in silicon-based coupled-cavity waveguides (CCWs)6,7,8,9,10,11 operating at telecom wavelengths.
Results and Discussion
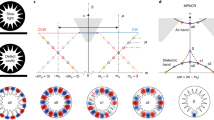
Our results rely on novel CCW designs, optimized using a genetic algorithm, and refined nanofabrication processes12. The schematic design of our CCW unit cell is shown in Fig. 1a. It comprises two L3 photonic crystal cavities13 (PCCs) separated by 5a in the x-direction and a√3 in the propagation direction y (where a is the lattice constant of the PC). Defining the CCW flat-band operation bandwidth as the spectral range Δω where the group index (ng = c dk/dω) deviates from a mean value 〈ng〉 by less than5 ±10%, we maximized the group-index bandwidth product (GBP) (=〈ng〉 Δω/ω for ng ~ 〈ng〉), while concomitantly minimizing losses, through the combination of three criteria. First, the shortest possible spatial period results in a large Brillouin zone and thus in a large GBP for a given bandwidth. Second, the first-neighbor coupling must be kept small, in order to minimize the influence of higher-order cavity modes, so that the guided band mainly arises from the coupling between the fundamental modes of each single PCC. To achieve this condition, we adopted the staggered geometry, where the mode overlap between first neighbors is naturally reduced. Third, the maximization of the quality factor (Q) of each single L3 PCCs14 does not play any role in determining the GBP, however, it minimizes the intrinsic losses of the CCW. Our PCCs, which are all strongly coupled, are expected to have a Q between the unmodified L3 PCC (~7700) and the singly optimized L3 PCC (~220,000) achieved through the modification of Δr3 and Δx. We carried out the optimization procedure via a genetic algorithm15,16 combined with the guided mode expansion (GME) method17. As an objective function, we choose the GBP with an additional price if the maximum radiation loss per unit time (Le) of the electric field intensity exceeded Le = 100 dB/ns. To maximize the objective function, we introduced four free parameters (Fig. 1a, Δr1,2,3 and Δx) that were varied simultaneously. Radii and positions of the blue air holes (Δr3 and Δx respectively) mostly affected the Q of each L3 PCCs. Radii of red and green air holes (Δr1 and Δr2 respectively) instead affected primarily the first- and second-neighbor couplings respectively. Figure 1b,c show the computed band structure of a genetically optimized CCW and the corresponding ng. (The folded band representation, indicated by the dashed line, helps to model forward and backward propagating modes measured via Fourier space imaging, as showed hereafter.) Our numerical simulations demonstrated a GBP value of 0.47, over an 18.0 nm bandwidth, for the set of parameters (Δr1, Δr2, Δr3, Δx) = (−0.0385a, −0.0279a, −0.0759a, 0.1642a). Higher theoretical GPB values of up to 0.66 were obtained at the expense of a narrower bandwidth (see Supplementary Section S3). To achieve CCW performance with a flat-band centered near 1550 nm and with standard silicon membrane thickness of d = 220 nm (see Methods), we locked the lattice constant a = 400 nm and bulk air hole radius r = 0.25a.
(a) Schematic of the CCW unit cell. The radii of the colored holes are modified (Δr1,2,3) with respect to the PC bulk holes. The blue holes are also shifted outward (Δx). (b) GME-simulated band structure and (c) corresponding ng in normalized frequency units (a/λ = ωa/2πc). The solid line corresponds to the guided mode in a representation where the period of the structure is assumed to be Ly. The dashed line indicates the folded band, in an equivalent representation where instead the period is taken as the elementary cell, of length 2Ly, containing the two staggered cavities. The operational bandwidth Δf is marked by the gray region [in panels (b and c)]. The pink region in (c) indicates the region where ng deviates from a mean value (〈ng〉 (by less than ±10%. (d) SEM top view image of a 50-CCW. Red arrows indicate the light input and output.
Figure 1d shows a top view scanning electron microscope image of one of our CCWs composed of 50 PCCs (50-CCW) fabricated in silicon-on-insulator (see Methods). As detailed in the Supplementary Section S1, all the CCWs were coupled to two separate input-output PC waveguides (red arrows in Fig. 1d) each of which (not shown in the figure) was butt-coupled to a silicon-strip waveguides and then to a spot size converter for efficient end-fire coupling. A nano-tether-based structure surrounding the device (not shown in figure) was engineered to achieve buckling-free suspended membranes18.
To study the transmission of the designed CCWs with respect to the number of PCCs composing the CCWs, we fabricated five groups of CCWs formed by 50, 100, 200, 400, and 800 total PCCs. Figure 2a shows the typical transmission profiles of those groups over their operation bandwidth. The transmission remained flat with variation <10 dB over a wide-band for CCWs containing up to 400 PCCs (400-CCW). For the 800-CCW, the transmission started dropping as extrinsic optical scattering losses (likely due to structural disorder and material absorption) became significant19, as also hinted by the more pronounced transmission fluctuations20. In general, for all CCW groups, part of the transmission fluctuations, especially at the extrema of the slow light band, display regularities and are thus likely caused by the abrupt coupling of the CCW to the input and output waveguides. A proper apodization of the design5 may prevent this effect and further improve the performance of the device. Figure 2b shows the real-space image of an 800-CCW as light propagates along the waveguide. The propagation loss of the CCW was estimated first by filtering out the strong scattering at the input edge of the CCW and then by integrating the real space profile along the x-direction. From the resulting intensity versus y-position, we fitted the loss per unit length21. By combining it with the measured ng (discussed later), the radiation loss per unit time at the center of the transmission band (1562.5 nm) was determined to be Le ~ 56 dB/ns (~76 dB/cm).
To comprehensively investigate our different CCWs we applied two complementary techniques: Fourier-space imaging (FSI)22 and Mach-Zehnder (MZ) interferometry23.
For FSI, the out-of-plane emission of the coupled PCCs is linked to the wave vector of the propagating mode through momentum conservation at the silicon/air interface. By measuring the far-field radiation angle, the in-plane Bloch wave vector ky of the mode is determined, and the dispersion relation can be reconstructed by scanning the light frequency. Figure 3a shows the measured dispersion relation for a 50-CCW and the excellent agreement with the simulated dispersion relation using the GME method (dashed white curve). From the measured dispersion relation, we obtained by numerical differentiation of the peak intensities the ng of the CCW (red crosses in Fig. 3b), which are compared with the ng curves obtained from the tight-binding (TB) model (blue curve) and the GME method (dashed black curve). By fitting the experimental data with the TB model, we determined 〈ng〉 = 41.0 and Δλ = 17.7 ± 0.5 nm, corresponding to GBP = 0.47 ± 0.01 (with the error accounting for the uncertainty in fitting the dispersion curves). The prediction of the GME model for the same device gave 〈ng〉 = 37 over an operational bandwidth of Δλ = 18.0 nm. To our knowledge, this is the highest experimental GBP ever reported in PC-based slow light devices. It is also worth noting the excellent agreement between experimental data and theory, with the measured GBP being nearly the same in all fabricated devices of nominally the same design (with the highest GBP observed in the 200-CCW). To explore the space of parameters around this optimal design we fabricated three additional series of CCW devices. For these devices, we measured a higher group index, at the expense of consistently lower GBP values, as detailed in the Supplementary Section S3.
(a) Photonic band structure of a CCW made up of 50 PCCS (50-CCW) measured by FSI overlaid with the GME simulation (white dashed line). (b) Red crosses: experimental ng calculated from data in (a). Blue continuous curve: fit of the experimental ng using the TB model. Black dashed curve: prediction of the GME simulation.
To confirm the FSI results, we carried out an alternative experimental investigation based on a MZ interferometer23 (Fig. 4a) consisting of a CCW in one arm (arm-A) and an external optical fiber in the second arm (arm-B). (See also Supplementary Section S4) Fig. 4b (inset) shows the change in the relative phase for three configurations of the MZ. Figure 4b shows the calculated group indices when an 800-CCW was inserted in the arm-A. The results are in excellent agreement with the ng measured via FSI. The two techniques are complementary, with the MZ method more suited for measuring longer CCWs (given that the uncertainty in ng scales with 1/Lc) and the FSI more suited to local investigations of the operating structure.
(a) Schematic of the optical fiber-based Mach-Zehnder interferometer set up. Each CCW was singly coupled to a left and right on-chip waveguide system (WG). (b) Calculated ng when a 800-CCW was present in arm-A. (Inset) Change in the relative phase, Δφ(ω) − Δφ(ω0), with respect to ω0 = 2πc/(1560.54 nm), as obtained from the MZ fringes when in arm-A there was: no CCW (blue), a 400-CCW (red), and a 800-CCW (black). The slope of the curves decreased when longer CCWs were inserted as the arm length difference decreased.
Together with setting a new record in the GBP of PCC-based CCWs, the nanophotonic structures reported in this letter have many potential applications as building blocks in on-chip slow-light-based devices. Particularly attractive are the implementations of slow-light in signal processing24 and slow-light-enhanced spectroscopic interferometers25. In the latter, the resolution can be increased by a factor as large as ng and, as demonstrated here, this performance can be extended over a ultra-broad bandwidth. High resolution spectrometers integrated in chip-scale platforms can find transformative applications in chemical and biosensing.
Materials and Methods
The silicon-on-insulator wafer consisted of a 220 nm top silicon layer and a 3 μm buffer oxide layer on a silicon substrate. The CCW pattern was defined by 100 kV electron beam lithography direct writing using a positive e-beam resist. The pattern was transferred from the resist (ZEP-520A) to the silicon top-layer by fluorine based inductively coupled plasma dry etching. To undercut the buried oxide layer, we used wet buffered oxide etchant while protecting the spot size converter by photo-resist. Engineered lateral openings in the membrane made the suspended structures free from buckling.
References
Milonni, P. W. Fast light, slow light and left-handed light. (Taylor & Francis, 2005).
Boyd, R. W. & Gauthier, D. J. Controlling the Velocity of Light Pulses. Science 326, 1074–1077 (2009).
Baba, T. Slow light in photonic crystals. Nature Photonics 2, 465–473 (2008).
Monat, C., Sterke, M. D. & Eggleton, B. J. Slow light enhanced nonlinear optics in periodic structures. Journal of Optics 12, 104003 (2010).
Schulz, S. A. et al. Dispersion engineered slow light in photonic crystals: a comparison. Journal of Optics 12, 104004 (2010).
Stefanou, N. & Modinos, A. Impurity bands in photonic insulators. Phys. Rev. B 57, 1212 (1998).
Yariv, A., Xu, Y., Lee, R. K. & Scherer, A. Coupled-resonator optical waveguide: a proposal and analysis. Optics Letters 24, 711 (1999).
O’Brien, D. et al. Coupled photonic crystal heterostructure nanocavities. Optics Express 15, 1228 (2007).
Jágerská, J. et al. Experimental observation of slow mode dispersion in photonic crystal coupled-cavity waveguides. Optics Letters 34, 359 (2009).
Takesue, H., Matsuda, N., Kuramochi, E., Munro, W. J. & Notomi, M. An on-chip coupled resonator optical waveguide single-photon buffer. Nature Communications 4 (2013).
Takesue, H., Matsuda, N., Kuramochi, E. & Notomi, M. Entangled photons from on-chip slow light. Scientific Reports 4, 3913 (2014).
Lai, Y. et al. Genetically designed L3 photonic crystal nanocavities with measured quality factor exceeding one million. Applied Physics Letters 104, 241101 (2014).
Akahane, Y., T. Asano, T., Song, B.-S. & Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 425, 944 (2003).
Notomi, M., Kuramochi, E. & Tanabe, T. Large-scale arrays of ultrahigh-Q coupled nanocavities. Nature Photonics 2, 741 (2008).
Minkov, M. & Savona, V. Automated optimization of photonic crystal slab cavities. Sci. Rep. 4, 5124 (2014).
Minkov, M. & Savona, V. Wide-band slow light in compact photonic crystal coupled-cavity waveguides. Optica 2, 631 (2015).
Andreani, L. C. & Gerace, D. Photonic-crystal slabs with a triangular lattice of triangular holes investigated using a guided-mode expansion method. Phys. Rev. B 73, 235114 (2006).
Iwase, E. et al. Control of buckling in large micromembranes using engineered support structures. J. of Micromech. Microeng. 22, 065028 (2012).
Hughes, S., Ramunno, L., Young, J. F. & Sipe, J. E. Extrinsic Optical Scattering Loss in Photonic Crystal Waveguides: Role of Fabrication Disorder and Photon Group Velocity. Physical Review Letters 94, 033903 (2005).
Mazoyer, S. et al. Statistical fluctuations of transmission in slow light photonic-crystal waveguides. Optics Express 18, 14654 (2010).
Mazoyer, S., Hugonin, J. P. & Lalanne, P. Disorder-Induced Multiple Scattering in Photonic-Crystal Waveguides. Physical Review Letters 103, 063903 (2009).
Le Thomas, N., Houdré, R., Kotlyar, M. V., O’Brien, D. & Krauss, T. F. Exploring light propagating in photonic crystals with Fourier optics. JOSA B 24, 2964 (2007).
Vlasov, Y. A., O’boyle, M., Hamann, H. F. & McNab, S. J. Active control of slow light on a chip with photonic crystal waveguides. Nature 438, 65–69 (2005).
Schweinsberg, A., Shi, Z., Vornehm, J. E. & Boyd, R. W. Demonstration of a slow-light laser radar. Optics Express 19, 15760 (2011).
Shi, Z., Boyd, R. W., Gauthier, D. J. & Dudley, C. C. Enhancing the spectral sensitivity of interferometers using slow-light media. Optics Letters 32, 915 (2007).
Acknowledgements
Y. L. and A. B. acknowledge funding from the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant RGPIN-2017-06859. M.M., V.S., M.S.M., and R.H. acknowledge funding from the Swiss National Science Foundation through projects 200021_146998, 200020_162657, 200020_149537 and 200020_169590. R.B. acknowledges funding from the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant RGPIN/2017-06880.
Author information
Authors and Affiliations
Contributions
R.H., V.S. and A.B. conceived the study. Y.L. and A.B. developed the nanofabrication. Y.L., M.S.M. and R.H. performed and analyzed the FSI. B.G., Y.L., R.W.B. and A.B. performed and analyzed the MZ experiments. M.M. and V.S. performed the theory and the numerical simulations that led to the optimized CCW design. Y.L., M.S.M., B.G., V.S., R.H. and A.B. wrote the manuscript, with extensive input from all other authors. All authors read, commented, and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lai, Y., Mohamed, M.S., Gao, B. et al. Ultra-wide-band structural slow light. Sci Rep 8, 14811 (2018). https://doi.org/10.1038/s41598-018-33090-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-33090-x
Keywords
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.