Abstract
Laser material deposition based restoration of high-value components can be a revolutionary technology in remanufacturing. The deposition process induces residual stresses due to thermomechanical behavior and metallurgical transformations. The presence of tensile residual stresses in the deposited layer will compromise the fatigue life of the restored component. We have developed a novel fully coupled metallurgical, thermal and mechanical (metallo-thermomechanical) model to predict residual stresses and identified a critical deposition height, which ensures compressive residual stresses in the deposited layer. Any lower deposition height will result in tensile residual stresses and higher deposition height will result in excessive dilution (substrate melting). We have validated the model using neutron and micro-focus X-ray diffraction measurements. This study highlights that the critical deposition height corresponds to the minimum cooling rate during solidification. It addresses one of the major outstanding problems of additive manufacturing and paves a way for “science-enabled-technology” solutions for sustainable restoration/remanufacturing.
Similar content being viewed by others
Introduction
Transformation of the global industrial ecology is essential to ensure the stability of the climate-sensitive tipping elements of the Earth System1,2,3,4,5 while maintaining sustainable industrial growth. For such a transformation, reorganizing the manufactured capital infrastructure towards repair and remanufacture of industrial products will reduce human impact on the environment as well as increase economic growth4,6,7,8. In this regard, the importance of maintenance, repair and overhaul (MRO) in the aerospace and automotive sectors can be understood from the fact that these sectors significantly leverage other sectors of a nation’s economy9. Even by conservative estimates ~18% increase by 202410 is predicted for the automotive collision repair industry and aircraft MRO market10,11. Central to these efforts for sustainable development in the automotive and aerospace sectors is extending the service life of molds/dies, engine parts and important structural components using energy efficient Directed Energy Deposition (DED) processes such as laser additive manufacturing12. Laser additive manufacturing provides numerous advantages over the traditional restoration techniques based on thermal spraying or welding, which are imprecise and ad hoc13,14,15,16,17,18,19,20,21,22,23,24,25. The precise and controlled deposition in these processes produces a relatively narrow dilution and heat affected zone15,16,17,19,26. However, it induces residual stresses (locked in post processing stresses). Note that the nature of the residual stresses (compressive or tensile) is the most important factor affecting the integrity and quality of the processed components as it directly affects the service life16,17,19,20,26,27. The residual stresses develop due to strains induced by thermomechanical effects and metallurgical transformations28,29,30. The deposition of the hot molten material on a relatively cold substrate and subsequent conduction-driven cooling results in differential thermal expansion and contraction between the deposited and substrate layers21,30,31,32,33. The thermomechanical strains depend on the temperature distribution, the coefficients of thermal expansion and the elastoplastic behavior of the clad and the substrate materials. In addition, the high rate of cooling can result in metallurgical transformations which contribute to the development of additional strains due to transformation induced plasticity and volumetric dilation34,35,36,37,38,39. It may be noted that the deposited layer is often the most critical region and tensile residual stresses in this region can aid in crack propagation17,18,27,30,31,40,41. One of the greatest challenges in laser additive manufacturing today is to determine a critical deposition height to ensure compressive residual stress in the clad (from the surface of the clad to the clad-substrate interface region).
Finite element (FE) models provide viable alternatives to expensive experiments for predicting the transient temperature field, the residual stresses and the microstructural transformations developed during the process15,16,17,19,26,27,35,42,43,44,45. Most of the finite element models reported in the literature for predicting the residual stresses use sequential coupling between the metallurgical and thermomechanical phenomena37,39,46,47. It may be noted that a fully coupled model can consider the effect of metallurgical transformations on the in-process stress evolution and can better predict the residual stress profile. Moreover, the existing models do not take into consideration of the shape of the deposited layer. In this work, we have investigated the residual stress distribution across a laser deposited layer on a substrate via a 3D fully coupled metallo-thermomechanical finite element model. Gaussian distribution of powder with uniform intensity moving heat source is considered in this analysis22,48.
To experimentally validate the model, laser cladding (deposition) experiments were conducted on H13 tool steel with Crucible Particle Metallurgy (CPM) steel powders with high Vanadium content. It is known that dies and molds of H13 tool steel are repaired using CPM9V18,22,23,24,49,50. The residual stresses predicted by the model have been compared with the results obtained from micro-focus X-ray diffraction for micro-scale local residual stress measurements at IIT Bombay, and neutron diffraction experiments for determining volume averaged residual stresses at ANSTO, Sydney, Australia. The following sections describe the formulation of the fully coupled 3D metallo-thermomechanical model and experimental details.
Methodology
Metallo-thermomechanical modeling of residual stresses
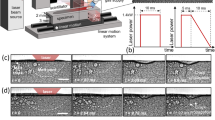
The 3D fully coupled metallo-thermomechanical finite element model utilizes various user-defined subroutines in the commercial finite element software ABAQUS® to model the complex interactions between the thermal, mechanical and metallurgical phenomena involved in laser cladding. Figure 1 describes the algorithm for the metallo-thermomechanical model along with the computational domain with details of mesh size and loading-boundary conditions. Note that the element activation happens only after the material temperature exceeds the melting temperature. As a result, the clad layer is deposited as a layer of molten material. The coefficient of thermal expansion of the molten material is reduced significantly via a user defined subroutine, so that no further thermal strain is accumulated in the element. Consequently, negligible stresses are present in the clad till the material is molten state (see Fig. 1(a)). To incorporate the strains due to metallurgical transformations, it is crucial to identify the various phase fractions using the kinetic model defined by the multi-utility user subroutine UEXPAN in ABAQUS®. The subroutine UEXPAN forms the crucial link between the thermal, metallurgical and mechanical interactions. For the elements that transform to martensite, the volume fraction of martensite (F) is calculated according to Eq. (1)51 (for details of governing equations see SI Appendix section S1).
where Fm is the maximum fraction of martensite permitted by the phase diagram, Fi is the volume fraction of pearlite, g is the grain size, Ce is the carbon content in austenite, Cc is the critical carbon content, D is the appropriate diffusion coefficient for carbon, t is the time required for the lateral diffusion of carbon over a distance λ (pearlite spacing). Apart from calculating F, UEXPAN also calculates the strains developed due to differential thermal expansion-contraction \((d{\varepsilon }_{ij}^{th{\rm{\_}}\alpha })\) 52,53 and metallurgical transformations \((d{\varepsilon }_{ij}^{TM})\) viz. transformation induced plasticity and volumetric dilation36,37,42,43,44, given by:
where KTP = 5.08 × 10−5 MPa−1 37, \({(\frac{{\rm{\Delta }}V}{V})}_{A\to B}\)is the volume change associated from one phase to other, i.e. from ferrite to austenite during heating, and austenite to ferrite or martensite during cooling. Xp corresponds to the resultant phase during the transformation, i.e. austenite during heating and ferrite or martensite during cooling39. The actual material behavior of H13 was determined in the thermomechanical simulator Gleeble (Fig. S1) and temperature dependent thermo-physical properties of H13 and CPM 9 V (Table S1, refer to Table S2 for microstructural properties of H13) have been used in the analysis54,55. The user defined subroutine UMAT has been used to define the mechanical constitutive behaviour of the material56,57,58, approximated by a modified Johnson-Cook plasticity model where strain rate hardening was ignored32,59 (Fig. S1), to calculate the elastic \(({\varepsilon }_{kl}^{e})\), plastic \(({\varepsilon }_{kl}^{p})\) strains and elasto-plastic constitutive matrix \((\,{C}_{ijkl}^{ep})\)52,53,60,61. Mesh convergence study was conducted to understand the behavior of the model for varying mesh sizes. Accordingly, the mesh size reported in Fig. 1(b) is obtained after mesh convergence study (see Fig. S3(a)).
Experimental details
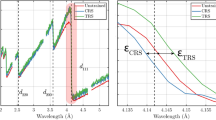
The volume averaged residual stresses in the laser cladded components were measured using Neutron diffraction at the KOWARI residual stress diffractometer at the Australian Nuclear Science and Technology Organization (ANSTO). For measurements, the Fe-211 reflection with neutron wavelength of 1.68 Å was used. The gauge volume for longitudinal measure was fixed at 2 mm × 2 mm × 3 mm. The limitation of the gauge volume used for neutron diffraction measurement restricted the measurement of the macroscale residual stresses to the clad zone. Consequently, the local micro-scale residual stress was measured using the Bruker D8 Discover X-ray diffractometer with a 300 μm spot size. The details of the neutron and micro-focus X-ray diffraction measurements are provided in Fig. 2 (for details of the calculation of residual stresses in diffraction measurements refer to SI Appendix section S3).
Results and Discussion
Influence of metallurgical transformations
Figure 2 shows a comparison of the normal residual stresses measured using diffraction techniques with the residual stresses predicted by the thermomechanical and the metallo-thermomechanical finite element models. Both the diffraction techniques showed the presence of tensile residual stresses near the melt front and compressive stresses in the deposited layer and the interface regions. The thermal stresses develop primarily due to different coefficients of thermal expansions between the deposited clad and substrate materials21,32 and the temperature difference due to the thermal gradient. In laser cladding, the shrinkage of the solidified deposited layer is constrained by the relatively large and cold substrate, which induces tensile stresses at the melt interface26,32,62. The force equilibrium and the metallurgical changes result in a complex residual stress profile (see Fig. 2). Figure 2 shows that the thermomechanical model could capture the nature of the residual stresses in the deposited layer and the substrate where the thermomechanical effects due to differential thermal expansion and contraction dominate; but fails to predict the compressive stress in the substrate. This is because the high cooling rates associated with laser cladding results in the formation of metastable martensite phase32,42,63,64. On inclusion of the metallurgical effects, the metallo-thermomechanical model can capture the presence of the compressive residual stresses in the substrate. Note that the thermomechanical model considers the stress developed due to thermal strains whereas the metallo-thermomechanical model considers the combined effect of thermal and metallurgical strains for calculation of residual stresses. The prediction error for compressive stresses in the clad layer significantly improves from ~26% for the thermomechanical model to ~2% for the metallo-thermomechanical model. Additionally, the prediction error for the tensile stresses near the melt depth region improves from ~29% to ~13% on considering the metallurgical effects. Additionally, the Electron Backscatter Diffraction (EBSD) images of the microstructures in the clad and substrate region are included in Fig. 2. From Fig. 2, it can be observed that very fine equiaxed alpha phase is present in the clad region with predominantly prior austenitic grain and a lath morphology is present in the substrate region27,33,63. Though the effect of the transformation induced plasticity is minor relative to the thermal strains and the volume dilation, the inclusion of metallurgical effects significantly improves the prediction of the residual stresses. Therefore, the subsequent analysis is conducted using the improved metallo-thermomechanical model.
Critical height of deposition
The critical height of deposition corresponds to the layer thickness which when deposited would ensure compressive residual stresses in the deposited layer. An iterative methodology has been devised (see Fig. 3(a)), wherein, for given input process variables, namely, powder feed rate, nozzle and beam diameter, a trial value of clad height and corresponding scanning speed (based on continuity equation for mass conservation as the powder feed rate is fixed) is selected. The next step is to determine the laser power required, to ensure that the entire deposited layer is melted with minimal substrate melting. The predicted residual stress distribution of this combination of trial height and laser power is calculated and checked if the residual stress in the clad layer is compressive and the clad-substrate interface is free of tensile residual stresses. If the above conditions are not satisfied, the trial-clad height is updated and the entire sequence of steps is repeated to identify the critical height of deposition. The converged clad height is termed as critical deposition height where the entire clad is under compressive stresses. Note that in this study, σ11 (the normal component of residual stress along the direction of deposition) is considered (see Fig. 2). It is important to point out that σ11 is not the principal stress but the normal residual stress component in the longitudinal (scan) direction. Previous studies have reported that the longitudinal residual stress is the dominant residual stress component for welding and laser assisted deposition operations41,44,65,66.
To obtain the critical height from the model proposed in this paper, the trial-clad height is increased from 600 µm to 690 µm for a powder feed rate of 5 g/min with a nozzle diameter and spot size of 3 mm (see Fig. 3(c)). The laser power required for completely melting the deposition height of 600 µm is 1500 W whereas for 690 µm deposition height, the laser power is 2250 W.
It may be noted that the scan speed will change for every trial clad height based on the conservation of mass. Even though a substantial portion of the clad is under compressive residual stresses, the clad-substrate interface is under tensile stresses for 600 and 630 µm deposition heights. However, if the clad height is increased to 660 µm, the residual stresses at the interface also become compressive. If the clad height is increased further to 690 µm, the residual stresses at the interface remain compressive, albeit at a higher magnitude. It may be noted that the melt depth increases substantially resulting in higher dilution in the substrate, which is detrimental. Consequently, 660 µm (at a laser power of 1800 W and a corresponding scan speed of 354 mm/s) has been identified as a critical deposition height, any lower or higher clad heights will result in unfavorable deposition conditions. To understand the physics underlying the residual stress generation, the effect of the cooling rate during solidification has been investigated at different deposition heights. The cooling rate during solidification R is given by63,64,67,68:
where TL is the liquidus temperature (~1811 K), TS is the solidus temperature (~1700 K)32 and Δts is the solidification time obtained from the variation of nodal temperature32 (see Fig. 3(b)). It is expected that R will govern the residual stress evolution as the onset of thermomechanical residual stresses occurs at solidification. It has been observed that R is 1593 K/s at a deposition height of 600 µm. R decreases with an increase of deposition height and at 660 µm R is 1360 K/s. It may be noted that beyond the critical deposition height, R increases to 1786 K/s at 690 µm. Hence, the critical deposition height corresponds to the lowest value of R (see Fig. 3(d)). The low cooling rate during solidification (R) ensures that the thermomechanical residual stresses are lower.
Summary and Concluding Remarks
In this work, we investigated the variation of residual stress across the cross-section of a laser cladded specimen, predicted using a fully coupled metallo-thermomechanical model to demonstrate the existence of a critical deposition height. Any deposition height lower than the critical height would yield detrimental tensile residual stresses at the interface whereas higher than the critical deposition height will result in undesired excessive dilution. It was also found that at the critical height of deposition, the solidification rate is minimum. The study also highlights the importance of strains developed due to metallurgical transformation on the final residual stress variation across the cross section of the repaired specimen. This study addresses one of the most important problems in additive manufacturing that whether a critical deposition height exists which can yield compressive residual stresses in the deposited layer and the interface. This study can form a basis of “science enabled technology solutions” for improving the quality of components produced using additive manufacturing techniques. It may be noted that if the restoration is carried out at this deposition height, the service life of the restored component will be enhanced. This could pave the way to sustainable restoration via energy-efficient laser additive manufacturing, thereby optimizing the total material cycles for industrial production.
Methods
All numerical simulations were performed utilizing various user-defined subroutines (DFLUX, UEXPAN and UMAT) in the commercial finite element software ABAQUS®. The subroutines are written to relate to the algorithm described in Fig. 1. Detailed explanation can be found in section ‘Methodology’.
Code Availability
All numerical codes in this paper are available upon request to the corresponding author.
Data Availability
All relevant data in this paper are available from the authors.
References
Weisz, H., Suh, S. & Graedel, T. E. Industrial Ecology: The role of manufactured capital in sustainability. Proc. Natl. Acad. Sci. USA 112, 6260–6264, https://doi.org/10.1073/pnas.1506532112 (2015).
Lenton, T. M. et al. Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. USA 105, 1786–1793, https://doi.org/10.1073/pnas.0705414105 (2008).
Intergovernmental Panel on Climate Change. Climate Change 2014: Mitigation of Climate Change. Working Group III Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press https://doi.org/10.1017/CBO9781107415416.008 (2014).
Riahi, K. et al. Energy Pathways for Sustainable Development. Global energy assessment toward sustainable future 1203–1306 (2012).
Brown, G. E. Remarks on industrial ecology. Proc. Natl. Acad. Sci. USA 89, 876–878, https://doi.org/10.1073/pnas.89.3.876 (1992).
Johansson, T. B., Patwardhan, A., Nakicenovic, N. & Gomez-Echeverri, L. Global Energy Assessment. Toward a Sustainable Future. Glob. Energy Assess. 3–93, https://doi.org/10.1017/CBO9780511793677 (2012).
Krausmann, F. et al. Growth in global materials use, GDP and population during the 20th century. Ecol. Econ. 68, 2696–2705, https://doi.org/10.1016/j.ecolecon.2009.05.007 (2009).
Peters, G. P. et al. Rapid growth in CO2 emissions after the 2008-2009 global financial crisis. Nat. Clim. Chang. 2, 2–4, https://doi.org/10.1038/nclimate1332 (2012).
Vaz, C. R., Rauen, T. R. S. & Lezana, A. G. R. Sustainability and innovation in the automotive sector: A structured content analysis. Sustainability 9, 880, https://doi.org/10.3390/su9060880 (2017).
Global Aircraft MRO Market (2017–2022). Bengaluru: Mordor Intelligence 1–35 (2017).
Vieira, D. R. & Loures, P. L. Maintenance, Repair and Overhaul (MRO) Fundamentals and Strategies: An Aeronautical Industry Overview. Int. J. Comput. Appl. 135, 975–8887, https://doi.org/10.5120/ijca2016908563 (2016).
ASTM. Standard Terminology for Additive Manufacturing Technologies. F2792-12a, 11–13, https://doi.org/10.1520/F2792-12A (2012).
Steen, W. M. & Mazumder, J. Laser Material Processing. Springer Science & Business MediaISBN 978-1-84996-062-5 (2010).
Toyserkani, E., Khajepour, A. & Corbin, S. F. (2004). Laser Cladding. CRC press., ISBN 9780849321726 (2004).
Dowden, J. T he Theory of Laser Materials Processing. Heat and Mass Transfer in Modern Technology (2009).
Vollertsen, F., Partes, K. & Meijer, J. State of the art of laser hardening and cladding. In Proc. of the 3nd Int. WLT-Conf. on Lasers in Manuf., Munich, Germany (2005).
Pinkerton, A. J., Wang, W. & Li, L. Component repair using laser direct metal deposition. Proc. Inst. Mech. Eng. Part B J. Mech. Eng. Sci. 222, 827–836, https://doi.org/10.1243/09544054JEM1008 (2008).
Leunda, J., Soriano, C., Sanz, C. & Navas, V. G. Laser cladding of vanadium-carbide tool steels for die repair. Phys. Procedia 12, 345–352, https://doi.org/10.1016/j.phpro.2011.03.044 (2011).
Wang, J., Prakash, S., Joshi, Y. & Liou, F. Laser aided part repair-a review. Proceedings of the Thirteenth Annual Solid Freeform Fabrication Symposium (2002).
Sexton, L., Lavin, S., Byrne, G. & Kennedy, A. Laser cladding of aerospace materials. J. Mater. Process. Technol. 122, 63–68, https://doi.org/10.1016/S0924-0136(01)01121-9, (2002).
Kattire, P., Paul, S., Singh, R. & Yan, W. Experimental characterization of laser cladding of CPM 9V on H13 tool steel for die repair applications. J. Manuf. Process. 20, 492–499, https://doi.org/10.1016/j.jmapro.2015.06.018 (2015).
Paul, S., Singh, R. & Yan, W. Thermal model for additive restoration of mold steels using crucible steel. J. Manuf. Process. 24, 346–354, https://doi.org/10.1016/j.jmapro.2016.06.012 (2016).
Chen, J. & Xue, L. Laser cladding of high-performance CPM tool steels on hardened H13 hot-work tool steel for automotive tooling applications. TMS 2012 141st Annual Meeting and Exhibition, Materials Processing and Interfaces 1, 11–18, https://doi.org/10.1007/s11837-012-0332-2, (2012).
Xue, L., Chen, J. & Wang, S. H. Freeform laser consolidated H13 and CPM 9V tool steels. Metallogr. Microstruct. Anal. 2, 67–78, https://doi.org/10.1007/s13632-013-0061-0, (2013).
Vilar, R. Laser Powder Deposition, Comprehensive Materials Processing 10, 163–216 ISBN: 978-0-08-096533-8 (2014).
Zhong, M. & Liu, W. Laser surface cladding: The state of the art and challenges. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 224, 1041–1060, https://doi.org/10.1243/09544062JMES1782, (2010).
Liu, Q., Janardhana, M., Hinton, B., Brandt, M. & Sharp, K. Laser cladding as a potential repair technology for damaged aircraft components. Int. J. Struct. Integr. 2, 314–331, https://doi.org/10.1108/17579861111162914 (2011).
Cottam, R., Luzin, V., Thorogood, K., Wong, Y. C. & Brandt, M. The role of metallurgical solid state phase transformations on the formation of residual stress in laser cladding and heating. Mater. Sci. Forum 777, 19–24, https://doi.org/10.4028/www.scientific.net/MSF.777.19 (2014).
Kumar, S., Awasthi, R., Viswanadham, C. S., Bhanumurthy, K. & Dey, G. K. Thermo-metallurgical and thermo-mechanical computations for laser welded joint in 9Cr-1Mo (V, Nb) ferritic/martensitic steel. Mater. Des. 59, 211–220, https://doi.org/10.1016/j.matdes.2014.02.046 (2014).
Palaniradja, K., Alagumurthi, N. & Soundararajan, V. Residual stresses in case hardened materials. Open Mater. Sci. J. 4, 92–102 (2010).
Paul, S., Ashraf, K. & Singh, R. Residual stress modeling of powder injection laser surface cladding for die repair applications. ASME 2014 International Manufacturing Science and Engineering Conference, MSEC. 2014 Collocated with the JSME 2014 International Conference on Materials and Processing and the 42nd North American Manufacturing Research Conference, https://doi.org/10.1115/MSEC.2014-4029 (2014).
Paul, S., Thool, K., Singh, R., Samajdar, I. & Yan, W. Experimental Characterization of Clad Microstructure and its Correlation with Residual Stresses. Procedia Manuf. 10, 804–818, https://doi.org/10.1016/j.promfg.2017.07.081, (2017).
Szost, B. A. et al. A comparative study of additive manufacturing techniques: Residual stress and microstructural analysis of CLAD and WAAM printed Ti-6Al-4V components. Mater. Des. 89, 559–567, https://doi.org/10.1016/j.matdes.2015.09.115 (2016).
Yang, Y. S. & Na, S. J. Effect of transformation plasticity on residual stress fields in laser surface hardening treatment. J. Heat Treat. 9, 49–56 (1991).
Oddy, A. S., Goldak, J. A. & McDill, J. M. J. Transformation plasticity and residual stresses in single-pass repair welds. J. Press. Vessel Technol. Trans. ASME 114, 33–38, https://doi.org/10.1115/1.2929009, (1992).
Denis, S. Considering stress-phase transformation interactions in the calculation of heat treatment residual stresses: Mechanics of Solids with Phase Changes. 293–317, https://doi.org/10.1007/978-3-7091-2660-8_10 (1997).
Ramesh, A. & Melkote, S. N. Modeling of white layer formation under thermally dominant conditions in orthogonal machining of hardened AISI 52100 steel. Int. J. Mach. Tools Manuf. 48, 402–414, https://doi.org/10.1016/j.ijmachtools.2007.09.007 (2008).
Leung, M. K., Man, H. C. & Yu, J. K. Theoretical and experimental studies on laser transformation hardening of steel by customized beam. Int. J. Heat Mass Transf. 50, 4600–4606, https://doi.org/10.1016/j.ijheatmasstransfer.2007.03.022 (2007).
Bailey, N. S., Tan, W. & Shin, Y. C. Predictive modeling and experimental results for residual stresses in laser hardening of AISI 4140 steel by a high power diode laser. Surf. Coatings Technol. 203, 2003–2012, https://doi.org/10.1016/j.surfcoat.2009.01.039 (2009).
Paydas, H., Mertens, A., Carrus, R., Lecomte-Beckers, J. & Tchoufang, T. J. Laser cladding as repair technology for Ti-6Al-4V alloy: Influence of building strategy on microstructure and hardness. Mater. Des. 85, 497–510, https://doi.org/10.1016/j.matdes.2015.07.035 (2015).
Teng, T. L., Chang, P. H. & Tseng, W. C. Effect of welding sequences on residual stresses. Comput. Struct. 81, 273–286, https://doi.org/10.1016/S0045-7949(02)00447-9, (2003).
Rohde, J. & Jeppsson, A. Literature review of heat treatment simulations with respect to phase transformation, residual stresses and distortion. Scand. J. Metall. 29, 47–62, https://doi.org/10.1034/j.1600-0692.2000.d01-6.x (2000).
Ion, J. C. Laser Transformation Hardening. Surf. Eng. 18, 14–31, https://doi.org/10.1179/026708401225001228 (2002).
Wang, X., Hu, L., Xu, Q., Chen, D. X. & Sun, S. T. Influence of martensitic transformation on welding residual stress in plates and pipes. Sci. Technol. Weld. Join. 22, 505–511, https://doi.org/10.1080/13621718.2016.1263711 (2017).
Murakawa, H. et al. Effect of phase transformation onset temperature on residual stress in welded thin steel plates. Trans. Join. Weld. Res. Inst. 37, 75–80, https://ridda2.utp.ac.pa/handle/123456789/2870 (2008).
Deng, D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater. Des. 30, 359–366, https://doi.org/10.1016/j.matdes.2008.04.052 (2009).
Geijselaers, H. J. M. Numerical simulation of stresses due to solid state transformations - The simulation of laser hardening. PhD dissertation, University of Twente, Faculty of Engineering Technology (2003).
Picasso, M., Marsden, C. F., Wagniere, J. D., Frenk, A. & Rappaz, M. A simple but realistic model for laser cladding. Metall. Mater. Trans. B 25, 281–291, https://doi.org/10.1007/BF02665211 (1994).
Paul, S., Singh, R., & Yan, W. Finite Element Simulation of Laser Cladding for Tool Steel Repair. In Lasers Based Manufacturing 139–156 Springer, New Delhi (2015).
Wang, S. H., Chen, J. Y. & Xue, L. A study of the abrasive wear behaviour of laser-clad tool steel coatings. Surf. Coatings Technol. 200, 3446–3458, https://doi.org/10.1016/j.surfcoat.2004.10.125 (2006).
Ashby, M. F. & Easterling, K. E. The transformation hardening of steel surfaces by laser beams-I. Hypo-eutectoid steels. Acta Metall. 32, 1935–1948, https://doi.org/10.1016/0001-6160(84)90175-5, (1984).
Neto, E. A., de S., Peric, D. & Owen, D. R. J. Computational Methods for Plasticity: Theory and Applications. Engineering. John Wiley & Sons https://doi.org/10.1002/9780470694626 (2009).
Dunne, F. & Petrinic, N. Introduction to Computational Plasticity. Oxford University Press (2006).
H13 datasheet, Crucible Industries LLC, 575 State Fair Blvd., Solvay, NY 13209, www.crucible.com, 800-365-1180 315-487-4111
CPM 9V datasheet, Crucible Industries LLC, 575 State Fair Blvd., Solvay, NY 13209, www.crucible.com, 800-365-1180 315-487-4111.
Dassault Systèmes Simulia, ABAQUS Documentation. Abaqus 6.12 53, 1689–1699 (2013).
Dassault Systèmes Simulia. Abaqus user subroutines. Abaqus 6.12 (2013).
Abaqus, Simulia, Writing User Subroutines with Abaqus. Abaqus 6.12 (2013).
Johnson, G. R. & Cook, W. H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. 7th International Symposium on Ballistics 541–547 https://doi.org/10.1038/nrm3209 (1983).
Hashiguchi, K. & Yamakawa, Y. Introduction to Finite Strain Theory for Continuum. John Wiley & Sons, https://doi.org/10.1002/9781118437711 (2013)
Bathe, K. -J. Finite Element Procedures. (2006)
Surez, A. et al. Study of residual stresses generated inside laser cladded plates using FEM and diffraction of synchrotron radiation. Surf. Coatings Technol. 204, 1983–1988, https://doi.org/10.1016/j.surfcoat.2009.11.037 (2010).
Shingu, P. H. & Ozaki, R. Solidification rate in rapid conduction cooling. Metall. Trans. A 6, 33–37 (1975).
Gowri, S. & Samuel, F. H. Effect of cooling rate on the solidification. Metall. Trans. A 23, 3369–3376 (1992).
Paradowska, A. M. et al. Residual stress distribution in steel butt welds measured using neutron and synchrotron diffraction. J. Phys. Condens. Matter 21, 124213, https://doi.org/10.1088/0953-984/21/12/124213 (2009).
Kong, F., Ma, J. & Kovacevic, R. Numerical and experimental study of thermally induced residual stress in the hybrid laser-GMA welding process. J. Mater. Process. Technol. 211, 1102–1111, https://doi.org/10.1016/j.jmatprotec.2011.01.012 (2011).
David, S. A., Babu, S. S. & Vitek, J. M. Welding: Solidification and microstructure. JOM 55, 14–20 (2003).
Sarreal, J. A. & Abbaschian, G. J. The effect of solidification rate on microsegregation. Metall. Trans. A 17, 2063–2073 (1986).
Acknowledgements
Ramesh Singh and Santanu Paul gratefully acknowledge the support of Department of Science and Technology-Swarana Jayanti Fellowship award [DST/SJF/ETA-02/2014–15]. Wenyi Yan acknowledges the support of Australian Research Council through the ITRH project IH13010000. Santanu Paul acknowledges Mr. Chaitanya Vundru, Prof. Xinhua Wu, Mr. Sheng Cao, Mr. Tom Jarvis and Mr. Simon Logsdail of the Monash Centre for Additive Manufacturing (MCAM) for their support and help during laser assisted deposition.
Author information
Authors and Affiliations
Contributions
S.P. performed the simulation and experimental work, analyzed the results and wrote the manuscript. R.S. conceived the idea. R.S. and W.Y. supervised the complete work., I.S., A.P. and M.R. supervised the experimental work. K.T. participated in the experimental work. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Paul, S., Singh, R., Yan, W. et al. Critical deposition height for sustainable restoration via laser additive manufacturing. Sci Rep 8, 14726 (2018). https://doi.org/10.1038/s41598-018-32842-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-32842-z
Keywords
This article is cited by
-
A Review on Effect of Cooling Rate on Metallurgical, Mechanical, Geometrical Characteristics and Defects of Laser Cladding Process
Lasers in Manufacturing and Materials Processing (2024)
-
Study on the Effect of Scanning Strategy on Residual Stress in Laser Additive Manufacturing with the Laser Ultrasound Technique
Experimental Mechanics (2022)
-
Development and Modeling of a Robotic Restoration System Based on Laser Directed Energy Deposition
Transactions of the Indian Institute of Metals (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.