Abstract
Comprehensive representation of nanoparticle dynamics is necessary for understanding nucleation and growth phenomena. This is critical in atmospheric physics, as airborne particles formed from vapors have significant but highly uncertain effects on climate. While the vapor–particle mass exchange driving particle growth can be described by a macroscopic, continuous substance for large enough particles, the growth dynamics of the smallest nanoparticles involve stochastic fluctuations in particle size due to discrete molecular collision and decay processes. To date, there have been no generalizable methods for quantifying the particle size regime where the discrete effects become negligible and condensation models can be applied. By discrete simulations of sub-10 nm particle populations, we demonstrate the importance of stochastic effects in the nanometer size range. We derive a novel, theory-based, simple and robust metric for identifying the exact sizes where these effects cannot be omitted for arbitrary molecular systems. The presented metric, based on examining the second- and first-order derivatives of the particle size distribution function, is directly applicable to experimental size distribution data. This tool enables quantifying the onset of condensational growth without prior information on the properties of the vapors and particles, thus allowing robust experimental resolving of nanoparticle formation physics.
Similar content being viewed by others
Introduction
Understanding the dynamics of nanoparticle populations is essential for probing nucleation, coalescence processes and phase transitions in various fields of fluid mechanics, soft matter physics and geosciences. Nanoparticle formation from condensable vapors is also a frequent phenomenon in the Earth’s atmosphere1. A substantial fraction of all airborne aerosol particles are estimated to originate from such gas-to-particle conversion2,3,4,5, but these estimates are highly sensitive to assumptions on (1) the formation mechanisms in different environments, and (2) the dynamics of the smallest nanoparticles (<5–10 nm in diameter)5,6. These questions are of central importance for the advancement of atmospheric physics: besides being a key component of air quality, aerosol particles have a potentially large, although highly uncertain, impact on clouds and climate7,8. As the smallest nanoparticles are easily lost from the air by removal processes, the early growth dynamics is a crucially important factor affecting particle survival to larger, climatically relevant sizes.
During the recent decade, experimental techniques measuring airborne nanoparticle concentrations down to the smallest molecular clusters of diameters of ca. 1–2 nm have been developed and deployed in laboratory and field9,10,11,12,13,14. While this is an important step forward, interpreting these observations is difficult due to unknown properties of the vapors and particles, namely the rate constants of the molecular collision and attachment (i.e. condensation), evaporation and coagulation processes. Evaporation rate constants, determined by the complex thermochemistry of the small particles, are the most challenging parameters to quantify, with uncertainties spanning up to orders of magnitude15,16,17,18.
Theoretical treatment of nanoparticle dynamics can be divided into (1) modeling the initial clustering with molecule-by-molecule models, and (2) describing the subsequent condensational growth assuming a macroscopic, continuous substance omitting stochastic collisions and evaporations of single molecules19,20. The initial cluster formation can occur via nucleation or barrierless clustering. In the former case, the particle evaporation frequency exceeds the collision frequency with vapor molecules at the smallest sizes, and stochastic fluctuations in particle size drive the growth until the collisions overcome evaporation at the critical size region19,21. Stochastic effects are likely non-negligible at the smallest sizes also for barrierless, collision-driven clustering22. However, due to the poorly known rate constants there has been no direct way to determine the particle sizes at which these effects become negligible. With no accurate knowledge on this limiting size range, experimentally observed size distributions are typically analyzed using continuous modeling frameworks from particle diameters of ca. 1–2 nm onward23,24,25,26,27. The validity of this assumption and the related errors have not been quantitatively addressed to date.
Reliably constraining the rate constants controlling observed nanoparticle formation phenomena is necessary for resolving the detailed physics and chemistry behind the process, and for predicting the size-dependent particle number. Assessing these parameters from experiments requires further development of sophisticated inverse modeling approaches26,28, and the first step for this is determining which type of physical model is suitable for the studied particle size range. The fundamental molecule-by-molecule approach cannot be expanded to very large sizes due to its vast computational burden and complexity, which increase drastically with increasing particle diameter. Accurately determining the threshold size for continuum growth is a key question, as it allows extending the simpler and computationally efficient continuous description down to as small sizes as possible. Here we present a simple, robust, and generalizable metric for quantifying the importance of stochastic vs. deterministic effects on nanoparticle populations, based on theoretical considerations of population dynamics. Simulations and experimental data in sub-10 nm size range confirm the validity and applicability of the approach. We show that the shape of the nanoparticle size distribution indicates the size regime below which stochastic effects cannot be omitted, with no need for prior knowledge of the related rate constants. Finally, we discuss the implications for interpretation of measurements and for prediction of airborne particle concentrations.
Results
Discrete and continuous descriptions of nanoparticle dynamics
The dynamics of an evolving nanoparticle population are fundamentally described by the discrete general dynamic equation (GDE)
Eq. (1) gives the time derivative of the number concentration Ci of particle i of a given molecular composition including all condensation, evaporation, particle coagulation and removal processes. The first summation includes molecular and coagulational collisions forming particle i, and the corresponding evaporations destroying it; the second summation corresponds to particle i colliding with vapor molecules and other particles j, and to evaporations resulting back to particle i. βi,j and γi+j → i,j are the collision and evaporation rate constants, respectively. The source term Qi normally applies only to vapor molecules, and the size-dependent sink rate constant Si to all molecules and particles. Generally, evaporation of only single vapor molecules is considered, as fissions are expected to be rare. Coagulation is negligible when particle concentrations are significantly lower than vapor concentrations, but becomes important when particle concentrations are increased due to high vapor sources, low sinks and/or suppressed evaporation.
The continuous form of the GDE is derived by transforming the concentration of discrete particle sizes into a continuous function of particle size and time. While the coagulation and removal terms of the continuous GDE are analogous to the discrete presentation, the condensation–evaporation terms are essentially different. In the discrete GDE, the attachment and evaporation of vapor molecules is described as
where subscript 1 refers to a single molecule. The continuous form of Eq. (2) is obtained via a Taylor expansion of C, β and γ around size i29,30. Including derivatives up to the second order gives the Fokker-Planck equation
where the continuous function c(i, t) is the concentration density per size interval. The first-order term, also called the drift term, describes the deterministic particle growth, governed by the driving force of condensation ∝ (βC1 − γ). The second-order term corresponds to diffusion in particle size space, driven by the stochastic molecular collisions and evaporations. Omitting the second-order term in Eq. (3) gives the standard continuous form, henceforth referred to as the continuous condensation description
A fundamental property of the continuous condensation equation is that it does not include stochastic effects: in Eq. (4), all particles of a given size i grow or shrink according to frequency βC1 − γ, and an initially monodisperse distribution always remains monodisperse. By contrast, the discrete condensation equation (Eq. (2)) and the Fokker-Planck equation (Eq. (3)) allow the stochastic widening of the size distribution, and describe both diffusion-driven nucleation and drift-driven growth.
As the studied particle size range increases, the GDE is more conveniently presented via particle diameter dp, and the distribution is described by the concentration density per diameter interval c′ = c × di/ddp. The condensational growth equation (Eq. (4)) becomes
where GRcond is the change rate of the particle diameter when stochastic effects are omitted. For an arbitrary number of condensing vapor species,
where mp and ρp are the mass and density of the particle of diameter dp, and the summation goes over the mass fluxes of vapors k of mass mk. Due to its apparent link to large-scale modeling and the thermochemical properties of the vapors, Eq. (6) is one of the key approaches used to interpret experimentally observed nanoparticle formation19,20,24,25. Coagulation and scavenging of particles by external surfaces, such as large aerosols in the atmosphere and chamber walls in the laboratory, can be accounted for when assessing GRcond from observations by applying the full GDE23,31. A fraction of vapors may also be bound to clusters of a few molecules, and the contribution of these clusters to the growth of larger particles can be included in GRcond.
Stochastic vs. deterministic effects on condensational growth
Here we simulate nanoparticle formation in sub-10 nm size regime by solving the discrete GDE including condensation, evaporation, coagulation and particle sinks (Eq. (1); see Methods). Possible particle-phase processes affecting particle chemistry are not included. We focus on situations where nucleation, condensation and evaporation are the main processes affecting particle formation, but include also cases where coagulation becomes significant. We use the discrete simulation data to evaluate standard data analysis approaches based on assuming continuous condensational growth. The default simulation conditions correspond to a chamber experiment26,32, and the molecules are representative of oxidized low-volatile organic compounds (LVOC), which are recognized as a major driver of atmospheric nanoparticle growth24,26,33,34,35. Complementary simulations are conducted including an extremely low-volatile compound (ELVOC). To treat the simulated particle concentrations similarly to measurable quantities, particles are grouped in size bins according to their mobility diameter, defined as dp,mass + 0.3 nm where dp,mass is the mass diameter36, with a bin width of 0.1 nm. Other measurement non-idealities, such as size-dependent detection efficiency and instrumental noise, are assumed to be corrected for.
To verify that the conclusions are independent of the simulation rate constants, additional simulations are performed using different compound properties and ambient conditions, and qualitatively and quantitatively different particle evaporation rates. The evaporation rates have a large impact on the size distribution dynamics, but quantifying these rates is extremely challenging: the classical Kelvin formula (Supplementary Eq. (S1)) is expected to give a qualitatively reasonable size dependence, as small molecular clusters are generally more prone to evaporation than larger nanoparticles due to their larger surface-to-volume ratio. However, the thermochemistry of these small complexes is affected by atom-scale phenomena such as the degree and patterns of hydrogen bonding and proton transfers, which are not expected to be similar to liquids and larger particles. The Kelvin formula is thus not considered to give accurate results for the smallest particle sizes. The most accurate method to assess the properties of small clusters is quantum chemistry37, but even the best quantum chemical methods involve high uncertainties stemming from, for instance, limitations in capturing the electron correlation especially for clusters of more than a couple of molecules. These issues may propagate to uncertainties of more than an order of magnitude in the evaporation rates15,16. Moreover, the available quantum chemical data is mainly for sulfuric acid and inorganic or organic basic species; clusters containing several oxidized organic molecules are too heavy for the current capacity of the methods. Therefore, we apply different evaporation rate profiles of a realistic order of magnitude: the evaporation rates are either approximated with the Kelvin formula (Supplementary Eq. (S1)), set to vary randomly while decreasing with particle size (Supplementary Eq. (S2)), or calculated from quantum chemical data for tests with representative acid–base systems. Details of all simulation set-ups and additional discussion are found in Supplementary Information.
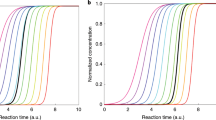
Figure 1a demonstrates the standard experimental analysis approach26,38,39. A vapor source is turned on in a laboratory chamber, and the appearance of subsequent particle sizes is observed as the size distribution builds up. Since the initial particle sizes do not form a clear growing mode, methods based on following the growth of such a mode40 cannot be used. Instead, each size bin dp is assigned an appearance time tapp at which the concentration in the bin reaches 50% of its maximum value. The apparent growth rate GRapp is defined as the slope of the (tapp, dp)-data
Panel (a): Simulated nanoparticle formation event at conditions of a chamber experiment for a representative LVOC species at a final vapor concentration of CLVOC = 2∙107 cm−3. White circles depict size bin appearance times tapp. Panel (b): GRapp determined from tapp (open circles; Eq. (7)), GRTREND determined by the TREND method (filled circles), and the condensational growth rate GRcond (Eq. (6)) with and without including collisions with very small clusters (solid and dashed black lines, respectively). The collision and evaporation frequencies from which GRcond is calculated are shown on the right-hand side y-axis.
This is compared to the continuous-GDE-based condensational growth rate GRcond (Eq. (6)), which here includes also clusters of a couple of molecules (see Methods), because in some simulation cases they may make a minor contribution to GRapp (see Fig. 1b). Figure 1b shows that at larger sizes (here dp ≳ 3 nm), GRapp approaches GRcond, but it is evident that at the smallest end of the size spectrum, GRapp and GRcond differ drastically as stochastics causes a fraction of particles of a given size to grow faster than the average rate GRcond. Specifically, in case of genuine nucleation where the first sizes are unstable against evaporation (here dp ≲ 2.3 nm), GRcond is negative for the initial sizes and approaches GRapp from below as the size increases. Predictions of condensation calculations can thus be expected to be inherently lower than the observed growth at the small end.
On the other hand, while the appearance-time-based method has become an established analysis approach, extracting growth rates from observations is not unambiguous. This applies especially to conditions at which particle sinks and coagulation have prominent effects on the distribution41. To confirm the conclusions, a recently developed growth rate analysis tool TREND31 that accounts for these effects was also applied. TREND determines the size- and time-resolved condensational growth rates by comparing regions of measured (here synthetic) and modeled particle size distributions (see Methods). The TREND results, also presented in Fig. 1b, show that also GRTREND is indeed higher than GRcond at the build-up of the initial sizes, similarly to GRapp.
Metric for determining the importance of stochastic effects
In real experiments, GRcond cannot be readily calculated due to uncertainties related to the properties and detection of various types of vapors17,18,26,27. However, fitting GRcond to reproduce GRapp outside the validity range of the continuous model (in Fig. 1b, below ca. 3 nm) results in erroneous conclusions on the condensational growth mechanisms. As stochastic effects are described by the second-derivative term in the Fokker-Planck equation (Eq. (3)), we propose that the first and second derivatives of the distribution c(i) or c′(dp) can be used to assess the sizes starting from which observed growth can be interpreted omitting stochastics. In Eq. (3), the derivatives are taken of fluxes, i.e. include both the particle concentration c and the rate constants βC1 and γ. While only c can be directly observed, a strong size-dependence in the rate constants is expected to propagate to a strong size-dependence in the concentration, and thus we hypothesize that studying the gradients of the distribution gives information on the size-diffusion effects (see also Supplementary Information Section 1.4).
Figure 2a shows the relative difference DGR between GRapp and GRcond together with the ratio of the second and first derivatives of the distribution (see Methods)
Panel (a): Relative difference DGR = abs[(GRcond − GRapp)/GRapp] between GRapp and GRcond (thin solid line), and the ratio ∂2:∂ of the second and first derivatives of the distribution at tapp (thick solid line) for LVOC at CLVOC = 2∙107 cm−3. Dotted grey line shows the difference between GRTREND and GRcond,vapor, where GRcond,vapor includes only vapor (see Methods). Black dashed line shows the particle stability as the ratio of the evaporation and condensation rates. Panel (b): The size at which GRapp and GRcond converge within 5%, and the size at which ∂2:∂ falls below 5% for different simulation cases (see Supplementary Information). The color and size of the markers depict the final vapor concentration Cvapor.
The differences between GRapp and GRcond become negligible at the sizes at which ∂2:∂ drops to a few percent. Furthermore, DGR and ∂ 2:∂ are generally of similar magnitude around the size of convergence, tentatively suggesting that ∂ 2:∂ gives a rough estimate of the magnitude of the error in GRcond around this size. Figure 2b compares the size around which GRapp and GRcond converge and the size around which ∂2:∂ becomes negligible for different simulation cases covering a variety of rate constant profiles and set-ups. The comparison is striking: the data falls around a 1:1 line, indicating that ∂2:∂ can be reliably used as a metric to quantify the limits of the continuum model.
The size range where GRapp and GRcond converge is largely affected by particle stability, which is depicted by the ratio of the evaporation and condensation frequencies in Fig. 2a. As the vapor concentration increases, the critical size region at which collisions overcome evaporation shifts towards smaller sizes. Since growth through stochastic collisions is more important when evaporation is relatively significant, also the convergence size of GRapp and GRcond becomes smaller at higher vapor concentrations (see data points corresponding to same set-up (symbol) but different vapor concentration (color and size) in Fig. 2b). Therefore, the ∂2:∂ analysis can be used to roughly fork the critical regime of clustering, which is connected to the overall thermodynamics of the initial particle formation20. However, DGR and ∂2:∂ are also affected by external conditions: the size distribution becomes steeper with increasing particle sink, shifting the convergence region towards slightly larger sizes (cf. the sink-free case (crosses) and the sink cases (diamonds, squares, and stars, in order of increasing sink) in Fig. 2b). In general, in addition to stochastics-driven growth, the early evolution of the distribution and the appearance of the smallest sizes may be significantly affected by particle sinks and vapor sources (see Supplementary Discussion Section 2.4). Simulations with evaporation rates modified to vary randomly around the values given by Supplementary Eq. (S1), or based on quantum chemistry, exhibit the same decreasing trend with respect to vapor concentration, but may differ somewhat more from the 1:1 line. This is due to non-smooth evaporation profiles, which cause larger fluctuations in DGR and to some extent also in ∂2:∂.
As GRapp does not allow separating the contribution of coagulation among the population, cases where coagulation becomes significant were examined with TREND as shown in Fig. 3 (see also Supplementary Discussion Section 2.2). In general, these include high vapor sources and the presence of strongly clustering compounds (here ELVOC), which lead to elevated particle concentrations. Regardless of coagulation, the general results are similar to GRapp: the condensational growth rate is distorted for the initial sizes (panels (a) and (b)), and the convergence size is smaller at higher vapor levels (panel (c)). TREND does not, however, give as high values for the small sizes as the appearance time method.
Panels (a) and (b): GRcond,vapor, GRTREND, and GRapp at particle appearance times tapp for LVOC and LVOC–ELVOC, respectively. Panel (c): The size at which GRTREND and GRcond,vapor converge within 5%, and the size at which ∂2:∂ falls below 5%. Note that GRcond,vapor is calculated here considering only single vapor molecules to be consistent with GRTREND.
It must be emphasized that the reasoning behind the metric ∂2:∂ is independent of the values and size dependences of the collision and evaporation rate constants β and γ. The rate constants of different dynamic processes shape the particle size distribution, creating gradients to the size-dependent concentration. If there is a strong size-dependence in the derivatives of the fluxes βC1c and γc between consecutive particle sizes (Eq. (3)), the simplified condensation equation (Eqs (4) and (5)) is not valid (see also Supplementary Information Section 1.4). Therefore, applying ∂2:∂ does not require prior knowledge of the rate constants, or of the physical and chemical processes affecting them. Due to its general considerations, the metric applies to different types of particle formation events and methods to deduce growth rates. This includes also e.g. the growth of a mode involving a seemingly sharp peak in the distribution. Even if a peak is distinct in terms of particle diameter, the growth can be described by continuous condensation if the second-order derivative around the peak is small in terms of molecular additions (Eqs (2, 3 and 11)). Finally, for the standard appearance time method, it can be noted that ∂2:∂ at each size is evaluated here at tapp, at which the bin reaches 50% of its maximum concentration. The growth rates and ∂2:∂ are, however, time-dependent, and thus DGR can vary with time (Supplementary Information Sections 2.2 and 2.3). Also other definitions of appearance time have been used, and Supplementary Fig. S8 demonstrates that DGR increases with decreasing threshold concentration for determining tapp. This is because the gradient ∂c/∂i varies more strongly at the beginning of the formation event.
Applying the metric ∂ 2:∂ on experimental data
The comprehensive set of test simulations was used to determine how to robustly capture the shape of a given particle size distribution c′(dp) and to obtain the metric ∂2:∂. Imperfect size resolution leads to a less smoothly behaving distribution, and the distribution may take different shapes depending on the conditions. The results indicate that an observed distribution can be used to quantify the size regime where particle growth mechanisms shift from stochastics-influenced clustering to deterministic, mass-flux-driven condensation by determining ∂2:∂ as follows (see Methods):
-
(1)
The size resolution at nanometer sizes needs to be fine enough. For the modeled molecule types, the resolution must be at least approximately 1.0 nm, but preferably higher.
-
(2)
The 1st and 2nd derivatives of the distribution c′(dp) with respect to particle diameter dp can be obtained as analytical derivatives of a 3rd order polynomial fit on the concentration, adjusting the fitted size range so that the function reliably captures the shape and gradients of the particle concentration. This was achieved using approximately ten adjacent data points for the model data.
-
(3)
Finally, ∂2:∂ is obtained from the 1st and 2nd derivatives by Eq. (11). This requires an estimate of the average molecular volume, but the results are not very sensitive to the accuracy of this estimate.
Figure 4 presents ∂2:∂ determined for an experimentally measured size distribution for particle formation from α-pinene oxidation products at the aerosol chamber of National Center for Atmospheric Research (NCAR)31. The metric exhibits a trend strikingly similar to the synthetic data: ∂2:∂ falls below a few percent at ca. 3–5 nm, indicating the onset of drift-driven condensational growth. While the chemical properties of the compounds present at the experiment remain to be quantified, Fig. 4 suggests to apply continuous-GDE-based models for sizes from ca. 5 nm upward for reliably resolving the particle growth mechanisms.
Discussion
The results raise important points regarding the interpretation of observations of very small particles. While continuous condensation models serve as a suitable first-order approximation, their limits and uncertainties have remained unquantified to date. The smallest particles require a discrete, molecule-by-molecule treatment32,42,43,44, and applying the continuous model outside of its validity range can lead to serious misinterpretations of observation data. However, extending the computationally efficient continuous description down to its lower limits is necessary due to the enormous computational burden of discrete modeling. For a mixture of vapors, the number of coupled differential equations in a discrete model rapidly increases to thousands and beyond even in the sub-5 nm size range. Finding an optimal and robust modeling approach is required for systematic and reliable assessment of particle evaporation rates and other key parameters from measured particle concentrations. This analysis is necessary for predicting the number and size distribution of newly-formed nanoparticles and their response to changes in ambient conditions. Correct modeling of the growth processes is relevant also for measurement techniques, e.g. for assessing the activation of particles to condensational growth inside condensation particle counters.
The presented results highlight the importance of accurately determining the threshold size for continuum approaches: fitting a deterministic condensation model to reproduce the observed apparent growth in situations where stochastics play a major role can lead to erroneous conclusions on (see e.g. the data in Fig. 1b) (1) the thermodynamic and other properties of the vapors and particles (when adjusting e.g. the Kelvin formula to match given data), (2) “missing” condensing species (the stochastic growth rate may be significantly higher than the deterministic prediction), and (3) the presence and magnitude of a Kelvin barrier at very small sizes26,38. The time evolution of the population at the initial sizes may be largely determined by stochastics-driven processes, particle sinks and the time dependence of vapor concentrations, and thus the size dependence of the apparent condensational growth rate is not necessarily related to particles growing past thermodynamic barriers. While the experimental growth rate may be quantified differently by different data analysis methods, these issues occur regardless of the method used. This is demonstrated e.g. in ref.41 by applying different methods to synthetic particle population data in the nanometer size range. Finally, the apparent growth may include also coagulation effects at elevated nanoparticle concentrations41,45. These need to be accounted for31, but the issue of stochastics vs. deterministic contributions on the growth due to vapor–particle exchange applies also in this case.
Within atmospheric sciences, correct representation of the initial growth is important not only for understanding local-scale particle pollution, but also for predictions of aerosol–cloud interactions which continue to be the single largest source of uncertainty in assessments of Earth’s radiation budget and global warming8. During atmospheric aerosol formation, small particles are lost to scavenging sinks due to their high mobility, but the loss rate decreases rapidly with increasing particle size. The early growth dynamics below ca. 5–10 nm are critical for aerosol number and size distribution, as faster growth leads to more particles reaching larger sizes20,46. The number of particles growing to ca. 50–100 nm, at which they can act as cloud condensation nuclei (CCN), is essential for the formation and properties of clouds. In large-scale models, production of particles of a few nanometers (often ≳ 3 nm) is commonly approximated based on assumed condensational growth by scaling the initial particle formation rate (at ca. 1 nm) by an exponential factor depending on the particle growth and loss rates6,46,47. At typical conditions, an overestimation of e.g. a factor of 2–5 in the growth rate of 1–3 nm particles results in an overestimation of a factor between ca. 2 and >>10 in the formation rate of >3 nm particles (see also Supplementary Discussion Section 2.5). The importance of these early growth stages on global aerosol and CCN concentrations has been demonstrated e.g. in ref.26 by atmospheric simulations assuming different parameterizations for the growth rate in the 1.7–3 nm size range: changing the parameterization resulted in up to 50% changes in the CCN concentrations. Misinterpretation of the apparent growth rate from e.g. laboratory data may thus lead to distorted assessments of the number, lifetime and impacts of newly-formed aerosol particles. This effect is expected to be particularly important for unpolluted regions which are sensitive to this secondary aerosol source48. This includes preindustrial conditions, which are an important source of uncertainty in the overall estimates on anthropogenic effects on clouds and climate6,49.
It can be noted that theoretical approaches other than the standard GDE-based-methods, such as Monte Carlo simulations50, can be applied to avoid the issues related to the continuum approximation. However, the GDE and especially the straight-forward continuum condensation rate calculations will undoubtedly remain a central tool to analyze measurements. The entire particle size range can be addressed by discrete-sectional GDE models, which include also coagulation and other dynamic processes. Furthermore, while the simulations of this work are in terms of measurable, dimensional quantities, GDE models can also be made non-dimensional for efficient probing of the parameter space51. The discrete-sectional models apply the discrete GDE for the smallest sizes and the continuous GDE for larger particles, once more highlighting the need to locate the size regime starting from which the continuous description is applicable.
We show that the onset of continuous condensational growth can be assessed based on an observed particle size distribution by using the ratio between the second- and first-order derivatives of the size distribution function as a metric. While the presented case studies address airborne nanoparticle formation, the rationale behind the metric applies to any physical and chemical systems involving particle formation and growth. The proposed tool gives direct information on the sizes at which the transition from discrete to continuous modeling can be done with reasonable accuracy, which (1) ensures correct interpretation of observations, and (2) enables reliable assessment of parameters controlling the particle formation process from experimental data.
Methods
Simulations based on the discrete GDE
The time evolution of the nanoparticle concentrations was simulated by solving the complete discrete GDE as given by Eq. (1), including collisions with and evaporations of vapor molecules, coagulation among the particles, and a sink reducing the vapor and particle concentrations. The collision rate constants βi,j were calculated as hard-sphere collision rates, and the evaporation rate constants γi+j → i,j were obtained as described in Supplementary Information Section 1. Particle fission was omitted. Details of the simulated compounds and simulation set-ups, and of the numerical solution method are found in Supplementary Information Section 1. To avoid unnecessary computational burden, the size distribution was truncated at ca. 5–10 nm depending on the chemical system, ensuring that the truncation size was beyond the sizes at which non-stochastic condensation begins to dominate.
GRapp based on the appearance times of different particle sizes
To analyze the data similarly to experiments, the apparent growth rate GRapp (Eq. (7)) was determined by applying linear fits on the (tapp, dp)-curve38,39,45. For each size bin, the fit included five adjacent data points centered at the bin. However, GRapp is not sensitive to the exact number of points included: including three points or simply taking the numerical derivative give similar, but slightly more scattered results.
GRcond calculated from molecular collision and evaporation rates
The continuous condensational growth rate GRcond was calculated according to Eq. (6), including in the mass flux also very small clusters in case that they were present at relatively high concentrations. The reason for this is that the concentrations of the smallest clusters consisting of only a couple of molecules may become non-negligible, and omitting them in the growth rates of larger particles leads to small underestimation of GRcond (Fig. 1b). For size-binned data, GRcond was determined by representing each bin with the particle size at the bin midpoint. For the LVOC–ELVOC mixture, the representative composition of a size bin was calculated as the weighted average over the compositions of all individual particles belonging to the bin.
The following approach was used to determine which small clusters are included in GRcond for each size bin: The collision frequencies βbinCbin of smaller bins with the given bin were compared to the collision frequency ∑βvaporCvapor of vapor molecules with the bin. The relative contribution of different smaller bins depends on the bin width; on the other hand, the particle concentration typically decreases as a function of size with the smallest sizes having clearly the highest concentrations. Therefore, all smaller size bins up to nbin,max were included in GRcond if the total collision frequency \(\,{\sum }_{1}^{{n}_{{\rm{bin}},{\rm{\max }}}}{\beta }_{{\rm{bin}}}{C}_{{\rm{bin}}}\) was at least 0.01 times the condensation frequency ∑βvaporCvapor, and including more bins in the sum had no further effect. It must be noted that this approach is applicable only if the coagulational growth involves solely the clustering of very small, vapor-like molecular clusters onto considerably larger particles. If self-coagulation among the studied particle size range is significant, the apparent growth cannot be described solely by mass flux calculations (Eq. (6)), but instead the full GDE must be applied. Therefore, simulation conditions that led to self-coagulation were excluded from the comparisons of GRapp and GRcond, and were analyzed by TREND instead.
GRTREND determined by the full-GDE-based analysis tool TREND
The details of the TREND method are found in ref.31. Briefly, the modeled distribution is calculated within TREND using as a starting point the measured (in this case synthetic) distribution at an earlier point in time. TREND solves the GDE for a given time interval and size resolution considering all quantifiable mechanisms that alter the aerosol size distribution, including coagulation and particle sinks. As a result, particle growth of any form, including both deterministic and stochastic contributions, remains the only unknown, and is determined by comparing fractions of the modeled and measured particle size distributions after the modeled time interval. The procedure starts at the largest particles of the modeled distribution and assigns size intervals containing a constant number of particles. This is repeated for the measured distribution and the corresponding size intervals containing the same number of particles are identified. Relating the count medium diameter of both intervals to each other allows assessing the growth rate, which may also be negative in case of particle shrinkage.
The analysis tool was adopted to the specifications of the synthetic molecular-resolution data. First, the toolkit was modified to accept the mass and number concentration data from the molecular-resolution model, converting them to size-binned concentration using a bin width of 2% of the corresponding lower bin limit. Second, only the largest 1%, or 10% in case of higher vapors source rates (4–5)∙104 cm−3s−1, of the particle size distribution were analyzed with the method. This is in order to avoid significantly limiting the size resolution of the TREND method, as the vast majority of the particles are contained within the first molecular clusters. However, note that all clusters except for the monomers are considered for simulating the aerosol dynamics, i.e. coagulation of the smallest molecular clusters is taken into account. The obtained growth rates GRTREND are thus compared to GRcond,vapor calculated considering only vapor monomers. It must be noted that as TREND considers size intervals instead of discrete molecule-by-molecule sizes, some differences in the description of coagulation compared to the accurate discrete model can be expected.
Determination of ∂ 2:∂
The gradients of the simulated discrete distribution can be straight-forwardly determined as numerical derivatives. In practice, molecular-resolution observations are not at present possible for arbitrary compounds, and instruments that are used to measure size-dependent particle concentrations classify the particles into size bins according to the mobility diameter. In addition, multi-compound systems may exhibit more than one parallel particle growth pathways, and thus following the growth molecule-by-molecule is not unambiguous even if molecular-resolution observations are available.
The metric ∂2:∂ (Eq. (8)) was thus determined for size-binned particle distributions c′(dp) by fitting a suitable function to the distribution. The reliability of this approach was tested by applying the fit to a molecular-resolution distribution, and comparing the obtained ratio ∂2:∂ of the second and first analytical derivatives of the fitted distribution to that determined from the numerical derivatives of the discrete distribution, ensuring that the fit is able to reproduce the gradients.
The evaluation of the fitting approach for ∂2:∂ was conducted as described below.
-
(1)
The numerical derivatives of c (in cm−3 molec.−1) at each discrete cluster size i0 (molec.) were determined according to standard numerical differentiation approaches as
$${\frac{\partial c}{\partial i}|}_{i={i}_{0}}=\frac{c({i}_{0}+{\rm{\Delta }}i)-c({i}_{0}-{\rm{\Delta }}i)}{2{\rm{\Delta }}i}$$(9)and
$${\frac{{\partial }^{2}c}{\partial {i}^{2}}|}_{i={i}_{0}}=\frac{c({i}_{0}+{\rm{\Delta }}i)-2c({i}_{0})+c({i}_{0}-{\rm{\Delta }}i)}{{({\rm{\Delta }}i)}^{2}},$$(10)where Δi = one molecule.
-
(2)
The number density c(i) with respect to the molecular content of the particles was converted to the number density c′(dp) with respect to particle diameter as c′ = c × di/ddp. A third-order polynomial function was fit to the base-10 logarithm of c′ around the size of interest as demonstrated in Supplementary Fig. S2a, and ∂c′/∂dp and ∂2c′/∂dp2 were obtained as analytical derivatives of the fit. The fit was applied piecewise around each particle size or size bin, as finding a function that is capable of reproducing the shape of a wider size range does not seem possible. For the limited size ranges, a 3rd order polynomial function is able to capture typical trends in the concentration density, including monotonously decreasing or increasing behavior, decrease or increase with a plateau, and local minima and maxima.
-
(3)
The derivatives of the fit c′(dp) give the changes in the number density and its slope per unit diameter. In order to assess the gradients of the distribution with respect to molecular additions, corresponding to Eqs (2–4), the ratio ∂2:∂ of the derivatives of c with respect to i was obtained from the derivatives of c′ with respect to dp as
In Eq. (11), ddp/di and its derivatives with respect to dp are calculated from the molecular volume assuming spherical particles.
Supplementary Fig. S2b shows that the fit-based ∂2:∂ reproduces the numerical-derivative-based results very well, indicating that the shape of the distribution can be reliably captured by the fit. In addition, the hypothesis that the relative importance of the drift and diffusion terms (\(-\,\frac{\partial }{\partial i}[(\beta {C}_{1}-\gamma )c]\) and \(\frac{1}{2}\frac{{\partial }^{2}}{\partial {i}^{2}}[(\beta {C}_{1}+\gamma )c]\), respectively) in Eq. (3) is reflected in the derivatives of the distribution ∂c/∂i and ∂2c/∂i2 was verified by comparing the ratio of the terms to the ratio of the derivatives, i.e. ∂2:∂, for representative simulation cases, as discussed in Supplementary Information Section 1.4.
Effect of size resolution on ∂ 2:∂
Sub-3 nm particle concentrations are often measured with diethylene-glycol-based particle counters, such as Particle Size Magnifier (PSM)13. We have thus chosen to by default bin the simulation data according to the best size resolution reported for PSM, namely 0.1 nm45, and tested the sensitivity of ∂2:∂ to the size resolution by using different bin widths between 0.2 and 1.0 nm. Supplementary Fig. S4a demonstrates the fitting approach applied on size-binned data. As the bins may contain different numbers of particles, the binned distribution is less smooth especially towards the smallest sizes. However, the shape of the distribution can still be represented by the fit, as shown in Supplementary Fig. S4b. ∂2:∂ obtained with bin widths of Δdp = 0.5 and 1.0 nm differ more from the accurate result, but reproduce the correct trend, order of magnitude, and size around which ∂2:∂ decreases to a few percent. It must be noted that for smaller molecules, a given bin Δdp contains more discrete particle compositions, and the resolution in terms of the molecular content becomes lower. However, for the largest bin widths studied, the bins contain up to tens or even hundreds of particle sizes, demonstrating that the overall behavior of ∂2:∂ is not distorted by an imperfect size resolution.
Data Availability
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.
References
Kulmala, M. et al. Formation and growth rates of ultrafine atmospheric particles: A review of observations. J. Aerosol Sci. 35, 143–176 (2004).
Spracklen, D. V. et al. Contribution of particle formation to global cloud condensation nuclei concentrations. Geophys. Res. Lett. 35 (2008).
Yu, F. & Luo, G. Simulation of particle size distribution with a global aerosol model: contribution of nucleation to aerosol and CCN number concentrations. Atmos. Chem. Phys. 9, 7691–7710 (2009).
Merikanto, J., Spracklen, D. V., Pringle, K. J. & Carslaw, K. S. Effects of boundary layer particle formation on cloud droplet number and changes in cloud albedo from 1850 to 2000. Atmos. Chem. Phys. 10, 695–705 (2010).
Kerminen, V.-M. et al. Cloud condensation nuclei production associated with atmospheric nucleation: a synthesis based on existing literature and new results. Atmos. Chem. Phys. 12, 12037–12059 (2012).
Gordon, H. et al. Reduced anthropogenic aerosol radiative forcing caused by biogenic new particle formation. Proc. Natl. Acad. Sci. USA 113, 12053–12058 (2016).
Boucher, O. et al. Clouds and aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) 571–658 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013).
Myhre, G. et al. Anthropogenic and natural radiative forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) 659–740 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013).
Jiang, J. et al. First measurements of neutral atmospheric cluster and 1-2 nm particle number size distributions during nucleation events. Aerosol. Sci. Technol. 45, ii–v (2011).
Vanhanen, J. et al. Particle size magnifier for nano-CN detection. Aerosol Sci. Technol. 45, 533–542 (2011).
Kirkby, J. et al. Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation. Nature 476, 429–433 (2011).
Bianchi, F. et al. New particle formation in the free troposphere: a question of chemistry and timing. Science 352, 1109–1112 (2016).
Kontkanen, J. et al. Measurements of sub-3 nm particles using a particle size magnifier in different environments: from clean mountain top to polluted megacities. Atmos. Chem. Phys. 17, 2163–2187 (2017).
Stolzenburg, D., Steiner, G. & Winkler, P. M. A DMA-Train for precision measurement of sub-10 nm aerosol dynamics. Atmos. Meas. Tech. 10, 1639–1651 (2017).
Myllys, N., Elm, J., Halonen, R., Kurtén, T. & Vehkamäki, H. Coupled cluster evaluation of the stability of atmospheric acid-base clusters with up to 10 molecules. J. Phys. Chem. A 120, 621–630 (2016).
Elm, J. et al. Formation of atmospheric molecular clusters consisting of sulfuric acid and a C8H12O6 tricarboxylic acid. Phys. Chem. Chem. Phys. 19, 4877–4886 (2017).
Kurtén, T. et al. α-pinene autoxidation products may not have extremely low saturation vapor pressures despite high O:C ratios. J. Phys. Chem. A 120, 2569–2582 (2016).
Barsanti, K. C., Kroll, J. H. & Thornton, J. A. Formation of low-volatility organic compounds in the atmosphere: recent advancements and insights. J. Phys. Chem. Lett. 8, 1503–1511 (2017).
Zhang, R., Khalizov, A., Wang, L., Hu, M. & Xu, W. Nucleation and growth of nanoparticles in the atmosphere. Chem. Rev. 112, 1957–2011 (2012).
Vehkamäki, H. & Riipinen, I. Thermodynamics and kinetics of atmospheric aerosol particle formation and growth. Chem. Soc. Rev. 41, 5160–5173 (2012).
Ford, I. J. Statistical mechanics of nucleation: A review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 218, 883–899 (2004).
Clement, C. & Wood, M. Equations for the growth of a distribution of small physical objects. Proceedings of the Royal Society of London A 368, 521–546 (1979).
Kuang, C. et al. Size and time-resolved growth rate measurements of 1 to 5 nm freshly formed atmospheric nuclei. Atmos. Chem. Phys. 12, 3573–3589 (2012).
Riipinen, I. et al. The contribution of organics to atmospheric nanoparticle growth. Nat. Geosci. 5, 453–458 (2012).
Yli-Juuti, T. et al. Model for acid-base chemistry in nanoparticle growth (MABNAG). Atmos. Chem. Phys. 13, 12507–12524 (2013).
Tröstl, J. et al. The role of low-volatility organic compounds in initial particle growth in the atmosphere. Nature 533, 527–531 (2016).
Chuang, W. K. & Donahue, N. M. Dynamic consideration of smog chamber experiments. Atmos. Chem. Phys. 17, 10019–10036 (2017).
Kupiainen-Määttä, O. A Monte Carlo approach for determining cluster evaporation rates from concentration measurements. Atmos. Chem. Phys. 16, 14585–14598 (2016).
Gelbard, F. & Seinfeld, J. H. The general dynamic equation for aerosols. Theory and application to aerosol formation and growth. J. Colloid Interface Sci. 68, 363–382 (1979).
Holten, V. & Van Dongen, M. E. H. Comparison between solutions of the general dynamic equation and the kinetic equation for nucleation and droplet growth. J. Chem. Phys. 130, 014102 (2009).
Pichelstorfer, L. et al. Resolving nanoparticle growth mechanisms from size- and time-dependent growth rate analysis. Atmos. Chem. Phys. 18, 1307–1323 (2018).
Kürten, A., Williamson, C., Almeida, J., Kirkby, J. & Curtius, J. On the derivation of particle nucleation rates from experimental formation rates. Atmos. Chem. Phys. 15, 4063–4075 (2015).
Winkler, P. M. et al. Identification of the biogenic compounds responsible for size-dependent nanoparticle growth. Geophys. Res. Lett. 39 (2012).
Riccobono, F. et al. Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles. Science 344, 717–721 (2014).
Ehn, M. et al. A large source of low-volatility secondary organic aerosol. Nature 506, 476–479 (2014).
Larriba, C. et al. The mobility-volume relationship below 3.0 nm examined by tandem mobility-mass measurement. Aerosol Sci. Technol. 45, 453–467 (2011).
Kurtén, T. & Vehkamäki, H. Investigating atmospheric sulfuric acid-water-ammonia particle formation using quantum chemistry. Adv. Quantum Chem. 55, 407–427 (2008).
Kulmala, M. et al. Direct observations of atmospheric aerosol nucleation. Science 339, 943–946 (2013).
Lehtipalo, K. et al. Methods for determining particle size distribution and growth rates between 1 and 3 nm using the Particle Size Magnifier. Boreal Environ. Res. 19, 215–236 (2014).
Kulmala, M. et al. Measurement of the nucleation of atmospheric aerosol particles. Nature Protocols 7, 1651–1667 (2012).
Li, C. & McMurry, P. H. Errors in nanoparticle growth rates inferred from measurements in chemically reacting aerosol systems. Atmos. Chem. Phys. 18, 8979–8993 (2018).
Lehtinen, K. E. J. & Kulmala, M. A model for particle formation and growth in the atmosphere with molecular resolution in size. Atmos. Chem. Phys. 3, 251–257 (2003).
Olenius, T., Riipinen, I., Lehtipalo, K. & Vehkamäki, H. Growth rates of atmospheric molecular clusters based on appearance times and collision-evaporation fluxes: growth by monomers. J. Aerosol Sci. 78, 55–70 (2014).
Olenius, T., Kupiainen-Määttä, O., Lehtinen, K. E. J. & Vehkamäki, H. Extrapolating particle concentration along the size axis in the nanometer size range requires discrete rate equations. J. Aerosol Sci. 90, 1–13 (2015).
Lehtipalo, K. et al. The effect of acid-base clustering and ions on the growth of atmospheric nano-particles. Nat. Commun. 7, 11594 (2016).
Kerminen, V.-M. & Kulmala, M. Analytical formulae connecting the ‘real’ and the ‘apparent’ nucleation rate and the nuclei number concentration for atmospheric nucleation events. J. Aerosol Sci. 33, 609–622 (2002).
Lehtinen, K. E. J., Dal Maso, M., Kulmala, M. & Kerminen, V.-M. Estimating nucleation rates from apparent particle formation rates and vice versa: Revised formulation of the Kerminen-Kulmala equation. J. Aerosol Sci. 38, 988–994 (2007).
Spracklen, D. V. et al. The contribution of boundary layer nucleation events to total particle concentrations on regional and global scales. Atmos. Chem. Phys. 6, 5631–5648 (2006).
Carslaw, K. S. et al. Large contribution of natural aerosols to uncertainty in indirect forcing. Nature 503, 67–71 (2013).
Khalili, S., Lin, Y., Armaou, A. & Matsoukas, T. Constant number Monte Carlo simulation of population balances with multiple growth mechanisms. AIChE J. 56, 3137–3145 (2010).
McMurry, P. H. & Li, C. The dynamic behavior of nucleating aerosols in constant reaction rate systems: dimensional analysis and generic numerical solutions. Aerosol Sci. Technol. 51, 1057–1070 (2017).
Acknowledgements
T.O. and I.R. kindly thank Formas project 2015-749 and Knut and Alice Wallenberg foundation (academy fellowship AtmoRemove) for funding. D. S. and P. M. W. acknowledge support by the European Research Council under the European Community’s 7th Framework Programme (FP7/2007 – 2013), ERC grant agreement No. 616075. Prof. Neil M. Donahue is acknowledged for useful discussions.
Author information
Authors and Affiliations
Contributions
T.O. planned the work and performed the discrete simulations and condensation rate calculations. L.P. and D.S. conducted the TREND modeling and provided the experimental data. I.R., K.E.J.L. and P.M.W. participated in discussion of the results and interpretation of the data. T.O. wrote the paper with contributions from L.P., D.S. and I.R. and all co-authors read and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Olenius, T., Pichelstorfer, L., Stolzenburg, D. et al. Robust metric for quantifying the importance of stochastic effects on nanoparticle growth. Sci Rep 8, 14160 (2018). https://doi.org/10.1038/s41598-018-32610-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-32610-z
Keywords
This article is cited by
-
Role of gas–molecular cluster–aerosol dynamics in atmospheric new-particle formation
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.