Abstract
The recent observation of extremely large magnetoresistance (MR) in the transition-metal dichalcogenide MoTe2 has attracted considerable interest due to its potential technological applications as well as its relationship with novel electronic states predicted for a candidate type-II Weyl semimetal. In order to understand the origin of the MR, the electronic structure of MoTe2−x (x = 0.08) is systematically tuned by application of pressure and probed via its Hall and longitudinal conductivities. With increasing pressure, a monoclinic-to-orthorhombic (1 T′ to Td) structural phase transition temperature (T*) gradually decreases from 210 K at 1 bar to 58 K at 1.1 GPa, and there is no anomaly associated with the phase transition at 1.4 GPa, indicating that a T = 0 K quantum phase transition occurs at a critical pressure (Pc) between 1.1 and 1.4 GPa. The large MR observed at 1 bar is suppressed with increasing pressure and is almost saturated at 100% for P > Pc. The dependence on magnetic field of the Hall and longitudinal conductivities of MoTe2−x shows that a pair of electron and hole bands are important in the low-pressure Td phase, while another pair of electron and hole bands are additionally required in the high-pressure 1 T′ phase. The MR peaks at a characteristic hole-to-electron concentration ratio (nc) and is sharply suppressed when the ratio deviates from nc within the Td phase. These results establish the comprehensive temperature-pressure phase diagram of MoTe2−x and underscore that its MR originates from balanced electron-hole carrier concentrations.
Similar content being viewed by others
Introduction
Transition-metal dichalcogenides (TMDs) MX2 have attracted interest because they display diverse ground states, such as charge density wave and superconductivity. Furthermore, they are considered as candidate type-II Weyl semimetals that could be controlled by tuning the dimensionality or the d-electron count of the transition metal M, providing a rich avenue to explore novel electronic states1,2,3,4,5. Semiconducting behavior is reported with an energy gap of 1 eV for group-6 TMDs with d2 configuration (M = Mo, W; X = S, Se, Te). Extremely large magnetoresistances (MR) have been reported in TMDs, including Dirac and Weyl semimetals, where topologically protected states and/or perfect compensation of electron and hole carriers are considered to be the origin of the anomalous MR6,7,8,9,10,11.
MoTe2 can exist in one of two polymorphs: a 2H-MoTe2 and a distorted 1 T form12,13,14. The 2H-MoTe2 phase is semiconducting. In this structure Mo is surrounded by a trigonal prism of Te atoms and the Te-Mo-Te layers are coupled by weak van der Waals forces along the crystalline c-axis, making it easy to exfoliate. In contrast, the distorted 1 T or 1 T′ phase is metallic and the Mo atoms are octahedrally surrounded by Te atoms and slightly translated from the center, resulting in zig-zag Mo chains along the b-axis. Here, the electrical conduction mainly originates from the bands formed from the Mo d-levels15,16. The octahedral or trigonal antiprismatic structure of monoclinic 1 T′-MoTe2, with space group P21/m illustrated in Fig. S1 of Supplementary Information, possesses inversion symmetry with the center located between Mo atoms in the chain direction12,17,18,19. Non-trivial Z2-band topology in 1 T′-MoTe2 and strong spin-orbit coupling present a unique opportunity for the realization of topological quantum devices1,2. The low-T orthorhombic Td phase, however, lacks inversion symmetry and the observation of Fermi arcs in the surface state is consistent with a type-II Weyl semimetal phase in MoTe2. Recent quantum oscillation measurements, however, revealed disagreement with the bulk Fermi surfaces predicted by band calculations, raising questions about the existence of Weyl points in the low-T Td phase of MoTe2−x20,21. Understanding the origin of the extremely large magnetoresistance (XMR) reported in MoTe2−x, therefore, is important for clarifying the realization of type-II Weyl semimetals as well as its possible technological applications22,23.
Here we report the effects of pressure on large magnetoresistance and the Hall and longitudinal conductivities in a single crystal of the transition-metal dichalcogenide MoTe2−x. Applied pressure suppresses the 1 T′-to-Td phase transition temperature (T*) from 210 K at 1 bar to 58 K at 1.1 GPa and there is no signature of T* at 1.4 GPa, indicating that a T = 0 K structural quantum phase transition occurs at a critical pressure Pc between 1.1 and 1.4 GPa. Concomitant with the suppression of T*, the superconducting transition temperature (Tc) sharply increases with pressure, from 0.4 K at 0.4 GPa to 2.8 K at 1.4 GPa near Pc. On the other hand, Tc gradually increases in the high-pressure 1 T′ phase (P > Pc) and the Meissner fraction becomes significant, indicating that superconductivity is of bulk nature in the Td phase of MoTe2. Large MR observed at 1 bar is strongly suppressed with increasing pressure and is almost saturated at 100% for P > Pc. The dependence on magnetic field of the Hall and longitudinal conductivities show that a pair of electron and hole bands are dominant in the Td phase, but another pair of electron and hole bands are additionally required in the 1 T′ phase, indicating a subtle change in the Fermi surface topology at Pc. The MR peaks sharply at a characteristic hole-to-electron concentration ratio (nc ≈ 0.82) and is suppressed as the ratio moves away from nc in the Td phase. These results establish the comprehensive temperature-pressure phase diagram of MoTe2 and underscore that the origin of its MR is the balanced electron-hole carrier concentration.
Results
The upper panel of Fig. 1 representatively displays the electrical resistivity (ρb) of MoTe2−x on a semi-logarithmic scale for current applied along the Mo-chain direction (b-axis) at ambient pressure. ρb decreases with decreasing temperature, characteristic of metallic behavior. The residual resistivity ratio (RRR) is 147, which is higher than 35 reported in ref.16, but is lower than 2000, which was obtained by the authors of ref.20. The amount of Te vacancies x has been shown to be pertinent to the RRR of MoTe2−x as well as Tc, e.g., RRR is 13 and Tc is 2.1 K for x = 0.13 (ref.24). Energy-dispersive spectroscopy (EDS) results show that the Te deficiency is x = 0.08 for the crystals that we study in this communication. A kink-like feature in ρb that appears near 210 K (= T*) is consistent with a structural phase transition from the monoclinic (1 T′) to orthorhombic phase (Td), where the monoclinic angle β changes from 93.55° to 90°25,26. A sharp peak in dρb/dT (red line), as shown in the right ordinate, clearly demarcates the structural phase transition near 210 K.
Transport property of MoTe2−x as a function of temperature. Upper panel: Electrical resistivity for current along the b-axis (=ρb) is shown on a semilogarithmic scale on the left ordinate. The first derivative of ρb with respect to temperature, dρb/dT, is displayed on the right ordinate. There are two features in dρb/dT: a sharp peak at 210 K, marked by the dashed line, and a broad peak at around 60 K, marked by the dash-dotted line. Regimes I, II, and III are demarcated by the peaks in dρb/dT. Middle panel: The Hall coefficient RH (the ratio of transverse resistivity dividied by applied field) is shown as a function of temperature, where squares, circles, and triangles correspond to RH for fields of 0, 2, and 9 T, respectively. Lower panel: Electron (Ne) and hole (Nh) carrier densities are plotted as a function of temperature. Hall and longitudinal resistivity measurements were used to estimate the carrier density, as detailed in Fig. S2 of the Supplementary Information.
The Hall coefficient of MoTe2−x at ambient pressure (RH) is plotted as a function of temperature for fields of 0, 2, and 9 T in the middle panel of Fig. 1, where the magnetic field is applied along the c-axis and the Hall voltage is measured across the a-axis. RH at room temperature is −3.65 × 10−4 cm3/C, indicating that electron carriers predominantly contribute to the transport. Analyses of the field dependence of the longitudinal (ρxx) and transverse resistivity (ρxy) show that the electron and hole carrier densities at room temperature are 1.36 × 1019 cm−3 and 2.1 × 1017 cm−3, respectively (see Fig. S2, Supplementary Information). The absolute value of RH gradually increases with decreasing temperature and plateaus below 210 K, the critical temperature T* where MoTe2−x goes through a structural phase transition from 1 T′ to Td phases. With further decrease of temperature, RH starts to decrease again below 60 K, the temperature at which a broad peak in dρb/dT appears, and the electron and hole carrier densities, Ne and Nh, respectively, become similar. We note that the strong change of the carrier density, the nearly compensated electron-hole carriers (Ne/Nh ≈ 1) at low temperatures, and a broad peak in the specific heat divided by temperature (C/T) are consistent with a Lifshitz-like transition in the candidate Weyl semimetal Td-phase of MoTe2−x24,27,28,29,30.
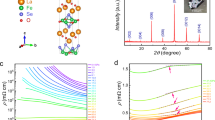
Figure 2(a) shows the pressure evolution of the electrical resistivity of MoTe2−x as a function of temperature. ρb at room temperature progressively decreases with increasing pressure at a rate of −7.9 ± 0.6 µΩ cm/GPa because of the increased overlap between adjacent Mo orbitals. The structural transition temperature T*, which was assigned to the peak in dρ/dT as a function of T, decreases to 58 K at 1.1 GPa and is completely suppressed to 0 K below 1.4 GPa, indicating that a T = 0 K structural quantum phase transition (=Pc) is located between 1.1 and 1.4 GPa. The temperature dependence of dρ/dT also shows a clear demarcation across Pc: the resistivity slope is strongly suppressed in the low-pressure regime (P < Pc), but it is gradually suppressed in the high-pressure regime (P > Pc). The low-T resistivity slopes collapse on top of each other in the two separate regimes, reflecting two different crystalline structures of Td and 1 T′ in the low and high-pressure regime, respectively. The critical pressure Pc observed in this work is similar to that in ref.31 but is much lower than that in refs16,32, which may be ascribed to the degree of Te vacancies that is relevant to Tc value at ambient pressure24. More systematic study, however, is necessary to understand the precise relationship between Tc and Pc.
Pressure evolution of electrical resistivity and temperature-pressure phase diagram (a) Pressure evolution of the electrical resistivity of MoTe2−x for current along the b-axis, ρb, plotted as a function of temperature. (b) First temperature derivative of the resistivity, dρb/dT, plotted versus temperature for several representative pressures. Arrows mark the peak in the slope where the monoclinic-to-orthorhombic structural phase transition occurs. (c) Electrical resistivity of MoTe2−x near the superconducting phase transition temperature Tc. (d) Temperature-pressure phase diagram of MoTe2−x, where Td and 1 T′ represent the orthorhombic and monoclinic structure, respectively. Squares and circles represent the structural transition temperature T* and SC transition temperature Tc, respectively. Open and closed circles were determined from the onset and zero-resistance temperature, respectively, of the SC phase transition.
Being commensurate with the suppression of T*, a superconducting (SC) state is induced and enhanced with increasing pressure, as shown in Fig. 2(c). The onset temperature of the SC phase transition, Tc,on, is 0.9 K at ambient pressure and gradually increases with pressure, developing a smooth dome shape over the whole pressure range. In contrast, a zero-resistance SC state is not observed down to 0.25 K at ambient pressure but appears at 0.47 K and 0.4 GPa. As pressure increases further, the transition temperature Tc sharply increases and becomes similar to Tc,on above Pc. As summarized in the temperature-pressure phase diagram in Fig. 2(d), the large difference between Tc,on and Tc in the Td phase disappears in the 1 T′ monoclinic phase, indicating that the pressure-induced SC state of MoTe2−x in the Td phase is not a bulk property. Substantial differences between Tc,on and Tc have been often observed when another competing phase coexists with superconductivity, for example in the quantum critical compound CeRhIn533 or in BiS2-based superconductors34. Supporting this conclusion, the Meissner effect in the magnetic susceptibility is negligible at low pressures, but it is significant for pressures higher than Pc (see Fig. S3, Supplementary Information). We note that recent neutron scattering experiments reported coexistence of Td and 1 T’ phases at moderate pressures below Pc (ref.35).
Figure 3(a) shows a MR contour plot of MoTe2−x at 9 T in the temperature-pressure plane. The large MR centered on the low-pressure and low-temperature regime is gradually suppressed with increasing temperature and pressure. Figure 3(b) shows the pressure dependence of the isothermal MR at 9 T for representative temperatures of 2, 10, 20, and 40 K. The large MR at 2 K is rapidly suppressed with increasing pressure and is almost saturated at 100% near Pc. The pressure dependence of MR at higher temperatures is similar to that at 2 K, showing a disparate behavior across Pc: rapid suppression with pressure in the Td phase, but saturation or slight upturn in the 1 T′ phase. As shown in Fig. 3(c), the pressure dependence of the Hall coefficient (RH) also shows different behaviors across Pc. At low pressures, RH is negative and becomes more prominent as temperature falls, indicating that the contribution from electron carriers is more prominent than that from hole carriers. Initially, the absolute value of RH decreases rapidly with pressure but is almost flat or changes gradually at higher pressures (P > Pc) – see Fig. S4, Supplementary Information. The pressure dependence of RH is more distinctive in the second pressure derivative (d2RH/dP2), as shown in Fig. 3(d). In the low-pressure regime (P < Pc), curvature of the Hall coefficient is negative at high temperatures in the 1 T′ phase and is positive at low temperatures in the Td phase; whereas, in the high-pressure regime (P > Pc), the curvature is almost negligible for both temperature regimes of the 1 T′ phase.
Pressure dependences of MR and Hall coefficients. (a) Three-dimensional contour of magnetoresistance (MR) of MoTe2 at 9 T plotted in the temperature-pressure plane. Blue color indicates the highest MR. The hashed area marks the critical pressure Pc, where the Td-to-1T′ structural transition occurs. (b) Isothermal magnetoresistance at 9 T plotted as a function of pressure for several representative temperatures. The MR saturates at pressures above Pc. (c) Hall coefficients at 2 T plotted as a function of pressure for several representative temperatures. (d) The second pressure derivatives of the Hall coefficients from (c) plotted as a function of pressure at 10, 40, 100, 200, and 300 K. There are disparate behaviors across Pc.
Discussion
The pressure-induced suppression of the large MR and the disparate curvature of the Hall coefficient RH across Pc indicate that electronic structure is important to the anomalous MR behavior in the Td phase of MoTe2. In order to probe the pressure-driven change in electronic structure, the dependence on magnetic field of the transverse (σxy) and longitudinal (σxx) conductivities was measured and analyzed using various multi-band models, as shown in Fig. 4(a,b), respectively. For clarity, low-pressure data in the Td phase are plotted in the left panel and high-pressure data in the 1 T′ phase are in the right panel. A two-band isotropic model, as described by the solid lines, reasonably explains the Hall and transverse conductivities in the Td phase (P < Pc). At higher pressures (P > Pc), however, the field dependence of σxy deviates significantly from the two-band model, indicating a change in the electronic structure in the 1 T′ phase. As shown in Fig. S5 in the Supplementary Information, simulations of three-band models do not fit σxy in the high-pressure 1 T′ phase either. Dashed lines in Fig. 4(a,b) are simulations of a four-band model, which reasonably explains both σxy and σxx, indicating that the effective two bands in the Td phase evolve into four bands in the 1 T′ phase.
Pressure dependences of Hall and longitudinal conductivities of MoTe2 at 2 K are plotted as a function of magnetic field in (a,b), respectively. Conductivities for selected pressures in the Td and 1 T′ phases are representatively shown in the left and right panels, respectively. Effective two- and four-band models are simulated to understand the field dependence of the conductivities and plotted as solid and dotted lines, respectively. (c) Top (bottom) panel: Electron and hole carrier densities (mobilities) obtained from the four-band simulations are plotted as a function of pressure. Nei (μei) and Nhi (μhi) represent, respectively, electron and hole carrier densities (mobilities), and the subscript i is the band index. The hashed area represents the critical pressure at low temperatures where the Td-to-1T′ transition occurs. (d) MR plotted as a function of the hole-electron concentration ratio, Nh/Ne. Red squares represent the pressure-tuned data at 2 K, while blue diamonds represent the temperature-tuned data at ambient pressure.
Figure 4(c) plots the pressure evolution of the carrier concentrations of MoTe2 at 2 K, which are obtained from simulations of the effective four-band model36:
where \({n}_{e,i}\)\(({\mu }_{e,i})\) and \({n}_{h,j}\)\(({\mu }_{h,j})\) are ith electron and jth hole carrier densities (mobilities), respectively. In the Td phase (P < Pc), it is effectively a two-band model because the carrier densities for the second electron (e2) and hole (h2) bands are negligible. At ambient pressure and 2 K, the carrier densities are 1.06 × 1019 and 0.93 × 1019 cm−3 for the first electron (e1) and hole (h1) bands, respectively, showing that they almost compensate each other. At 0.5 GPa, both e1 and h1 carrier densities are enhanced to 1.62 × 1019 and 1.70 × 1019 cm−1, respectively, but the carrier density ratio between e1 and h1 is reversed. With further increasing pressure, up to the highest measured pressure of 2.4 GPa, both carrier densities increase gradually. The additional two bands, in contrast, are not negligible anymore in the high-pressure 1 T′ phase (P > Pc). The carrier concentrations are 3.21 × 1018 and 2.38 × 1018 cm−3 at 1.6 GPa for the e2 and h2 bands, respectively, which accounts for 8.4% of Ne1 and 4.2% of Nh1 at this pressure. The evolution of the carrier densities is plotted in the pressure-temperature plane in Fig. S6, Supplementary Information. As shown in the bottom panel of Fig. 4(c), the mobilities of e1 and h1 bands gradually decrease with pressure, while those of the minority bands (e2 and h2) sharply increase above Pc and become larger than the mobilities of the major bands.
Electronic band structure calculations in the Td and pressure-induced 1 T′ phases were performed via the WIEN2k package with the full-potential linearized augmented plane-wave method and spin-orbit coupling. As shown in Fig. 5, two major pockets (one electron and one hole) and two minor pockets (one electron and one hole) exist along the X-Γ-Y direction in the Brillouin zone. The Fermi surfaces of the four pockets are enlarged when the structural change occurs from the Td to the 1 T′ phase. In the Td phase (P < Pc), two major pockets contribute to the anomalously large MR and other physical properties, while the two minor pockets become important in the 1 T′ phase (P > Pc). These results are consistent with the analysis of the pressure dependence of the Hall and longitudinal conductivities, underlining that the change in electronic structure plays a critical role in producing the anomalously large MR in MoTe2. Supporting this conclusion, the MR peaks sharply at a characteristic electron-hole concentration ratio, i.e., Nh/Ne = 0.83, as shown in Fig. 4(d). In the Td phase, the MR is rapidly suppressed as the electron-hole concentration ratio moves away from this critical value. In the pressure-induced 1 T′ phase, the ratio slightly changes with pressure and the MR is almost constant (~100%). The Saturation of MR above Pc seems related to the saturation of Nh/Ne (~1.4) in 1 T′ phase (P > Pc). Even though the difference between the major electron and hole carriers gradually increases with increasing pressure, the total carrier concentration ratio is almost saturated due to the contribution from the minor electron and hole carrier, leading to the saturation of MR in 1 T′ phase. We note that the critical ratio deviates from the equal electron-hole concentration point because of different hole and electron mobilities, showing that subtleties of the Fermi surface topology are important in understanding the large MR in MoTe2.
Electronic structure of the Td and pressure-induced 1 T′ phases. (a) Schematic T-P phase diagram of MoTe2. Electronic structure calculations are performed for (A), (B), and (C), which are marked by the arrows, and their Fermi surfaces are plotted at the right of the panel. (b) Representative electronic structures are comparatively plotted along the Y-Γ-X direction at 1 bar (blue) and 2 GPa (red). Electronic structures at 1 bar (c) and 2 GPa (d) are magnified near the Fermi level along the Y-Γ-X direction.
The possibility of realizing topological superconductivity in the low-T Td phase of MoTe2 has been raised. Recent muon-spin relaxation/rotation measurements claimed a topologically non-trivial s+− gap symmetry in the pressure-induced SC phase32. However, Takahashi et al. pointed out an anticorrelation between superconductivity and the topological Td phase31. These contradicting claims stem from controversy about the phase diagrams, especially with respect to the pressure evolution of the Td-to-1T′ structural transition16. Our systematic transport study under pressure, as shown in Fig. 2(d), resolves this controversy and establishes the comprehensive phase diagram, showing that the structural phase transition is suppressed to 0 K between 1.1 and 1.4 GPa. Ac magnetic susceptibility measurements under pressure revealed that the SC Meissner fraction in the Td phase is negligible but becomes significant in the 1 T′ phase (see Fig. S3, Supplementary Information). The large difference between Tc,on and Tc in the Td phase is consistent with the negligible SC volume fraction, underlining that bulk superconductivity in MoTe2 exists in the non-polar 1 T′ phase, while there is a possibility of non-bulk superconductivity in the polar Td phase. Surface sensitive studies under pressure will be important for probing the realization of topological superconductivity in the low-pressure Td phase.
Conclusion
We have reported the dependence on pressure of the large magnetoresistance (MR) and superconductivity in the candidate type-II Weyl semimetal MoTe2. With increasing pressure, the monoclinic-to-orthorhombic (T′-to-Td) structural phase transition temperature gradually decreases and extrapolates to 0 K at Pc between 1.1 and 1.4 GPa. Supporting the existence of Pc, the first temperature derivative of electrical resistivity displays disparate scaling behaviors across Pc and the second pressure derivative of the Hall coefficient becomes saturated above Pc. The magnetic field dependence of the Hall and longitudinal conductivities are analyzed by an effective four-band model, where the carrier density ratio between the hole and electron types (Nh/Ne) grows with pressure and becomes saturated above Pc. The large non-saturating MR is peaked when Nh/Ne is 0.83 and is suppressed rapidly as the ratio deviates from the critical value in the Td phase, showing that the origin of the anomalously large MR is a consequence of balancing electron-hole contributions. The small SC volume fraction in the Td phase indicates that bulk superconductivity resides in 1 T′ phase, and thus surface sensitive measurements under pressure are required to properly understand the possible topological nature of its superconductivity.
Methods
MoTe2−x single crystals were synthesized by a NaCl-flux method, for which the detailed methods are described elsewhere2. A clamp-type hybrid cell with Daphne 7373 as a pressure transmitting medium was used up to a pressure of 2.5 GPa. A sharp resistivity drop at the superconducting transition temperature of Pb, which was used to determine the pressure inside the cell, is indicative of a quasi-hydrostatic pressure environment38,39. A conventional six-probe technique was used to measure the electrical resistivity and Hall effect under an external magnetic field37. A Quantum Design Physical Properties Measurement System (PPMS) and a 3He Heliox system (Oxford Inst. Nanotechnology) are used to regulate temperature down to 1.8 K and 0.25 K, respectively.
References
Qian, X., Liu, J., Fu, L. & Li, J. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides. Science 346, 1344 (2014).
Keum, D. H. et al. Bandgap opening in few-layered monoclinic MoTe2. Nat. Phys. 11, 482 (2015).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263 (2013).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotech 6, 147 (2013).
Duerloo, K. –A. N., Li, Y. & Reed, E. J. Structural phase transitions in two-dimensional Mo- and W-dichalcogenide monolayers. Nat. Comm. 5, 4214, https://doi.org/10.1038/ncomms5214 (2014).
Lagallo, A. et al. Tuning of quantum interference in top-gated graphene on SiC. Phys. Rev. B 88, 235406 (2013).
Tikhonenko, F. V., Kozikov, A. A., Savchenko, A. K. & Gorbachev, R. V. Transition between Electron Localization and Antilocalization in Graphene. Phys. Rev. Lett. 103, 226801 (2009).
Gopinadhan, K. et al. Extremely large magnetoresistance in few-layer graphene/boron-nitride heterostructures. Nat. Comm. 6, 8337, https://doi.org/10.1038/ncomms9337 (2015).
Zhang, C. –L. et al. Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Comm. 7, 10735, https://doi.org/10.1038/ncomms10735 (2016).
Wang, Y. et al. Gate-tunable negative longitudinal magnetoresistance in the predicted type-II Weyl semimetal WTe2. Nat. Comm. 7, 13142, https://doi.org/10.1038/ncomms13142 (2016).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2. Nature 514, 205 (2014).
Dawson, W. G. & Bullett, D. W. Electronic structure and crystallography of MoTe2 and WTe2. J. Phys. C: Solid State Phys. 20, 6159 (1987).
Hughes, H. P. & Friend, R. H. Electrical resistivity anomaly in β-MoTe2. J. Phys. C: Solid State Phys. 11, L103 (1978).
Vellinga, M. B., Jonge, R. & Haas, C. Semiconductor to metal transition in MoTe2. J. Solid State Chem. 22, 299 (1970).
Clarke, R., Marseglia, E. & Hughes, H. P. A low-temperature structural phase transition in β-MoTe2. Philos. Mag. 38, 121 (1978).
Qi, Y. et al. Superconductivity in Weyl semimetal candidate MoTe2. Nat. Comm. 7, 11038, https://doi.org/10.1038/ncomms11038 (2016).
Chen, S. –Y., Goldstein, T., Venkataraman, B., Ramasubramaniam, A. & Yan, J. Activation of New Raman Modes by Inversion Symmetry Breaking in Type II Weyl Semimetal Candidate T′-MoTe2. Nano Lett. 16, 5852 (2016).
Brown, B. E. The crystal structures of WTe2 and high-temperature MoTe2. ActaCrystallogr. 20, 268 (1966).
Puotinen, D. & Newnham, R. E. The crystal structure of MoTe2. ActaCrystallogr. 14, 691 (1961).
Rhodes, D. et al. Bulk Fermi surface of the Weyl type-II semimetallic candidate γ− MoTe2. Phys. Rev. B 96, 165134 (2017).
Wang, Z. et al. MoTe2: A Type-II Weyl Topological Metal. Phys. Rev. Lett. 117, 056805 (2016).
Pei, Q. L. et al. Origin of the turn-on phenomenon in Td− MoTe2. Phys. Rev. B 96, 075132 (2017).
Yang, J. et al. Elastic and electronic tuning of magnetoresistance in MoTe2. Sci. Adv. 3, eaao4949 (2017).
Cho, S. et al. Te vacancy-driven superconductivity in orthorhombic molybdenum ditelluride. 2D Mater. 4, 021030 (2017).
Kang, D. et al. Superconductivity emerging from a suppressed large magnetoresistant state in tungsten ditelluride. Nat. Comm. 6, 7804, https://doi.org/10.1038/ncomms8804 (2015).
Liu, C. et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nat. Phys. 6, 419 (2010).
Zhou, Q. et al. Hall effect within the colossal magnetoresistive semimetallic state of MoTe2. Phys. Rev. B 94, 121101(R) (2016).
Liang, A. et al. Electronic Evidence for Type II Weyl Semimetal State in MoTe2. Preprint at https://arxiv.org/abs/1604.01706 (2016).
Chen, F. C. et al. Extremely large magnetoresistance in the type-II Weyl semimetal MoTe2. Phys. Rev. B 94, 235154 (2016).
Wu, Y. et al. Temperature-Induced Lifshitz Transition in WTe2. Phys. Rev. Lett. 115, 166602 (2015).
Takahashi, H. et al. Anticorrelation between polar lattice instability and superconductivity in the Weyl semimetal candidate MoTe2. Phys. Rev. B 95, 100501 (2017).
Guguchia, Z. et al. Signatures of the topological s+− superconducting order parameter in the type-II Weyl semimetal Td-MoTe2. Nat. Comm. 8, 1082, https://doi.org/10.1038/s41467-017-01066-6 (2017).
Park, T. et al. Hidden Magnetism and Quantum Criticality in the Heavy Fermion Superconductor CeRhIn5. Nature 440, 65 (2006).
Luo, Y. et al. Pressure-enhanced superconductivity in Eu3Bi2S4F4. Phys. Rev. B 90, 220510 (2014).
Heikes, C. et al. Mechanical control of crystal symmetry and superconductivity in Weyl semimetal MoTe2. Phys. Rev. Mater. 2, 074202 (2018).
Luo, Y. et al. Hall effect in the extremely large magnetoresistance semimetal WTe2. Appl. Phys. Lett. 107, 182411 (2015).
van der Pauw, L. J. A Method of Measuring the Resistivity and Hall Coefficient on Lamellae of Arbitrary Shape. Philips Technical Review 20, 220 (1958).
Walker, I. R. Nonmagnetic piston–cylinder pressure cell for use at 35 kbar and above. Rev. Sci. Instrum. 70, 3402 (1999).
Eiling, A. & Schilling, J. S. Pressure and temperature dependence of electrical resistivity of Pb and Sn from 1-300 K and 0-10 GPa-use as continuous resistive pressure monitor accurate over wide temperature range; superconductivity under pressure in Pb, Sn and In. J. Phys. F: Metal Phys. 11, 623 (1981).
Acknowledgements
We acknowledge a fruitful discussion with Yongkang Luo, Sangmo Cheon, Youngkuk Kim, and J. D. Thompson. Work at Sungkyunkwan University was supported by a NRF grant funded by the Ministry of Science, ICT and Future Planning (No. 2012R1A3A2048816). J. Y. R and J. J acknowledge support from NRF-2014R1A1A2058975 and NRF-2016R1A6A3A11933107. S.-G. Jung was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2015R1D1A1A01060382).
Author information
Authors and Affiliations
Contributions
All authors discussed the results and commented on the manuscript. S.C. and S.W.K. grew MoTe2 and performed the XRD analysis. S.L., S.–G.J. and J.K. measured transport properties under pressure. S.L. analyzed the corresponding data. S.K. performed measurements of magnetic susceptibility under pressure. J.J. and J.Y.R. calculated electronic structure. S.L., K.P. and T.P. wrote the manuscript with assistance from all authors.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lee, S., Jang, J., Kim, SI. et al. Origin of extremely large magnetoresistance in the candidate type-II Weyl semimetal MoTe2−x. Sci Rep 8, 13937 (2018). https://doi.org/10.1038/s41598-018-32387-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-32387-1
Keywords
This article is cited by
-
Electronic band tuning under pressure in MoTe2 topological semimetal
npj Quantum Materials (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.