Abstract
The steady two dimensional magnetohydrodynamic (MHD) boundary layer flow and heat transfer over a stretching/shrinking permeable wedge is numerically investigated. The partial differential equations governing the flow and heat transfer are transformed into a system of ordinary differential equations using a similarity transformation. These equations are then solved numerically using the boundary value problem solver, bvp4c in Matlab software. It is found that dual solutions exist for a certain range of the shrinking strength. A stability analysis is performed to identify which solution is stable and physically reliable.
Similar content being viewed by others
Introduction
One of the family of boundary layer similarity solutions was discovered by Falkner and Skan1, for the study of flow over a static wedge. The numerical solutions were then calculated by Hartree2. With a similarity transformation, the boundary layer equation reduces to an ordinary differential equation, which is well known as the Falkner-Skan equation. This problem reduces to the classical Blasius flow if the angle of the wedge is set to zero, while it reduces to the stagnation-point flow (Hiemenz flow) if the angle is 180°. The Falkner-Skan flow past a stretching wedge was considered by Postelnicu and Pop3 and Su et al.4, while very recently Nadeem et al.5 studied the Falkner-Skan problem for a static and moving wedge in the presence of induced magnetic field.
Magnetohydrodynamic (MHD) flow is the study of magnetic properties on electrically conducting fluids. Given its significance in engineering industrial applications, this has led to numerous studies of MHD flow in electrically conducting fluids, such as Ishak6, Jafar et al.7, Mat Yasin et al.8, Hayat et al.9,10, Lu et al.11, etc. Dual solutions were found for the unsteady flow over a shrinking sheet by Soid et al.12. Meanwhile, Sharma et al.13 in their study of two dimensional MHD stagnation point flow over a stretching/shrinking sheet found dual solutions exist for a certain range of the shrinking parameter. The stability analysis revealed that the first solution is stable while the second solution is not.
With that, the present study examines the steady boundary layer flow and heat transfer over a stretching/shrinking wedge immersed in a viscous and incompressible electrically conducting fluid, with uniform surface temperature. The analysis is conducted numerically by using bvp4c function and once the dual solutions are obtained, the stability analysis is performed to determine which solution is stable and physically reliable.
Mathematical Formulation
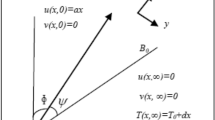
Figure 1 depicts the physical model and coordinate system for the stretching/shrinking wedge, where x and y are respectively the Cartesian coordinates measured along the surface and normal to it, while u and v are the velocity components along the Cartesian coordinates x and y, respectively. It is assumed that the velocity of the stretching/shrinking wedge is represented by \({u}_{w}(x)={U}_{w}{x}^{m}\), where \({U}_{w} > 0\) corresponds to stretching and \({U}_{w} < 0\) corresponds to shrinking. It is also assumed that the velocity of the external flow outside the boundary layer is represented by \({u}_{e}(x)={U}_{\infty }{x}^{m}\), where m and U∞ are positive constants. A variable magnetic field of strength represented by B(x) is applied in the positive direction of y-axis. The induced magnetic field is assumed small and neglected. In Fig. 1, β is the Hartree pressure gradient parameter which corresponds to β = Ω/π for a total angle Ω of the wedge. We note that \(0\le m\le 1\) with m = 0 for the boundary-layer flow over a stationary flat plate (Blasius problem) and m = 1 for the flow near the stagnation point on an infinite wall.
The governing equations based on the above-mentioned assumptions are (Ishak et al.14)
while the boundary conditions are
where ν is the kinematic viscosity, T is the fluid temperature, Tw is the uniform surface temperature, σ is the electrical conductivity, α is the thermal diffusivity of the fluid, ρ is the fluid density and vw(x) is the mass flux velocity with \({v}_{w}(x) < 0\) for suction and \({v}_{w}(x) > 0\) for injection.
To obtain similarity solutions of equations (1) to (3) subject to boundary conditions (4), we introduce the following similarity variables (Ishak et al.15,16):
where ψ is the stream function, which is defined as u = ∂ψ/∂y and v = −∂ψ/∂x which satisfies the continuity equation (1). Thus, resulting to:
where prime denotes differentiation with respect to η. At the boundary where η = 0, the transpiration rate is given by
where s = f(0), a constant parameter with s > 0 for suction and s < 0 for injection. To obtain similarity solution, all parameters must be constant. For this purpose, we take \(B(x)={B}_{0}{x}^{(m-1)/2}\), where B0 is a positive constant (see Kudenatti et al.17).
Substituting equations (5) and (6) into equations (2) and (3), the following ordinary (similarity) differential equations are obtained:
which is subject to the boundary conditions:
where λ is the stretching/shrinking parameter, β is the pressure gradient parameter, M is the magnetic parameter (Hartmann number), Pr is the Prandtl number and s is the suction/injection parameter, which are defined as:
where \(\lambda > 0\) refers to the stretching and \(\lambda < 0\) is for the shrinking case. Notably, it should be mentioned that in the absent of magnetic field (M = 0), Eq. (8) reduces to the classical Blasius equation when β = 0 and it reduces to the classical Hiemenz equation when β = 1.
The physical quantities of interest in this study are the skin friction coefficient Cf and the local Nusselt number \(N{u}_{x}\) which can be expressed as:
where τw is the wall shear stress along the stretching/shrinking surface and qw is the surface heat flux, which are defined as:
Substituting (6) into (13), one obtains
where Rex = ue(x)x/ν is the local Reynolds number.
Results and Discussions
In this study, the nonlinear ordinary differential equations (8) and (9) subject to the boundary conditions (10) were solved numerically using the bvp4c function available in Matlab software (see Shampine et al.18). The relative error tolerance was set to10−7 with the configured convergence criterion to achieve an accuracy of six decimal places. Dual solutions exist in the current study. These solutions are obtained by using different initial guesses for the values of f ″(0) and θ′(0) where all of the velocity and temperature profiles satisfy the far field boundary conditions (equation 10) asymptotically. For this purpose, we need to set different values of the boundary layer thickness, η∞. The range of η∞ for the first solution is between 10 and 20 while for the second solution is between 30 and 40. The initial guesses and the boundary layer thickness vary for different values of parameters. In the numerical computations, we have to make sure that all profiles satisfy the infinity boundary conditions asymptotically, otherwise the numerical results are not valid. Besides, we compare our results with previously published one by other researchers.
Table 1 shows the comparison of numerical results of the skin friction coefficient, f ″(0) with those reported by White19, Ishak et al.14 and Postelnicu and Pop3 for the case when λ = 0 (fixed surface), M = 0 (magnetic field is absent) and s = 0 (impermeable surface), which shows a favorable agreement. This gives confidence to the other numerical results that reported in the present study. For the sake of brevity, the value of Prandtl numer, Pr was set as 1 (such as ionized gases) and magnetic parameter, M was set as 0.2.
Figure 2 depicts the variation of the skin friction coefficient, f ′′(0) versus λ while Fig. 3 depicts the variation of the local Nusselt number, −θ′(0) versus λ, where \(\lambda < 0\) denotes the shrinking case and \(\lambda > 0\) denotes the stretching case. Variations illustrated in both figures are for different values of s, namely s = 0.5, 0.7 and 1 at constant values of β and M, i.e. β = 0.1 and M = 0.2. Both Figs 2 and 3 reveal the existence of dual solutions (first and second solutions) of equations (8) and (9), subject to the boundary conditions, Eq. (10), for a certain range of λ which depends on the suction strength, s. The solutions bifurcate at λ = λc, where λc is the critical value of λ for which equations (8–10) have no solutions for \(\lambda < {\lambda }_{c}\). The values of λc are given in Figs 2 and 3. It is observed that dual solutions are found for the shrinking case, while for the stretching case, the solution is unique. Figure 2 also shows that the skin friction coefficient f ″(0) increases when the suction strength is increased. Meanwhile, Fig. 3 reveals that the local Nusselt number, −θ′(0) which represents the heat transfer rate at the surface, decreases as the effect of suction increases.
Figure 4 illustrates the velocity profiles, f ′(η) while Fig. 5 illustrates the temperature profiles, θ(η) for different values of λ when s = 1, β = 0.1 and M = 0.2. Based on these figures, the boundary layer thickness for the first solution is lower than that of the second solution and the infinity boundary conditions (f → 1 and θ → 0 as η → ∞) are satisfied asymptotically which support the validity of the numerical results obtained.
Figure 6 demonstrates the variation of the skin friction coefficient, f ″(0) against the stretching/shrinking parameter λ for β = 0.17, 0.25 and 0.33 when s = 1 and M = 0.2, while Fig. 7 demonstrates the variation of the associated local Nusselt number, −θ′(0) for Pr = 1. The numerical results presented in these figures show that dual solutions are obtained for a certain range of the shrinking strength, while the solution is unique for the stretching case. Also, there is no solution for \(\lambda < {\lambda }_{c}\) where these values of λc are presented in Figs 6 and 7. These values of λc increase in absolute sense, when the values of β are increased. Thus, the range of λ (for which the solution exists) increases as the angle of the wedge increases. Besides that, the results also indicate that the skin friction coefficient f ″(0) increases as β increases for the first solutions, whereas it decreases for the second solution. Similar behaviour is observed for the absolute local Nusselt number, |−θ′(0)| as presented in Fig. 7.
The graphical results for the velocity profiles f ′(η) are presented in Fig. 8, while Fig. 9 graphically illustrates the temperature profiles θ(η) for different values of λ for β = 0.33, s = 1, M = 0.2 and Pr = 1. Both profiles reveal that the boundary layer thickness for the second solution is higher than that of the first solution and both satisfy the infinity boundary conditions asymptotically, which support the validity of the numerical results obtained.
Stability Analysis
Since the solutions are not unique for a certain range of the shrinking strength, a stability analysis is performed to determine which one of the solutions is stable and thus physically reliable. There have been several studies on stability analysis such as Merkin20, Weidman et al.21, Roşca and Pop22, Merril et al.23 and Awaludin et al.24. An analysis of the temporal stability is performed to identify which solution is stable when time passes. The new governing equations for the unsteady state flow are given as
where t denotes the time while equation (1) holds. The new similarity variables are introduced as
where τ denotes dimensionless time.
Substituting equation (17) into equations (15) and (16) yields
which is subject to the boundary conditions:
To test the stability of the steady flow solution f(η) = f0(η) and θ(η) = θ0(η) of equations (8) to (10) we write (see Merril et al.23):
where γ is an unknown eigenvalue; F(η) and G(η) are small relative to f0(η) and θ0(η). We take perturbation in exponential form since it will increase or decrease more rapidly compared to the power functions. This form of perturbation has also been considered by Merkin20, Weidman et al.21, Roşca and Pop22, Merril et al.23 and Awaludin et al.24, among others.
Equations (18) to (20) present an infinite set of eigenvalues, \({\gamma }_{1} < {\gamma }_{2} < \mathrm{...}\) . If the smallest eigenvalue is positive, there is an initial decay which is the flow is stable. Besides, there is an initial growth of disturbance if the smallest eigenvalue is negative which mean the flow is unstable. Substituting equation (21) into equations (18) and (19), the following linear eigenvalue problems are obtained:
along with the boundary conditions:
The stability of the steady state flow are determined by the smallest eigenvalue γ1. Since equations (22) and (23) satisfy homogeneous boundary and far-field conditions (24), without loss of generality we set F″(0) = 1 to determine the eigenvalues γ. There are more that one value of γ in equations (22) and (23) that give F″(0) = 1. A search for the lowest eigenvalues γ1 satisfying equations (22) to (24) was carried out and the results are plotted in Fig. 10.
Based on equation (21), the unsteady solution f(η, τ) converges to the steady state solution F(η) as time passes (τ → ∞) if γ1 is positive. The sign of γ1 determines either there is an initial decay or initial growth of disturbance. Figure 10 shows that γ1 is positive for the first solution, and negative for the second solution. Thus, the first solution is stable and physically reliable, whereas the second solution is unstable.
Conclusions
This study examined the steady two dimensional MHD flow and heat transfer of an incompressible and electrically conducting fluid over a permeable stretching/shrinking wedge. Numerical results, which were obtained using the bvp4c function in Matlab software, proved the existence of dual solutions for the shrinking case but unique solution for the stretching case. For the shrinking case, the existence of the solution depends on the shrinking strength λ and the angle of the wedge Ω. The range of λ (for which the solution exists) increases as the angle of the wedge Ω increases. Discussion on the skin friction coefficient and the local Nusselt number were carried out for the effect of all parameters involved. The boundary layer thickness for the second solution was found to be higher than that of the first solution, which gave a picture of its stability. To confirm this observation, a stability analysis was conducted and it was revealed that the first solution is stable and physically reliable while the second solution is not.
References
Falkner, V. M. & Skan, S. W. Some approximate solutions of the boundary layer equations. Philos. Mag. 12, 865–896 (1931).
Hartree, D. R. On an equation occurring in Falkner and Skan’s approximate treatment of the equations of the boundary layer. Proc. Cambridge Philos. Soc. 33, 223–239 (1937).
Postelnicu, A. & Pop, I. Falkner-Skan boundary layer flow of a power-law fluid past a stretching wedge. Applied Mathematics and Computation 217, 4359–4368 (2011).
Su, X., Zheng, L., Zhang, X. & Zhang, J. MHD mixed convective heat transfer over a permeable stretching wedge with thermal radiation and ohmic heating. Chemical Engineering Science 78, 1–8 (2012).
Nadeem, S., Ahmad, S. & Muhammad, N. Computational study of Falkner-Skan problem for a static and moving wedge. Sensors and Actuators B: Chemical 263, 69–76 (2018).
Ishak, A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malaysiana. 40, 391–395 (2011).
Jafar, K., Nazar, R., Ishak, A. & Pop, I. MHD boundary layer flow due to a moving wedge in a parallel stream with the induced magnetic field. Boundary Value Problems. 2013, Article ID 20 (2013).
Mat Yasin, M. H., Ishak, A. & Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. Journal of Magnetism and Magnetic Materials. 407, 235–240 (2016).
Hayat, T., Sajjad, R., Muhammad, T., Alsaedi, A. & Ellahi, R. On MHD nonlinear stretching flow of Powell-Eyring nanomaterial. Results in Physics. 7, 534–543 (2017).
Hayat, T., Ijaz Khan, M., Tamoor, M., Waqas, M. & Alsaedi, A. Numerical simulation of heat transfer in MHD stagnation point flow of cross fluid model towards a stretched surface. Results in Physics. 7, 1824–1827 (2017).
Lu, D., Ramzan, M., Huda, N., Chung, J. D. & Farooq, U. Nonlinear radiation effect on MHD Carreau nanofuid flow over a radially stretching surface with zero mass flux at the surface. Scientific Reports. 8, Article ID 3709 (2018).
Soid, S. K., Ishak, A. & Pop, I. Unsteady MHD flow and heat transfer over a shrinking sheet with ohmic heating. Chinese Journal of Physics. 55, 1626–1636 (2017).
Sharma, R., Ishak, A. & Pop, I. Stability analysis of magnetohydrodynamic stagnation-point flow toward a stretching/shrinking sheet. Comp. Fluids. 102, 94–98 (2014).
Ishak, A., Nazar, R. & Pop, I. Falkner-Skan equation for flow past a moving wedge with suction or injection. J. Appl. Math. & Computing. 25, 67–83 (2007).
Ishak, A., Nazar, R. & Pop, I. MHD boundary-layer flow of a micropolar fluid past a wedge with variable wall temperature. Acta Mech. 196, 75–86 (2008).
Ishak, A., Nazar, R. & Pop, I. MHD boundary-layer flow of a micropolar fluid past a wedge with constant wall heat flux. Communications in Nonlinear Science and Numerical Simulation 14, 109–118 (2009).
Kudenatti, R. B., Kirsur, S. R., Achala, L. N. & Bujurke, N. M. Exact solution of two-dimensional MHD boundary layer flow over a semi-infinite flat plate. Communications in Nonlinear Science and Numerical Simulations. 18, 1151–1161 (2013).
Shampine, L. F., Kierzenka, J. & Reichelt, M. W. Solving Boundary Value Problems for Ordinary Differential Equations in MATLAB with bvp4c. Retrieved from http://200.13.98.241/~martin/irq/tareas1/bvp_paper.pdf (2000).
White, F. M. Viscous Fluid Flow (ed. White, F. M.) 233 (McGraw-Hill, 2006).
Merkin, J. H. On dual solutions occuring in mixed convection in a porous medium. Journal of Engineering Mathematics. 20, 171–179 (1985).
Weidman, P. D., Kubitschek, D. G. & Davis, A. M. J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. International Journal of Engineering Science. 44, 730–737 (2006).
Roşca, A. V. & Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. International Journal of Heat and Mass Transfer. 60, 355–364 (2013).
Merrill, K., Beauchesne, M., Previte, J., Paullet, J. & Weidman, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. International Journal of Heat and Mass Transfer. 49, 4681–4686 (2006).
Awaludin, I. S., Weidman, P. D. & Ishak, A. Stability analysis of stagnation-point flow over a stretching/shrinking sheet. AIP Advances. 6, Article ID 045308 (2016).
Acknowledgements
The authors would like to acknowledge the financial support received from the Universiti Kebangsaan Malaysia (Project Code: DIP-2017-009). The authors are also thankful for the constructive suggestions and comments from the competent reviewers. The work of I. Pop has been supported from the grant PN-III-P4-ID-PCE-2016-0036, UEFISCDI, Romania.
Author information
Authors and Affiliations
Contributions
I.S.A. and A.I. performed the numerical analysis and wrote the manuscript. IP carried out the literature review and co-wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Awaludin, I.S., Ishak, A. & Pop, I. On the Stability of MHD Boundary Layer Flow over a Stretching/Shrinking Wedge. Sci Rep 8, 13622 (2018). https://doi.org/10.1038/s41598-018-31777-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-31777-9
Keywords
This article is cited by
-
Stability of hydromagnetic boundary layer flow of non-Newtonian power-law fluid flow over a moving wedge
Engineering with Computers (2022)
-
On solution existence of MHD Casson nanofluid transportation across an extending cylinder through porous media and evaluation of priori bounds
Scientific Reports (2021)
-
Hybrid nanofluid flow towards a stagnation point on a stretching/shrinking cylinder
Scientific Reports (2020)
-
Multiple nature analysis of Carreau nanomaterial flow due to shrinking geometry with heat transfer
Applied Nanoscience (2020)
-
MHD flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking wedge
Applied Mathematics and Mechanics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.