Abstract
Measuring single-electron charge is one of the most fundamental quantum technologies. Charge sensing, which is an ingredient for the measurement of single spins or single photons, has been already developed for semiconductor gate-defined quantum dots, leading to intensive studies on the physics and the applications of single-electron charge, single-electron spin and photon–electron quantum interface. However, the technology has not yet been realized for self-assembled quantum dots despite their fascinating transport phenomena and outstanding optical functionalities. In this paper, we report charge sensing experiments in self-assembled quantum dots. We choose two adjacent dots, and fabricate source and drain electrodes on each dot, in which either dot works as a charge sensor for the other target dot. The sensor dot current significantly changes when the number of electrons in the target dot changes by one, demonstrating single-electron charge sensing. We have also demonstrated real-time detection of single-electron tunnelling events. This charge sensing technique will be an important step towards combining efficient electrical readout of single-electron with intriguing quantum transport physics or advanced optical and photonic technologies developed for self-assembled quantum dots.
Similar content being viewed by others
Introduction
Self-assembled quantum dots (QDs) have been a fascinating platform for the investigation of microscopic quantum physics and applications to nanoelectronics, spintronics and photonics. In InAs QD-based single-electron transistors1, a variety of quantum transport experiments have been reported, including electrical control of the spin–orbit interaction2 and g-factor3,4, Josephson junction5,6, spin valve7,8 and terahertz spectroscopy9. In quantum information processing, the coupling between photons and InAs QDs offers key technologies, such as a single-photon source10, single-spin manipulation11 and entanglement between spins and photons12,13. Moreover, site-selective growth techniques are being developed14,15, which are indispensable for constructing large-scale quantum devices comprising a number of dots.
For further developments of the potential abilities of self-assembled QDs, a charge sensing technique, which has greatly contributed to the development of gate-defined QDs towards spin-based quantum information processing16, is strongly needed to be realized in the self-assembled QDs. Charge sensing has been realized by using a quantum point contact17 or a single electron transistor18 fabricated near the dots as a sensor. The conductance through the sensor is sensitive to the electrostatic environment at certain gate-voltage conditions. Because the sensor is placed close to the dot, the single-electron charging in the dot significantly changes the sensor conductance, enabling single-electron charge sensing. This technique works even if dot conductance is too small to measure, enabling detection of single-electron tunnelling events in real-time18,19,20. In addition, this real-time charge sensing allows for measurement of other physical quantities by converting them into electron charge: single-photon detection has been demonstrated by detecting single photo-excited electrons21,22, and the readout of single-electron spin has been implemented by detecting spin-dependent tunnelling events23,24,25,26. Moreover, a few works on charge sensing have been reported for vertical QDs27, carbon nanotube QDs28 and nanowire QDs29,30,31 by placing a sensor near a QD or by connecting a sensor and a QD with a floating gate. However, this has not yet been achieved for self-assembled QDs. Realizing charge sensing in a single-electron transistor based on a self-assembled QD may be challenging because the metal electrodes directly contacting the QD may effectively screen the single-electron charge in the QD6.
In this work, we report single-electron charge sensing experiments in InAs self-assembled QDs by using another adjacent QD as a sensor. Metal electrodes contacting the QDs are made narrow for reducing the screening effect. The capacitive coupling between the two QDs is large enough to show the distinct change in the dot current induced by the single-electron charging in the adjacent dot. We also demonstrate charge sensing in real-time at the dot-reservoir resonance having the tunnel rate lower than the measurement bandwidth.
Results
Device
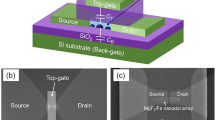
Two samples, A and B, studied in this work consist of two uncapped self-assembled InAs QDs, each contacted by a pair of Ti/Au (10/20 nm) electrodes as source and drain [see Fig. 1(a)]. The two QDs have a diameter and height of approximately 100 nm and 20 nm, respectively, which are suitable for stable single-electron transistor devices1,2,3,4,5,6,7,8,9,32,33. These dots are separated by approximately 150 nm from centre-to-centre. The source-drain electrode has a nanogap separation of approximately 50 nm and a width of approximately 50 nm. The latter is intentionally made narrow compared to the devices used in preceding studies1,2,3,4,5,6,7,8,9,32,33, in order to reduce the screening effect6 and hence enhance the charge sensitivity of the dots. Ti/Au electrodes surrounding the dots and a degenerately Si-doped GaAs layer buried 300 nm below the surface are used as local side gates and a global back gate, respectively, to control the electrostatic potential of the dots. For sample A, the 20 × 20 μm region around the dots is covered by a 50-nm-thick SiNx film to increase the capacitance between the two dots. In the following, we denote the two QDs as QDi (i = 1,2), and the side gates as SGiL and SGiR for each sample, as illustrated in Fig. 1(a). We measure the current through QDi, Ii, at the source–drain bias voltage, VSDi, across the dot, the side-gate voltages, VSGiL and VSGiR, and the back-gate voltage, VBG. All measurements discussed below have been performed in a dilution refrigerator at a base temperature of 20 mK and an electron temperature of 290 mK.
Basic characterization of devices
Figure 1(b) shows the differential conductance of QD2 in sample A, dI2/dVSD2, as a function of VSD2, and the side-gate voltage VSG2 = VSG2L = VSG2R at VBG = 0 V. We observe a series of diamond-shaped Coulomb blockade regions. Some of the diamonds are truncated because of inelastic co-tunnelling processes. Note that the electron numbers in both QD1 and QD2 in both samples A and B are not experimentally determined, but we speculate that each of the QDs contains few tens of electrons. From the aspect ratio of the diamonds, we evaluate the lever-arm factor, α, which converts the gate voltage to the change in the electrochemical potential of a QD. We find that α varies with the electron number in the dot, as implied by different aspect ratios of the diamonds in Fig. 1(c). We suppose that α may depend on the spatial distribution of the wave function in the dot and thus the screening effect, which may change with the electron number. In Fig. 1(c), we show averaged α values of each dot in samples A and B for VSG1 = VSG1L = VSG1R, VSG2 and VBG. Error bars indicate the range of the α values evaluated for single diamonds. For the side gates, the values of α are larger than 40 meV/V, which is an order of magnitude larger than those reported in preceding works2,3. These large α values of the side gates are attributed to the gates’ locations close to the dots, increased number of side gates, and the reduced screening effect by the narrow source and drain electrodes. The α values of the side gates in samples A are larger than those in sample B, whereas the α values of the back gates are almost the same for both samples. This may indicate the increase in the capacitance between the dot and the side gates by the SiNx dielectric layer; this is not, however, conclusive because of the electron number dependence of α.
Charge sensing experiments
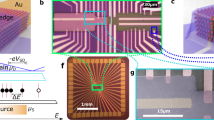
To investigate the transport properties of one dot in response to single-electron charging in the other, we measure I1 and I2 simultaneously. Fig. 2(a,b) show I1 and I2, respectively, in sample A as a function of VSG1R and VSG2L at VBG = 0 V and VSD1 = VSD2 = 70 μV. We observe two Coulomb peak ridges in each dot in the measured side-gate voltage range. These ridges exhibit a finite slope because each dot has capacitive couplings to both the side gates. Each ridge shows a distinct shift at the gate voltage where the two ridges in the different dots intersect each other. The gate voltage of the ridges shifts towards positive when the electron number in the other dot increases, resulting in a honeycomb pattern [see also Fig. 2(c)] typical of double QDs with an inter-dot capacitive coupling34. These features indicate that these shifts of ridges result from the capacitive coupling between the two dots, and thus, the charge sensing of either dot by using the other dot as a sensor is achieved. Note that the inter-dot tunnel coupling is negligibly small. We observed similar charge sensing features in sample B as shown in Fig. 2(d,e).
(a,b) Intensity plots of I1 (a) and I2 (b) in sample A as a function of VSG1R and VSG2L at VBG = 0 V and VSD1 = VSD2 = 70 μV. The dashed lines in (a) and (b) represent the positions of the Coulomb peak ridges in QD2 and QD1, respectively. Capacitive coupling between the two QDs and thus charge sensing features are observed at the gate voltage conditions denoted as Pj (j = 1–4), where the two ridges in different QDs intersect. (c) Superposition plots of (a) and (b) showing the honeycomb pattern. (d,e) Intensity plots of I1 (d) and I2 (e) in sample B as a function of VSG1 and VSG2 at VBG = 0 V and VSD1 = VSD2 = 70 μV, showing the charge sensing features at Qk (k = 1–3).
We evaluate the change in the electrochemical potential of the dot, Δμ, induced by single-electron charging in the other dot at the gate voltage conditions Pj (j = 1–4) shown in Fig. 2(a) for sample A and Qk (k = 1–3) shown in Fig. 2(d) for sample B. For sample A, Δμ is 220 ± 20 μeV at P1 and P2, and 110 ± 20 μeV at P3 and P4. For sample B, Δμ is 110 ± 20 μeV at Q1 and 150 ± 20 μeV at Q2 and Q3. For each of Pj and Qk, the values of Δμ evaluated from I1 [Fig. 2(a,d)] are almost the same as those evaluated from I2 [Fig. 2(b,e)]. It is difficult to compare Δμ directly between samples A and B because Δμ reflects the details in the wave function geometry in both dots as discussed above for the lever-arm factors in Fig. 1(c). It has been reported that asymmetrically applied side-gate voltage affects the lateral position and the extension of the wave function because of the modulation of the lateral confinement potential of the QDs4,5. As seen in Fig. 2(b), for QD2 in sample A, the electronic state responsible for the lower Coulomb peak ridge couples more strongly to SG2L than the state for the upper ridge. This implies that the orbital wave function in QD2 is located closer to SG2L and thus farther from QD1, which is consistent with the smaller Δμ for the lower ridge than the upper one.
Demonstration of real-time charge sensing
We demonstrate the real-time detection of single-electron tunnelling events. Fig. 3(a) shows I1 in sample B as a function of VSG1 = VSG1L = VSG1R and VSG2L for different electron numbers in both QD1 and QD2 from Fig. 2(d,e) with VBG = −0.5 V, VSD1 = 200 μV and VSD2 = 0 μV. We observe the shift in the Coulomb peak ridge for I1 similar to that observed in Fig. 2(a) to (e), indicating the change in the electron number of QD2 between N2 and N2 + 1. The amplitude of I2 is smaller than the noise floor of approximately 20 fA in the same gate-voltage range, suggesting small tunnel coupling between QD2 and the leads. We measure I1 in real-time at the resonance of the charge state transition in QD2 in Fig. 3(a). For the charge sensing measurements, the gate voltages are set such that the sensor QD1 is always set on one side of a Coulomb peak. The measurement bandwidth and the sampling frequency are 5 kHz and 2 kHz, respectively. Figure 3(b) shows the real-time traces of I1 measured at slightly different gate voltage conditions for QD2 along the red line in Fig. 3(a). We observe distinct random telegraph signals between I1 values of ~0.2 nA and ~0.5 nA. These low and high I1 signal levels correspond to the N2 and N2 + 1 charge states in QD2, respectively, indicating the detection of single-electron tunnelling events in and out of QD2. The charge-sensing signal amplitude is ~0.32 nA and the noise amplitude is ~0.08 nA, resulting in the signal-to-noise ratio of ~4. To further confirm the real-time charge sensing, we analyse the gate voltage dependence of the fraction of the N2 and N2 + 1 charge states. When the electrochemical potential of QD2, μQD2, changes with the gate voltages, the fraction of the N2 and N2 + 1 charge states also changes, reflecting the energy difference between μQD2 and the thermally broadened energy distributions of electrons in the source and drain electrodes. In Fig. 3(b), as VSG2L decreases across the charge state resonance in QD2 from top to bottom I1 traces, the fraction of the N2 + 1 state decreases as expected for increasing μQD2. Figure 3(c) shows the N2 + 1 state fraction as a function of μQD2. The estimation of the lever-arm factor in this condition is described in Supplementary Information. Numerical fitting using the Fermi distribution function gives an electron temperature of 280 ± 20 mK, which is in good agreement with that estimated from the Coulomb peak width. We define tin and tout for the dot as the lengths of time it resides at the N2 + 1 and N2 charge states, respectively, and show their histograms in Fig. 3(c,d). Each histogram shows a single exponential distribution. By fitting them to exp(−Γin(out)tin(out)), where Γin(out) is the rate of electron tunnelling into (out of) the dot, we obtain the tunnel coupling γ = Γin + Γout = 84 ± 2 Hz between the dot and the lead. The utility of the real-time charge sensing will be further improved by the ability to independently control the tunnel rate and the charge state in individual QDs. This will be viable by changing voltages on both side and back gates simultaneously so as to modulate the overlap between the lead state and the electronic wave function in the QD while keeping the electrochemical potentials of the QD unchanged5. The control of the tunnel rate for arbitrary charge states is to be investigated in our devices in future experiments.
(a) Intensity plot of I1 in sample B as a function of VSG1 and VSG2L at VBG = −0.5 V, VSD1 = 200 μV and VSD2 = 0 μV. (b) Real-time traces of I1 measured at VSG2L = −1.306 V (top), −1.309 V (middle), and −1.312 V (bottom) along the red line in (a). Each curve is offset by 0.6 nA for clarity. (c) N2 + 1 state fraction as a function of μQD2. A red curve is a fit to the data with the Fermi distribution function. (d,e) Histograms of tin (d) and tin (e) obtained at VSG2L = −1.306 V, the same condition as the middle I2 trace in (b).
Summary and Prospect
In summary, we have demonstrated charge sensing experiments in InAs self-assembled quantum dots by using one of two adjacent dots as a target and the other as a sensor. We have observed distinct shifts in the Coulomb peak ridges in the sensor dot when the electron number changes by one in the target dot, which is a signature of single-electron charge sensing. We have also demonstrated real-time detection of single-electron tunnelling events, which is an ingredient for the measurement of single spins or single photons. The charge sensing technique presented in this work will be applicable for self-assembled QDs made of other materials, such as GaN35 and SiGe36; this would bring opportunities to investigate intriguing physics of charge and spin in self-assembled QDs. Moreover, the technology can be applicable for self-assembled multiple QD systems6,37 and QDs coupled to superconductors5,6 or ferromagnets7,8, enabling to study the correlated electron spin dynamics. In terms of the applications to photonics, the charge sensing may be realized for single-electron transistors using on optically active QDs having a thin capping layer38. Our demonstration of the charge sensing in self-assembled QDs will be an important step towards combining efficient electrical readout of single electron with a variety of transport phenomena and advanced optical and photonic technologies.
Methods
Device fabrication
Uncapped InAs self-assembled QDs are grown by molecular beam epitaxy in the Stranski-Krastanov mode on a semi-insulating (001) GaAs substrate. The growth layers consist of a 300-nm-thick degenerately Si-doped GaAs layer, used as the back gate, followed by a 100-nm-thick Al0.3Ga0.7As barrier layer and a 200-nm-thick undoped GaAs buffer layer. Among the randomly positioned QDs with various sizes, we identify using scanning electron microscope two QDs with size and position suitable for subsequent fabrication. In this work, we choose QDs having diameter and height of approximately 100 nm and 20 nm, respectively, and separated by approximately 150 nm from centre-to-centre. A pair of source and drain electrodes and side-gate electrodes are fabricated on each dot using electron beam lithography and electron beam evaporation of Ti/Au (10/20 nm) [Fig. 1(a)]. Prior to the evaporation, an oxidized layer on the dot surface is removed using in situ Ar plasma etching. For sample A, a 50-nm-thick SiNx film is deposited by the catalytic chemical vapour deposition method.
Measurement details
Measurements are performed in a dilution refrigerator with a base temperature of 20 mK. The measurement lines are filtered with a two-stage RC low-pass filter with a cut-off frequency of 1 MHz. The electron temperature is estimated to be approximately 290 mK from the width of the narrowest Coulomb peaks in our samples.
References
Jung, M. et al. Shell structures in self-assembled InAs quantum dots probed by lateral electron tunneling structures. Applied Physics Letters 87, 203109 (2005).
Kanai, Y. et al. Electrically tuned spin-orbit interaction in an InAs self-assembled quantum dot. Nature Nanotechnology 6, 511–516 (2011).
Deacon, R. S. et al. Electrically tuned g tensor in an InAs self-assembled quantum dot. Physical Review B 84, 041302(R) (2011).
Takahashi, S. et al. Electrically tunable three-dimensional g-factor anisotropy in single InAs self-assembled quantum dots. Physical Review B 87, 161302(R) (2013).
Kanai, Y. et al. Electrical control of kondo effect and superconducting transport in a side-gated InAs quantum dot josephson junction. Physical Review B 82, 054512 (2010).
Deacon, R. S. et al. Cooper pair splitting in parallel quantum dot josephson junctions. Nature Communications 6, 7446 (2015).
Hamaya, K. et al. Spin transport through a single self-assembled InAs quantum dot with ferromagnetic leads. Applied Physics Letters 90, 053108 (2007).
Hamaya, K. et al. Electric-field control of tunneling magnetoresistance effect in a Ni/InAs/Ni quantum-dot spin valve. Applied Physics Letters 91, 022107 (2007).
Shibata, K., Umeno, A., Cha, K. M. & Hirakawa, K. Photon-assisted tunneling through self-assembled InAs quantum dots in the terahertz frequency range. Physical Review Letters 109, 077401 (2012).
Michler, P. et al. A quantum dot single-photon turnstile device. Science 290, 2282 (2000).
Press, D., Ladd, T. D., Zhang, B. & Yamamoto, Y. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature 456, 218 (2008).
De Greve, K. et al. Quantum-dot spin-photon entanglement via frequency downconversion to telecom wavelength. Nature 491, 421 (2012).
Gao, W., Fallahi, P., Togan, E., Miguel-Sánchez, J. & Imamoglu, A. Observation of entanglement between a quantum dot spin and a single photon. Nature 491, 426 (2012).
Schneider, C. et al. Lithographic alignment to site-controlled quantum dots for device integration. Applied Physics Letters 92, 183101 (2008).
Cha, K. M., Shibata, K. & Hirakawa, K. Single electron transport through site-controlled InAs quantum dots. Applied Physics Letters 101, 223115 (2012).
Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Reviews of Modern Physics 79, 1217–1265 (2007).
Field, M. et al. Measurements of coulomb blockade with a noninvasive voltage probe. Physical Review Letters 70, 1311–1314 (1993).
Lu, W., Ji, Z., Pfeiffer, L., West, K. & Rimberg, A. Real-time detection of electron tunnelling in a quantum dot. Nature 423, 422–425 (2003).
Schleser, R. et al. Time-resolved detection of individual electrons in a quantum dot. Applied Physics Letters 85, 2005–2007 (2004).
Vandersypen, L. M. K. et al. Real-time detection of single-electron tunneling using a quantum point contact. Applied Physics Letters 85, 4394–4396 (2004).
Pioda, A. et al. Single-shot detection of electrons generated by individual photons in a tunable lateral quantum dot. Physical Review Letters 106, 146804 (2011).
Fujita, T. et al. Nondestructive real-time measurement of charge and spin dynamics of photoelectrons in a double quantum dot. Physical Review Letters 110, 266803 (2013).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Hanson, R. et al. Single-shot readout of electron spin states in a quantum dot using spin-dependent tunnel rates. Physical Review Letters 94, 196802 (2005).
Barthel, C., Reilly, D. J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Rapid single-shot measurement of a singlet-triplet qubit. Physical Review Letters 103, 160503 (2009).
Kiyama, H., Nakajima, T., Teraoka, S., Oiwa, A. & Tarucha, S. Single-shot ternary readout of two-electron spin states in a quantum dot using spin filtering by quantum hall edge states. Physical Review Letters 117, 236802 (2016).
Zaitsu, K., Kitamura, Y., Ono, K. & Tarucha, S. Vertical quantum dot with a vertically coupled charge detector. Applied Physics Letters 92, 033101 (2008).
Biercuk, M. J. et al. Charge sensing in carbon-nanotube quantum dots on microsecond timescales. Physical Review B 73, 201402(R) (2006).
Wallin, D. et al. Detection of charge states in nanowire quantum dots using a quantum point contact. Applied Physics Letters 90, 172112 (2007).
Shorubalko, I. et al. Self-aligned charge read-out for InAs nanowire quantum dots. Nano Letters 8, 382–385 (2008).
Vukušić, L., Kukucka, J., Watzinger, H. & Katsaros, G. Fast hole tunneling times in germanium hut wires probed by single-shot reflectometry. Nano Letters 17, 5706–5710 (2017).
Shibata, K., Yuan, H., Iwasa, Y. & Hirakawa, K. Large modulation of zero-dimensional electronic states in quantum dots by electric-double-layer gating. Nature Communications 4, 2664 (2013).
Shibata, K., Jung, M., Cha, K. M., Sotome, M. & Hirakawa, K. Effect of in-ga intermixing on the electronic states in self-assembled inas quantum dots probed by nanogap electrodes. Applied Physics Letters 94, 162107 (2009).
van der Wiel, W. G. et al. Electron transport through double quantum dots. Reviews of Modern Physics 75, 1–22 (2002).
Nakaoka, T., Kako, S., Arakawa, Y. & Tarucha, S. Coulomb blockade in a self-assembled GaN quantum dot. Applied Physics Letters 90, 162109 (2007).
Katsaros, G. et al. Hybrid superconductor-semiconductor devices made from self-assembled SiGe nanocrystals on silicon. Nature Nanotechnology 5, 458–464 (2010).
Baba, S. et al. Superconducting transport in single and parallel double InAs quantum dot josephson junctions with Nb-based superconducting electrodes. Applied Physics Letters 107, 222602 (2015).
Nakaoka, T., Watanabe, K., Kumagai, Y. & Arakawa, N. A single-electron probe for buried optically active quantum dot. AIP advances 2, 032103 (2012).
Acknowledgements
We thank S. Baba for help with device fabrication, and T. Hirayama, R. Shikishima for useful discussions. This work was supported by Grant-in-Aid for Young Scientists B (No. 15K17681), Grants-in-Aid for Scientific Research S (No. 17H06120, No. 26220710), Scientific Research A (16H02333), Innovative Areas “Nano Spin Conversion Science” (No. 26103004), Innovative Areas “Science of hybrid quantum systems” (No. 15H05868), Project for Developing Innovation Systems of MEXT, CREST, Japan Science and Technology Agency (JST) (JPMJCR15N2), the Murata Science Foundation, the Asahi Glass foundation, Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials from MEXT, “Nanotechnology Platform Project (Nanotechnology Open Facilities in Osaka University)” of Ministry of Education, Culture, Sports, Science and Technology, Japan (No. F-17-OS-0030, No. S-17-OS-0030), and the PROMOS program of the German Academic Exchange Service.
Author information
Authors and Affiliations
Contributions
H.K. fabricated the devices, performed the measurements, analysed the results and wrote the manuscript. A.K. contributed to the device fabrication and the measurements. N.N. and K.H. grew the uncapped InAs QDs. Y.K. and K.M. deposited the SiNx layer. A.O. contributed to the interpretation of results and supervised the work. All authors contributed to the discussions and writing of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kiyama, H., Korsch, A., Nagai, N. et al. Single-electron charge sensing in self-assembled quantum dots. Sci Rep 8, 13188 (2018). https://doi.org/10.1038/s41598-018-31268-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-31268-x
This article is cited by
-
Single-electron detection utilizing coupled nonlinear microresonators
Microsystems & Nanoengineering (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.