Abstract
The multiplexing capacity of conventional fluorescence materials are significantly limited by spectral overlap and background interference, mainly due to their short-lived fluorescence lifetimes. Here, we adopt a novel Gd3+ doping strategy in NaYF4 host materials, realized tuning of upconversion photoluminescence (UCPL) lifetimes at selective emissions. Time-correlated single-photon counting (TCSPC), was applied to measure the photoluminescence lifetimes accurately. We demonstrated the large dynamic range of lifetimes of upconversion nanoparticles with good upconversion quantum yields, mainly owing to the dominance of high efficient energy transfer upconversion mechanism. The exceptional tunable properties of upconversion materials allow great potential for them to be utilized in biotechnology and life sciences.
Similar content being viewed by others
Introduction
Upconversion nanoparticles, capable of displaying high-energy luminescent emission through absorption of two or more low-energy photons, have attracted tremendous research attention in past decade due to their remarkable and unique optical properties including sharp emission, low background signal, long decay time et al.1,2. UCNPs have been widely exploited in many emerging applications such as biological imaging, molecular detection, drug delivery and optoelectronics3,4. In particular, with versatile surface modification strategies, it has been demonstrated biocompatibility of UCNPs, significantly boosting their prospect for biomedical applications1. Optical multiplexing gains significant attention in biotechnology and life science due to the capability of identifying and quantifying multiple biomolecular species5. To realize efficient multiplexing, one of the great challenges is the exploration of optical markers possessing a matrix of optical codes, which could be identified with minimal time, high sensitivity and accuracy. However, conventional fluorescence materials, including quantum dots and organic dyes, only exhibit lifetimes in the order of nanoseconds6 and are simply too short for the temporal identification of fluorescence interference from scattered excitation photons. In contrast to these short-lived fluorescence counterparts, lanthanide ions doped upconversion nanoparticles (UCNPs) demonstrate distinct photoluminescence lifetimes from microseconds to even milliseconds7,8. Upconversion photoluminescence nanoparticles, not only can realize frequency conversion via converting two (or more) low-energy photons into one high-energy photon, but also exhibit unique optical proper- ties such as high resistance to optical blinking, sharp and multiple luminescence peaks, as well as high photostability9. All these advantages make UCNPs a great candidate for multiplexing, allowing the creation of extra coding dimensions. Current research has already suggested that Ln-doped fluorides (i.e., NaYF4:Yb3+ 20%, Er3+ 2%) are the most promising and efficient nanomaterial to achieve desirable UCPL10,11,12. However, poor upconversion efficiencies of UCNPs remains to be one of the most critical limitation for a range of applications13,14.
Further studies of the enhancement of upconversion quantum yield (UCQY) of UCNPs are needed to fulfil their full potential for practical applications. Recent advances demonstrated the availability of systematically tuning various properties of UCNPs, including phase, morphology, and quantum yield through designing lanthanide doping strategy and novel nanostructure, such as core-shell structure15, nanoarrays structure16, etc. Liu realized simultaneous phase and size control of UCNPs with strong UCPL by additional doping of Gd3+ ions17. Despite these progresses have been achieved, it remains a challenge to precisely tune the UCPL lifetimes of NaYF4 nanocrystals, with high efficiency UCPL to overcome the limitation in emission selectivity for the multiplexed applications.
In this work, we developed a facile Gd3+ doping strategy in a hydrothermal process to synthesize a set of upconversion nanomaterials with distinct luminescent properties. The dominant role of energy transfer upconversion (ETU) process in Sensitizer–Activator-coupled UCNPs system was identified by accurate lifetime measurement (TCSPC), as shown in Fig. 1a. Accordingly, we observed that the lanthanide Gd3+ ion doping approach leads to a clear prolonged lifetimes of photoluminescence, and the lifetimes of both green emission (at 540 nm) and red emission (at 656 nm) exhibit as a function of the internal upconversion quantum yield (iUCQY), shown in Fig. 1b. In addition, X-ray power diffraction (XRD), field emission scanning electron microscopy (FE-SEM), and were used to characterize the UCNPs. Our results indicate that tuneable UCPL lifetimes have remarkable potential for optical multiplexing applications.
Methods
Time-correlated single-photon counting (TCSPC), which is considered as the most sensitive digital technique for determining photoluminescence lifetime to date, was used to obtain a dynamic picture of the upconversion photoluminescence of the as-prepared samples18. With well-defined Poisson statistics, TCSPC is a method based on the detection of the arrival time of individual photon after optical excitation of a sample. Importantly, this mechanism allows only one photon can be counted at any one time and the measured lifetimes are not affected by changes in source intensity. It is worth to mention that the lifetimes of UCNPs in general cases are independent of excitation power density in the low power regime (<100 Wcm−2)19. We precisely modulated the pulse duration of the 980 nm pulsed laser to statistically characterize the time dependent photoluminescence emission profiles of the as-synthesized UCNPs by repeating the excitation-emission process to 10000 counts.
Results
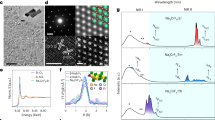
All samples were first examined by X-ray powder diffraction. Figure 2 shows the XRD patterns of NaYF4:Yb3+, Er3+ materials doped with 0–70% Gd3+ ions synthesized at 200 C for 20 hours. The diffraction spectra show evidence of the co-existence of cubic phase (JCPDS File No. 772042) and hexagonal phase NaYF4 (JCPDS File No. 16-0334) without Gd3+ doping prepared in this synthesis condition17. Notably, the XRD patterns demonstrate the formation of hexagonal phase NaYF4:Yb3+, Er3+ when doping additional 30% Gd3+ according to standard hexagonal XRD spectra of NaYF4. This suggests extra dopant Gd3+ ions can effectively induced an cubic to hexagonal phase transition under this synthesize condition. No extra diffraction peaks appeared with further increase of the Gd3+ concentration from 30 mol% to 70 mol%, which implies the formation of a homogeneous Y-Gd solid solution. Since the Y3+ ions were substituted by larger Gd3+ ions in the host lattice, the diffraction peaks shifted to lower diffraction angles with the increasing of Gd3+ ions concentration and the expansion of unit-cell volume.
To study the crystallite size and phase of NaYF4:Yb3+, Er3+ doped with different concentrations of Gd3+ ions, all the samples were synthesized under a same heating condition and characterized by scanning electron microscopy (SEM), respectively. A brief summary of the synthetic parameters of NaYF4:Yb3+, Er3+, Gd3+ materials are listed in Table S1. The influences of Gd3+ doping on crystallite size distribution and crystal phase of NaYF4:Yb3+, Er3+ nanoparticles are listed in Table S2. Figure 3a confirmed the co-existence of hexagonal phase and cubic phase NaYF4. Clearly, there were significant differences on morphology as a function of the dopant con- centration of Gd3+. Figure 3(b) demonstrated that pure hexagonal phase of NaYF4 was formed when the Gd3+ ion concentration reached 30 mol%, and this as-prepared sample was of good crystallite size uniformity. In addition, the length of the nanorods decreased gradually when the Gd3+ doping concentration increased from 30 mol% to 70 mol%. The transition from cubic phase to hexagonal phase could be well controlled by modulating the doping concentration of Gd3+.
(a–d) SEM characterization of NaYF4:Yb3+, Er3+ (20, 2 mol%) nanoparticles doped with various concentrations of Gd3+ ions. (a) shows the SEM image of the NaYF4:Yb3+, Er3+ (20, 2 mol%) UC nanoparticles. (b) shows the SEM image of the NaYF4:Yb3+, Er3+ (20, 2 mol%) @Gd3+ doping (30 mol%) UC nanoparticles. (c) shows the SEM image of the NaYF4:Yb3+, Er3+ (20, 2 mol%) @Gd3+ doping (50 mol%). (d) shows the SEM image of the NaYF4:Yb3+, Er3+ (20, 2 mol%) @Gd3+ doping (70 mol%) UC nanoparticles. The scale bars in figure (a–d) are 500 nm.
In view of geometry of UCNPs, 30 mol% Gd3+ doped sample shows larger physical dimen- sion, smaller surface defect, high crystallinity and a smaller ratio of surface area to volume. On the contrary, both 50 mol% and 70 mol% Gd3+ doping samples have a relatively smaller size, less homogenous morphology, and lower crystallinity. High Gd3+ concentrations are associated with an increase of unwanted surface impurities, ligands and lattice defects, which could change the ori- gin phonon energy of the host matrix. Moreover, the size ranges become broader when the Gd3+ doping content is raised from 30 mol% to 70 mol%, indicates the tendency of less homogeneity with a higher concentration of lanthanide doping. Notably, when the Gd3+ ions are doped into the NaYF4:Yb3+, Er3+ nanoparticles, hexagonal tubes have a protruding centre and distortional tubular structure with the end face convex in the centre and concave between the centre and the edge. When the Gd3+ doping concentration is 30 mol%, and F−/Ln3+ molar ratio is calculated as 8:1, the obtained UCNPs are the most uniform ones and have the smoothest morphologies among the three lanthanide doping samples. The evolution of morphology can be partly attributed to the surface modification effect of dopant Gd3+ ions on crystal growth20.
In a typical Sensitizer–Activator-coupled UCNPs system (shown in Fig. 4), ground state absorption/excited state absorption (GSA/ESA), energy transfer upconversion (ETU) and cooperative sensitization (CS) are three main mechanisms for upconversion21. ETU, which comprises multiple competing transitions between multiple energy levels in the Yb3+ - Er3+ couples system, is considered to be the most efficient mechanisms in upconversion process22,23. NaYF4:Er3+,Yb3+ exhibits a combination of ESA and ETU process. Er3+ ion is excited from the ground-state 4I15/2 to the excited-state 4I11/2 by one of the two following processes: ground-state absorption by absorbing one 980 nm laser photon (GSA), or energy transfer (ET) from the excited Yb3+ ions
Energy level diagram and upconversion mechanism for the Yb3+ and Er3+ co- doped UCNPs system upon 980 nm laser excitation. Three major emission peaks centered at 520 nm, 540 nm, and 656 nm are observed in the range of UV to visible light spectrum, where two green emissions at 520 nm and540 nm are assigned to the 2H11/24I15/2 and 4S3/24I15/2 transition, respectively; and the red emission at 656 nm is assigned to the 4F9/24I15/2 transition. The UCPL of Er3+ and Yb3+ ions co-doped nanoparticles excited by a 980 nm laser emit yellowish green light, which is a combination of green and red colour emissions.
Then, the ions in the 4I11/2 state can be immediately excited to the 4F7/2 level of Er3+ ions by absorbing another Yb3+ ion. The Er3+ ions could decay non-radiatively to the luminescent states 2H11/24,S3/2, and 4F9/2. Furthermore, the Er3+ ions at the excited state 4I11/2 could undergo a non-radiative decay to the 4I13/2 level and subsequently be excited to the 4F9/2 state by absorbing a second 980 nm photon24. Recently, other UCNPs systems, with core-shell nanostructures, were proposed with more complicated upconversion mechanisms1 including the non-steady-state upconversion for emissions generated from triply-doped systems and energy transfer mechanism in nanodumbbells nanostructures25.
In brief, the unique properties of UCPL are owing to the intra 4f-4f orbital electronic-dipole transitions of lanthanide ions. The long-lived intermediate energy states in lanthanide ions can be attributed to the quantum mechanical forbidden nature of the 4f-4f transition, which allows energy transfers between two or more ions and favour the successive excitations in a single lanthanide ion26. Since Yb3+ ions have a much broader absorption cross-section than that of Er3+ ions for 980 nm light, the ETU process should plays a predominant role among these mechanisms27. To investigate the ETU process, Fig. 5(a,b) signify the time evolution of upconversion photoluminescence intensity measured under different excitation duration times of the pulsed laser (109 µs 1092 µs, 4368 µs, 4586 µs, respectively). These figures comprise both the rise and decay curves of photoluminescence intensity versus time, which are proportional to the population of the excited states of Er3+ as a function of time. In terms of decay lifetime, longer time indicates slower decay rate and favours the accumulation of population28.
where I(t) represent the photoluminescence intensity at a specific time point corresponding to the on and off of the pulsed laser. τD is decay lifetime of the UCPL, which can be influenced by the lifetime of excited emitting level and the lifetime of energy levels that feed the emitting level via the ET process. While τR represents the rise time, which is also influenced by the lifetime of the emitting state and ET rate. We observed a pronounced rise lifetime dependence on excitation duration for 30% Gd3+ doped NaYF4 sample. Within the entire measurement range of 11,000 µs, as the pulsed laser duration times prolonged from 109 µs to 1092 µs, the rise time was delayed from 74.6 µs to 125.3 µs. It was revealed that all GSA/ESA excitation only occurs within the duration of a short laser pulse, when the sample is irradiated29. In contrast, the contribution of ETU process can be identified by the slower increase rate and delayed maximum in the time evolution picture of the GSA/ESA and ETU co-existence upconversion photoluminescence. Interestingly, a four times longer duration time, 4368 µs, leads to only a slight increased rise time, compared with the 1092 µs duration time measurement. With further extension of the duration time to 4586 µs, there were negligible changes of rising time. This result could be attributed to the saturation of the intermediate levels10. The appearance of a secondary peak at 4600 µs in Fig. 5(b) corresponds to the initiation of re-excitation of the ground state when the duration time (4586 µs) reached a critical period of time (Tc). Thus, in the following measurements, duration time of 4368 µs was selected to overcome the restriction of re-excitation effect.
(a) Time evolution of upconversion photoluminescence intensity measured under four different excitation duration times (109 µs 1092 µs, 4368 µs, respectively) of the pulsed laser. We observed the dynamic picture of rise time versus excitation duration for 30% Gd3+ doped NaYF4 sample. We fitted the values of decay lifetimes and rise lifetimes by using algorithm in DAS6 Analysis software, which allows deconvolution analysis of time-domain luminescence data with two exponentials. (b) Time evolution of upconversion photoluminescence intensity measured under two different excitation duration times (4368 µs and 4586 µs, respectively) of the pulsed laser. The temporal evolution of the photoluminescence of NaYF4 as a function of time can be described by a Vial’s type equation32.
In order to demonstrate the Gd3+ dopant concentration dependent photoluminescence dynamics, the lifetime decay curves of the green (550 nm) and red (656 nm) emissions of NaYF4:Yb3+, Er3+, Gd3+ were measured in samples with increased concentration of Gd3+ dopant under excitation of 980 nm pulsed laser, as shown in Fig. 6.
The results in Table 1 shows that the decay lifetime τ increased with the variation of Gd3+ concentration. Clearly, the photoluminescence lifetimes of both green and red emissions were prolonged accordingly as a function of increasing the molar concentration of Gd3+ doping in NaYF4. In case of samples doped with 30 mol%, 50 mol% Gd3+ ions, the green lifetimes increase slightly from 209.62 µs to 211.61 µs, and from 495.1 µs to 499.8 µs for red emission. Theoretically, the lifetime (τ) of an excited state is expressed as30,
where τrad represents the radiative decay, τnr represents the non-radiative decay lifetime, and kET is energy transfer rate. As previously results informed, the upconversion process is dominated by ETU mechanisms in the sensitizer to activator (S-A) couples system (Fig. 7). Dexter’s theory31 described the relationship of energy transfer probability (WS-A) and the S-A separation (rS-A), which can be simplified as,
This relationship indicates that S-A separation is a significant factor influencing the energy transfer probability. The strong dependence of energy transfer rate on the interionic distance, (rS-A) directly leads to the significance of sensitizer and activator ions concentration in the host of UCNPs. With the increased Gd3+ ions doped into the NaYF4 nanocrystals, more Y3+ and Yb3+ ions were substituted by Gd3+ in the crystal lattice of NaYF4. With the average S-A separation (rS-A) increases accordingly, a decreased energy transfer rate between sensitizer and activator could lead to the prolonged lifetime of NaYF4 Nanocrystals.
To investigate the photoluminescence of NaYF4:Yb3+, Er3+ UCNPs as a function of the Gd3+ concentration, the absolute quantum yields of upconversion nanoparticles were measured (Fig. 8a). Clearly, the absolute quantum yield of both green light emission (500 nm–570 nm) and red light emission (620 nm–700 nm) varied as a function of the Gd3+ ions doping concentration. The calculated quantum yields at different emission bands with various Gd3+ concentrations are summarized in Table S3. In Fig. 8a, the shapes of the emission spectra for the four samples are similar, which suggests the same combination of upconversion pathways for these as-prepared samples. Besides, the intensity ratio of green and red emission demonstrated a remarkable change as a result of the incorporation of Gd3+ ions into NaYF4:Yb3+, Er3+ host lattice. With 30 mol% Gd3+ doping, the UC luminescence efficiency is enhanced at 540 nm and 520 nm, compared to those without doping. However, the highest emission peak occurs at 656 nm when Gd3+ ions are not doped into the NaYF4:Yb3+, Er3+ UC systems. These results reveal that the suitable lanthanide doping and controlled dopant ion concentration are able to modify the UCPL efficiency at selective wavelengths. In the perspective of the ladder-like energy levels in the sensitizer and activator, Gd3+ doping induces large local distortion in crystal lattice, and reducing the site symmetry of the activators. Therefore, the probabilities of different pathways in the ETU process could be changed due to the modified lattice symmetry, unit cell parameters and intra-4f transition probability. In addition, the iUCQY were proved to be in correlation with the evolution trend of UCPL lifetimes. Therefore, both the UCPL lifetimes and iUCQY were proved to be influenced by the tailoring of ETU efficiency.
(a) demonstrates the absolute irradiance of UC photoluminescence emission spectra of the resulting NaYF4:Yb3+, Er3+ when tuning the Gd3+ dopant molar concentration from 0 to 70 mol% upon 980 nm laser excitation. (b) shows the UC luminescence emission intensity at 656 nm, 540 nm, and 520 nm versus different Gd3+ doping concentration (0, 30 mol%, 50 mol%, and 70 mol%).
Conclusions
In summary, we demonstrate that UCPL lifetimes and iUCQY at selective emissions can be tuned by varying the molar concentration of the Gd3+ ions. In addition, the properties of UCPL are identified highly sensitive to the energy transfer rate between the sensitizer and activator. Based on the precise control of UCPL lifetimes in the wide range timescale, this doping strategy make it possible to create extra temporal-domain coding dimension, promising significant potential for practical multiplexed applications.
References
Zhou, B., Shi, B., Jin, D. & Liu, X. Controlling upconversion nanocrystals for emerging applications. Nature Nanotechnology 10, 924, https://doi.org/10.1038/nnano.2015.251 (2015).
Liu, X. et al. Probing the nature of upconversion nanocrystals: instrumentation matters. Chemical Society Reviews 44, 1479–1508, https://doi.org/10.1039/C4CS00356J (2015).
Liu, K. et al. Stable gadolinium based nanoscale lyophilized injection for enhanced MR angiography with efficient renal clearance. Biomaterials 158, 74–85, https://doi.org/10.1016/j.biomaterials.2017.12.023 (2018).
Wang, W.-N. et al. Controlled synthesis of upconverting nanoparticles/ZnxCd1-xS yolk-shell nanoparticles for efficient photocatalysis driven by NIR light. Applied Catalysis B: Environmental 224, 854–862, https://doi.org/10.1016/j.apcatb.2017.11.037 (2018).
Lu, Y. et al. Tunable lifetime multiplexing using luminescent nanocrystals. Nature Photonics 8, 32, https://doi.org/10.1038/nphoton.2013.322 https://www.nature.com/articles/nphoton.2013.322#supplementary-information (2013).
Resch-Genger, U., Grabolle, M., Cavaliere-Jaricot, S., Nitschke, R. & Nann, T. Quantum dots versus organic dyes as fluorescent labels. Nature Methods 5, 763, https://doi.org/10.1038/nmeth.1248 https://www.nature.com/articles/nmeth.1248#supplementary-information (2008).
Gnach, A. & Bednarkiewicz, A. Lanthanide-doped up-converting nanoparticles: Merits and challenges. Nano Today 7, 532–563, https://doi.org/10.1016/j.nantod.2012.10.006 (2012).
Deng, R. & Liu, X. Tunable lifetime nanocrystals. Nature Photonics 8, 10, https://doi.org/10.1038/nphoton.2013.353 (2013).
Wang, F. & Liu, X. Multicolor Tuning of Lanthanide-Doped Nanoparticles by Single Wavelength Excitation. Accounts of Chemical Research 47, 1378–1385, https://doi.org/10.1021/ar5000067 (2014).
Zhou, J., Liu, Q., Feng, W., Sun, Y. & Li, F. Upconversion Luminescent Materials: Advances and Applications. Chemical Reviews 115, 395–465, https://doi.org/10.1021/cr400478f (2015).
Li, C. & Lin, J. Rare earth fluoride nano-/microcrystals: synthesis, surface modification and application. Journal of Materials Chemistry 20, 6831–6847, https://doi.org/10.1039/C0JM00031K (2010).
Dyck, N. C., van Veggel, F. C. J. M. & Demopoulos, G. P. Size-Dependent Maximization of Upconversion Efficiency of Citrate-Stabilized β-phase NaYF4:Yb3+, Er3+ Crystals via Annealing. ACS Applied Materials & Interfaces 5, 11661–11667, https://doi.org/10.1021/am403100t (2013).
Wang, J. et al. Photon energy upconversion through thermal radiation with the power efficiency reaching 16%. Nature Communications 5, 5669, https://doi.org/10.1038/ncomms6669 https://www.nature.com/articles/ncomms6669#supplementary-information (2014).
Wu, X. et al. Upconversion Nanoparticles: A Versatile Solution to Multiscale Biological Imaging. Bioconjugate Chemistry 26, 166–175, https://doi.org/10.1021/bc5003967 (2015).
Li, Z. et al. Multicolor Core/Shell‐Structured Upconversion Fluorescent Nanoparticles. Advanced Materials 20, 4765–4769, https://doi.org/10.1002/adma.200801056 (2008).
Zhang, F., Wan, Y., Shi, Y., Tu, B. & Zhao, D. Ordered Mesostructured Rare-Earth Fluoride Nanowire Arrays with Upconversion Fluorescence. Chemistry of Materials 20, 3778–3784, https://doi.org/10.1021/cm800489e (2008).
Wang, F. et al. Simultaneous phase and size control of upconversion nanocrystals through lanthanide doping. Nature 463, 1061, https://doi.org/10.1038/nature08777 https://www.nature.com/articles/nature08777#supplementary-information (2010).
Wahl, M., Rahn, H.-J., Gregor, I., Erdmann, R. & Enderlein, J. Dead-time optimized time-correlated photon counting instrument with synchronized, independent timing channels. Review of Scientific Instruments 78, 033106 (2007).
Gargas, D. J. et al. Engineering bright sub-10-nm upconverting nanocrystals for single-molecule imaging. Nature Nanotechnology 9, 300, https://doi.org/10.1038/nnano.2014.29 https://www.nature.com/articles/nnano.2014.29#supplementary-information (2014).
Shang, Y. et al. Synthesis of Upconversion β-NaYF4:Nd3+/Yb3+/Er3+ Particles with Enhanced Luminescent Intensity through Control of Morphology and Phase. Nanomaterials 5, https://doi.org/10.3390/nano5010218 (2015).
Villanueva-Delgado, P., Krämer, K. W. & Valiente, R. Simulating Energy Transfer and Upconversion in β-NaYF4: Yb3+, Tm3+. The Journal of Physical Chemistry C 119, 23648–23657, https://doi.org/10.1021/acs.jpcc.5b06770 (2015).
Park, W., Lu, D. & Ahn, S. Plasmon enhancement of luminescence upconversion. Chemical Society Reviews 44, 2940–2962, https://doi.org/10.1039/C5CS00050E (2015).
Lu, D., Mao, C., Cho, S. K., Ahn, S. & Park, W. Experimental demonstration of plasmon enhanced energy transfer rate in NaYF4:Yb3+, Er3+ upconversion nanoparticles. Scientific Reports 6, 18894, https://doi.org/10.1038/srep18894 https://www.nature.com/articles/srep18894#supplementary-information (2016).
Ding, M. et al. Simultaneous morphology manipulation and upconversion luminescence enhancement of β-NaYF4:Yb3+/Er3+ microcrystals by simply tuning the KF dosage. Scientific Reports 5, 12745, https://doi.org/10.1038/srep12745 https://www.nature.com/articles/srep12745#supplementary-information (2015).
Ding, B., Peng, H., Qian, H., Zheng, L. & Yu, S. Unique Upconversion Core–Shell Nanoparticles with Tunable Fluorescence Synthesized by a Sequential Growth Process. Advanced Materials Interfaces 3, 1500649, https://doi.org/10.1002/admi.201500649 (2016).
Chen, G., Qiu, H., Prasad, P. N. & Chen, X. Upconversion Nanoparticles: Design, Nanochemistry, and Applications in Theranostics. Chemical Reviews 114, 5161–5214, https://doi.org/10.1021/cr400425h (2014).
Xu, S. et al. Upconversion fluorescence spectroscopy of Er3+/Yb3+-codoped lead oxyfluorosilicate glass. Chemical Physics Letters 385, 263–267, https://doi.org/10.1016/j.cplett.2003.12.104 (2004).
Wei, T. et al. Mid-infrared fluorescence, energy transfer process and rate equation analysis in Er3+ doped germanate glass. Scientific Reports 4, 6060, https://doi.org/10.1038/srep06060 (2014).
Yersin, H. & Donges, D. In Transition Metal and Rare Earth Compounds: Excited States, Transitions, Interactions II (ed. Hartmut Yersin) 81–186 (Springer Berlin Heidelberg, 2001).
Chen, G., Liu, H., Liang, H., Somesfalean, G. & Zhang, Z. Upconversion Emission Enhancement in Yb3+/Er3+ -Codoped Y2O3 Nanocrystals by Tridoping with Li+ Ions. The Journal of Physical Chemistry C 112, 12030–12036, https://doi.org/10.1021/jp804064g (2008).
Dexter, D. L. A Theory of Sensitized Luminescence in Solids. The Journal of Chemical Physics 21, 836–850, https://doi.org/10.1063/1.1699044 (1953).
Yu, W., Xu, W., Song, H. & Zhang, S. Temperature-dependent upconversion luminescence and dynamics of NaYF4:Yb3+/Er3+ nanocrystals: influence of particle size and crystalline phase. Dalton Transactions 43, 6139–6147, https://doi.org/10.1039/C3DT53562B (2014).
Author information
Authors and Affiliations
Contributions
Q.H. designed the experiment. D.W. and Q.H. performed the upconversion nanoparticles synthesis. Q.H. and D.W. contributed to the draft writing. Q.H. performed the characterizations including SEM, TEM, Lifetime and XRD measurements. J.S. Q.H. and X.X. performed the quantum yield measurements. Q.H. and X.X. contributed to the graphic work. All authors contributed to scientific discussions. F.X. conceived the original idea and supervised the project.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qin, H., Wu, D., Sathian, J. et al. Tuning the upconversion photoluminescence lifetimes of NaYF4:Yb3+, Er3+ through lanthanide Gd3+ doping. Sci Rep 8, 12683 (2018). https://doi.org/10.1038/s41598-018-30983-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-30983-9
This article is cited by
-
Upconversion Spectral Modulation and Temperature Sensing of NaYF4:Yb3+/Ho3+/Tm3+/Gd3+ Nanorods with Resistance to Thermal Quenching
Journal of Electronic Materials (2024)
-
Near-infrared excitation/emission microscopy with lanthanide-based nanoparticles
Analytical and Bioanalytical Chemistry (2022)
-
Upconversion and Near Infrared Emission of Rare Earth Ions in Chalcohalide Glass at the Early Stage of Crystallization
Journal of Wuhan University of Technology-Mater. Sci. Ed. (2022)
-
Fast wide-field upconversion luminescence lifetime thermometry enabled by single-shot compressed ultrahigh-speed imaging
Nature Communications (2021)
-
Assessing the protective effects of different surface coatings on NaYF4:Yb3+, Er3+ upconverting nanoparticles in buffer and DMEM
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.