Abstract
Here we show how the size of a body affects its maximum average speed of movement through its environment. The theoretical challenge was to predict that ‘outliers’ must exist, such as the cheetah for terrestrial animals and the jet fighter for airplanes. We show that during a travel that starts from rest and continues at cruising speed, the body size for minimum travel time, or maximum average speed, is not the biggest. The results are compared with extensive data for military aircraft for chase, attack and reconnaissance, in addition to data for commercial aircraft. The paper also explains why in earlier studies of flying (animals, airplanes) the airplane data deviated upward (toward greater speeds) relative to the theoretical trend followed by flying animals, and why the fastest animal flyers are one thousand times smaller than the fastest swimmers. Unlike the biggest animals and airplanes (elephant, whale, commercial jet), which move constantly, the fastest animals and airplanes spend most of their lives at rest. When judged for speed averaged over lifetime, the fastest ‘sprinters’ are in fact the slowest movers (as in Aesop’s fable ‘The Tortoise and the Hare’).
Similar content being viewed by others
Introduction
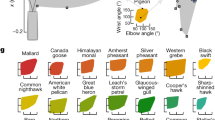
Bigger bodies tend to move faster on land, in water, and in the air. This broad trend is supported by the speed-size data collected from many sources for flying, running and swimming (Fig. 1)1. On this unifying background, outliers exist. The burst speed of the cheetah is greater than the steady speed of the elephant. The tuna can swim faster than the steady whale. There are outliers that are even more distant from the general trend, but they should not be confused with the fastest runners, swimmers and fliers. For example, there are insects (e.g., the flea) that snap and jump at speeds much greater than what their speed-mass scaling law would predict. The ant odontomachus holds this kind of speed record (of order 200 km/h) by snapping its jaws shut, in order to jump to the side, to get out of the way of danger. This is a one-shot event, not cyclical locomotion. Most of her life, this ant walks on land at ant speed, in accord with the speed-mass scaling law for animal locomotion1.
Animal speed-mass data (fliers, runners, swimmers) compiled from sources indicated in ref.1.
Hirt et al.2 addressed this aspect of animal locomotion with a model chosen to account for the starting (accelerating) period in the movement of the fastest animals. The model consisting of elastic fast-twitch fibers was constructed such that the speed emerges as a concave function of body size, with its peak at a body size that is not the largest size (Fig. 2). Bejan3 observed that the existence of body size for peak speed also rules the evolutionary design of jet fighter aircraft, which is the human made counterpart of the animal of prey, with a high burst speed followed by a long period of inactivity on the ground.
The following analysis is a theoretical treatment of this physics aspect of locomotion. It is a generalization of the unifying theory of animate, inanimate and vehicle movement, which includes the lifetime and life travel of animate and inanimate movement4.
Additionally, the following theory accounts for several features of the alignment of locomotion data that have not been questioned. One is the fact that the data for airplanes in Fig. 1 are not aligned with the data for animal fliers. Why are the airplane data trending above the animal speed-mass correlation? Why do the airplane data fall on a steeper line than the data for animal fliers? Moving over to Fig. 2, why does the body size for peak speed decrease in the direction from swimming to running and flying?
Theory
Consider the body of a vehicle or animal of size M [kg] moving horizontally on the earth’s surface to a distance L. The body starts from rest (V = 0), is then accelerated to the cruising speed Vc over the distance La and time interval ta. The body continues its travel at cruising speed Vc over the distance Lc and time interval tc. We ask what size (M) enables the body to travel the distance L = La + Lc the fastest.
The body M moves because it is driven by power. The power comes from an engine (animal, or human made). The power produced by the engine for the purpose of forcing the motion is4
where \(\dot{{\rm{Q}}}=\dot{{\rm{m}}}H\) is the rate of heat transfer that drives the engine, \(\dot{{\rm{m}}}\,[{\rm{kg}}/{\rm{s}}]\) is the rate of fuel (or food) consumption, and H [J/kg] is the heating value of the consumed fuel.
Recent physics articles5,6 showed that for maximum efficiency the engine size must have the same scale as the body size M, which is why in the following analysis M is the scale of the body plus the engine. In other words, the moving body has a single size scale, M. Next, the phenomenon of economies of scale requires the efficiency to increase monotonically with the body size,
where the exponent α is less than 1, for example, α = 1/4 for helicopter engines7, and α = 5/12 for animal locomotion (flying, running, swimming)4. In Fig. 3 we show that economies of scale are also present in the evolution of jet engines for aircraft, and that the exponent α is of order 0.14. The data8 plotted in Fig. 3 are tabulated in Supplementary Material. The R2 value is 0.52 and the P value is below 0.001, therefore the correlation is statistically significant9. Combining Eqs (1) and (2) we find that the power that drives the body is
The power is dissipated in three ways:
-
(i)
To accelerate the body,
-
(ii)
To lift the body (or an equivalent body of water in the case of swimmers1), and
-
(iii)
To overcome the drag posed by the medium relative to which the body is moving.
We distinguish two sequential regimes of movement: acceleration, defined such that (ii) and (iii) are negligible compared with (i), and cruise, in which (i) is negligible compared with (ii) and (iii).
Acceleration
During acceleration, the power exerted by the motor on the body is matched by the force of accelerating the mass (MdV/dt) times the instantaneous speed V,
Integrating this equation from t = 0 to t = ta, where V = Vc, we find
where ma is the amount of fuel used over the acceleration period, and \(\overline{{\dot{{\rm{m}}}}_{{\rm{a}}}}\) is the average fuel consumption rate (ma/ta) during that period.
The theoretical cruising speed Vc emerged1 as the trade off between the power spent on lifting (ii) and the power spent on overcoming drag (iii). The cruising speed depends monotonically on body size,
where C2 = rg1/2 ρ−1/6, where ρ is the body density, and r accounts for the medium in which the body is moving: r = (ρ/ρa)1/3, where ρ is the body density and ρa is the density of the ambient. Representative ranges of values are r ~ 10 for fliers, r ~ 1 for swimmers, and 1 < r < 10 for terrestrial locomotion. Combined, Eqs (6) and (8) confirm one side of the trade off noted at the start: bigger bodies take longer to be accelerated to their cruising speed:
Cruise
The corresponding analysis for the cruising period begins with Eq. (8), where Vc = Lc/tc. The engine work spent over Lc is
The travel time tc is shorter when the body is bigger, and this confirms the second side of the trade off,
The size trade off
A first glimpse at the trade off that determines the body size for shortest travel time is possible if we assume that the fuel consumption rate is represented by a known constant, \({\dot{{\rm{m}}}}_{{\rm{a}}}={\dot{{\rm{m}}}}_{{\rm{c}}}\). The analysis begins with Eq. (11) by replacing Lc with (L − La), where L is fixed and La is given by Eq. (7). The total travel time, or the inverse of the speed averaged over the distance L, is
with the condition that La < L. Equation (12) can be nondimensionalized by introducing the cruising speed of a reference body of fixed unit mass, M0 = 1 kg, namely \({{\rm{V}}}_{0}={{\rm{C}}}_{2}{{\rm{M}}}_{0}^{1/6}\). Equation (12) becomes
where \({\tilde{{\rm{V}}}}_{{\rm{avg}}}={{\rm{V}}}_{{\rm{avg}}}/{{\rm{V}}}_{0}\,{\rm{and}}\,{{\rm{V}}}_{{\rm{avg}}}={\rm{L}}/({{\rm{t}}}_{{\rm{a}}}+{{\rm{t}}}_{{\rm{c}}}),\)
Equation (13) shows that the total travel time has a minimum with respect to body size. Alternatively, the speed averaged over the total travel has a maximum with respect to body size. The design for peak velocity is represented by
where
Figure 4 shows that the factors BM and BV are both of order 1, and are relatively insensitive to changes in the exponent α.
These results are in accord with the model of Hirt et al.2: the largest animal is not necessarily the fastest. The fastest travel emerges at an intermediate size in animals (and vehicles) where the accelerating period is not negligible in comparison with the total travel time. This feature belongs to animals of prey and jet fighters. Another conclusion is that even the fastest [Eqs (17) and (18)] obey the theoretical1 proportionality between speed and mass raised to the power 1/6, as in Eq. (8), namely
The analysis presented above is based on the simplifying assumption that the fuel consumption rate \(\dot{{\rm{m}}}\) is a constant. If we also account for the body size effect on \(\dot{{\rm{m}}}\), we can repeat the analysis by replacing \(\dot{{\rm{m}}}\) with C3Mβ, where, as we show next, the exponent β is approximately 1/2. The β exponent has been found previously in two ways, empirically for commercial airplanes6, and theoretically for animals4. Specifically, for airplanes the fuel load is roughly M/3, the range is statistically proportional to M0.64, and if we take the average speed to be proportional to M1/6 we conclude that β ≅ 0.53. For animals, the analysis detailed in ref.10 concluded with β = 0.5. This means that in the results presented above C1 is replaced by C1C3, and α is replaced by α + β. In other words, the value of the exponent \({\rm{\alpha }}\lesssim {\rm{0.5}}\), which was used until now, is replaced by an exponent with a value \({\rm{\alpha }}+{\rm{\beta }}\lesssim {\rm{1}}\). Looking at Fig. 4, we see that the change from 0.5 to 1 on the abscissa does not have a meaningful effect on BM, BV and Eq. (21).
The fastest airplanes
The quest for speed in human flight has a rich history dominated by the development of military aircraft for attack and reconnaissance10. Highlights are collected chronologically in Fig. 5 (top) and Fig. 6. The data plotted in these figures are tabulated in Supplementary Material. The sequence of frames in Fig. 6 focuses progressively on earlier stages of the development of fast models. Figure 7 (top) shows the evolution of the speeds of military aircraft over time.
The broad view conveyed by Figs 5–7 is that during the past eight decades the fastest models have been joined by even faster models that are also bigger. The theoretical trend derived in Eq. (21) matches the cloud of data of commercial aircraft and early military models compiled in Fig. 5 (top). Several approximating assumptions were made in tracing the two lines, namely r ≈ 10, Bv ≈ 1.5 and BM ≈ 0.2. For the average density of the aircraft [ρ in the C2 formula under Eq. (8)] we used the method of ref.11, which shows that the density of the fuselage of the B747-400 is 31.9 kg m−3, or 3 percent of the density of water. We indicated this order of magnitude as the band between ρ = ρwater/100 and ρ = ρwater/10.
Most of the data for the fastest military models fall above the trend traced with Eq. (21) in Fig. 5 (top). The explanation has its origin in the fact that the early military models flew at subsonic speeds and at altitudes comparable with those of contemporary commercial models. Although the fastest military models since the 1950s have supersonic speeds, they also fly at higher altitudes.
Figure 7 (bottom) complements Fig. 5 (top) by showing the altitude ceiling of each of the models. At higher altitudes the air density is lower, and the r factor (in C2, and later in Vpeak) is greater. Specifically, if in the r definition
ρa is the air density at low altitudes that are comparable with ground level, then the correct r factor that belongs in the theoretical result for Vpeak [Eq. (21)] is
where
The new factor R is monotonically greater than 1 as the ceiling altitude plotted in Fig. 7 (bottom) increases.
Why airplanes deviate from flying animals
The flying altitude has a predictable effect on the maximum theoretical speed, Eq. (23), because Vpeak is proportional to r. To bring this effect into view, in Fig. 5 (bottom) we repeated the data of Fig. 5 (top) by plotting on the ordinate V/R in place of V. This way we removed the effect of altitude, in other words, we referenced all the theoretical speeds to the r value that corresponds to air density at ground level.
The R values employed in Fig. 5 (bottom) come from Eq. (24) and the relationship between altitude and atmospheric air density12. For example, at an altitude of 10 km the air density is 0.41 kg/m3 at −50 °C, while at ground level at 20 °C it is 1.2 kg/m3. In this numerical example R is approximately 0.15.
Compare Fig. 5 (bottom) with Fig. 5 (top). The speed data collapse on the theoretical trend obeyed by animals when the altitude effect (R) is taken into account. The correctness of the theory is strengthened if we replot the classical animal speed data of Fig. 1 as V/R versus M, in place of V versus M. This new representation is provided in Fig. 8. It is now evident why in the original version of Fig. 1 the airplane data deviate above the theoretical trend. With the effect of altitude taken into account, the theory covers correctly all the speed data, from animals (Fig. 1) to commercial and military aircraft (Figs 5–7). Noteworthy is also that the airplane data condensed now in the V/R-revised Fig. 5 (bottom) and Fig. 8 show a hump (i.e., a maximum speed at an intermediate size), which is reminiscent of the animal data plotted in Fig. 2.
Revised version of Fig. 1, showing that the aircraft data line up with the animal fliers when the effect of lower air density and drag at higher altitudes is taken into account.
Why the fastest fliers are significantly smaller than the fastest swimmers
The animal data compiled in Fig. 2 show that the peak speeds of animals have the same order of magnitude (100 km/h), but the fastest flier is three orders of magnitude smaller than the fastest swimmer. Here is why this effect is in accord with the theory that concluded with Eqs (17–20):
Note that the body size for peak speed (Mpeak) is proportional to A raised to the power −1/(3/2–α), where α is positive and smaller than 1. In other words, the theoretical Mpeak is expected to vary roughly as 1/A, where A is proportional to \({{\rm{C}}}_{2}^{3}\), or r3g3/2ρ−1/2. In conclusion, Mpeak should vary roughly as r−3, that is in proportion with the density of the ambient, ρa.
The density of the ambient decreases by a factor of 103 from animal swimmers to animal fliers. Figure 2 shows that the body size of the fastest animals decreases by the same factor from swimmers to fliers. This suggests that the clouds of data for swimmers and fliers would fill the same cloud if on the abscissa the body sizes (M) are multiplied by r3, with r ~ 10 for fliers, r ~ 1 for swimmers, and an in-between r value such as 3 for runners.
The theory advanced in this paper is less conclusive with regard to the effect of the ambient on the peak speeds of animals, fliers versus swimmers. According to Eq. (18), the peak speeds should vary as \({{\rm{M}}}_{{\rm{peak}}}^{1/6}\), which means that Vpeak should vary roughly as r−1/2, or (ρ/ρa)−1/6. Taking r ≈ 10 for fliers and r ≈ 1 for swimmers, the prediction is that Vpeak for fliers should be 1/3 of the Vpeak for swimmers. The opposite trend is exhibited by the data in Fig. 2.
Economies of scale
Bigger movers are more efficient movers. This aspect of the physics of powered locomotion is the basis of the present theory, starting with Eq. (2) with α < 1, and Fig. 3. This phenomenon is recognized more generally as economies of scale. Here we have the opportunity to show that the phenomenon is visible not only after plotting engine efficiencies versus size, as in Fig. 3, but also by looking at how airplanes are configured.
In Fig. 9 and Table 1 we used three airplane models to illustrate the evolution of the biggest transport aircraft that flies today. From the B52 to the B747 and the B777, the engine thrust (the force) and size (mass) increased by a factor of order 10. The number of engines decreased by a similar factor, from 8 to 4, and finally 2.
The evolution of the thrust and number of jet engines on three of the largest aircraft in service today (Table 1).
From the point of view of the whole vehicle, the evolution means something different. The data on the right side of Fig. 9 show the total thrust and total mass of the engines that drive the airplane. The data line up on the vertical, which means that the B52 from 1956 is driven by the same engine mass as the B747 of 1984 and the B777 of 2004. The difference and the message are on the vertical. From the 1950s to the 1980s, the total engine mass is essentially the same, the total thrust increased by an order of magnitude, and the size of the vehicle increased by a factor of the same order, from the B52 to the B747 and B777.
In sum, the evolution has been toward bigger force, bigger size, and more efficient engines, over time.
Concluding remarks
In this paper we relied on physics to show how the body size controls the maximum speed through the environment. The original challenge was to predict from theory that ‘outliers’ such as the cheetah must exist. The physical reason for outliers is that animals do not move the same way during their daily life. Grazing animals move constantly and eat constantly, while predators move and eat in spurts. In fact, predators spend most of their lives at rest, sleeping or watching the prey.
We showed that what accounts for the animal outlier (higher speed at smaller body mass) also accounts for the vehicle outlier. Military aircraft for chase, attack and reconnaissance are smaller and reach speeds higher than the biggest commercial aircraft. Yet, like the cheetah, the jet fighter spends most of its active life at rest, on the ground, out of sight.
The theoretical line pursued in this paper revealed two unexpected opportunities to complete the physics theory of animal and human flight. One was the deviation of the commercial aircraft data (upward, relative to animal data) in Fig. 1. The cause is the higher altitude of flying aircraft, where the air density is lower than close to the ground, and consequently the theoretical speeds must be higher. When the flying altitude effect is taken into account, the animal and aircraft data line up together (Fig. 8).
The second unexpected opportunity was to explain why the fastest animal fliers are 103 times smaller than the fastest animal swimmers (Fig. 2). The explanation is in the theoretical formulas for maximum-speed locomotion. The body size for maximum speed depends on the density of the medium (ρa) through which the animal is moving. The theoretical body size is approximately proportional to ρa/ρ, and this ratio decreases by a factor of 103 from the ρa of water to the ρa of air.
The practical usefulness of these theoretical advances is that they help us fast-forward the evolution of vehicle technology. This benefit was already demonstrated with the transition from the physics theory of all animal locomotion1,4, which revealed the main scaling laws of all moving animal design, to predicting the scaling laws of commercial airplanes6 and helicopters7, which have ‘converged’ naturally (from numerous disconnected designers and groups) during the documented lives of these technologies. It stands to reason that with the new theory and the morphological trends of modern aircraft reported in the present paper (e.g., sections 2–8 and Figs 5–10), designers, teams and industries will see more directly and more clearly the future of such vehicles. This predictive power of evolutionary design returns the favor to biology, for which it provides ample evidence of the natural phenomenon of evolution, which is observable in our lifetime13.
The lifetime-averaged speeds of current aircraft, showing the new ‘outlier’ position of the jet fighter (Table 2).
The speed ‘outlier’ phenomenon covered in this paper can be read from the much older perspective offered in Aesop’s fable “The Tortoise and the Hare”. What matters in the life of the mover is the movement (the territory covered, the speed averaged) over the lifetime. In Table 2 and Fig. 10 we brought together the lifetime speed and distance data of the work horses of commercial aviation and one jet fighter, the F-18A. This new presentation gives the word ‘outlier’ an entirely different meaning: the jet fighter is the outlier because during its lifetime it is slower than the bigger, the commercial aircraft. This new meaning is in fact the oldest, taught by Aesop.
References
Bejan, A. & Marden, J. M. Unifying constructal theory for scale effects in running, swimming and flying. J. Exp. Biol. 209, 238–248 (2006).
Hirt, M. R., Jetz, W., Rall, B. C. & Brose, U. A general scaling law reveals why the largest animals are not the fastest. Nat. Ecol. Evol. 1, 1116–1122 (2017).
Bejan, A. interviewed in S. Devos, Sa vitesse cache une théorie de la masse. Science & Vie 75–77 (2017).
Bejan, A. Why the bigger live longer and travel farther: animals, vehicles, rivers and the winds. Sci. Rep. 2, 594 (2012).
Bejan, A., Almerbati, A. & Lorente, S. Economies of scale: The physics basis. J. Appl. Phys. 121, 594, 044907 (2017).
Bejan, A., Charles, J. D. & Lorente, S. The evolution of airplanes. J. Appl. Phys. 116, 044901 (2014).
Chen, R., Wen, C. Y., Lorente, S. & Bejan, A. The evolution of helicopters. J. Appl. Phys. 120, 014901 (2016).
Meier, N. Jet Engine Specification Database. Available at: http://jet-engine.net/ (Accessed: 28th February 2018).
Vogt, W. P. & Johnson, B. Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. (SAGE Publications, 2011).
Fighter Planes. Fighter Planes Available at: https://www.fighter-planes.com/ (Accessed: 21st May 2018).
Chambers, M. C. et al. Analytical Fuselage and Wing Weight Estimation of Transport Aircraft. (1996).
U. S. Standard Atmosphere Supplements, 1966. 292 (NASA, 1966).
Bejan, A. The Physics of Life: The Evolution of Everything (St. Martin’s Press, New York, 2016).
777-300ER. GE Aviation Available at: https://www.swiss.com/CMSContent/web/SiteCollectionDocuments/777/SWISS_Factsheet_B777-300ER_EN.pdf (Accessed: 28th February 2018).
Boeing 747–400. Boeing Available at: http://www.boeing.com/resources/boeingdotcom/company/about_bca/startup/pdf/historical/747-400-passenger.pdf (Accessed: 28th February 2018).
B-52 Stratofortress. U.S. Air Force Available at: http://www.af.mil/About-Us/Fact-Sheets/Display/Article/104465/b-52-stratofortress/ (Accessed: 28th February 2018).
Connors, J. & Allen, N. The Engines of Pratt & Whitney: A Technical History. (American Institute of Aeronautics and Astronautics, 2010).
The CF6 Engine. GE Aviation Available at: https://www.geaviation.com/commercial/engines/cf6-engine (Accessed: 28th February 2018).
The GE90 Engine. GE Aviation Available at: https://www.geaviation.com/commercial/engines/ge90-engine (Accessed: 28th February 2018).
F/A-18 Hornet strike fighter. The US Navy Fact FileAvailable at: http://www.navy.mil/navydata/fact_display.asp?cid=1100&tid=1200&ct=1 (Accessed: 28th February 2018).
Boeing 737–800. Boeing Available at: http://www.airliners.net/aircraft-data/boeing-737-800900/96 (Accessed: 28th February 2018).
Airbus A320-200. GE Aviation Available at: http://www.airbus.com/aircraft/passenger-aircraft/a320-family/a320neo.html (Accessed: 28th February 2018).
Airbus A330-300. GE AviationAvailable at: http://www.airbus.com/aircraft/passenger-aircraft/a330-family/a330-300.html (Accessed: 28th February 2018).
Cooper, C. Bridging the Gap: Extending the Life of the F18 Hornet. (Master of Military Studies United States Marine Corps Command and Staff College Marine Corps University, 2011).
Aircraft and Related Datasets. MIT Global Airline Industry Program – Airline Data Project Available at: http://web.mit.edu/airlinedata/www/Aircraft&Related.html (Accessed: 21st May 2018).
Chang, F.-K. Structural Health Monitoring 2000. (CRC Press, 1999).
Jiang, H. Key Findings on Airplane Economic Life. Boeing White Pap. 9 (2013).
Acknowledgements
Prof. Bejan’s work was supported by the US National Science Foundation. Umit Gunes’ visit at Duke University was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK).
Author information
Authors and Affiliations
Contributions
A. Bejan and B. Sahin constructed the model. U. Gunes, and J. Charles performed the analysis numerically, and collected the new data for fast airplanes compiled in Supplementary Material. The text was written in multiple iterations by A. Bejan, B. Sahin, J. Charles and U. Gunes. The figures were made in multiple iterations by U. Gunes. and J. Charles.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bejan, A., Gunes, U., Charles, J.D. et al. The fastest animals and vehicles are neither the biggest nor the fastest over lifetime. Sci Rep 8, 12925 (2018). https://doi.org/10.1038/s41598-018-30303-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-30303-1
This article is cited by
-
Locomotion rhythm makes power and speed
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.