Abstract
Twisted light, having a helical spatial phase structure and carrying orbital angular momentum (OAM), has given rise to many developments ranging from optical manipulation to optical communications. The laser excitation of twisted light in a reconfigurable and tunable way is of great interest. Here, we propose and experimentally demonstrate an OAM reconfigurable and wavelength tunable twisted light laser with achievable high-order OAM modes on a hybrid free-space and fiber platform. The excited twisted light laser is enabled by a ring resonator incorporating spatial light modulators (SLMs) and bandpass filter (BPF). By appropriately switching the phase pattern loaded onto SLMs and adjusting the BPF, twisted light laser with reconfigurable OAM and tunable wavelength is implemented. In the experiment, the OAM value is varied from −10 to +10 and the wavelength is adjusted from 1530 to 1565 nm covering the whole C band. The obtained results indicate successful implementation of a reconfigurable and tunable twisted light laser with favorable operation performance. Reconfigurable and tunable twisted light laser may open up new perspectives to more extensive OAM-enabled applications with improved flexibility and robustness.
Similar content being viewed by others
Introduction
In recent years, the space domain of lightwaves has gained great interest in diverse applications. Exploiting the spatial structure of lightwaves enables a new kind of light beam called structured light beyond the well-known Gaussian light beam. In general, structured light manifests distinct spatial amplitude/phase/polarization distribution1,2,3,4,5. Among different kinds of structured light, a promising one is called twisted light, featuring a helical phasefront, a phase singularity, and a doughnut intensity profile. Since the early recognition in 1992 by Allen and co-workers that lightwaves comparising a helical phasefront exp(ilφ) have an orbital angular momentum (OAM) of lħ per photon (l: topological charge, φ: azimuthal angle, ħ: reduced Plank’s constant)2, OAM-carrying twisted light has given rise to many developments in optical manipulation, tweezer, microscopy, imaging, metrology, astronomy and quantum information processing6,7,8,9,10,11,12,13,14,15,16. Very recently, twisted light has also seen its potential applications in free-space, fiber-based and underwater optical communications with increased transmission capacity and efficient spectral usage17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36.
Remarkably, for all of the above OAM-enabled extensive applications, the generation of OAM-carrying twisted light is of great importance. Various techniques for generating OAM-carrying twisted light beams have been proposed and demonstrated over the past years6,7,8,18,19,20. In general, there are two kinds of techniques, i.e. external beam shaping and internal beam lasing. The external beam shaping technique usually transforms a Gaussian beam into an OAM-carrying twisted light beam, e.g. computer-generated hologram7,37, mode converte38, spiral phase plate39, inhomogeneous anisotropic media40, fiber41, metamaterials42,43,44,45,46,47 and photonic integrated devices48,49. These tehniques relying on external beam shaping, however, suffer from relatively low conversion efficiency, degradation of beam quality, high power handling limitation, and added complexity with extra bulky mode conversion devices. Alternatively, using internal beam lasing technique, OAM-carrying twisted light can be also generated inside a laser resonator (i.e. twisted light laser), which may overcome some drawbacks of external beam shaping technique. To date there have been lots of prior seminal works related to OAM-carrying twisted light laser and an increasing interest has been gained to control light’s helicty at the source (i.e. OAM states from lasers)50. For instance, (1) Laguerre-Gaussian (LG) modes were generated in Nd:YAG lasers51,52; (2) LG modes seletection was demonstrated in diode-pumped solid-state lasers53; (3) a doughnut laser beam was generated as an incoherent superposition of two petal beams54; (4) high-order mode excitation was demonstrated in end-pumped solid-state lasers55; (5) the controlled generation of higher-order Poincaré sphere beams was demonstrated from a laser56; (6) OAM microlaser was fabricated and demonstrated on the InGaAsP/InP platform57. These works showed impressive lasing performance. Beyond the basic realization of OAM-carrying twisted light laser, the functionality and robustness are also worth taking full consideration. For a robust OAM-carrying twisted light laser, one would expect reconfigurable OAM and tunable wavelength. Fortunately, several approaches have been reported to add OAM reconfigurability or wavelength tunability to the twisted light laser. For example, (1) a digital laser for reconfigurable on-demand laser modes was demonstrated by using a phase-only spatial light modulator (SLM) as the back optical element of the cavity58; (2) a tunable midinfrared (6.0–12.5 μm) vortex laser was demonstrated by rotating the cascaded KTP crystals59. Wavelength-versatile optical vortex lasers were also reported60. In the demonstrated reconfigurable digital laser and wavelength-tunable optical vortex laser, free-space resonator cavities were employed. Very recently, all-fiber based resonator cavity was also employed for generating optical vortex beams61,62. However, the achievable OAM modes (e.g. OAM±1) were limited by the few-mode fiber. The generation of high-order OAM modes is full of challenge. Actually, the resonator cavity can be also constructed by a hybrid configuration, i.e. the combined free-space and fiber resonator cavity. For instance, a low-noise stretched-pulse Yb3+-doped fiber laser was demonstrated using free-space resonator cavity incorporating a piece of Yb3+-doped fiber as the gain medium63. Using fiber as the gain medium to form free-space to fiber resonator cavities can add enhanced flexibility to the laser configuration, i.e. one can have more choices on either bulky gain medium or fiber-doped gain medium for the desired lasing wavelength range. For example, for the potential application of twisted light in optical communications, twisted light laser in the 1.55 μm wavelength range is highly desired. In such case, a piece of erbium-doped fiber (EDF), commonly used in the communication band fiber laser, is preferred. Meanwhile, the all-fiber approach has great limitation in the achievable OAM modes. Hence, a possible approach could be to incorporate the EDF inside a free-space resonator cavity. The EDF serves as the gain medium for lasing in the 1.55 μm wavelength range, and the free-space resonator cavity allows more achievable OAM modes (high-order OAM modes). Remarkably, although most of the previously demonstrated twisted light lasers on various platforms (free space, fiber, chip) with favorable performance might achieve either high-order modes, or mode reconfigurability, or wavelength tunability, simultaneous implementation of all of these functions is still challengeable. To meet the increasing demand on a diverse of OAM-enabled applications with variable OAM values and wavelengths, robust twisted light laser with achievable high-order OAM modes, OAM reconfigurability and wavelength tunability is highly desired. In this scenario, a laudable goal would be to develop an OAM reconfigurable and wavelength tunable twisted light laser.
In this article, we propose and demonstrate a twisted light laser with achievable high-order OAM modes, OAM reconfigurability and wavelength tunability. The ring resonator of the twisted light laser is built upon a hybrid free-space and fiber platform. SLMs and a bandpass filter (BPF) are inserted into the laser resonator. Twisted light laser with reconfigurable OAM value from −10 to 10 and tunable wavelength from 1530 to 1565 nm (C band) is demonstrated in the experiment.
Results
Concept and principle
In general, a Fabry-Perot (FP) cavity formed by two mirrors is employed to construct a laser64,65,66. For a laser with cavity that is cylindrically symmetric, the lasing beam profile is also circularly symmetric often best solved using the Laguerre-Gaussian (LG) modal decomposition. The lasing beam functions can be written in cylindrical coordinates using generalized Laguerre polynomials. Taking the OAM-carrying LG beam laser as an example, the electrical field of a typical LG beam at a distance z from the waist in the paraxial approximation can be expressed as7
where w(z) = w0[(z2 + zR2)/zR2]1/2 is the 1/e radius of the LG beam at distance z from the beam waist w0, ρ is the radial distance from the beam center, φ is the azimuthal angle, l is the topological charge, zR is the Rayleigh range, Lp|l| is the generalized Laguerre polynomial, k = 2π/λ is the wavenumber, λ is the wavelength, and (2p + |l| + 1)tan−1(z/zR) is the Gouy phase. Remarkably, LG0,+l with right-handed helical phase trajectory and LG0,−l with left-handed phase trajectory have the same spatial intensity distribution according to Eq. (1). Taking the typical FP cavity laser as an example, the scalar instantaneous electric field for LG0,+l and LG0,−l propagating in the forward direction can be written by
where w is the angular frequency and u(r) is a complex function denoting the amplitude of the electric field. After the reflection by a cavity mirror, the scalar instantaneous electric field for LG0,+l and LG0,−l propagating in the backward direction can be expressed as
The superposition of forward and backward propagating electric fields gives the standing-wave electric field distribution for LG0,+l and LG0,−l as follows
As a result, the instantaneous standing-wave intensity distribution is expressed as
From Eq. (5), one can clearly see that in a traditional LG beam laser with two mirrors forming an FP cavity, LG0,+l and LG0,−l beams have 2|l|-lobed transverse intensity distribution and always exist simultaneously. Note that although the forward and backward propagating electric fields overalp at a plane inside the cavity, the actual output even from a FP cavity is only the traveling wave. In particular, for a unidirectional ring resonator configuration, the electric field for LG0,+l and LG0,−l propagating in the ring resonator can be expressed as
The superposition of LG0,+l and LG0,−l (zero radial order and azimuthal order l) with different intermodal phase shift can be written by54
Eqs (7) and (8) give even and odd petal modes with 2|l|-lobed transverse intensity distributions expressed as
From Eqs (6–10), one can understand the laser principle in another way. The phase only azimuthal terms are not real-valued functions. It is the even and odd petal modes that are the real solutions to the wave equation.
In order to realize either LG0,+l or LG0,−l lasing, one may break the degeneracy of a standard laser cavity. One possible way is to insert an extra carefully designed mode-selection element (MSE) into the cavity64,66. Using pump control to produce desired modes or developing micro-chip laser could avoid the use of MSE inside the cavity51,52,57. Alternatively, a unidirectional ring resonator configuration with determined OAM value assisted by intra-cavity SLMs could be considered to overcome the shortcoming of the traditional FP cavity based laser.
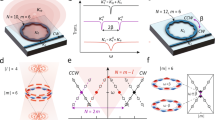
The concept and schematic structure of the proposed reconfigurable and tunable twisted light laser is illustrated in Fig. 1. The gain medium of erbium-doped fiber (EDF) pumped with a 980 nm laser enables the lasing wavelength in the C band. For a ring resonator both clockwise (CW) and counterclockwise (CCW) propagation beams are supported. To ensure the unidirectional lasing, an isolator (ISO) is inserted into the ring resonator. To avoid simultaneous lasing of two OAM modes with opposite topological charges, a free-space Gaussian-OAM-Gaussian conversion module is inserted into the ring resonator. Hence, the twisted light laser shown in Fig. 1 is based on the hybrid free-space and fiber platform. The fiber part using fiber pigtailed components constructs the main ring resonator and provides the gain. The free-space part determines the desired OAM value of the twisted light for lasing. The Gaussian-OAM-Gaussian conversion module includes Gaussian-to-OAM conversion, OAM-to-Gaussian back conversion, and OAM output, as depicted in the inset of Fig. 1. Remarkably, the Gaussian-to-OAM conversion is enabled by an SLM loaded with a spiral phase pattern, simply expressed as
Concept and principle of the reconfigurable and tunable twisted light laser. It is a ring resonator configuration based on hybrid free-space and fiber platform. The gain medium of erbium doped fiber (EDF) pumped by a 980 nm laser enables lasing wavelength in the C band. An isolator (ISO) ensures unidirectional lasing. A Gaussian-OAM-Gaussian conversion module, including Gaussian-to-OAM and OAM-to-Gaussian by spatial light modulators (SLMs) and OAM output, supports determined reconfigurable OAM-carrying twisted light lasing. A tunable bandpass filter (BPF) enables wavelength tunable lasing.
The spiral phase pattern converts the planar phasefront of a Gaussian beam from fiber to the helical phasefront of an OAM-carrying twisted light beam. A part of the twisted light serves as the OAM output. The OAM-to-Gaussian back conversion is realized by another SLM loaded with an inverse spiral phase pattern written by
The inverse spiral phase pattern removes the helical phasefront of the OAM-carrying twisted light beam and back convert it to a Gaussian-like beam, which is further fed into the fiber. The key components are SLMs supporting determined reconfigurable OAM-carrying twisted light lasing. The OAM conversion from Gaussian beam and back conversion to Gaussian-like beam ensure the seamless connection between the fiber part and free-space part on the hybrid free-space and fiber platform. To realize the wavelength tunable lasing, a tunable bandpass filter (BPF) is inserted into the ring resonator. As a consequence, by properly switching the phase patterns loaded onto SLMs to determine the desired OAM value and adjusting the BPF to change the lasing wavelength, an OAM reconfigurable and wavelength tunable twisted light laser can be implemented using the modified ring resonator configuration shown in Fig. 1 based on the hybrid free-space and fiber platform.
Experimental Configuration
Figure 2 shows the experimental configuration of the reconfigurable and tunable twisted light laser. It has a ring resonator incorporating an EDF as the gain medium pumped by a 980 nm laser, an ISO for unidirectional lasing, a Gaussian-OAM-Gaussian conversion module for determined OAM reconfigurable operation and OAM output, and a tunable BPF for wavelength tunable operation. The 980 nm pump laser is fed into the ring resonator via a coupler. The gain medium of EDF supports lasing in the 1.55 μm band (C band). A polarization controlled (PC) is used to adjust the polarization to be aligned to the polarizer (Pol.) for optimized efficiency. An ISO ensures only CCW propagation inside the ring resonator. After a collimator (Col.), the collimated fiber output Gaussian beam passes through a Pol. and a half-wave plate (HWP1) before shining on the SLM1. Pol. ensures a pure linear polarization. HWP1 adjusts the polarization to be aligned to the working direction of the SLM for efficient generation of OAM beam. SLM1 is loaded with a spiral phase pattern for converting incident Gaussian beam to an OAM beam (Gaussian-to-OAM conversion). After SLM1, another HWP2 and a polarization beam splitter (PBS) are used to properly control the output power of the twisted light laser. The reflection port of PBS delivers the OAM output. The transmitted twisted light laser via the through port of PBS is sent to another SLM2 for OAM-to-Gaussian conversion. SLM2 loaded with another phase pattern converts the OAM beam back to a Gaussian-like beam, which is coupled back to the fiber. The followed tunable BPF enables the changeable lasing wavelength. The output of BPF is connected to the coupler together with the 980 nm pump laser for constructing the ring resonator. The intensity profile of the output OAM-carrying twisted light laser is observed by a camera not shown in Fig. 2. The OAM values of twisted light can be determined by its interferogram (interference with a reference Gaussian beam) or back conversion to a Gaussian-like beam by a third SLM3 loaded with the detection phase pattern. An optical spectrum analyzer (OSA) is used to observe the spectra. With proper update of phase patterns loaded onto SLMs and adjustment of BPF, OAM reconfigurable and wavelength tunable twisted light laser is achievable.
Experimental configuration of reconfigurable and tunable twisted light laser. EDF:erbium-doped fiber; PC: polarization controller; ISO: isolator; Col: collimator; Pol.: polarizer; HWP: half-wave plate; SLM: spatial light modulator; PBS: polarization beam splitter; BPF: bandpass filter; OSA: optical spectrum analyzer.
Results
In order to realize OAM reconfigurable twisted light laser (OAM value: −10 to 10) in the following experiment, we prepare corresponding spiral phase patterns to be switchably loaded onto the SLMs, which are shown in Fig. 3. We also simulate the generation of different OAM modes during the Gaussian-to-OAM conversion process shown in the inset of Fig. 1. Figure 4 shows the simulated intensity and interferogram of different OAM modes. One can see the generated OAM beams appear to be hypergemetric (with many rings). This might be explained with the fact that directly adding a spiral phasefront to a Gaussian beam gives an OAM beam but not a perfect OAM-carrying LG mode (zero radial order and azimuthal order l). Nevertheless, such OAM beams using straightforward and easy generation method and having all typical properties of OAM, are also widely used in different applications6,7,8,9,17,18,19,20,22. The interferograms (number of twists and twist direction) confirm the helical phase structures (OAM properties) of OAM beams.
In the experimental configuration shown in Fig. 2, the combined use of HWP2 and PBS facilitates flexible output power adjustment by properly changing the relative angle between HWP2 and PBS. In the experiment, we first adjust the HWP2 to get the lowest output power and record its position as the start angle of 0 degree between the HWP2 and the through port polarization direction of PBS. Figure 5(a) shows measured output power for OAM+1 and OAM−5 as a function of the relative angle between the HWP2 and the through port polarization direction of PBS. With the increase of the relative angle, the output power increases first and then decreases. Note that when HWP2 rotates by α degree, the output light rotates by 2α degree compared to the incident light. Hence, one can clearly see the periodical behavior in Fig. 5(a) with a period of 90 degree. In particular, it is expected to achieve the maximum output power under a relatively angle of 45 degree when the HWP2 outputs light polarization aligned to the reflection port polarization direction of PBS. However, such maximum output power is not observed in Fig. 5(a), but a drop of output power is obtained instead. Such interesting phenomena can be briefly explained as follows. When adjusting the HWP2 and increasing the output power, the loss introduced in the ring resonator also increases. The maximum output power corresponds to the minimum power left in the ring resonator, leading to the failure of lasing. The shadow regions in Fig. 5(a) correspond to the amplified spontaneous emission (ASE) noise output, which should be avoided for the twisted light laser. To verify the laser output and ASE noise output, we measure the typical spectra outside and within the shadow regions, as shown in Fig. 5(b,c) for OAM+1 and Fig. 5(d,e) for OAM−5. One can clearly see the narrow lasing spectra in Fig. 5(b,d) and broad ASE noise spectra (limited by the filtering shape of BPF) in Fig. 5(c,e).
Measured results for flexible output power adjustment and typical lasing and ASE noise spectra. (a) Output power of twisted light laser versus relative angle between the HWP2 and the through port polarization direction of PBS in Fig. 2. Shadow regions: failure of lasing (ASE noise output). (b) Lasing spectrum for OAM+1. (c) ASE noise spectrum for OAM+1. (d) Lasing spectrum for OAM−5. (e) ASE noise spectrum for OAM−5. (b, d) Outside shadow regions in (a). (c,e) Within shadow regions in (a).
We first demonstrate OAM reconfigurable twisted light laser. As shown in Fig. 6(a), the OAM value is varied from −10 to 10 simply by switching the order of spiral phase patten loaded onto SLMs. The lasing wavelength is 1550 nm. The typical enlarged spectra for OAM+3 and OAM−10 are depicted in Fig. 6(b,c), respectively. To confirm the successful lasing output of twisted light, we observe the intensity profiles and interferograms of twisted light by a camera, as shown in Fig. 6(d,e). The intensity profiles of OAM beams have doughnut shape with null intensity at the beam center due to phase singularity. The radius of the doughnut shape also increases with the order of OAM beam. One can also observe hypergeometric intensity profiles (multiple rings), which agree with the simulation results shown in Fig. 4. In the interferograms, the numer of twists and the twist direction indicate the magnitude of sign of OAM, respectively. From Fig. 6(d,e) one can confirm the successful output of OAM+3 and OAM−10 carrying twisted light laser.
Measured results for OAM reconfigurable twisted light laser. (a) Measured spectra for twisted light laser with variable OAM values from −10 to 10. The lasing wavelength is 1550 nm. (b, c) Enlarged spectra for OAM+3 and OAM−10. (d,e) Measured intensity profiles and interferograms for OAM+3 and OAM−10. (b,d) OAM+3. (c,e) OAM−10.
We then demonstrate wavelength tunable twisted light laser. As shown in Fig. 7(a), the lasing wavelength is changed from 1530 to 1565 nm simply by adjusting the tunable BPF in the ring resonator. The twisted light laser is OAM+1. The typical enlarged spectra for 1550 nm and 1565 nm are depicted in Fig. 7(b,c), respectively. The recorded intensity profiles and interferograms of twisted light OAM+1 at 1550 nm and 1565 nm are shown in Fig. 7(d,e), respectively.
Measured results for wavelength tunable twisted light laser. (a) Measured spectra for twisted light laser with tunable wavelength from 1530 to 1565 nm. The twisted light laser is OAM+1. (b,c) Enlarged spectra for 1550 and 1565 nm. (d,e) Measured intensity profiles and interferograms for 1550 and 1565 nm. (b,d) 1550 nm. (c,e) 1565 nm.
We further study the threshold of the twisted light laser. Figure 8 plots measured output power of twisted light laser as a function of the pump power for OAM+1 and OAM−5. It is shown that the twisted light laser has a lasing threshold of ~180 mW.
The obtained results shown in Figs 4–8 indiciate the successful implementation of OAM reconfigurable and wavelength tunable twisted light laser with favorable operation performance.
Discussion
In summary, we design and demonstrate a reconfigurable and tunable OAM-carrying twisted light laser on a hybrid free-space and fiber platform. Instead of using traditional FP cavity, a ring resonator structure is employed. It consists of an EDF serving as the gain medium, a 980 nm pump laser, an ISO ensuring unidirectional lasing, a Gaussian-OAM-Gaussian conversion module supporting determined OAM reconfigurable operation and OAM output, and a tunable BPF enabling wavelength tunable operation. We study in detail the flexible output power adjustment, OAM reconfigurable twisted light laser, wavelength tunable twisted light laser, and the lasing threshold. In the experiment, twisted light laser with reconfigurable OAM from −10 to 10 and tunable wavelength from 1530 to 1565 nm covering the C band is demonstrated. The lasing threshold is measured to be ~180 mW (980 nm pump power).
The demonstrated reconfigurable and tunable twisted light laser features two distinct features as follows.
-
(1)
The hybrid free-space and fiber platform provides added flexibility to construct the laser configuration, offering more choices on either bulky or fiber-doped gain medium for the desired lasing wavelength range.
-
(2)
Simultaneous high-order OAM modes, OAM reconfigurability and wavelength tunability are realized by incorporating SLMs and BPF inside the ring cavity, which are challengeable in previous demonstrations.
Because of the above two advantages, the presented twisted light laser shows successful lasing of high-order OAM modes, reconfigurable OAM (−10 to 10) and tunable wavelength (1530 to 1565 nm) in the optical communication band (C band), which has not yet been demonstrated before.
Remarkably, the demonstrated twisted light laser also has several aspects worth improving.
-
(1)
The generated OAM beams appear to be hypergeometric with multiple rings as shown in both simulations and experiments. Although the OAM properties are still preserved and already widely used in many applications, one would expect to obtain perfect OAM modes such as LG modes. Fortunately, LG mode generation using SLMs has already been demonstrated67,68,69, which might be used for future performance improvement of the mode quality.
-
(2)
The constructed ring cavity resonator could lead to longitudinal modes instability for many cases (e.g. mechanical vibrations, thermal influences), which might become a potential cause for performance degradation of the twisted light laser. To overcome the longitudinal modes instability, several approaches have been proposed in the past decade. Recently, the combination of self-injection locking and stimulated thermal Rayleigh scattering was reported to enable longitudinal modes stability70,71, which might be used for future performance improvement of the mode stability.
In addition to the demonstrated continuous wave twisted light laser, other types of lasers such as single-longitudinal-mode twisted light laser and mode-locked fs pulsed twisted light laser could be considered with future improvement.
The demonstrations, indicating successful realization of reconfigurable and tunable twisted light laser, may further find a diverse of applications relying on flexible and robust generation of OAM-carrying twisted light beams. The hybrid free-space and fiber platform forming a laser resonator cavity with enhanced flexibility might be further developed to enable more general structured light laser.
References
Rubinsztein-Dunlop, H. Roadmap on structured light. J. Opt. 19, 013001 (2016).
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992).
Du, J. & Wang, J. High-dimensional structured light coding/decoding for free-space optical communications free of obstructions. Opt. Lett. 40, 4827–4830 (2015).
Zhao, Y. & Wang, J. High-base vector beam encoding/decoding for visible-light communications. Opt. Lett. 40, 4843–4846 (2015).
Liu, J. et al. Direct fiber vector eigenmode multiplexing transmission seeded by integrated optical vortex emitters. Light Sci. Appl. 7, 17148 (2018).
Franke‐Arnold, S., Allen, L. & Padgett, M. Advances in optical angular momentum. Laser Photon. Rev. 2, 299–313 (2008).
Yao, A. M. & Padgett, M. J. Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photon. 3, 161–204 (2011).
Forbes, A., Dudley, A. & McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photon. 8, 200c227 (2016).
Padgett, M. J. Orbital angular momentum 25 years on. Opt. Express 25, 11265–11274 (2017).
Dholakia, K. & Čižmár, T. Shaping the future of manipulation. Nature Photon. 5, 335–342 (2011).
Padgett, M. & Bowman, R. Tweezers with a twist. Nature Photon. 5, 343–348 (2011).
Bernet, S., Jesacher, A., Fürhapter, S., Maurer, C. & Ritsch-Marte, M. Quantitative imaging of complex samples by spiral phase contrast microscopy. Opt. Express 14, 3792–3805 (2006).
Lavery, M. P., Speirits, F. C., Barnett, S. M. & Padgett, M. J. Detection of a spinning object using light’s orbital angular momentum. Science 341, 537–540 (2013).
Fang, L., Padgett, M. J. & Wang, J. Sharing a common origin between the rotational and linear Doppler effects. Laser Photon. Rev. 11, 1700183 (2017).
Elias, N. M. II. Photon orbital angular momentum in astronomy. Astron. Astrophys. 492, 883–922 (2008).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001).
Willner, A. E., Wang, J. & Huang, H. A different angle on light communications. Science 337, 655–656 (2012).
Willner, A. E. et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 7, 66–106 (2015).
Wang, J. Advances in communications using optical vortices. Photon. Res. 4, B14–B28 (2016).
Wang, J. Data information transfer using complex optical fields: a review and perspective. Chin. Opt. Lett. 15, 030005 (2017).
Gibson, G. et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 12, 5448–5456 (2004).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nature Photon. 6, 488–496 (2012).
Bozinovic, N. et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 340, 1545–1548 (2013).
Wang, A. et al. Demonstration of hybrid orbital angular momentum multiplexing and time-division multiplexing passive optical network. Opt. Express 23, 29457–29466 (2015).
Huang, H. et al. Mode division multiplexing using an orbital angular momentum mode sorter and MIMO-DSP over a graded-index few-mode optical fiber. Sci. Rep. 5, 14931 (2015).
Wang, A. et al. Characterization of LDPC-coded orbital angular momentum modes transmission and multiplexing over a 50-km fiber. Opt. Express 24, 11716–11726 (2016).
Chen, S. et al. Full-duplex bidirectional data transmission link using twisted lights multiplexing over 1.1-km orbital angular momentum fiber. Sci. Rep. 6, 38181 (2016).
Zhu, L. et al. Orbital angular momentum mode groups multiplexing transmission over 2.6-km conventional multi-mode fiber. Opt. Express 25, 25637–25645 (2017).
Wang, A. et al. Directly using 8.8-km conventional multi-mode fiber for 6-mode orbital angular momentum multiplexing transmission. Opt. Express 26, 10038–10047 (2018).
Zhu, L., Wang, A., Chen, S., Liu, J. & Wang, J. Orbital angular momentum mode multiplexed transmission in heterogeneous few-mode and multi-mode fiber network. Opt. Lett. 43, 1894–1897 (2018).
Zhu, L. et al. 18 km low-crosstalk OAM + WDM transmission with 224 individual channels enabled by a ring-core fiber with large high-order mode group separation. Opt. Lett. 43, 1890–1893 (2018).
Ren, Y. et al. Orbital angular momentum-based space division multiplexing for high-capacity underwater optical communications. Sci. Rep. 6, 33306 (2016).
Zhao, Y. et al. Performance evaluation of underwater optical communications using spatial modes subjected to bubbles and obstructions. Opt. Lett. 42, 4699–4702 (2017).
Zhao, Y. et al. Demonstration of data-carrying orbital angular momentum-based underwater wireless optical multicasting link. Opt. Express 25, 28743–28751 (2017).
Wang, A. et al. Adaptive water-air-water data information transfer using orbital angular momentum. Opt. Express 26, 8669–8678 (2018).
Zhao, Y. et al. Feedback-enabled adaptive underwater twisted light transmission link utilizing the reflection at the air-water interface. Opt. Express 26, 16102–16112 (2018).
Heckenberg, N. R., McDuff, R., Smith, C. P. & White, A. G. Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 17, 221–223 (1992).
Beijersbergen, M. W., Allen, L., Van der Veen, H. E. L. O. & Woerdman, J. P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 96, 123–132 (1993).
Beijersbergen, M. W., Coerwinkel, R. P. C., Kristensen, M. & Woerdman, J. P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 112, 321–327 (1994).
Marrucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).
Li, S., Mo, Q., Hu, X., Du, C. & Wang, J. Controllable all-fiber orbital angular momentum mode converter. Opt. Lett. 40, 4376–4379 (2015).
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Zhao, Z., Wang, J., Li, S. & Willner, A. E. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams. Opt. Lett. 38, 932–934 (2013).
Du, J. & Wang, J. Design of on-chip N-fold orbital angular momentum multicasting using V-shaped antenna array. Sci. Rep. 5, 9662 (2015).
Du, J. & Wang, J. Dielectric metasurfaces enabling twisted light generation/detection/(de)multiplexing for data information transfer. Opt. Express 26, 13183–13194 (2018).
Zhao, Y., Du, J., Zhang, J., Shen, L. & Wang, J. Generating structured light with phase helix and intensity helix using reflection-enhanced plasmonic metasurface at 2 μm. Appl. Phys. Lett. 112, 171103 (2018).
Wang, J. Metasurfaces enabling structured light manipulation: advances and perspectives. Chin. Opt. Lett. 16, 050006 (2018).
Cai, X. et al. Integrated compact optical vortex beam emitters. Science 338, 363–366 (2012).
Su, T. et al. Demonstration of free space coherent optical communication using integrated silicon photonic orbital angular momentum devices. Opt. Express 20, 9396–9402 (2012).
Forbes, A. Controlling light’s helicity at the source: orbital angular momentum states from lasers. Phil. Trans. R. Soc. A 375, 20150436 (2017).
Bisson, J. F., Senatsky, Y. & Ueda, K. I. Generation of Laguerre-Gaussian modes in Nd: YAG laser using diffractive optical pumping. Laser Phys. Lett. 2, 327–333 (2005).
Okida, M., Omatsu, T., Itoh, M. & Yatagai, T. Direct generation of high power Laguerre-Gaussian output from a diode-pumped Nd: YVO4 1.3-μm bounce laser. Opt. Express 15, 7616–7622 (2007).
Senatsky, Y. et al. Laguerre-Gaussian modes selection in diode-pumped solid-state lasers. Opt. Rev. 19, 201–221 (2012).
Litvin, I. A., Ngcobo, S., Naidoo, D., Ait-Ameur, K. & Forbes, A. Doughnut laser beam as an incoherent superposition of two petal beams. Opt. Lett. 39, 704–707 (2014).
Barré, N., Romanelli, M. & Brunel, M. Role of cavity degeneracy for high-order mode excitation in end-pumped solid-state lasers. Opt. Lett. 39, 1022–1025 (2014).
Naidoo, D. et al. Controlled generation of higher-order Poincaré sphere beams from a laser. Nature Photon. 10, 327–332 (2016).
Miao, P. et al. Orbital angular momentum microlaser. Science 353, 464–467 (2016).
Ngcobo, S., Litvin, I., Burger, L. & Forbes, A. A digital laser for on-demand laser modes. Nature Commun. 4, 2289 (2013).
Horikawa, M. T., Ogawa, A., Miyamoto, K., Yusufu, T. & Omatsu, T. Handedness control in a tunable midinfrared (6.0–12.5 μm) vortex laser. J. Opt. Soc. Am. B 32, 2406–2410 (2015).
Omatsu, T., Miyamoto, K. & Lee, A. J. Wavelength-versatile optical vortex lasers. J. Opt. 19, 123002 (2017).
Wang, T. et al. Generation of femtosecond optical vortex beams in all-fiber mode-locked fiber laser using mode selective coupler. J. Lightwave Technol. 35, 2161–2166 (2017).
Yao, S. et al. Tunable orbital angular momentum generation using all-fiber fused coupler. IEEE Photon. Technol. Lett. 30, 99–102 (2017).
Lefort, L. et al. Practical low-noise stretched-pulse Yb3+-doped fiber laser. Opt. Lett. 27, 291–293 (2002).
Lin, D., Daniel, J. M. O. & Clarkson, W. A. Controlling the handedness of directly excited Laguerre–Gaussian modes in a solid-state laser. Opt. Lett. 39, 3903–3906 (2014).
Kim, D. J. & Kim, J. W. Direct generation of an optical vortex beam in a single-frequency Nd:YVO4 laser. Opt. Lett. 40, 399–402 (2015).
Zhou, N. & Wang, J. Metasurface-assisted orbital angular momentum carrying Bessel-Gaussian Laser: proposal and simulation. Sci. Rep. 8, 8038 (2018).
Ohtake, Y. et al. Universal generation of higher-order multiringed Laguerre–Gaussian beams by using a spatial light modulator. Opt. Lett. 32, 1411–1413 (2007).
Ando, T., Ohtake, Y., Matsumoto, N., Inoue, T. & Fukuchi, N. Mode purities of Laguerre–Gaussian beams generated via complex-amplitude modulation using phase-only spatial light modulators. Opt. Lett. 34, 34–36 (2009).
Zhu, L. & Wang, J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators. Sci. Rep. 4, 7441 (2014).
Cui, J. et al. Stimulated Brillouin scattering evolution and suppression in an integrated stimulated thermal Rayleigh scattering-based fiber laser. Photon. Res. 5, 233–238 (2017).
Dang, H. et al. Spectral purity improvement by combining self-injection locking and stimulated thermal Rayleigh scattering in fiber lasers. IEEE Photon. J 10, 1–9 (2018).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC) (61761130082, 11574001, 11774116, 11274131), the Royal Society-Newton Advanced Fellowship, the National Program for Support of Top-notch Young Professionals, the National Basic Research Program of China (973 Program) (2014CB340004), the Yangtze River Excellent Young Scholars Program, the Natural Science Foundation of Hubei Province of China (2018CFA048), and the Program for HUST Academic Frontier Youth Team. The authors would like to thank Chi Zhang and Liao Chen for their technical supports and helpful discussions.
Author information
Authors and Affiliations
Contributions
J.W. developed the concept. N.Z. and J.W. conceived the design. N.Z. and J.L. carried out the experiments. N.Z. and J.W. analyzed the experimental data. N.Z. and J.W. contributed to writing and finalizing the paper. J.W. supervised the project. N.Z. and J.L. contributed equally to this work.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhou, N., Liu, J. & Wang, J. Reconfigurable and tunable twisted light laser. Sci Rep 8, 11394 (2018). https://doi.org/10.1038/s41598-018-29868-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-29868-8
This article is cited by
-
Orbital angular momentum lasers
Nature Reviews Physics (2024)
-
Detection and elimination of pulse train instabilities in broadband fibre lasers using dispersion scan
Scientific Reports (2020)
-
Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities
Light: Science & Applications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.