Abstract
Raman scattering measurements of monolayer WS2 are reported as a function of the laser excitation energies from the near-infrared (1.58 eV) to the deep-ultraviolet (4.82 eV). In particular, we observed several strong Raman peaks in the range of 700∼850 cm−1 with the deep-ultraviolet laser lights (4.66 eV and 4.82 eV). Using the first-principles calculations, these peaks and other weak peaks were appropriately assigned by the double resonance Raman scattering spectra of phonons around the M and K points in the hexagonal Brillouin zone. The relative intensity of the first-order \({{\boldsymbol{E}}}_{{\bf{2}}{\boldsymbol{g}}}^{{\bf{1}}}\) to A1g peak changes dramatically with the 1.58 eV and 2.33 eV laser excitations, while the comparable relative intensity was observed for other laser energies. The disappearance of the \({{\boldsymbol{E}}}_{{\bf{2}}{\boldsymbol{g}}}^{{\bf{1}}}\) peak with the 1.58 eV laser light comes from the fact that valley polarization of the laser light surpasses the \({{\boldsymbol{E}}}_{{\bf{2}}{\boldsymbol{g}}}^{{\bf{1}}}\) mode since the \({{\boldsymbol{E}}}_{{\bf{2}}{\boldsymbol{g}}}^{{\bf{1}}}\) mode is the helicity-exchange Raman mode. On the other hand, the disappearance of the A1g peak with the 2.33 eV laser light might be due to the strain effect on the electron-phonon matrix element.
Similar content being viewed by others
Introduction
Layered transition metal dichalcogenides of hexagonal crystal structure (2H-TMDs) have attracted considerable attention in recent years. These materials exhibit distinct properties from their bulk counterparts because of reduced dimensionality and symmetry1,2,3,4,5, and offer unique opportunities for applications such as nanoelectronics, optoelectronics, spintronics, valleytronics, gas sensor, energy storage, and information processing6,7,8,9,10,11,12,13,14,15,16,17,18,19. Among 2H-TMDs, monolayer tungsten disulfide (WS2) is special in many respects. It has the largest direct band gap of about 2.1 eV at the K and \(K^{\prime} \) points in the Brillouin zone4,5,20, resulting in the highest quantum efficiency of photoluminescence yield4,5,21. Furthermore, it exhibits sufficiently large exciton binding energy in the range of 0.3 ∼0.7 eV20,22,23, featuring stable A and B exciton absorptions even at room temperature. Additionally, it shows significant spin-orbit coupling that induces a large splitting of the valence band of about 0.4 eV5,20,24 at the K and \(K^{\prime} \) points, leading to coupled spin and valley physics25. These superior properties make monolayer WS2 a very attractive material for use in field-effect transistors26,27, photodetectors28,29,30, solar cells31, light-emitting21, biosensing32, and spin valve devices33.
For many of these practical applications, knowledge of the lattice dynamics and electronic band structure of monolayer WS2 is important not only to characterize the structure but also to understand the optical and electronic properties of devices. Resonant Raman scattering spectroscopy has been proved to be an effective tool for probing such properties of monolayer WS234,35, providing critical information about the phononic and electronic excitations in WS2 systems. In earlier studies, Berkdemir et al.36 examined the resonant Raman scattering spectra of monolayer WS2 with 488 nm (∼2.54 eV), 514.5 nm (∼2.41 eV), and 647 nm (∼1.92 eV) laser excitations. Gaur et al.37 studied the resonant enhancement of the first-order and second-order Raman phonon modes in monolayer WS2 with six different laser excitation wavelengths of 457.9 nm (∼2.71 eV), 476.5 nm (∼2.60 eV), 488 nm (∼2.54 eV), 496.5 nm (∼2.50 eV), 501.7 nm (∼2.47 eV), and 514.5 nm (∼2.41 eV). They both36,37 found that many second-order Raman phonon modes appear and an increase in the intensity of the longitudinal acoustic 2 LA(M) mode at 351 cm−1 occurs only when a 514.5 nm (∼2.41 eV) laser is resonant to the B exciton. This resonance can be explained in terms of the electron-phonon coupling based upon double resonant Raman scattering process. Corro et al.38 presented the results of Raman scattering spectra of monolayer WS2 using up to 25 laser excitation wavelengths in the visible range. They observed that the resonant excitation profiles of first-order A1g and \({E}_{2g}^{1}\) and the second-order 2 LA(M) phonon modes show the intensity enhancements at 2.0, 2.4, and 2.7 eV, corresponding to three exciton absorption energies, revealing strong exciton-phonon interactions in monolayer WS2. Very recently, Yang et al.39 and Tan et al.40 investigated the excitation energy dependence of low-frequency Raman scattering spectra in few-layer WS2. Their results showed the quantum interference effects between low-frequency discrete phonon and exciton continuum under resonant excitation. Moreover, Miranda et al.41 explained the experimentally observed different resonant behavior of first-order \({A^{\prime} }_{1}\) and \(E^{\prime} \) modes of monolayer MoTe2 in terms of the quantum interference between electronic transitions at differernt parts in the Brillouin zone.
Despite intense research having been conducted on resonant Raman scattering measurements of monolayer WS2 using the visible laser lines, their ultraviolet (especially for deep-ultraviolet) Raman scattering spectra have not been reported so far. Only our earlier study of the ultraviolet Raman scattering spectrum of monolayer MoS2 with the smaller band gap exhibits the rich second-order phonon structures42. Many high energy absorption peaks for monolayer WS2 were observed in the ultraviolet regime, showing much larger intensity than those of the A and B excitons5,20, which is due to the nesting effect at the Λ valley43,44 or Van Hove singularity at the M point. More recently, the stable, highly-responsive, and broadband (from 370 to 1064 nm) photodetection has been discovered in multilayer WS229. These results show the great potential to use monolayer WS2 in the ultraviolet photodetector applications. Therefore, to gain further insight into the resonant Raman scattering spectra of monolayer WS2 using the ultraviolet laser lines is crucial for future design of effective ultraviolet photodetector based on this material. In this paper, we report a resonant Raman scattering study of monolayer WS2 with increasing laser excitation energies ranging from the near-infrared 785 nm (∼1.58 eV) to the deep-ultraviolet 257 nm (∼4.82 eV), and we compare our results with the predictions of first-principles calculations. We find that the anomalously strong enhancement of the Raman scattering spectra in the range of 700 ∼850 cm−1 as the second-order phonon modes by the deep-ultraviolet excitation wavelength 266 nm (∼4.66 eV) and 257 nm (∼4.82 eV). Furthermore, we observe the disappearance of \({E}_{2g}^{1}\) and A1g peaks, respectively, with the 1.58 eV and 2.33 eV laser excitations. We discuss theoretically the origin of this disappearance.
The organization of the paper is as follows. In section II, we describe the technical details of the experiment and theoretical calculations. In section III, we present the experimental data and discuss the origin of the Raman scattering spectra by comparing with the results of first-principles calculations. Finally, the paper is summarized in Section IV.
Technical Details
Experiment
Monolayer WS2 thin films were grown on the sapphire substrates by chemical vapor deposition45. These thin films were single layer materials verified by atomic force microscopy46. Resonant micro-Raman scattering measurements were performed at room temperature using two deep-ultraviolet lasers at λ = 257 and 266 nm, a ultraviolet laser at λ = 354 nm47,48, two visible lasers at λ = 488 and 532 nm, and a near-infrared laser at λ = 785 nm. The power of all laser lines used was kept below 1.0 mW to avoid possible heating effects. The typical duration time of measuring the Raman scattering spectra was 300 seconds (λ = 257, 266, 354, and 785 nm) and 120 seconds (λ = 488 and 532 nm). A detailed description of the experimental Raman scattering setup is given elsewhere42. Spectroscopic ellipsometric measurements were performed for multiple angles of incidence between 60° and 75° by using a Woollam M-2000U ellipsometer over the spectral range from 0.73 to 6.42 eV. Optical absorption spectra were obtained through spectroscopic ellipsometry analysis using the stacked layer model (sapphire substrate/thin film/surface roughness/air ambient structure). The sample was placed in a continuous-flow helium cryostat for optical absorption measurement at 4.5 K.
Theoretical model
We calculated the electronic band structure and phonon dispersion relation of monolayer WS2 based on first-principles density functional theory within the local density approximation (LDA) as implemented in the Quantum-Espresso code49. The monolayer WS2 separation from one unit cell to another unit cell was taken as 20 Å in the calculation to eliminate the inter-layer interaction. Projector augmented-wave (PAW) pseudopotentials50,51 was used with a plane-wave cutoff energy of 65 Ry to describe the interaction between electrons and ions. The electronic band structure with spin-orbit interaction considered was calculated using fully relativistic pseudopotentials derived from an atomic Dirac-like equation52. The atomic structure was fully relaxed with atomic force less than 10−5 Ry/Bohr. The Brillouin zone (BZ) was sampled over a k-mesh of 12 × 12 × 1 under the Monkhorst-Pack scheme53. The phonon energy dispersion relation of monolayer WS2 was calculated based on density functional perturbation theory54. The non-resonant Raman scattering intensity was calculated based on the Placzek approximation as introduced by Lazzeri and Mauri55. It is noted that in Quantum Espresso code, non-resonant Raman spectra based on the Placzek approximation can so far be taken care of only within local density approximation.
The optical absorption spectrum was calculated by the real (ε′) and imaginary (\(\varepsilon ^{\prime\prime} \)) parts of the dielectric function as a function of photon energy, respectively, based on the PAW methodology56 and the conventional Kramers-Kronig transformation. The absorption coefficient α is described by α = 4 πκ EL/(hc), where EL is the incident laser excitation energy, h is the Planck constant, c is the speed of light, and κ is the extinction coefficient57, that is, \(\kappa =\sqrt{(\sqrt{\varepsilon {^{\prime} }^{2}+\varepsilon {^{\prime\prime} }^{2}}-\varepsilon ^{\prime} )/2}\).
To evaluate the optical absorption as a function of laser energy EL and wave vector in the BZ, the optical absorption probability42 was calculated as follows and normalized by \(({{\rm{W}}}_{0}=\frac{2\pi {e}^{2}{\hslash }^{3}I}{{m}^{2}c{\varepsilon }_{0}})\),
in which m is the electron mass, I is the intensity of the incident laser, ε0 is the dielectric constant for vacuum, \(\overrightarrow{D}\)(c, v, \(\overrightarrow{k}\)) (=\(\langle {\psi }_{c}(\overrightarrow{k})|\nabla |{\psi }_{v}(\overrightarrow{k})\rangle \)) is the dipole vector, and \(\overrightarrow{P}\) is the laser polarization.
In order to evaluate the electron-phonon matrix element as a function of electron wavevector \(\overrightarrow{k}\) in the first BZ for q = 0 phonon, we adopted the EPW package58,59 independently.
Results and Discussion
In Fig. 1(a), we show the Raman scattering spectrum of monolayer WS2 at room temperature excited by a 532 nm laser line. The spectrum exhibits two first-order Raman peaks with the labels of \({E}_{2g}^{1}\) and A1g and several weak double resonant Raman structures as denoted by asterisks. We fitted these peaks by using a standard Lorentzian function. The two main peaks at approximately 356 and 417 cm−1 are associated with the zone center and first-order one-phonon emission for in-plane and out-of-plane vibrations with \({E}_{2g}^{1}\) and A1g symmetries, respectively. The peak frequencies (356 cm−1 and 417 cm−1) well reproduce the previous Raman scattering measurements, indicating a single-layer signature4,36,37,38. Moreover, the spatial maps of the Raman frequency within 356 ± 2 cm−1 for the \({E}_{2g}^{1}\) mode (Fig. 1(b)) show uniform color contrast in each triangular WS2 domain. This evidence indicates that our monolayer WS2 is a high-quality sample. The assignment of the second-order Raman phonon modes will be discussed later.
(a) The Raman scattering spectrum of monolayer WS2 excited by a 532 nm laser line. The asterisks denote the second-order Raman phonon modes. (b) The Raman mapping of the \({E}_{2g}^{1}\) peak frequency over the sample. The white dot in the middle of the image shows the place where the spectrum was collected in (a).
In order to further investigate the vibrational properties of monolayer WS2, we extended the Raman scattering measurements with excitation energies ranging from the near-infrared to deep-ultraviolet. In Fig. 2, we plot the Raman scattering spectra of monolayer WS2 excited by the near-infrared 785 nm (∼1.58 eV), visible 532 nm (∼2.33 eV) and 488 nm (∼2.54 eV), ultraviolet 354 nm (∼3.50 eV), and deep-ultraviolet 266 nm (∼4.66 eV) and 257 nm (∼4.82 eV) laser lights. There are three important features in the spectra. First, when the monolayer WS2 is excited at 785 nm, only A1g and weak \({E}_{2g}^{1}\) Raman modes can be seen. The \({E}_{2g}^{1}\) mode is almost suppressed compared with the A1g mode. By contrast, the opposite behavior is observed in the intensities of the \({E}_{2g}^{1}\) and A1g modes for the 532 nm excitation. The possible origins of the disappearance of \({E}_{2g}^{1}\) or A1g will be discussed later. Second, both \({E}_{2g}^{1}\) and A1g modes show the prominent intensities excited by 488 nm, 354 nm, 266 nm, and 257 nm lasers. Additionally, many weak phonon modes appear in the Raman scattering spectra with 532 nm and 488 nm excitations as shown by arrows in Fig. 2. The peak positions of these weak modes shift to higher frequencies with increasing EL, suggesting that these modes are due to the second-order Raman scattering process60,61,62. Third, the intensities of these second-order phonon modes in the range of 700∼850 cm−1 become significant when the 266 nm and 257 nm lasers are applied.
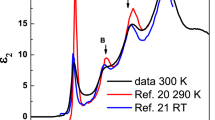
To understand the origins of Raman scattering spectra due to different laser energies, we first calculate the electronic band structure and optical absorption. In Fig. 3(a), we show electronic band structure and density of states. The band splitting Δsoc on top of valence band due to spin-orbit interaction is around 0.44 eV, which agrees very well with the energy splitting (∼0.42 eV) between A and B excitons in our experimental optical absorption data as indicated in Fig. 3(b) and also in the data by Rigosi et al.63. Electronic density of states (DOS) in Fig. 3(a) shows some typical features, such as constant value of DOS due to quadratic band dispersion at band edge of both valence and conduction bands around the zone-corner K point; and also Van-Hove singularity of DOS due to saddle points in the band structure around the zone-edge center M point. We expect a strong optical transition or Raman intensity for the optical transition for the transition energy of laser light at the Van-Hove singular DOS. Worth pointing out that due to an underestimate of optical band gap from density functional calculation, we upshift all conduction bands by 0.46 eV. With this band shift, our calculated optical absorption result in blue solid line in Fig. 3(b) agrees reasonably well with the experimental data (measured at 4.5 K) given in red empty dots, except for the absorption intensity that is calculated based on the single-particle picture without taking into account of electron-hole (exciton) interaction. Nevertheless, this difference is not relevant to the present analysis since we discuss the optical absorption for the transition energy with much larger energy than the exciton energies. It is noted that the A and B exciton peaks shift from 2.12 and 2.51 eV, respectively, at 4.5 K to 2.04 and 2.43 eV at 300 K. In Fig. 3(a), we mark the possible vertical optical transition by solid arrows for the laser lines used in the experiment. The electron excitation due to the laser lines of 532 nm (∼2.33 eV) and 488 nm (∼2.54 eV) takes place with wave vector close to the K point, suggesting that the Raman scattering spectra are due to the A or B excitons near the K point. In the case of EL = 1.58 eV, since EL is much smaller than the energy gap at the K point, the Raman scattering spectrum is non-resonant in which the dominant contribution of the Raman scattering intensity comes from the K point.
The vertical transition by the laser line in the ultraviolet 354 nm (∼3.50 eV) occurs more widely in the Brillouin zone, which gives a peak in the joint density of states at 3.50 eV. This situation explains the reason why the Raman peaks other than \({E}_{2g}^{1}\) and A1g are almost invisible (the peaks become broad) compared with other laser lines because the double resonance wavevectors of phonon exists over the Brillouin zone. By contrast, the two laser lines 266 nm (∼4.66 eV) and 257 nm (∼4.82 eV) in the deep-ultraviolet region give rise to singular joint density of states (JDOS) at the Λ point (around \(\frac{1}{2}\overrightarrow{{\rm{\Gamma }}{\rm{K}}}\)), which leads to specified resonant electron-photon process for prominent double resonance Raman peaks42,64.
To assign the multiple resonant Raman peaks observed in Fig. 2, it is more straightforward to analyze the electron-photon resonant process in the whole Brillouin zone. In Fig. 4, we plot laser energy EL dependence of optical absorption probability W of monolayer WS2 in the BZ. Consistent with the previous analysis in the band structure in Fig. 3(a), the wave vector keγ of electron-photon resonance process for the laser excitation energies of 2.33 and 2.54 eV is around K point, as shown in Fig. 4(b) and (c) while there is no resonant optical absorption in Fig. 4(a). Therefore the Γ-point or K-point phonons are expected to contribute to the intra-band or inter-band resonant Raman peaks, respectively. However, the keγ for the ultraviolet and deep-ultraviolet lasers is more complicated. Nevertheless, keγ for the ultraviolet and deep-ultraviolet lasers is along \(\overrightarrow{{\rm{\Gamma }}K}\) line, as seen from Fig. 4(d–f).
To extract the phonon wave vector q of resonance electron-phonon scattering process for the ultraviolet and deep-ultraviolet lasers, we analyze the possible intervalley/intravalley scattering between λ or \(\lambda ^{\prime} \) points as shown in Fig. 5(a). λ point is defined as a k point along \(\overline{{\rm{\Gamma }}K}\) line and becomes Λ point at 1/2 \(\overline{{\rm{\Gamma }}K}\) line. Starting at the λ points with keγ = β \(\overline{{\rm{\Gamma }}K}\), the phonon wavevector q can be either qK = β \(\overline{{\rm{\Gamma }}K}\), or qM = 2 β \(\overline{{\rm{\Gamma }}M}\), or qK = 2 β \(\overline{{\rm{\Gamma }}K}\). Here the value of β is a function of EL, as seen from Fig. 4, for example, β takes two values (β = 0.21 and 0.43) for EL = 4.66 eV, and another two values (β = 0.17 and 0.50) for EL = 4.82 eV. The corresponding phonon wave vectors q which satisfied the double resonant condition, including qM near the M point and qK close to the K point, are marked in blue lines in the phonon dispersion relation as shown in Fig. 5(b). We have pointed out in the previous work42,65 that Van Hove singularity of both electronic and phonon density of states at the M point can give rise to the resonant electron-photon and electron-phonon process, which can significantly enhance the Raman scattering intensity. The Raman peaks above 700 cm−1 with large intensity due to both 266 nm and 257 nm laser lines, as seen from Fig. 2, are assigned to the combination mode or overtone mode at the M point (qM1) or close to the M point (qM2 = 0.86 \(\overline{{\rm{\Gamma }}M}\)), as indicated in Fig. 5(b) and summarized in Table 1.
(a) The intervalley wave vector q e−ph of resonance electron-phonon scattering process between λ and \(\lambda ^{\prime} \) where electron-photon resonance process occurs. λ point is defined as a k point along \(\overline{{\rm{\Gamma }}M}\) line and becomes Λ point at 1/2 \(\overline{{\rm{\Gamma }}M}\) line. (b) Phonon dispersion relation of monolayer WS2. The blue vertical lines denote the wave vectors of double resonance Raman scattering. (c) Optical phonon dispersion relation. Dashed lines in color are used to highlight the dispersion of different optical phonon bands.
Since all these resonant Raman peaks for the ultraviolet and deep-ultraviolet lasers are due to optical phonon modes, we show the optical phonon dispersion relation as shown in Fig. 5(c). Compared to the well dispersive B2g (dashed blue line) and E1g modes (dashed green lines) along the high-symmetry line, A1g (dashed purple line) and E2g (red solid lines) modes are relatively flat and believed to contribute to the small shift of those resonant Raman peaks around 700 cm−1 to 708 cm−1 due to both 266 nm and 257 nm laser lines. In particular, the \({E}_{2g}^{1}\) (M) and \({E}_{2g}^{2}\)(M) modes have an opposite energy dispersion to each other, the combinational resonant Raman peak from the two modes should have no obvious laser-energy dependence, such as the pronounced Raman peak at 708 cm−1 from 266 nm to 257 nm laser line.
In Table 1, we list up the observed weak Raman scattering spectra excited by 2.33, 2.54, 4.66, and 4.82 eV laser lines and the assignment to the double resonance Raman scattering spectra. The upper part of the Table 1 gives the assignment of the Raman peaks excited by the visible light (2.33 and 2.54 eV). Since all the assigned combination, difference combination and overtone modes are due to the K-point phonons, no laser energy dependence of Raman frequency is expected. The lower part of the Table 1 shows the assignment of Raman peaks due to the deep-ultraviolet lasers (4.66 and 4.82 eV). As discussed above, phonon at or near the M point are responsible for the pronounced Raman peaks. Except for the 2 LA(M) and \({E}_{2g}^{1}\) + \({E}_{2g}^{2}\) modes, an obvious laser energy dependence of Raman peaks due to the deep-ultraviolet lasers is observed both in the experiment and theory, which is an evidence that the assignment of double resonance Raman peak is consistent with phonon dispersion relation.
Let us briefly discuss the disappearance of A1g intensity at EL = 2.33 eV and \({E}_{2g}^{1}\) intensity at EL = 1.58 eV. In order to check the reproducibility of the relative intensity, we measured the Raman scattering spectra at three different spots. The relative intensity at EL = 2.33 eV is almost identical to that measured by Corro et al.38 at 530.9 nm laser line. Corro et al.38 attributed this to the exciton-phonon interaction between the B exciton and A1g phonon. However, Carvalho et al.66 observed in MoS2 and MoSe2 an enhancement of A1g peak at the energy of the B exciton and explained that the \({d}_{{z}^{2}}\) orbital can couple with the A1g mode other than with the \({E}_{2g}^{1}\) mode. Following the analysis by Carvalho et al.66, we calculated the wavefunctions of the 5 \({d}_{{z}^{2}}\) orbital of W and the 4 \({d}_{{z}^{2}}\) orbital of Mo, we found that the delocalization of atomic orbitals is similar to each other. In fact, the lattice constants of WS2 (c = 3.19 Å) and MoS2 (c = 3.19 Å) are almost identical. But the result for WS2 is opposite to that of MoS2 and MoSe2. The previous exciton-phonon effect between the A1g mode and the B exciton can not apply to WS2. It is pointed out that the disappearance of the A1g mode at the energy of the C exciton (MoS2 at EL = 2.75 eV, MoSe2 at EL = 2.60 eV) can be explained by the exciton-phonon interaction according to the discussion by Carvalho et al.66. Though we do not have the Raman scattering spectra of WS2 at the C exciton energy (2.80 eV), Corro et al. showed the disappearance of A1g mode at 457.9 nm and 472.7 nm laser lines38.
Here we try to consider two possible origins of the disappearance of the A1g mode. One of possible origins is due to the node of electron-phonon matrix element around the K point64. Since we do not calculate directly the exciton-phonon matrix element that is given by weighted sum of electron-phonon matrix element67, we can not specify the energy in which the exciton-phonon matrix element becomes zero. It should be mentioned that the laser energy that gives zero electron-phonon matrix element is 3.06 eV that is much larger than 2.33 eV even if we consider the exciton binding energy. Another possible reason for the disappearance of the A1g mode is the strain effect of the Raman scattering intensity. In Fig. 6(a,b), we show the non-resonant Raman scattering spectra calculated based on the Placzek polarizability theory55 at both (a) zero and (b) 2% isotropic tensile strain. In Fig. 6(c), we show the strain dependence of A1g intensity as a function of strain and A1g intensity exponentially decreases with increasing isotropic tensile strain. It is noted that the A1g intensity does not decrease much for uniaxial strain. We expect that the A1g disappearance at 2.33 eV may have something to do with lattice tensile strain effect possibly due to laser heating. However, since we did not study power dependence of Raman scattering spectra, we could not see if the strain effect is essential of not. And 2% strain is relatively large from the thermal expansion or the interlayer interaction between WS2 and the sapphire substrate.
As for the disappearance of \({E}_{2g}^{1}\) at EL = 1.58 eV, since this Raman scattering process is non-resonance, the main contribution to Raman scattering intensity is the K-point optical absorption which is valley-polarized. That means that only left-handed (or right-handed) component of the circular polarized light is absorbed and emitted at the K(or \(K^{\prime} \)) point. Since \({E}_{2g}^{1}\) mode changes the helicity of circular polarized light in the scattered light, the Raman scattering process of \({E}_{2g}^{1}\) is suppressed by valley polarization. It is the reason why \({E}_{2g}^{1}\) is suppressed for 1.58 eV. It is important to note that this effect of valley polarization occurs even when incident light is linearly polarized. The linear polarized light is expressed by the sum of left-handed and right-handed circular light for each of which the optical absorption occurs at the K and \(K^{\prime} \) points.
Summary
In summary, we report a combined experimental and theoretical study of the deep-ultraviolet Raman scattering spectra of monolayer WS2 in which we observed new intense Raman peaks in the range of 700∼850 cm−1, which can be assigned to the double resonance Raman scattering spectra with the phonon wave vector connecting the Λ points. Though the peaks show dispersive behavior of Raman frequency with increasing EL, the other Raman peaks show non-dispersive nature because of the opposite phonon dispersion to each other for a combination modes of the \({E}_{2g}^{1}\) and \({E}_{2g}^{2}\) modes. The disappearance of A1g peak with the 2.33 eV laser excitation is probably from a lattice tensile strain due to laser heating, while disappearance of \({E}_{2g}^{1}\) peak with the 1.58 eV laser excitation is due to valley polarization effect and helicity exchanged Raman process of the \({E}_{2g}^{1}\) mode.
References
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271 (2010).
Tongay, S. et al. Thermally driven crossover from indirect toward direct bandgap in 2D semiconductors: MoSe2 versus MoS2. Nano Lett. 12, 5576 (2012).
Gutuerrez, H. R. et al. Extraordinary room-temperature photoluminescence in triangular WS2 monolayers. Nano Lett. 13, 3447 (2013).
Zhao, W. et al. Evolution of electronic structure in atomically thin sheets of WS2 and WSe2. ACS Nano 7, 791 (2013).
Yoon, Y., Ganapathi, K. & Salahuddin, S. How good can monolayer MoS2 transistors be? Nano Lett. 11, 3768 (2011).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nature Nanotech. 6, 147 (2011).
Radisavljevic, B., Whitwick, M. B. & Kis, A. Integrated circuits and logic operations based on single-layer MoS2. ACS Nano 5, 9934 (2011).
Wang, Q. H., Kourosh, K. Z., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nature Nanotech. 7, 699 (2012).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenides nanosheets, Nature. Chemistry 5, 263 (2013).
Larentis, S., Fallahazad, B. & Tutuc, E. Field-effect transistors and intrinsic mobility in ultra-thin MoSe2 layers. Appl. Phys. Lett. 101, 223104 (2012).
Bernardi, M., Palummo, M. & Grossman, J. C. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 13, 3664 (2013).
Zhang, W. et al. High-gain phototransistors based on a CVD MoS2 monolayer. Adv. Mater. 25, 3456 (2013).
Xia, F., Wang, H., Xiao, D., Dubey, M. & Ramasubramaniam, A. Two-dimensional material nanophotonics. Nature Photonics 8, 899 (2014).
Cho, B. et al. Charge-transfer-based gas sensing using atomic-layer MoS2. Sci. Rep. 5, 8052 (2015).
Eginligil, M. et al. Dichroic spin-valley photocurrent in monolayer molybdenum disulphide. Nature Commun. 6, 7636 (2015).
Ye, Y. et al. Electrical generation and control of the valley carriers in a monolayer transition metal dichalcogenide. Nature Nanotech. 11, 598 (2016).
Yang, X. et al. Plasmon-exciton coupling of monolayer MoS2-Ag nanoparticles hybrids for surface catalytic reaction, Materials Today. Energy 5, 72 (2017).
Lin, W. et al. Physical mechanism on exciton-plasmon coupling revealed by femtosecond pump-probe transient absorption spectroscopy. Materials Today Physics 3, 33 (2017).
Liu, H. L. et al. Optical properties of monolayer transition metal dichalcogenides probed by spectroscopic ellipsometry. Appl. Phys. Lett. 105, 201905 (2014).
Peumyoo, N. et al. Nonblinking, intense two-dimensional light emitter: monolayer WS2 triangles. ACS Nano 7, 10985 (2013).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2. Phys. Rev. Lett. 113, 076802 (2014).
Zhu, B., Chen, X. & Cui, X. D. Exciton binding energy of monolayer WS2. Sci. Rep. 5, 9218 (2015).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlöl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phy. Rev. B 84, 153402 (2011).
Di Xiao, G.-B., Liu, W. X., Feng, X. D., Xu & Yao, W. Coupled spin and valley physics in monolayer of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Ovchinnikov, D., Allain, A., Huang, Y.-S., Dumcenco, D. & Kis, A. Electrical transport properties of single-layer WS2. ACS Nano 8, 8174 (2014).
Withers, F., Bointon, T. H., Hudson, D. C., Craciun, M. F. & Russo, S. Electron transport of WS2 transistors in a hexagonal boron nitride dielectric environment. Sci. Rep. 4, 4967 (2014).
Perea-López, N. et al. Photosensor device based on few-layered WS2 films. Adv. Funct. Mater. 23, 5511 (2013).
Yao, J. D., Zheng, Z. Q., Shao, J. M. & Yang, G. W. Stable, highly-responsive and broadband photodetection based on large-area multilayered WS2 films grown by pulsed-laser deposition. Nanoscale 7, 14974 (2015).
Zeng, L. H. et al. High-responsivity UV-Vis photodetectro based on transferable WS2 film deposited by magnetron sputtering. Sci. Rep. 6, 20343 (2016).
Shanmugam, M., Bansal, T., Durcan, C. A. & Yu, B. Schottky-barrier solar cell based on layered semiconductor tungsten disulfide nanofilm. Appl. Phys. Lett. 101, 263902 (2012).
Ge, J. et al. A WS2 nanosheet based sensing platform for highly sensitive detection of T4 polynucleotide kinase and its inhibitors. Nanoscale 6, 6866 (2014).
Iqbal, M. Z., Iqbal, M. W., Siddique, S., Khan, M. F. & Ramay, S. M. Room temperature spin valve effect in NiFe/WS2/Co junctions. Sci. Rep. 6, 21038 (2016).
Zhang, X. et al. Phonon and Raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 44, 2757 (2015).
Mu, X. et al. Analysis and design of resonance Raman reporter molecules by density functional theory. Journal of Raman Spectroscopy 48(9), 1196 (2017).
Berkdemir, A. et al. Identification of individual and few layers of WS2 using Raman spectroscopy. Sci. Rep. 3, 1755 (2013).
Gaur, A. P. S., Sahoo, S., Scott, J. F. & Katiyar, R. S. Electron-phonon interaction and double-resonance Raman studies in monolayer WS2. J. Phys. Chem. C 119, 5146 (2015).
del Corro, E. et al. Atypical exciton-phonon interactions in WS2 amd WSe2 monolayers revealed by resonance Raman spectroscopy. Nano Lett. 16, 2363 (2016).
Yang, J., Lee, J.-U. & Cheong, H. Excitation energy dependence of Raman spectra of few-layer WS2. FlatChem. 3, 64 (2017).
Tan, Q.-H. et al. Observation of forbidden phonons, Fano resonance and dark exciton by resonance Raman scattering in few-layer WS2. 2D Materials 4, 031007 (2017).
Miranda, H. P. C. et al. Quantum interference effects in resonant Raman spectroscopy of single- and triple-layer MoTe2 from first-principles. Nano Lett. 17, 2381 (2017).
Liu, H. L. et al. Anomalous lattice vibrations of monolayer MoS2 probed by ultraviolet Raman scattering. Phys. Chem. Chem. Phys. 17, 14561 (2015).
Carvalho, A., Ribeiro, R. M. & Castro Neto, A. H. Band nesting and the optical response of two-dimensional semiconducting transition metal dichalcogenides. Phys. Rev. B 88, 115205 (2013).
Kozawa, D. et al. Photocarrier relaxation pathway in two-dimensional semiconducting transition metal dichalcogenides. Nat. Commun. 5, 4543 (2014).
Shi, Y. M., Li, H. N. & Li, L. J. Recent advances in controlled synthesis of two-dimensional transition metal dichalcogenides via vapour deposition techniques. Chem. Soc. Rev. 44, 2744 (2015).
Lee, Y. H. et al. Synthesis and transfer of single-layer transition metal disulfides on diverse surfaces. Nano Lett. 13, 1852 (2013).
Kumamoto, Y., Taguchi, A., Smith, N. I. & Kawata, S. Deep UV resonant Raman spectroscopy for photodamage characterization in cells. Biomed. Opt. Express 2, 927 (2011).
Kumamoto, Y., Taguchi, A., Smith, N. I. & Kawata, S. Deep ultraviolet resonant Raman imaging of a cell. J. Biomed. Opt. 17, 076001 (2012).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Theurich, G. & Hill, N. A. Self-consistent treatment of spin-orbit coupling in solids using relativistic fully separable ab initio pseudopotentials. Phys. Rev. B 64, 073106 (2001).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Baroni, S., de Gironcoli, S., Corso, A. D. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515 (2001).
Lazzeri, M. & Mauri, F. First-principles calculation of vibrational Raman spectra in large systems: signature of small rings in crystalline SiO2. Phys. Rev. Lett. 90, 036401 (2003).
Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J. & Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 73, 045112 (2006).
H. Zimmermann Integrated Silicon Optoelectronics, Springer Series in Optical Sciences (Springer, New York, 2000).
Poncé, S., Margine, E. R., Verdi, C. & Giustino, F. EPW: Electron-phonon coupling, transport and superconducting properties using maximally localied Wannier functions. Comput. Phys. Comm. 209, 116 (2016).
Giustino, F., Cohen, M. L. & Louie, S. G. Electron-phonon interaction using Wannier functions. Phys. Rev. B 76, 165108 (2007).
A. Jorio, M. Dresselhaus, R. Saito and G. Dresselhaus Raman Spectroscopy in Graphene Related Systems (Wiley-VCH, 2011).
Saito, R. et al. Probing phonon dispersion relations of graphite by double resonance Raman scattering. Phys. Rev. Lett. 88, 027401 (2002).
Saito, R. et al. Double resonance Raman spectroscopy of single-wall carbon nanotubes. New J. Phys. 5, 157 (2003).
Rigosi, A. F., Hill, H. M., Li, Y. L., Chernikov, A. & Heinz, T. F. Probing interlayer interactions in transition metal dichalcogenide heterostructure by optical spectroscopy: MoS2/WS2 and MoSe2/WSe2. Nano Lett. 15, 5033 (2015).
Y. Tatsumi & R. Saito Phys. Rev. B, accepted (2018).
Guo, H. H. et al. Double resonane Raman modes in monolayer and few-layer MoTe2. Phys. Rev. B 91, 205415 (2015).
Carvalho, B. R., Malard, L. M., Alves, J. M., Fantini, C. & Pimenta, M. A. Symmetry-dependent exciton-phonon coupling in 2D and bulk MoS2 observed by resonance Raman scattering. Phys. Rev. Lett. 114, 136403 (2015).
Jiang, J. et al. Chirality dependence of exciton effects in single-wall carbon nanotubes: tight-binding model. Phys. Rev. B 75, 035407 (2007).
Acknowledgements
H.L.L. thanks financial support from the Ministry of Science and Technology of Republic of China under Grants No. MOST 105-2112-M-003-013-MY3 and Academia Sinica under thematic project Grant No. AS-105-TP-A03. T.Y. and Z.D.Z. acknowledge the National Key R&D Program of China (No. 2017YFA0206301) and the Major Program of Aerospace Advanced Manufacturing Technology Research Foundation NSFC and CASC, China (No. U1537204). H.G. acknowledges NSFC Grant No. 51702146 and Liaoning Province Doctor Startup Fund (No. 201601325). L.J.L. thanks the support from Taiwan Consortium of Emergent Crystalline Materials (TCECM), Ministry of Science and Technology, and USA AFOSR BRI (FA238615100015). R.S. acknowledges MEXT-Japan Grants Nos. JP25107005, JP15K21722, and JP18H01810. Y.K. and S.K. acknowledge JSPS-Japan Grants No. JP21226003. Y.T. acknowledges World Premier International Research Center Initiative (WPI), MEXT, Japan.
Author information
Authors and Affiliations
Contributions
H.L.L., Y.K. and S.K. conceived the idea and designed the experiments. H.L.L. and Y.K. performed the experiments. M.Y.L. and L.J.L. prepared the samples. T.Y., Y.T., Y.Z., B.D., H.G., Z.D.Z. and R.S. performed the first-principles calculations and theoretical analyses. H.L.L. and T.Y. wrote the paper. All the authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, HL., Yang, T., Tatsumi, Y. et al. Deep-ultraviolet Raman scattering spectroscopy of monolayer WS2. Sci Rep 8, 11398 (2018). https://doi.org/10.1038/s41598-018-29587-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-29587-0
This article is cited by
-
Study of thermo-optic and thermo-polarizability coefficients of ions in congruent LiNbO3 open-type optical waveguide using point dipole approximation
Indian Journal of Physics (2024)
-
Temperature-dependent optical constants of monolayer \({\text {MoS}}_2\), \({\text {MoSe}}_2\), \({\text {WS}}_2\), and \({\text {WSe}}_2\): spectroscopic ellipsometry and first-principles calculations
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.