Abstract
The C2v surface symmetry of W(110) strongly influences a spin-orbit-induced Dirac-cone-like surface state and its characterization by spin- and angle-resolved photoelectron spectroscopy. In particular, using circular polarized light, a distinctive k-dependent spin texture is observed along the \(\overline{{\boldsymbol{\Gamma }}{\boldsymbol{H}}}\) direction of the surface Brillouin zone. For all spin components Px, Py, and Pz, non-zero values are detected, while the initial-state spin polarization has only a Py component due to mirror symmetry. The observed complex spin texture of the surface state is controlled by transition matrix element effects, which include orbital symmetries of the involved electron states as well as the geometry of the experimental set-up.
Similar content being viewed by others
Introduction
Topological insulators (TI) and Rashba systems attract great attention with regard to manipulation and generation of spin currents without magnetic field1,2,3. The lack of space-inversion symmetry at the surface of these materials leads to spin-polarized surface states driven by the spin-orbit interaction. The electron spin is locked to its crystal momentum, forming a unique helical spin texture. As a consequence of spin-orbit interaction, the spin-polarized surface state, by hybridization, consists of both spin-up and spin-down components with different weight of their partial wave functions4,5,6,7, except for the special case of wavevectors with C3 symmetry8,9,10,11.
The spin mixture causes spin entanglement of photoelectrons in topological materials as well as Rashba systems. Consequently, when spin-up and spin-down components in such initial bands are simultaneously excited by photons with a coherent mixture of s- and p-polarized light or by circular polarized light, a spin component other than that in the initial state is caused by the superposition of complex transition matrix elements.
Recently, by utilizing the above-mentioned effect, a fascinating idea was proposed: the manipulation and control of spin polarization of the photoelectron signal by a proper selection of the light polarization, experimental geometry and photon energy5,6,12,13,14,15,16,17,18,19. These phenomena are promising in view of the material-light-spin relationship for potential applications in optospintronics devices with multiple functionalities. So far, most studies of the photoelectron spin are restricted to surfaces with C3v symmetry or to cases with normal electron emission20,21,22,23,24.
A surface state on W(110) within a spin-orbit-induced symmetry gap25,26,27,28,29 shows Dirac-cone-like dispersion with a spin texture reminiscent of a topological surface state (TSS)30. The surface state is strongly influenced by the twofold symmetry (C2v) of the crystal surface: it shows a flattened dispersion behavior along the \(\overline{{\rm{\Gamma }}N}\) line of the surface Brillouin zone and a linear dispersion along \(\overline{{\rm{\Gamma }}H}\) and \(\overline{{\rm{\Gamma }}S}\)31,32,33. Only \(\overline{{\rm{\Gamma }}N}\) and \(\overline{{\rm{\Gamma }}H}\) possess mirror planes. Based on several theoretical and experimental studies, along \(\overline{{\rm{\Gamma }}H}\), the surface state exhibits predominant Σ1 (\({d}_{{z}^{2}}\)) and Σ3 (dzx) symmetry (single-group representation) with minor Σ2 (dxy) and Σ4 (dyz) contributions. We have demonstrated by angle-resolved photoelectron spectroscopy (ARPES) using linear p- and s-polarized light4 that the spin polarization depends on the orbital symmetry in agreement with theoretical calculations7. Moreover, recent theoretical research has shown that this surface state is topologically protected by mirror symmetry along \(\overline{{\rm{\Gamma }}H}\). Therefore, W(110) is called a topological crystalline transition metal34.
In this work, we use spin-resolved ARPES with left and right circular polarized light to measure the three spin-polarization components of photoelectrons emitted from the Dirac-cone like surface state along \(\overline{{\rm{\Gamma }}H}\) on W(110) with C2v symmetry. We show that the observed complex spin-polarization texture as a function of momentum can be explained by multiple contributions of the dipole-transition matrix element for the given highly symmetric experimental geometry. The observed spin polarization of the photo-emitted electrons is not only determined by the intrinsic spin polarization, i.e. the spin polarization of the initial state under investigation, but also by extrinsic spin polarization, which is induced and controlled by experimental parameters. In detail, the latter is given by phase differences between complex partial transition matrix elements, which contain the orbital components of initial and final states as well as experimental parameters such as the crystal symmetry, light polarization and its angle of incidence. In short, using the example of the Dirac-like surface state on W(110), we show how the spin polarization of photo-emitted electrons can be controlled experimentally.
Results and Discussion
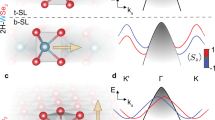
Figure 1(a) shows spin-integrated ARPES data of W(110) along \(\overline{{\rm{\Gamma }}H}\), obtained with right circular polarized light (C+) of photon energy hν = 43 eV. In agreement with established results for linear polarized light4,31, there are two characteristic surface states (S1 and S2) and bulk continuum states at binding energies EB higher than 1.45 eV. In this paper, we only discuss the surface state S1 with clear Dirac-cone-like dispersion and a crossing point at EB = 1.25 eV at \(\overline{{\rm{\Gamma }}}\).
(a) Spin-integrated ARPES data taken with right circular polarized light of hν = 43 eV. (b) Spin-resolved energy distribution curves (EDCs) for all three spin-polarization components presented for selected emission angles θe along the \(\overline{{\rm{\Gamma }}H}\) line, obtained for right circular polarized light (C+) of hν = 43 eV. The spin-dependent intensities are presented as red and blue lines. (c) Same as (b) but for left circular polarized light (C−). The dashed lines in (a) correspond to the EDCs given in (b) and (c). (d) Experimental geometry including the detection plane, which coincides with the mirror plane mxz of the crystal.
Figure 1(b,c) show spin-ARPES data as energy distribution curves (EDC’s) for selected emission angles θe along \(\overline{{\rm{\Gamma }}H}\), excited by right (C+) and left (C−) circular polarized light. Left, middle and right columns present spin-ARPES results for Px, Py and Pz, respectively. Spin-up and spin-down intensities are plotted as red and blue solid lines, respectively.
At first, we will discuss spin-EDC’s for Py in the middle panel of Fig. 1(b). A sharp peak S1 in the spin-up (spin-down) channel is located at EB = 1.42 eV (1.05 eV) for θe = −4° and moves to lower (higher) EB with increasing θe. At θe = 0°, the bands cross, yet with spin-dependent intensities. This behavior is reminiscent of our previous results obtained for p-polarized light4. Moreover, according to the middle panel of Fig. 1(c), the observed spin features remain unchanged upon switching the circular polarization.
For Pz in Fig. 1(b), the spin texture of S1 is similar to Py but with reduced spin difference. For Px, the spin-up intensities always exceed the spin-down intensities for both the upper and lower part of the Dirac cone. Note that, in contrast to Py, Px and Pz switch sign upon reversing the circular polarization of the light (see Fig. 1(c)).
In Fig. 2, our spin-ARPES results are summarized as E vs k|| plots, where the spin-polarized photoemission intensities and their differences are given as colored contours. In the following, we focus on the spin differences for the three spin-polarization components in the right columns of Fig. 2(a) for C+ light and Fig. 2(b) for C− light. Two major observations stand out and have to be explained:
-
(i)
By switching the circular polarization, the sign of Px and Pz is reversed but Py is unchanged.
-
(ii)
By reversing the sign of k|| or θe, Py and Pz change sign, while Px is unchanged.
For measurements along \(\overline{{\rm{\Gamma }}H}\), due to the mxz mirror plane as shown in Fig. 1(d), the initial-state spin polarization is restricted to Py. As a consequence, the observed non-zero Px and Pz spin components are caused by the photoemission process itself, which is described by the full dipole-transition matrix element including the final state. The following discussion focuses on the photoemission-induced effect for Px and Pz.
First, we discuss the origin of observation (i). It can be explained by considering the symmetry of the experimental geometry including the mirror plane mxz as illustrated in Fig. 1(d). Upon reflection at the mirror plane, the circular polarization of the light is reversed, while the light incidence angle and the electron emission angle are unchanged. In addition, Py is unchanged, while Px and Pz change sign. As a consequence, Px and Pz are expected to change sign upon switching the circular polarization of the light. This situation is generally realized in experiments, where the detection plane coincides with a mirror plane, which is the case for \(\overline{{\rm{\Gamma }}H}\) on W(110).
Second, observation (ii) can be explained in the framework of a group-theoretical analysis of spin-dependent photoemission on the basis of dipole-transition matrix elements including final states of Σ1 representation (without spin-orbit interaction)21. In general, an initial state consisting of a mixture of spin-up and spin-down states may result in a spin polarization of the photo-emitted electron, which is different from the initial-state spin polarization.
Following the approach of ref.21, we can derive the total photoemission intensity I and the intensity differences \({I}_{{\rm{up}}}^{{\rm{x}},{\rm{y}},{\rm{z}}}-{I}_{{\rm{down}}}^{{\rm{x}},{\rm{y}},{\rm{z}}}=I{{\rm{P}}}_{{\rm{x}},{\rm{y}},{\rm{z}}}\). The orbital-dependent spin polarization of the initial states is considered, while the final states have Σ1 symmetry. The latter follows from the fact that there is no spin-orbit interaction at the detector (vacuum), spin-orbit coupling is very weak for electronic states with energies much higher than the Fermi level, and only even states can be detected.
θp and ϕp represent polar and azimuthal angles of the incident photons, respectively. In our experimental geometry, ϕp = 0°. As a consequence, only the first terms of eqs (2–4) are relevant for the discussion of the observed spin polarization. \({M}_{p\perp }^{\mathrm{(1)}}\) and \({M}_{p||}^{\mathrm{(3)}}\) (\({M}_{s}^{\mathrm{(4)}}\)) indicate the complex partial matrix elements for Σ1 and Σ3 (Σ4) orbital contributions in the initial state, excited by normal and parallel electric field vector components of p-polarized (s-polarized) light within circular polarized light, respectively. For normal electron emission and small θe, we neglect photoemission contributions of Σ2 states because they are forbidden by selection rules at \(\overline{{\rm{\Gamma }}}\)31. From these equations, Py originates from a mixing of Σ1 and Σ3 even-symmetry orbitals with respect to the mxz mirror plane. This photoemission-induced effect of Py is caused by only the p-polarized component of the light. The intensity difference for Px (Pz) is generated by a mixing of Σ1 (Σ3) even-symmetry orbitals and Σ4 (Σ4) odd-symmetry orbitals. The unexpected intensity differences for Px and Pz are due to coherent superposition of p− and s−polarization components within the circular polarized light. In the experiment, we varied the photoelectron emission angle θe between −5° and +5°. Consequently, according to our set-up, the light incidence angle θp varies between 45° and 55°, which will not strongly influence the intensity differences. The variation of θe is taken into account in the complex partial matrix elements \({M}_{p\perp }^{\mathrm{(1)}}\), \({M}_{p||}^{\mathrm{(3)}}\), and \({M}_{s}^{\mathrm{(4)}}\).
Next, we discuss the symmetry of the partial matrix elements in more detail, as illustrated in Fig. 3. The partial matrix elements contain the wave function of the final state, the electric field vector of the photons, and the wave function of the initial state with C2v symmetry, namely, Σ1, Σ3, and Σ4. (In double-group representation, only one representation (Σ5) exists which can be decomposed into the four single-group representations). The surface with C2v symmetry includes two mirror planes: mxz and myz. In our experimental geometry, final state, electric field vector components Ez and Ey, and Σ1 and Σ4 initial states have even symmetry with respect to myz. However, the photoelectron emission angle is reversed upon reflection at myz. As a consequence, \({M}_{p\perp }^{\mathrm{(1)}}({{\rm{\theta }}}_{e})={M}_{p\perp }^{\mathrm{(1)}}(\,-\,{\theta }_{e})\) and \({M}_{s}^{\mathrm{(4)}}({{\rm{\theta }}}_{e})={M}_{s}^{\mathrm{(4)}}(\,-\,{\theta }_{e})\). For \({M}_{p||}^{\mathrm{(3)}}\), we can estimate the symmetry properties. In a simple model, a matrix element is the Fourier transform of the initial state’s orbitals; thus, it obeys the same even-odd properties in k-space as the orbital itself. Therefore, \({M}_{p||}^{\mathrm{(3)}}\) has odd symmetry with respect to myz: \({M}_{p||}^{\mathrm{(3)}}({{\rm{\theta }}}_{e})=-\,{M}_{p||}^{\mathrm{(3)}}(\,-\,{\theta }_{e})\). By considering the θe-dependent partial matrix elements, IPx (IPy and IPz) show even (odd) symmetry, with respect to myz. Therefore, the intensity differences for Pz are reversed, when θe changes sign, while Px does not change.
Figure 4 shows first-principles calculations within the relativistic one-step model calculation for W(110) along \(\overline{{\rm{\Gamma }}H}\). The calculation includes the full photoemission process for excitation with circular polarized light and the geometrical set-up of our experiment. EDC’s for C+ and C− light are presented for all three spin polarization components in Fig. 4(a,b), respectively. The intensity differences are shown in Fig. 4(c). We find good qualitative agreement between experimental and theoretical results, even details, such as spin-dependent intensities for Py at θe = 0°, are well reproduced.
In conclusion, we have clarified the origin of circular-polarized-light-induced spin signals in photoemission results from the Dirac-cone-like surface state on W(110) with C2v crystal symmetry. We observed non-zero spin polarization in all spin components Px, Py, and Pz. In our case, for photoelectrons from the Dirac-like state on W(110) with hν = 43 eV, we obtained spin-polarization values of up to 20% for Px, 90% for Py, and 25% for Pz. While Py is dominated by the intrinsic spin polarization of the initial states, Px and Pz are exclusively extrinsic and originate from the photoemission process. Our detailed analysis of the complex partial transition matrix elements shows how the orbital contributions of the initial state and the geometrical details of the experiment, such as light incidence angle and light polarization, and the crystal symmetry lead to the experimentally observed spin texture. Within limits, this approach opens the way for manipulating and controlling the spin polarization of photo-emitted electrons. The limits are given by the sample and its symmetry, the orbital characters of the respective electron states, and the experimental parameters. The challenge is to find optimum conditions for sample and experimental parameters that lead to maximum spin-polarization values.
The discussed mechanism of inducing spin polarization by circular polarized light is a general phenomenon depending on the specific orbital characters of the bands as well as geometrical parameters of the experiment. While the described test case of an occupied Dirac state at the metallic W(110) surface is not well suited for spin-selective transport, the general idea may be applied to optical-induced spin-polarized transport in optospintronic devices (see, e.g.,35). One may even speculate about spin-selective anisotropic transport phenomena by exploiting anisotropically dispersing states similar to the Dirac state on W(110)31.
Methods
A clean surface of W(110) was obtained and evaluated by the same procedure as described elsewhere30,31. The ARPES and spin-ARPES experiments were performed with synchrotron radiation generated by a quasi-periodic variable polarizing undulator at BL-9B at Hiroshima Synchrotron Radiation Center (HiSOR), equipped with highly efficient three-dimensional spin-polarization analysis of the ESPRESSO machine36,37. At BL-9B, the electric field vectors between left (C−) and right circular (C+) can be switched by changing the magnetic phase of the variable polarizing undulator. The angle of light incidence was 50° relative to the lens axis of the electron analyzer in all experiments as shown in Fig. 5. The spin-ARPES system with high angular- and energy-resolution can resolve all three spin polarization components: out-of-plane (Pz) and in-plane (Px and Py). The positive (negative) sign of spin polarization is parallel (antiparallel) to the arrows of the x, y, and z axes in the sample coordinate system. The emission angle θe of the photoelectrons is defined as positive (negative), when the surface normal is moved away from (toward) the light propagation vector. The overall experimental energy and angular resolutions of ARPES (spin-ARPES) at BL-9B were set to 50 meV (50 meV) and 0.3° (0.75°), respectively. All measurements have been performed at a sample temperature of 80 K.
The first-principles calculations include the photoemission process in the one-step model and are described in ref.7.
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Bychkov, Y. A. & Rashba, E. I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 39, 78 (1984).
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665 (1990).
Miron, I. M. et al. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nature Mater. 9, 230 (2010).
Miyamoto, K. et al. Orbital-symmetry-selective spin characterization of Dirac-cone-like state on W(110). Phys. Rev. B. 93, 161403(R) (2016).
Kuroda, K. et al. Coherent control over three-dimensional spin polarization for the spin-orbit coupled surface state of Bi2Se3. Phys. Rev. B. 94, 165162 (2016).
Yaji, K. et al. Spin-dependent quantum interference in photoemission process from spin-orbit coupled states. Nature Commun. 8, 14588 (2017).
Mirhosseini, H., Fliege, M. & Henk, J. Dirac-cone-like surface state in W(110): dispersion, spin texture and photoemission from first principles. New J. Phys. 15, 033019 (2013).
Sakamoto, K. et al. Abrupt rotation of the Rashba spin to the direction perpendicular to the surface. Phys. Rev. Lett. 102, 096805 (2009).
Sakamoto, K. et al. Valley spin polarization by using the extraordinary Rashba effect on silicon. Nature Commun. 4, 2073 (2013).
Stolwijk, S. D., Schmidt, A. B., Donath, M., Sakamoto, K. & Krüger, P. Rotating spin and giant splitting: Unoccupied surface electronic structure of Tl/Si(111). Phys. Rev. Lett. 111, 176402 (2013).
Suzuki, R. et al. Valley-dependent spin polarization in bulk MoS2 with broken inversion symmetry. Nature Nanotech. 9, 611 (2014).
Jozwiak, C. et al. Photoelectron spin-flipping and texture manipulation in a topological insulator. Nature Phys. 9, 293 (2013).
Zhang, H., Liu, C.-X. & Zhang, S.-C. Spin-orbital texture in topological insulators. Phys. Rev. Lett. 111, 066801 (2013).
Xie, Z. et al. Orbital-selective spin texture and its manipulation in a topological insulator. Nature Commun. 5, 3382 (2014).
Zhu, Z.-H. et al. Photoelectron spin-polarization control in the topological insulator Bi2Se3. Phys. Rev. Lett. 112, 076802 (2014).
Sánchez-Barriga, J. et al. Photoemission of Bi2Se3 with circularly polarized light: Probe of spin polarization or means for spin manipulation? Phys. Rev. X 4, 011046 (2014).
Wissing, S. N. P. et al. Ambiguity of experimental spin information from states with mixed orbital symmetries. Phys. Rev. Lett. 113, 116402 (2014).
Donath, M. In or out of control? Electron spin polarization in spin-orbit-influenced systems, in: Wandelt, K., (Ed.) Encyclopedia of Interfacial Chemistry: Surface Science and Electrochemistry 2, 131–137 (2018).
Miyamoto, K. et al. Peculiar Rashba spin texture induced by C 3v symmetry on the Bi(111) surface revisited. Phys. Rev. B. 97, 085433 (2018).
Tamura, E., Piepke, W. & Feder, R. New spin-polarization effect in photoemission from nonmagnetic surfaces. Phys. Rev. Lett. 59, 934 (1987).
Henk, J., Scheunemann, T., Halilov, S. V. & Feder, R. Magnetic dichroism and electron spin polarization in photoemission: analytical results. J. Phys.: Condens. Matter 8, 47 (1996).
Heinzmann, U. & Dil, H. Spin-orbit-induced photoelectron spin polarization in angle-resolved photoemission from both atomic and condensed matter targets. J. Phys.: Condens. Matter 24, 173001 (2012).
Wortelen, H. et al. Tuning the spin signal from a highly symmetric unpolarized electronic state. Phys. Rev. B. 91, 115420 (2015).
Bentmann, H. et al. Strong linear dichroism in spin-polarized photoemission from spin-orbit-coupled surface states. Phys. Rev. Lett. 119, 106401 (2017).
Gaylord, R. H. & Kevan, S. D. Spin-orbit-interaction-induced surface resonance on W(011). Phys. Rev. B. 36, 9337 (1987).
Feydt, J. et al. Photoemission from bulk bands along the surface normal of W(110). Phys. Rev. B. 58, 14007 (1998).
Rotenberg, E., Chung, J. W. & Kevan, S. D. Spin-orbit coupling induced surface band splitting in Li/W(110) and Li/Mo(110). Phys. Rev. Lett. 82, 4066 (1999).
Hochstrasser, M., Tobin, J. G., Rotenberg, E. & Kevan, S. D. Spin-resolved photoemission of surface states of W(110)-(1×1)H. Phys. Rev. Lett. 89, 216802 (2002).
Rybkin, A. G. et al. Topology of spin polarization of the 5 d states on W(110) and Al/W(110) surfaces. Phys. Rev. B. 86, 035117 (2012).
Miyamoto, K. et al. Spin-polarized Dirac-cone-like surface state with d character at W(110). Phys. Rev. Lett. 108, 066808 (2012).
Miyamoto, K. et al. Massless or heavy due to two-fold symmetry: Surface-state electrons at W(110). Phys. Rev. B. 86, 161411(R) (2012).
Miyamoto, K., Kimura, A., Okuda, T. & Donath, M. Spin polarization of surface states on W(110): Combined influence of spin-orbit interaction and hybridization. J. Electron Spectrosc. Relat. Phenom. 201, 53 (2015).
Braun, J. et al. Exceptional behavior of d-like surface resonances on W(110): the one-step model in its density matrix formulation. New. J. Phys. 16, 015005 (2014).
Thonig, D. et al. Existence of topological nontrivial surface states in strained transition metals: W, Ta, Mo, and Nb. Phys. Rev. B. 94, 155132 (2016).
Yan, Y. et al. Topological surface state enhanced photothermoelectric effect in Bi22Se3 nanoribbons. Nano Letters 14, 4389 (2014).
Okuda, T. et al. Efficient spin resolved spectroscopy observation machine at Hiroshima Synchrotron Radiation Center. Rev. Sci. Instrum. 82, 103302 (2011).
Okuda, T., Miyamoto, K., Kimura, A., Namatame, H. & Taniguchi, M. A double VLEED spin detector for high-resolution three dimensional spin vectorial analysis of anisotropic Rashba spin splitting. J. Electron Spectrosc. Relat. Phenom. 201, 23 (2015).
Acknowledgements
This work was financially supported by KAKENHI (Grant Nos 23340105, 23244066, 25800179, 16K13823), Grant-in-Aid for Scientic Research (A), (B) and for Young Scientists (B) of JSPS. K.M. gratefully acknowledges the hospitality of the Physikalisches Institut at the University of Münster and support by the Alexander von Humboldt foundation (Humboldt research fellowship for experienced researcher). The measurements were performed with the approval of the Proposal Assessing Committee of HSRC (Proposal No. 13-B-2). H.W. and M.D. gratefully acknowledge the hospitality of the Hiroshima Synchrotron Radiation Center.
Author information
Authors and Affiliations
Contributions
K.M. and M.D. conceived the experiments. K.M., H.W., T.O., and M.D. conducted the experiments. J.H. provided the SARPES calculations. K.M., M.D., and J.H. analyzed and discussed the results. K.M. and M.D. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Miyamoto, K., Wortelen, H., Okuda, T. et al. Circular-polarized-light-induced spin polarization characterized for the Dirac-cone surface state at W(110) with C2v symmetry. Sci Rep 8, 10440 (2018). https://doi.org/10.1038/s41598-018-28693-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-28693-3
This article is cited by
-
Quantum spin mixing in Dirac materials
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.