Abstract
Magnetic skyrmions are topologically protected spin-whirls currently considered as promising for use in ultra-dense memory devices. Towards achieving this goal, exploration of the skyrmion phase response and under external stimuli is urgently required. Here we show experimentally, and explain theoretically, that in the magnetoelectric insulator Cu2OSeO3 the skyrmion phase can expand and shrink significantly depending on the polarity of a moderate applied electric field (few V/μm). The theory we develop incorporates fluctuations around the mean-field that clarifies precisely how the electric field provides direct control over the free energy difference between the skyrmion and the surrounding conical phase. The quantitative agreement between theory and experiment provides a solid foundation for the development of skyrmionic applications based on magnetoelectric coupling.
Similar content being viewed by others
Introduction
To realise skyrmion-based applications (skyrmionics)1,2,3,4,5, research into the creation, control and stabilisation of skyrmions is in an active phase1,6,7,8,9,10,11,12,13. In this context, it could seem problematic that in bulk materials the skyrmion phase is stable only for a narrow interval at finite temperature (T) just below the magnetic ordering temperature TC, and under an applied magnetic field (H)6,14,15,16,17. In Cu2OSeO3 for example, the skyrmion phase spreads down in T by just 3.5% of TC, occupying no more than 1% of the total ordered phase space that is otherwise dominated by topologically trivial helical or conical phases7,17,18. This limited skyrmion phase space is observed also in other known bulk hosts of skyrmions14,15,16,19. On the other hand, the finite extent of the skyrmion phase pocket can be considered to present an interesting advantage, since relatively small perturbations can dramatically influence the skyrmion phase stability. It follows that the ability to enhance or suppress the skyrmion phase space in a sample can provide a flexible platform for the respective creation or destruction of skyrmions, a process that can be technologically useful. Here we describe a simple and reliable mechanism for the stabilisation and destabilisation of the skyrmion lattice (SkL) phase by exploiting electric (E) fields applied to the insulating magnetoelectric material Cu2OSeO3.
To date, several approaches for skyrmion manipulation have been demonstrated that make use of either moderate electric currents, electric fields, or thermal gradients6,8,9,10,11,12,13,20,21,22,23. In addition, progress towards tuning the bulk skyrmion phase stability was also demonstrated using both applied uniaxial24,25 and hydrostatic pressure18. For possible applications however, the use of E fields to manipulate skyrmions and skyrmion phase stability in insulators offers several potential advantages for applications, yet this approach remains still little-explored experimentally6,8,23,26. Moreover, the E field control of the SkL phase stability remains an outstanding theoretical issue.
Here we report a combined experimental and theoretical study of skyrmion phase stability under moderate E-fields (V/μm) in the model insulating skyrmion host Cu2OSeO3. We use the microscopic probe of small-angle neutron scattering (SANS) to show that in Cu2OSeO3, the extent of the skyrmion phase stability either expands or shrinks in both T and H, dependent on the E field polarity. Theoretically, we address the role of the E field using first order perturbation theory to evaluate the free energy of the underlying phases. We show how an applied E field causes a relatively small shift of the SkL free energy that is nonetheless commensurate with the mean-field free energy difference between the competing skyrmion and conical phases, and thus dramatically controls the SkL phase stability. For the quantitative description of the experimental phase diagram, we develop a new approach for treating the fluctuative part of the free energy contributed by quasiparticle modes around TC. The inclusion of these modes proves pivotal for the correct evaluation of the free energy difference between the competing skyrmion and conical phases, both with and without E field, and thus represents an improved approach more generally for the calculation of the skyrmion phase diagram.
Results
Controlling skyrmion phase stability using electric fields
From recent bulk susceptibility χ(H) measurements of Cu2OSeO323, it was suggested that skyrmions may be “created” or “annihilated” by applying a dc E-field in suitable parts of the temperature–magnetic field (T,H) phase diagram. In that study23 the skyrmion phase is identified by a small drop in χ(H), which serves as an indirect indication for the existence of the skyrmion phase.
We have used the tool of SANS to observe directly the microscopic skyrmionic magnetism in Cu2OSeO3 and its response to an applied dc E-field. In SANS the SkL phase is typically evidenced by a sixfold symmetric diffraction pattern, consistent with the so-called multi-q (triple-q) magnetic structure ansatz for the SkL described by three propagation q-vectors rotated by 120° with respect to each other (note that both ±q each give a SANS diffraction spot)6,14,27. In our SANS experiments we oriented the sample so that E||H|| [111], since according to previous bulk measurements7, the effect of the E field is expected to be maximal in this geometry. By measuring with the neutron beam also along [111], scattered intensity is only observed due to the SkL phase; for both the conical phase with q||H and the zero field helical phase with q||{100} type directions6, the expected scattering lies well out of the detector plane.
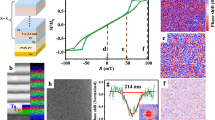
Figure 1 summarizes the direct E-field control of the SkL phase stability in Cu2OSeO3. Representative SANS data collected at constant T = 56.8 K, and at (H,E) coordinates selected to emphasise the E field effect, are shown in Fig. 1a–d. The initial states at T = 56.8 K were always prepared after zero-field cooling. By applying H = 17 mT at E = 0, the system the system is located on the border of the SkL phase and mostly in the conical phase, as evidenced by a weak SkL signal on the SANS detector (Fig. 1a). Without changing T or H, applying a positive E field of +5.0 V/μm leads to the appearance of the characteristic 6-fold diffraction pattern in the SANS image (Fig. 1b), demonstrating the creation of a well-developed SkL. Conversely, starting from the SkL state at H = 0 38 mT and E = 0 (Fig. 1c), application of a negative electric field E = −2.5 V/μm erases the SkL as evidenced by the disappearance of the SANS diffraction peaks (Fig. 1d).
Skyrmion phase tuning by electric fields. (a–d) Representative SANS diffraction patterns obtained from the SkL phase at a temperature of 56.8 K, and various (H, E) conditions for \(E\Vert H\Vert \mathrm{[111]}\). Here the [111] direction is into the page. Starting with only a weak intensity from the SkL at T = 56.8 K and H = 17 mT (a nearly conical state) (a), applying a positive E field enhances the SkL stability as evidenced by a significantly enhanced SkL intensity (b). Conversely, starting from a well-developed SkL state at T = 56.8 K and H = 38 mT (c), applying a negative E field erases the SkL (d). For the systematic analysis of the SANS data shown later in Figs 1(e) and 2(a–c), we evaluate the entire SANS intensity due to all SkL domains within the annular integration windows denoted by white rings in (a–d). This allows us to cater for scattering due to the major SkL domain (six strongest spots), and also any minority domains present that are signified by weaker diffraction spots in-between the strong ones. (e) shows the extent of the skyrmion phase pockets in the phase diagram for various E fields as determined by SANS. The skyrmion pocket doubles in temperature extent under a positive E field of +5.0 V/μm, while shrinks to half its size at E = 0 under a negative E field of −2.5 V/μm. The white and yellow stars on figure (e) mark experimental conditions of SANS patterns (a–d) on the phase diagram.
Since in our experimental geometry it is only scattering from the SkL that contributes to the observed SANS intensity, we determined the extent of the SkL phase by evaluating the total intensity within the region of interest on the detector (the annular range within the white rings shown in Fig. 1a–d) as a function of T, H, and E. The resulting stability range of the skyrmion phase is shown in Fig. 1e for zero (green), positive (red) and negative (blue) E fields. We find that a positive E field of +5.0 V/μm expands the skyrmion pocket so that it becomes twice larger (in temperature), while a negative E field of just E = −2.5 V/μm shrinks the pocket by a factor of two. These SANS results provide microscopic experimental evidence for the electric field control of the skyrmion phase. Moreover, the results are quantitatively consistent with those of the indirect measurements reported in ref.23 after rescaling the data to take into account the difference between the ranges of applied electric field explored in the two studies.
Optimum conditions for stabilising and destabilising the skyrmion phase
Examining our SANS data more closely reveals the systematic manner by which applied E fields modify the SkL stability in the phase diagram. Figure 2a,b, show H-scans of the total scattered SANS intensity from the SkL for various E fields, and at T = 55.8 K and 56.8 K, respectively. At each T, the extent in H over which the SkL intensity is observed at E = 0 becomes enhanced under positive E fields, and suppressed under negative E fields. This demonstrates clearly the importance of the E field polarity on either enhancing or suppressing SkL stability. The effect is very pronounced as seen in Fig. 2a; at T = 55.8 K a negative E field can completely destabilise the SkL that is otherwise stable in the unperturbed state (E = 0).
Skyrmion lattice stability in electric field: experiment and theory (a,b) E- and H-field dependence of the total scattered SANS intensity from SkLs in the sample at (a) T = 55.8 K, and (b) T = 56.8 K. The intensity evaluated is that observed within the annular sectors defined by white rings in Fig. 1a–d. (c) The E- and T-dependence of the peak SANS intensity in the H-scans like those shown in (a,b). In (a–c), symbols and lines in red, green and blue denote data obtained under E = +5kV/mm, E = 0 and E = −2.5 kV/mm, respectively. The dotted lines in (c) are guides for the eye. (d,e) The H-dependence of the calculated free energy difference between skyrmion and conical phases at (d) T = 55.8 K and (e) T = 56.8 K, for various E-fields. (f) The T-dependence of the minima in the calculated free energy differences like those shown in (d,e). In (d–f) calculations for E = +5 kV/mm, E = 0 kV/mm, E = −5 kV/mm are shown in red, green, blue, respectively (asymmetric \({{\rm{\ae }}}^{2}\) effects neglected). The skyrmion phase stability is preferred over the conical phase when the calculated free energy differences are negative.
Since the total scattered SANS intensity is indicative of both the population (relative to the conical phase) and quality of SkLs in the sample, the maximum intensity in the H scans like those shown in Fig. 2a,b is identified to represent the optimal SkL stability at each E and T. We present the T-dependence of this intensity peak at each E field in Fig. 2c, along with T windows identified as optimal for either enhancing or suppressing the SkL stability using the E field. Within the T window of 53–55.5 K, positive E fields enhance the SkL phase stability relative to the case at E = 0, while in the T-window of 55–56.5 K the SkL phase stability is readily suppressed by the negative E field relative to the E = 0 case. Positioning a sample at 55.5 K allows the demonstration of either a significant enhancement or suppression of the skyrmion phase at E = 0 by using E-fields of opposite polarity. In what follows, we develop a theory capable of explaining these observations quantitatively.
Free energy in electric fields
The underlying mechanism for the E field driven enhancement or suppression of the skyrmion phase stability relies upon the magnetoelectric (ME) coupling in insulating Cu2OSeO3, which microscopically originates from the d-p hybridisation mechanism27,28,29,30,31. The emergent electric dipole moment P = λ(SySz, SzSx, SxSy) is generated by the underlying spin structure S(r) = (Sx, Sy, Sz), with the coupling between the magnetic and electric degrees of freedom described by a ME coupling parameter λ of relativistically small magnitude. Crucially, because the skyrmion phase now carries a non-vanishing electric-dipole moment, the ME coupling results in a P·E shift of the skyrmion free energy in E-field. This perturbation renormalises the elementary helices upon which the skyrmion phase is built, and slightly distorts the SkL6,32.
In this work, we apply the ME perturbation to the free energy described by an effective Ginsburg-Landau functional with Dzyaloshinski-Moriya interaction (DMI), and consider carefully the critical fluctuations that favour the skyrmion phase with respect to the competing conical phase (see Methods). Due to the relativistically small size of λ, the dimensionless E-field itself is rather small so that, \({\rm{\ae }}=\lambda E\mathrm{/4}D{k}_{0}\ll 1\), and we can build a perturbation theory in \({\rm{\ae }}\); for the modified free energy, neglecting all the terms of order \({{\rm{\ae }}}^{{\rm{2}}}\) and higher. Our finding is that perturbations of the fluctuative terms are important only at second order, while the mean-field energy already shifts in the first order due to direct ME and nonlinear contributions (see Methods). The corresponding shift in free energy of the skyrmion phase depends on the direction of E-field (see Fig. 2d–f), thus either enhancing (E > 0) or suppressing (E < 0) the skyrmion phase stability. While at first sight it can be surprising that the perturbation due to only a moderate applied E-field can play such a crucial role here, this is facilitated by the very close competition between the skyrmion and conical phases already in the mean-field.
Calculation of the phase diagram
To calculate the response of the phase diagram to applied E-field, we use a new approach developed on the basis of effective models presented in refs6,14,33 (see Methods). Compared with these earlier studies, the new approach is self-consistent in the way that it reproduces the phase diagram, provides a deeper understanding of the role of quasiparticle modes near TC, and includes the path-integral approach presented previously for calculating the fluctuative free energy14 as a limiting case. We thus treat the first-order perturbation in E field on top of the mean-field solution, and add the fluctuative contributions that stabilise the SkL in the bulk. The main contribution of the E field here is captured by the shift of the mean-field free energy difference between the SkL and conical phases, while the fluctuative shift under voltage remains quadratically small.
Figure 2d,e each show calculations of the H and E field-dependent free energy difference between the skyrmion and conical phases, at T = 55.8 K and T = 56.8 K, respectively. In general, the calculations show the minima of the free energy difference curves deepen with increasingly positive E field. At T = 55.8 K changing between sufficiently negative and positive E fields can shift the curve so that the conical phase favoured for all H in a negative E field becomes unstable towards the skyrmion phase formation in the positive E field. This result is consistent with the experimental data shown in Fig. 2a. We also identify semi-quantitative agreement between these calculations and our experiments; the H location of the minima in the calculated free-energy difference curves [Fig. 2d,e] correspond well to the values of H where the peaks of SANS intensity are observed in the scans shown in Fig. 2a,b. In addition, we can link the calculated T and E field dependence of the free energy difference minima shown in Fig. 2f to our experimental data. The T s at which the free energy difference between the SkL and conical phases vanish for the theoretical E fields correspond to the T windows identified from the experimental data as optimal for either enhancing or suppressing SkL stability with E [Fig. 2c]. This correspondence between experiment and theory provides firm support for the validity of our theoretical treatment of the E-field effect on the SkL phase stability.
Independent of any applied E field, our theory provides a more general understanding of SkL stability on an intuitive, pictorial level: the critical fluctuations (waves) are superposed on top of the variationally minimised free energies. There are three critical modes \({\omega }_{{\bf{k}}}^{\mathrm{(0,1,2)}}\) around the mean-field (see Methods), with \({\omega }_{{\bf{k}}}^{\mathrm{(0)}}\) soft on the sphere \(|{\bf{k}}|={k}_{0}\), which means that it costs very little energy to add many such fluctuations if they are coherent with the helix k0. Thus \({\omega }_{{{\bf{k}}}_{0}}^{\mathrm{(0)}}\) is the so-called “dangerous” mode since it results in a Van-Hove-like singularity at TC and eventually breaks down the ordered phases into the disordered (paramagnetic) phase33. Below TC the symmetry-breaking can be observed using SANS by either a six-fold pattern (SkL phase) or a two-fold pattern (helical or conical phases), both circumscribed on a sphere of radius \(|{\bf{k}}|={k}_{0}\) in reciprocal space. Our calculation shows that the skyrmion phase is favoured because adding fluctuations generates more entropy in the skyrmion phase. This analysis also leads to a qualitative criterion for capturing the magnetic-field-independent breakdown of the ordered phases at TC (see Methods). Asymptotically, the main contribution of the fluctuative free energy is given in the short-scale physics, where Cu2OSeO3 is “almost” a ferromagnet, thus reproducing the result of the path-integral approach14 as a limiting case. The model described here captures the qualitative physics of the system, as exemplified by the theoretical phase diagram shown in Fig. 3. To date, a quantitative theory for the skyrmion phase diagram under electric fields has been missing.
Calculation of the skyrmion phase in electric fields Calculated H and T extent of the skyrmion phase for E > 0 (red shading), E = 0 (green shading), E < 0 (blue shading) for the \(E\Vert H\Vert \mathrm{[111]}\) geometry, and for the symmetric-response approach \(({{\rm{\ae }}}^{1})\). The extent of each phase corresponds to the range over which the free energy of the skyrmion phase is less than that of the surrounding conical phase. Dashed lines denote phase boundaries, including the vertical breakdown regime at TC.
Discussion
In some respects, the effect of E field observed here resembles that achieved due to applied uniaxial pressure24,25 since, the SkL phase stability can be either enhanced or suppressed by appropriate selection of the uniaxial stress direction relative to the direction of H. However, integrating the pressure effect on skyrmion stability into a technological setting is very challenging. In contrast, the E field is a versatile and reliable external parameter; providing an efficient control of both the skyrmion position6,8,26 and, as we show here the stability of the phase as a whole. Since the E field controlled expansion or contraction of the skyrmion phase can occur in general for an insulating ME skyrmion host with any TC, our findings are very attractive for applications at room T; for a device layer of thickness 100 nm the skyrmion phase in a sample can be entirely destabilised (erased) or restabilised (written) with less than 1 V, a voltage compatible with modern microelectronics.
The present study further lays both theoretical and experimental foundations for fully exploring alternative H and E field configurations, not only in reciprocal-space measurements like SANS, but also by real-space imaging techniques such as cryo-Lorentz transmission electron microscopy (LTEM) on technologically-relevant, nanometrically-thin specimens. Crucial next steps experimentally concerning the skyrmion writing and erasing includes exploring directly the expected E field-driven switching hysteresis between the competing conical and skyrmion states, and the associated volatility of remnant states in zero biasing E field. In addition, learning how E field influences out-of-equilibrium and metastable skyrmion configurations in confined geometries can provide progressive insights for assessing the merits of insulating skyrmions for practical uses.
In conclusion, we have demonstrated both theoretically and experimentally the mechanism by which a moderate electric field can either enhance or suppress skyrmion phase stability in the magnetoelectric chiral magnet Cu2OSeO3. In addition, we have provided the parameters by which our theoretical approach achieves quantitative agreement with experiment, and which can be extended towards describing the effect of E field on both stable and metastable skyrmion states, these being of paramount technological importance.
Methods
Small-angle neutron scattering (SANS)
For the SANS experiment, we used a single crystal crystal grown using chemical vapour transport34. The crystal with a TC = 58 K was of mass 6 mg and volume 3.0 × 2.0 × 0.50 mm3 with the thinnest axis ||[111], and \([\bar{1}\bar{1}2]\) vertical. The sample was mounted onto a bespoke sample stick designed for applying dc E-fields35, and oriented with the orthogonal \([\bar{1}\bar{1}2]\) and \([1\bar{1}0]\) directions lying in the SANS scattering plane. For the SANS images shown in Fig. 1, the \([\bar{1}\bar{1}2]\) direction is aligned with the vertical axis, and the \([1\bar{1}0]\) direction aligned with the horizontal axis. In our experiments we achieved E-fields ranging from +5.0 kV/mm to −2.5 kV/mm. Evidence of electrical breakdown was detected for E-fields outside this range.
The sample was loaded into a horizontal field cryomagnet at the SANS-II beamline, SINQ, PSI. The magnetic field (μ0H) was applied parallel to both the [111] direction of the sample and the incident neutron beam to give the experimental geometry E||μ0H||[111]. In this geometry, the SANS signal is only detected from the skyrmion phase, which typically presents as a hexagonal scattering pattern with propagation vectors q ⊥μ0H. In this geometry, we avoid detecting any SANS signal due to either of the neighbouring helical (q ||{100}) or conical phases (q ||μ0H), since the propagation vectors of these phases lie well out of the SANS detector plane.
We used incident neutrons with a wavelength of 10.8 Å (Δλ/λ = 10%). The scattered neutrons were detected using a position-sensitive multidetector. The SANS measurements were done by rotating (‘rocking’) the sample and cryomagnet ensemble over angles that brought the various SkL diffraction spots onto the Bragg condition at the detector. Data taken at 70 K in the paramagnetic state were used for background subtraction. Before starting each μ0H-scan, the sample was initially zero field-cooled from 70 K to a target temperature, with the E-field applied when thermal equilibrium was achieved. The E-field was maintained during the μ0H-scan. At each T we define the μ0H extent of the SkL phase as that over which SANS intensity is detected. We use this criterion to extract the parametric extent of the SkL phase for (μ0H,T,E) as shown in Figs 1 and 2. See Supplemental Material for more details.
Mean-field free energy
The effective mean-field theory is based on the coarse-grained magnetisation approach \(M({\bf{r}})={M}_{s}{\bf{S}}({\bf{r}})\) as described in14. One starts with the mean-field approach with free energy
with spatial average \(\langle \mathrm{...}\rangle =\int \frac{dV}{V}\mathrm{...}\), and \({{\rm{\Theta }}}_{T}\propto \alpha (T-{T}_{C})\) near TC, J is the Heisenberg stiffness and D is DMI, H is the magnetic field, and the higher-order term U grants the formation of the crystalline phase14. In the mean-field, the interplay between Heisenberg and DMI energies determines the helical vector as k0 = D/2J. The long-range-ordered hexagonal skyrmion lattice is approximated as \({\bf{S}}({\bf{r}})\simeq {\bf{m}}+\mu {\sum }_{{{\bf{q}}}_{n}}{{\bf{S}}}_{{{\bf{q}}}_{n}}{e}^{i{{\bf{q}}}_{n}{\bf{r}}+i{\varphi }_{n}}+{\rm{c}}{\rm{.c}}{\rm{.}}\), where the summation runs over the magnetocrystalline wave vectors q1 + q2 + q3 = 0. In the mean-field, the skyrmion phase is slightly gapped with respect to the conical phase, however the two are closely competing. Further details of the mean-field theory described in ref.14.
Perturbation theory in electric fields
The magneto-electric coupling in Cu2OSeO3 is relativistically small, so the perturbation parameter is \({\rm{\ae }}=\lambda E\mathrm{/4}D{k}_{0}\ll 1\). It is sufficient to use the first order perturbation theory on top of the non-perturbed free energy. We go to the rotated frame defined by the magnetic field direction along [111], and re-write the free energy. The first order perturbation theory gives eigenvectors:
which are now the basis for constructing the distorted skyrmion lattice. For other (H, E)-field configurations, we re-do the calculations in the new rotated frames. See Supplemental Materials for further details.
Fluctuation-induced phase stabilisation
We use a new approach, which captures as a limiting case the fluctuation free energy from14. The essential physics is captured already in Gaussian (noninteracting) fluctuations with free energy density
where Λ = 2π/a is the natural cut-off, \({f}_{{\bf{k}}}^{(i)}\) is the critical modes distribution, and the entropy of Gaussian fluctuations is
in the case of bosons. Fluctuations around mean-field are described by the generalised susceptibility \({\chi }_{ij}^{-1}({\bf{r}},{\bf{r}}\text{'})=\frac{1}{T}\frac{{\delta }^{2}F}{\delta {M}_{i}({\bf{r}})\delta {M}_{j}({\bf{r}}\text{'})}\), giving rise to several collective modes (See Supplemental Material). On the local scale \((k\gg J/D)\), the chiral magnet is reminiscent of a ferromagnet, so the modes behave asymptotically ωk ∝ k2 for large k, thus asymptotically \({F}_{{\rm{fluct}}}\simeq \,\mathrm{log}\,\beta {\omega }_{{\bf{k}}}\propto \,\mathrm{log}\,{k}^{2}\), which covers the model of ref.14. The main contribution to (5) is given by the short length-scale (“ferromagnetic”) physics,
The electric field also slightly affects the fluctuative energy, because it modifies the correlation length near TC and so renormalises Jeff, which is neglected here as a higher-order \(({{\rm{\ae }}}^{2})\) effect. See [Supplemental Material] for further details.
Parameters of the effective model
For our numerical calculations we use TC = 58 K, which approximately sets the Heisenberg stiffness as J = 4.85 × 10−23 Jm/A2. From the SANS measurement we establish directly the modulation period of 60 nm, which estimatively differs by a few percents from the mean-field value 2π/k0, because the mean-field ordering vector k0 = D/2J is slightly renormalised by the fluctuations near TC. This sets the “bare” DM interaction entering (1) as D = −9.85 × 10−15 J/A2. The lattice parameter is a = 8.91 × 10−10 m, which gives the natural cutoff Λ = 2π/a ≈ 70k0. The saturation magnetization in Cu2OSeO3 is Ms = 1.11 × 105 A/m and scales with temperature as \({M}_{s}(T)={M}_{s}{(1-{(T/{T}_{C})}^{{\alpha }_{1}})}^{{\alpha }_{2}}\), with α1 = 1.95 and α2 = 0.39336. We choose the nonlinear coupling responsible for SkL formation U = 6.2 × 10−6 Jm−1 A−2 and Landau parameter \({\alpha }_{T}={\theta }_{T}/J{k}_{0}^{2}(T-{T}_{C}^{{\rm{m}}{\rm{.f}}{\rm{.}}})=3.5\,{{\rm{K}}}^{-1}\). For the qualitative phase diagram shown in Fig. 3, we use a symmetric-response model \(({\text{ae}}^{1})\), for which the best fit to SANS data is for \({\text{ae}}^{1}=0.02\), which corresponds here to E = ±5 × 106 V/m coupled with λ/Dk0 = 9.23 × 10−3 μm/V to the underlying spin structure through ME mechanism.
References
Fert, A., Cros, V. & Sampaio, J. Skyrmions on the track. Nat. Nanotech. 8(3), 152–156 (2013).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotech. 8(12), 899–911 (2013).
Tomasello, R. et al. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 4, 6784, https://www.nature.com/articles/srep0678410.1038/srep06784 (2014).
Zhang, X. et al. Skyrmion-skyrmion and skyrmion-edge repulsions in skyrmion-based racetrack memory. Sci. Rep. 5, 7643, https://www.nature.com/articles/srep0764310.1038/srep07643 (2015).
Zhang, X., Ezawa, M. & Zhou, Y. Magnetic skyrmion logic gates: conversion, duplication and merging of skyrmions. Sci. Rep. 5, 9400, https://www.nature.com/articles/srep0940010.1038/srep09400 (2015).
White, J. S. et al. Electric-field-induced skyrmion distortion and giant lattice rotation in the magnetoelectric insulator Cu2OSeO3. Phys. Rev. Lett. 113(10), 107203 (2014).
Seki, S., Yu, X. Z., Ishiwata, S. & Tokura, Y. Observation of skyrmions in a multiferroic material. Science 336(6078), 198–201 (2012).
White, J. S. et al. Electric field control of the skyrmion lattice in Cu2OSeO3. J. Phys. Condens. Matter. 24(43), 432201 (2012).
Jonietz, F. et al. Spin transfer torques in MnSi at ultralow current densities. Science 330(6011), 1648–1651 (2010).
Yu, X. Z. et al. Skyrmion flow near room temperature in an ultralow current density. Nat.Commun. 3, 988 (2012).
Jiang, W. et al. Blowing magnetic skyrmion bubbles. Science 349(6245), 283–286 (2015).
Everschor, K. et al. Rotating skyrmion lattices by spin torques and field or temperature gradients. Phys. Rev. B. 86(5), 054432 (2012).
Mochizuki, M. et al. Thermally driven ratchet motion of a skyrmion microcrystal and topological magnon Hall effect. Nat. Mater. 13(3), 241 (2014).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323(5916), 915–919 (2009).
Münzer, W. et al. Skyrmion lattice in the doped semiconductor Fe1xCoxSi. Phys. Rev. B 81(4), 041203 (2010).
Tokunaga, Y. et al. A new class of chiral materials hosting magnetic skyrmions beyond room temperature. Nat. Commun. 6, 7638, https://www.nature.com/articles/ncomms863810.1038/ncomms8638 (2015).
Adams, T. et al. Long-wavelength helimagnetic order and skyrmion lattice phase in Cu2OSeO3. Phys. Rev. Lett. 108(23), 237204 (2012).
Levatić, I. et al. Dramatic pressure-driven enhancement of bulk skyrmion stability. Sci. Rep. 6, 21347, https://www.nature.com/articles/srep2134710.1038/srep21347 (2016).
Wilhelm, H. et al. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 107, 127203 (2011).
Mochizuki, M. & Watanabe, Y. Writing a skyrmion on multiferroic materials. Appl. Phys. Lett. 107(8), 082409 (2015).
Mochizuki, M. Creation of Skyrmions by Electric Field on Chiral Lattice Magnetic Insulators. Adv. Electron. Mater. 2(1), https://doi.org/10.1002/aelm.20150018010.1002/aelm.201500180 (2016).
Upadhyaya, P., Yu, G., Amiri, P. K. & Wang, K. L. Electric-field guiding of magnetic skyrmions. Phys. Rev. B 92(13), 134411 (2015).
Okamura, Y., Kagawa, F., Seki, S. and Tokura, Y. Transition to and from the skyrmion lattice phase by electric fields in a magnetoelectric compound. Nat. Commun. 7, 12669, https://www.nature.com/articles/ncomms1266910.1038/ncomms12669 (2016).
Chacon, A. et al. Uniaxial pressure dependence of magnetic order in MnSi. Phys. Rev. Lett. 115(26), 267202 (2015).
Nii, Y. et al. Uniaxial stress control of skyrmion phase. Nat. Commun. 6, 8539, https://www.nature.com/articles/ncomms953910.1038/ncomms9539 (2015).
Omrani, A. A. et al. Exploration of the helimagnetic and skyrmion lattice phase diagram in Cu2OSeO3 using magnetoelectric susceptibility. Phys. Rev. B 89(6), 064406 (2014).
Seki, S., Ishiwata, S. & Tokura, Y. Magnetoelectric nature of skyrmions in a chiral magnetic insulator Cu2OSeO3. Phys. Rev. B 86(6), 060403 (2012).
Liu, Y. H., Li, Y. Q. & Han, J. H. Skyrmion dynamics in multiferroic insulators. Phys. Rev. B 87(10), 100402 (2013).
Jia, C., Onoda, S., Nagaosa, N. & Han, J. H. Microscopic theory of spin-polarization coupling in multiferroic transition metal oxides. Phys. Rev. B 76(14), 144424 (2007).
Arima, T. H. Ferroelectricity induced by proper-screw type magnetic order. J. Phys. Soc. Jpn. 76, 073702 (2007).
Belesi, M. et al. Magnetoelectric effects in single crystals of the cubic ferrimagnetic helimagnet Cu2OSeO3. Phys. Rev. B 85(22), 224413 (2012).
Kruchkov, A. J. & Rønnow, H. M. Preprint at https://arxiv.org/abs/1702.08863 (2017).
Janoschek, M. et al. Fluctuation-induced first-order phase transition in Dzyaloshinskii-Moriya helimagnets. Phys. Rev. B 87(13), 134407 (2013).
Belesi, M. et al. Ferrimagnetism of the magnetoelectric compound Cu2OSeO3 probed by 77Se NMR. Phys. Rev. B 82(9), 094422 (2010).
Bartkowiak, M., White, J. S., Rønnow, H. M. & Prša, K. Note: Versatile sample stick for neutron scattering experiments in high electric fields. Rev. Sci. Instrum. 85, 026112 (2014).
Živković, I. et al. Two-step transition in a magnetoelectric ferrimagnet Cu2OSeO3. Phys. Rev. B 85(22), 224402 (2012).
Acknowledgements
We thank Achim Rosch, Naoto Nagaosa and Jiadong Zang for fruitful discussions. The work was supported by the Swiss National Science Foundation, its Sinergia networks “NanoSkyrmionics” and “Mott Physics Beyond the Heisenberg Model (MPBH)”, and projects 153451, 166298 and P2ELP2_175278. Neutron scattering experiments were carried out at the Swiss Spallation Neutron Source (SINQ), Paul Scherrer Institut, Switzerland.
Author information
Authors and Affiliations
Contributions
A.J.K. performed calculations, J.S.W. performed SANS measurements, H.M.R. planned the project. A.J.K., J.S.W., H.M.R. interpreted results. A.M. provided crystals for SANS, M.B. and I.Z. provided technical support. A.J.K., J.S.W., H.M.R. wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kruchkov, A.J., White, J.S., Bartkowiak, M. et al. Direct electric field control of the skyrmion phase in a magnetoelectric insulator. Sci Rep 8, 10466 (2018). https://doi.org/10.1038/s41598-018-27882-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-27882-4
This article is cited by
-
Direct Visualisation of Skyrmion Lattice Defect Alignment at Grain Boundaries
Nanoscale Research Letters (2022)
-
Magnetic skyrmions in curved geometries
Rare Metals (2022)
-
Generation and manipulation of skyrmions and other topological spin structures with rare metals
Rare Metals (2022)
-
Frustration-driven magnetic fluctuations as the origin of the low-temperature skyrmion phase in Co7Zn7Mn6
npj Quantum Materials (2021)
-
Noncollinear spintronics and electric-field control: a review
Rare Metals (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.