Abstract
The use of gas cluster media as a target for an intense femtosecond laser pulses is considered to be uniquely convenient approach for the development of a compact versatile pulsed source of ionizing radiation. Also, one may consider cluster media as a nanolab to investigate fundamental issues of intense optical fields interaction with sub-wavelength scale structures. However, conventional diagnostic methods fail to register highly charged ion states from a cluster plasma because of strong recombination in the ambient gas. In the paper we introduce high-resolution X-ray spectroscopy method allowing to study energy spectra of highly charged ions created in the area of most intense laser radiation. The emission of CO2 clusters were analyzed in experiments with 60 fs 780 nm laser pulses of 1018 W/cm2 intensity. Theory and according X-ray spectra modeling allows to reveal the energy spectra and yield of highly charged oxygen ions. It was found that while the laser of fundamental frequency creates commonly expected monotonic ion energy spectrum, frequency doubled laser radiation initiates energy spectra featuring of distinctive quasi-monoenergetic peaks. The later would provide definite advantage in further development of laser-plasma based compact ion accelerators.
Similar content being viewed by others
Introduction
During the past decades, the interaction of laser radiation with nanostructured media (clusters, nano-wires, nano-spheres, carbon nano-tubes, snow targets and etc.) has attracted much attention in the context of studying fundamental properties of matter under extreme conditions1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26. Cluster plasma offers a potential for various applications, including nuclear fusion reactions2,27,28,29,30, laser-driven high-energy ion1,31,32,33,34,35,36,37,38 and electron sources39,40,41, and X-ray and betatron emission42,43,44,45,46,47,48,49,50. The benefits of cluster targets include not only the possibility of efficiently generating various particle and radiation beams, i.e., high-energy electron and ion beams, bright flashes of X-rays and radioactivity, but also the absence of debris that can damage optics and a quick renewal of the initial target parameters after each laser action. Cluster targets are also unique because of the possibility of attaining a high rate of absorbing laser radiation up to the total, which can boost further potential applications.
We note that despite about 20 years of intensive investigations, a complete understanding of the interaction of short laser pulses with clusters is still far from clear. For example, the formation of very pronounced peaks in the contour of the OVIII Ly α line emitted by a CO2 cluster plasma created by the second harmonic of Ti:Sa laser light with an intensity of the order of 1018 W/cm2 was observed32. These X-ray spectra features have not yet been explained during practically 20 years. This paper is intended to contribute to understanding the observed spectroscopic features. The key supposition that could explain them is the generation of quasimonoenergetic high-Z oxygen ions of different energies, and we follow this direction below. We note that quasimonoenergetic protons were recently observed when an intense laser pulse irradiated a nanosized water spray. This was interpreted in terms of the contribution of many Coulomb exploding clusters in a focal volume to produce a peaked spectrum of accelerated protons51. Nevertheless, highly charged oxygen ions were not detected in this experiment in measurements with a Thomson parabola because of fast oxygen recombination as a result of propagation inside the spray. Similar was the case in the experiment by F. Abicht et al.52, where water droplets were irradiated by powerful laser radiation at intensities up to 5 · 1019 W/cm2 and no highly charged carbon and oxygen ions were observed with the Thomson parabola technique. This situation is typical for cluster targets51,52,53,54,55. Recombination in the surrounding gas leads to a production of neutrals and negative ions, which is well detected in laser–cluster experiments54,55.
There are many direct methods for registering ions, such as time-of-flight measurements with a microchannel plate detector (MPD), radiochromic film (RCF)56, CR-39 track detector57, and Thomson parabola58. However, those conventional methods fail for characterization of ion enery spectrum in cluster plasma, as they utilize measurements outsize of the interaction volume. Although the X-ray spectral method has already been used to detect multicharged ions some time ago10,32, it is still not widely used. We believe that this method can be applied for registration of high-charge-state ions in the future for relevant experiments similar to such as in refs51,52,53,54,55,59,60. The standard methods mentioned above require measurements outside of the interaction region (e.g., with Thomson parabola) and are not able to diagnose the presence of highly charged ions due to electron capture in an ambient medium. Ultimately, even while the developed method utilizes quantitative approach (see Sec. Methods for details), it is the only one available till now to measure high-charge-state ions inside the interaction volume. In our experiments, we used a spectroscopic measurement that allowed registering highly charged oxygen states and reconstructing high-Z ion spectra. Our aim is to use numerical simulations and analytic theory to interpret these experiments and prove that the X-ray spectroscopic method for measuring the ion spectrum is well complementary to the traditional methods and has an advantage for a large-volume gas target.
It is well known that there are two basic regimes of plasma expansion depending on the ratio between the electron Debye radius λD and the cluster diameter D: quasineutral expansion (or close to it), where \({\lambda }_{{\rm{D}}}/D\ll 1\) 61,62,63,64, and cluster explosion with strong charge separation (Coulomb explosion in the limit case λD → ∞), where \({\lambda }_{{\rm{D}}}/D\gg 1\) 21,51,65. These regimes are very well studied for short (femtosecond) energy input because simplified theories are now well developed for small and large ratios λD/D. They are relevant to either low (typically, subrelativistic) or ultra-high laser intensities. But the intermediate regime with \(D\gtrsim {\lambda }_{{\rm{D}}}\) is theoretically more complicated and requires numerical modeling. Our experimental results for moderate laser intensities \({I}_{{\rm{L}}}\simeq {10}^{18}\) W/cm2 satisfy this condition. The interaction of laser pulses with cluster targets in this regime is also relevant for laser-triggered thermonuclear reactions as possible neutron sources.
To interpret the experimental data, we here adapt a numerical approach for studying a kinetic collisionless expansion of multispecies plasma clusters in a self-consistent electric field driven by laser-heated electrons66 and the theory of the quasineutral adiabatic expansion of a hot macroscopic gas plasma61,63,64 of the focal volume. We use both a simplified electrostatic kinetic numerical model and PIC (particle-in-cell) simulations below to model cluster expansion in the case where an ultrashort second-harmonic laser pulse interacts with CO2 clusters. Namely, in the case of 2ω interaction, the laser contrast suffices for clusters to intact, while in the 1ω case, the clusters are expected to be significantly destroyed. Correspondingly, ion acceleration results from the focal hot plasma expanding as a whole in the 1ω case. Because the laser hot spot has a cylinder-like shape in our experiment, this is predominantly radial expansion. Given the general impossibility of directly measuring highly charged state ions from cluster targets using conventional methods, we here present a theoretical background for measuring highly charged ions indirectly with high-resolution X-ray spectroscopy. Interpreting spectra using the developed theory and numerical simulations clearly show the prospects for such a diagnostic tool.
Experimental Setup and Diagnostics
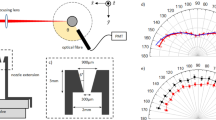
The experiments32 were performed on the laser facility at the Center d’Etudes de Saclay (France). The experimental scheme is shown in Fig. 1a. A titanium–sapphire laser with a 60 fs pulse duration and energy up to 70 mJ at the fundamental frequency (λL ≈ 0.8 μm) or up to 20 mJ at the second harmonic (λL/2 ≈ 0.4 μm) was used to heat the cluster target. Focusing the radiation with a parabolic mirror gave a radiation flux density up to 1018 W/cm2 in a focal spot of \(\simeq 5\,\mu {\rm{m}}\) diameter. The cluster target was produced by adiabatic expansion into vacuum of a small amount of CO2 gas emerging from a gas valve through a pulsed nozzle 0.3 mm in diameter. The gas pressure in the valve was varied from 10 to 40 bar. The X-ray radiation of the plasma was detected by a focusing spectrometer with spatial resolution (FSSR)67,68 with a spherically bent mica crystal with a curvature radius R = 150 mm. The spectral resolution of the spectrometer was λ/δλ ~ 3000 with a spatial resolution ~20 μm. The spectral range covered by the spectrometer was 18.5 to 19.2 Å, which allowed observing the 1s3p1P1 − 1s2 (n > 3) line of He-like OVII and the 2p2P − 1s2S Ly α line of H-like OVIII. An example of the spectrograms and densitometer traces obtained by heating clusters with laser pulses of the first and second harmonic of the Ti:Sa laser are shown in Fig. 1b. The laser and CO2 gas parameters used in the experiments are presented in Table 1. It was previously found32 that the X-ray spectra of H-like oxygen have very unique structures (see Fig. 1b and c) in the shapes of the emission lines when CO2 clusters are heated by 2ω radiation of a Ti:Sa laser with intensity of about 1018 W/cm2.
Results
Two main characteristic features of the emission spectra of a CO2 plasma can be seen in Fig. 1b and c. The emission spectra of a plasma produced by the interaction of a femtosecond laser pulse at the fundamental frequency (λL ≈ 0.8 μm) with CO2 clusters clearly show the presence of a strong asymmetry of the profile of the spectral lines of H- and He-like oxygen ions. The same asymmetry is also seen in the case where the second harmonic of Ti:Sa radiation with λL/2 ≈ 0.4 μm is used. This feature is due to the presence of a strong asymmetry of the profiles of the spectral lines of H- and He-like oxygen ions. Such an asymmetric line shape cannot be due to thermal Doppler or Stark broadening of the spectral lines in plasma. A simple model was proposed32 that explains the observed shape of the spectral lines. The main fundamentals of such model are (i) line broadening due to macroscopic motion (expansion) of the cluster plasma and (ii) appearance of asymmetry of the shapes of the lines of oxygen ions as a result of the photoionization absorption on H- and He-like carbon ions present in the CO2 plasma. Nevertheless, the second feature of the emission spectra the appearance of multiple clearly resolved peaks at the observed spectral lines and, in particular, at the shape of the Ly α of H-like oxygen emitted by CO2 cluster plasma created by a pulse at the second harmonic of the Ti:Sa laser has not yet been explained. The experiments do not show such clearly pronounced peaks for the laser pulse at the fundamental frequency. Below, we explain the different spectral features in the cases of 1ω and 2ω radiation and the nature of the deep modulation of the O+8 ion spectrum from a cluster plasma heated by the second harmonic.
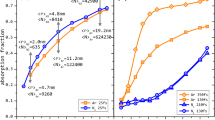
First, we note that because the spectral line broadening in our experiments was due to the directed motion of plasma particles, the analysis of the line profiles can be used to measure the distribution of ions with respect to the expansion velocity, i.e., distribution of the number N(ε) of ions with respect to their energy ε. It can be seen that the experimental spectra clearly show two slopes corresponding to two different ion temperatures for low and high ion energy ranges. In Fig. 2, we show the reconstruction of the shapes of the Ly α of H-like oxygen spectra (see Methods for details) emitted by CO2 clusters irradiated by 1ω and 2ω Ti:Sa laser pulses. It is important that our spectroscopy method allows reproducing ion spectra directly in the laser–plasma interaction region, which is not often possible with other methods.
Theoretical description and comparison with experiment
To treat the experimental results theoretically, we use models based on the analytic 1D solution of the kinetic equations for electrons and ions of a hot plasma column radially expanding in a quasineutral manner, a simplified electrostatic PIC method for a spherically symmetric cluster with a given initial electron distribution, which models a short laser pulse, and full 3D PIC simulations of the laser–cluster interaction. These approaches are not intended to be all-inclusive, i.e., to include the effect of a finite laser contrast ratio (prepulse). They model only the main pulse interaction with a plasma target, and the prepulse is taken into account by modifying the initial target density profile. Note, that it is hardly possible to obtain quantitative agreement from comparison of theoretical model with experimental results, because the number of clusters in the focal volume, distances between them, their maximum density and density profiles are not well predictable. However, that is in fact the first explanation of high-charge-state ion energy distribution for cluster plasma.
As a starting point, we assume that clusters in a gas are not fully destroyed as a result of the laser prepulse in the case of 2ω laser pulse radiation, because the 2ω radiation has much better contrast than the 1ω radiation. As a result, the laser pulse interaction with clusters produces a spectrum of highly charged state ions with deep modulations due to the contribution of some number of clusters from a focal volume (see Fig. 2b). On the other hand, it is unlikely that clusters survived before main pulse arrival in the 1ω case because of the low laser contrast (due to the prepulses and pedestal). We believe that the clusters in this case are significantly or fully destroyed and the propagating laser pulse in fact interacts with gas and strongly heats the plasma in the caustic domain, which evolves in the form of a radially expanding cylindrical multispecies plasma (laser–plasma channel). Obviously, such an expanding macroplasma (unlike the cluster microplasmas) should lead to the formation of a quasimonotonic ion energy spectrum with no deep modulations63,64. The corresponding energy spectrum from observation is shown in Fig. 2a.
Therefore, we proceed from the fact that ions are accelerated from a radially expanding plasma column in the 1ω case and from both a quasi-homogeneous gas macroplasma of laser caustics and single clusters within it in the 2ω case. To describe ion acceleration from the heated gas laser–plasma channel, we use the plasma expansion model63,64 in a symmetric cylindrical geometry with adiabatic ion acceleration in the radial direction immediately after the 1ω ultra-short (60 fs) laser pulse terminates. In our theoretical model, we assume a two-temperature electron distribution with hot and cold electrons typically observed in laser–plasma interactions. The hot-electron density is typically much smaller than the cold-electron density, but the temperature and pressure of hot electrons are larger than the temperature and pressure of the cold electrons. The plasma expansion is hence mostly determined by the hot electrons. The temperature of laser-heated hot electrons is a key parameter in our model. We estimate it from the standard ponderomotive scaling69 \({T}_{{\rm{h}}}=\mathrm{((1}+{a}_{0}^{2}{)}^{\mathrm{1/2}}-\mathrm{1)}{m}_{e}{c}^{2}\), where \({a}_{0}=0.85{\lambda }_{{\rm{L}}}[\mu m]\sqrt{{I}_{{\rm{L}}}{\mathrm{[10}}^{18}\,{\rm{W}}/{{\rm{cm}}}^{2}]}\) is the dimensionless laser field amplitude. For the pulse with the maximum laser intensity of 1018 W/cm2, this gives Th ≈ 100 keV and Th ≈ 30 keV respectively for 1ω and 2ω radiation. Because the laser pulse duration is much shorter than the ion acceleration time, we neglect the direct ponderomotive ion acceleration and regard the ion acceleration as triggered by the temperature effect in the adiabatic plasma expansion regime. For simplicity in our analytic model, we assume that the plasma column contains two ion species (denoted by the subscripts 1 and 2): the ion bulk with the average charge 〈Z〉1 = 3 and atomic number 〈A〉1 = 15 and the high-Z impurity with 〈Z〉2 = 8 and 〈A〉2 = 16. Because the ionization potential of the two inner levels of oxygen exceeds the laser ponderomotive potential, the ions O+7 and O+8 should indeed be treated as impurities. Making an insignificant simplification, we neglect the difference between O+7 and O+8 and consider a single impurity O+8. Similarly, we also treat the ions C+5 and C+6 as a single impurity. Their charge-to-mass ratio is nearly the same as for O+8, and we therefore replaced all impurities O+7, O+8, C+5, and C+6 with the approximate effective impurity with 〈Z〉2 = 8 and 〈A〉2 = 16 because only the charge-to-mass ratio is important. We used the approximation of an average ion with 〈Z〉1 = 3 and 〈A〉1 = 15 (〈Z〉1/〈A〉1 = 1/5) to describe the entire multispecies bulk for oxygen from O+1 to O+6 and for carbon from C+1 to C+4.
The dynamics of the adiabatic cylindrical plasma expansion is determined by the solution of the kinetic equation system for ions and electrons with initial Maxwellian distributions for all kinds of particles. For a two-ion component plasma with two-temperature electrons (hot and cold components), the spectrum of the light ion impurity can be expressed as64
where θ(x) is the unit step function and \({\varepsilon }_{ch}\simeq {\langle Z\rangle }_{2}{T}_{{\rm{c}}}\,\mathrm{ln}\,({n}_{{\rm{c}}}/{n}_{{\rm{h}}})\). We impose the quasineutrality condition 〈Z〉1n10 + 〈Z〉2n20 = nh + nc, and C is a constant that can be found from the normalization condition \({\int }_{0}^{\infty }d\varepsilon \,dN/d\varepsilon ={N}_{20}\), where N20 is the total number of impurity ions. Equation (1) holds under the natural assumptions \({T}_{{\rm{h}}}\gg {T}_{{\rm{c}}}\), \({n}_{{\rm{h}}}\ll {n}_{{\rm{c}}}\), and \({\langle Z\rangle }_{2}{n}_{20}\ll {\langle Z\rangle }_{1}{n}_{10}\). There is a direct connection between the two-temperature electron distribution and two slopes of the high-Z ion energy spectrum. The quasineutrality approximation used is applicable for a hot plasma gas under the experimental conditions because λ D /L < 1, where \({\lambda }_{D}=\sqrt{{T}_{{\rm{h}}}\mathrm{/4}\pi {n}_{{\rm{h}}}{e}^{2}}\) and L is the characteristic scale of plasma inhomogeneity. The result of theory (1) for the ion impurity energy spectrum is shown by the black dashed curve together with the experimental findings in Fig. 2a. To fit the experimental data for the 1ω radiation, we chose the electron parameter relations Th/Tc = 300 and nh = 0.03nc, where Th ≈ 100 keV in accordance with the ponderomotive estimate given above. Radial expansion of the hot spot gas plasma also well describes the averaged (over spectral oscillations) shape of the O+8 spectrum in the 2ω case, as shown in Fig. 2b (black dashed line). The theoretical curve presented in the figure corresponds to Th ≈ 30 keV, Th/Tc ≈ 90, and nh ≈ 0.1nc.
The above value of hot electron densities have been taken to achieve best agreement with experimental spectra. In the case of high contrast laser pulse clusters should sustain solid under heating by prepulse, what consistenly results in more effective hot electron generation and 3 times higher electron densities. By modeling for the ratio of OVIII Ly α to He β line intensities the estimate for bulk cold electron temperature was obtained to be around 140–150 eV. At the same time, the observed spectrum introduces rather weak dependence on hot electron density.
The nonmonotonic behavior of the O+8 spectrum in the 2 ω case can be explained by ion acceleration from expansions of clusters in the focal volume. We model such cluster expansion by the electrostatic gridless spherical particle code (EGSPC) and by the full 3D relativistic PIC code Mandor. In these simulations, we consider 50 to 160 nm diameter clusters with two ion species, i.e., ions with 〈Z〉1 ≈ 3 and 〈A〉1 ≈ 15 as a bulk and small impurity (few percent) of a high 〈Z〉2/〈A〉2 ratio, \({\langle Z\rangle }_{2}/{\langle A\rangle }_{2}\simeq \mathrm{1/2}\). We used smoothed density distributions of the clusters in our simulation because we believe that a steplike density profile (ideal clusters) is unlikely to occur even in the 2 ω case because of the nonideal contrast ratio at the 1 to 10 ps time scale, similar to the argument in ref.70. This is because the ps-prepulse leads to some cluster expansion before interaction with the main pulse. In this context, we assume that the ion cluster density profiles are Gaussian (as shown in Fig. 3a), i.e., \(n\sim \exp (\,-\,\mathrm{ln}\,\mathrm{(2)}{r}^{2}/{r}_{0}^{2})\), where 2r0 is the FWHM cluster size. The energy spectra for the expanding clusters from the EGSPC simulation are shown in Fig. 3b for the 2ω pulse with a peak intensity of 1018 W/cm2. We chose the following electron parameters based on the results of PIC simulations (see below): Th ≈ 100, 120, and 140 keV, n h /n c ≈ 0.05, Tc ≈ 10 keV for 160, 120, and 100 nm clusters, which contain \(\lesssim {10}^{7}\) atoms. We note that the hot electron temperature of clusters could be higher than for a smooth gas macroplasma because of possible resonant heating of clusters. It can be seen that the spectra have a sharp cutoff with a pronounced quasimonoenergetic feature close to the cutoff. These features can be explained as a result of light ions accelerating at the expanding plasma cloud front, similar to what was described in ref.66. With this simple electrostatic model, we can take both cluster size dispersion and different initial radial cluster positions in the focal volume into account, reducing electron temperatures that can also be attributed to off-axis positions of clusters with respect to the laser beam axis. This model qualitatively reproduces the characteristic energies of high-Z impurity ions accelerated from clusters corresponding to the experimental findings. Thus, in our theoretical modeling we were able to describe spectral peaks that correspond to different clusters (with different size, different densities, and different density profiles smoothing due to the prepulse effect). Because of chaotic appearance of the clusters in a focal volume, exact characterization of these peaks in experiment is impossible and qualitative picture is the only thing that is possible, similar to refs51,52 for quasimonoenergetic protons from a water spray. However, as mentioned above, even qualitative explanation of high-Z ion energy distribution allows identify highly charged ions as well as relevant cluster characteristics.
(a) The initial electron density distribution (in critical density units \({n}_{cr}={m}_{e}{\omega }_{L}^{2}\mathrm{/4}\pi {e}^{2}\)) used in the simulations corresponding to clusters of 160 nm (blue), 120 nm (green), and 100 nm (red) diameter. (b) Spectra from EGSPC simulations for impurity ions (for 160, 120 and 100 nm clusters) for the maximum laser intensity IL = 1018 W/cm2.
The results of the 3D PIC simulation are summarized in Fig. 4. Nonmomotonic features can be clearly seen in the spectra: there are quasimonoenergetic distributions with well-pronounced energy peaks (with widths of the order of 100 keV) shifted to the cutoff energies (300 to 800 keV). The characteristic peak energies are proportional to the hot electron temperatures. For cluster diameters of 100, 120, and 160 nm, our PIC simulations give the corresponding hot electron temperatures Th ≈ 140, 120, and 80 keV. The electron distributions are two-temperature-like with T c ≈ 10 to 30 keV. The steeper initial density profile (smaller cluster size), the higher cutoff energy of the spectrum, and the corresponding peak energy agree with the qualitative results of the electrostatic modeling. The reduction of the pulse intensity from 1018 W/cm2 to 3 · 1017 W/cm2 results in a decrease of the electron temperature and maximum (cutoff) ion energy by a factor of two. The corresponding energy spectra are shown in Fig. 4 (right panel). The energy range of the oxygen impurity is consistent with the experimental findings including the nonmonotonic features of the ion spectra.
Spectra of impurity cluster ions from the PIC simulations corresponding to density profiles shown in Fig. 3a for (a) IL = 1018 W/cm2 and (b) IL = 3 · 1017 W/cm2 (b).
We have thus demonstrated that for the 2ω laser pulse interaction with a cluster plasma, the theory reproduces the experimental spectrum of O8+ ions in the form of a monotonically decreasing slope (due to gas plasma expansion) of two different steepnesses with peaks (from cluster expansions) on it. Both the electrostatic and the full PIC numerical models show the existence of well-pronounced spectral peaks for moderately smoothed clusters expected in the rather high-contrast 2ω experiment. It cannot be excluded that strongly expanded but not entirely destroyed clusters from the prepulse stage could also lead to a weak modulation of the observed ion spectrum in the 1ω case (cf. Fig. 2a).
Discussion
This paper reports theoretical modeling of multicharged ion acceleration from a CO2 cluster plasma and justifies the result of an experiment demonstrating unusual features in the X-ray spectra of H-like oxygen observed when a cluster gas is irradiated by the second harmonic of a Ti:Sa laser with intensities about 1018 W/cm2. The performed theoretical modeling based on a three-dimensional PIC simulation, a simplified electrostatic kinetic model, and an analytic solution of the Vlasov equations allowed proving the nonmonotonic features of the ion spectra, thus providing the first interpretation of the experimental findings since their original publications32,33.
We showed that the shape of the spectra of highly charged state ions is defined by particles accelerated from both the gas and clusters. Ions originating from clusters provide pronounced peaks in the spectra for 2ω high-contrast radiation. These peaks are very smoothed or even absent for a low-contrast laser pulse, which is the case for laser interaction at the fundamental frequency, where the experiment does not show noticeable spectral modulations. In the cases of both high and low laser contrast (the 2ω and 1ω cases), the overall integral shape of the spectra for highly charged state ions shows two different steepnesses, identifying two kinds electrons with low and high energies. Finally, we conclude that a theoretical basis for X-ray spectroscopic measurements of ion spectra is now established. We have shown that high-resolution X-ray spectroscopy is an effective tool that allows measuring the spectra of multicharged laser-accelerated ions, even with a very complicated fine structure, with good accuracy.
Methods
Spectrum reconstruction
Because the broadening of spectral lines in our experiment is due to plasma motion, the analysis of line profiles can be used to measure the distribution of ions with respect to the expansion energies. Most simply (and precisely), this can be done in the case of an optically thin plasma where photoionization absorption is absent and the profile F ik (ω − ω ik ) of a spectral line resulting from the radiative i − k transition is directly proportional to the distribution of ions with respect to the velocities:
Here, N i (v) is the density of ions in the excited state i moving with the velocity v and the values of frequency and velocity are linked by relation ω − ω ik = v/c. In the case of an optically thick plasma, it is impossible to measure N i (v) directly because the spectral line profile is significantly affected by broadband photoionization absorption.
Ions emitted toward the spectrometer are absorbed less the faster the ions leave the absorbing media. In contrast, ions emitted away from the spectrometer are absorbed more as the distance from the detector increases and the linear density of the absorbing plasma media accordingly rapidly increases with time. Hence, the red-shifted part (long-wavelength wing) of the spectral line profile is strongly depressed by absorption (as can be seen in Figs 1 and 2), while the absorption is insignificant for the far short-wavelength wing of spectral lines. Consequently, even in the case of an optically thick plasma, relation (2) can be applied in particular to the blue-wing part of the line profile to determine the ion distribution.
We note that some depression due to absorption also occurs in the central part of the spectral lines, but it does not affect the spectral line position nor the position of local extremes in the ion distribution function. We consider that the ion distribution function is the same for the ion excited and ground states and use formula (2) to reconstruct the functions dN/dv and dN/dε shown in Fig. 2.
Simulations
To describe ion spectra from a cluster plasma, we use the electrostatic model EGSPC66 for the expansion of a single spherical plasma cluster. The input parameters are cold and hot electron temperatures, partial particle densities, and the ion composition. This code allows simulating the adiabatic multi-ion species expansion of a charged or quasineutral spherical plasma cluster for a wide range of the parameter λ D /D with homogeneous or inhomogeneous density distributions. This numerical model provides a quick, easy-to-use, and physically crystal clear tool with which we can preliminarily study cluster evolution qualitatively. The aim of the PIC simulations is to improve the fundamental understanding of the cluster expansion mechanism more quantitatively and rigorously. Going beyond the simple electrostatic approach, we also performed PIC simulations of the laser–cluster interaction and cluster expansion in a real 3D geometry using the PIC code Mandor71. Clusters were placed in the focal domain of a laser pulse with maximum intensities 1018 W/cm2 and 3 · 1017 W/cm2 with the pulse having a Gaussian shape in time (the FWHM duration was 55 fs) and in the transverse direction (the FWHM focal spot size was 4λL). The clusters (with initial density profiles shown in Fig. 3a) were composed of electrons, heavy ions with 〈Z〉1/〈A〉1 = 1/5, and 1% of light ions with 〈Z〉2/〈A〉2 = 1/2. The PIC code used a numerical mesh with a cell size x × y × z = 0.02λL × 0.05λL × 0.05λL and 36 macroparticles of each species per cell.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Ditmire, T. et al. High-energy ions produced in explosions of superheated atomic clusters. Nature 386, 54–56 (1997).
Ditmire, T. et al. Nuclear fusion from explosions of femtosecond laser-heated deuterium clusters. Nature 398, 489–492 (1999).
Rajeev, R. et al. A compact laser-driven plasma accelerator for megaelectronvolt-energy neutral atoms. Nature Physics 9, 185–190 (2013).
Purvis, M. A. et al. Relativistic plasma nanophotonics for ultrahigh energy density physics. Nature Photonics 7, 796–800 (2013).
Lübcke, A. et al. Scientific Reports 7, 44030 (2017).
Bargsten, C. et al. Energy penetration into arrays of aligned nanowires irradiated with relativistic intensities: Scaling to terabar pressures. Science Advances 3, e1601558, https://doi.org/10.1126/sciadv.1601558 (2017).
Zigler, A. et al. Enhanced proton acceleration by an ultrashort laser interaction with structured dynamic plasma targets. Phys. Rev. Lett. 110, 215004 (2013).
Margarone, D. et al. Laser-driven proton acceleration enhancement by nanostructured foils. Phys. Rev. Lett. 109, 234801 (2012).
Bin, J. H. Ion Acceleration Using Relativistic Pulse Shaping in Near-Critical-Density Plasmas. Phys. Rev. Lett. 115, 064801 (2015).
Ditmire, T., Donnelly, T., Falcone, R. W. & Perry, M. D. Strong x-ray emission from high-temperature plasmas produced by intense irradiation of clusters. Phys. Rev. Lett. 75, 3122–3125 (1995).
Ditmire, T., Gumbrell, E. T., Smith, R. A., Djaoui, A. & Hutchinson, M. H. R. Time-resolved study of nonlocal electron heat transport in high temperature plasmas. Phys. Rev. Lett. 80, 720–723 (1998).
Tajima, T., Kishimoto, Y. & Downer, M. C. Optical properties of cluster plasma. Phys. Plasmas 6, 3759–3764 (1999).
Rusek, M., Lagadec, H. & Blenski, T. Cluster explosion in an intense laser pulse: Thomas-Fermi model. Phys. Rev. A 63, 013203 (2000).
Hagena, O. F. Cluster ion sources. Rev. Sci. Instrum. 63, 2374 (1992).
Saalmann, U., Siedschlag, C. & Rost, J. M. Mechanisms of cluster ionization in strong laser pulses. J. Phys. B. 39, R39–R77 (2006).
Gavrilenko, V. P. et al. Observation of modulations in Lyman–α line profiles of multicharged ions in clusters irradiated by femtosecond laser pulses: Effect of a dynamic electric field. Phys. Rev. A 73, 013203 (2006).
Boldarev, A. S., Gasilov, V. A., Faenov, A. Y., Fukuda, Y. & Yamakawa, K. Gas-cluster targets for femtosecond laser interaction: Modeling and optimization. Rev. Sci. Instr. 77, 083112 (2006).
Davis, J., Petrov, J. M. & Velikovich, A. Nonlinear energy absorption of rare gas clusters in intense laser field. Phys. Plasmas 14, 060701 (2007).
Faenov, A. Y. et al. Non-adiabatic cluster expansion after ultrashort laser interaction. Laser and Particle Beam 26, 69–81 (2008).
Taguchi, T., Antonsen, T. A., Palastro, J., Milchberg, H. & Mima, K. Particle in cell analysis of a laser-cluster interaction including collision and ionization processes. Optics Express 18, 2389–2405 (2010).
Bychenkov, V. Yu. & Kovalev, V. F. Relativistic Coulomb explosion of spherical microplasma. JETP Letters 94, 97–100 (2011).
Erk, B. et al. Observation of shells in Coulomb explosions of rare-gas clusters. Phys. Rev. A 83, 043201 (2011).
Skobelev, I. Y. et al. Effects of the self-absorption of X-ray spectral lines in the presence of the laser-cluster interaction. JETP Letters 94, 270–276 (2011).
Faenov, A. Y. et al. Diagnostics of the early stage of the heating of clusters by a femtosecond laser pulse from the spectra of Hollow ions. JETP Letters 94, 187–193 (2011).
Hoffmann, K. et al. Rare-gas-cluster explosions X-ray spectroscopy diagnoses of clusters under irradiation by intense short XUV pulses. Phys. Rev. A 83, 043203 (2011).
Oks, E. et al. Revealing the second harmonic generation in a femtosecond laser-driven cluster-based plasma by analyzing shapes of Ar XVII spectral lines. Optics Express 23, 31991 (2015).
Grillon, G. et al. Deuterium-Deuterium Fusion Dynamics in Low-Density Molecular-Cluster Jets Irradiated by Intense Ultrafast Laser Pulses. Phys. Rev. Lett. 73, 013203 (2002).
Kishimoto, Y., Masaki, T. & Tajima, T. High energy ions and nuclear fusion in laser-cluster interaction. Phys. Plasmas 9, 589–601 (2002).
Last, I., Ron, S. & Jortner, J. Aneutronic H + 11B nuclear fusion driven by Coulomb explosion of hydrogen nanodroplets. Phys. Rev. A. 83, 043202 (2011).
Lu, H. Y. et al. Efficient fusion neutron generation from heteronuclear clusters in intense femtosecond laser fields. Phys. Rev. A 80, 051201(R) (2009).
Ditmire, T. et al. High energy ion explosion of atomic clusters: transition from molecular to plasma behavior. Phys. Rev. Lett. 78, 2732–2735 (1997).
Dobosz, S. et al. Characteristic features of the X-Ray spectra of a plasma, produced by heating CO2 clusters by intense femtosecond laser pulses with λ = 0.8 μm and 0.4 μm. JETP Letters 68, 454–459 (1998).
Dobosz, S. et al. Observation of ions with energies above 100 keV produced by the interaction of a 60-fs laser pulse with clusters. JETP 88, 1122–1129 (1999).
Faenov, A. Y. et al. Generation of quantum beams in large clusters irradiated by super-intense, high-contrast femtosecond laser pulses. Contrib. Plasma Phys. 53, 148–160 (2013).
Faenov, A. Y., Pikuz, T. A. & Kodama R. In laser-driven particle acceleration towards radiobiology and medicine. High Resolution Ion and Electron Beam Radiography with Laser-Driven Clustered Sources (Giulietti, A. ed.), Chapter 12, pp. 271–294 Heidelberg, New York: Springer (2016).
Fukuda, Y. et al. Energy increase in multi-MeV ion acceleration in the interaction of a short pulse laser with a cluster gas target. Phys. Rev. Lett. 103, 165002 (2009).
Fukuda, Y. et al. Generation of X rays and energetic ions from superintense laser irradiation of micron-sized Ar clusters. Laser Part. Beams 22, 215–220 (2004).
Makarov, S. Ion pinhole imaging diagnostics on fast ion source in femtosecond laser plasma of cluster targets. et al. Optics Express 25, 16419 (2017).
Zhang, L. et al. Electron acceleration via high contrast laser interacting with submicron clusters. Appl. Phys. Lett. 100, 014104 (2012).
Bussolino, G. C. et al. Electron radiography using a table-top laser-cluster plasma accelerator. J. Phys. D. Appl. Phys. 46, 245501 (2013).
Koester, P. et al. High-charge divergent electron beam generation from high-intensity laser interaction with a gas-cluster target. Laser and Particle Beams 33, 331–338 (2015).
McPherson, A., Thompson, B. D., Borisov, A. B., Boyer, K. & Rhodes, C. K. Multiphoton-induced X-ray emission at 4–5 keV from Xe atoms with multiple core vacancies. Nature 370, 631–634 (1994).
Sherrill, M. E. et al. Spectroscopic characterization of an ultrashort laser driven Ar cluster target incorporating both Boltzmann and particle-in-cell models. Phys. Rev. E 73, 066404 (2006).
Zhang, L. et al. Enhanced Kα output of Ar and Kr using size optimized cluster target irradiated by high-contrast laser pulses. Optics Express 19, 25812–25822 (2011).
Kim, K. Y. et al. X-Ray spectroscopy of 1 cm channels produced by self-focusing pulse propagation in elongated cluster jets. Phys. Rev. E 78, 066463 (2006).
Fukuda, Y. et al. X-ray study of microdroplet plasma formation under the action of superintense laser radiation. JETP Lett. 78, 115–118 (2003).
Abdallah, J. Jr. et al. Time-dependent Boltzmann kinetic model of x-rays produced by ultrashort-pulse laser irradiation of argon clusters. Phys. Rev. A 68, 063201 (2003).
Berkelbach, T. C. et al. Modeling energy dependence of the inner-shell x-ray emission produced by femtosecond-pulse laser irradiation of xenon clusters. Phys. Rev. E 79, 016407 (2009).
Chen, L. M. et al. Bright betatron X-ray radiation from a laser-driven-clustering gas target. Sci. Rep. 3, 1912 (2013).
Colgan, J. et al. Observation and modeling of high resolution spectral features of the inner-shell X-ray emission produced by 10−10 contrast femtosecond-pulse laser irradiation of argon clusters. High Energy Density Phys. 7, 77–83 (2011).
Ramakrishna, B. et al. Laser-driven quasimonoenergetic proton burst from water spray target. Phys. Plasmas 17, 083113 (2010).
Abicht, F. et al. Energetic beams of negative and neutral hydrogen from intense laser plasma interaction. Appl. Phys. Lett. 103, 253501 (2013).
Rajeev, R., Dalui, M., Trivikram, T. M., Rishad, K. P. M. & Krishnamurthy, M. Anisotropic negative-ion emission from cluster nanoplasmas. Phys. Rev. A 91, 063403 (2015).
Rajeev, R., Trivikram, T. M., Rishad, K. P. M., Narayanan, V. & Krishnamurthy, M. Generation of energetic negative ions from clusters using intense laser fields. New Journal of Physics 15, 043036 (2013).
Nakamura, T. et al. High energy negative ion generation by Coulomb implosion mechanism. Phys. Plasmas 16, 113106 (2009).
Kaufman, J. et al. Radiochromic film diagnostics for laser-driven ion beams. Proc. SPIE 9515, 95151J (2015).
Jeong, T. W. et al. CR-39 track detector for multi-MeV ion spectroscopy. Scientific Reports 7, Article number: 2152 (2017).
Alejoa, A. et al. Recent developments in the Thomson Parabola Spectrometer diagnostic for laser-driven multi-species ion sources. JINST 11, C10005 (2016).
Zhvaniya, I. A., Dzhidzhoev, M. S. & Gordienko, V. M. Femtosecond laser excitation of mixed Ar/Kr clusters: peculiarities of K-line x-ray production from nanoplasma under varied fraction of initial gas components. Laser Phys. Lett. 14 (2017).
Kanasaki, M. et al. Plasma Phys. Control. Fusion 58, 034013 (2016).
Kovalev, V. F., Bychenkov, V. Yu. & Tikhonchuk, V. T. Particle dynamics during adiabatic expansion of a plasma bunch. JETP 95, 226–242 (2002).
Dorozhkina, D. S. & Semenov, V. E. Exact solution of the problem of quasineutral expansion into vacuum of a localized collisionless plasma with cold ions. JETP Lett. 67, 573–578 (1998).
Kovalev, V. F. & Bychenkov, V. Yu. Analytic solutions to the Vlasov equations for expanding plasmas. Phys. Rev. Lett. 90, 185004 (2003).
Kovalev, V. F., Bochkarev, S. G. & Bychenkov, V. Yu. Radial acceleration of ions during adiabatic expansion of a multicomponent cylindrical plasma. Quantum Electronics 47, 1023–1030 (2017).
Murakami, M. & Mima, K. Efficient generation of quasimonoenergetic ions by Coulomb explosions of optimized nanostructured clusters. Phys. Plasmas 16, 103108 (2009).
Popov., K. I., Bychenkov, V. Yu., Rozmus, W. & Ramunno, L. A detailed study of collisionless explosion of single- and two-ion-species spherical nanoplasmas. Phys. Plasmas 17, 083110 (2010).
Faenov, A. Y. et al. High-performance X-ray spectroscopic devices for plasma microsources investigations. Physica Scripta 50, 333–338 (1994).
Alkhimova, M. A., Pikuz, S. A., Faenov, A. Y. & Skobelev, I. Y. Determination of spectral reflectivity of spherically bent mica crystals applied for diagnostics of relativistic laser plasmas. J. Phys. CS 774, 012115 (2016).
Wilks, S. C., Kruer, W. L., Tabak, M. & Langdon, A. B. Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383–1386 (1992).
Ter-Avetisyan, S. et al. Generation of a quasi-monoergetic proton beam from laser-irradiated sub-micron droplets. Phys. Plasmas 19, 073112 (2012).
Romanov, D. V., Bychenkov, V. Y., Rozmus, W., Capjack, C. E. & Fedosejevs, R. Self-organization of a plasma due to 3D evolution of the Weibel instability. Phys. Rev. Lett. 93, 215004 (2004).
Acknowledgements
The theoretical part and interpretation of the experimental results were supported by the Russian Science Foundation (Grant No. 17-12-01283). The X-ray data measurements and analysis were performed by JIHT RAS and NRNU MEPHi team with support of the Russian Foundation for Basic Research (Grant No. 18-52-53033) and Competitiveness Program of NRNU MEPhI. This paper is dedicated to the memory of brilliant scientist and our wonderful colleague, Prof. Anatoly Ya. Faenov, who recently passed away.
Author information
Authors and Affiliations
Contributions
The simulations were performed by S.G.B., A.V.B., K.I.P. and V.F.K. All the authors have discussed the results thoroughly and contributed to the writing and review of the manuscript. T.P., I.S., A.F. and S.P. conducted the experiments and reconsructed the energy spectra from the experimental data. A.F. and R.K. analyzed the results. S.G.B., V.Yu.B., A.F., S.P. and I.S. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bochkarev, S.G., Faenov, A., Pikuz, T. et al. Ion energy spectra directly measured in the interaction volume of intense laser pulses with clustered plasma. Sci Rep 8, 9404 (2018). https://doi.org/10.1038/s41598-018-27665-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-27665-x
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.