Abstract
The effect of mixed partial occupation of metal sites on the phase stability of the γ-Cr23−xFe x C6 (x = 0–3) carbides is explored as function of composition and temperature. Ab initio calculations combined with statistical thermodynamics approaches reveal that the site occupation of the carbides may be incorrectly predicted when only the commonly used approach of full sublattice occupation is considered. We found that the γ-M23C6 structure can be understood as a familiar sodium chloride structure with positively charged rhombic dodecahedron (M(4a) M12(48h)) and negatively charged cubo-octahedron (M8(32f) C6(24e)) super-ion clusters, together with interstitial metal atoms at the 8c sites. The stability of the partially occupied phase can be easily rationalized on the basis of a super-ion analysis of the carbide phase. This new understanding of γ-M23C6 carbides may facilitate further development of high-chromium heat-resistant steels.
Similar content being viewed by others
Introduction
The phase stability of carbide precipitates plays a crucial role in improving the creep lifetime of steels1,2. For instance, a high density of γ-M23C6 carbides (in which M denotes a metal element), increases the creep rupture strength, as grain boundary sliding and surface cracking are reduced. Although the chemical compositions of some of these carbides have been determined, experimental studies on their mechanism of formation, atomic site occupation, and chemical interactions between species in multicomponent phases have seldom been reported3,4.
The partial/full occupation of a sublattice site refers to the fraction of the site that is occupied by a particular atomic species, averaged over many unit cells. To date, the vast majority of ab initio total energy studies have considered only configurations in which sublattice sites were fully occupied by a single atomic species5,6,7,8,9,10,11,12,13,14,15,16,17,18,19, in particular with regard to Frank-Kasper structures20. When mixed occupancy of sublattice sites was considered it was only to the extent as necessitated by the cluster expansion method, say when nearest neighbor interactions between sites of the same type needed to be evaluated, such as is the case in the σ structure21,22,23,24. Mixed occupancy was considered in the specific context of the coherent potential approximation25, and for several configurations in the Fe-Cr σ structure26 but an in-depth analysis including associated effects such as due to lattice vibrations remains lacking. Here, we address this issue by considering many partially occupied configurations of a non-trivial technically important carbide phase, Cr23C6, while including vibrational effects.
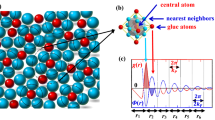
The γ-M23C6 crystal has a face-centered cubic (fcc) structure with the \(Fm\bar{3}m\) space group. The supercell contains four (M23C6) unit cells and consists of 92 metal atoms occupying four inequivalent metallic sites, namely, the 4a, 8c, 32f, and 48h sites, and 24 non-metallic atoms occupying the 24e sites, as represented using Wyckoff notation, according to the results of X-ray powder diffraction27. Figure 1a shows the crystal structure of γ-Cr23C6, and Fig. 1b shows a simplified view of the super-ion arrangement originally already recognized by Westgren27. In this structure, each 4a site is surrounded by 12 metal atoms in 48h sites, forming a cubo-octahedron with the composition Cr(4a)Cr12(48h). On the other hand, the neighboring 32f sites form a cube, and protruding from the faces of the cube are the 24e sites that together form a concentric octahedron. The closely positioned 32f and 24e sites together form a rhombic dodecahedron with the composition Cr8(32f)C6(24e) and eight Cr(8c) atoms lie at the interstitial positions. In this work, we treat only the mixed, i.e. partial, occupation of the metallic sites, and not the C occupied sites. We suppose that C atoms are fully occupying the 24e sites. Partial occupancy of the carbon sublattice can be important in some carbides28,29, but in this carbide we do not expect it to play a role of significance because the carbon vacancy formation enthalpy is very large (~1.05 eV/C vacancy)30.
(a) The γ-Cr23C6 supercell consists of one conventional unit cells with four inequivalent metal sites, namely, the 4a, 8c, 32f, and 48h sites, according to Wyckoff notation. The C atoms are located at the 24e sites. (b) The carbide NaCl super-ion morphology and interstitial (8c) atomic arrangement in γ-Cr23C6. The supercell is constructed from four Cr(4a)Cr12(48h) clusters and four Cr8(32f)C6(24e) clusters, together with eight Cr atoms in the 8c sites.
Experimentally, according to single-crystal X-ray diffraction data, there is evidence of the selective metallic site occupation of Fe in γ-Cr23−xFe x C6 in the range of 0 ≤ x ≤ 7.3631,32. At a low Fe fraction, the Fe atoms occupy the 4a and 8c sites, and they simultaneously begin to occupy the 48h and 32f sites at higher Fe fractions. The occupancy sequence was found for 4a and 8c sites from atomistic simulations using pair potentials obtained through the lattice inversion technique33. However, simple pair potentials generally favor topologically close packed structures and generally cannot yield complex structures such as the present carbide as a true ground state. Therefore, in an MD simulation at finite temperatures, these pair potentials quickly lead to an unrealistic complete collapse of the crystal structure33. Moreover, the pair potentials do not account for changes in magnetic order, cannot reproduce elastic anisotropy, and fail to reproduce non-isotropic structural relaxations. Clearly, ab initio approaches which properly account for many-body interactions are much preferred for studies of the occupancy sequence in M23C6.
A few ab initio studies considered partial site occupation in M23C6. Medvedeva et al.34 considered Cr22Fe1C6, where Fe either fully occupies the 4a site, or partially occupies an 8c, 32f, or 48h site. It was found that Fe prefers to occupy the 4a site and that Cr22Fe1(4a)C6 is more stable than a mixture of Cr23C6 and Fe23C635,36, whereas other substitutions (Fe1(8c), Fe1(32f) and Fe1(48h)) decrease the stability of Cr22Fe1C6. A similar result was reported by Fang et al.37. However, in contrast to the present work, previous work neglects important thermal excitations such as the effect of vibrational entropy on stability. This severely limits a comparison between previous ab initio results and experiment.
In this paper, we investigated the impact of site occupancy of Fe in the γ-Cr23–xFe x C6 (x = 0–3) carbide phase in detail using the cluster-expansion method (CEM) and the cluster-variation method (CVM) based on first-principles as function of composition and temperature. We found that if the partial site occupation is more properly taken into account in the cluster expansion, the preferred site occupancy is substantially different from the case when the cluster expansion mostly relies on full occupation configurations.
Results and Discussion
γ-Cr23−xFe x C6 (x = 0–3): super-ion cluster morphology
Although subsequently forgotten, Westgren27,38 already recognized that the Cr23C6 structure can be viewed as composed of Cr(4a)Cr12(48h) and Cr8(32f)C6(24e) clusters in a NaCl arrangement with Cr(8c) atoms as interstitials, see Fig. 1b. A Bader charge analysis39,40 coupled with an analysis of the electron levels of the isolated clusters supports the ionic NaCl interpretation of the structure, as evidenced by Figs 2 and 3. The Bader charges as a function of Fe fraction (xFe = x/23), shown in Fig. 2, reveal that Cr(4a)Cr12(48h) is more than 6 electrons deficient, rather independent of Fe content, and Cr8(32f)C6(24e) has more than 7 additional electrons, while the interstitial 8c sites balance the charges. As is typical of ionic configurations we expect to see a significant gap between the highest occupied and the lowest unoccupied molecular orbitals (HOMO–LUMO gap) for this charge state. Figure 3 confirms this: isolated Cr(4a)Cr12(48h) features a large HOMO–LUMO gap for 70, 74, and 80 valence electrons, implying preferred charges of 8+, 4+, and 2−, the former corresponding nicely to the Bader charge of more than 6 electron deficient. The isolated Cr8(32f)C6(24e) cluster has a large HOMO-LUMO gap for 72, 75, and 80 valence electrons, implying preferred charges of 0, 3−, and 8−, the latter agreeing well with the Bader charge of more than seven excess electrons.
The Fe-Cr substitution behavior can be understood in terms of the HOMO-LUMO gaps of the Cr(4a)Cr12(48h) and Cr8(32f)C6(24e) super-ions. When some Fe atoms substitute for Cr atoms on the 48h sites in the Cr(4a)Cr12(48h) or on the 32f sites in the Cr8(32f)C6(24e) super-ions, the high symmetry of the super-ions is lost. Such symmetry breaking lowers the degeneracies of electron levels and therefore also reduces the HOMO-LUMO gap. Large HOMO-LUMO gaps indicate favorable electronic configurations. Therefore, Fe substitutions on 48h or 32f sites destabilize the super-ions and thus the whole carbide structure. When Fe substitutes for Cr on the 4a site in Cr(4a)Cr12(48h), or Fe substitutes Cr on the 8c sites, the symmetry remains exactly the same, the favorable large HOMO-LUMO gap of the super-ions is maintained, and the structure remains stable. Therefore, incorporation of Fe in Cr23C6 is energetically preferred on the 4a and 8c sites.
Free energy and vibrational entropy contribution
Consideration of the vibrational effect in the free energy calculations can significantly alter the predicted carbide phase stability obtained at T = 0 K. Indeed, the vibrational free energy contributions can cause a re-ranking of the most stable structures (Table S1) in the lowest energy search. In this regard, the phase stability of the precipitates can be deduced by accounting for the enthalpy of formation, whereby the lattice vibration of the compounds is also included in the total free energy using CVM calculations within the Debye model41,42. The configurations studied for the full and partial occupations are summarized in Table S2 in the Supplementary information. Each structure is denoted in the form MMMM where sequentially reference is made to the 4a, 8c, 32f, 48h sites and M = −(Fe) when a site is occupied by Cr (partially by Fe). Subscript for Fe indicates fraction Fe atoms with remaining fraction Cr. We used the Debye model because a full phonon calculation was not feasible for all structures. Our method for obtaining the Debye temperature is described in detail in the supplementary information (see Table S2). The free energy of a supercell, \(\tilde{G}(T)\), is obtained by adding the temperature dependent vibrational free energy, GDebye(T), to the ab initio computed ground state enthalpy, H,
where T is the absolute temperature. The tilde superscript is a reminder that the configurational entropy term has not been accounted for. The Debye vibrational free energy43,44,45 is computed with
where kB is Boltzmann’s constant, θD is the Debye temperature, and D3 is the Debye integral.
The first term on the right-hand side denotes the zero-point vibrational contribution and the second indicates the temperature dependent vibrational contribution.
The formation free energies of the perfectly periodic supercells, \({\rm{\Delta }}{\tilde{G}}_{{\rm{f}}}(T)\), without including the entropic contribution from configurational disorder, can then be defined with respect to the terminal carbides as
where the composition of the supercell is written in square brackets.
The free energies, \({\rm{\Delta }}{\tilde{G}}_{{\rm{f}}}(T)\), are used in a cluster expansion to yield temperature dependent effective cluster interactions. The effective cluster interactions are used in the CVM to obtain the formation free energy, ΔGf(T), with full inclusion of configurational entropy and configurational enthalpy associated with temperature dependent partial site occupancy. The thermodynamically favored site occupation is determined by minimizing ΔGf(T). In our calculations, we have neglected the effects of thermal volume expansion.
Figure 4 shows \({\rm{\Delta }}{\tilde{G}}_{{\rm{f}}}\) of the carbides as a function of xFe for the cases of both full and partial occupation at various temperatures. It is apparent that many Fe substituted carbides have lower energy than mixtures of the terminal carbides (Cr23C6 and Fe23C6) at the same composition. As a function of temperature, it is apparent that even when configurational entropy effects are ignored, the vibrational free energy contribution by itself causes shifts in the most favorable carbide structures: at T = 0 K (Fig. 4a) the (Fe – – –) configuration is most favorable at xFe ≈ 0.043. At T = 600 K (Fig. 4b), the same configuration remains favored, while at 1200 K (Fig. 4c), the partial occupancy (– – Fe1/8 –) configuration becomes preferred. At xFe ≈ 0.087, (Fe – Fe1/8 –) and (Fe – – Fe1/12) configurations have similar low free energies at T = 0 K. Vibrational free energy contributions increasingly favor the (Fe – – Fe1/12) configuration over the (Fe – Fe1/8 –) configuration as temperature is raised. When even more Fe atoms substitute for Cr (xFe ≈ 0.130), even more partial occupied configurations (Fe – Fe1/8 Fe1/12), (Fe – Fe2/8 –), and (Fe – – Fe2/12), have free energies very close to the fully occupied (Fe Fe – –) configuration at 0 K. However, at higher temperatures, the vibrational excitations cause a gradual preference for the (Fe – Fe2/8 –) configuration. This is not an isolated case, at higher temperatures several partial occupancy structures sink below the convex hull formed by full occupancy structures only. So a general trend emerges where vibrational excitations increasingly favor partial occupancy configurations over full occupancy configurations as temperature is raised. Clearly the vibrational effects by themselves already can produce shifts in site occupation behavior. The volume per atom decreases monotonically with xFe, as shown in Fig. S1a. The atomic volumes of the most stable configurations were linearly fitted as (10.045 − 0.549 xFe [Å3]), where the negative slope is in agreement with the reported linear fits to experimental results of (10.439 − 0.574 xFe [Å3]) by Yakel32, (10.385 − 0.390 xFe [Å3]) by Shaw32,46, and (10.443 − 0.536 xFe [Å3]) by Westgren32,47. The computed atomic volumes are smaller than the reported experimental values. This is a well-known deficiency of the generalized gradient approximation (GGA) of the exchange-correlation functional48, especially for systems containing early 3d-elements49,50. For very Cr-rich carbides there is no net magnetization, however, already at an iron concentration xFe ≈ 0.043 a transition to the ferromagnetic state occurs, see Fig. S1b.
To understand the nature of chemical bonding in the most stable γ-Cr23−xFe x C6 (x = 0–3) carbide structures, and the relevant changes with increased Fe content, we examined the electron localization function (ELF)51. ELF contour plots in the (110) plane of the carbide phase are displayed for four different Fe occupations, ranging from xFe = 0.0 to 0.130, see Fig. S2b. It is readily apparent that with increasing Fe content the character of bonding locally changes. While the ELF usually indicates degree of covalency, here it nicely illustrates changes in spin polarization. The arrows indicate the area in the bonding region between nearest neighbor 48h-48h Cr atoms perpendicular to the cross section plane where the spin polarization is strongly increased due to the presence of extra Fe atoms.
At T = 1200 K, \({\rm{\Delta }}{\tilde{G}}_{{\rm{f}}}\) of the most stable carbide at xFe ≈ 0.087 (Fe – – Fe1/12), was calculated as approximately −4.09 eV/supercell, quite comparable with the experimental enthalpy of −3.34 eV/supercell52 and higher than the value of −12.12 eV/supercell reported using a thermodynamic Calphad assessment of the Fe–Cr–C system53.
Site occupation parameter
Finally, Fig. 5 shows the site fraction of Fe at each metal site computed with the CVM, both without (Fig. 5a,b) and with (Fig. 5c,d) inclusion of vibrational contributions. Experimental site occupations along with their error bars are also plotted for comparison32. In the results without the vibrational contribution, we found that inclusion of partial occupation structures in the cluster expansion gave improvement with experiment for the 4a and 48 h sites at both 600 K and 1200 K. However, for the 8c and 32f sites no such clear improvement could be seen. The results with vibrational contributions show more often that including the partial occupation structures in the cluster expansion does not improve the agreement with experimentally measured site occupations, the only exception to this being the 4a site at 600 K. The inclusion of vibrational effects seems to improve the agreement with experiment in particular for the results for the 4a site, for the other sites no such clear-cut conclusion can be drawn. Overall, we see a fair agreement with the experimental results, in particular for the 4a, 32f and 48h sites theoretical results are found within the experimental error bars. For the 8c sites agreement, in all theoretical treatments we considered is less good.
Iron site occupation on the inequivalent metal sites of γ-Cr23−xFe x C6 (x = 0–3) as a function of xFe, (a,b) without and (c,d) with vibrational effects at T = 600 K and T = 1200 K. The experimental data with error bars are plotted also for comparison32.
Fe is found to preferentially substitute for Cr at the 4a site, which is consistent with earlier work34,35,36,37. With increasing iron content, in contrast to the experimental findings, we find that the 4a sites saturate before the 8c sites take Fe occupancy. The Fe uptake in the 32f and 48h sites increases gradually with iron content, and in the 48h sites a little more rapidly than in the 32f sites, in good agreement with experiment31,32.
Conclusion
In this work, we revived an old interpretation of the Cr23C6 structure as an NaCl arrangement of super-ions. We show that such super-ions can be recognized with approximate constant charges irrespective of composition, at least within the range 0 ≤ x ≤ 3 in Cr23–xFe x C6. The super-ion description not only gives a rationalization for the crystal structure, but also gives an understanding for the site preference of Fe in Cr23C6. As this reasoning does not rely on the specifics of Fe, but merely assumes that elastic strain effects play an subordinate role, we expect that other alloying elements, with an atomic size comparable to Cr, can be predicted and understood as well.
It is also shown that including vibrational effects changes which structures populate the convex hull. With increasing temperature, it is seen that the vibrational free energy causes structures with partial site occupancy to sink below the convex hull formed by the full occupancy structures, even when configurational entropy effects are neglected. Of course, configurational free energy terms would further favor partial occupancy structures over full occupancy structures. This implies that vibrational effects cannot be ignored in the prediction of site preference.
Including partial occupancy structures in the cluster expansion gives significant changes in the site occupation. However, these changes did not give a univocal improvement with the experimental data. Inclusion of vibrational effects however, did give a systematic improvement of computed site occupancies with experimental results.
Methods
Cluster Expansion Method (CEM) & Cluster Variation Method (CVM)
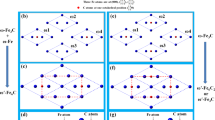
In this work, we have used CEM and CVM54 to study the effect of the partial occupation of inequivalent metallic sites in the γ-Cr23−xFe x C6 (x = 0–3) carbide phase, where the interactions were used to compute the entropy and Gibbs energy of the phase as function of the temperature and composition within the tetrahedron approximation21. The cluster expansion was carried out using a pool of clusters generated by the condition that no two sites in a cluster are separated more than 0.31 times the M23C6 lattice parameter. As the lattice parameter is about 1 nm, this means no sites are further than about 0.3 nm apart. Using this criterion, five distinct types of 4-site clusters are the largest clusters that can be generated55. These clusters are shown in Fig. 6. Further details of the method are given in the Supplementary information.
Ab initio calculations
As inputs for the CEM, we performed total energy calculations using pseudopotentials generated by the projected augmented wave (PAW) method as implemented in the Vienna Ab initio Simulation Package (VASP)56,57. The number of valence electrons are 4, 6, and 8 for C:(2s22p2), Cr:(3d54s1), and Fe:(3d74s1), respectively. We considered collinear spin-polarization for all structures within the generalized gradient approximation (GGA) for the exchange–correlation functional as formulated by Perdew, Burke, and Ernzerhof (PBE)48. All of the calculations were performed using the supercell technique, where periodic boundary conditions and full relaxation of internal coordinates and lattice parameters were considered. The adopted supercell contains one conventional cubic unit cell consisting of 92 metal atoms and 24 carbon atoms. The cutoff energy for plane wave expansion was 520 eV and the k-point sampling grid was 7 × 7 × 7. The calculations were considered converged when the change of the total energy between successive self-consistency iterations reached 10−5 eV or less and simultaneously the magnitude of the greatest force on any atom was less than 10−4 eV/Å.
References
Kondo, M., Tabuchi, M., Tsukamoto, S., Yin, F. & Abe, F. Suppressing type IV failure via modification of heat affected zone microstructures using high boron content in 9Cr heat resistant steel welded joints. Sci. Technol. Weld. Join. 11, 216–223 (2006).
Tabuchi, M., Hongo, H. & Takahashi, Y. Effect of Boron on Microstructures and Creep Properties of Welded Joint for High Cr Heat Resisting Steels. J. Soc. Mater. Sci. Japan 58, 108–114 (2009).
Tytko, D. et al. Microstructural evolution of a Ni-based superalloy (617B) at 700 °C studied by electron microscopy and atom probe tomography. Acta Mater. 60, 1731–1740 (2012).
Godec, M. & Skobir Balantič, D. A. Coarsening behaviour of M23C6 carbides in creep- resistant steel exposed to high temperatures. Sci. Rep. 6, 29734 (2016).
Grånäs, O., Korzhavyi, P. A., Kissavos, A. E. & Abrikosov, I. A. Theoretical study of the Mo–Ru sigma phase. Calphad 32, 171–176 (2008).
Pavlů, J., Vřeštál, J. & Šob, M. Ab initio study of energetics and magnetism of sigma phase in Co–Mo and Fe–Mo systems. Modelling Simul. Mater. Sci. Eng. 24, 025009 (2016).
Palumbo, M., Abe, T. & Kocer, C. Murakami, H. & Onodera, H. Ab initio and thermodynamic study of the Cr–Re system. Calphad 34, 495–503 (2010).
Pavlů, J., Vřeštál, J. & Šob, M. Ab initio study of formation energy and magnetism of sigma phase in Cr–Fe and Cr–Co systems. Intermetallics 18, 212–220 (2010).
Kabliman, E. A., Mirzoev, A. A. & Udovskii, A. L. First-principles simulation of an ordered sigma phase of the Fe-Cr system in the ferromagnetic state. Phys. Met. Metallography 108, 435–440 (2009).
Havránková, J., Vřeštál, J., Wang, L. G. & Šob, M. Ab initio analysis of energetics of σ-phase formation in Cr-based systems. Phys. Rev. B 63, 174104 (2001).
Ackland, G. J. Ordered sigma-type phase in the Ising model of Fe-Cr stainless steel. Phys. Rev. B 79, 094202 (2009).
Crivello, J.-C. & Joubert, J.-M. First principles calculations of the σ and χ phases in the Mo–Re and W–Re systems. J. Phys.: Condens. Matter 22, 035402 (2010).
Crivello, J.-C., Breidi, A. & Joubert, J.-M. χ and σ Phases in Binary Rhenium–Transition Metal Systems: a Systematic First-Principles Investigation. Inorg. Chem. 52, 3674–3686 (2013).
Palumbo, M. et al. First-principles-based phase diagrams and thermodynamic properties of TCP phases in Re–X systems (X=Ta, V, W). Comp. Mater. Sci. 81, 433–445 (2014).
Nakano, J., Malakhov, D. V. & Purdy, G. R. A crystallographically consistent optimization of the Zn–Fe system. Calphad 29, 276–288 (2005).
Fries, S. G. & Sundman, B. Using Re-W σ-phase first-principles results in the Bragg-Williams approximation to calculate finite-temperature thermodynamic properties. Phys. Rev. B 66, 012203 (2002).
Zhang, Y., Ozoliņš, V., Morelli, D. & Wolverton, C. Prediction of New Stable Compounds and Promising Thermoelectrics in the Cu–Sb–Se System. Chem. Mater. 26, 3427–3435 (2014).
Palumbo, M., Abe, T., Fries, S. G. & Pasturel, A. First-principles approach to phase stability for a ternary σ phase: Application to Cr-Ni-Re. Phys. Rev. B 83, 144109 (2011).
Seister, B., Hammerschmidt, T., Kolmogorov, A. N., Drautz, R. & Pettifor, D. G. Theory of structural trends within 4d and 5d transition metal topologically close-packed phases. Phys. Rev. B 83, 224116 (2011).
Joubert, J.-M. & Crivello, J.-C. Non-Stoichiometry and Calphad Modeling of Frank-Kasper Phases. Appl. Sci. 2, 669–681 (2012).
Sluiter, M. H. F., Esfarjani, K. & Kawazoe, Y. Site Occupation Reversal in the Fe−Cr σ Phase. Phys. Rev. Lett. 75, 3142–3145 (1995).
Berne, C., Sluiter, M., Kawazoe, Y., Hansen, T. & Pasturel, A. Site occupancy in the Re-W sigma phase. Phys. Rev. B 64, 144103 (2001).
Berne, C., Sluiter, M. & Pasturel, A. Theoretical approach of phase selection in refractory metals and alloys. J. Alloys Compd. 334, 27–33 (2002).
Berne, C., Sluiter, M., Kawazoe, Y. & Pasturel, A. Ordering effects in the Re–W and Re–Ta sigma phases. J. Phys.: Condens. Matter. 13, 9433–9443 (2001).
Kabliman, E., Ruban, A. V., Blaha, P., Peil, O. & Schwarz, K. Ab Initio Study of Lattice Site Occupancies in Binary Sigma Phases Using a Single-Site Mean Field Model. Appl. Sci. 2, 654–668 (2012).
Cieslak, J., Tobola, J. & Dubiel, S. M. Study of phase stability in the σ-FeCr system. Intermetallics 24, 84–88 (2012).
Westgren, A. Snabbstålskarbiden Kristallstruktur. Jernkontorets Ann. 117, 501–512 as cited in ref. 38 (1933).
Zhang, Y., Liu, B. & Wang, J. Self-assembly of carbon vacancies in sub-stoichiometric ZrC1–x. Sci. Rep 5, 18098 (2015).
Zhang, Y., Liu, B., Wang, J. & Wang, J. Theoretical investigations of the effects of ordered carbon vacancies in ZrC1–x on phase stability and thermo-mechanical properties. Acta Mater. 111, 232–241 (2016).
Fang, C. M., Van Huis, M. A., Sluiter, M. H. F. & Zandbergen, H. W. Stability, structure and electronic properties of γ-Fe23C6 from first-principles theory. Acta Mater. 58(8), 2968–2977 (2010).
Yakel, H. L. & Brynestad, J. Non-random site-occupation parameters in (Cr,Fe)23C6 phases. Scripta Metall. 16, 453–454 (1982).
Yakel, H. L. Atom distributions in tau-carbide phases: Fe and Cr distributions in (Cr23–xFe x )C6 with x=0, 0.74, 1.70, 4.13 and 7.36. Acta Cryst. B43, 230–238 (1987).
Xie, J. Y., Chen, N. X., Teng, L. D. & Seetharaman, S. Atomistic study on the site preference and thermodynamic properties for Cr23−xFe x C6. Acta Mater. 53, 5305–5312 (2005).
Medvedeva, N. I., Van Aken, D. C. & Medvedeva, J. E. Stability of binary and ternary M23C6 carbides from first principles. Comput. Mater. Sci. 96, 159–164 (2015).
Han, J. J., Wang, C. P., Liu, X. J., Wang, Y. & Liu, Z.-K. First-principles calculation of structural, mechanical, magnetic and thermodynamic properties for γ-M23C6 (M = Fe, Cr) compounds. J. Phys.: Condens. Matter 24, 505503 (2012).
Henriksson, K. O. E., Sandberg, N. & Wallenius, J. Carbides in stainless steels: Results from ab initio investigations. Appl. Phys. Lett. 93, 191912 (2008).
Fang, C., van Huis, M. A. & Sluiter, M. H. F. Formation, structure and magnetism of the γ-(Fe,M)23C6 (M = Cr, Ni) phases: A first-principles study. Acta Mater. 103, 273–279 (2016).
Bowman, A. L., Arnold, G. P., Storms, E. K. & Nereson, N. G. The crystal structure of Cr23C6. Acta Cryst B28, 3102–3103 (1972).
Tang, W., Sanville, E. & Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys: Cond. Matter 21, 084204 (2009).
W. Orville-Thomas In: Bader R. F. W. (Ed.), Atoms inMolecules—a Quantum Theory, Clarendon Press, Oxford, UK, 1994. 438, Elsevier, 1996.
Florez, M., Recio, J. M., Francisco, E., Blanco, A. M. & Pendas, M. A. First-principles study of the rocksalt–cesium chloride relative phase stability in alkali halides. Phys. Rev. B 66, 144112 (2002).
Ma, D., Grabowski, B., Körmann, F., Neugebauer, J. & Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 100, 90–97 (2015).
Toher, C. et al. High-throughput computational screening of thermal conductivity, Debye temperarure, and Grüneisen parameter using a quasiharmonic Debye model. Phys. Rev. B 90, 174107 (2014).
Shang, S.-L., Wang, Y., Kim, D. & Liu, Z.-K. First-principles thermodynamics from phonon and Debye model: Application to Ni and Ni3Al. Comput. Mater. Sci. 47, 1040–1048 (2010).
Wang, Y., Ahuja, R. & Johansson, B. Mean-field potential approach to the quasiharmonic theory of solids. Int. J. Quantum Chem. 96, 501–506 (2004).
Shaw, S. W. K. & Quarrell, A. G. The Formation of Carbides in Low-Carbon, Chromium-Vanadium Steels at 700 °C. J. Iron Steel Inst. 185, 10–22 (1957).
Westgren, A., Phragmén, G. & Negresco, T. R. On the Structure of the Iron-Chromium-Carbon System. J. Iron Steel Inst. 117, 383–400 (1928).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Haas, P., Tran, F. & Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 79, 085104 (2009).
Schimka, L., Gaudoin, R., Klimeš, Marsman, M. & Kresse, G. Lattice constants and cohesive energies of alkali, alkaline-earth, and transition metals: Random phase approximation and density functional theory results. Phys. Rev. B 87, 214102 (2013).
Becke, A. D. & Edgecombe, K. E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 92, 5397–5403 (1990).
Kulkarni, A. D. & Worrell, W. L. High-Temperature Thermodynamic Properties of the Chromium Carbides Determined Using the Torsion-Effusion Technique. Metall. Trans. 3, 2363–2369 (1972).
Khvan, A. V., Hallstedt, B. & Broeckmann, C. A thermodynamic evaluation of the Fe–Cr–C system. Calphad 46, 24–33 (2014).
Kikuchi, R. A Theory of Cooperative Phenomena. Phys. Rev. 81, 988–1003 (1951).
Sluiter, M. H. F., Colinet, C. & Pasturel, A. Ab initio calculation of the phase stability in Au-Pd and Ag-Pt alloys. Phys. Rev. B 73, 174204 (2006).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
This work is partially supported by JSPS KAKENHI Grant Number 15H04117. We gratefully acknowledge the support of the staff of the Numerical Materials Simulator at the National Institute for Materials Science (NIMS) for providing the computational resources. The authors are also grateful to Professor Hiroshi Numakura (Osaka Prefecture University) for useful comments and enlightening discussions.
Author information
Authors and Affiliations
Contributions
M. Souissi conducted the ab initio calculations and prepared the manuscript. M.H.F. Sluiter carried out CEM and CVM and co-wrote the manuscript. T. Matsunaga, M. Tabuchi and M.J. Mills analyzed the results and helped with interpretation of experimental results. R. Sahara has initiated and supervised this research project.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Souissi, M., Sluiter, M.H.F., Matsunaga, T. et al. Effect of mixed partial occupation of metal sites on the phase stability of γ-Cr23−xFe x C6 (x = 0–3) carbides. Sci Rep 8, 7279 (2018). https://doi.org/10.1038/s41598-018-25642-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-25642-y
This article is cited by
-
High-Temperature Phases in the Fe–Mo–Cr–C System
Powder Metallurgy and Metal Ceramics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.