Abstract
Two-mode squeezing is a fascinating example of quantum entanglement manifested in cross-correlations of non-commuting observables between two subsystems. At the same time, these subsystems themselves may contain no quantum signatures in their self-correlations. These properties make two-mode squeezed (TMS) states an ideal resource for applications in quantum communication. Here, we generate propagating microwave TMS states by a beam splitter distributing single mode squeezing emitted from distinct Josephson parametric amplifiers along two output paths. We experimentally study the fundamental dephasing process of quantum cross-correlations in continuous-variable propagating TMS microwave states and accurately describe it with a theory model. In this way, we gain the insight into finite-time entanglement limits and predict high fidelities for benchmark quantum communication protocols such as remote state preparation and quantum teleportation.
Similar content being viewed by others
Introduction
Propagating quantum microwave signals in the form of squeezed states are natural candidates for quantum communication1,2,3 and quantum information processing4,5,6,7 with continuous variables. This assessment stems from the fact that they belong to the same frequency range and are generated using the same material technology as quantum information processing platforms based on superconducting circuits8,9,10,11. Utilizing propagating quantum microwaves, one can potentially realize quantum illumination protocols12,13,14,15,16, hybrid computation schemes with continuous variables6,17,18 and a high-fidelity seamless connection between distant superconducting quantum computers19. In two-mode squeezed microwave states, entanglement is expressed in strong correlations between two nonlocal field quadratures3,5. The physical limits of this entanglement are of broad interest regarding both quantum information theory and applications. In this context, finite-time correlation properties of propagating squeezed states provide necessary information about the tolerance to unwanted delays, and therefore, determine whether delay lines are required. From the fundamental point of view, finite-time correlation measurements grant a quantitative physical insight into the dephasing processes of propagating entangled microwave signals.
In this Article, we experimentally show how the entanglement in the two-mode squeezed state decays depending on a time delay τ in one of the propagation paths. This entanglement decrease can be attributed to a dephasing process between the two modes propagating along each path. According to our experimental results and the corresponding theoretical model, the dephasing time, characterising the entanglement decay, is inversely proportional to the squeezing level and the measurement filter bandwidth. In contrast to earlier works20,21, we perform direct state tomography of highly symmetric frequency-degenerate microwave TMS states with a record entanglement strength quantified by the negativity of \({\mathscr{N}}\simeq 3.9\).
We use two superconducting flux-driven Josephson parametric amplifiers (JPAs) operated at f0 = 5.323 GHz for the generation of squeezed microwave states (see supplementary information for details). The task of each JPA is to perform a squeezing operation on the incident vacuum state \(\hat{S}(\xi \mathrm{)|0}\rangle \), where \(\hat{S}(\xi )=\exp (\frac{1}{2}\xi \ast {\hat{a}}^{2}-\frac{1}{2}\xi {({\hat{a}}^{\dagger })}^{2})\) is the squeezing operator, \({\hat{a}}^{\dagger }(\tau )\) and \(\hat{a}(\tau )\) are the creation and annihilation operators of the f0 mode, and ξ = reiϕ is the complex squeezing amplitude. Here, the phase ϕ determines the squeezing angle in phase space, while the squeezing factor r parameterizes the amount of squeezing. We conveniently characterize the degree of squeezing of the quantum state in decibels as \(S=-\,10\,\,{\mathrm{log}}_{10}[{\sigma }_{{\rm{s}}}^{2}\mathrm{/0.25]}\), where \({\sigma }_{{\rm{s}}}^{2}\) is the variance of the squeezed quadrature and the vacuum variance is 0.25. Positive values of S indicate squeezing below the vacuum level. In experiments, the JPAs are nonideal, meaning that they effectively squeeze a thermal state with a mean noise photon number n. In this scenario, the squeezed and antisqueezed quadratures can be expressed as \({\sigma }_{{\rm{s}}}^{2}=\mathrm{0.25(1}+2n)\,\exp \,(\,-\,2r)\) and \({\sigma }_{{\rm{a}}}^{2}=\mathrm{0.25(1}+2n)\,\exp \,\mathrm{(2}r)\), respectively (see supplementary information for details). This expressions allow us to rewrite the squeezing level as \(S=-\,10\,{\mathrm{log}}_{10}\mathrm{[(1}+2n)\,\exp \,(\,-\,2r)]\). Although n is typically small, it must be accounted for in a quantitative analysis of actual data.
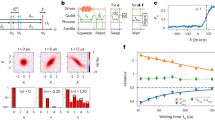
Finite-time correlations of a propagating single-mode squeezed state can be captured using the normalized second order correlation function \({g}^{\mathrm{(2)}}(\tau )=\langle {\hat{a}}^{\dagger }\mathrm{(0)}{\hat{a}}^{\dagger }(\tau )\hat{a}(\tau )\hat{a}\mathrm{(0)}\rangle /{\langle {\hat{a}}^{\dagger }\mathrm{(0)}\hat{a}\mathrm{(0)}\rangle }^{2}\). It describes the decay of the correlations in propagating light and relates an autocorrelation time to this process. To measure g(2)(τ) of propagating squeezed microwaves, we employ the experimental setup shown in Fig. 1a. In order to reconstruct the squeezed vacuum states, we apply a variant of the dual-path reconstruction scheme22,23,24. To this end, the input signal is first distributed over two paths using a hybrid ring beam splitter. After amplification, auto- and cross-correlation measurements are performed on the output paths. In this way, we can correct for the amplifier noise and retrieve all moments of the signal mode incident at the beam splitter up to fourth order in amplitude. An important modification in our setup is the introduction of a digital time-delay τ in one of the detection paths (see Fig. 1). This modification allows us to extend the dual-path technique to measure finite-time correlations g(2)(τ). For further technical details, we refer the reader to the supplemental material.
Circuit schematic for the generation of squeezed propagating microwave states. In case (a) JPA2 is in the vacuum state (the respective microwave pump is switched off) is depicted. In case (b) both JPAs are operated such that symmetric TMS states are generated at the outputs of the hybrid ring. State detection, in both cases, is realized with the dual-path detector23,28 based on cross-correlation quadrature measurements. For finite-time correlation measurements, we introduce a time delay τ in one of the paths.
Figure 2 shows the experimental results. As expected from theory25, the super-Poissonian character of squeezed microwave states is demonstrated by g(2)(0) > 1. We observe a smooth decay of g(2)(τ) to the coherent-state limit g(2)(τ) = 1 on a timescale of \(\tau \gtrsim 1\,\mu \)s. In order to describe our results, we use an extended variant of the input-output theory presented in ref.26. It yields
where Ω is a width of a measurement bandpass filter centered at f0. By fitting experimental data with Eq. (1), as depicted in Fig. 2a, we extract the experimental filter bandwidth Ω ≃ 420 kHz. This value agrees very well with the bandwidth of the digital finite-impulse response (FIR) filter used in our measurement protocol, ΩFIR = 430 kHz. As can be seen from Eq. (1), the fitted squeezing factor r and noise photon number n define the value of g(2)(0), but neither one influences the temporal shape of g(2)(τ). A noticeable scatter in g(2)(τ) for low squeezing levels (4–5 dB) is caused by low respective average photon numbers \(\langle {\hat{a}}^{\dagger }\mathrm{(0)}\hat{a}\mathrm{(0)}\rangle \). The latter lead to a decreased experimental signal-to-noise ratio and an increased uncertainty of g(2)(τ).
Finite-time correlations of single-mode squeezed microwave states at the frequency f0 = 5.323 GHz. Top graph (a) illustrates the second order correlation function g(2)(τ) of single-mode squeezed states fitted with Eq. (1). Bottom graph (b) depicts the impact of a finite-time delay on the path entanglement quantified via the negativity kernel N k (τ), which can be accurately fitted using Eq. (2). In both graphs, symbols depict experimental data, lines show corresponding theoretical fits, S e is the experimental squeezing level in JPA1, while S is the fitted one, and n is the fitted noise photon number. Fitting parameters and color codes are the same for (a,b). When not shown, statistical error bars are smaller than the symbol size.
So far, we have investigated the correlations of single-mode squeezed states. Now, in order to evaluate the suitability of our setup for actual quantum microwave communication protocols, we go one step further and study the finite-time behaviour of quantum entanglement between the outputs of the hybrid ring. In general, the amount of quantum entanglement can be assessed using the negativity \({\mathscr{N}}\). It is defined as \({\mathscr{N}}\equiv \,{\rm{\max }}\,\{0,{N}_{k}\}\), where the negativity kernel N k is a function of the density matrix of the investigated state. In the relevant case of Gaussian states, N k is expressed in terms of the covariance matrix27, and \({\mathscr{N}}\) constitutes an entanglement measure. Then, condition N k > 0 implies the presence of entanglement. By varying τ in our experiment, we measure the τ-dependent negativity kernel N k (τ) which provides information about the temporal length of the propagating entangled signal. Here, we introduce a maximally acceptable delay τ d which still allows for existence of entanglement in a TMS state. This condition is given by N k (τ d ) = 0 for a monotonically decreasing N k (τ). Assuming all other system properties to be equal, a large τ d is beneficial in quantum communication. The expression for the negativity kernel N k (τ) for an arbitrary two-mode squeezed state produced by two independent JPAs is given by (see supplementary information for details).
where \(\tilde{n}\equiv \mathrm{(1}+2{n}_{1})(1+2{n}_{2})\), \(C\equiv {\cosh }^{2}({r}_{1}+{r}_{2})\), D ≡ sinh (2r1 + 2r2); r1 (r2) and n1 (n2) are the squeezing factor and number of noise photons of JPA1 (JPA2), respectively. For the scenario depicted in Fig. 1a, where JPA2 is off, we consider r2 = n2 = 0 and accurately fit the experimental data with Eq. (2) as it can be seen in Fig. 2b. The negativity kernel N k depends on the squeezing level S and the corresponding values of r since the delay τ d clearly decreases with increasing S. This is in strong contrast with the behavior of g(2)(τ) where the temporal shape only provides information on Ω. The increasing noise photon numbers n for higher squeezing levels are caused by larger microwave pump powers required to reach these values of S. As a result, stronger microwave fields lead to a stronger coupling to environmental loss channels, a process that increases n.
Finally, we consider the case of propagating symmetric TMS states, which is most relevant for our envisioned applications. To this end, we operate both JPAs with orthogonal squeezing angles as shown in Fig. 1b. The resulting TMS states are essential for quantum microwave communication as they allow for entanglement distribution between separate distant parties. First, we are interested in the full tomography of the path-entangled two-mode states. We achieve this goal by using the reference state method17,22,28,29 and zero time delay τ = 0. The result is depicted in Fig. 3. We tune the squeezing levels and angles of both JPAs by adjusting the amplitude and phase of the microwave pump tone to obtain symmetric TMS states. In this way, we eliminate residual single-mode squeezing in the marginal distributions in the self-correlated subspaces {p1, q1} and {p2, q2} of the resulting Wigner function (see Fig. 3a). We achieve close to perfect local thermal states in both paths. The strong two-mode squeezing between them is clearly observed in the cross-correlation subspaces {q2, p1} and {p2, q1} in Fig. 3b. This result is very different from the case shown in Fig. 1a, where, in addition to the two-mode squeezing, also a residual local single-mode squeezing is generated at the hybrid ring outputs. The latter is unwanted in certain communication protocols since it partially reveals the encoded information. To describe the entanglement for this case, we use Eq. (2) in the approximation of identical squeezing factors r1 = r2 = r (accordingly, S1 = S2 = S) and noise photon numbers n1 = n2 = n in both JPAs. Figure 4 describes the entanglement dephasing in the propagating TMS states with respect to the finite-time delay τ of the second path for various input squeezing levels and different filter bandwidths. The fit to the experimental data has been implemented using the squeezing factor and number of noise photons as free fitting parameters while setting the filter bandwidth Ω to the value predefined by FIR characteristics (430 kHz or 770 kHz). Figure 4 shows an excellent agreement between theory and experiment. Moreover, the entanglement dephasing time τ d strongly decreases with the increasing squeezing levels S, and consequently, the squeezing factors r. Additionally, high squeezing levels lead to a substantial increase in the added noise photons n, which leads to weaker entanglement N k (τ = 0) but does not affect τ d . Both contributions may be seen in Eq. (2). Another important experimental observation is that increasing the filter bandwidth Ω leads to shorter dephasing times τ d which is also described by Eq. (2). In the limit Ω → ∞, τ d is eventually limited by the internal JPA bandwidth Δf ≃ 5 MHz. Quantum entanglement can be also evaluated using the entanglement of formation N F . The amount of entanglement in the TMS state for N F = 1 is equivalent to a maximally entangled pair of qubits30,31. This link allows us to estimate an equivalent entangled-bit rate transferred via the propagating TMS states. By measuring the entanglement of formation N F ≃ 0.86 within the full JPA bandwidth Δf (which corresponds to N k ≃ 1.08 and S ≃ 5.3 dB), we arrive at the entangled-bit rate of 4.3 × 106 ebits · s−1 usable in quantum communication protocols.
Experimental marginal distributions of the Wigner function of TMS states created via interference of two orthogonally squeezed single-mode states with the squeezing levels S1 ≃ S2 ≃ 8 dB in a hybrid ring. The quantities p and q are dimensionless variables representing quadratures of the electromagnetic field. Color reflects the quasiprobability amplitude. Left box (a) illustrates transformation of the hybrid ring inputs in the self-correlated subspaces {p1, q1} and {p2, q2}. Its respective outputs show no quantum signatures and coincide with thermal states with an average number of photons nTMS = 2.7. Right box (b) depicts the output distributions in the cross-correlated subspaces {q2, p1} and {p2, q1} which uncover quantum entanglement in the form of two-mode squeezing with STMS = 7.2 dB and corresponds to the negativity kernel of N k = 2.1.
Entanglement dephasing of propagating TMS states. The negativity kernel N k is plotted as a function of the delay time τ. Left graphs (a,b) show experimental data measured with the filter bandwidth Ω = 430 kHz. Right graphs (c,d) show the data obtained with Ω = 770 kHz. The red line in (a,c) marks the boundary between the entangled (N k > 0) and classical (N k < 0, separable) regions. The circles in (b,d) represent the experimental data, the lines show the corresponding fits using Eq. (2), S e values in the insets represent the experimental squeezing levels for both JPA1 and JPA2, S values denote the fitted squeezing levels, and n denotes the corresponding noise photon numbers. When not shown, statistical error bars are smaller than the symbol size.
The demonstrated dephasing process of TMS states allows us to estimate fidelities for two relevant quantum communication protocols based on propagating squeezed microwaves. The first one is remote state preparation (RSP)19. It can be viewed as the creation of a remote quantum state with local operations. Here, we consider the case of Ω = 430 kHz and S e ≃ 5.7 dB. A straightforward estimation based on the observed N k (τ) and otherwise ideal conditions provides the drop in fidelity from unity FRSP (τ = 0) = 1 to FRSP (τ) = 0.95 for τ ≃ 90 ns. The situation improves significantly when aiming at the remote preparation with lower squeezing level S e ≃ 3.8 dB, where the same drop does not happen until τ ≃ 250 ns. A similar analysis for the quantum teleportation (QT) protocol19 shows that the initial fidelities are lower (since it ultimately depends on the initial squeezing level and FQT → 1 only for S → ∞), but decrease slower with increasing τ. For S e = 5.7 dB, the change from FQT (τ = 0) ≃ 0.80 to FQT (τ) ≃ 0.75 occurs in τ ≃ 380 ns. These timescales make the implementation of RSP and QT with propagating squeezed microwaves possible without implementing delay lines, since the required delays due to feedback operations in these protocols are estimated to be around τ ≃ 100–200 ns.
In conclusion, we have confirmed that the autocorrelation time of microwave single-mode squeezed states depends on the minimum filter bandwidth Ω in the measurement setup. In our specific setup, Ω is defined by the bandwidth of the digital FIR filter. We have uncovered that, for propagating microwave TMS states, the entanglement quantified via N k (τ) survives for finite-time delays τ. We express the negativity kernel N k (τ) as a function of the squeezing level S and the noise photon number n in addition to Ω. This function is given by Eq. (2) and accurately describes the experimental results. The measurement bandwidth Ω also influences the timescale of entanglement decay due to dephasing in the case of propagating TMS states. High squeezing levels and accompanying large noise photon numbers additionally reduce the entanglement for finite delays between the paths. With respect to applications, a key result of this work is the observation of the characteristic dephasing timescale τ d for two-mode entanglement which can be longer than 1 μs for squeezing levels S ≃ 3 dB. This result confirms that propagating TMS microwave states are suitable for the remote preparation of squeezed states and short-to-medium distance quantum teleportation10,11.
References
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998).
Madsen, L. S., Usenko, V. C., Lassen, M., Filip, R. & Andersen, U. L. Continuous variable quantum key distribution with modulated entangled states. Nat. Commun. 3, 1083 (2012).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005).
Lloyd, S. & Braunstein, S. L. Quantum computation over continuous variables. Phys. Rev. Lett. 82, 1784 (1999).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Andersen, U. L., Neergaard-Nielsen, J. S., van Loock, P. & Furusawa, A. Hybrid discrete- and continuous-variable quantum information. Nat. Phys. 11, 713–719 (2015).
Marshall, K. et al. Continuous-variable quantum computing on encrypted data. Nat. Commun. 7, 13795 (2016).
Devoret, M. H. & Schoelkopf, R. J. Superconducting Circuits for Quantum Information: An Outlook. Science 339, 1169–1174 (2013).
Xiang, Z., Ashhab, S., You, J. Q. & Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623–653 (2013).
Mallet, F. et al. Quantum state tomography of an itinerant squeezed microwave field. Phys. Rev. Lett. 106, 220502 (2011).
Zhong, L. et al. Squeezing with a flux-driven Josephson parametric amplifier. New J. Phys. 15, 125013 (2013).
Lloyd, S. Enhanced sensitivity of photodetection via quantum illumination. Science 321, 1463–1465 (2008).
Zhang, Z., Mouradian, S., Wong, F. N. C. & Shapiro, J. H. Entanglement-enhanced sensing in a lossy and noisy environment. Phys. Rev. Lett. 114, 110506 (2015).
Las Heras, U. et al. Quantum illumination reveals phase-shift inducing cloaking. Sci. Rep. 7, 9333 (2017).
Sanz, M., Las Heras, U., García-Ripoll, J. J., Solano, E. & Di Candia, R. Quantum estimation methods for quantum illumination. Phys. Rev. Lett. 118, 070803 (2017).
Barzanjeh, S. et al. Microwave quantum illumination. Phys. Rev. Lett. 114, 080503 (2015).
Fedorov, K. G. et al. Displacement of propagating squeezed microwave states. Phys. Rev. Lett. 117, 020502 (2016).
Liu, N. et al. Power of one qumode for quantum computation. Phys. Rev. A 93, 052304 (2016).
Di Candia, R. et al. Quantum teleportation of propagating quantum microwaves. EPJ Quantum Technology 2, 25 (2015).
Flurin, E., Roch, N., Mallet, F., Devoret, M. H. & Huard, B. Generating entangled microwave radiation over two transmission lines. Phys. Rev. Lett. 109, 183901 (2012).
Ku, H. S. et al. Generating and verifying entangled itinerant microwave fields with efficient and independent measurements. Phys. Rev. A 91, 042305 (2015).
Menzel, E. P. et al. Path entanglement of continuous-variable quantum microwaves. Phys. Rev. Lett. 109, 250502 (2012).
Menzel, E. P. et al. Dual-path state reconstruction scheme for propagating quantum microwaves and detector noise tomography. Phys. Rev. Lett. 105, 100401 (2010).
Goetz, J. et al. Photon statistics of propagating thermal microwaves. Phys. Rev. Lett. 118, 103602 (2017).
Walls, D. F. & Milburn, G. J. Quantum Optics. Springer (2007).
Grosse, N. B., Symul, T., Stobinska, M., Ralph, T. C. & Lam, P. K. Measuring photon antibunching from continuous variable sideband squeezing. Phys. Rev. Lett. 98, 153603 (2007).
Adesso, G. & Illuminati, F. Gaussian measures of entanglement versus negativities: Ordering of two-mode Gaussian states. Phys. Rev. A 72, 032334 (2005).
Di Candia, R. et al. Dual-path methods for propagating quantum microwaves. New J. Phys. 16, 015001 (2014).
Eichler, C. et al. Observation of two-mode squeezing in the microwave frequency domain. Phys. Rev. Lett. 107, 113601 (2011).
Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998).
Wootters, W. K. Entanglement of formation and concurrence. Quantum. Inf. Comput. 1, 27–44 (2001).
Acknowledgements
We acknowledge support by the German Research Foundation through FE 1564/1-1, Spanish MINECO/FEDER FIS2015-69983-P, UPV/EHU PhD grant, Basque Government Grant IT986-16, European Project AQuS (Project No. 640800), Elite Network of Bavaria through the program ExQM, the projects JST ERATO (Grant No. JPMJER1601) and JSPS KAKENHI (Grant No. 26220601 and Grant No. 15K17731). E.S. acknowledges support from a TUM August-Wilhelm Scheer Visiting Professorship and hospitality of Walther-Meißner-Institut and TUM Institute for Advanced Study. We would like to thank K. Kusuyama for assistance with part of the JPA fabrication.
Author information
Authors and Affiliations
Contributions
K.G.F. and F.D. planned the experiment. K.G.F. and S.P. performed the measurements and analysed the data. K.G.F., S.P., P.Y. and P.E. programmed the data acquisition software. U.L.H., M.S., R.D.C., and E.S. provided the theory support. K.I. and Y.N. provided the JPA samples. F.D., A.M. and R.G. supervised the experimental part of this work. K.G.F. wrote the manuscript. All authors contributed to discussions and proofreading the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fedorov, K.G., Pogorzalek, S., Las Heras, U. et al. Finite-time quantum entanglement in propagating squeezed microwaves. Sci Rep 8, 6416 (2018). https://doi.org/10.1038/s41598-018-24742-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-24742-z
This article is cited by
-
Demonstration of microwave single-shot quantum key distribution
Nature Communications (2024)
-
Beyond the standard quantum limit for parametric amplification of broadband signals
npj Quantum Information (2021)
-
Secure quantum remote state preparation of squeezed microwave states
Nature Communications (2019)
-
Quantum illumination reveals phase-shift inducing cloaking
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.