Abstract
Transition-metal chalcogenides host various phases of matter, such as charge-density wave (CDW), superconductors, and topological insulators or semimetals. Superconductivity and its competition with CDW in low-dimensional compounds have attracted much interest and stimulated considerable research. Here we report pressure induced superconductivity in a strong spin-orbit (SO) coupled quasi-one-dimensional (1D) transition-metal chalcogenide NbTe4, which is a CDW material under ambient pressure. With increasing pressure, the CDW transition temperature is gradually suppressed, and superconducting transition, which is fingerprinted by a steep resistivity drop, emerges at pressures above 12.4 GPa. Under pressure p = 69 GPa, zero resistance is detected with a transition temperature T c = 2.2 K and an upper critical field μ0Hc2 = 2 T. We also find large magnetoresistance (MR) up to 102% at low temperatures, which is a distinct feature differentiating NbTe4 from other conventional CDW materials.
Similar content being viewed by others
Introduction
Transition-metal chalcogenides possess rich structural chemistry and a wide variety of unusual physical properties1,2,3. The latter includes, for instance, charge density wave (CDW)3, superconductivity4,5,6,7 and recently reported extremely large magnetoresistance in WTe28,9,10,11,12,13. Among chalcogenides, tellurides are usually different from sulfides and selenides in crystal structures, electronic structures and physical properties, due to the diffusive nature of the tellurium valence orbitals14 and thus more covalent character of tellurium1. While sulfides and selenides, such as NbS2, NbSe2 and NbSe3, were intensively studied in the context of CDW and/or superconductivity3,4,15, tellurides have not received much attention until recently8,9,10,11,12,13. One import feature of tellurides is that the atomic number of Te is very large, resulting in a strong spin-orbital (SO) coupling. Nowadays, topological materials with strong SO coupling have been drawing plenty of attention in condensed matter physics16. It is highly desirable to discover noval superconductors with strong SO coupling for understanding the nature of topological superconductivity. On the other hand, low dimensionality is accompanied by strong lattice instability. Additional interest for pursuing a quasi-1D material with itinerant electrons comes from the possible realization of Luttinger liquid, in which an exotic spin-charge separation is expected17. Thus, it should be of great interest to study superconductivity in quasi-1D tellurides with large atomic number14,18, where competing interactions might give rise to interacting ground states.
The magnetoresistance (MR) in ordinary non-magnetic metals is a relatively weak effect and usually at the level of a few percent19,20. Materials exhibiting large MR are not only utilized to enlarge the sensitivity of read/write heads of magnetic storage devices, e.g., magnetic memory21 and hard drives22, but also stimulating many fundamental researches8,23. Typically, large negative MR occurs in thin-film metals24, manganese based perovskites25,26 and some disordered systems27,28, while large positive MR has been observed in semiconductors29 and semimetals8,30. In general, there exists only a few of CDW materials, which show large positive MR31,32,33. The origin of the huge positive MR effect in the CDW state is still under debate. Exploring more CDW materials with large MR may help to clarify the controversial explanations.
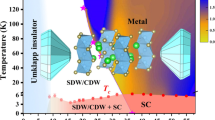
NbTe4 and TaTe4 belong to the same group of quasi-1D CDW materials (space group P4/mcc). The structure of NbTe4 was first determined by Selte and Kjekshus in 196434. The metal atoms Nb form linear chains along the tetragonal c-axis and the Te atoms form square antiprismatic formulae in which the metal atoms confined (Fig. 1(a,b)). Superlattice reflections indicate that the a-axis is doubled and the c-axis is tripled, leading to an enlarged unit cell 2a* × 2a* × 3c* 34,35. NbTe4 undergoes a strong lattice distortion around room temperature to form an incommensurate charge density wave (CDW) phase35,36,37. The resulting CDW superstructure in NbTe4 was visualized by scanning tunneling microscopy (STM)37. Intriguingly, the CDW ordering in NbTe4 is highly anisotropic due to the quasi-1D chain structure. Strikingly, there exist three CDW orders in NbTe4, two are incommensurate with wave vectors \({\overrightarrow{q}}_{1}\) = (0, 0, 0.311c*) and \({\overrightarrow{q}}_{2}\) = (0.5a*, 0.5b*, 0.344c*), respectively, and the third is commensurate with \({\overrightarrow{q}}_{3}\) = (0.5a*, 0, \(\frac{1}{3}\)c*)35. The crystal structure of NbTe4 is depicted in Fig. 1(a,b). The displacements of Nb ion in a single column for the commensurate phase are shown in Fig. 1c, which can also be found in previous literature38. Indeed, NbTe4 and TaTe4 are the only two reported crystals in which three CDWs coexist35. In this paper, we report large magneto-resistance and high pressure induced superconductivity in NbTe4. The CDW transition temperature is strongly suppressed by applied pressure, and superconductivity fingerprint of steep resistivity drop emerges when pressure exceeds 12.4 GPa. Under pressure p = 69 GPa, zero resistance is reached with a transition temperature T c = 2.2 K and an upper critical field of 2 T. We also observed large magnetoresistance (MR) up to 102% at low temperatures in NbTe4, which is rarely observed in conventional CDW systems.
Structural characterization by x-ray diffractions for NbTe4. (a,b) The basic crystal structure of NbTe4 projected along the [010] (a) and [001] (b) directions. (c) The red solid circles represent equidistant Nb ions on the axis of a single column of the basic structure; the arrows show the displacements and resultant trimerizations of the Nb ions in the commensurate phase. (d) XRD structure characterization of a NbTe4 single crystal. Only (0 l 0) peaks can be observed. The inset: The enlarged XRD curve of (030) peak. (e) A typical crystal of NbTe4, with crystallographic directions marked.
Results and Discussions
Figure 1d displays the X-ray diffraction pattern of NbTe4 single crystal. Only multiple reflections of the (0 l 0) planes can be detected, consistent with the quasi-one-dimensional crystal structure depicted in Fig. 1(a,b). The interplane spacing is determined to be 6.499 \({\rm{\AA }}\), agreeing with the previous reported value of the NbTe4 phase34. For the (030) peak, the full width at half-maximum is only 0.03°, indicating high quality of the crystals.
The temperature dependence of resistivity under various applied magnetic fields (μ0H up to 15 T) is summarized in Fig. 2a. In zero field, the room temperature resistivity is 59.2 \(\mu {\rm{\Omega }}\cdot {\rm{cm}}\) and decreases to 9.4 \(\mu {\rm{\Omega }}\cdot {\rm{cm}}\) at T = 2 K, yielding a residual resistivity ratio (RRR) of 6.3. Low RRR in NbTe4 single crystals has been commonly reported, which is irrespective of growth conditions39,40. To understand the origin of the poor RRR, we performed the measurements of energy dispersive X-ray spectroscopy (EDXS). The chemical composition determined by EDXS gives the atomic ratio Nb:Te = 0.8:4, with a measurement error of ±3.5% depending on the elements measured. This result indicates that there exists significant deficiency for Nb, which may be responsible for the poor RRR. To get further insight into the resistivity data, we take the partial derivative of resistivity with respect to temperature, as shown in the inset of Fig. 2a. At T* = 200 K a cusp is observed, consistent with the previous reports39,40. It is known that the two incommensurate superlattices with \({\overrightarrow{q}}_{1}\) = (0, 0,0.311c*) and \({\overrightarrow{q}}_{2}\) = (0.5a*, 0.5b*, 0.344c*) are stable at room temperature in NbTe4. Below room temperature, additional superlattice ordering with \({\overrightarrow{q}}_{3}\) = (0.5a*, 0, \(\frac{1}{3}\)c*) ermerges at about 200 K. The change of the slope in the temperature dependence of resistivity at 200 K should be due to the appearance of the \({\overrightarrow{q}}_{3}\) superlattice39,40. Usually, more drastic anomalies in resistivity should be observed at the CDW transition temperatures. For example, two sharp increases in resistivity were observed in NbSe3 at 145 and 59 K15, corresponding to about 20% and 48% of conduction electrons condensating into the CDW states, respectively15,33. The observed small change of resistivity around 200 K in NbTe4 is indicative of a finite but slight decrease of free carrier density associated with the reconstruction of the Fermi surface by Brillouin zone refolding. The anomaly at around T L = 50 K may be due to the lock-in transition into the 2a* × 2a* × 3c* superstructure, which is worthy of further clarification40. The anomies at T* = 200 K and T L = 50 K, which were also observed in previous reports39,40, further confirm the CDW features observed in NbTe4.
Transport properties of NbTe4 at ambient pressure. (a) Plots of resistivity against temperature under μ0H = 0, 5, 10, and 15 T. The current is along the c-axis, and the field is along the b-axis. Inset: Plots of dρ/dT versus temperature. (b) Field dependence of \({\rm{MR}}=[\rho (H)-\rho \mathrm{(0)]/}\rho \mathrm{(0)}\) under various temperatures.
The field (H//b) dependence of resistance (I//c) at various temperatures is shown in Fig. 2b. The magneto-resistance (MR), which is defined as \({\rm{MR}}=[\rho \mathrm{(15}T)-\rho \mathrm{(0)]/}\rho \mathrm{(0)}\), rises up to 102% under a magnetic field of 15 T at T = 2 K. Although the MR value of NbTe4 is orders of magnitude smaller than that of WTe28 and Bi30, it is much larger than that of a usual single-band weakly interacting electron system, in which the MR is usually at the level of a few percent8,20. For a single-band noninteracting electron system, the Hall field exactly balances the Lorentz force, and the electron moves as if in zero field without being deflected; thus, there is no remarkable magnetoresistance20,41.
Figure 3 displays the field (H//b) dependence of Hall resistivity (I//c) ρ yx at various temperatures. At 2 K, ρ yx is positive under low fields but switches to negative sign in higher fields. With increasing temperature, the required field where ρ yx changes its sign decreases. The curvature and sign reversal in the Hall resistivity indicate the coexistence of hole-type minority carriers with high mobility and electron-type majority carriers with low mobility42,43. The multiband nature of NbTe4 is also manifested in the breakdown of the Kohler’s rule, as plotted in the inset of Fig. 3. According to the Kohler’s rule, if only one relaxation time τ exists in metals, then MR can be characterized by a function of \({\mu }_{0}H/\rho \mathrm{(0)}\), and the results for different temperatures should collapse into a single curve41,44. As shown clearly in the inset of Fig. 3, the Kohler’s rule is violated in NbTe4, as evident by the non-overlapping of the MR curves at different temperatures. The observeation indicates more than one relaxation time τ exist, supporting the multiband result obtained by the Hall measurements.
Materials exhibiting a large magneto-resistance have potential device applications and thus have been attracting researchers’ interest45. The most well-known examples are the giant magnetoresistance in magnetic multilayers24 and colossal magnetoresistance in manganites26, both of them rely on the coupling between spin configuration and charge transport. However, even among nonmagnetic materials, extremely large magnetoresistance (MR) may arise in semimetals with electron-hole Fermi surface (FS) compensation46,47,48,49.
As a discussion of the multiband effects in NbTe4, we define the direction of the current (Hall voltage) as the x-axis (y-axis). Even though no net current should exist in the y-direction, the currents in the y-direction by one particular type of carriers may be non-zero in a multiband system. When we applied magnetic field, the y-direction currents should be affected by the Lorentz force which is antiparallel to the x-direction50. The back flow of carriers provides a substantial source of the large magnetoresistance in metals with multiple bands like MgB241 and semimetals like Bi48 and WTe28. Owing to the coexistence of both electron- and hole-type carriers, the large MR in NbTe4 may be attributed to multiband effects. We employed a two band mode to fit the ρ xx and ρ yx data simultaneously in the low field region (See supplementary material for a simultaneous fitting of ρ xx and ρ xx data by the two band semiclassical model). The values of n e and n h are close to each other at all the measured temperatures, which suggests that the large MR should result from the electron-hole compensation effect. The mobilities μ e and μ h increase with decreasing temperatures as the usual metals. Meanwhile, the carrier concentrations decrease significantly at low temperatures, which occurs commonly in a CDW system. At T = 2 K, μ e is 0.22 m2V−1s−1, while μ h is 0.29 m2V−1s−1. Actually large magnetoresistance was also observed in the CDW materials NbSe331,33 and AMo6O17 (A = Na, K, and Tl)32. It has been proposed that the large MR in these CDW systems may result from the magnetic-field-induced enhancement of the CDW gap31, but a study by Tritt et al.51 presented negative results on such a claim. Until now, the nature of the huge positive MR effect in the CDW state is still ambiguous. Actually, only a few CDW materials show large positive MR31,32,33. The origin of the large MR in NbTe4 deserves further investigation.
Superconductivity often occurs in the proximity of other competing ordered states. Both high-T c cuprates and Fe-based superconductors are close to antiferromagnetic (AFM) ordered states52,53. The AFM order in Fe-based superconductor is of a spin density wave (SDW)-type. For CDW materials, high pressure or chemical doping can continuously suppress the CDW order, and then superconducting transition temperature is enhanced or superconducting state emerges after the suppression of CDW state54,55. The weakening of competing orders normally favors superconductivity56. The CDW order of NbTe4 survives up to very high temperatures. Thus it is interesting to investigate whether superconductivity can be induced by pressure.
Figure 4a shows the evolution of resistance (I//c) as a function of temperature of the NbTe4 single crystal at various pressures from 5 GPa to 69 GPa. The samples used in high pressure and ambient pressure measurements are two different ones, but they are from the same batch. Under an applied pressure of p = 5 GPa, the cusp associated with the appearance of the \({\overrightarrow{q}}_{3}\)-superlattice CDW transition is suppressed to T* = 173 K, as shown in Fig. 4b. The MR decreases to less than 10% with an applied pressure of 5 GPa, and becomes smaller and smaller with an increasing pressure, as shown in Fig. 4c. When the pressure increases up to 12.4 GPa, the cusp associated with the CDW transition is suppressed and becomes too weak to be distinguished in the resistivity curve, instead, a sudden resistivity decrease presents at T~2.4 K, which could be a fingerprint of superconductivity. So we keep increasing the pressure to trace the superconducting transition. Upon further increasing pressure, at T = 1.7 K, which is the base temperature of our high pressure measurement system, the resistance drops to very small. Finally, under p = 69 GPa, which is the highest pressure we can apply, zero resistance has been detected. The low-T resistance appears to increase monotonically with pressure. In contrast, the room-temperature resistance keeps increasing up to 12.4 GPa, and then steadily decreases, which coincides with the disappearance of the CDW phase. Whether the variation in room-temperature resistance is correlated with the CDW order deserves further clarification. T c around 2.2 K is stabilized for the pressure range from 10 to 69 GPa. Such a wide stabilization pressure range could be a result of heavy doping due to Nb deficiency up to 0.2. Figure 4d shows the suppression of superconductivity under magnetic fields (H//b). The inset gives the temperature dependence of the upper critical field \({\mu }_{0}{H}_{c2}(T)\), determined by using 90% normal state resistivity criterion. The temperature dependence of \({\mu }_{0}{H}_{c2}(T)\) is nearly linear in the investigated temperature range. According to the Ginzburg-Landau theory, the upper critical field Hc2 evolves with temperature following the formula \({H}_{c2}(T)={H}_{c2}\mathrm{(0)}(1-{t}^{2})/(1+{t}^{2})\), where t is the renormalized temperature T/T c . It is found that the experimental upper critical field \({\mu }_{0}{H}_{c2}(T)\) can be well fitted by this model and its zero-temperature limit is extracted to be 2.0 T. Due to the limited temperature range, the estimated \({\mu }_{0}{H}_{c2}\mathrm{(0)}\) by this way may be of considerable error.
Transport properties for single crystal NbTe4 under pressure. (a) The plot of resistance versus temperature for the pressure ranging from 5 GPa to 69 GPa. The current is along the c-axis. The inset: The enlarged plot of resistance at low temperatures under p = 12.4 GPa. (b) Plots of d R/d T versus temperature under p = 5 GPa. (c) Field dependence of MR under p = 0, 5 and 7 GPa. (d) Temperature dependence of resistance for several different magnetic fields under p = 69 GPa. The inset displays the upper critical fields as a function of temperatures.
The temperature-pressure phase diagram is summarized in Fig. 5. The CDW transition temperature in NbTe4 is strongly suppressed with an applied high pressure. Accompanying the suppression of the CDW order, superconductivity fingerprint appears. Such superconducting phase diagrams, where superconductivity may compete with different kind of orders, have been observed in many systems, including high-T c cuprates, Fe-based superconductors, NbSe2 and Cu x TiSe252,53,54,55. Barath et al. proposed that the superconducting paring mechanism in Cu x TiSe2 could be associated with the quantum criticality, stemming from the fluctuations of CDW order57. There are also many theoretical works on the superconducting dome in transition metal dichalcogenides (TMDCs), and pursuing the nature of the observed superconducting states is still on-going58,59. High temperature high pressure treatment could induce phase transformation in NbTe460, which may be relevant to the occurrence of superconductivity. Further investigation on this issue is of potential interest. Since the physical properties of NbTe4 and TaTe4 show numerous similar features, the further research on pressure effect of TaTe4 should be gainful61. As a low dimensional chalcogenide, it could be fascinating to explore whether intercalation or doping could induce superconductivity, or at least decrease the critical superconducting pressure, as the case in Cu x TiSe257, Cu x Bi2Se362, Ir1−x Pd x Te216, (NbSe4)3.33I63. Primarily because of the strong SO coupling, the appealing Majorana surface state has been suggested to exist in Cu x Bi2Se3 superconductor62,64. Due to the large atom number in NbTe4, it is expected to own strong SO coupling. Furthermore, a recent theoretical work has proposed monolayer hole-doped TMDCs as candidates for topological superconductors65, which makes transition metal chalcogenide systems more fascinating. Thus it becomes quite interesting to explore the possible presence of nonconventional quantum states in NbTe4. Our work may provide another promising system for exploring novel topological superconductors.
Summary
In conclusion, we discovered unusually large magnetoresistance(MR) and pressure induced superconductivity with a maximum T c of 2.2 K in a quasi-one-dimensional (1D) transition-metal chalcogenide NbTe4 with strong spin-orbit coupling. Superconductivity appears when the CDW order is suppressed by high pressure. Although T c is relatively low, the large MR and strong SO coupling make NbTe4 a promising candidate for the exploration of novel superconductors.
Methods
Sample synthesis and characterization
The NbTe4 crystals were grown by a self-flux method. Powders of the elements Nb (99.97%) and Te (99.99%), all from Alfa Aesar, in an atomic ratio of Nb:Te = 1:8 were thoroughly mixed together, loaded, and sealed into an evacuated quartz ampule. The ampule was slowly heated up to 1273 K and held for 25 h. After that, it was slowly cooled to 873 K at a rate of 3 K/h, followed by furnace cooling down to room temperature. Shiny, gray-black soft crystals in flattened needle shapes were harvested with a typical dimension of 1.2 × 0.02 × 0.02 mm3, as shown in Fig. 1(e). Single crystal X-ray diffraction (XRD) was performed at room temperature using a PANalytical X-ray diffractometer (Model EMPYREAN) with a monochromatic CuKα1 radiation. Energy-dispersive x-ray spectroscopy (EDXS) was collected by an Octane Plus Detector (AMETEX EDAX), equipped in a field-emitting scanning electron microscope (SEM, Hitachi S-4800).
Measurements
The resistance data was collected using standard four-probe method in a screw-pressure-type diamond anvil cell (DAC), which is made of non-magnetic Cu-Be alloy. The diamond culet was about 300 μm in diameter. A T301 stainless steel gasket was pre-indented from a thickness of 250 μm to 35 μm, leaving a pit inside the gasket. A hole with diameter of 300 μm was drilled in the center of the pit by laser ablation. The pit of the indented gasket was then covered with a mixture of epoxy and fine cubic boron nitride (c-BN) powder and compressed tightly to insulate the electrode leads from the metallic gasket. Next, the c-BN-covered pit served as the sample chamber, where a NbTe4 single crystal in dimension of 200 μm × 35 μm × 5 μm was inserted without the pressure-transmitting medium, together with a ruby ball served as a pressure marker at the top of the sample. The value of the pressure was determined by the ruby fluorescence method. Platinum (Pt) foil with a thickness of 5 μm was used as electrodes. The gasket surface outside the pit was insulated from the electrode leads by a layer of Scotch tape. The DAC was put inside a home-made multifunctional measurement system (1.8–300 K, JANIS Research Company Inc.; 0–9 T, Cryomagnetics Inc.) with helium (He) as the medium for heat conduction to obtain high efficiency of heat transfer and good precision of temperature control. Two Cernox resistors (CX-1050-CU-HT-1.4 L) located near the DAC were employed to ensure the accuracy of temperature in the presence of magnetic field. The ambient-pressure electrical transport measurements were carried out in a Oxford cryostat system with magnetic field up to 15 T and temperature down to 1.5 K. Ohmic contacts were made with gold wires and silver paste.
References
Mar, A., Jobic, S. & Ibers, J. A. Metal-Metal vs Tellurium-Tellurium Bonding in WTe2 and Its Ternary Variants TaIrTe4 and NbIrTe4. J. Am. Chem. Soc. 114, 8963–8971 (1992).
Monceau, P. Electronic crystals: an experimental overview. Adv. Phys. 61, 325–581 (2012).
Moncton, D. E., Axe, J. D. & DiSalvo, F. J. Neutron scattering study of the charge-density wave transitions in 2H-TaSe2 and 2H-NbSe2. Phys. Rev. B 16, 801–819 (1977).
Morris, R. C., Coleman, R. V. & Bhandari, R. Superconductivity and magnetoresistance in NbSe2. Phys. Rev. B 5, 895–901 (1972).
Gamble, F. R. et al. Superconductivity in Layered Structure Organometallic Crystals. Science 168, 568–570 (1970).
Pan, X. C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
Kang, D. et al. Superconductivity emerging from a suppressed large magnetoresistant state in tungsten ditelluride. Nat. Commun. 6, 7804 (2015).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2. Nature 514, 205–208 (2014).
Cai, P. L. et al. Drastic pressure effect on the extremely large magnetoresistance in WTe2: quantum oscillation study. Phys. Rev. Lett. 115, 057202 (2015).
Zhu, Z. et al. Quantum Oscillations, Thermoelectric Coefficients, and the Fermi Surface of Semimetallic WTe2. Phys. Rev. Lett. 114, 176601 (2015).
Jiang, J. et al. Signature of Strong Spin-Orbital Coupling in the Large Nonsaturating Magnetoresistance Material WTe2. Phys. Rev. Lett. 115, 166601 (2015).
Zhao, Y. et al. Anisotropic magnetotransport and exotic longitudinal linear magnetoresistance in WTe2 crystals. Phys. Rev. B 92, 041104(R) (2015).
Pletikosić, I. et al. Electronic Structure Basis for the Extraordinary Magnetoresistance in WTe2. Phys. Rev. Lett. 113, 216601 (2014).
Jiao, W. H. et al. Superconductivity in a Layered Ta4Pd3Te16 with PdTe2 Chains. J. Am. Chem. Soc. 136, 1284–1287 (2014).
Ong, N. P. & Monceau, P. Anomalous transport properties of a linear-chain metal: NbSe3. Phys. Rev. B 16, 3443–3455 (1977).
Yang, J. J. et al. Charge-Orbital Density Wave and Superconductivity in the Strong Spin-Orbit Coupled IrTe2:Pd. Phys. Rev. Lett. 108, 116402 (2012).
Voit, J. One-Dimensional Fermi Liquids. Rep. Prog. Phys. 58, 977 (1995).
Bao, J. K. et al. Superconductivity in Quasi-One-Dimensional K2Cr3As3 with Significant Electron Correlations. Phys. Rev. X 5, 011013 (2015).
Lin, X. et al. Superconductivity induced by La doping in Sr1−xLa x FBiS2. Phys. Rev. B 87, 020504(R) (2013).
Pippard, A. B. Magnetoresistance in Metals (Cambridge University, Cambridge, 1989).
Moritomo, Y. et al. Giant magnetoresistance of manganese oxideswith a layeredperovskite structure. Nature 380, 141–144 (1996).
Daughton, J. M. GMR applications. J. Magn. Magn. Mater. 192, 334–342 (1999).
Urushibara, A. et al. Insulator-metal transition and giant magnetoresistance in La1-xSr x MnO3. Phys. Rev. B 51, 14103–14109 (1995).
Egelhoff, W. F. et al. Magnetoresistance values exceeding 21% in symmetric spin valves. J. Appl. Phys. 78, 273–277 (1995).
Ramirez, A. P., Cava, R. J. & Krajewski, J. Colossal magnetoresistance in Cr-based chalcogenide spinels. Nature 386, 156–159 (1997).
Jin, S. et al. Colossal magnetoresistance in La-Ca-Mn-O ferromagnetic thin films. J. Appl. Phys. 76, 6929–6933 (1994).
Yang, X. et al. Sr0.9K0.1Zn1.8Mn0.2As2: A ferromagnetic semiconductor with colossal magnetoresistance. EPL 107, 67007 (2014).
Yang, X. et al. K and Mn co-doped BaCd2As2: A hexagonal structured bulk diluted magnetic semiconductor with large magnetoresistance. J. Appl. Phys. 114, 223905 (2013).
Xu, R. et al. Large magnetoresistance in non-magnetic silver chalcogenides. Nature 390, 57–60 (1997).
Alers, P. B. & Webber, R. T. The magnetoresistance of bismuth crystals at low temperatures. Phys. Rev. 91, 1060–1065 (1953).
Yasuzuka, S. et al. Pressure effect on large magnetoresistance in the lower charge-density-wave transition of NbSe3. Phys. Rev. B 60, 4406–4409 (1999).
Tian, M., Yue, S. & Zhang, Y. Magnetoresistance of quasi-two-dimensional purple bronzes Amo6O17 (A = Na, K, and Tl). Phys. Rev. B 65, 104421 (2002).
Shen, J. Q. et al. The magnetoresistance of the quasi-one-dimensional conductor NbSe3. J. Phys.: Condens. Matter 15, 5353–5358 (2003).
Selte, K. & Kjekshus, A. On the Crystal Structure of NbTe4. Acta Chem. Scand. 18, 690–696 (1964).
Boswell, F. W., Prodan, A. & Brandon, J. K. Charge-density waves in the quasi-one-dimensional compounds NbTe4 and TaTe4. J. Phys. C: Solid State Phys. 16, 1067–1076 (1983).
Mahy, J., Landuyt, J. V. & Amelinckx, S. Electron Diffraction Evidence for Superstructures in TaTe4 and NbTe4. Phys. Status Solidi A 77, K1 (1983).
Prodan, A. et al. Scanning tunneling microscope study of charge-density-wave modulations in NbTe4. Phys. Rev. B 57, 6235–6238 (1998).
Walker, M. B. & Morelli, R. NbTe4: A model for a class of incommensurate-to-incommensurate phase transitions. Phys. Rev. B 38, 4836–4839 (1988).
Ikari, T., Berger, H. & Levy, F. Electrical Properties of NbTe4 and TaTe4. Phys. Stat. Sol. (b) 139, K37–K40 (1987).
Tadaki, S. et al. Electrical properties of NbTe4 and TaTe4. Synthetic Metals 38, 227–234 (1990).
Li, Q. et al. Large Anisotropic Normal-State Magnetoresistance in Clean MgB2 Thin Films. Phys. Rev. Lett. 96, 167003 (2006).
Luo, Y. et al. Pressure-enhanced superconductivity in Eu3Bi2S4F4. Phys. Rev. B 90, 220510(R) (2014).
Wang, K. et al. Anisotropic giant magnetoresistance in NbSb2. Sci. Rep. 4, 7328 (2014).
Ziman, J. M. Electrons and Phononss, Classics Series (Oxford University Press, New York, 2001).
Takatsu, H. et al. Extremely Large Magnetoresistance in the Nonmagnetic Metal PdCoO2. Phys. Rev. Lett. 111, 056601 (2013).
Yang, F. Y. et al. Large Magnetoresistance of Electrodeposited Single-Crystal Bismuth Thin Films. Science 284, 1335–1337 (1999).
Yang, X. et al. Giant linear magneto-resistance in nonmagnetic PtBi2. Appl. Phys. Lett. 108, 252401 (2016).
Du, X. et al. Metal-Insulator-Like Behavior in Semimetallic Bismuth and Graphite. Phys. Rev. Lett. 94, 166601 (2005).
Kasahara, Y. et al. Exotic Superconducting Properties in the Electron-Hole-Compensated Heavy-Fermion “Semimetal” URu2Si2. Phys. Rev. Lett. 99, 116402 (2007).
Singleton, J. Band Theory and Electronic Properties of Solids. (Oxford University Press, 2001).
Tritt, T. M. et al. Charge-Density-Wave Carrier Concentration in NbSe3 as a Function of Magnetic Field and Temperature. Phys. Rev. Lett. 61, 1776 (1988).
Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xF x FeAs systems. Nature 453, 899–902 (2008).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Morosan, E. et al. Superconductivity in Cu x TiSe2. Nat. Phys. 2, 544–550 (2006).
Morris, R. C. Connection between charge-density waves and superconductivity in NbSe2. Phys. Rev. Lett. 34, 1164–1166 (1975).
Regueiro, M. N., Mignot, J. M. & Castello, D. Superconductivity at High Pressure in NbSe3. EPL 18, 53–57 (1992).
Barath, H. et al. Quantum and Classical Mode Softening Near the Charge-Density-Wave-Superconductor Transition of Cu x TiSe2. Phys. Rev. Lett. 100, 106402 (2008).
Das, T. & Dolui, K. Superconducting dome in MoS2 and TiSe2 generated by quasiparticle-phonon coupling. Phys. Rev. B 91, 094510 (2015).
Rösner, M., Haas, S. & Wehling, T. O. Phase diagram of electron-doped dichalcogenides. Phys. Rev. B 90, 245105 (2014).
Bjerkelund, E., Kjekshus, A. & Meisalo, V. High Pressure Induced Transformations in NbTe4 and TaTe4. Acta. Chem. Scand. 22, 3336 (1968).
Luo, X. et al. Resistivity plateau and large magnetoresistance in the charge density wave system TaTe4. Appl. Phys. Lett. 110, 092401 (2017).
Hor, Y. S. et al. Superconductivity in Cu x Bi2Se3 and its Implications for Pairing in the Undoped Topological Insulator. Phys. Rev. Lett. 104, 057001 (2010).
Wang, Z. Z. et al. Charge density transport in a novel halogened transition metal tetrachalcogenide (NbSe4)3.33I. Solid State Commun. 47, 439–443 (1983).
Fu, L. & Berg, E. Odd-Parity Topological Superconductors: Theory and Application to Cu x Bi2Se3. Phys. Rev. Lett. 105, 097001 (2010).
Hsu, Y. et al. Topological superconductivity in monolayer transition metal dichalcogenides. Nat. Commun. 8, 14985 (2017).
Acknowledgements
We thank Yi Zheng and Guanghan Cao for valuable discussions and helpful suggestions. This work is supported by the Ministry of Science and Technology of China (Grant No. 2016YFA0300402 and 2016YFA0401804), NSF of China (Contract Nos. U1332209, 11574323, and U1632275). X. C. thanks for the support from the Natural Science Foundation of Anhui Province (1708085QA19).
Author information
Authors and Affiliations
Contributions
Zhu-an Xu and Xiaojun Yang designed the research. Zhu-an Xu administered the experiment. Xiaojun Yang synthesized the samples. Xiaojun Yang and Yonghui Zhou performed the measurements. Mengmeng Wang, Hua Bai, Xuliang Chen, Chao An, Ying Zhou, Qian Chen, Yupeng Li, Zhen Wang, Jian Chen, Chao Cao, Yuke Li, Yi Zhou and Zhaorong Yang presented helpful suggestions in the measurements and in the data analysis. Zhu-an Xu, Xiaojun Yang and Zhaorong Yang analyzed the data, interpreted the results, and wrote the paper.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, X., Zhou, Y., Wang, M. et al. Pressure induced superconductivity bordering a charge-density-wave state in NbTe4 with strong spin-orbit coupling. Sci Rep 8, 6298 (2018). https://doi.org/10.1038/s41598-018-24572-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-24572-z
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.