Abstract
Solid solutions of Zr(Mo,W)2O7(OH,Cl)2∙2H2O with a preset ratio of components were prepared by a hydrothermal method. The chemical composition of the solutions was determined by energy dispersive X-ray spectroscopy (EDX). For all the samples of ZrMoxW2−xO7(OH,Cl)2∙2H2O (x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0), TGA and in situ powder X-ray diffraction (PXRD) studies (300–1100 K) were conducted. For each case, the boundaries of the transformations were determined: Zr(Mo,W)2O7(OH,Cl)2∙2H2O → orthorhombic-ZrMoxW2−xO8 (425–525 K), orthorhombic-ZrMoxW2−xO8 → cubic-ZrMoxW2−xO8 (700–850 K), cubic-ZrMoxW2−xO8 → trigonal-ZrMoxW2−xO8 (800–1050 K for x > 1) and cubic-ZrMoxW2−xO8 → oxides (1000–1075 K for x ≤ 1). The cell parameters of the disordered cubic-ZrMoxW2−xO8 (space group Pa-3) were measured within 300–900 K, and the thermal expansion coefficients were calculated: −3.5∙10−6 – −4.5∙10−6 K−1. For the ordered ZrMo1.8W0.2O8 (space group P213), a negative thermal expansion (NTE) coefficient −9.6∙10−6 K−1 (300-400 K) was calculated. Orthorhombic-ZrW2O8 is formed upon the decomposition of ZrW2O7(OH,Cl)2∙2H2O within 500–800 K.
Similar content being viewed by others
Introduction
Both applied material science and academic research fields are interested in substances with negative thermal expansion (NTE)1,2,3,4. Due to its unique behaviour, ZrMoxW2−xO8 is an advanced filler material used to produce composites with controlled expansion. The main advantage of the family of cubic-ZrMoxW2−xO8 materials over other materials is their large isotropic NTE over a wide temperature range. The most famous and well-studied ZrW2O8 has an NTE coefficient of −8.8∙10−6 K−1 for oxygen-ordered cubic α-ZrW2O8 from 0.3 K to 430 K and −4.8∙10−6 K−1 for dynamically disordered cubic β-ZrW2O8 from 430 K to 1050 K5. Cubic γ-ZrMo2O8 is isostructural to cubic β-ZrW2O8, and it has an NTE coefficient of −5.0∙10-6 K−1 from 11 to 573 K, as reported in ref.6. Simon Allen and J.S.O. Evans made precise measurements of the NTE coefficient of γ-ZrMo2O8: −6.9∙10−6 K−1 from 2 to 200 K and −5.0∙10−6 K−1 from 250 to 502 K7.
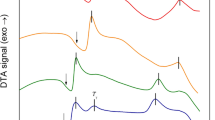
This material can be obtained by dehydration and topotactic recrystallization from a hydrated precursor, ZrMoxW2−x(OH,Cl)2∙2H2O8. According to the thermogravimetric results presented by us in a previous paper9, the thermal decomposition of the precursor ZrW2O7(OH,Cl)2∙2H2O starts at 500 K and results in the appearance of an amorphous intermediate, which crystallizes as cubic β-ZrW2O8 above 850 K. The strong exothermic effect at 1100 K is related to the decomposition of cubic β-ZrW2O8 into oxides. The transformation of cubic α-ZrW2O8 into cubic β-ZrW2O8 is not registered by differential thermal analysis (DTA).
The DTA curve for ZrMoxW2−xO7(OH,Cl)2∙2H2O showed the expected endothermic peak, corresponding to the weight loss and formation of the orthorhombic phase of β-ZrMo2O8, while the two exothermic peaks at 700 and 800 K can be assigned to the crystallization of the cubic γ-ZrMo2O8 and trigonal α−ZrMo2O8 phases, respectively10.
The solid solutions of ZrW2−xMoxO8 (with different values of “x”) have been prepared by a number of scientific groups7,8,11,12,13,14. A significant number of solid solutions of the precursor ZrMoxW2−xO7(OH)2∙2H2O was prepared by Ling Huang and co-authors12. Cubic phases were obtained for x = 0.2, 0.4, 0.6, 0.7 and 0.8, but the NTE coefficients were not measured. Accurate measurement of the NTE coefficient for ZrMoxW2−xO8 (x = 1.0) was reported in work6. For the cubic, ordered phase, the NTE was −9.0∙10−6 K−1 from 2 to 200 K, and −5.5∙10−6 K−1 from 250 to 502 K for the disordered phase. Solid solutions of ZrMoxW2−xO8 (x = 0.4, 0.6, 0.7, 1.0 1.2, 1.4 and 1.5) were prepared by C. Closmann8. The phase composition was determined for all the samples after heating them to 723, 823, and 923 K and quenching. For one of these solutions (ZrMo0.4W1.6O8), the NTE coefficient was −11.8∙10−6 K−1 (273-298 K) and –7.4∙10−6 K−1 (383–473 K). The NTE coefficient –11.8∙10–6 K−1 is the largest known (in absolute value).
We assumed that one of the cubic-ZrMoxW2−xO8 solutions may have a larger coefficient than that previously determined. We carefully investigated the conditions for obtaining cubic-ZrMoxW2−xO8 (x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0) from precursors and measured their NTE coefficients.
Results and Discussion
Synthesis of the precursors and their characterization
We synthesized ZrMoxW2−xO7(OH,Cl)2∙2H2O by a hydrothermal method10. Stoichiometric amounts of Na2WO4•2H2O, Na2MoO4 and ZrOCl2•8H2O were placed in a flask with 2.3 M HCl (solid: liquid ~1: 10) and stirred for 30 minutes. The obtained reaction mixture was placed in an autoclave with a Teflon liner and heated at 450 K for 48 hours. After cooling, ZrMoxW2−xO7(OH,Cl)2∙2H2O was filtered, washed with water and dried at 380 K for 24 hours. Eleven samples were obtained. The colours of the powders of ZrMoxW2−xO7(OH,Cl)2∙2H2O changed from white to bluish as a function of the value of “x”.
The powders of ZrMoxW2−xO7(OH,Cl)2∙2H2O were examined by powder X-ray diffraction (Fig. 1) on a DRON-RM4 diffractometer (CuKα source, graphite monochromator at the diffracted beam, room temperature, 2θ range 5–60°). The experimental data were processed with the PowderCell program v.2.415, and the data from the powder structural database powder diffraction file (PDF) were used as the reference16. The EDX spectral analysis was performed using a Hitachi TM3030 desktop scanning electron microscope and the Quantax70 microanalysis system.
The PXRD data showed that all the samples were single phase. We performed an EDX investigation for all the prepared samples and found that the preset stoichiometry was retained in the products of the reaction within the experimental uncertainty. Determining the content of molybdenum and tungsten in ZrMoxW2−xO7(OH,Cl)2∙2H2O by the Zen-Retgers rule is extremely difficult because of the extreme similarity of the unit cell volumes (Table 1).
DTA and high-temperature PXRD of ZrMoxW2–xO7(OH,Cl)2∙2H2O
A thermal analysis was performed on an “STA 449 F1 Jupiter” in a platinum crucible under an oxygen–argon atmosphere (20% O2) in the temperature range 298–1073 K.
High-temperature experiments were carried with time-resolved diffractometry at channel 5b of the Siberian Synchrotron and Therahertz Radiation Centre17,18. The wavelength used was 1.516 A. The diffraction patterns were recorded by a one-coordinate detector (OD-3) developed in Budker Institute of Nuclear Physics of Siberian Branch Russian Academy of Sciences19. The exposure time for a frame was set to 1 minute. The samples were heated in air up to 1123 K at a rate of 10 K/min.
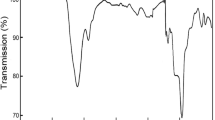
The behaviours of the ZrMoxW2−xO7(OH,Cl)2∙2H2O samples upon thermal decomposition are similar (Fig. 2a), but some features depend on the value of “x”. The decomposition of ZrMoxW2−xO7(OH,Cl)2∙2H2O begins at 450 K for x = 2 and increases linearly up to 500 K for x = 0. The first stage is accompanied by an endothermic effect and a weight loss (Fig. 3). The data from the high-temperature PXRD confirmed the following reaction:
We calculated the molar ratio of the chloride ion to the hydroxide ion (In all the samples, the ratio was approximately 1:3.) based on the loss of the mass, which was measured by DTA, as described in article9.
The diffraction peaks of ZrMoxW2−xO7(OH,Cl)2∙2H2O decreased to zero, and the diffraction pattern of orthorhombic-ZrMoxW2−xO8 appeared. The peaks of the formed orthorhombic-ZrMoxW2−xO8 had large widths, and the crystallite size was small, approximately 10–15 nm (The Scherer equation was used to calculate the crystallite sizes).
The crystallite sizes did not increase with the temperature in our experiments. Allen20 used a long heat treatment (8 hours at 573 K) to prepare good crystalline samples of orthorhombic-ZrMoxW2−xO8.
The second transformation did not have a weight loss and was accompanied by an exothermal effect. The temperatures of the transformation (650–800 K) had a complex dependence on the parameter “x” (Fig. 2a). We observed the appearance of the peaks of a nicely crystalline cubic-phase ZrMoxW2−xO8 in the powder pattern. The width of the synthetic “window” for single-phase, cubic ZrMoxW2−xO8 was not large: 70–200 K (x = 0–1.4) and 30–50 K (x = 1.4–2.0). Preparation of pure cubic, single-phase samples required accurate work. The precursor had to be heated to the minimal possible temperature (blue line on Fig. 2b) and held for 10–60 minutes (60 minutes for x = 0 and 10 minutes for x = 2).
Further heating led to the formation of trigonal ZrMoxW2−xO8 at 500–700 K (x = 1.2–2.0) or decomposition of the material into constituent oxides at 1050 K (x = 0–1.0) (Fig. 2b). In study14, it was found that the resulting products with x ≤ 0.5 would decompose to WO3/MoO3 and ZrO2 upon a temperature increase, while for x > 0.5, the cubic phase would transform into the trigonal phase. Shi Yongfang11 noted that the appearance of the trigonal phase occurs at relatively low temperatures, i.e., 861 K (x = 0.73) and 889 K (x = 0.53). This fact was confirmed in our work. Trace amounts of the trigonal phase were often present in all the PXRD patterns, while the cubic compound was the main phase. However, we did not observe the exothermal effect for the cubic-to-trigonal transformation for x = 0.2–0.8, 1.6, and 1.8 in the DTA experiments.
Trigonal ZrMoxW2−xO8 (x = 1.2–1.8) had a good thermal stability, and we found no evidence of its decomposition for x = 1.4, 1.6 and 1.8 under the conditions in our experiment. Trigonal ZrMoxW2−xO8 (x = 1.2) decomposed at 1150 K. However, trigonal ZrMo2O8 decayed into oxides with an exo-effect at 925 K.
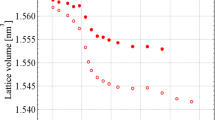
We should note that all the transformations of orthorhombic-cubic-trigonal-oxides are exothermic. This can be explained if all those phases (with the exception of the oxides) are metastable in our experimental temperature ranges. The transformations were accompanied by a decrease in the volume of the formula unit (V/Z), e.g., for x = 1.2 (Fig. 4):
Our data directly indicated the formation of a poorly crystalline orthorhombic phase (Pmn21) of zirconium tungstate (ZrW2O8) in the temperature range 550–825 K (Fig. 2).
NTE coefficient of cubic-ZrMoxW2−xO8
The thermal expansion of cubic-ZrMoxW2−xO8 was investigated using variable temperature PXRD. Diffraction data were measured using a Bruker D8 Advance diffractometer (CuKα radiation) with a parallel-beam geometry with Göbel Mirrors. In situ experiments were carried out using an Anton Paar XRK900 reaction chamber. The patterns were measured in the 2θ range from 10 to 70° with a step of 0.05° and a collection time of 3 s per point. The heating rate was 12 K/min. The acquisition of the X-ray patterns was started when the given temperature was reached. Sample cooling was immediately performed. The profile analysis and structural refinement by the LeBail method were performed using the TOPAS v.4.3 program21, and the data from the powder structural database PDF were used as the standards16. The lengths of the coherent scattering domain were calculated using LVol-IB values (i.e., volume weighted mean column height based on the integral breadth).
When measuring the NTE coefficient, it is important to realize which form of cubic ZrMoxW2−xO8 is being measured, i.e., ordered or disordered. For ZrW2O8, this transition is called α → β. In article13, the thermal effects for the transition (ordered → disordered) were measured, and a formula describing the temperature of the α → β transitions for cubic-ZrMoxW2−xO8 was proposed: T (K) = 432–168.45•x. We used it in our work to estimate whether the NTE coefficient belongs to the corresponding ordered or disordered form (Table 2). Of course, the dependence is not linear for x > 1; this is clearly visible when comparing the calculated and experimental values for x = 1.8 and 2.0 (Table 2).
We were able to obtain reliable data for the NTE coefficients for only the disordered phase, except for x = 1.8. The calculated coefficients have similar values (from −3.5∙10−6 K−1 to −4.5∙10−6 K−1) and almost did not differ from those of the “pure components”. Our value of the NTE coefficient, 3.5∙10−6 K−1, for x = 0.4 did not coincide with the value8 obtained earlier, −7.4∙10−6 K−1. Only for cubic ZrMo1.8W0.2O8 could the calculated NTE coefficient, −9.6∙10−6 K−1 (300−400 K), be attributed to the ordered cubic ZrMoxW2−xO8W2−xO8 (space group P213).
Conclusion
All the investigated phases of ZrMoxW2−xO7(OH,Cl)2∙2H2O and ZrMoxW2−xO8 are metastable at T < 1200 K and P(air) = 1 bar. All transformations that occur during heating are irreversible.
The precursors ZrMoxW2−xO7(OH,Cl)2∙2H2O (average size of individual particles 50 nm) with pre-determined chemical compositions can be obtained by a hydrothermal method.
Heating of the precursors up to T = 525–50•x K affords crystals of orthorhombic ZrMoxW2−xO8 (10–15 nm).
Cubic ZrMoxW2−xO8 solid solutions with a small crystal grain size (30–100 nm) can be obtained by thermal decomposition of the corresponding precursor or orthorhombic ZrMoxW2−xO8 at a temperature up to 850–900 K at x ≤ 1.8 and T = 2200–750•x K at x > 1.8.
Trigonal ZrMoxW2−xO8 (only for x > 1) can be prepared by heating the precursor or cubic ZrMoxW2−xO8 or orthorhombic ZrMoxW2−xO8 up to 850–1050 K, depending on the exact composition.
Solid solutions of cubic ZrMoxW2−xO8 in the ordered form have a higher coefficient of thermal expansion (CTE) in comparison to that of other materials, but they exist in a very limited and relatively low-temperature range, which limits their possible applications.
The disordered form of cubic ZrMoxW2−xO8 solid solutions does not have an advantage over that of the “pure components” in the value of CTE. The use of solid solutions is justified in the case when it is necessary to have a uniform CTE material for a certain temperature range (e.g., 250–800 K for x = 1.0).
References
Sleight, A. W. Compounds that contract on heating. Inorg. Chem. 37, 2854–2860 (1998).
Sleight, A. W. Negative thermal expansion materials. Curr. Opin. in Solid State and Mater. Sci. 3, 128–131 (1998).
Sleight, A. W. Isotropic negative thermal expansion. Annu. Rev. Mater. Sci. 28, 29–43 (1998).
Evans, J. S. O. Negative thermal expansion materials. J. Chem. Soc. Dalton Transactions 19, 3317–3326 (1999).
Mary, T. A., Evans, J. S. O., Vogt, T. & Sleight, A. W. Negative thermal expansion from 0.3 to 1050 Kelvin in ZrW2O8. Science 272, 90–92 (1996).
Lind, C., Wilkinson, A. P., Hu, Z., Short, S. & Jorgensen, J. D. Synthesis and properties of the negative thermal expansion material cubic ZrMo2O8. Chem. Mater. 10, 2335–2337 (1998).
Allen, S. & Evans, J. S. O. Negative thermal expansion and oxygen disorder in cubic ZrMo2O8. Phys. Rev. B: Condens. Matter. 68, 134101-1–134101-3 (2003).
Closmann, C., Sleight, A. W. & Haygarth, J. C. Low tempetetures Synthesis of ZrW2O8 and Mo-Substituted ZrW2O8. J. Solid State Chem. 139, 424–426 (1998).
Gubanov, A. I. et al. Some peculiarities of zirconium tungstate synthesis by thermal decomposition of hydrothermal precursors. Thermochim. Acta. 597, 19–26 (2014).
Lind, C., Wilkinson, A. P., Rawn, C. J. & Payzant, E. A. Preparation of the negative thermal expansion material cubic ZrMo2O8. J. Mater. Chem. 11, 3354–3359 (2001).
Shi, Y. et al. Phase transition behavior for ZrW2−xMoxO8 compositions at elevated temperatures. J. Solid State Chem. 182, 2030–2035 (2009).
Ling, H. et al. Phase Behaviors of the ZrW2−xMoxO8 (x = 0.2–2.0) System and the Preparation of an Mo‐Rich Cubic Phase. Eur. J. Inorg. Chem. 4521–4526 (2005).
Ahmad, Md. I., Lindley, K. & Akinc, M. Hydrothermal Synthesis of ZrW2−δMoδO8 (δ = 0–0.91) and its α → β Transformation. J. Am. Ceram. Soc. 94, 2619–2624 (2011).
Yang, J., Liu, Q., Sun, X., Xu, G. & Cheng, X. Synthesis of negative thermal expansion materials ZrW2−xMoxO8 (0 ≤ x ≤ 2) using hydrothermal method. Ceram. Int. 35, 441–445 (2009).
Kraus, W., Nolze. G. PowderCell 2.4, Рrogram for the representation and manipulation of crystal structures and calculation of the resulting X-ray powder patterns, Federal Institute for Materials Research and Testing. Berlin, Germany (2000).
ICDD PDF-2 Release 2014, Swarthmore: International Centre for Diffraction Data, PA, USA (2014).
Evdokov, O. V., Titov, V. M., Tolochko, B. P. & Sharafutdinov, M. R. In situ time-resolved diffractometry at SSTRC, Nucl. Instrum. Methods Phys. Res., Sect. A: Accelerators, Spectrometers, Detectors and Associated Equipment 603(1–2), 194–195 (2009).
Piminov, P. A. et al. Synchrotron Radiation Research and Application at VEPP-4. Physics Procedia 84, 19–26 (2016).
Aulchenko, V. M. et al. One-coordinate X-ray detector OD–3 M. Nucl. Instrum. Methods Phys. Res., Sect. A: Accelerators, Spectrometers Detectors and Associated Equipment 603, 76–79 (2009).
Allen, S., Warmingham, N. R., Gover, R. K. B. & Evans, J. S. O. Synthesis, Structure and Thermal Contraction of a New Low-Temperature Polymorph of ZrMo2O8. Chem. Matter. 15, 3406-1–3410 (2003).
TOPAS, version 4. 2., Bruker AXS Inc., Madison, Wisconsin, USA, (n.d.) (2009).
Acknowledgements
Diffraction patterns were obtained using the infrastructure of the Shared-Use Center “Siberian Synchrotron and Terahertz Radiation Center (SSTRC)” based on VEPP-3/VEPP-4 M/NovoFEL of BINP SB RAS. The authors are grateful to Professor V. Chernyshev (Moscow State University) for his help (#ma-3313 ESRF). The research is funded by the Tomsk Polytechnic University Competitiveness Enhancement Program grant, Project Number TPU CEP_IHTP_73\2017 and the grant of “BP plc” for a scientific team led by Gubanov Alexander Iridievich (without a number). The NIIC team thanks Federal Agency for Scientific Organizations for funding. The work is supported by the RFBR Grant 18-33-00493-mol_a (M.Yu. Petrushina).
Author information
Authors and Affiliations
Contributions
M.Y.P., E.S.D. and G.A.I. synthesized all samples; M.Y.P. and E.S.D. performed EDX experiments; M.Y.P., E.Y.F. and E.A.Z. performed PXRD experiments; P.E.P. performed DTA experiments; M.Y.P. and M.R.S. performed high-temperature PXRD experiments; M.Y.P., S.V.K., S.N.K., E.A.D. and G.A.I. analysed the data; M.Y.P., S.V.K., S.N.K. and G.A.I. designed the experiments; G.A.I. supervised the project; and all authors wrote the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Petrushina, M.Y., Dedova, E.S., Filatov, E.Y. et al. Preparation of Zr(Mo,W)2O8 with a larger negative thermal expansion by controlling the thermal decomposition of Zr(Mo,W)2(OH,Cl)2∙2H2O. Sci Rep 8, 5337 (2018). https://doi.org/10.1038/s41598-018-23529-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-23529-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.