Abstract
Absolute measurements of the radiolytic yield of Fe3+ in a ferrous sulphate dosimeter formulation (6 mM Fe2+), with a 20 keV x-ray monoenergetic beam, are reported. Dose-rate suppression of the radiolytic yield was observed at dose rates lower than and different in nature to those previously reported with x-rays. We present evidence that this effect is most likely to be due to recombination of free radicals radiolytically produced from water. The method used to make these measurements is also new and it provides radiolytic yields which are directly traceable to the SI standards system. The data presented provides new and exacting tests of radiation chemistry codes.
Similar content being viewed by others
Introduction
The accurate determination of radiolytic yields underlies all radiation research. The applications of such research include novel cancer therapy options, innovative industrial chemical process and the management of nuclear waste products1,2,3,4,5.
Previous work on the determination of radiolytic yields (G-values) with synchrotron sources used soft X-rays deposited in thick samples6, resulting in a large dose rate variation along the sample’s depth. The work of Hoshi et al.7 investigated the G-values for a ferrous sulphate dosimeter using a similar technique. In contrast, the measurements reported here were made using thin samples compared to the attenuation length of the radiation and hence the variation in dose and doses rate throughout the irradiated region is much smaller, leading to better defined experimental conditions. In this work, the power absorbed was measured to determine the total energy absorbed by the sample. Also, automated irradiation allows for higher throughput of samples. The results obtained could be used to benchmark computer models of radiation chemistry8,9,10,11,12,13 that will be used in applications of radiation research. This method was benchmarked using a variation of the standard chemical dosimeter, the ferrous sulphate dosimeter, which is used in most basic radiation research to measure energy deposited with irradiation (dose)5,14,15,16,17,18 and has been used as a dosimeter on the beamlines used in this study1.
In this paper we used the radiation chemistry research platform of Polin et al.19, and an add-on developed to enable a new, accurate method for the measurement of radiolytic yields in thin liquid samples. Essentially, photons from a synchrotron x-ray source pass through a thin-walled sample chamber that holds a known volume of sample with the attenuated beam being detected by a calibrated photodiode downstream of the sample chamber. By comparing the photodiode signal with and without sample in place, the absolute power absorbed by the sample during irradiation is deduced. From this a dose rate is calculated taking into account the time structure of radiation production of the synchrotron x-ray source, which is a pulsed x-ray source20.
Results and Discussion
G-values as a function of dose rate
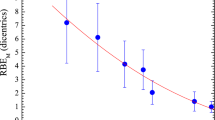
The variation of the G-value of Fe3+ in the ferrous sulphate dosimeter against the average dose rate during a pulse is seen in Fig. 1. Measurements were made at a photon energy of 20 keV (monoenergetic beam). Each data point is derived from a set of measurements like those shown in Fig. 2, made at a specific dose rate, the G-value being determined from the resultant slope. The line shown in Fig. 1 was determined using a total least squares linear fit (i.e. accounting for errors in both dose rate and G-value)21. At low dose rates the G(Fe3+) is 1.51 ± 0.06 μmol/J. This value compares well to model values from Yamaguchi (1.4852 μmol/J under these conditions)22 suggesting that the absolute G-values obtained are reliable. The G-value has been noted to be dose rate independent up to 20 kGy/s5. However, the results presented here show dose rate dependence in the G value of −0.35 ± 0.09 (nmol/J)/(Gy/s) for dose rates below 1 kGy/s. This previously unobserved dose rate dependence is only noticeable due to the sensitivity of the technique. It is noteworthy that the contours of likelihood of fit shown in Fig. 1 (right hand panel B) indicate the conclusion that there is a decrease in the G-value as the dose rate increases is valid with greater than 5-sigma confidence (i.e. it is an extremely robust conclusion).
Total least squares fit of the data. Part A showing the best linear fit plotted (c = 1.51 ± 0.06 μmol/J and m = −0.37 ± 0.09 (nmol/J)/(Gy/s), as indicated on the graph) against the data and error bars (plotted as ellipses). In part B, there is a contour plot of the likelihood that a fit fits the data. Each contour is about a standard deviation further away from the best fit, which is indicated by the point in the center of the contours21. The intercept of the best fit line agrees well with the model by Yamaguchi22. The blue line shows the predicted change in G-value due to spectral hardening effects. With an intercept at 1.498 μmol/J and a slope of −2.11 × 10−2 (nmol/J)/(Gy/s), i.e. two orders of magnitude smaller than the observed effect.
Measured amount of Fe3+ as a function of radiation energy absorbed by the sample. The slope of the line of best fit through the data is the G-value (1.42 ± 0.08 μmol/J). Error bars (indicated by ellipses) are ± two standard errors and indicate statistical errors alone. These measurements were taken with a dose rate of 150 ± 20 Gy/s.
Consideration of artifactual effects
It is worth considering the source of this decrease in G-value as a possible experimental artifact. Initially, we might consider whether oxygen depletion plays a role in the observed effect. The presence of molecular oxygen in the medium is of particular importance23,24, mainly through the reaction
This reaction chain markedly increases the Fe3+ yield in the ferrous sulphate dosimeter– with no oxygen present in solution, the number of Fe2+ ions oxidized by H• is reduced from three to one24, markedly reducing the yield. In an aerated solution, the yield after Co-60 γ-ray irradiation is typically 15.5 ± 0.2 ions per 100 eV16,17,24,25 versus only 8.2 ± 0.3 ions per 100 eV in an anoxic solution16,17,24,25,26,27. We expect oxygen to be steadily depleted over the course of irradiation, with each reaction down the oxic pathway removing a single molecule, and with higher dose rates increasing ionization and depletion rates. To investigate this effect we estimated the number density of oxygen molecules in the medium, through a method previously described28, and simulated the removal of oxygen through ionization events. However, this analysis suggested that oxygen depletion could not account for the observed effect, and was dependent on total dose received rather than the dose rate. The same analysis also predicted that the switch from oxic to anoxic reactions following oxygen depletion would occur rapidly rather than gradually, and indeed previous literature indicates a rapid switch in yield following oxygen depletion5, with no obvious dose rate effects up to 10 Gy/min5,18. Furthermore, if oxygen (or an other substance) is being depleted sufficiently to alter the dosimeter’s response then this would be reflected in a departure from the linear trend shown in Fig. 2. Statistical analysis of the dose dependences observed at different dose rates rules out consumption effects as is discussed in supplementary information.
To illustrate the depletion effect, we performed a similar experiment but at a lower photon energy (16 keV) thereby allowing us to achieve higher energy depositions in a reasonable time. As can be seen in Fig. 3, the lowering of the yield occurs at a higher deposited energy than the range over which the G-values were determined. Since the data shown in Fig. 2 and all other such plots (taken at different dose rates to derive the data shown in Fig. 1(A)) are linear across the whole dose range studied, depletion effects can not account for the effect observed.
Measured amount of Fe3+ as a function of radiation energy absorbed by the sample; showing the turnover in production from the depletion of oxygen. Error bars are ± two standard errors and indicate statistical errors alone. These measurements were taken on B1629,31 with 16 keV X-rays (monoenergetic beam) at a dose rate of 575 ± 17 Gy/s.
Another possible mechanism responsible for this effect on the radiolytic yield is spectral hardening. This occurs because when aluminum attenuators are introduced they preferentially remove the lower photon energy x-rays. Higher photon energy x-rays produce a higher radiolytic yield22. As these higher energy photons form a greater and greater proportion of the spectrum the radiolytic yield will consequentially rise. The mono-energetic x-rays that irradiate the sample are selected from the x-ray spectrum produced, on I15 by a wiggler and on B16 by a bending magnet, followed by transmission through a monochromator. A RuB4C double multilayer mirror monochromator was used on B1629,30,31. A Si(111) double crystal monochromator (DCM) was used on I15. These monochromators can reflect, at a much lower intensity, higher photon energy photons that are an integer multiple photon energy of the selected photon energy (i.e. higher orders of light), as e.g. in case of DCM on I1532 the 3rd harmonic of fundamental/primary photon energy selected. The spectrum, S (E), produced by the double multilayer mirror monochromator on B16 was simulated (see supplementary information). The attenuated spectrum, S′(E), after attenuation by an aluminium with thickness (t) is calculated from the aluminium attenuation coefficients (μ Al ) for each different photon energy (E), from equation 333.
The relative absorption as a function of the photon energy Δ(E), for this attenuated spectrum in a sample with thickness (x) using the sample’s energy-absorption coefficients (μen:F), is given by equation 433.
The measured G-value, G m (Fe3+) by the radiation spectrum S′(E) can be determined by taking a weighted average of the energy dependent G-values G(Fe3+) taken from22, using equation 5.
Using the spectrum shown in supplementary information, the variation in the measured G-values was determined using equation 5. The results of this simulation is depicted on Fig. 1 as the blue line. Since this line has a far lower (almost negligable) slope than the one observed, it is safe to conclude that spectral hardening is not the reason for the effect observed.
Consideration of these effects as a result of recombination
Having considered the readily apparent sources of artifacts and shown that they are unable to account for the trend observed, we must consider alternate mechanics to explain this effect. While ferrous sulphate dosimeters have long been employed, the underlying radiation chemistry is in fact rather complex, with Monte Carlo simulations requiring in excess of 60 possible interactions to capture the observed dynamics of radiation with oxygenated water25, including radical interactions. Radical recombination may explain the observed effect. It is well known4,15,34 that recombination in heavy ion tracks acts to reduce the G-value of Fe3+ in the ferrous sulphate dosimeter. A similar effect has been observed at similar dose rates with electrons35,36. Recombination occurs when radicals interact with each other to produce non-radicals. Most of these non-radicals will be inert to oxidation pathways of Fe2+, reducing the G-value of Fe3+.
For any ionizing radiation, recombination is dependent on dose rate. As dose rates increase, radicals from separate primaries are produced closer together in time so recombination occurs more often. This is because radicals form and react within a reactive micro-zone around an ionization event called a spur5,17. At higher dose rates these spurs interact with each-other increasing the recombination rate.
The calculations of Hill and Smith37 are instructive since they consider the physical and chemical development of a complete track compared to the situation where the effect of short tracks (i.e. where isolated spurs are considered). In Fig. 1 of this paper, there is a clear difference between the G(Fe3+) as calculated with short and full tracks at 20 keV, with full tracks producing a lower G-value. Hence it is clear that spur-spur interactions act to significantly lower the G-value at this energy. As the dose rate increases, so too will the interactions between spurs originating from different primary photons. Accordingly the G-value is expected to lower, in line with our observations. These dose-rate effects are small at the dose-rates considered, which is why they have not been previously observed with x-rays, whereas the technique outlined has sufficient sensitivity to detect these dose-rate effects. This suggests the method outlined could improve understanding of water radiation chemistry, with the data set presented here (Fig. 1) providing new reference data against which computer codes simulating radiation chemistry8,9,10,11,12,13 can be validated. The synchrotron provides high dose rates with mono-energetic photon beams, hence giving stringent tests of such codes. However, this method is not limited to use on synchrotrons it can be used with any type of radiation source; provided means of establishing the power in the beam are available.
Methods
Sample handling
For the radiation chemistry research platform of Polin et al.19, an add-on was developed to enable the measurement of radiolytic yields in geometrically thin liquid samples. This add-on needs only two syringe pumps and a means to translate the sample catcher, so it could easily be implemented as a standalone system. Essentially, photons from a synchrotron X-ray source pass through a thin-walled sample chamber that holds a known volume of sample with the attenuated beam being detected by a calibrated photodiode downstream of the sample chamber. By comparing the photodiode signal with and without sample in place, one can deduce the absolute power absorbed by the sample during irradiation. Using this system to irradiate a sample for a known time and measuring the absolute yield of chemical products (e.g. photometrically) gives rise to an absolute determination of the radiolytic yield under investigation (i.e. the one corresponding to the product measured). Details of the sample chamber are shown in Fig. 4. This is coupled to a sample delivery and flushing system, consisting of an airtight chamber with a cylindrical hole in a polyethylene terephthalate (PETE) block. Chamber o-rings and kapton windows are held together with PETE blocks on either side - the back PETE block connects the chamber to a support structure of the end station, with the chamber connected by polyether ether ketone (PEEK) tubing lines to and from the sample delivery and flushing system, the operation of which is described in the supplementary information.
Irradiation and preparation
The ferrous sulphate dosimeter samples were irradiated at the B16 and I15 beamlines of the Diamond Light Source29,31,32. The samples (0.4 M sulphuric acid, 6 mM ammonium ferrous sulphate and 1 mM potassium chloride) were prepared with ultra-pure water and well-agitated to ensure that the solution is saturated with air, to insure that sufficient oxygen was present5,14,15,16,18. Figure 5 illustrates the irradiation geometry employed with a rectangular collimated X-ray beam. The apparatus was aligned so that the X-ray beam propagated through the sample chamber and other elements. Sheets of aluminium of varying thickness were used to attenuate the X-ray beam before it entered the sample chamber. These attenuators are used to reduce the intensity of the beam, and thus the dose rate. Behind the sample chamber a PD300-500CB photodiode (Canberra, United States)38, calibrated by the Physikalish-Technische Bundesanstalt, was set up to measure the power in the beam after propagating through the chamber. On B16, the photodiode was set 46.5 cm behind the chamber. On I15, the photodiode was set 162.5 cm behind the chamber. In both cases the absorption of X-rays in the air was taken into account as is described below. The shutter and an x-y translator were used to move different sample-catching wells under the ejection nozzle by a PC situated outside of the experimental hutch19. The shutter was controlled with electronic pulses that signaled when it should be open or closed. This means that the beam could only pass through the chamber at the above-mentioned times during the operation of the system. The length of time when the shutter is open with a sample in the chamber is recorded and associated with that sample. As noted above, there are times when the shutter is opened when there is no sample in the chamber. This enables the determination of the beam power with and without the sample present. The readings from the photodiode during these two set ups are used in the analysis to determine the energy deposited in the sample.
The Diamond Light Source’s EPICS-based data acquisition system39 was used to extract the readings from the photodiode and the concurrent current in the synchrotron ring (the ring current)20. These values were then recorded in a tab delimited text file, with the time at which they were taken. This text file is passed through a script to determine the power absorbed by the sample. Under irradiation the photodiode produces a current proportional to the power in the beam. The sensitivity of the photodiode is the ratio of the current produced to the power in the beam and it is calibrated for different energies of X-rays, to the Physikalish-Technische Bundesanstalt standards. This current is converted into a voltage through an amplifier; this voltage is the reading from the photodiode.
Determination of Power Absorbed
The power absorbed by the sample is dependent on the power in the beam, during the irradiation. The power in the beam is proportional to the X-ray production of the synchrotron, which is dependent on the current in the synchrotron storage ring (electron beam ring current). Accordingly, a photodiode value equivalent to one produced by this power can be calculated from the readings without the sample, the baseline readings, and concurrent ring current. These baseline readings are divided by their concurrent ring current to calculate the average reading to ring current ratio, for the empty chamber. This ratio is used to get the equivalent reading that would be produced if the sample chamber were empty for any ring current. This is then used to get equivalent readings for the times when the sample is being irradiated, as in equation 6:
where I ring (t) is the ring current measured at time t and R out is the signal measured at the photodiode when there is no sample in the chamber (the baseline reading). The angle brackets represent the average taken over a long-time series (sufficiently long that the errors in this term are negligible) and R equiv (t) is the equivalent signal to R out (t) deduced from ring-current measurement, i.e. it can be determined even when sample is in the sample chamber. The power deposited in the sample is given by:
where R in refers to the photodiode readings taken during irradiation while the sample is in the chamber, S is the product of the calibrated photodiode’s sensitivity and the gain of the amplifier used prior to digitization of the photodiode signal and d is distance from the chamber to the photodiode. Here x is the thickness of the sample chamber determined both by geometric measurement of the sample chamber and from the relationship:
where μ and μ air are the attenuation coefficients of the sample and air respectively, and μ en and μen:air are the absorption coefficients of the sample and air respectively. These coefficients can be found in a database, maintained by NIST, developed from the ICRU reports40. The value of x determined from this is 4.06 ± 0.09 mm. All of the terms involving exponents represent small corrections for absorption of X-rays by the air. Errors in power absorbed and hence dose and dose rate were determined from a standard quadrature error propagation of equation 7. The dominant contribution to this error comes from the determination of x and the error in the calibrated diode’s sensitivity.
Determination of G-Values
The ferrous sulphate dosimeter is based on quantifying the radiolytic oxidation of iron, the production of Fe3+ from Fe2+ by irradiation5,14,15,18. The amount of Fe3+ produced by irradiation is determined from its concentration in the irradiated sample. The concentration of Fe3+ was measured by taking an absorbance reading at 304 nm, and dividing by the difference between the molar attenuation coefficients of Fe3+ and Fe2+ at 304 nm5,14,18. Absorbance readings were taken with a 1800 spectrophotometer (Shimazdu, Japan).
The density of the ferrous sulphate dosimeters prepared for this paper, was measured as 1.025 ± 0.003 kg/L. The expected density for the ferrous sulphate dosimeter is 1.024 kg/L5. The sample masses were determined to be 146 ± 5 mg for the ferrous sulphate dosimeter described below, correspond to an average volume of 142 ± 5 μl.
This volume of the sample was multiplied by the concentration of Fe3+ to calculate the amount produced during irradiation. This amount divided by the energy absorbed, during its production, gives the G-value for Fe3+. Note that although the irradiated volume is considerably less than the total sample volume, provided the production increases linearly with increased energy deposition, the G-value is reliably determined with the method described above. The linearity of production is discussed below. The axis of the chamber may be at a small angle to the beam. This would not affect the G-value measured, because this would only negligibly increase the relative pre-sample air attenuation of the beam on one side of the chamber. The mass of the sample, measured as described above, is then combined with the density of the sample to calculate the volume of the sample. The volume of the sample was multiplied by the concentration of the end product to calculate the amount of end product in the irradiated sample. Many such measurements were made for different irradiation times. An example of the resultant data is illustrated in Fig. 2.
A computer script was written to determine times when the shutter is open by looking for groups of photodiode readings with low variation (i.e. one opening and closing of the shutter gives rise to a top-hat function in the photodiode signal). These readings are separated into those taken while the sample is in the chamber and those taken when the chamber is empty using the magnitude of the readings. The power attenuated due to the sample from the beam is determined by taking the photodiode reading difference between these two states and converting it with the sensitivity of the photodiode to an absolute power. This value was then corrected for the attenuation of the beam by the air between the chamber and the photodiode, according to equation 7, and converted to total energy with a record of the irradiation time. This record can then be verified by comparison to the record of photodiode signal.
Determination of the average dose rate during X-ray pulses in the irradiated volume
Although the G-value does not depend on the volume of sample irradiated, the instantaneous dose rate in the sample does. The power absorbed can also be used with the mass of the sample to calculate the average dose rate. The volume irradiated was calculated by multiplying the area of the beam by the thickness of the sample from equation 8. The area of the beam can be taken from the set size of the slits. It was also empirically determined by measuring the burn marks on a piece of EBT3 Gafchromic film39 irradiated at the front of the sample chamber. The area was found to be 6.4 ± 0.2 mm2, by both methods. The volume irradiated is then given by:
where V irrad is the volume that is irradiated by the beam, A beam is the area that the beam projected perpendicular to the beam axis and the thickness of the sample is x (as defined above in Equation 8). The volume irradiated in the ferrous sulphate dosimeter was 25.6 ± 0.2 μl on B16, and 24.8 ± 0.3 μl on I15. The dose rate determined from the power absorbed is an average over many pulses. However, the synchrotron is not a continuous source of photons. X-rays are produced when bunches of electrons in the synchrotron ring are accelerated in a bending magnet or wiggler producing a train of X-ray pulses. Accordingly, the sample absorbs energy only during these pulses. The average time structure of the electron bunches was measured by a streak camera, confirming a Gaussian distribution centered at 93 ps with a FWHM of approximately 55 ps. On I15 a wiggler was used to generate the X-rays20,32,41. This means that the X-rays are produced by the electron bunches traveling through a series of magnets. Because the X-rays produced at the start of the wiggler travel faster than the electrons producing the X-rays, the time structure of the X-rays is slightly expanded in time. The distance between the X-rays produced at the start of the wiggler determines the pulse length extension time. Electrons move at 0.999997195c through the I15 wiggler which is 147 cm long20,32,41. Over the length of the wiggler the distance between the electron bunch and the first produced X-rays grows to 4 microns extending the pulse by 13 fs; this is a negligible increase in the pulse length. Accordingly, the X-ray pulses have the same time structure as the electron bunches. In a single revolution of electrons in the synchrotron there is a train of 900 bunches separated by 2 ns intervals and then a 72 ns pause and then the pattern repeats20,32. Each bunch has a full width at half maximum (FWHM) length of 43.36 ± 0.02 ps. The time structure of the bunch gives the time structure of the production of X-ray pulses. This means that during irradiation the sample absorbs energy during the pulse. The amount of energy absorption is proportional to the intensity of X-ray production, which is driven by the intensity of the electron bunch. The equivalent length of actual irradiation is 39.02 ± 0.09 ns in every 1.873 μs of irradiation, which means the average dose rate during a pulse is 48.01 ± 0.11 times the average dose rate integrated over many pulses (i.e. as seen by the photodiode)38. The instantaneous dose rate varies within a pulse, however in order to meaningfully study the variation of G-value with dose rate, it is necessary to define an average dose rate in the pulse. We define this average power as the total energy delivered in a pulse divided by the FWHM time of the pulse.
Conclusions
An accurate technique to determine absolute G-values for radiolytic processes with direct reference to the physical standards (through the use of a calibrated photodiode, weighing scales and volumetric flasks) is described. Although applicable to a wide range of photon or particle beam delivery systems, its use with synchrotron beams has been illustrated. This technique has been used to generate a new benchmark measurement, which could test radiation chemistry simulation codes8,9,10,11,12,13 over a wide range of dose rates. This technique produces an extremely accurate measure of the radiolytic yield of a product.
References
Sicard-Roselli, C. et al. A new mechanism for hydroxyl radical production in irradiated nanoparticle solutions. Small 10, 3338–3346 (2014).
LaVerne, J. A. & Tandon, L. H2 and cl2 production in the radiolysis of calcium and magnesium chlorides and hydroxides. The Journal of Physical Chemistry A 109, 2861–2865 (2005).
LaVerne, J. A. Oh radicals and oxidizing products in the gamma radiolysis of water. Radiation research 153, 196–200 (2000).
LaVerne, J. A. Track effects of heavy ions in liquid water. Radiation research 153, 487–496 (2000).
Spinks, J. W. T. & Woods, R. J. An introduction to radiation chemistry (1990).
Watanabe, R., Usami, N. & Kobayashi, K. Oxidation yield of the ferrous ion in a fricke solution irradiated with monochromatic synchrotron soft x-rays in the 1. 8–10 kev regio. n. International journal of radiation biology 68, 113–120 (1995).
Hoshi, M. et al. Iron (ii) sulphate (fricke solution) oxidation yields for 8. 9 and 13. 6kev x-rays from synchrotron radiation. International journal of radiation biology 61, 21–27 (1992).
Incerti, S. et al. The geant4-dna project. International Journal of Modeling, Simulation, and Scientific Computing 1, 157–178 (2010).
Alloni, D., Campa, A., Friedland, W., Mariotti, L. & Ottolenghi, A. Track structure, radiation quality and initial radiobiological events: considerations based on the partrac code experience. International journal of radiation biology 88, 77–86 (2012).
Solov’yov, I. A., Yakubovich, A. V., Nikolaev, P. V., Volkovets, I. & Solov’yov, A. V. Mesobionano explorer–a universal program for multiscale computer simulations of complex molecular structure and dynamics. Journal of computational chemistry 33, 2412–2439 (2012).
Bernal, M. et al. Track structure modeling in liquid water: a review of the geant4-dna very low energy extension of the geant4 monte carlo simulation toolkit. Physica Medica 31, 861–874 (2015).
Karamitros, M. et al. Modeling radiation chemistry in the geant4 toolkit. Progress in nuclear science and technology 2, 503–508 (2011).
Boscolo, D., Scifoni, E., Kramer, M. & Durante, M. Gsi scientific report 2015. https://doi.org/10.15120/GR-2016-1 (2016).
Fricke, H. & Hart, E. J. Chemical dosimetry. Radiation dosimetry 2, 167–239 (1966).
Chatterjee, A. & Magee, J. L. Radiation chemistry of heavy-particle tracks. 2. fricke dosimeter system. The Journal of Physical Chemistry 84, 3537–3543 (1980).
Fricke, H., Hart, E., Attix, F. & Roesch, W. Radiation dosimetry. Radiation Dosimetry. Academic Press, New York 167 (1966).
Allen, A. O. The radiation chemistry of water and aqueous solutions (van Nostrand New York, 1961).
Klassen, N., Shortt, K., Seuntjens, J. & Ross, C. Fricke dosimetry: the difference between g (fe3+) for 60co-rays and high-energy x-rays. Physics in medicine and biology 44, 1609 (1999).
Polin, C. et al. A novel experimental approach to investigate radiolysis processes in liquid samples using collimated radiation sources. Review of Scientific Instruments 86, 035106 (2015).
Diamond Light Source Diamond machine science. http://www.diamond.ac.uk/Science/Machine.html. Accessed: 2017-06-23.
VanderPlas, J., Connolly, A. J., Ivezić, Ž. & Gray, A. Introduction to astroml: Machine learning for astrophysics. In Intelligent Data Understanding (CIDU), 2012 Conference on, 47–54 (IEEE, 2012).
Yamaguchi, H. A spur diffusion model applied to estimate yields of species in water irradiated by monoenergetic photons of 50 ev–2 me. v. International Journal of Radiation Applications and Instrumentation. Part C. Radiation Physics and Chemistry 34, 801–807 (1989).
Schreiner, L. Review of fricke gel dosimeters. In Journal of Physics: Conference Series, vol. 3, 9 (IOP Publishing, 2004).
Meesat, R. et al. Utilization of the ferrous sulfate (fricke) dosimeter for evaluating the radioprotective potential of cystamine: experiment and monte carlo simulation. Radiation research 177, 813–826 (2012).
McAuley, K. & Nasr, A. Fundamentals of gel dosimeters. In Journal of Physics: Conference Series, vol. 444, 012001 (IOP Publishing, 2013).
Katsumura, Y., Takeuchi, Y. & Ishigure, K. Radiation chemistry of high temperature water–i. degradation products in acid by gamma radiolysis. International Journal of Radiation Applications and Instrumentation. Part C. Radiation Physics and Chemistry 32, 259–263 (1988).
on Radiation Units, I. C. & Measurements. Radiation Dosimetry: X Rays and Gamma Rays with Maximum Photon Energies Between 0.6 and 50 MeV. (International Commission on Radiation Units and Measurements, 1969).
Grimes, D. R. & Partridge, M. A mechanistic investigation of the oxygen fixation hypothesis and oxygen enhancement ratio. Biomedical physics & engineering express 1, 045209 (2015).
Sawhney, K. et al. A test beamline on diamond light source. In AIP conference proceedings, vol. 1234, 387–390 (AIP, 2010).
Sawhney, K. et al. A double multilayer monochromator for the b16 test beamline at the diamond light source. In Advances in X-Ray/EUV Optics and Components VI, vol. 8139, 813908 (International Society for Optics and Photonics, 2011).
Diamond L Source Diamond B16 information. http://www.diamond.ac.uk/Beamlines/Materials/B16.html. Accessed: 2017-06-23.
Diamond L Source Diamond I15 information. http://www.diamond.ac.uk/Beamlines/Engineering-and-Environment/I15-Extreme.html. Accessed: 2017-06-23.
Hubbell, J. H. & Seltzer, S. M. X-ray coefficients. http://www.nist.gov/pml/data/xraycoef/index.cfm. Accessed: 2017-06-23.
LaVerne, J. A. & Schuler, R. H. Radiation chemical studies with heavy ions: oxidation of ferrous ion in the fricke dosimeter. Journal of Physical Chemistry 91, 5770–5776 (1987).
Schuler, R. H. & Allen, A. O. Yield of the ferrous sulfate radiation dosimeter: An improved cathode-ray determination. The Journal of Chemical Physics 24, 56–59 (1956).
Anderson, A. A calorimetric determination of the oxidation yield of the fricke dosimeter at high dose rates of electrons1a. The Journal of Physical Chemistry 66, 180–182 (1962).
Hill, M. & Smith, F. Is the response of the fricke dosimeter constant for high energy electrons and photons? Radiation Physics and Chemistry 47, 637–647 (1996).
Canberra Canberra partially depleted series diode. http://www.canberra.com/products/detectors/pips-detectors-standard.asp. Accessed: 2017-06-23.
Knott, M., Gurd, D., Lewis, S. & Thuot, M. Epics: A control system software co-development success story. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 352, 486–491 (1994).
I. C. on Radiation Units & Measurements. Tissue substitutes in radiation dosimetry and measurement (International commission on radiation units and measurements, 1989).
Winick, H., Brown, G., Halbach, K. & Harris, J. Wiggler and undulator magnets. Physics Today 34, 50–63 (1981).
Acknowledgements
The authors acknowledge Diamond Light Source for time on beamlines B16, I15 and the side laboratories no. 67 and 94 under sessions MT11529-1 and EE10228-1. The authors thank the beamline teams from both beamlines and other support staff who made these measurements possible. Samples were also analysed using equipment in the Research Complex at Harwell. The authors also thank to Lorraine Bobb and Ed Rail for information on the bunch structure of electrons in the synchrotron. The authors thank the Queens University Belfast physics workshop for construction of the chamber. The work was partly supported by the EU FP7 project ARGENT (grant agreement n. 608163). The work was partly supported by NNL, NDA, DISTINCTIVE and EnvRadNet.
Author information
Authors and Affiliations
Contributions
M.O.L., F.J.C., N.B., D.B., J.B., C.E., C.F., V.I., C.P., N.W. and A.M. performed the experimental work, M.O.L. performed data analysis and wrote the manuscript, including the production of figures. D.R.G. performed oxygen analysis and co-wrote the manuscript. O.J.L.F., A.K.K., I.P., and I.P.D. tuned the beamlines, provided the required radiation and modeled the X-ray optics leading to the spectrum shown in Figure S2. C.P. and N.W. built the experimental system and the control software. F.J.C. proposed the experiment, was awarded the beam time, identified the significance of the effect, assisted with all aspects of the study and co-wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
O’Leary, M., Boscolo, D., Breslin, N. et al. Observation of dose-rate dependence in a Fricke dosimeter irradiated at low dose rates with monoenergetic X-rays. Sci Rep 8, 4735 (2018). https://doi.org/10.1038/s41598-018-21813-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-21813-z
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.