Abstract
Spontaneous activity found in neural networks usually results in a reduction of computational performance. As a consequence, artificial neural networks are often operated at the edge of chaos, where the network is stable yet highly susceptible to input information. Surprisingly, regular spontaneous dynamics in Neural Networks beyond their resting state possess a high degree of spatio-temporal synchronization, a situation that can also be found in biological neural networks. Characterizing information preservation via complexity indices, we show how spatial synchronization allows rRNNs to reduce the negative impact of regular spontaneous dynamics on their computational performance.
Similar content being viewed by others
Introduction
Random recurrent neural networks (rRNNs) are popular models to investigate basic principles of information processing inside the human brain. Although brain connectivity cannot be assumed to be fully random1,2, there is experimental support suggesting that some parts of the brain are described by stochastic architectures. For example, in insect’s olfactory systems the odour recognition process is performed by olfactory receptor neurons with structureless (random) synaptic connections3,4. The random weights of these networks also serve as tools for dimensionality reduction5,6. In models investigating such situations, the synaptic neural links, defined by the elements of a random matrix, would follow a Gaussian distribution7,8,9,10.
Despite the fact that interactions inside rRNNs are governed according to random coupling, these networks can still achieve highly coherent collective behavior1,11,12,13. Under such conditions they can experience phase synchronized dynamics, which have been identified to play an important role in biological memory processes14, neural communication15,16,17 and plasticity18,19,20,21. Synchronization therefore is a relevant mechanism in biological neural networks. Such synchronous phenomena take the form of regular spatio-temporal patterns, showing the presence of self-organization. These patterns can also be found in homogeneous22 as well as in heterogeneous artificial neural networks23,24. Dynamics of the here discussed rRNNs can be tuned via a single parameter, which typically results in a bifurcation phenomena as a route to chaos25,26,27. Furthermore, this transition in their dynamical properties possibly influences the network’s spatio-temporal synchronization.
Besides their function as model systems in biological neuroscience, rRNNs have been widely studied in the machine learning community due to their excellent computational properties. In rRNNs, special attention was given to computation at the transition from a steady state to chaotic dynamics, defined as the edge of chaos. Essential for solving complex tasks, operating a network at the edge of chaos ensures a high susceptibility to perturbations and hence its excitability25,26,27,28,29. Beyond the edge of chaos, the network typically experiences non-regular dynamics even in the absence of an external stimulus. Such spontaneous dynamics are considered a nuisance as they disrupt the causality between input and network state. Nevertheless, information processing might not depend on individual node dynamics. In other words: local details of an autonomous rRNN’s dynamical state might be of secondary importance, as long as the network as a whole can preserve the information content of the injected signal. Global dynamical properties and their influence on computation therefore deserve a closer inspection.
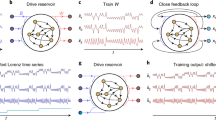
In this work, we study a rRNN predicting a chaotic time series. Identifying each node as a spatial-position, the network’s state variable can be interpreted in terms of spatio-temporal dynamics. Motivated by the impact of spatio-temporal dynamical properties, we particularly focus on beyond fixed point operation. We employ a variation to classical rRNNs25,26,27,30 by using nodes with a sinusoidal activation function. A broad range of autonomous dynamics are the consequence, among which we most importantly find multiple non-fixed point states with surprisingly high computational performance. We show that spatial synchronization between nodes and bifurcation point play essential roles in information processing. The underlying mechanisms are analysed based on the mutual information between each node of rRNN and the input time signal, as well as the rRNN’s maximal Lyapunov exponent. Our choice of system is directly motivated by its randomness: we can exclude structural modifications induced by learning being the cause behind spatial synchronization.
Results
Random recurrent neural networks
Our rRNN consists of a set of N = 500 nodes in state x n , internally connected via a random, uniformly distributed internal weight matrix W of dimensionality N × N. The resulting random networks have a temporal evolution governed by
where {W, Woff, Wfb} are matrices defining the random weight connectivity of the rRNN for the network itself, b = 0.2 the offset operating points at each node, and the input layer connectivity with the signal \(\alpha \cdot {y}_{n+1}^{T}\) (α the input scaling), respectively. μ is the feedback amplification. The connectivity matrix W is constructed with 500 × 500 random, uniformly distributed coefficients in [0, 1], from a matrix with connectivity 0.99. The rRNN is schematically illustrated in Fig. 1(a), where nodes (symbol ⊕) add and nonlinearly transform all inputs \(\{{{\bf{x}}}_{n},b,{y}_{n+1}^{T}\}\) according to random weights {W, Woff, Wfb}.
In its bifurcation diagram this neural network experience multiple windows of regular dynamics. In Fig. 1(b), we show a single node’s bifurcation diagram. The windows of regular dynamics appear at distinct values which are highly comparable for all nodes. Dynamics are obtained for μ in [0, 50] and for a randomly chosen node, i.e. node 34 (\({x}_{n+1}^{34}\)) of the autonomous system (α = 0). Non-chaotic regimes can be found in several regions: R1, R2, R3, R4, and R5, for μ ∈ [0.1, 2.8], μ ∈ [4.8, 5.4], μ ∈ [8.5, 8.9], μ ∈ [12.4, 12.7], and μ ∈ [17.6, 18.4], respectively. These regions are part of the multistability present in this particular rRNN, consequence of the sinusoidal nonlinear function. Standard rRNNs typically have a hyperbolic tangent as their nonlinear function30. In that case, a steady state only exists for μ < 1.4. However, once it bifurcates there are no additional steady state windows that can be used for investigating their information processing properties, i.e. the network’s dynamic falls in a chaotic regime. In such a system one could not compare results obtained under similar dynamical states. As we intent to investigate general properties for computation in non-steady state systems, we opted for our modified rRNN.
Autonomous rRNN dynamics (α = 0) for different values of the bifurcation parameter μ are shown in Fig. 2. The left column shows the functional input-output relationship of Eq. (1) for node 34. The central column displays exemplary individual time series for the same node, referred to as local dynamics, while the right column shows the dynamical state of the full rRNN. For μ = 5 (regime R2) the node state is symmetrically concentrated along the nonlinear function’s extrema, see panel (a) of Fig. 2. The resulting dynamics of \({x}_{n+1}^{34}\) and the full networks state xn+1 is shown in Fig. 2(b,c), respectively. Autonomous dynamics of \({x}_{n+1}^{34}\) are therefore periodic, and according to Fig. 2(c) such local periodic dynamics strongly synchronize across the rRNN. When increasing bifurcation parameter μ to 10, dynamics span an increasing number of the nonlinear function’s periods, see Fig. 2(d). The consequence is a local dynamical state with considerably higher complexity, see Fig. 2(e). Yet, synchronization between individual nodes still proofs to be robust. According to Fig. 2(f), regular spatial patterns are still present and synchronization across the network is preserved despite the chaotic dynamics of individual nodes31. Finally, when further increasing μ to 50, dynamics spanning up to 14 extrema (Fig. 2(g)) result in hyper-chaotic node responses, see Fig. 2(h). As illustrated in Fig. 2(i), only for such large bifurcation values the regular spatio-temporal structures across the network have vanished and synchronization is lost.
Dynamical evolution of the rRNN. Nonlinear response of nodes with f(x) = sin(x) (left column), time series recorded for node \({x}_{n+1}^{34}\) (center column), and spatio-temporal evolution of the rRNN (right column): (a–c) μ = 5, (d–f) μ = 10, and (g–i) μ = 50. All dynamics obtained for the autonomous system (α = 0).
Mitigating autonomous dynamics by learning
All previously discussed dynamical properties have been exclusively obtained in the absence of an external stimulus. However, as an information processing system, the rRNN realizes computation on the bases of rich dynamical responses to external, i.e. sensory input. We therefore activate the rRNN’s input by setting α = 0.8 and investigate its dynamics when fed by a chaotic time series. We add an output layer that provides the computational result according to
A divergence of the system’s output yout for large μ is avoided by limiting the range of yout through the hyperbolic tangent in Eq. (2). The output weight vector Wout is calculated according to a supervised learning rule based on a teacher/target signal \(\alpha {y}_{n+1}^{T}\), Eq. (3).
Once trained, the input signal is replaced by the network’s own output30 \({y}_{n+1}^{T}={y}_{n+1}^{out}\) in Eq. (1), and the system autonomously approximates dynamics learned from the teacher system, here the Mackey-Glass (MG) sequence from Eq. (7)32. Computational performance is determined after a free evolution of 35 time steps, twice the time-delay of the MG sequence (τ m = 17 in Eq. (7))32,33. In Fig. 3(a) the prediction NMSE (Eq. (4)) is shown for 0 < μ ≤ 10. At each μ we repeated the previously introduced training procedure. The optimal performance (NMSE = 5.5 × 10−4) is found for a very narrow regime around μ = 0.9, which comes at no surprise as it corresponds to the often employed computation close to the self organizing criticality25. However, additionally we identify multiple broader regions of acceptable performance with a prediction error of roughly NMSE ≈10−2. A comparison to the rRNN’s bifurcation diagram of Fig. 1(b) reveals that these regions directly correspond to R1, R2 and R3, where rRNN dynamics are regular and nodes are synchronized. Regimes R4 and R5 are not treated in our analysis since small perturbations result in their destabilization, driving the rRNN instantaneously into the next chaotic regime. In all other regions the error is orders of magnitude higher.
rRNN prediction performance, noise supression and synchronization. (a) Average NMSE as a function of μ (blue stars), and the noise-like standard deviation in rRNN output σα=0 for the autonomous system (black circles) with error-limits presented by envelops of dotted-curves. (b) Average synchronization error across the rRNN for the driven (α = 0.8) and autonomous system (α = 0) in black dots and blue stars, respectively. Data was averaged over 100 different realizations of the rRNN.
As previously introduced, in the self-driven mode the rRNN’s output becomes its own input. If not suppressed, perturbation-like autonomous rRNN dynamics can therefore freely propagate through the system due to this recurrent input/output relationship. This raises the question as to how the network can mitigate internal dynamics so efficiently. The answer lies within the learning process. We demonstrate this by creating the rRNN’s output \({y}_{n+1}^{out}\) for α = 0, however using the Wout previously learned for approximating \({y}_{n+1}^{T}\) for the driven system at α = 0.8. From the resulting signal we discard the first 10 data points to avoid possible transient behavior. From the remaining 25 samples we calculate the average output amplitude variation σα=0 via Eq. (5). This measure σα=0 evaluates the output weights’ performance for suppressing autonomous dynamics, and the black data in Fig. 3(a) demonstrates how intricate σα=0 and the NMSE are related. Within regions R1, R2 and R3, learning efficiently separates autonomous dynamics from transients induced by the rRNN’s input. As revealed by the low values of σα=0, the rRNN can there approximate \({y}_{n+1}^{T}\) well because the impact of autonomous rRNN dynamics on yout is strongly reduced. As a consequence, perturbations not present in the training data can be isolated from dynamics in the target data.
In general, the spontaneous internal activity of each node has an impact on the collective evolution of the network. As illustrated in the right column of Fig. 2, this recurrent network architecture can cause different levels of dynamical diversity through out the rRNN, which in turn potentially influences the propagation of information within the network. The spatio-temporal evolution of the rRNN can be quantified by the spatial synchronization between the nodes. The standard deviation, described by Eq. (6), globally measures spatial synchronization between nodes24. Figure 3(b) shows how uniformly synchronous the nodes are depending on the value of μ when the network presents autonomous (black dots) and driven activity (blue stars). The nodes of the rRNN are less synchronized in the non-regular windows when the network is perturbed by an external signal. In regions R1, R2 and R3, however, synchronization is nearly preserved in both cases. As demonstrated by Fig. 3(b), the global rRNN synchronization error significantly decreases in regions R1, R2 and R3. Thus, the dependence of synchronization δ on bifurcation parameter μ is highly comparable for, both, the driven and the autonomous system. Region R1 can clearly be separated into two sections. For μ ≤ 1 node responses consists of constant states; the system is operating in the linear section of the nonlinear function. For μ > 1 the network states also cover the nonlinear function’s extrema and nodes start evolving in synchrony. Region R3 is significantly more sensitive to μ when compared to R1 and R2. This is due to the proximity to parameters resulting in chaotic dynamics. Such a sensitive operating point is less recommendable when for example we use a noisy hardware or biological rRNN for prediction. In fact, in R3 we find that the nodes are in steady states with small or vanishing amplitude dynamics, however not as well synchronized as in R1, and R 2. The comparison between panels (a) and (b) of Fig. 3 highlights the importance of spatial synchronization for good prediction performance. Data shown in Fig. 3 shows the statistical average obtained from 100 realizations of W.
An extensive qualitative analysis of the dynamics associated with good prediction performance is shown by Fig. 4. For μ = 0.8, Fig. 4(a) shows the spatio-temporal plot of all nodes when the input is injected in steady state regime R1. Column-shaped patterns throughout the entire spatio-temporal plot are induced by the external data and therefore indicate information preservation. One example of how input information is preserved within the rRNN is shown by Fig. 4(b), where the randomly chosen node 31 (\({x}_{n+1}^{31}\)) shows a nonlinearly transformed version of the input. For a geometrical illustration of the information carried by the node, we illustrate the system’s dynamic by reconstructing the attractor of node 31 through Takens embedding Theorem34. We used embedding parameters of delay τ = 12 and dimensions D = 4 which are the ones obtained for delay embedding the original MG attractor35, also see Methods section. A 2D projection of resulting state space is shown by Fig. 4(c), which is qualitatively comparable with the structure of the chaotic MG attractor shown in the Methods section.
Spatio-temporal evolution of the rRNN (left column), time series recorded for node \({x}_{n+1}^{31}\) (center column), and 2D projections of the reconstructed time series from node 31 (right column). (a–c) μ = 0.8, (d–f) μ = 5, and (g–i) μ = 8.7. All dynamics obtained for the driven system (α = 0.8).
At μ = 5 (regime R2) we find the previously described periodic oscillations. The spatio-temporal plot of the driven rRNN shows once again a constant phase relation across all nodes, see Fig. 4(d). Spatio-temporal features corresponding to the input timetrace masked by the autonomous oscillations. Consequently, the closer inspection of individual node evolutions shows that the spontaneous rRNN internal dynamics are still present, see Fig. 4(e). We find that node dynamics consist of two contributions. Large amplitude oscillations at fast timescales correspond to the autonomous dynamics, while nonlinear transients induced by the input information are encoded in the slowly varying envelope. Such specific and well separated time scales are a requirement for suppressing the crosstalk of autonomous dynamics to yout. Combined with Fig. 4(f), the impact of regular autonomous rRNN dynamics becomes clear. The fast autonomous oscillations separate the node’s attractor into two regions of its state space. Within each of these regions, the local attractor again resembles the one of the injected MG sequence. As such, removing this division by training corresponds to σα=0, and the system should still be able to approximate the target attractor36. Periodic dynamics ensure the discussed separation between timescales, while synchronization minimizes the resources learning has to dedicate for their suppression, leaving more freedom for optimizing prediction performance.
Upon increasing the bifurcation parameter to μ = 8.7 (regime R3), the collective dynamics shown by Fig. 4(g) have similarities to the one shown in panel (a), even experiencing a degree of synchronization. In this case, the node’s responses to the external information is perturbed by irregularly appearing, noise-like epochs, see Fig. 4(h). The fixed point of R3 is a quasi-steady state, yet due to the narrow width of R3 the rRNN is forced outside this stability window even by small fluctuations which in turn can induce noise like epochs. Figure 4(i) shows the effect of the noise on the reconstructed attractor. The noise strongly distorts the node responses away from the MG attractor. As induced by noise-like epochs, these distortions strongly hamper the determinism in the rRNN’s response to the injected information.
Preservation of information in destabilized rRNNs
Spontaneous dynamics in the rRNN therefore result in distortions of its response. At this point it is important to recall that the input sequence is chaotic, yet by no means random. It is the result of complex, yet causal deterministic processes. Predicting such a signal therefore demands these causal relationships to be preserved within the neural network’s dynamical state, providing a functional relationship to currently and previously injected information. For low error prediction it is therefore an essential condition that the network can serve as carrier and short term storage of injected information. Synchronization is not sufficient to estimate if a rRNN complies with this condition. Quantifying the information content preserved within the rRNN when stimulated by an input, we calculate the mutual information (MI) between the rRNN and the input signal. This provides an estimation of how well the network is able to maintain the input information content25, and hence is capable to capitalize from these internal causal relationships for computation.
We consequently evaluate the network by estimating the memory capacity C via the mutual information between each node and the input, see Eq. (8), and maximal Lyapunov exponent λ max , as functions of the bifurcation parameter. In Fig. 5 we show the rRNN’s C and λ max as black dots and blue stars, respectively. As during our previous analysis, we find that regimes R1, R2, and R3 show their capabilities to accurately preserve previous input information. In steady state regimes R1 and R3 the memory capacity C is higher than in R2, where the rRNN’s spontaneous behavior is periodic in general. Our Lyapunov component analysis reveals that λ max is kept small inside R1, R2, and R3 due to their non-chaotic spontaneous features. In fact, for μ ≤ 1 in R1, λ max of the network approaches with the one estimated for the input signal (\({\lambda }_{max}^{MG}\sim 3.6\times {10}^{-3}\)), indicated by the dashed line in Fig. 5. For μ > 1, oscillatory, spontaneous rRNN’s dynamics are combined with the injected input information. As the internal dynamics of the rRNN begin to exert influence over dynamics induced by the MG input, λ max starts increasing accordingly. This behavior agrees well with the decrease of memory capacity, where the internal rRNN’s dynamics will modify the probability distribution of the nodes. This demonstrates a strong correlation between the decline of spatio-temporal synchronization and the reduction in the system’s memory capacity to approximate the deterministic, functional relationship of the prediction task.
rRNN mermory capacity and maximal Lyapunov exponent. Memory capacity C (black dots), and maximal Lyapunov exponent λ max (blue stars) of the rRNN, as functions of μ. Sections without λ max values exhibit hyper-chaotic dynamics with more than one positive Lyapunov exponent. The dashed/dotted line indicates \({\lambda }_{max}^{MG}/{C}_{max}\), respectively.
Conclusion
Unlike neural networks run on a data-center, the human brain is not a special purpose computing machine, but parameters will most likely be optimized according to a compromise between partially competing demands. We therefore demonstrated that information preservation and synchronization inside a random network allow good prediction performance at parameters where learning in biological neural networks benefits. Based on a rRNN with a periodic nonlinear function we compare various regions of regular dynamics and highlight their importance of spatial synchronization upon prediction performance, mutual information and the stability of the neural network. Synchronization between nodes plays an essential role, but it is not sufficient to understand how information processing is successful in a rRNN beyond its fixed point. On the contrary, when linear regression is used to realize supervised learning, a causal relation between processed information and target is required.
We describe a rRNN predicting the future time-steps of a chaotic trajectory. Our results illustrate the importance of information flow, divergence and the suppression of signal components not present in the training data set. The rRNN’s damped autonomous deviation σα=0, mutual information MI and maximal Lyapunov exponent can be seen as complexity indicators for interpreting neural networks based on dynamical systems. Other than for the oscillatory state, chaotic responses were not capable to maintain important features of the input dynamic, resulting in a low prediction performance. Finally, delay systems exploiting an identical nonlinearity have been reported37,38 and it would be of interest to investigate such hardware systems based on the here introduced methodology.
Methods
Training of the rRNN
For the training step we use 2000 values from the MG system and α = 0.830,32,33. The training target is equivalent to the input signal, shifted by a single time step. Via the teacher we estimate the optimal output weight vector \({W}_{op}^{out}\)
via its pseudo-inverse according to singular value decomposition. Equation (3) therefore minimizes the error between output tanh(Wout ⋅ xn +1) and teacher \({y}_{n+1}^{T}\). As training error measure we use the normalized mean squared error (NMSE) between output \({y}_{n+1}^{out}\) and target signal \({y}_{n+1}^{T}\), normalized by the variance of teacher signal \({y}_{n+1}^{T}\):
where σ is the standard deviation.
Statistical amplitude variation
The average output amplitude variation:
where n = 2010, 2011, …, 2035.
Standard deviation
The standard deviation of all node responses individually averaged over time is measured against the rRNN’s mean-field dynamical state:
with i∈ [1, 500]. A normalization by μ then allows to associate δn+1 to a synchronization error in phase of the nonlinear function in Eq. (1).
The Mackey-Glass system
The MG system is a first order nonlinear delay differential equation32, whose time-discrete version is the following33:
where \({y}_{{\tau }_{m}}=y(n-{\tau }_{m}/\delta )\), τ m = 17 as the time delay, and δ = 1/10 is the stepsize indicating that the time series is subsampled by 10. Where 1 increment of the resultant time series correspond to 10 time units of the Mackey-Glass equation. The MG time series is shifted to oscillate around zero. For the reconstruction of the attractor we apply Takens embedding Theorem34 to the time series yn+1. We used embedding parameters of delay τ = 12 and dimensions D = 4 which are the ones obtained for delay embedding the original MG attractor35. Figure 6 shows a 3D projection of the MG attractor.
Mutual information
Mutual information quantifies the amount of information shared between node responses \({x}_{n+1}^{i}\) and input signal \({y}_{n+1}^{T}\)39
Mutual information MI therefore depends on the joint probability density function of \({x}_{n+1}^{i}\) and \({y}_{n+1}^{T}\), \({\mathscr{P}}({x}_{n+1}^{i},\,{y}_{n+1}^{T})\), as well as \({\mathscr{P}}({x}_{n+1}^{i})\), \({\mathscr{P}}({y}_{n+1}^{T})\) which are the probability density functions of xi and yT, respectively. If MI i >> 0 for the ith node, it preserves most dynamical properties of input \({y}_{n+1}^{T}\). Under these conditions the rRNN as a whole therefore is capable to preserve the input information without significant loss of information, hence learning should be possible in principle. By accumulating all MI i in the global measure C = ∑ i (MI i ) defined as memory capacity26.
Maximal Lyapunov exponent
Complex dynamical systems are typically classified using the rate of exponential divergence between neighbor trajectories, corresponding to their Lyapunov exponent. Specifically chaotic systems have a positive maximal Lyapunov exponent λ max 40. The maximal Lyapunov exponent40,41,42 is at first calculated for each i-th node, \({\lambda }_{max}^{i}\). Then the maximal Lyapunov exponent of the rRNN is \({\lambda }_{max}=\,{\rm{\max }}({\lambda }_{max}^{i})\).
References
MacGregor, R. Neural and Brain Modeling (ACADEMIC PRESS, 1987).
Sporns, O. The non-random brain: efficiency, economy, and complex dynamics. Front. Comput. Neurosci. 5, 5 (2011).
Gutiérrez, A. & Marco, S. Biologically Inspired Signal Processing for Chemical Sensing (Springer, 2009).
Caron, S. J. C., Ruta, V., Abbott, L. F. & Axel, R. Random convergence of olfactory inputs in the drosophila mushroom body. Nature 497, 113 (2013).
Indyk, P. & Motwani, R. Approximate nearest neighbors: towards removing the curse of dimensionality (ACM Press, 1998).
Dasgupta, S. & Gupta, A. An elementary proof of a theorem of johnson and lindenstrauss. Random Struct. Alg. 22, 60 (2002).
Bruckstein, A. M., Donoho, D. L. & Elad, M. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Review 51, 34 (2009).
Ganguli, S. & Sompolinsky, H. Compressed sensing, sparsity, and dimensionality in neuronal information processing and data analysis. Ann. Rev. Neurosci. 35, 485 (2012).
Babadi, B. & Sompolinsky, H. Sparseness and expansion in sensory representations. Neuron 83, 1213 (2004).
Schottdorf, M., Keil, W., Coppola, D., White, L. E. & Wolf, F. Random wiring, ganglion cell mosaics, and the functional architecture of the visual cortex. PLoS Comput. Biol. 11, e1004602 (2015).
Harth, E. M., Beek, B., Csermely, T. J. & Lindsay, R. D. Brain functions and neural dynamics. J. Theor. Biol. 26, 93 (1970).
Sompolinsky, H., Crisanti, A. & Sommers, H. J. Chaos in random neural networks. Phys. Rev. Lett. 61, 259 (1988).
Wainrib, G. & Touboul, J. Topological and dynamical complexity of random neural networks. Phys. Rev. Lett. 110, 118101 (2013).
Fell, J. & Axmacher, N. The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 12, 105 (2011).
Konig, P., Engel, A. K. & Singer, W. Integrator or coincidence detector? the role of the cortical neuron revisited. Trends Neurosci. 19, 130 (1996).
Azouz, R. & Gray, C. M. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc. Natl Acad. Sci. USA 97, 8110 (2000).
Daoudal, G. & Debanne, D. Long-term plasticity of intrinsic excitability: learning rules and mechanisms. Learn. Mem. 10, 456 (2003).
Miltner, W. H., Braun, C., Arnold, M., Witte, H. & Taub, E. Coherence of gamma-band eeg activity as a basis for associative learning. Nature 397, 434 (1999).
Weiss, S. & Rappelsberger, P. Long-range eeg synchronization during word encoding correlates with successful memory performance. Brain Res. Cogn. Brain Res. 9, 299 (2000).
Fell, J., Ludowig, E., Rosburg, T., Axmacher, N. & Elger, C. E. Phase-locking within human mediotemporal lobe predicts memory formation. Neuroimage 43, 410 (2008).
Benchenane, K. et al. Coherent theta oscillations and reorganization of spike timing in the hippocampal- prefrontal network upon learning. Neuron 66, 921 (2010).
Singh, R., Menon, S. N. & Sinha, S. Complex patterns arise through spontaneous symmetry breaking in dense homogeneous networks of neural oscillators. Sci. Rep. 6, 22074 (2016).
Stern, M., Sompolinsky, H. & Abbott, L. F. Dynamics of random neural networks with bistable units. Phys. Rev. E 90, 062710 (2014).
Wei, D. Q. & Luo, X. S. Ordering spatiotemporal chaos in discrete neural networks with small-world connections. EPL 78, 68004 (2007).
Natschlager, T., Bertschinger, N. & Legenstein, R. At the edge of chaos: Realtime computations and self-organized criticality in recurrent neural networks (Advances in Neural Information Processing Systems, 2005).
Bertschinger, N. & Natschlager, T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput. 16, 1413 (2004).
Sussillo, D. & Abbott, L. F. Generating coherent patterns of activity from chaotic neural networks. Neuron 63, 544 (2009).
Langton, C. G. Computation at the edge of chaos: Phase transitions and emergent computation. Physica D 42, 12 (1990).
Packard, N. Dynamic Patterns in Complex: Adaptation towards the edge of chaos (World Scientific, 1988).
Jaeger, H. & Haas, H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304, 78 (2004).
Pecora, L. M. & Carroll, T. L. Synchronization of chaotic systems. Chaos 25, 097611 (2015).
Mackey, M. C. & Glass, L. Oscillation and chaos in physiological control systems. Science 197, 287–289 (1977).
Jaeger, H. Fraunhofer Institute for Autonomous Intelligent Systems, Tech. rep. 148 (2001).
Takens, F. Detecting strange attractors in turbulence (Dynamical Systems and Turbulence, Lecture Notes in Mathematics, 1981).
Farmer, J. D. & Sidorowich, J. J. Predicting chaotic time series. Phys. Rev. Lett. 59, 845 (1987).
Marquez, B. A. et al. Nonlinear attractor embedding: the mechanism behind prediction in reservoir computing. Submitted (2017).
Paquot, Y. et al. Optoelectronic reservoir computing. Sci. Rep. 2, 287 (2012).
Larger, L. et al. Photonic information processing beyond turing: an optoelectronic implementation of reservoir computing. Opt. Express 20, 3241 (2012).
Shannon, C. E. & Weaver, W. The mathematical theory of communication (University of Illinois Press, 1949).
Kantz, H. & Schreiber, T. Nonlinear Time Series Analysis (Cambridge University Press, 1997).
Sato, S., Sano, M. & Sawada, Y. Practical methods of measuring the generalized dimension and the largest lyapunov exponent in high dimensional chaotic systems. Prog. Theor. Phys. 77, 1 (1987).
Rosenstein, M. T., Collins, J. J. & Luca, C. J. D. A practical method for calculating largest lyapunov exponents from small data sets. Physica D 65, 117 (1993).
Acknowledgements
The authors acknowledge the support of the Region Bourgogne Franche-Comté. This work has been performed in cooperation with Labex ACTION program (contract ANR-11-LABX-0001-0), the Volkswagen Foundation NeuroQNet project and the ANR project BiPhoProc from the OH-Risque call (ANR-14-OHRI-0002-02).
Author information
Authors and Affiliations
Contributions
The concepts of the manuscript were developed by B.M. and D.B.; B.M. carried out the computational and data analysis of the manuscript. D.B. and L.L. supervised the work. All authors contributed to writing of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marquez, B.A., Larger, L., Jacquot, M. et al. Dynamical complexity and computation in recurrent neural networks beyond their fixed point. Sci Rep 8, 3319 (2018). https://doi.org/10.1038/s41598-018-21624-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-21624-2
This article is cited by
-
Application of cellular automata in neuroscience: dynamic models of neuron populations
Multiscale and Multidisciplinary Modeling, Experiments and Design (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.