Abstract
We investigate theoretically thermal and electrical conductances for the system consisting of a quantum dot (QD) connected both to a pair of Majorana fermions residing at the edges of a Kitaev wire and two metallic leads. We demonstrate that both quantities reveal pronounced resonances, whose positions can be controlled by tuning of an asymmetry of the couplings of the QD and a pair of MFs. Similar behavior is revealed for the thermopower, Wiedemann-Franz law and dimensionless thermoelectric figure of merit. The considered geometry can thus be used as a tuner of heat and charge transport assisted by MFs.
Similar content being viewed by others
Introduction
Majorana fermions (MFs) are particles that are equivalent to their antiparticles. The corresponding concept was first proposed in the domain of high-energy physics, but later on existence of the elementary excitations of this type was predicted for certain condensed matter systems. Particularly, MFs emerge as quasiparticle excitations characterized by zero-energy modes1,2 appearing at the edges of the 1D Kitaev wire3,4,5,6,7. Kitaev model is used to describe the emerging phenomena of p-wave and spinless topological superconductivity.
Kitaev topological phase can be experimentally achieved in the geometry consisting of a semiconducting nanowire with spin-orbit interaction put in contact with s-wave superconducting material and placed in external magnetic field8,9. Other condensed matter systems were also proposed as candidates for the observation of MFs. They include ferromagnetic chains placed on top of superconductors with spin-orbit interaction10,11, fractional quantum Hall state with filling factor ν = 5/212, three-dimensional topological insulators13 and superconducting vortices14,15,16.
MFs residing at the opposite edges of a Kitaev wire are elements of a robust nonlocal qubit which appears to be immune to the environment decoherence. This attracted the interest of the researchers working in the domain of quantum information and transport, as systems with MFs17,18,19 can be in principle used as building blocks for the next generation of nanodevices20,21, including current switches20 and quantum memory elements21. At the same time, similar systems were proposed as thermoelectric nanodevices22,23,24,25.
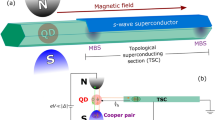
In this work, following the proposals of thermoelectric detection of MF states22,23,24,25, we explore theoretically zero-bias thermal and electrical transport through one particular geometry consisting of an individual QD coupled both to a pair of MFs and metallic leads as shown in the Fig. 1(a). The MFs reside at the edges of a topological U-shaped Kitaev wire, similar to the case of ref.19. The QD coupling to the MFs is considered to be asymmetric, while coupling to the metallic leads is symmetric, and MFs are supposed to overlap with each other. The results of our calculations clearly show that thermoelectric conductance, thermopower, Wiedemann-Franz law26 and dimensionless thermoelectric figure of merit (ZT) as function of the QD electron energy demonstrate resonant behavior. Moreover, the position of the resonance can be tuned by changing the coupling amplitudes between the QD and the MFs, which allows the system to operate as a tuner of heat and charge assisted by MFs.
(a) The sketch of the geometry we consider. Topological U-shaped Kitaev wire with a pair of MFs η A and η B is placed in contact with a QD, which is connected as well to two metallic reservoirs. The coupling of the QD to the MFs is asymmetric and is characterized by tunneling matrix elements λ A and λ B , while coupling to the metallic leads is symmetric and is characterized by the tunneling matrix element V. ε2 denotes the coupling between two MF states. (b) Equivalent auxiliary setup (Kitaev dimer) resulting from the mapping of the original system onto the system with nonlocal fermion residing in QD2. t is tunneling matrix element between the QDs 1 and 2, Δ is the binding energy of the Cooper pair delocalized between them.
Model
For theoretical treatment of the setup depicted in the Fig. 1(a), we use the Hamiltonian proposed by Liu and Baranger27:
where the electrons in the leads α = H, C (for hot and cold reservoirs, respectively) are described by the operators \({c}_{\alpha k}^{\dagger }\) (c αk ) for the creation (annihilation) of an electron in a quantum state labeled by the wave number k and energy ε k . For the QD \({d}_{1}^{\dagger }\) (d1) creates (annihilates) an electron in the state with the energy ε1. The energies of both electrons in the leads and QD are counted from the chemical potential μ (we consider only the limit of small source-drain bias, thus assuming that chemical potential is the same everywhere). V stands for the hybridization between the QD and the leads. The asymmetric coupling between the QD and MFs at the edges of the topological U-shaped Kitaev wire is described by the complex tunneling amplitudes λ A and λ B . Introduction of an asymmetry in the couplings can account for the presence of the magnetic flux which can be introduced via Peierls phase shift27. ε2 stands for the overlap between the MFs.
Without loss of generality, we can put: \({\lambda }_{A}=\frac{(t+{\rm{\Delta }})}{\sqrt{2}}\) and \({\lambda }_{B}=i\frac{({\rm{\Delta }}-t)}{\sqrt{2}}\), respectively for the left \(({\eta }_{A}={\eta }_{A}^{\dagger })\) and right \(({\eta }_{B}={\eta }_{B}^{\dagger })\) MFs, and introduce an auxiliary nonlocal fermion \({d}_{2}=\tfrac{1}{\sqrt{2}}({\eta }_{A}+i{\eta }_{B})\)20,21. The expressions for \({\lambda }_{A}=|{\lambda }_{A}|{e}^{i{\varphi }_{A}}\) and \({\lambda }_{B}=|{\lambda }_{B}|{e}^{i{\varphi }_{B}}\) constitute a convenient gauge for our problem. We put ϕ A = 0 and \({\varphi }_{B}=(n+\tfrac{1}{2})\pi \) with integer n = 0, 1, 2, … corresponding to the total flux through the ring of Fig. 1. This parameter is experimentally tunable by changing the external magnetic field. This fact gives certain advantages to our proposal with respect to the previous works with asymmetric couplings between a single QD and a pair of MFs at the ends of a topological Kitaev wire28,29,30,31. According to ref.32 the parameter ε2 describing the overlap between the MFs depends on magnetic field in an oscillatory manner, the amplitudes \(|{\lambda }_{A}|=\frac{t+{\rm{\Delta }}}{\sqrt{2}}\) and \(|{\lambda }_{B}|=\frac{|{\rm{\Delta }}-t|}{\sqrt{2}}\) demonstrate the same behavior (see Sec. III-A of ref.30) and thus external magnetic field affects not only the relative phase between λ A and λ B but their absolute values as well. To fulfill the condition |λ B | < |λ A | one should place the QD closer the MF η A than to the MF η B .
We map the original Hamiltonian into one where the electronic states d1 and d2 are connected via normal tunneling t and bounded as delocalized Cooper pair, with binding energy Δ:
This expression represents a shortened version of the microscopic model for the Kitaev wire corresponding to the Kitaev dimer (see Fig. 1(b)). As it was shown in the refs33 and34 this model allows clear distinguishing between topologically trivial and Majorana-induced zero-bias peak in the conductance.
In what follows, we use the Landauer-Büttiker formula for the zero-bias thermoelectric quantities \({ {\mathcal L} }_{n}\)22,23:
where h is Planck’s constant, \({\rm{\Gamma }}=2\pi {V}^{2}\,{\sum }_{k}\,\delta (\varepsilon -{\varepsilon }_{k})\) is Anderson broadening35 and f F stands for Fermi-Dirac distribution. The quantity
is electronic transmittance through the QD, with \({\tilde{{\mathscr{G}}}}_{{d}_{1}{d}_{1}}\) being retarded Green’s function for the QD in the energy domain ε, obtained from the Fourier transform \({\tilde{{\mathscr{G}}}}_{{\mathscr{A}} {\mathcal B} }=\int \,d\tau {\tilde{{\mathscr{G}}}}_{{\mathscr{A}} {\mathcal B} }{e}^{\frac{i}{\hslash }(\varepsilon +i{0}^{+})\tau }\), where
corresponds to the Green’s function in time domain τ, expressed in terms of the Heaviside function θ(τ) and thermal density matrix ρ for Eq. (1).
Experimentally measurable thermoelectric coefficients can be expressed via \({ {\mathcal L} }_{0}\), \({ {\mathcal L} }_{1}\) and \({ {\mathcal L} }_{2}\) as:
and
for the electrical and thermal conductances and thermopower, respectively (T denotes the temperature of the system).
We also investigate the violation of Wiedemann-Franz law, given by
in units of Lorenz number L0 = (π2/3) (k B /e)2 and corresponding behavior of the dimensionless figure of merit22,23
For Eq. (4), we use equation-of-motion (EOM) method36 summarized as follows:
with \({\mathscr{A}}= {\mathcal B} ={d}_{1}\).
As our Hamiltonian given by Eqs (1) and (2) is quadratic, the set of the EOM for the single particle Green’s functions can be closed without any truncation procedure37. We find the following four coupled linear algebraic equations:
where Σ = −iΓ is the self-energy of the coupling with the metallic leads
and
with
and
This gives the Green’s function of the QD:
where the part of self-energy
describes the hybridization between MFs and QD.
Importantly, for the low temperatures regime, the substitution of Eq. (19) into Eq. (3) and its decomposition into Sommerfeld series23,26 allows to get analytical expressions for thermoelectric coefficients:
where
with
Comparison of the Eqs (21) and (22) allows us to conclude that the peak values of the electric conductance are reached when S = 0 for which \(d\,{\mathscr{T}}/d\varepsilon =0\) which happens when
As we will see below, fulfillment of this condition corresponds to the presence of an electron-hole symmetry in the system. Note that as ε2 enters in the denominator of the Eq. (25), even slight differences between t and Δ will be enough to change drastically the position of the resonance if hybridization between the MFs is small.
Results and Discussion
In our further calculations, we scale the energy in units of the Anderson broadening \({\rm{\Gamma }}=2\pi {V}^{2}\,{\sum }_{k}\,\delta (\varepsilon -{\varepsilon }_{k})\)35 and take the temperature of the system k B T = 10−4Γ. The Anderson broadening Γ defines the coupling between the QD and the metallic leads, which is assumed to be symmetrical for a sake of simplicity.
We start our analysis from the case when only a single MF (η A ) is coupled to the QD. In terms of the amplitudes t,Δ this corresponds to t = Δ. To be specific, we fix t = Δ = 4Γ. Looking at Eq. (2), we see that the terms \({d}_{1}{d}_{2}^{\dagger }+{\rm{H}}.{\rm{c}}.\) and \({d}_{2}^{\dagger }{d}_{1}^{\dagger }+{\rm{H}}.{\rm{c}}.\) enter into Hamiltonian with equal weights, and thus we are in the superconducting (SC)-metallic boundary phase.
Figure 2(a) shows the electrical conductance \(G={e}^{2}\,{ {\mathcal L} }_{0}\) scaled in units of the conductance quantum G0 = e2/h as a function of the QD energy level ε1, for several coupling amplitudes ε2 between the MFs. Note that, if MFs are completely isolated from each other (ε2 = 0), the conductance reveals a plateau with G = G0/2 whatever the value of ε1 (black line), and similar trend is observed in the thermal conductance shown in the Fig. 2(b). The effect is due to the leaking of the Majorana fermion state into the QD38. The MF zero-mode becomes pinned at the Fermi level of the metallic leads, but within the QD electronic-structure. With increase of the coupling between the wire and the QD, the MF state of the Kitaev wire leaks into the QD. As a result, a peak at the Fermi energy emerges in the QD density of states (DOS), while in the DOS corresponding to the edge of the wire the corresponding peak becomes gradually suppressed. Consequently, the QD effectively becomes the new edge of the Kitaev wire. This scenario was reported experimentally in the ref.9.
Electrical and thermal conductances of the system corresponding to SC-metallic boundary phase, t = Δ = 4Γ: (a) Electrical conductance as function of the QD energy level ε1 for several ε2 values of the couplings between MFs. (b) Corresponding thermal conductance. For both cases the resonance at the Fermi energy ε1 = 0 occurs if ε2 ≠ 0. For ε2 = 0 the conductance plateau is observed (see main text for the corresponding discussion). The inset shows the equivalent circuit with an auxiliary fermion d2 constructed from MFs η A and η B (red half-circles).
To get resonant response of the thermoelectric conductances one should consider the case ε2 ≠ 0, corresponding to the splitting of the MF zero-bias peak. The resonant behavior of G and K can be understood as arising from the presence of an auxiliary fermion d2, in the Hamiltonian [Eq. (2)], whose energy ε2 is now detuned from the Fermi level (see inset of Fig. 2(b)). In this case, the regular fermion state instead of the corresponding half-fermion provided by MF η A gives the main contribution to the charge and heat current. In this scenario, filtering of the electricity and heat emerges: the maximal transmission occurs at ε1 = 0. Our Fig. 2(a,b) recover the findings of Fig. 5(a) in ref.23. Our work, however, have an important novel dimension: we demonstrate that even small deviations of the system from the SC-metallic boundary phase which can be achieved by the control of the asymmetry of the couplings allows realization of the efficient tuners of electricity and heat. This effect is shown in the Fig. 3(a,b). As one can see, even small detuning of the coefficient t from the value t = Δ leads to substantial blueshift (for the case t > Δ) or redshift (for the case t < Δ) of the conductance resonances. Such sensitivity is a direct consequence of the Eq. (25) defining the position of the resonances.
Electrical and thermal conductances as functions of the QD energy level outside SC-metallic boundary phase. Slight deviations from the condition t = Δ result in the shift of the resonance peak for the electrical (panel (a)) and thermal (panel (b)) conductances. The corresponding resonances are blueshifted for t > Δ and redshifted for t < Δ as compared to the case of the SC-metallic boundary phase. Insets show the equivalent circuit with auxiliary fermion d2 constructed from MFs η A and η B (red half-circles).
To shed more light on the effect of the tuning of charge and heat transport in the system, we make a plot of the quantity \({\mathscr{T}}=-{\rm{\Gamma }}\text{Im}({\tilde{{\mathscr{G}}}}_{{d}_{1}{d}_{1}})\) appearing in the Eqs (3) and (4), as function of ε1 and ε, see Fig. 4(a–d). Figure 4(a) corresponds to the case t = Δ, ε2 = 0. One can recognize a “cat eye”-shaped central structure, corresponding to the vertical line at ε = 0. Everywhere along this line \({\mathscr{T}}={\rm{constant}}\), which according to the Eq. (21) means that changes in ε1 do not affect the conductance. This corresponds well to the conductance plateau in the Fig. 2. If ε2 is finite, the “cat eye” structure transforms into a double-fork profile as it is shown in the Fig. 4(b). Note that in this case, movement along the vertical line corresponding to ε = 0 lead to the change of the function \({\mathscr{T}}\), which according to the Eq. (21) leads to the modulation of the conductance. The maximal value is achieved at the point ε1 = 0, which corresponds well to the resonant character of the curves shown in the Fig. 2. The introduction of the finite value of ε2 and the asymmetry of the coupling between the QD and MFs (t ≠ Δ) leads to the shifts of the double-fork structure either upwards by ε1 scale for t > Δ (panel (c), blueshift of the resonant curves in the Fig. 3) or downwards by ε1 scale for t < Δ (panel (d), redshift of the resonant curves in the Fig. 3). It should be noted that similar results to the transmittance were reported both theoretically (ref.30) and experimentally (ref.31) for the geometry of a linear Kitaev wire with a QD attached to one of its ends placed between source and drain metallic leads. Differently from the case considered in our work, the authors account for the spin degree of freedom and particularly for ref.31, they evaluate the dependence of the conductance on the energy level of the QD and magnetic field, while we further analyze ε and asymmetry of couplings dependencies relevant for the understanding of the tuner regime. Despite the distinct geometry and spinless regime, our results and those reported in refs30,31 are in good correspondence with each other, thus validating the mechanism pointed out in refs30,32 of field-assisted overlapping between MFs and tunnel-couplings with the QD.
Transmittance \({\mathscr{T}}\) spanned by the axes of ε1 and ε. Panels (a,b) show the regime corresponding to SC-metallic boundary phase with t = Δ, for ε2 = 0 and finite ε2, respectively. Panel (a) reveals characteristic “cat eye”-shaped central structure at the Fermi level responsible for the onset of the conductance plateau. Panel (b) exhibits a double-fork structure responsible for the resonant character of the conductance for ε2 ≠ 0. Introduction of the asymmetry of the QD to MFs coupling leads to the vertical shift of the double-fork feature resulting in the blueshift (panel (c)) or redshift (panel (d)) of the resonant conductance curve. The bright arcs visualized in all panels represent poles of the Green’s function of the QD.
The possibility to tune electric and thermal conductances opens a way for tuning the thermopower (S), Wiedemann-Franz law (WF) and dimensionless figure of merit (ZT) as it is shown in the Fig. 5(a–c). In the Fig. 5(a) the dependence of the thermopower on ε1 is demonstrated. If t > Δ, at ε1 = 0, S > 0 and the setup behaves as a tuner of holes. On the contrary, for t < Δ, at ε1 = 0, S < 0 and the setup behaves as a tuner of electrons. Figure 5(b,c) illustrate the violation of WF law and the behavior of the dimensionless thermoelectric ZT, respectively. Note that ZT does not reach pronounced amplitudes, i.e., ZT < 126, even for finite values of G and K as dependence on S2 prevails if we take into account Eq. (21) into Eq. (10).
Conclusions
In summary, we considered theoretically thermoelectric conductances for the device consisting of an individual QD coupled to both pair of MFs and metallic leads. The charge and heat conductances of this system as functions of an electron energy in the QD reveal resonant character. The position of the resonance can be tuned by changing the degree of asymmetry between the QD and the MFs, which allows us to propose the scheme of the tuner of heat and charge. Thermopower, Wiedemann-Franz law and the figure of merit are found to be sensitive to the asymmetry of the coupling as well. Our findings will pave way for the development of thermoelectric nanodevices based on MFs.
References
Alicea, J. Rep. Prog. Phys. 75, 076501 (2012).
Elliott, S. R. & Franz, M. Rev. Mod. Phys. 87, 137 (2015).
Kitaev, A. Y. Phys. Usp. 44, 131 (2001).
Zyuzin, A. A., Rainis, D., Klinovaja, J. & Loss, D. Phys. Rev. Lett. 111, 056802 (2013).
Rainis, D., Klinovaja, J., Trifunovic, L. & Loss, D. Phys. Rev. B 87, 024515 (2013).
Zazunov, A., Sodano, P. & Egger, R. New J. Phys 15, 035033 (2013).
Roy, D., Bolech, C. J. & Shah, N. Phys. Rev. B 86, 094503 (2012).
Mourik, V. et al. Science 336, 1003 (2012).
Deng, M. T. et al. Science 354, 6319 (2016).
Perge, S. N. et al. Science 346, 602 (2014).
Pawlak, R. et al. Nature Partner Journals Quantum Information 2, 16035 (2016).
Moore, G. & Read, N. Nucl. Phys. B 360, 362 (1991).
Fu, L., Kane, C. L. & Mele, E. J. Phys. Rev. Lett. 98, 106803 (2007).
Fu, L. & Kane, C. L. Phys. Rev. Lett. 100, 096407 (2008).
Sau, J. D., Lutchyn, R. M., Tewari, S. & Das Sarma, S. Phys. Rev. Lett. 104, 040502 (2010).
Kawakami, T. & Hu, X. Phys. Rev. Lett. 115, 177001 (2015).
Flensberg, K. Phys. Rev. Lett. 106, 090503 (2011).
Leijnse, M. & Flensberg, K. Phys. Rev. Lett. 107, 210502 (2011).
Chiu, C.-K., Sau, J. D. & Das Sarma, S. arXiv:1709.04475 (2017).
Dessotti, F. A. et al. Phys. Rev. B 94, 125426 (2016).
Ricco, L. S. et al. Phys. Rev. B 93, 165116 (2016).
Andrade, J. P. R., Ovando, O. Á., Orellana, P. A. & Ulloa, S. E. Phys. Rev. B 94, 155436 (2016).
López, R., Lee, M., Serra, L. & Lim, J. S. Phys. Rev. B 89, 205418 (2014).
Leijnse, M. New J. Phys. 16, 015029 (2014).
Valentini, S., Fazio, R., Giovannetti, V. & Taddei, F. Phys. Rev. B 91, 045430 (2015).
Dubi, Y. & Di Ventra, M. Rev. Mod. Phys. 83, 131 (2011).
Liu, D. E. & Baranger, H. U. Phys. Rev. B 84, 201308(R) (2011).
Clarke, D. J. Phys. Rev. B 96, 201109(R) (2017).
Schuray, A., Weithofer, L. & Recher, P. Phys. Rev. B 96, 085417 (2017).
Prada, E., Aguado, R. & Jose, P. S. Phys. Rev. B 96, 085418 (2017).
Deng, M. T. et al. arXiv:1712.03536v1.
Danon, J., Hansen, E. B. & Flensberg, K. Phys. Rev. B 96, 125420 (2017).
Stanescu, T. D. & Tewari, S. Phys. Rev. B 89, 220507(R) (2014).
Roy, D., Bondyopadhaya, N. & Tewari, S. Phys. Rev. B 88, 020502(R) (2013).
Anderson, P. W. Phys. Rev. 124, 41 (1961).
Haug, H. & Jauho, A. P. Quantum Kinetics in Transport and Optics of Semiconductors, Springer Series in Solid-State Sciences. (Springer, New York, 1996; 123.
Ricco, L. S., Marques, Y., Dessotti, F. A., de Souza, M. & Seridonio, A. C. Phys. E 78, 25 (2016).
Vernek, E., Penteado, P. H., Seridonio, A. C. & Egues, J. C. Phys. Rev. B 89, 165314 (2014).
Acknowledgements
This work was supported by the Brazilian funding agencies CNPq Grant No. 307573/2015-0, CAPES and São Paulo Research Foundation (FAPESP) Grant No. 2015/23539-8. I.A.S. acknowledges support from Horizon2020 RISE project CoExAN and the project No. 3.8884.2017/8.9 of the Ministry of Education and Science of the Russian Federation.
Author information
Authors and Affiliations
Contributions
A.C.S., M.S.F. and I.A.S. formulated the problem and wrote the manuscript. L.S.R. and A.C.S. derived the expressions and M.S.F. performed their numerical computing. F.A.D. and L.S.R. plotted the figures. All co-authors taken part in the discussions and reviewed the manuscript as well.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ricco, L.S., Dessotti, F.A., Shelykh, I.A. et al. Tuning of heat and charge transport by Majorana fermions. Sci Rep 8, 2790 (2018). https://doi.org/10.1038/s41598-018-21180-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-21180-9
This article is cited by
-
Thermoelectric properties of topological chains coupled to a quantum dot
Scientific Reports (2023)
-
Topological isoconductance signatures in Majorana nanowires
Scientific Reports (2021)
-
Detecting Spin Heat Accumulation by Sign Reversion of Thermopower in a Quantum Dot Side-Coupled to Majorana Bound States
Journal of Low Temperature Physics (2021)
-
Thermoelectric Effect in a Correlated Quantum Dot Side-Coupled to Majorana Bound States
Nanoscale Research Letters (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.