Abstract
Monitoring the in vivo dose distribution in proton therapy is desirable for the accurate irradiation of a tumor. Although positron emission tomography (PET) is widely used for confirmation, the obtained distribution of positron emitters produced by the protons does not trace the dose distribution due to the different physical processes. To estimate the accurate dose from the PET image, the cross sections of nuclear reactions that produce positron emitters are important yet far from being sufficient. In this study, we measured the cross sections of 16O(p,x)15O, 16O(p,x)13N, and 16O(p,x)11C with a wide-energy range (approximately 5–70 MeV) by observing the temporal evolution of the Cherenkov radiation emitted from positrons generated via β+ decay along the proton path. Furthermore, we implemented the new cross sectional data into a conventional Monte Carlo (MC) simulation, so that a direct comparison was possible with the PET measurement. We confirmed that our MC results showed good agreement with the experimental data, both in terms of the spatial distributions and temporal evolutions. Although this is the first attempt at using the Cherenkov radiation in the measurements of nuclear cross sections, the obtained results suggest the method is convenient and widely applicable for high precision proton therapy.
Similar content being viewed by others
Introduction
Proton therapy is one of several radiation therapies to treat cancer. The most important advantage of using protons is the depth of the dose distribution as the protons deposit the highest dose near the end of their paths, at the Bragg peak. Owing to these characteristics, the dose can be concentrated to a tumor while minimizing the damage to normal tissues. Moreover, the protons have a sharp dose gradient; however the accurate estimation of dose distributions in human bodies is difficult owing to the uncertainties in the proton range in the human body. In the treatment planning of proton therapy, the patients undergo an X-ray computed tomography (CT) of the irradiation area. The conversion of X-ray CT numbers into proton stopping powers has uncertainties of the order of a few percent, which is equal to a few millimeter uncertainties of the proton range1,2,3,4. In addition, the position, motion, and anatomical changes of a patient can produce even more uncertainties. For these reasons, normal tissues may be fatally damaged if appropriate irradiation is not performed or an insufficient dose is delivered to the tumor. It is thus preferable to monitor the actual dose distribution in vivo.
During proton therapy, an incident proton that exceeds the Coulomb barrier bombards a target nucleus in the human body. This process is called nuclear fragmentation. To detect the gamma rays from the annihilation, positron emission tomography (PET) is used to visualize the distribution of positron emitters during or after irradiation5,6,7,8,9,10,11,12,13,14,15,16. However, the physical processes that produce positron emitters via the nuclear reactions is different from the energy loss process of protons through the electromagnetic interaction; as a result, the PET image does not reflect the dose information along the proton path. To estimate the dose from the PET image, a spatial distribution of positron emitters corresponding to various proton dose distributions must be known a priori17,18,19,20,21,22. Therefore, cross sectional data of the nuclear reactions that produce positron emitters are important, particularly for the components of the human body, for e.g., oxygen, carbon, and calcium. However, the current database of such nuclear reactions is insufficient below 250 MeV, which are important for proton therapy6,7,8,10,11,14,23,24. The lower energy region (under ∼70 MeV) is especially important because decelerated protons damage tumors most effectively14,23,24. Moreover, as the proton flux rapidly decreases, the straggling effect becomes stronger, and the cross sections vary drastically. Because the nuclear cross sections reported by previous studies have large uncertainties with a limited energy range, the precise measurement for the wide energy range has not yet been performed.
In this study, we developed a novel method of measuring nuclear reaction cross sections toward high-precision proton therapy by using Cherenkov radiation after proton irradiation. We used an electron multiplying charge-coupled device (EM-CCD) camera as a detector to visualize weak Ceherenkov radiation from the irradiated target. A synthetic quartz glass SiO2, containing oxygen, was irradiated with 72.0-MeV proton. We acquired cross sections of 16O(p,x)15O, 16O(p,x)13N, and 16O(p,x)11C, and compared them with the archival data. In addition, we used the obtained cross sections with Monte Carlo (MC) simulation code, the Particle and Heavy Ion Transport Code System (PHITS). Finally, we present a quantitative comparison between the MC simulation and PET measurements of water to validate the proposed method.
Results and Discussion
Cherenkov image
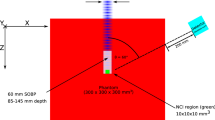
To measure the proton-induced nuclear reaction cross sections in oxygen, we chose a synthetic quartz glass SiO2 as a target. Figure 1 shows the temporal evolution of EM-CCD image, covering 120 s to 1205 s after the proton irradiation. The background subtractions followed by the median filter processing was performed for each image. Clearly, the distribution of Cherenkov radiation gradually changed with time. Note that intensity of the image, represented by “pixel value”, decreased with time. Moreover, the peak emission, which was hardly visible in the left panel, newly appeared in the middle and right panels, suggesting that the dominant positron emitters changed as time passed, due to the different decay times.
We used data sets of 120 to 3600 s for the analysis to remove the very fast components of positron emitters generated from silicon (half-lives: under 10 s). The positron emitters generated from oxygen were 14O, 15O, 13N, and 11C, with half-lives 70.62, 122.2, 597.9, and 1222 s25, respectively, in the energy range of proton therapy11,12. In this study, 15O, 13N, and 11C were considered to contribute to the Cherenkov radiation because the half-life of 14O is shorter than 120 s and the cross section values of 14O were very small (estimated at a few mbarns). By fitting the decay curve (see Supplementary information) at each depth, we resolved the contribution of each of the three components, namely, 15O, 13N, and 11C. An example of the decay curve fitting is shown in Fig. 2 (left) and the obtained distributions of the Cherenkov radiation decomposed by the decay curve fitting are presented in Fig. 2 (right). Note that the sudden drop in Cherenkov intensity at a depth below 0.12 cm was artificial, as the irradiated sample had a finite size, and the slightly different viewing angles, when measuring with the EM-CCD, affected the edge region of the target image.
Nuclear reaction cross sections
By processing the Cherenkov blur deconvolution and flux correction (see Supplementary information), we acquired the relative cross section values of each of the positron emitters. As the normalization of the Cherenkov radiation intensity as measured by the EM-CCD was arbitrary, the resultant cross sections were only given in relative units and difficult to quantify. As the first attempt in this study, we used the archival data of 16O(p,x)15O23,26 that was the most densely sampled with the least uncertainty, and the results agreed with others in literature. Note that the acquired cross section and archival data peaked at almost same energy, 35 MeV. Therefore, we normalized the acquired cross sections determined from the Cherenkov radiation to match with the archival maximal cross section of 76.8 mbarns ± 2.45% at 35 MeV. By choosing an absolute value, the cross sections of 16O(p,x)15O, 16O(p,x)13N, and 16O(p,x)11C were determined simultaneously. In this way, we acquired the three nuclear reaction cross sections in the energy range of 5–70 MeV. They are listed in Supplementary Table. We compared the acquired cross sections to those reported in the National Nuclear Data Center (NNDC)23,26,27,28,29,30,31,32,33 and the Intra-Nuclear Cascade of Liège (INCL) code34 as a general nuclear reaction model (Fig. 3). It is notable that our acquired cross sections have many more data points, smaller deviations, and smaller error values than the previous experimental values, as long as the normalization of the cross section is performed correctly.
We compared our data with previous experimental values and refer to the INCL briefly. Our data for 16O(p,x)15O around 10–30 MeV was consistent with previous experimental values23,26,28,29 within 1-σ uncertainty. In the energy range over 40 MeV, our acquired cross section values gradually decreased. This trend was more significant compared to that observed by Akagi et al., Albouy et al, and Valentin. It is noted that this tendency was also supported by other research groups35 and is also verified in the next subsection. The trend of the INCL was similar to that of our acquired cross section, but the absolute value was approximately 30% larger.
16O(p,x)13N is considered to be the sum of 16O(p,α)13N and 16O(p,2p2n)13N. The distinct features seen in the low energy range of approximately 10–20 MeV of 16O(p,α)13N were due to a combination of multiple peaks, explained by the nuclear resonance between 16O and a proton. Compared to Sajjad et al., Furukawa et al., and Whitehead et al., the peak width was broader and the peak value was approximately three times smaller in our data. This discrepancy can be explained by the energy resolution. There were several excitation energies of 16O(p,α)13N around 10–20 MeV. Our acquired cross section values for 10–20 MeV have uncertainties of a few MeV due to the straggling effect, and the typical width of the nuclear resonance line was several hundred keV; therefore, narrow peaks formed by the excitation energies were not separated in our data. As the straggling effect is also observed at the time of the actual proton therapy, our data is applicable, and this is discussed further in the next subsection. For higher energies, greater than 30 MeV, our data was consistent with that of Akagi et al., Kitwanga et al., Kettern et al., and the INCL. A gradual increase from 30 to 50 MeV was considered to be contamination from the 16O(p,2p2n)13N, with a threshold energy of approximately about 30 MeV.
The acquired cross section values of 16O(p,x)11C were roughly consistent with the previous experimental values and the INCL, but had a sharp gradient for the increasing area near 30–45 MeV. Considering the sparse data points and large uncertainties in previous reports, we succeeded in performing the precise measurement of the 16O(p,x)11C cross section.
Comparison with PET measurement
First, we simulated the PET measurement of water using the INCL cross section, which was used in various MC simulation codes36. We refer to the current status of the MC simulation for PET-based proton therapy. Then, to verify the newly obtained cross sections, we implemented them as a new library of the PHITS simulation code and compared these to the PET measurements.
In the PET measurements, the total exposure dose was 95.5 Gy, corresponding to 1.96 × 1011 of the incident protons. We then measured the number of positrons generated by an incident proton at each depth. The results are presented in Figs. 4 and 5, and all results took into account the statistic and systematic uncertainties.
It was clear that the existing nuclear reaction model was not valid in the energy range of proton therapy. An accurate estimation of the dose from the PET image was not possible with using these data. In contrast, our MC simulation results at each time interval were in good agreement with the PET measurements, within 1-σ uncertainty, for all regions. This result validates the normalization method and the obtained cross section values of 16O(p,x)15O, 16O(p,x)13N, and 16O(p,x)11C. We focused on the peak values at a depth of approximately 3.6–3.7 cm, where 16O(p,x)13N was dominant. The time evolutions of the PET measurements and our MC simulation around the peak were consistent, suggesting that our measured 16O(p,x)13N data was accurate enough to reproduce the PET imaging data. On the other hand, a small discrepancy at a depth near 3.0–3.2 cm was observed at 15–17 min, 20–22 min, and 25–27 min. It is probable that the sensitivity correction of the PET detector was not performed precisely. We conclude that our acquired cross sections are promising choice for realizing the proton dose estimation from the PET images.
Methods
Principles of measuring the cross sections from Cherenkov radiation
Protons that exceed the Coulomb barrier bombard a target nucleus, some of which produce positron emitters via various nuclear reaction channels. Positrons can therefore emit weak light along their path, namely Cherenkov radiation37,38, which has been receiving attention as a new tool for luminescence imaging39,40. Therefore, the observed light after proton irradiation traces the distribution of generating positron emitters41,42,43 and the temporal evolution of the Cherenkov radiation reflects the decay time. As protons travel through the material while depositing energy, the depth distribution can be converted into the proton energy distribution. Then, by acquiring the light intensity in the depth direction, we can convert it into the nuclear reaction cross section depending on the incident proton energy.
We acquired the spatial and temporal evolution of Cherenkov radiation by using a CCD camera as the detector. We plotted the pixel values versus the time at each depth. By directly fitting a decay curve, we resolved the contributions of each of the positron emitters. The distribution of the resolved Cherenkov radiation was slightly different from the spatial distribution of the positron emitters themselves, because Cherenkov radiation is generated along the tracks of positrons. We then performed Cherenkov blur deconvolution, and converted the depth into the proton energy. It is noted that the total proton flux gradually decreased with increasing depth, which was also corrected in our calculation. The absolute values of the cross sections could not be determined. Hence, we used the archival data of 16O(p,x)15O in the NNDC.
In this study, we used the MC simulation code PHITS Ver.2.93, which was mainly developed by the Japan Atomic Energy Agency (JAEA)44, and the nuclear reaction model INCL Ver.4.634. The INCL code describes protons, neutrons, pions and light-ions(d, t, 3He, or α) induced reactions. This code is also available in the Geant4 particle-transport toolkit and Monte Carlo N-Particle Transport Code (MCNPX)36. To calculate all reactions precisely, the event generator mode45,46,47 Ver.2 was also used.
Experimental setup
We performed two differential experiments, both of which were conducted at the National Institute of Radiological Sciences (NIRS), Japan, and the protons were provided by the AVF930 cyclotron.
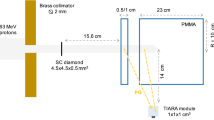
To measure the Cherenkov radiation, we used an EM-CCD camera (BU-66EM-UV, BITRAN) with a C-mount F-1.4 lens (LM16JC1MS, Kowa Optical Products). The Cherenkov radiation was so weak that the EM gain was configured at a maximum 20, with a cooling temperature of −20 °C and exposure time of 5 s. In the energy range of proton therapy, the nuclear fragmentation between hydrogen and protons does not occur, so that oxygen is the main component of the positron emitters for the PET monitor. We chose a 3 × 3 × 3.5 cm3 synthetic quartz glass SiO2 as a target, which contained only a very small amount of impurities, of the order of ppb. The decay time of the positron emitters from the silicon and oxygen were completely different30. Therefore, the contamination of the positron emitters from the silicon was less than 1%, at 120 s after irradiation (Fig. 6). SiO2 is a transparent material, enabling the Cherenkov radiation to be measured from outside the material by the CCD camera. The distance between the target and the CCD camera was 50 cm, where the pixel length of the CCD camera corresponded to 133 μm. The target was shielded from light except for the readout surface, and the measurement was performed with the experimental room completely dark. The SiO2 was irradiated with a 72.0-MeV pencil beam at 30 nA for 30 min. The beam size was 0.400 × 0.246 cm2 (FWHM). After the proton irradiation, we measured the Cherenkov radiation for an hour.
To verify our acquired cross sections, we also performed a PET measurement of a water target. We used planar-type PET (PPIS-4800-01, Hamamatsu Photonics)48, whose field of view (FOV) is 16.72 × 16.5 cm2. In each detector unit, 36 blocks of Position Sensitive PMT (R8520-00-C12, Hamamatsu Photonics) were equipped with 11 × 10 BGO scintillators. Each BGO scintillator of size 2.0 × 2.0 × 20 mm3 ware placed with a 2.2 mm pitch. The distance between the two detectors was 30 cm with a spatial resolution of 2.0 mm at FWHM. The absolute value of the PET count was calibrated with a 22Na point source (96.3 kBq ± 3%). The water target with 2% gelatin was contained by a 6.6 × 6.6 × 12.6 cm3 acrylic container with a thickness of 3 mm. To eliminate the influence of the positron emitters from the acrylic, the beam entrance region was covered with only a very thin film. The water was irradiated with a 72.0-MeV pencil beam at 5 nA for 5 s, with the 3 mm polyethylene (PE) inserted on the upstream side to decelerate the incident protons, whose energy decreased to 69.2 MeV. The number of incident protons were evaluated using a beam monitor, which was calibrated with an ionization chamber (Markus Ion Chamber 23343, PTW) in advance. After the proton irradiation, the PET measurement was performed for 30 min. These two experimental setups are illustrated in Fig. 7.
Data availability
The acquired cross sections of 16O(p,x)15O, 16O(p,x)13N, and 16O(p,x)11C are included in this Supplementary information files. The other datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Schneider, U., Pedroni, E. & Lomax, A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys. Med. Biol. 41, 111–124 (1996).
Kanematsu, N., Matsufuji, N., Kohno, R., Minohara, S. & Kanai, T. A CT calibration method based on the polybinary tissue model for radiotherapy treatment planning. Phys. Med. Biol. 48, 1053–1064 (2003).
Paganetti, H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys. Med. Biol. 57, 99–117 (2012).
Yang, M. et al. Comprehensive analysis of proton range uncertainties related to patient stopping-power-ratio estimation using the stoichiometric calibration. Phys. Med. Biol. 57, 4095–4115 (2012).
Vynckier, S. et al. Is it possible to verify directly a proton-treatment plan using positron emission tomography? Radiother. Oncol. 26, 275–277 (1993).
Oelfke, U., Lam, G. K. Y. & Atkins, M. S. Proton dose monitoring with PET: quantitative studies in Lucite. Phys. Med. Biol. 41, 177–196 (1996).
Parodi, K. & Enghardt, W. Potential application of PET in quality assurance of proton therapy. Phys. Med. Biol. 45, 151–156 (2000).
Parodi, K., Enghardt, W. & Haberer, T. In-beam PET measurements of β + radioactivity induced by proton beams. Phys. Med. Biol. 47, 21–36 (2002).
Hishikawa, Y. et al. Usefulness of positron-emission tomographic images after proton therapy. Int. J. Radiat. Oncol. Biol. Phys. 53, 1388–1391 (2002).
Parodi, K., P¨onisch, F. & Enghardt, W. Experimental Study on the Feasibility of In-Beam PET for Accurate Monitoring of Proton Therapy. IEEE Trans. Nucl. Sci. 52, 778–786 (2005).
Nishio, T., Sato, T., Kitamura, H., Murakami, K. & Ogino, T. Distributions of β + decayed nuclei generated in the CH2 and H2O targets by the target nuclear fragment reaction using therapeutic MONO and SOBP proton beam. Med. Phys. 32, 1070–1082 (2005).
Nishio, T., Ogino, T., Nomura, K. & Uchida, H. Dose-volume delivery guided proton therapy using beam on-line PET system. Med. Phys. 33, 4190–4197 (2006).
Parodi, K. et al. Patient study of in vivo verification of beam delivery and range, using positron emission tomography and computed tomography imaging after proton therapy. Int. J. Radiat. Oncol. Biol. Phys. 68, 920–934 (2007).
Attanasi, F. et al. Experimental validation of the filtering approach for dose monitoring in proton therapy at low energy. Phys. Med. 24, 102–106 (2008).
Zhu, X. & Fakhri, G. E. Proton Therapy Verification with PET Imaging. Theranostics 3, 731–740 (2013).
Kraan, A. C. et al. Online monitoring for proton therapy: A real-time procedure using a planar PET system. Nucl. Instr. and Meth. A 786, 120–126 (2015).
Parodi, K. & Bortfeld, T. A filtering approach based on Gaussian-powerlaw convolutions for local PET verification of proton radiotherapy. Phys. Med. Biol. 51, 1991–2009 (2006).
Inaniwa, T. et al. Measurements of deposited dose with induced β + activity in proton and heavy-ion therapy. Nucl. Instr. and Meth. A 580, 1135–1138 (2007).
Fourkal, E., Fan, J. & Veltchev, I. Absolute dose reconstruction in proton therapy using PET imaging modality: feasibility study. Phys. Med. Biol. 54, N217–N228 (2009).
Remmele, S., Hesser, J., Paganetti, H. & Bortfeld, T. A deconvolution approach for PET-based dose reconstruction in proton radiotherapy. Phys. Med. Biol. 56, 7601–7619 (2011).
Frey, K. et al. TPS PET -A TPS-based approach for in vivo dose verification with PET in proton therapy. Phys. Med. Biol. 59, 1–21 (2014).
Schumann, A. et al. From prompt gamma distribution to dose: a novel approach combining an evolutionary algorithm and filtering based on Gaussian powerlaw convolutions. Phys. Med. Biol. 61, 6919–6934 (2016).
Akagi, T. et al. Experimental study for the production cross sections of positron emitters induced from 12C and 16O nuclei by low-energy proton beams. Radiat. Meas. 59, 262–269 (2013).
Matsushita, K. et al. Measurement of proton-induced target fragmentation cross sections in carbon. Nucl. Phys. A. 946, 104–116 (2016).
Nuclear Data Center, N. Nuclear structure & decay Data (NuDat). https://www.nndc.bnl.gov/nudat2/.
Sajjad, M., Lambrecht, R. M. & Wolf, A. P. Cyclotron Isotopes and Radiopharmaceuticals. XXXVI. Investigation of Some Excitation Functions for the preparation of 15O, 13N and 11C. Radiochim. Acta. 38, 57–64 (1985).
Albouy, M. G. et al. Spallation of oxygen by protons with 20 to 150 MeV. Phys. Lett. 2, 306–307 (1962).
Kitwanga, S. W., Leleux, P., Lipnik, P. & Vanhorenbeeck, J. Production of 13N radioactive nuclei from 13C(p, n) or 16O(p,) reactions. Phys. Rev. C40, 306–307 (1989).
Valentin, L. Réactions (p, n) et (p, pn) Induites à moyenne énergie sur des noyaux légers. Nucl. Phys. 62, 81–102 (1965).
Kettern, K. et al. Formation of short-lived positron emitters in reactions of protons of energies up to 200 MeV with the target elements carbon, nitrogen and oxygen. Appl. Radiat. Isot. 60, 939–945 (2004).
Furukawa, M. et al. Excitation Function for the Reaction 11B(p, n)11B up to E p =15 MeV and Energy Levels of 12C. Phys. Soc. Jpn. 15, 2167–2170 (1960).
Whitehead, A. B. & Foster, J. S. Activation cross sections for 12C(p, pn)11C, 16O(p,)13N, and 19F(p, pn)18F. Can. J. Phys. 36, 1276–1285 (1958).
Bimbot, R. & Gauvin, H. Spallation reactions of light nuclei induced by protons from 50, 100 to 153 MeV. Compte. Rendu. 273, 1054 (1971).
Boudard, A., Cugnon, J., David, J. C., Leray, S. & Mancusi, D. New potentialities of the liège intranuclear cascade model for reactions induced by nucleons and light charged particles. Phys. Rev. C87, 014606 (2013).
Espana, S. et al. The reliability of proton-nuclear interaction cross-section data to predict proton-induced PET images in proton therapy. Phys. Med. Biol. 56, 2687–2698 (2011).
CEA-Irfu and the University of Liège. the Liège intranuclear cascade model (INCL). http://irfu.cea.fr/Sphn/Spallation/incl.html.
Cherenkov, P. A. Visible emission of clean liquids by action of gamma radiation. Doklady Akad. Nauk SSSR 2, 451 (1934).
Tamm, I. E. & Frank, I. M. Coherent Radiation of Fast Electrons in a Medium. Doklady Akad. Nauk SSSR 14, 107 (1937).
Gregory, S. M., Ruby, K. G., David, L. B., Changqing, L. & Simon, R. C. in vivo Cerenkov luminescence imaging: a new tool for molecular imaging. Phil. Trans. R. Soc. A 369, 4605–4619 (2011).
B Yann, C Bertrand, and A D Richard. Redshifted Cherenkov Radiation for in vivo Imaging: Coupling Cherenkov Radiation Energy Transfer to multiple Forster Resonance Energy Transfers. Sci. Rep., 7, 2017.
Helo, Y., Kacperek, A., Rosenberg, I., Royle, G. & Gibson, A. P. The physics of Cherenkov light production during proton therapy. Phys. Med. Biol. 59, 7107–7124 (2014).
Glaser, A. K., Zhang, R., Gladstone, D. J. & Pogue, B. W. Optical dosimetry of radiotherapy beams using Cherenkov radiation: the relationship between light emission and dose. Phys. Med. Biol. 59, 3789–3811 (2014).
Yamamoto, S. et al. High resolution Cherenkov light imaging of induced positron distribution in proton therapy. Med. Phys. 41, 111913 (2014).
Sato, T. et al. Particle and Heavy Ion Transport Code System PHITS, Version 2.52. Nucl. Sci. Technol. 50, 913–923 (2013).
Iwamoto, Y., Niita, K., Sakamoto, Y., Sato, T. & Matsuda, N. Validation of the event generator mode in the PHITS code and its application. In Proc. of International Conference on Nuclear data and science and Technology (2007).
Niita, K. et al. A new treatment of radiation behavior beyond one-body observables. In Proc. of International Conference on Nuclear data and science and Technology (2007).
Iwamoto, Y. et al. Application and Validation of Event Generator in the PHITS Code for the Low-Energy Neutron-Induced Reactions. Prog. Nucl. Sci. Technol. 2, 931–935 (2011).
Uchida, H. et al. A compact planar positron imaging system. Nucl. Instr. Meth. A 516, 564–574 (2004).
Author information
Authors and Affiliations
Contributions
T.Ma. and J.K. conceived the concept of the study. T.Ma., M.A., and M.T. conducted the measurements of the Cherenkov radiation. T.Ma., T.N., K.M., and T.Mi. conducted the PET measurement. T.N., K.M., S.Y., T.I., and T.T. provided technical advice. T.Ma. analyzed all of the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Masuda, T., Kataoka, J., Arimoto, M. et al. Measurement of nuclear reaction cross sections by using Cherenkov radiation toward high-precision proton therapy. Sci Rep 8, 2570 (2018). https://doi.org/10.1038/s41598-018-20906-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-20906-z
This article is cited by
-
Discovery of the luminescence of water during irradiation of radiation at a lower energy than the Cherenkov light threshold
Radiological Physics and Technology (2021)
-
Precision imaging of 4.4 MeV gamma rays using a 3-D position sensitive Compton camera
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.