Abstract
In the exceedingly rare event of nuclear reactor core meltdown, uranium dioxide fuel reacts with Zircaloy cladding to produce eutectic melts which can subsequently be oxidized by coolant/moderator water. Oxidized corium liquids in the xUO2·(100 − x)ZrO2 system were produced via laser melting of UO2-ZrO2 mixtures to temperatures in excess of 3000 K. Contamination was avoided by floating the droplets on a gas stream within an aerodynamic levitator and in-situ high-energy x-ray diffraction experiments allowed structural details to be elucidated. Molecular dynamics simulations well reproduced diffraction and density data, and show less compositional variation in thermal expansion and viscosity than suggested by existing measurements. As such, corium liquids maintain their highly penetrating nature irrespective of the amount of oxidized cladding dissolved in the molten fuel. Metal-oxygen coordination numbers vary with both composition and temperature. The former is due to mismatch in native values, nUO(x = 100) ≈ 7 and nZrO(x = 0) ≈ 6, and the requirement for oxygen site stabilization. The latter provides a thermal expansion mechanism.
Similar content being viewed by others
Introduction
Multiscale modelling of material processes is essential for both forensic investigation of historically rare fission reactor core meltdowns, as well as development and design of future power reactors with improved safety and performance1,2,3. At the smallest, atomic length scales, molecular dynamics based on semi-empirical interatomic potentials remains a popular and powerful tool4,5,6,7,8, allowing access to wider length and time scales as compared to full quantum mechanical treatments of the electronic structure. Experimental validation of such simulations is of paramount importance1, but data at the extreme temperatures reached during core meltdown is scarce owing to the inherent practical challenges. Recently measurements pertaining to the atomistic structure of molten fuel and fuel-bearing phases have become possible9,10,11. Herein we seek to apply such techniques to the molten corium phase, obtained during extensive fuel-clad interaction, and to exploit these measurements by evaluating promising interatomic potentials which, in turn, are used to predict key structural and bulk physical properties including thermal expansion and viscosity. Melt viscosity in particular is an important property governing the spreading, and thereby the cooling, of corium in core-catchers12. The potentials and properties derived are suitable for larger scale simulations, including solid-melt interfaces between core materials, or to study the incorporation and behaviour of fission products. Moreover the predicted physical properties can be used to inform higher level finite element codes as part of multiscale reactor models.
A severe accident scenario involving melting of the reactor core leads to the formation of corium lavas which are initially composed primarily of fuel and cladding materials. The most common such materials are based on UO2 and zirconium respectively. Subsequent interaction with water present as coolant and/or neutron moderator leads to oxidation of U-Zr-O liquids and H2 generation. In this paper, we study the structure and properties of oxidized molten corium in the UO2-ZrO2 pseudobinary obtained by laser heating ~100 mg quantities of ceramic material during levitation on a gas jet13,14 within a hermetically sealed chamber9,10, Fig. 1B. In-situ measurements using high-energy synchrotron x-rays yield the melt’s structure factors, S(Q), which provide atomistic level structural information used to verify the efficacy of molecular dynamics (MD) models, themselves based on interatomic potentials refined to similar measurements on the molten endmember dioxides11,15. The UO2 potentials employed herein are derived from those of Yakub, et al.4.
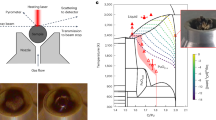
Comparison of measured (black circles) and MD modelled (red curves) x-ray diffraction data for liquid 27UO2·73ZrO2 at 3070 K. (A) Interference functions Q(S(Q) – 1), (B) schematic sample environment showing levitator within sealed chamber10, (C) close-up schematic of corium sample showing x-rays impinging on the top few hundred microns, (D) structure factors, S(Q) – 1, (E) close-up of two-dimensional data before integration of the above-plane scattering, (F) Fourier transforms of the data in (A) – the total correlation functions, T(r), as well as the weighted partial pair contributions w ij (r)⊗t ij (r). A Qmax = 17 Å−1 was used, without any Q-dependent window or modification function. The various reciprocal- and real-space functions are defined in22,40.
Results and Discussion
The agreement obtained between modelled and experimental x-ray S(Q) and real-space Fourier transforms T(r) is excellent, Figs 1 and 2. The real-space goodness-of-fit parameters Rχ16 are reported in Table S1. Rχ is actually smallest for the binary 27 mol% UO2 melt, even compared to the pure endmembers (Figs S2 and S3), which may be attributed to the increased structural and chemical disordering arising from the presence of two different cationic species. The slightly larger Rχ for the 4, 20 and 21 mol% UO2 corium melts (Fig. 2) is likely due to a marginally higher mean UO2 content being represented in the x-ray measurements, as compared to the MD simulations. Since UO2 is volatilized throughout these short measurements, even integrating over only the last few seconds (Table S2) results in a time averaged UO2 content that is higher than that of the recovered material, at which MD simulations were run. This interpretation is supported by the excess intensity in the measured T(r) circa 2.55 Å due to U-O bonds (Fig. 2), and the fact that this increases in magnitude at earlier times. The data in Fig. 2 further indicate negligible differences between measurements made in Ar and highly reducing Ar:5%H2 gases (cf. 20 and 21 mol% UO2 samples). It is important to bear in mind that at such high temperatures, and at low oxygen potentials, the formation of low valence states of uranium, initially U3+, can be significant. However, previous work on UO2-x melts9 revealed only subtle changes in the liquid diffraction patterns under different oxygen fugacities, from which a U3+ content of ≲ 27% was estimated in Ar:5%H2. Since U4+ is favored thermodynamically in Ar9,17 (owing to ppm levels of oxygen) and, based on the previous work, can be maintained kinetically even at lower oxygen potentials, we neglect the presence of lower valence states in our analyses.
Stack plot comparisons of all six diffraction measurements (open points) and corresponding MD modelled functions (red curves), with measured compositions marked. (A) Q(S(Q) – 1), (B) T(r) with Qmax = 11.77 Å−1 and without any Q-dependent window or modification function. The inset shows the full detector panel with masked regions in red (mainly beamstop). In both parts A and B, the blue points correspond to the nominally 30 mol% UO2 sample measured in Ar:5%H2 which overlay those of the sample of the same nominal composition measured in Ar, demonstrating that the data are essentially indistinguishable.
Simulated melt densities were also obtained within reasonably good agreement with existing measurements18,19,20,21, Fig. 3, despite considerable uncertainty in the experimental density of molten ZrO2. The experimental verification of the MD models by x-ray diffraction and comparison of their densities to the literature, as well as their basis in the well-tested Yakub potentials for UO24,11, encourages further interrogation of their statistical structure and properties.
Densities of liquids in the xUO2·(100 − x)ZrO2 system. Symbols correspond to selected MD models of the present work. Molten UO2 density is that measured by Breitung and Reil19 (Pu bearing) in close agreement with Drotning21 and recommended by Fink29, with shaded region corresponding to the recommended uncertainty. Molten ZrO2 density is that measured by Kohara, et al.18 with uncertainty region shaded. The various broken curves correspond to the regular solution model of Asmolov, et al.20 which is constrained to be consistent with their recommendation for the density of molten ZrO2 (red dashed), the Breitung and Reil19 density, and their measurements for a 60.4 mol% UO2 corium liquid. The various literature relations have been extrapolated beyond the measured regions, including into the supercooled states, below the melting points. Temperature error bars on the UO2 MD model points are representative of those for the other MD models. Standard deviations in the modelled densities are similar to half the symbol heights. Recent MD results employing CRG EAM potentials from Kim, et al.5 are also shown. Note that we have plotted our own fits to the digitized data from Kim et al.’s Fig. 5 because their original Table 5 equations do not reproduce their graphical data and are erroneous.
Composition Dependent Coordination Numbers
Several interesting phenomena are revealed in Fig. 4A, which shows that the cation-oxygen coordination numbers, nZrO and nUO, as well as their mean, nRO, depend on both composition and temperature (see also Fig. S4).
(A) Composition and temperature dependence of metal-oxygen coordination numbers in xUO2·(100 − x)ZrO2 liquids. Note that average R-O coordination is nRO = x’nUO + (1 − x’)nZrO, with x’ = x/100 the mole fraction UO2. The right hand ordinate axis gives the oxygen-metal coordination nOR = (1/2)nRO and corresponds only to the average O-R coordination, and not to O-U or O-Zr which are given by nOj = (c j /cO)njO. Points correspond to the MD models, using radial cutoffs of 3.03 Å for Zr-O and 3.25 Å for U-O bonds. Broken curves are linear fits to the points (excluding x = 4 and 20 mol% UO2), solid curves connect the nRO points which follow non-linear, quadratic trends owing to the fact nUO(x) and nZrO(x) are not parallel. Six temperatures are represented, from 3670 K down to 2670 K in 200 K increments. B-F) Schema of oxygen site electrostatic bond strength sums (ζO) in amorphous MO2 with native nMO = 6, upon doping with M’O2, native nM’O = 8. (B) Stable 3-fold oxygen site in an MO2 material with 6-fold cation coordination. (C) The 3-fold site becomes unstable when an 8-fold M’ cation is substituted in. (D) Assuming the 8-fold cation is too large to reduce its coordination number to 6, in order to stabilize the 3-fold site some of the 6-fold cations reduce their coordination number. (E) As the M’O2 concentration increases, the average oxygen-cation coordination exceeds 3 and some 4-fold sites are necessary. These are also unstable without some adjustment of the cation environments. (F) To stabilize the 4-fold site, some cation coordination numbers must increase. These cannot be the M cations because they have decreased their (average) coordination to stabilize the 3-fold sites, and therefore the M’-O coordination must increase. See Fig. S7 for the complementary schema considering doping of M’O2 by MO2.
At high temperatures solid UO2-ZrO2 binaries form a cubic solid solution, with all cations coordinated to 8 oxygen ions. Further increasing the temperature leads to melting, upon which nZrO and nUO have both been shown to decrease in the pure endmember dioxides11,15,18, as observed for several other oxides15,22, but importantly the effect is larger for zirconium. As such, molten ZrO2 has a different structure from molten UO2, akin to the difference in room temperature crystal structures, where monoclinic zirconia contains 7-fold Zr, while UO2 maintains the cubic structure with 8-fold U. The insight provided by our models of the binary melts is that this mismatch in endmember or ‘native’ R-O coordination numbers gives rise to linear composition dependence of both nZrO(x) and nUO(x). Since the slopes ∂nZrO/∂x ≠ ∂nUO/∂x, interpolation of nRO(x) between endmembers, Fig. 4A, is non-linear, and specifically, quadratic. A similar effect is observed for the alkali cations in chemically more complex mixed alkali silicate glasses23,24. Further support for the existence of this effect is provided by comparison of the appropriately weighted gUO(r) and gZrO(r) taken from simulations of the endmember dioxides, to the x-ray diffraction data for the 27 mol% UO2 corium binary. Figures S5 and S6 show that use of the endmember cation-oxygen bond length distributions leads to poorer agreement with the experimental corium T(r) in the region of the first peak, than does the simulation of the binary itself (Fig. 1F). We propose that the variation in local structure with composition can be qualitatively understood in terms of the stabilization of the various oxygen environments present.
Oxygen site stabilization
The concept of the Pauling electrostatic bond strength (EBS)25 has been shown to be helpful in understanding amorphous structures26. Within this approach the M-O bonds are assigned an EBS of s = Z M /nMO and then the stability of the anionic oxygen sites are assessed by the proximity of the EBS sum,
to its ideal value of |ZO| = 2, where the sum is taken over all O-M bonds to the given O2− anion. Figure 4B shows a schematic representation of a 3-fold oxygen site in a material built up of only 6-fold M4+ cations, similar to molten zirconia. The oxygen must be on average 3-coordinated given the universal relationship n jk = (c k /c j ) n kj where c k and c j are atomic fractions of the kth and j th atomic species respectively, or nOM = (1/2) nMO for MO2 stoichiometry (Fig. 4A right hand ordinate). In this case, ζO = 2 and the site stability is maximized (Fig. 4B). Figure 4C to F illustrate the effect of introducing a larger cation, M’, with larger native nM’O(100) = 8. We have chosen the value 8, which is larger than nUO(100) ≈ 7, in order to simplify the discussion by means of an integer native O-M’ coordination of nOM’(100) = 4. Figure 4C considers the dilute case, where M’O2 is doped into the MO2 melt such that the most likely ‘mixed cation’ oxygen sites are 3-fold, with two M and a single M’. With native coordination numbers maintained, ζO = 1.83 < 2 and the site is less stable than in the undoped melt. One way to stabilize the site would be for the M’ cations to adopt the 6-fold coordination environments of the host M cations. However, this is not what we observe in the corium MD models, and if this mechanism is unavailable, then the only option for O site stabilization is for the M cations to reduce their coordination. This behavior is illustrated in Fig. 4D where the arrows illustrate the shortening of the M-O bonds, which typically accompany a reduction in coordination number. This is exactly what is observed in the lower left of Fig. 4A, where nZrO(x) begins to decrease as uranium is introduced. As the M’O2 concentration increases, 4-fold oxygen sites become more abundant, Fig. 4E, and these can be stabilized via an increase in cation coordination. Since nMO(x) is already decreasing to stabilize the 3-fold oxygen sites, the only option available is for nM’O(x) to increase, as in Fig. 4F. This is the behavior observed in the upper left of Fig. 4A, where nUO(x) is larger than its native value at x = 100. One obtains a complementary picture if the dilution is reversed and MO2 is doped into the M’O2 melt, Fig. S7. The same general conclusions are reached in this way, whereby the right hand side of Fig. 4A is qualitatively described. Overall, for ∂nRO/∂x > 0, the individual derivatives, ∂nMO/∂x < 0 and ∂nM’O/∂x < 0, must have the opposite sign.
Clearly the EBS approach is highly simplified, not all bonds to a given cation are equal, and in the actual melts there are wide bond-length distributions, Figs 1F and 2B, as well as distributions of coordination environments, Fig. S8. The flexibility introduced through variable bond lengths allows oxygen sites to be stabilized without necessarily any coordination changes. For example, a given cation can simultaneously form longer bonds to 4-fold oxygen sites, and shorter ones to 3-fold oxygen sites. The magnitude of the coordination changes within the EBS approach are suggested by the coordination numbers given in Figs 4D,F, S7C, S7E, which are those required to yield ζO = 2. We reason that bond length variability will significantly depress the magnitude of these coordination changes. Furthermore, if one iterates around Figs 4B–F or S7 there is positive feedback, i.e. the two cation coordination numbers simply diverge in a runaway process. The limiting mechanism preventing this is the existence of minimum and maximum stable coordination numbers, which are controlled by the form of the pair potentials. Finally, the effect is smaller in our MD simulations given the smaller difference in native coordination numbers (nZrO(0) ≳ 6, nUO(100) ≈ 7) than illustrated. Nonetheless, similar non-ideal mixing behavior can be expected to occur in related (Ti,Zr,Hf)O2-(Th,U,Pu,…)O2 melts, but likely becomes negligibly small in more ideal cases, where cation radii are more closely matched, such as molten (U,Pu)O2 MOX fuels. In real Pu bearing melts, hypostoichiometry and the occurrence of reduced Pu3+ would play an important role, potentially again giving rise to composition dependent structures.
Temperature Dependent Coordination Numbers and Thermal Expansion
Also revealed in Fig. 4A is that nZrO(x,T) and nUO(x,T) both decrease linearly with T, and this is plotted explicitly in Fig. S4, which reveals that the temperature coefficients are approximately independent of composition (Table S1). The values ∂nZrO/∂T ≈ −3.2(1)×10−4 K−1 and ∂nUO/∂T ≈ −4.9(2)×10−4 K−1 are comparable to that calculated for titanium in molten TiO2, ∂nTiO/∂T = −3.0(1)×10−4 K−122, and it is evident that the magnitude of the effect increases with decreasing field strength, Ti4+ → Zr4+ → U4+, and increasing anharmonicity of the metal-oxygen pair potential. As with the thermal coordination number reduction, the temperature dependencies of the melt densities, Fig. 3, are also linear. This is suggestive of coordination change playing a key role as a thermal expansion mechanism. Positive correlation between coordination number and density is observed in many other settings, for example: the tetragonal and cubic phases of ZrO2 (8-fold Zr) are more dense than the monoclinic phase (7-fold Zr); both density and coordination numbers tend to increase with increasing pressure27,28; and materials like amorphous SiO2 and GeO2, composed of open networks of 4-fold tetrahedral cations, have lower atom number densities, despite their smaller cations, compared to melts of Ti, Zr, U dioxides, or the (U,Zr) corium melts, all of which contain more highly coordinated cations11,15,18,22. The calculated thermal expansion coefficients (TECs) of the corium melts at 3070 K are shown in Fig. 5A,B. They show remarkably little dependence on the corium composition, and lie between higher measured values for the endmembers19,20 and the lower value measured for a corium binary20. As such the models show no deep minimum in TEC as implied by the regular solution interpolation of Asmolov, et al.20. Such a deep minimum would require much larger structural variations with composition than observed by our diffraction measurements and MD simulations.
Physical properties of the MD modelled corium melts. (A,B) Volume thermal expansion coefficients at 3070 K compared to experimental data from Asmolov, et al.20 whose regular solution model is constrained to be consistent with the value for molten UO2 from Breitung and Reil19 (Pu bearing). (A) shows the same data as (B) over an extended ordinate range. (C) Self-diffusion coefficients plotted as ln D i against 104/T from which the activation energies, E i , and infinite temperature limits, D0i, can be obtained by linear regression of ln D i = ln D0i − E i /kBT. Temperature error bars on the UO2 MD model points are representative of those for the other MD models. The slopes yield the activation energies plotted in Fig. S9. (D) Viscosities estimated from the O2− ion diffusivities using the Stokes-Einstein relationship, Eqn. 2, with slip boundary condition and hydrodynamic radius equal to the Shannon ionic radius aO = 1.37 Å44. Similar estimates are obtained from the M4+ cation diffusivities as long as the hydrodynamic radius is set to encompass the first coordination shell33,34,35, Fig. S10. Statistical uncertainties are < 2%, within the size of the symbols. Measurements are also plotted; for molten UO2 from Woodley30 (extrapolated trend) with uncertainties recommended by Fink29 shaded, and for a 62 mol% UO2 corium melt from Abalin, et al.31. The latter authors report the kinematic viscosity, and we have therefore multiplied by the melt density (Asmolov, et al.20) to obtain the shear viscosities shown. The same viscosity data are plotted by Sudreau and Cognet12 with about 15% lower magnitude, presumably due to use of smaller densities, the provenance of which are not stated by those authors. Recent MD results from Kim et al5. are also shown, the shaded region corresponding to their range of interpolated corium viscosities (their Fig. 8c). The solid and chained curves for ZrO2 are based on Teter and EAM potentials, respectively. Note that we have plotted our own fits to the digitized data from Kim et al.’s Fig. 8a and b because their equations 38 and 39 (and their Table 5) are erroneous and do not reproduce their graphical data.
Diffusivity and Viscosity
The self-diffusion coefficients calculated for the corium liquids are large, of order 10−5 to 10−4 cm2s−1 (Fig. 5C), similar to the Yakub, et al.4 model for UO2 upon which our potentials are based11. Since no measurements of D i in corium liquids have been made, we have used the Stokes-Einstein (SE) relation to estimate the liquid viscosities from the DO:
Figure 5D. The result for UO2 is slightly smaller than the recommended29 measurements made by Woodley30 in the 3140 to 3300 K range, although the agreement is reasonable given the experimental uncertainties and assumption of the SE relation. As with the TECs, little variation in viscosity is observed across the range of corium compositions, and little increase with ZrO2 content is observed, in contrast to that implied by the comparison of the corium measurement of Abalin, et al.31 to that of Woodley30. Abalin, et al. explain this discrepancy as due to build up of pressure within Woodley’s apparatus as T increases – leading to an apparent suppression of the activation energy for viscous flow. Note however that the difference between Abalin, et al.31 and Woodley30 (or our SE estimates) amounts to a factor ≲ 1.4 (1.8), which is small – smaller than the change in viscosity of liquid water between room temperature and its freezing point. Considering that liquid viscosity varies over at least 16 orders of magnitude, from 1012 Pas for supercooled liquids near their glass transition, down to 10−4 Pas for boiling or supercritical water, a factor of < 2 is of little practical importance. The less precise molten UO2 viscosity measurements of Tsai and Olander32 are in fact larger than Woodley’s, and similar to Abalin et al.’s corium measurement.
The key observation is that the corium liquids have incredibly low viscosities of only a few mPas, approaching that of cold water. Combined with their high mass densities, these fluids are highly penetrating and capable of traveling large distances within a reactor vessel during meltdown, independent of the amount of cladding incorporated into the molten fuel. This fluidity can enhance the spreading and cooling of melts within suitable core-catcher designs.
It is noteworthy that similar viscosities are obtained using the cationic self-diffusion coefficients in the Stokes-Einstein relation only if the diffusion of [MO n ] coordination complexes are considered, such that the hydrodynamic radii are significantly larger than the ionic radii (Fig. S10). This has been explicitly validated in mixtures of molten halides33,34,35.
Arima6 has modelled other transport properties of corium melts, such as the thermal conductivities, and shown that they also show little variation with composition. Note however that the potential parameterizations used by Arima6 are based on those of Pedone, et al.36 (ξ = 0.60), which typically require further refinement to yield good agreement with liquid diffraction measurements at experimental temperatures15,22. Kim, et al.5 recently computed similar UO2 and ZrO2 melt viscosities to ours by means of the Green-Kubo stress autocorrelation approach (Fig. 5D). The authors used embedded atom method (EAM) many-body CRG potentials7,8, and additionally tested Teter pair potentials37 for ZrO2. They found some dependence on the choice of ZrO2 interatomic potential, but nonetheless inferred by compositional interpolation little variation in viscosity across the corium pseudobinary, in accord with our findings.
We note that EAM potentials, unlike simple pair potentials, allow for violation of the Cauchy relations between elastic tensor components, and have been shown7 to yield an improved bulk modulus for UO2 as compared to the Yakub model upon which our potentials are based. Direct comparisons of the EAM models5 to diffraction data for the molten end-members (Figs S11 to S13) reveal good agreement for UO2, but poorer agreement for ZrO2. Furthermore, whilst the density of molten UO2 appears well predicted by the EAM CRG potentials, that of ZrO2 is rather large, as compared to the measurements of Kohara, et al.18 and the function used by Asmolov, et al.20, see Fig. 3. The Teter potentials37 tested by Kim, et al.5 conversely yield a rather low melt density (very similar number density to UO2) and we have shown previously22 that these potentials require refinement to yield agreement with experimental densities and melt diffraction data.
Conclusions
High energy x-ray diffraction from levitated droplets of molten corium has been used to validate classical molecular dynamics models of the same liquids. These models were based upon the well-tested UO2 interatomic potentials of Yakub et al.4 subsequently refined to similarly measured x-ray structure factors and densities of the UO2 and ZrO2 molten endmembers. Modelled properties including thermal expansion, self-diffusion coefficients and melt viscosities show very little dependence on U/Zr ratio in the UO2-ZrO2 pseudobinary, and confirm the extremely fluid and highly penetrating nature of these liquids. Corium liquids are therefore capable of traveling large distances within a reactor vessel during meltdown, independent of the amount of cladding incorporated into the molten fuel. Such high fluidity can be beneficial for spreading and cooling core melts within suitable core-catcher designs. Mismatch between the native metal-oxygen coordination numbers, nUO ≈ 7 in molten UO2 and nZrO ≈ 6 in molten ZrO2, results in their variation with composition. In particular, both nUO and nZrO decrease with increasing UO2 content, while their mean value increases. This behavior is explained on the basis of the stabilization of the various 3- and 4-fold oxygen sites present in the melts. Temperature dependent coordination numbers are also observed, and this is suggested to be a primary mechanism for liquid thermal expansion. Temperature derivatives ∂nUO/∂T ≈ −5 × 10−4 K−1 and ∂nZrO/∂T ≈ −3 × 10−4 K−1, imply an increasing temperature dependence with increasing cation coordination and anharmonicity of the pair potentials. Our experimental verification of interatomic potentials for molten corium suggests their suitability for larger scale simulations, including melt-solid interface interaction, incorporation and behaviour of fission products, and for informing higher level finite element codes as part of multiscale reactor models.
Methods
Diffraction experiments, using 100.23 keV x-rays, were performed at beamline 6-ID-D of the Advanced Photon Source, Argonne, Il, using an aerodynamic levitator, 400 W, 10.6 μm laser heating, and a hermetically sealed chamber, Fig. 1B,C, as described previously9,10. For a single sample formed in-situ, a sample to detector distance of 306.6 mm was used, whilst for later experiments on sintered ceramic beads, the distance was 837.7 mm, both of which were calibrated using a crystalline CeO2 standard. In the latter measurements a second ZnSe laser window was installed to increase redundancy in the containment of radioactive samples. The argon gas between the two windows was held at a slight overpressure such that a sensor could detect breach of either window and cut power to the laser.
One corium sample was produced by in-situ fusion of individual UO2 and ZrO2 ceramic beads in the levitator nozzle via laser melting. Based on the masses of the initial beads (28 mg ZrO2 and 69 mg UO2), a composition of 52.9 mol% UO2 was obtained, Table S2. However, due to the high vapor pressure of UO2 above the melt, significant enrichment in ZrO2 occurred during the in-situ synthesis of the bead. This compositional change was assumed to take place primarily during the initial stages of fusion, which was confirmed by comparison of the individual 1 s diffraction patterns collected during the final 27 s melting stage (Fig. S1). The diffraction pattern was observed to be invariant over the latter 16 s, and only these data were averaged together and analyzed. The composition of the recovered material was determined by inductively coupled plasma optical emission spectrometry (ICP-OES) to be 27(3) mol% UO2, and this composition was used for the analysis.
Further samples were made by milling together powders of −270 mesh (53 μm) depleted UO2 and 1 μm ZrO2. The mixtures were pressed into a tungsten die to form a pellet that was then sintered at 1700 ◦C for 1 hr in an argon atmosphere using an induction furnace. The pellets were removed from the die and ground using a 400 grit silicon carbide polishing wheel to form roughly spherical samples 2.5–3.0 mm in diameter, suitable for levitation. Details of three samples successfully measured in the molten state are recorded in Table S2. ICP-OES analyses reveal final sample compositions of 20, 21 and 4 mol% UO2, compared to their nominal values of 30, 30 and 15 mol% UO2 respectively, consistent with the high vapor pressure of UO2 and estimates based on the mass losses. Measurements on nominal compositions of 50 and 75 mol% UO2 were attempted but samples were only partially melted and are not reported here. The likely reasons for a lack of complete melting are the scattering of laser light by airborne particles of condensed volatilized UO2, along with the effective laser power loss associated with an additional laser window.
Either Ar or 5%H2:95%Ar levitation gases were used. Although the latter is highly reducing, the effects on diffraction patterns of molten UO2−x have been shown to be small9, and are expected to be correspondingly smaller in dilutions with zirconia. This is confirmed by the strong similarity of the diffraction data for the two samples with the same nominal, 30 mol% UO2, compositions measured in different gases. As such, the UO2 component is considered stoichiometric in our analyses. Future investigations into the effect of U3+ content on melt structure and properties would be of great value, but extremely challenging experimentally, e.g. by in-situ U LIII edge XANES. Modelling of hypostoichometric melts on the other hand poses a more tractable avenue. The fully corrected structure factors, S(Q) – 1, are available as supplementary data online. Residual background intensity varying slowly with Q was removed using the top-hat convolution method (6.0 Å−1 top-hat width) and real-space intensity below 1.0 Å was supressed38, which is important for direct comparison to the MD simulated functions.
Atomistic models of corium melts were obtained by classical molecular dynamics (MD) simulation using the DL_POLY classic code39. Seven compositions were investigated, including the two endmembers, the ICP-OES measured final corium compositions of 4, 20 and 27 mol% UO2, and additionally 50 and 75 mol% UO2. As a starting point Morse potential parameterizations previously refined to measured x-ray structure factors of molten UO2 at 3270 K11 and molten ZrO2 at 3170 K15 were chosen. Those for UO2 are based on the well-tested Yakub potentials4, but with simplified interatomic pair-potentials taking the form
The second term is the short range Morse potential, parameterized by E jk , a jk and r0jk, and the first term represents the Coulombic energy between ions of formal charge, Z j , in units of the electron charge, e, and 0 < ξ ≤ 1 is the ionicity parameter. Since the two starting models are incompatible due to their different ξ = 0.55 and 0.60, for UO2 and ZrO2 respectively, a new model was derived for liquid ZrO2 using ξ = 0.55 and identical O-O interactions to the UO2 model11. EZrO and r0ZrO were refined to the x-ray S(Q) and measured density18,20, Fig. 3, within the isothermal-isobaric, NPT ensemble. The starting point for all MD trajectories was the 4800 atom configuration used in a study of molten TiO222, which has the same stoichiometry, and similar atom number density (0.0726 Å−3) to the corium melts. The ZrO2 refinement runs began with 5 ps of equilibration (forces capped at 103 kBT/Å), followed by a further 20 ps NPT trajectory, using a 1 fs timestep. A further 25 ps in the isothermal-isochoric NVT ensemble were used for calculation of the pair distribution functions, g jk (r)40, which were appropriately weighted, Fourier transformed and summed to yield the x-ray S(Q) (Figs S2, S3, 1,2). Ultimately the parameter EZrO was increased, resulting in an increase in system density toward the measured values18,20, Fig. 3, and r0ZrO was adjusted to maintain the UZrO(r) potential minimum at the same distance as that of the reference potential15. Any further increase in EZrO, and thereby the density, had a detrimental effect on the agreement between measured and simulated x-ray S(Q), Fig. S3, which may explain the low density of 0.068 Å−3 obtained by Skinner, et al.15 during the original ξ = 0.60 refinement. The finalized potential parameters are given in Table S3. These were used for modelling of binary corium melts where U and Zr cations were decorated randomly onto the starting configuration22. For each composition the models were equilibrated at 3670 K for 50 ps followed by a further 50 ps (NPT) over which reported volume (density), mean-square-displacement (MSD) and coordination data were collected. The temperature was then reduced by 200 K and the procedure repeated (with just 25 ps equilibration) until T = 2670 K. Note that several of the lowest temperature points sampled correspond to supercooled liquids. This allows for interpolation of results through the melting points, as well as for isothermal comparisons across the full composition range. The liquidus temperature ranges from 3120 K (pure UO2), down to a minimum of 2850 K at 40 mol% UO241. An additional 3170 K step was included for pure ZrO2 to match the x-ray experimental temperature15. A further 50 ps (NVT) was simulated for collection of g jk (r) for comparison to experimental S(Q), and to calculate coordination number and bond-angle distributions using the RINGS code42. In comparisons of x-ray and MD simulated S(Q) and T(r), the MD simulation closest to the experimental temperature (Table S2) was chosen, and the average density term, T 0(r) = 4πρ0r, added to the experimental T(r) = D(r) + T 0(r), was based on the MD simulated atom number density, ρ0. Deviations from a statistical distribution of U and Zr cations were not detected, based on the observed U-U, Zr-Zr and Zr-U coordination numbers.
Note that any effects of charge transfer or disproportionation via 2U4+ ⇄U3+ + U5+ have been neglected in our simulations. Gillan43 estimates the free energy for this process in molten UO2 at ΔF = 0.7 to 1.7 eV which yields between 4% and 18% of each of the [U3+] = [U5+] populations at the melting point. Over the 1000 K T range of our simulations, these become 2–6% and 15–20%. Clearly this is non-negligible from the point of view of electronic processes, whereby small polaron hopping provides a conduction mechanism. However, we expect the effect on structure and bulk properties such as viscosity to be much weaker. Consider the success of our and previous approaches4,5,6,7 in correctly predicting a wide range of properties in the absence of charge transfer. Nonetheless future investigation into the effects of charge transfer is of interest. For example, models such as ours could be used as the basis for more accurate predictions of ΔF than those of Gillan43 who used the Ornstein–Zernike equation with hypernetted-chain closure relation to estimate the melt structure.
Data availability
The fully corrected structure factors, S(Q) – 1, are available as supplementary data online. All other data are available upon request from the corresponding authors.
References
Bartel, T. J. et al. State-of-the-Art Report on Multi-scale Modelling of Nuclear Fuels. (OECD Nuclear Energy Agency, 2015).
Grimes, R. W., Konings, R. J. M. & Edwards, L. Greater tolerance for nuclear materials. Nat. Mater. 7, 683–685 (2008).
Konings, R. J. M., Wiss, T. & Benes, O. Predicting material release during a nuclear reactor accident. Nat. Mater. 14, 247–252, https://doi.org/10.1038/nmat4224 (2015).
Yakub, E., Ronchi, C. & Staicu, D. Molecular dynamics simulation of premelting and melting phase transitions in stoichiometric uranium dioxide. J. Chem. Phys. 127, 094508 (2007).
Kim, W. K., Shim, J. H. & Kaviany, M. Thermophysical properties of liquid UO2, ZrO2 and corium by molecular dynamics and predictive models. J. Nucl. Mater. 491, 126–137, https://doi.org/10.1016/j.jnucmat.2017.04.030 (2017).
Arima, T. Melting Point and Thermal Conductivity of UO2-ZrO2 Solid Solution: Molecular Dynamics Simulation. Journal of Computer Chemistry, Japan 14, 97–104 (2015).
Cooper, M. W. D., Rushton, M. J. D. & Grimes, R. W. A many-body potential approach to modelling the thermomechanical properties of actinide oxides. J. Phys.: Condens. Matter 26, 105401 (2014).
Liu, X. Y. et al. Molecular Dynamics Simulation of Thermal Transport in UO2 Containing Uranium, Oxygen, and Fission-product Defects. Phys. Rev. Appl. 6, 044015 (2016).
Alderman, O. L. G. et al. The structure of liquid UO2−x in reducing gas atmospheres. Appl. Phys. Lett. 110, 081904, https://doi.org/10.1063/1.4977035 (2017).
Weber, J. K. R. et al. Aerodynamic Levitator for In Situ X-ray Structure Measurements on High Temperature and Molten Nuclear Fuel Materials. Rev. Sci. Instrum. 87, 073902 (2016).
Skinner, L. B. et al. Molten uranium dioxide structure and dynamics. Science 346, 984–987, https://doi.org/10.1126/science.1259709 (2014).
Sudreau, F. & Cognet, G. Corium viscosity modelling above liquidus temperature. Nucl. Eng. Des. 178, 269–277, https://doi.org/10.1016/S0029-5493(97)00137-4 (1997).
McMillan, P. F. Levitating Liquids. Nat. Mater. 7, 843–844, https://doi.org/10.1038/Nmat2313 (2008).
Price, D. L. High-temperature levitated materials. (Cambridge University Press, 2010).
Skinner, L. B. et al. Low cation coordination in oxide melts. Phys. Rev. Lett. 112, 157801 (2014).
Grimley, D. I., Wright, A. C. & Sinclair, R. N. Neutron-Scattering from Vitreous Silica .4. Time-of-Flight Diffraction. J. Non-Cryst. Solids 119, 49–64 (1990).
Lindemer, T. B. & Besmann, T. M. Chemical thermodynamic representation of <UO2±x>. J. Nucl. Mater. 130, 473–488 (1985).
Kohara, S. et al. Atomic and electronic structures of an extremely fragile liquid. Nature Communications 5, 5892 (2014).
Breitung, W. & Reil, K. The density and compressibility of liquid (U, Pu)-mixed oxide. Nucl. Sci. Eng. 105, 205–217 (1990).
Asmolov, V. G. et al. The Density of UO2–ZrO2 Alloys. High Temp. 41, 627–632 (2003).
Drotning, W. In Proceedings of the Eighth Symposium on Thermophysical Properties. Gaithersburg, MD, National Bureau of Standards (1981).
Alderman, O. L. G., Skinner, L. B., Benmore, C. J., Tamalonis, A. & Weber, J. K. R. Structure of Molten Titanium Dioxide. Phys. Rev. B 90, 094204 (2014).
Yu, Y., Mauro, J. C. & Bauchy, M. Stretched exponential relaxation of glasses: Origin of the mixed-alkali effect. Am. Ceram. Soc. Bull. 96, 34–36 (2017).
Yu, Y. et al. Thermometer Effect: Origin of the Mixed Alkali Effect in Glass Relaxation. Phys. Rev. Lett. 119, 095501 (2017).
Pauling, L. The principles determining the structure of complex ionic crystals. J. Am. Chem. Soc. 51, 1010–1026 (1929).
Hannon, A. C. Bonding and structure in network glasses. J. Non-Cryst. Solids 451, 56–67, https://doi.org/10.1016/j.jnoncrysol.2016.04.035 (2016).
Kono, Y. et al. Ultrahigh-pressure polyamorphism in GeO2 glass with coordination number > 6. Proc. Natl. Acad. Sci. USA 113, 3436–3441, https://doi.org/10.1073/pnas.1524304113 (2016).
Zeidler, A., Salmon, P. S. & Skinner, L. B. Packing and the structural transformations in liquid and amorphous oxides from ambient to extreme conditions. Proc. Natl. Acad. Sci. USA, 201405660 (2014).
Fink, J. K. Thermophysical properties of uranium dioxide. J. Nucl. Mater. 279, 1–18, https://doi.org/10.1016/S0022-3115(99)00273-1 (2000).
Woodley, R. E. The viscosity of molten uranium dioxide. J. Nucl. Mater. 50, 103–106, https://doi.org/10.1016/0022-3115(74)90066-X (1974).
Abalin, S. S. et al. Corium kinematic viscosity measurement. Nucl. Eng. Des. 200, 107–115, https://doi.org/10.1016/S0029-5493(00)00238-7 (2000).
Tsai, H. C. & Olander, D. R. The viscosity of molten uranium dioxide. J. Nucl. Mater. 44, 83–86, https://doi.org/10.1016/0022-3115(72)90132-8 (1972).
Dewan, L. C., Simon, C., Madden, P. A., Hobbs, L. W. & Salanne, M. Molecular dynamics simulation of the thermodynamic and transport properties of the molten salt fast reactor fuel LiF–ThF4. J. Nucl. Mater. 434, 322–327, https://doi.org/10.1016/j.jnucmat.2012.12.006 (2013).
Brookes, R., Davies, A., Ketwaroo, G. & Madden, P. A. Diffusion coefficients in ionic liquids: relationship to the viscosity. J. Phys. Chem. B 109, 6485–6490 (2005).
Salanne, M., Simon, C., Turq, P. & Madden, P. A. Conductivity− Viscosity− Structure: Unpicking the Relationship in an Ionic Liquid. J. Phys. Chem. B 111, 4678–4684 (2007).
Pedone, A., Malavasi, G., Menziani, M. C., Cormack, A. N. & Segre, U. A new self-consistent empirical interatomic potential model for oxides, silicates, and silica-based glasses. J. Phys. Chem. B 110, 11780–11795, https://doi.org/10.1021/Jp0611018 (2006).
Du, J., Devanathan, R., Corrales, L. R., Weber, W. J. & Cormack, A. N. Short- and medium-range structure of amorphous zircon from molecular dynamics simulations. Phys. Rev. B 74, 214204 (2006).
Soper, A. K. & Barney, E. R. Extracting the pair distribution function from white-beam X-ray total scattering data. J. Appl. Cryst. 44, 714–726, https://doi.org/10.1107/S0021889811021455 (2011).
Smith, W. & Forester, T. R. DL_POLY_2.0: A general-purpose parallel molecular dynamics simulation package. J. Mol. Graphics 14, 136–141, https://doi.org/10.1016/S0263-7855(96)00043-4 (1996).
Keen, D. A. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Cryst. 34, 172–177 (2001).
Quaini, A. et al. High temperature investigation of the solid/liquid transition in the PuO2–UO2–ZrO2 system. J. Nucl. Mater. 467, 660–676 (2015).
Le Roux, S. & Jund, P. Ring statistics analysis of topological networks: New approach and application to amorphous GeS2 and SiO2 systems. Comp. Mater. Sci. 49, 70–83, https://doi.org/10.1016/j.commatsci.2010.04.023 (2010).
Gillan, M. Estimation of the free energy of charge transfer in molten UO2. Philos. Mag. B 46, 191–206 (1982).
Shannon, R. D. Revised Effective Ionic-Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. A 32, 751–767, https://doi.org/10.1107/S0567739476001551 (1976).
Acknowledgements
Thanks to Woong Kee Kim and Prof. Massoud Kaviany for discussion and provision of EAM model data from Ref.5. Work was supported by U.S. Department of Energy (DOE) under grant number SBIR DE-SC0015241 (OLGA, AJT, SS, JKRW). This research used resources of the Advanced Photon Source, a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
O.L.G.A., C.J.B., J.K.R.W., L.B.S., A.J.T. and S.S. performed the experiments. A.H. and M.A.W. synthesized samples and directed post diffraction experiment analyses of sample compositions. A.J.T. and J.K.R.W. designed the sample containment used at the synchrotron beamline, with input from the rest of the team. O.L.G.A. analyzed diffraction data, designed and performed molecular dynamics simulations and wrote the paper. C.J.B., J.K.R.W., M.A.W. conceived the idea to measure corium melts by high-energy x-ray diffraction. All authors made contributions to the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alderman, O.L.G., Benmore, C.J., Weber, J.K.R. et al. Corium lavas: structure and properties of molten UO2-ZrO2 under meltdown conditions. Sci Rep 8, 2434 (2018). https://doi.org/10.1038/s41598-018-20817-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-20817-z
This article is cited by
-
Thermophysical Properties of Liquid Zirconia Measured by Aerodynamic Levitation at High Temperature
International Journal of Thermophysics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.