Abstract
Ligaments provide stability to the human knee joint and play an essential role in restraining motion during daily activities. Compression-tension nonlinearity is a well-known characteristic of ligaments. Moreover, simpler material representations without this feature might give reasonable results because ligaments are primarily in tension during loading. However, the biomechanical role of different constitutive representations and their fibril-reinforced poroelastic properties is unknown. A numerical knee model which considers geometric and material nonlinearities of meniscus and cartilages was applied. Five different constitutive models for the ligaments (spring, elastic, hyperelastic, porohyperelastic, and fibril-reinforced porohyperelastic (FRPHE)) were implemented. Knee joint forces for the models with elastic, hyperelastic and porohyperelastic properties showed similar behavior throughout the stance, while the model with FRPHE properties exhibited lower joint forces during the last 50% of the stance phase. The model with ligaments as springs produced the lowest joint forces at this same stance phase. The results also showed that the fibril network contributed substantially to the knee joint forces, while the nonfibrillar matrix and fluid had small effects. Our results indicate that simpler material models of ligaments with similar properties in compression and tension can be used when the loading is directed primarily along the ligament axis in tension.
Similar content being viewed by others
Introduction
Stability of the knee joint is provided by different structures such as ligaments, menisci, and muscles which exhibit a complex mechanical behavior and affect the articular cartilage response under different loading conditions1. In particular, ligaments play an essential role in providing stability in more than one degree of freedom as well as restraining knee joint motion during external loads. However, the contributions of the individual ligaments and their structural constituents, and the importance of the material models of ligaments are not well known2,3,4. Research on the effect of these ligament properties in the knee joint contributes to understanding joint disorders and injury mechanisms.
The experimental and clinical studies have been complemented with computational knee models to overcome inherent limitations such as high cost, difficulties to obtain accurate measures in vivo, and reproduce degenerative situations in the knee. Previous numerical knee models have investigated the mechanical behavior of knee joint ligaments under different loading conditions5,6,7,8,9,10,11,12,13,14,15,16. For instance, some studies simulated ligaments as nonlinear elastic springs and cartilage and menisci as a simple linear elastic material or rigid12,17,18,19. Other studies have included realistic geometries of ligaments, but cartilage and menisci were treated as linear elastic materials14,20. Models with more complicated properties for cartilage have not typically incorporated fibril-reinforced biphasic properties for ligaments during dynamic gait21,22.
Nonlinear tensile properties of ligaments along axis have been extensively documented23,24,25, however, less studies have reported the anisotropy and the compressive mechanical response of the tendon or ligament tissue26,27,28. Nonetheless, the anisotropy of these tissues has been primarily suggested to results from the collagen fibril orientation26. During in vivo loading, the contribution of the compressive properties of ligaments may occur to some extent when ligaments are exposed to multiaxial states of stresses, bending, and transverse compressive loads. However, many finite element (FE) studies4,12,14,29,30 and musculoskeletal models18,31 have considered that, due to the ligament and tendon structure and composition, their contribution in tension is much greater than that in compression. This variance in compression and tension along the main axis of loading (strong in tension and soft in compression) has also been documented thoroughly for other fibril-reinforced poroelastic tissues, such as articular cartilage and meniscus32,33,34,35,36.
In order to apply knee joint models for clinical cases with large patient groups, they should be simple and fast but at the same time accurate and reliable. Because ligaments are primarily in tension during joint loading, it might be that the aforementioned compression-tension characteristic is not always needed. Then the properties along the tensile direction mainly control the ligament response and the compressive properties are not necessarily that important. For this reason, ligaments modeled in the knee with similar properties in compression and tension might give reasonable results at those time points of loading when there is minimal amount of bending and therefore local compression. This approach would simplify the model generation applied for clinical purposes, reducing computational demands (run time) and labour required to generate personalized knee models. Specifically, reliable and simplified models could potentially provide expeditious diagnostics for improving clinical outcomes in patients with orthopedic disorders.
Thus, the aim for this study was to investigate the effect of different constitutive representations and structural constituents (fibrillar matrix, nonfibrillar matrix, fluid) of ligaments on knee joint mechanics during the stance phase of gait. A finite element model of the knee joint which takes into account geometric and material nonlinearities of meniscus and cartilages was applied. Particularly, we simulated the effect of fibril-reinforced porohyperelastic properties of ligaments on the knee joint function as well as forces, stresses and strains in the tibial and patellar cartilages during walking. These results were compared with knee models with simpler geometries (springs) and 3-D constitutive models for ligaments. We hypothesize that the collagen network of ligaments contributes strongly to the knee joint mechanics while the contribution of the nonfibrillar matrix and especially fluid is minimal. However, we also hypothesize that at certain time points of stance when ligaments are elongated primarily along their axis it is possible to obtain similar mechanical response with a simple representation for ligaments compared to a complex formulation (fibril-reinforced porohyperelastic).
Methods
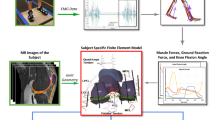
A general workflow of this study is shown in Fig. 1a.
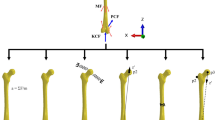
(a) Study workflow. (b) Gait input data for the numerical knee joint model, as obtained directly from21. (c) External-internal, valgus-varus moments, and flexion-extension rotation. (d) Anterior-posterior, distal-proximal and medial-lateral forces. Components of the total quadriceps force. (e) A posterior-lateral view of the three-dimensional finite element model of the knee shows articular cartilages, ligaments and tendons. The original model was compared to experiments in21.
Finite element model
A previously developed finite element model was applied and modified here22. A knee joint of an asymptomatic male subject (28 years, 80 kg) was imaged using MRI and the joint tissues (femoral, tibial and patellar cartilages, and meniscus) were segmented and meshed as described in our earlier study22. This MR imaging was conducted according to the ethical guidelines of Kuopio University Hospital, Finland. MR imaging was conducted with the permission (94/2011) from the local ethical committee of the Kuopio University Hospital, Kuopio, Finland, and written informed consent was obtained from the volunteer. Based on the same knee joint, patellar and quadriceps tendons (PT and QT) and six ligaments were segmented in this study. The six ligaments were anterior and posterior cruciate ligaments (ACL and PCL), medial and lateral collateral ligaments (MCL and LCL), and medial and lateral patellofemoral ligaments (MPFL and LPFL) (Fig. 1). Ligament and tendon geometries were segmented using the MR images (a clinical 3.0 T scanner, Philips, Best, Netherlands) which were taken using 3D fast spin-echo sequence (VISTA) (in-plane resolution = 0.5 mm, slice thickness = 0.5 mm, TR = 1300 ms, TE = 32.3 ms). Ligaments and their exact insertion sites were determined by consulting two orthopedic surgeons during the segmentation process. The segmented geometries were meshed in Abaqus v.6.13 (Dassault Systémes, Providence, USA). Gait input, properties of the patellofemoral ligaments and boundary conditions for the knee model were identical to an earlier study21,22 (Fig. 1b–d). In the simplified models, the ligaments and tendons were represented using an array of spring elements22,37 or meshed with tetrahedral pore pressure elements (type = C3D4P) in the 3D continuum models. In the most complex model, ACL, PCL, LCL and MCL were modeled as a fibril-reinforced porohyperelastic material. Cartilages were defined as a fibril-reinforced poroviscoelastic material38,39,40, while menisci were considered as a fibril-reinforced porohyperelastic material; our previous studies have validated the materials and applied these to the knee joint models37,41. The cartilage-bone interfaces were defined as rigid boundary conditions. Frictionless surface-to-surface contact was defined for all the contacting surfaces, i.e., interactions between cartilages and menisci, the external surfaces of solid ligaments and cartilages, and ACL and PCL. The master surfaces were determined as a surface, whereas the slave surfaces were defined as a node surface. Numerical simulations were run on a high performance workstation with 48x Intel Xeon E5-2690 v3 CPU (2.60 GHz) and 264 GB of memory.
Models with different mechanical properties for ligaments
Five knee joint models were constructed with different constitutive models for the ligaments: 1) spring, 2) linear elastic, 3) hyperelastic, 4) porohyperelastic and 5) fibril-reinforced porohyperelastic (FRPHE) material, which we briefly describe here (see the supplementary material for more details about the implementation of these constitutive models). In all cases, stress-strain behavior of the ligaments was defined such that the ligaments produced force in tension (strain > 0) but not in compression (strain < 0) during the gait. For the first two cases, Hooke´s law represents the relation between stresses (or forces) and strains (or elongations)
where \({{\boldsymbol{\sigma }}}_{{\bf{t}}{\bf{o}}{\bf{t}}}\) is the Cauchy stress tensor, ε is the infinitesimal strain tensor, and C is the fourth-order stiffness matrix, which is defined by the Young’s modulus (E) and Poisson’s ratio (ν). For the spring model, the stiffness is defined by a spring constant ks. The third model was defined using a neo-Hookean material, in which the stresses are given by
where Km is the bulk modulus, Gm is the shear modulus, J is the determinant of the deformation gradient tensor F and I is the unit tensor. For the fourth model, the ligaments were described as a biphasic tissue in which the porous solid matrix is fully saturated with water. The total stress in the tissue is then given by
where \({{\boldsymbol{\sigma }}}_{{\rm{tot}}}\) is the total stress tensor, \({{\boldsymbol{\sigma }}}_{{\rm{s}}}\) is the stress in the solid matrix, \({{\boldsymbol{\sigma }}}_{{\rm{fl}}}\) is the stress in the fluid matrix, p is the hydrostatic pressure and \({{\boldsymbol{\sigma }}}_{{\rm{eff}}}\) is the effective solid stress. In this model, \({{\boldsymbol{\sigma }}}_{{\rm{eff}}}\) was described by equation (2). Additionally, the permeability \(k\) was assumed to be strain-dependent and is as follows:
where k0 is the initial permeability, M is a positive constant, ϕ0 is the initial volume fraction of the solid phase, ϕf is the current volume fraction of the fluid phase and ϕs is the current volume fraction of the solid phase.
Finally, the FRPHE model considers that the solid matrix is divided into a non-fibrillar part, describing primarily the proteoglycan matrix, and a fibrillar elastic network, representing the collagen fibers. The total stress in the ligament tissue is then given by
where \({{\boldsymbol{\sigma }}}_{{\rm{f}}}\) and \({{\boldsymbol{\sigma }}}_{{\rm{nf}}}\) are the stresses in the collagen fibers and the non fibrillar matrix, respectively. The non-fibrillar component of the ligament is defined using a neo-Hookean material with biphasic properties as was described in equation (3). The fibril stress \({\sigma }_{{\rm{f}}}\) is given by
where Ef is the fibril network modulus and εf is the fibril strain. The fibril network stress arises from the sum of primary and secondary collagen fibril stresses, which is calculated separately for each integration point in each element40. Stresses for these fibrils in tension were
where \({\sigma }_{{\rm{f}},{\rm{p}}}\) and \({\sigma }_{{\rm{f}},{\rm{s}}}\) are the fibril stresses for primary and secondary fibrils, respectively, C is the density ratio between primary and secondary fibrils and \({\rho }_{z}\) is the relative collagen density.
Analysis
For the initial analysis, we estimated the initial group of material constants for each constitutive model based on experimental studies (Table 1). A Gaussian distribution was generated with a relative standard deviation (RSD) of 0.62, 0.60, 0.70, 0.71, 0.52 and 0.43 for the ACL, PCL, LCL, MCL, PT and QT (Fig. 2) 14,16,42,43. Based on these constants we performed a preliminary evaluation for all models on the tibial reaction force. A detailed list of material parameters used in the initial analysis for each constitutive model is given in Table 1.
Probabilistic density function of Young’s modulus of the ACL2,15,25,75,76,77,78,79,80,81,82,83, PCL2,15,75,77,80,82,84,85,86,87, MCL2,16,24,25,42,88,89,90,91,92,93,94, LCL2,23,88,91,92,94,95,96,97,98,99,100,101, PT81,88,95,102,103,104,105,106,107,108,109,110,111,112,113,114, and QT81,112,113,115. In this study, biphasic properties for ligaments were selected based on43 and MPFL and LPFL were defined as elastic truss elements with a Young’s modulus equal to 19 MPa and Poisson’s ratio was set to 0.499.
After the preliminary assessment of the mechanical parameters for every constitutive model, we modified the stiffness in the spring model and the fibril network modulus in the FRPHE model iteratively in the ligaments until the obtained “adjusted” values matched the first peak of the tibial reaction force with respect to the rest of the knee models. Then, the FRPHE model was used for evaluating the influence of the fibril network modulus and the nonfibrillar matrix modulus of ligaments. Furthermore, the initial permeability k0 and material constant M were also varied in this analysis. Finally, in the biphasic models, we analyzed two boundary conditions on the external surface of ligaments: sealed and free draining. A list of the ranges of the material parameters used in the parametric study is given in Table 2.
In order to assess the effect of the ligament representation (springs and 3D continuum) and the contributions of different structural constituents (fibril network, nonfibrillar matrix, fluid), knee joint reaction forces, rotations and translations as well as stresses, strains and pore pressures of the tibiofemoral and patellofemoral contact were determined for all models during the stance phase of gait.
Results
Comparison between the constitutive models
Stress distribution in cartilages and menisci at different phases of stance is seen in Fig. 3. By using the values of the material parameters in the preliminary analysis (Table 1), tibial reaction forces in the models with elastic, hyperelastic and porohyperelastic properties for ligaments showed similar behavior throughout the stance, while the model with ligaments modeled as spring elements and FRPHE properties yielded a similar trend, but the last case exhibited lower joint reaction forces in terms of body weight (BW) during the entire stance phase of gait (Fig. 4a). After this first evaluation, we matched the first peak force among the models through a decrease of 50% of the stiffness for all ligaments in the spring model as well as modifying the fibril network modulus values in the FRPHE model (Table 1). For these “adjusted” values, both the modified spring and FRPVE models yielded lower joint reaction forces after the first peak load (Fig. 4b), and the spring model exhibited slightly lower forces in the mid-stance of the gait compared to the FRPHE model. Additionally, the model with the FRPHE ligaments displayed high tensile stresses and essentially no compressive stresses, while the other models with solid ligaments experienced both tensile and compressive stresses at the second half of the stance phase (Fig. 5).
Tensile and compressive stresses for σ22 in PCL for the hyperelastic (left) and fibril-reinforced poroelastic material (right) at the second peak of the stance phase. The hyperelastic model experiences both tensile (positive values) and compressive (negative values) stresses, though the tensile stresses are dominant, while the FRPHE model exhibited tensile stresses and virtually no compressive stresses.
Based on these models with “adjusted” material parameters, inferior-superior translations and varus-valgus rotations in the knee were similar in all models. However, the models with solid ligaments yielded a maximum reduction of 73% (1.72 mm) in the anterior femoral translation, as compared to the spring model, at the beginning of stance (Fig. 6). The medial-lateral translation was similar in the solid models with exception of the FRPHE model for ligaments, where lateral translation was higher throughout the stance (Fig. 6c). Though, the change in the translation during the stance (min – max) was similar in all solid models. Compared to the solid models, the spring model showed slightly higher medial translation at 60% of stance. Further, the FRPHE model displayed a smaller external-internal rotation at ~60% of the stance. In the FRPHE model, the patellar force was ~24% higher at ~25% of the stance compared with the spring model (Fig. 6e and f). Again, all other solid models gave consistent results and these forces were slightly higher than those in the FRPHE and spring models.
Tibial translations (a–c), rotations (d,e) with respect to femur and patellar forces (f) during the stance phase of gait for different constitutive models for the ligaments. (a) Posterior-anterior translation. (b) Inferior-superior translation. (c) Medial-lateral translation. (d) Valgus-varus rotation. (e) External-internal rotation. (f) Patellar force.
Similarly with joint reaction forces and motions, elastic, hyperelastic, and porohyperelastic models displayed quite similar behavior in the quantitative analysis of average contact pressures, maximum principal strains and stresses, fibril strains and fluid pressures in the contact area of the medial and lateral compartments of tibial cartilage during the entire stance phase of gait (Fig. 7). In contrast, the FRPHE model revealed lower values of contact and fluid pressures, and higher values of maximum principal stresses and fibril strains in the medial compartment, while contact and fluid pressures, stresses and strains in the lateral compartment were mostly highest in the FRPHE model. This result was related to the different contact area in the FRPHE model resulting from slightly different medial-lateral translation and external-internal rotation (Fig. 6).
The run time for the spring model was 605 minutes, whereas those for the hyperelastic and FRPHE models were 331 and 823 minutes, respectively.
Parametric analysis of the effect of fibrillar and non-fibrillar components
Parametric analysis within the FRPHE model by varying the fibril network modulus in every ligament (Table 2) showed a considerable influence of PCL, ACL and LCL on tibial and patellar forces (Fig. 8a and b); minimal impact was observed by the rest of the ligaments (data not shown). Variation of the PCL fibril network modulus showed the largest changes; increasing the modulus reduced the first peak force at the tibiofemoral contact and increased the second peak but decreasing the modulus value caused an opposite behavior. On the other hand, the fibril network modulus of the ACL and LCL modulated joint forces similarly during the entire stance phase; increasing the fibril network modulus increased tibiofemoral joint forces consistently (Fig. 8a). Modifications in the PCL, ACL, and LCL fibril network properties demonstrated similar effect in the force on patellar cartilage; with the chosen range of the fibril network modulus values, PCL controlled mostly this force as well (Fig. 8b).
Tibiofemoral (a) and patellofemoral joint reaction forces (b) in the FRPHE model after parametric variation of the fibrillar network modulus in ligaments (Table 2), while the other model parameters were kept unchanged (Table 1). Tibiofemoral (c) and patellofemoral joint reaction forces (d) in the FRPHE model after parametric variation of the nonfibrillar modulus in ligaments from 0.1 to 50 MPa, while the other material parameters were kept unchanged (Table 1).
In contrast, variation of the nonfibrillar matrix modulus in all ligaments exhibited only a small influence on the tibiofemoral and patellofemoral reaction forces; increasing substantially the nonfibrillar matrix modulus reduced the first peak force at the tibiofemoral contact but augmented the forces after ~40% of the phase stance (Fig. 8c). In addition, variations in the initial permeability k0 and material constant M, as well as the two boundary conditions on the external surface of ligaments (sealed and free draining) in the FRPHE model, did not change the results on the tibiofemoral contact (the maximum difference in joint reaction forces was 2%).
Discussion
In the present study, computational analysis showed that different geometrical representations (springs versus solid) and constitutive formulations of ligaments, particularly the compression-tension behavior, affect the human knee motion and tibial cartilage responses. This was mainly explained by the fibril-reinforcement attribute causing large tensile stresses and almost negligible compressive stresses. On the other hand and with a proper choice of material parameters, during the first ~50% of the stance all constitutive models could produce similar results. Further parametric analysis also demonstrated that the effect of the fibril network modulus of ligaments on the joint forces was predominant, and its variation, particularly in the PCL, modulated joint forces substantially. The nonfibrillar matrix modulus of ligaments had only a small influence on the forces, while fluid flow had virtually no influence on the joint forces and cartilage responses.
The original model with cartilage and menisci meshed, ligaments modeled as springs, and knee motion implemented was developed earlier and compared to experiments22,44. In the present study, we generated new ligament and tendon geometries for this model and implemented several different constitutive models for ligaments. For these reasons, we only briefly mention here how the current model results compare with experiments and computational studies. The magnitude of the joint reaction forces (2–3 BW) obtained from all the generated numerical knee models agree with recent experimental data45,46,47 and numerical studies48,49. Knee motion, contact pressures, and cartilage stresses and strains were also consistent with several earlier experimental and computational studies29,50,51,52. Varus-valgus and internal-external rotations matched well with the measured values of the same subject. Find more details about the validation of this model from the supplementary material.
Although the contribution of the compressive properties of ligaments may occur to some extent in vivo where ligaments are exposed to multiaxial states of stresses, bending, and transverse compressive loads during locomotion26,27,28, it is evident that this contribution is much smaller than that in tension12,14,29. The FRPHE model was able to capture this compression-tension characteristic, thereby giving slightly different knee joint forces and cartilage responses during loading as compared to the other solid models without this feature. The effect of the lack of the compressive properties of ligaments with the fibril-reinforced model was particularly observed at the end of stance, where particularly the PCL experienced also bending and subsequent local compressive loads and then the force obviously was slightly higher in the models without this compression-tension difference in the ligaments. Yet, local tensile stresses also in these simpler solid models were substantially higher than local compressive stresses because ligaments obviously are primarily in tension during gait.
In terms of joint reaction forces, the simplest model with spring elements representing ligaments was actually the closest match with the FRPHE model. The reason for this is that this model has no compressive resistance to load. The difference between these models came from the ligament geometry and nonfibrillar matrix contribution in the FRPHE model. Particularly, in ligaments as 3D continuum, cruciate ligaments had varying degrees of twisting during loading and collateral ligaments bent dissimilarly and inhomogeneously throughout the knee motion but especially from 50% to 90% of the stance. This complex interplay caused changes in length and fibril orientation of ligaments, causing combined loading states in the ligaments e.g. shear and bending, and showing an intricate interaction between the fibril network and nonfibrillar matrix. Moreover, the FRPHE model could produce the same response with the rest of models during certain time points of the stance. These findings indicate that simpler formulations of ligaments could be used to solve particular biomechanical problems, without the need to develop an elaborated constitutive representation for ligaments.
Tibial lateral and anterior translations and external rotation were the most sensitive kinematic parameters under varying ligament constitutive models which also contributed to the different joint reaction forces particularly at about 50 to 100% of the stance. Complex mechanical interactions in and between solid cruciate ligaments provided a reduced elongation and therefore smaller translation. In contrast, spring ligaments possessed more space to elongate, consequently this simplified model experienced higher translations. Additionally, FRPHE ligaments were able to bend and were supported partly by tensile forces at certain edges and virtually no compressive loads, while spring elements, which are constantly loaded along their axis, have a reduced capacity to twist during the knee motion. Interestingly, fibers in ligaments as 3D continuum contributed to reduce the elongation of ligaments, and accordingly the FRPHE model exhibited slightly different medial-lateral translation and smaller external-internal rotation regarding the other three-dimensional models for ligaments.
Due to slightly different knee motion in the FRPHE model compared to the other models, the tibiofemoral contact area was relocated in the medial tibial plateau and the contact area increased slightly. Therefore, the average contact and fluid pressures, and maximum principal strain in cartilage were smaller in the fibril-reinforced model, while elevated average fibril strains and tensile stresses were generated in the cartilage contact area. On the other hand, and primarily due to different medial-lateral translation, stresses, strains, and contact and fluid pressures in the lateral joint compartment were the highest in the FRPHE model.
It is known that the mechanical properties of ACL, PCL, and LCL have a notable effect on the biomechanical response of the knee joint18,20,52. Our parametric study with the FRPHE model showed also that tibiofemoral and patellofemoral joint forces were strongly influenced by the collagen network modulus of ACL, PCL, and LCL. This result is consistent with numerical studies which have examined the integrated interplay of knee ligaments29,52,53,54. Interestingly, while increasing the fibril network modulus of both the ACL and LCL increased joint reaction forces consistently throughout the gait, by increasing the fibril network modulus of the PCL first reduced the joint reaction forces (till ~50% of stance) and then increased the forces (from ~50% till 90% of stance) above the other models. On the other hand, reduction in the PCL fibril network modulus caused increased joint reactions forces through the stance. This implies an increase of anterior tibial translation and shift of the tibiofemoral contact area toward posterior direction, increasing the stress concentration in specific areas of the tibial cartilage. In addition, the ACL influence is consistent with our previous study22 and the remarkable PCL impact is congruent with recent studies55,56,57,58. In addition, this particular PCL influence is consistent with experimental studies that have reported a significant increase in joint contact forces and pressure concentrations on the medial compartment in a posterior cruciate deficient knee59,60. This could be the mechanism that causes joint degeneration after PCL deficiency58.
The parametric results within the FRPHE model suggest that fluid flow of ligaments (permeability and fluid flow boundary condition) has a negligible role for the cartilage response during the knee joint motion primarily due to tensile forces generated on ligaments. This result is consistent with several earlier studies on soft tissues, suggesting that the transient response of these tissues in tension is controlled by intrinsic properties of the solid matrix36,61,62, not by fluid flow which controls the transient response in compression63,64. Consistently, the effect of the nonfibrillar matrix modulus (range 0.1–50 MPa) on knee joint forces was small. This is also consistent with several other studies on fibril-reinforced poroelastic soft tissues36,65,66,67,68, and is a result of the high ratio between the fibril network and nonfibrillar matrix moduli.
Since the density ratio between the primary, organized fibrils and secondary, randomly organized fibrils (C) in the FRPHE models is not known for ligaments, in ACL and PCL it was assumed to be the same than that given for cartilage. However, lower C values had to be given for MCL and LCL since high values in these ligaments started to control the end part of the stance differently than with any other model. Since the collagen network stress (Eq. 9) is controlled by both the fibril network modulus and C, alternative combinations of these values could give the same result. Therefore, the modulus values in the fibril-reinforced model should not be directly related to the elastic tensile modulus values obtained from experiments.
Some limitations exist in this study regarding the model generation, input and assumptions. First, tissue geometries and gait input data were based on a single healthy male subject, as obtained from an earlier study22, except ligaments and tendons which were segmented separately for the purposes of this investigation. We also modeled only walking because it is the most typical type of movement. However, the fundamental behavior of ligaments should not change by modeling another subject and this methodology can be easily extended for other daily motor tasks (e.g. stair climbing, sit-to-stand, squatting). Second, the ligament pre-strains were taken from an earlier numerical study69 although PCL might be lax and it may not be active at full extension17,70. Also ligament collagenous part was simplified (bilinear) and not fully nonlinear with the toe region as has been presented in the literature71 because ligaments were assumed to function primarily at the linear region in the knee8,30. However, the ligament pre-strains and bilinearities were assumed to be the same for all the models analyzed in this study and the conclusion about the effect of different material representations should not change by different pre-strains and ligament properties. Though, if the PCL strain would be much smaller during loading, then likely the contribution of the fibril network modulus of the PCL would not be that drastic. Nonetheless, with these assumptions the maximum tibial reaction forces obtained (2–3 BW) concurred well with selected previous studies46,48.
The run time for the spring model was shorter than that for the FRPHE model but longer than that for the hyperelastic model. Also, the pre-processing steps for the spring model were faster than those for the hyperelastic and FRPHE models due to segmentation. On the other hand, the development and implementation of the fibril-reinforced properties of ligaments is demanding and time-consuming. These differences might be important in medical applications. However, as shown by the results, simpler models do not necessarily produce the same results with more complex fibril-reinforced models throughout the stance phase. Hence, simple representations for tissues could be used if they produce results close to the more realistic fibril-reinforced materials72 in certain steps of the phase stance. Moreover, automatic segmentation and meshing techniques would also be desirable to speed up the creation of the knee models73,74. The models with higher complexity might be better for investigation of local changes in the tissues such as rupture and biophysical adaptations of ligaments, tendons, cartilage and menisci.
In conclusion, the results of the current study suggest that the compression-tension relationship in ligaments due to the fibril-reinforcement contributes substantially to the knee joint motion and forces as well as cartilage responses during stance, while the roles of the nonfibrillar matrix and fluid are small or negligible. On the other hand, at certain phases of stance and with a proper choice of material parameters, knee models with simpler material models of ligaments (either springs or other solid constitutive models) are suggested to be able to reproduce similar results. These findings and suggestions are relevant to consider in biomechanical models to explore treatments (surgical or conservative) associated with knee ligament injuries.
References
Madeti, B. K., Chalamalasetti, S. R. & Pragada, S. K. S. siva rao B. Biomechanics of knee joint — A review. Front. Mech. Eng. 10, 176–186 (2015).
Chokhandre, S., Colbrunn, R., Bennetts, C. & Erdemir, A. A Comprehensive Specimen-Specific Multiscale Data Set for Anatomical and Mechanical Characterization of the Tibiofemoral Joint. PLOS ONE 10, e0138226 (2015).
Halloran, J. P. et al. Multiscale mechanics of articular cartilage: potentials and challenges of coupling musculoskeletal, joint, and microscale computational models. Ann. Biomed. Eng. 40, 2456–2474 (2012).
Galbusera, F. et al. Material models and properties in the finite element analysis of knee ligaments: a literature review. Biomechanics 2, 54 (2014).
Adouni, M. & Shirazi-Adl, A. Evaluation of knee joint muscle forces and tissue stresses-strains during gait in severe OA versus normal subjects. J. Orthop. Res. 32, 69–78 (2014).
Atkinson, T. S., Haut, R. C. & Altiero, N. J. A Poroelastic Model That Predicts Some Phenomenological Responses of Ligaments and Tendons. J. Biomech. Eng. 119, 400–405 (1997).
Freutel, M., Schmidt, H., Dürselen, L., Ignatius, A. & Galbusera, F. Finite element modeling of soft tissues: Material models, tissue interaction and challenges. Clin. Biomech. 29, 363–372 (2014).
Gardiner, J. C. & Weiss, J. A. Subject-specific finite element analysis of the human medial collateral ligament during valgus knee loading. J. Orthop. Res. 21, 1098–1106 (2003).
Kiapour, A. et al. Finite Element Model of the Knee for Investigation of Injury Mechanisms: Development and Validation. J. Biomech. Eng. 136, 011002–011002 (2013).
Mesfar, W. & Shirazi-Adl, A. Knee joint mechanics under quadriceps–hamstrings muscle forces are influenced by tibial restraint. Clin. Biomech. 21, 841–848 (2006).
Mesfar, W. & Shirazi-Adl, A. Biomechanics of the knee joint in flexion under various quadriceps forces. The Knee 12, 424–434 (2005).
Orsi, A. D. et al. The effects of knee joint kinematics on anterior cruciate ligament injury and articular cartilage damage. Comput. Methods Biomech. Biomed. Engin. 19, 493–506 (2016).
Peña, E., Peña, J. A. & Doblaré, M. On modelling nonlinear viscoelastic effects in ligaments. J. Biomech. 41, 2659–2666 (2008).
Peña, E., Calvo, B., Martínez, M. A. & Doblaré, M. A three-dimensional finite element analysis of the combined behavior of ligaments and menisci in the healthy human knee joint. J. Biomech. 39, 1686–1701 (2006).
Wang, L. et al. Anterior cruciate ligament reconstruction and cartilage contact forces—A 3D computational simulation. Clin. Biomech. 30, 1175–1180 (2015).
Weiss, J. A., Gardiner, J. C. & Bonifasi-Lista, C. Ligament material behavior is nonlinear, viscoelastic and rate-independent under shear loading. J. Biomech. 35, 943–950 (2002).
Harris, M. D. et al. A Combined Experimental and Computational Approach to Subject-Specific Analysis of Knee Joint Laxity. J. Biomech. Eng. 138 (2016).
Smith, C. R., Vignos, M. F., Lenhart, R. L., Kaiser, J. & Thelen, D. G. The Influence of Component Alignment and Ligament Properties on Tibiofemoral Contact Forces in Total Knee Replacement. J. Biomech. Eng. 138, 021017–021017 (2016).
Steinbrück, A. et al. Posterior cruciate ligament balancing in total knee arthroplasty: a numerical study with a dynamic force controlled knee model. Biomed. Eng. OnLine 13, 91 (2014).
Dhaher, Y. Y., Kwon, T.-H. & Barry, M. The effect of connective tissue material uncertainties on knee joint mechanics under isolated loading conditions. J. Biomech. 43, 3118–3125 (2010).
Halonen, K. S. et al. Importance of Patella, Quadriceps Forces, and Depthwise Cartilage Structure on Knee Joint Motion and Cartilage Response During Gait. J. Biomech. Eng. 138 (2016).
Halonen, K. S. et al. Optimal graft stiffness and pre-strain restore normal joint motion and cartilage responses in ACL reconstructed knee. J. Biomech. 49, 2566–2576 (2016).
Mommersteeg, T. J. A. et al. The effect of variable relative insertion orientation of human knee bone-ligament-bone complexes on the tensile stiffness. J. Biomech. 28, 745–752 (1995).
Moon, D. K., Woo, S. L.-Y., Takakura, Y., Gabriel, M. T. & Abramowitch, S. D. The effects of refreezing on the viscoelastic and tensile properties of ligaments. J. Biomech. 39, 1153–1157 (2006).
Woo, S. L.-Y., Hollis, J. M., Adams, D. J., Lyon, R. M. & Takai, S. Tensile properties of the human femur-anterior cruciate ligament-tibia complex The effects of specimen age and orientation. Am. J. Sports Med. 19, 217–225 (1991).
Böl, M., Ehret, A. E., Leichsenring, K. & Ernst, M. Tissue-scale anisotropy and compressibility of tendon in semi-confined compression tests. J. Biomech. 48, 1092–1098 (2015).
Lee, S.-B. et al. The bursal and articular sides of the supraspinatus tendon have a different compressive stiffness. Clin. Biomech. 15, 241–247 (2000).
Williams, L. N., Elder, S. H., Bouvard, J. L. & Horstemeyer, M. F. The anisotropic compressive mechanical properties of the rabbit patellar tendon. Biorheology 45, 577–586 (2008).
Yang, N. H., Nayeb-Hashemi, H., Canavan, P. K. & Vaziri, A. Effect of frontal plane tibiofemoral angle on the stress and strain at the knee cartilage during the stance phase of gait. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 28, 1539–1547 (2010).
Blankevoort, L. & Huiskes, R. Ligament-Bone Interaction in a Three-Dimensional Model of the Knee. J. Biomech. Eng. 113, 263–269 (1991).
Kiapour, A. M. et al. The Effect of Ligament Modeling Technique on Knee Joint Kinematics: A Finite Element Study. 2013 (2013).
Ateshian, G. A. et al. The Role of Osmotic Pressure and Tension-Compression Nonlinearity in the Frictional Response of Articular Cartilage. Transp. Porous Media 50, 5–33 (2003).
Danso, E. K. et al. Characterization of site-specific biomechanical properties of human meniscus-Importance of collagen and fluid on mechanical nonlinearities. J. Biomech. 48, 1499–1507 (2015).
Danso, E. K., Honkanen, J. T. J., Saarakkala, S. & Korhonen, R. K. Comparison of nonlinear mechanical properties of bovine articular cartilage and meniscus. J. Biomech. 47, 200–206 (2014).
Huang, C.-Y., Stankiewicz, A., Ateshian, G. A. & Mow, V. C. Anisotropy, inhomogeneity, and tension-compression nonlinearity of human glenohumeral cartilage in finite deformation. J. Biomech. 38, 799–809 (2005).
Korhonen, R. K. & Jurvelin, J. S. Compressive and tensile properties of articular cartilage in axial loading are modulated differently by osmotic environment. Med. Eng. Phys. 32, 155–160 (2010).
Halonen, K. S. et al. Deformation of articular cartilage during static loading of a knee joint–experimental and finite element analysis. J. Biomech. 47, 2467–2474 (2014).
Wilson, W., van Donkelaar, C. C. & Huyghe, J. M. A comparison between mechano-electrochemical and biphasic swelling theories for soft hydrated tissues. J. Biomech. Eng. 127, 158–165 (2005).
Wilson, W., van Donkelaar, C. C., van Rietbergen, B. & Huiskes, R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. J. Biomech. 38, 1195–1204 (2005).
Wilson, W., van Donkelaar, C. C., van Rietbergen, B., Ito, K. & Huiskes, R. Stresses in the local collagen network of articular cartilage: a poroviscoelastic fibril-reinforced finite element study. J. Biomech. 37, 357–366 (2004).
Julkunen, P., Kiviranta, P., Wilson, W., Jurvelin, J. S. & Korhonen, R. K. Characterization of articular cartilage by combining microscopic analysis with a fibril-reinforced finite-element model. J. Biomech. 40, 1862–1870 (2007).
Quapp, K. M. & Weiss, J. A. Material Characterization of Human Medial Collateral Ligament. J. Biomech. Eng. 120, 757–763 (1998).
Weiss, J. A. & Maakestad, B. J. Permeability of human medial collateral ligament in compression transverse to the collagen fiber direction. J. Biomech. 39, 276–283 (2006).
Halonen, K. S., Mononen, M. E., Jurvelin, J. S., Töyräs, J. & Korhonen, R. K. Importance of depth-wise distribution of collagen and proteoglycans in articular cartilage—A 3D finite element study of stresses and strains in human knee joint. J. Biomech. 46, 1184–1192 (2013).
Damm, P., Kutzner, I., Bergmann, G., Rohlmann, A. & Schmidt, H. Comparison of in vivo measured loads in knee, hip and spinal implants during level walking. J. Biomech., https://doi.org/10.1016/j.jbiomech.2016.11.060.
Kutzner, I. et al. Loading of the knee joint during activities of daily living measured in vivo in five subjects. J. Biomech. 43, 2164–2173 (2010).
Schwachmeyer, V. et al. Medial and lateral foot loading and its effect on knee joint loading. Clin. Biomech. 30, 860–866 (2015).
Komistek, R. D., Stiehl, J. B., Dennis, D. A., Paxson, R. D. & Soutas-Little, R. W. Mathematical model of the lower extremity joint reaction forces using Kane’s method of dynamics. J. Biomech. 31, 185–189 (1997).
Tanska, P., Mononen, M. E. & Korhonen, R. K. A multi-scale finite element model for investigation of chondrocyte mechanics in normal and medial meniscectomy human knee joint during walking. J. Biomech. 48, 1397–1406 (2015).
Kozanek, M. et al. Tibiofemoral kinematics and condylar motion during the stance phase of gait. J. Biomech. 42, 1877–1884 (2009).
Kutzner, I., Trepczynski, A., Heller, M. O. & Bergmann, G. Knee Adduction Moment and Medial Contact Force – Facts about Their Correlation during Gait. PLOS ONE 8, e81036 (2013).
Smith, C. R., Lenhart, R. L., Kaiser, J., Vignos, M. F. & Thelen, D. G. Influence of Ligament Properties on Tibiofemoral Mechanics in Walking. J. Knee Surg. 29, 99–106 (2016).
Adouni, M., Shirazi-Adl, A. & Shirazi, R. Computational biodynamics of human knee joint in gait: From muscle forces to cartilage stresses. J. Biomech. 45, 2149–2156 (2012).
Li, G., Gil, J., Kanamori, A. & Woo, S. L. A validated three-dimensional computational model of a human knee joint. J. Biomech. Eng. 121, 657–662 (1999).
Abubakar, M. S. et al. Influence of Posterior Cruciate Ligament Tension on Knee Kinematics and Kinetics. J. Knee Surg. 29, 684–689 (2016).
Kang, K.-T. et al. The effects of posterior cruciate ligament deficiency on posterolateral corner structures under gait- and squat-loading conditions. Bone Jt. Res. 6, 31–42 (2017).
Varma, R. K., Duffell, L. D., Nathwani, D. & McGregor, A. H. Knee moments of anterior cruciate ligament reconstructed and control participants during normal and inclined walking. BMJ Open 4, e004753 (2014).
von Eisenhart-Rothe, R. et al. Tibiofemoral and patellofemoral joint 3D-kinematics in patients with posterior cruciate ligament deficiency compared to healthy volunteers. BMC Musculoskelet. Disord. 13, 231 (2012).
MacDonald, P., Miniaci, A., Fowler, P., Marks, P. & Finlay, B. A biomechanical analysis of joint contact forces in the posterior cruciate deficient knee. Knee Surg. Sports Traumatol. Arthrosc. Off. J. ESSKA 3, 252–255 (1996).
Skyhar, M. J., Warren, R. F., Ortiz, G. J., Schwartz, E. & Otis, J. C. The effects of sectioning of the posterior cruciate ligament and the posterolateral complex on the articular contact pressures within the knee. J. Bone Joint Surg. Am. 75, 694–699 (1993).
Khayyeri, H., Longo, G., Gustafsson, A. & Isaksson, H. Comparison of structural anisotropic soft tissue models for simulating Achilles tendon tensile behaviour. J. Mech. Behav. Biomed. Mater. 61, 431–443 (2016).
Li, L. P., Korhonen, R. K., Iivarinen, J., Jurvelin, J. S. & Herzog, W. Fluid pressure driven fibril reinforcement in creep and relaxation tests of articular cartilage. Med. Eng. Phys. 30, 182–189 (2008).
Langelier, E. & Buschmann, M. D. Increasing strain and strain rate strengthen transient stiffness but weaken the response to subsequent compression for articular cartilage in unconfined compression. J. Biomech. 36, 853–859 (2003).
Li, L. P., Buschmann, M. D. & Shirazi-Adl, A. The asymmetry of transient response in compression versus release for cartilage in unconfined compression. J. Biomech. Eng. 123, 519–522 (2001).
Khayyeri, H. et al. A Fibre-Reinforced Poroviscoelastic Model Accurately Describes the Biomechanical Behaviour of the Rat Achilles Tendon. PLOS ONE 10, e0126869 (2015).
Korhonen, R. K. et al. Fibril reinforced poroelastic model predicts specifically mechanical behavior of normal, proteoglycan depleted and collagen degraded articular cartilage. J. Biomech. 36, 1373–1379 (2003).
Li, L. P., Buschmann, M. D. & Shirazi-Adl, A. A fibril reinforced nonhomogeneous poroelastic model for articular cartilage: inhomogeneous response in unconfined compression. J. Biomech. 33, 1533–1541 (2000).
Seifzadeh, A., Wang, J., Oguamanam, D. C. D. & Papini, M. A Nonlinear Biphasic Fiber-Reinforced Porohyperviscoelastic Model of Articular Cartilage Incorporating Fiber Reorientation and Dispersion. J. Biomech. Eng. 133, 81004–NaN (2011).
Gantoi, F. M., Brown, M. A. & Shabana, A. A. Finite Element Modeling of the Contact Geometry and Deformation in Biomechanics Applications1. J. Comput. Nonlinear Dyn. 8, 041013–041013 (2013).
Nakagawa, S. et al. The posterior cruciate ligament during flexion of the normal knee. J. Bone Joint Surg. Br. 86, 450–456 (2004).
Blankevoort, L., Huiskes, R. & de Lange, A. Recruitment of knee joint ligaments. J. Biomech. Eng. 113, 94–103 (1991).
Klets, O. et al. Comparison of different material models of articular cartilage in 3D computational modeling of the knee: Data from the Osteoarthritis Initiative (OAI). J. Biomech. 49, 3891–3900 (2016).
Rodriguez-Vila, B., Sánchez-González, P., Oropesa, I., Gomez, E. J. & Pierce, D. M. Automated hexahedral meshing of knee cartilage structures - application to data from the osteoarthritis initiative. Comput. Methods Biomech. Biomed. Engin. 20, 1543–1553 (2017).
Liukkonen, M. K. et al. Application of a semi-automatic cartilage segmentation method for biomechanical modeling of the knee joint. Comput. Methods Biomech. Biomed. Engin. 20, 1453–1463 (2017).
Butler, D. L., Sheh, M. Y., Stouffer, D. C., Samaranayake, V. A. & Levy, M. S. Surface strain variation in human patellar tendon and knee cruciate ligaments. J. Biomech. Eng. 112, 38–45 (1990).
Chandrashekar, N., Mansouri, H., Slauterbeck, J. & Hashemi, J. Sex-based differences in the tensile properties of the human anterior cruciate ligament. J. Biomech. 39, 2943–2950 (2006).
Hagena, F. W., Hofmann, G. O., Mittlmeier, T., Wasmer, G. & Bergmann, M. The cruciate ligaments in knee replacement. Int. Orthop. 13, 13–16 (1989).
Jones, R. et al. Mechanical properties of the human anterior cruciate ligament. Clin. Biomech. 10, 339–344 (1995).
McLean, S. G., Mallett, K. F. & Arruda, E. M. Deconstructing the Anterior Cruciate Ligament: What We Know and Do Not Know about Function, Material Properties, and Injury Mechanics. J. Biomech. Eng. 137 (2015).
Mommersteeg, T. J. et al. The fibre bundle anatomy of human cruciate ligaments. J. Anat. 187, 461–471 (1995).
Noyes, F. R., Butler, D. L., Grood, E. S., Zernicke, R. F. & Hefzy, M. S. Biomechanical analysis of human ligament grafts used in knee-ligament repairs and reconstructions. J. Bone Joint Surg. Am. 66, 344–352 (1984).
Pioletti, D. P., Rakotomanana, L. R., Benvenuti, J.-F. & Leyvraz, P.-F. Viscoelastic constitutive law in large deformations: application to human knee ligaments and tendons. J. Biomech. 31, 753–757 (1998).
Rachmat, H. H., Janssen, D., Verkerke, G. J., Diercks, R. L. & Verdonschot, N. In-situ mechanical behavior and slackness of the anterior cruciate ligament at multiple knee flexion angles. Med. Eng. Phys. 38, 209–215 (2016).
Harner, C. D., Vogrin, T. M. & Woo, S. L.-Y. Anatomical and Biomechanical Considerations of the PCL. J. Sport Rehabil. 8, 260–278 (1999).
Race, A. & Amis, A. A. The mechanical properties of the two bundles of the human posterior cruciate ligament. J. Biomech. 27, 13–24 (1994).
Wright, J. O. et al. Microstructural and Mechanical Properties of the Posterior Cruciate Ligament: A Comparison of the Anterolateral and Posteromedial Bundles. J. Bone Joint Surg. Am. 98, 1656–1664 (2016).
Zhou, A.-G., Yu, T., Chen, P. & Ma, H.-S. Tensile mechanical properties of knee posterior cruciate ligament. J. Clin. Rehabil. Tissue Eng. Res. 12, 1085–1088 (2008).
Eleswarapu, S. V., Responte, D. J. & Athanasiou, K. A. Tensile Properties, Collagen Content, and Crosslinks in Connective Tissues of the Immature Knee Joint. PLOS ONE 6, e26178 (2011).
Bonifasi-Lista, C., Lakez, S. P., Small, M. S. & Weiss, J. A. Viscoelastic properties of the human medial collateral ligament under longitudinal, transverse and shear loading. J. Orthop. Res. 23, 67–76 (2005).
Robinson, J. R., Bull, A. M. & Amis, A. A. Structural properties of the medial collateral ligament complex of the human knee. J. Biomech. 38, 1067–1074 (2005).
Wan, C. et al. An update on the constitutive relation of ligament tissues with the effects of collagen types. J. Mech. Behav. Biomed. Mater. 50, 255–267 (2015).
Wilson, W. T., Deakin, A. H., Payne, A. P., Picard, F. & Wearing, S. C. Comparative analysis of the structural properties of the collateral ligaments of the human knee. J. Orthop. Sports Phys. Ther. 42, 345–351 (2012).
Woo, S. L., Orlando, C. A., Gomez, M. A., Frank, C. B. & Akeson, W. H. Tensile properties of the medial collateral ligament as a function of age. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 4, 133–141 (1986).
Woo, S. L.-Y., Abramowitch, S. D., Kilger, R. & Liang, R. Biomechanics of knee ligaments: injury, healing, and repair. J. Biomech. 39, 1–20 (2006).
Butler, D. L., Kay, M. D. & Stouffer, D. C. Comparison of material properties in fascicle-bone units from human patellar tendon and knee ligaments. J. Biomech. 19, 425–432 (1986).
Ciccone, W. J., Bratton, D. R., Weinstein, D. M., Walden, D. L. & Elias, J. J. Structural properties of lateral collateral ligament reconstruction at the fibular head. Am. J. Sports Med. 34, 24–28 (2006).
Jeffcote, B., Nicholls, R., Schirm, A. & Kuster, M. S. The variation in medial and lateral collateral ligament strain and tibiofemoral forces following changes in the flexion and extension gaps in total knee replacement. A laboratory experiment using cadaver knees. J. Bone Joint Surg. Br. 89, 1528–1533 (2007).
LaPrade, R. F., Bollom, T. S., Wentorf, F. A., Wills, N. J. & Meister, K. Mechanical Properties of the Posterolateral Structures of the Knee. Am. J. Sports Med. 33, 1386–1391 (2005).
Meister, B. R., Michael, S. P., Moyer, R. A., Kelly, J. D. & Schneck, C. D. Anatomy and Kinematics of the Lateral Collateral Ligament of the Knee. Am. J. Sports Med. 28, 869–878 (2000).
Sugita, T. & Amis, A. A. Anatomic and biomechanical study of the lateral collateral and popliteofibular ligaments. Am. J. Sports Med. 29, 466–472 (2001).
Zens, M. et al. Mechanical tensile properties of the anterolateral ligament. J. Exp. Orthop. 2, 1 (2015).
Blevins, F. T., Hecker, A. T., Bigler, G. T., Boland, A. L. & Hayes, W. C. The effects of donor age and strain rate on the biomechanical properties of bone-patellar tendon-bone allografts. Am. J. Sports Med. 22, 328–333 (1994).
Chandrashekar, N., Slauterbeck, J. & Hashemi, J. Effects of cyclic loading on the tensile properties of human patellar tendon. The Knee 19, 65–68 (2012).
Flahiff, C. M., Brooks, A. T., Hollis, J. M., Vander Schilden, J. L. & Nicholas, R. W. Biomechanical analysis of patellar tendon allografts as a function of donor age. Am. J. Sports Med. 23, 354–358 (1995).
Haraldsson, B. T. et al. Region-specific mechanical properties of the human patella tendon. J. Appl. Physiol. Bethesda Md 1985 98, 1006–1012 (2005).
Hashemi, J., Chandrashekar, N. & Slauterbeck, J. The mechanical properties of the human patellar tendon are correlated to its mass density and are independent of sex. Clin. Biomech. 20, 645–652 (2005).
Haut, R. C. & Powlison, A. C. The effects of test environment and cyclic stretching on the failure properties of human patellar tendons. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 8, 532–540 (1990).
Johnson, G. A. et al. Tensile and viscoelastic properties of human patellar tendon. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 12, 796–803 (1994).
Müller, S. S. et al. Comparative analysis of the mechanical properties of the patellar ligament and calcaneus tendon. Acta Ortopédica Bras. 12, 134–140 (2004).
O’Brien, T. D., Reeves, N. D., Baltzopoulos, V., Jones, D. A. & Maganaris, C. N. Mechanical properties of the patellar tendon in adults and children. J. Biomech. 43, 1190–1195 (2010).
Rupp, S., Seil, R., Kohn, D. & Müller, B. The influence of avascularity on the mechanical properties of human bone-patellar-tendon-bone grafts. J. Bone Joint Surg. Br. 82, 1059–1064 (2000).
Schatzmann, L., Brunner, P. & Stäubli, H. U. Effect of cyclic preconditioning on the tensile properties of human quadriceps tendons and patellar ligaments. Knee Surg. Sports Traumatol. Arthrosc. 6, S56–S61 (1998).
Stäubli, H. U., Schatzmann, L., Brunner, P., Rincón, L. & Nolte, L. P. Mechanical tensile properties of the quadriceps tendon and patellar ligament in young adults. Am. J. Sports Med. 27, 27–34 (1999).
Stäubli, H. U., Schatzmann, L., Brunner, P., Rincón, L. & Nolte, L. P. Quadriceps tendon and patellar ligament: cryosectional anatomy and structural properties in young adults. Knee Surg. Sports Traumatol. Arthrosc. Off. J. ESSKA 4, 100–110 (1996).
Miller, R. M. et al. Tensile properties of a split quadriceps graft for ACL reconstruction. Knee Surg. Sports Traumatol. Arthrosc. 25, 1249–1254 (2017).
Acknowledgements
The authors appreciate the support of the University of Eastern Finland and Aalborg University to undertake this study. This project has received funding from the Doctoral Programme in Science, Technology and Computing (SCITECO), University of Eastern Finland; the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 713645; the European Research Council (ERC) under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No 281180 and the European Union’s Horizon 2020 research and innovation programme (grant agreement No 755037); Academy of Finland (grant No 286526, 305138); and Sigrid Juselius Foundation. CSC-IT Center for Science Ltd is acknowledged for providing FE software. Mikko Venäläinen, Ph.D. and Mimmi Liukkonen, M.Sc. are acknowledged for technical support.
Author information
Authors and Affiliations
Contributions
G.O. design of the study, conducting simulations and analysis, preparing all figures and tables, main writer (responsible for the integrity of the work as a whole). P.T. design of the study, interpretation of the results, critical revision of the manuscript for important intellectual content. M.E.M. design of the study, interpretation of the results, critical revision of the manuscript for important intellectual content. K.H. develop the previous model used in this article, critical revision of the manuscript for important intellectual content. R.K.K. original design of the concept, interpretation of the results, critical revision of the manuscript for important intellectual content.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Orozco, G.A., Tanska, P., Mononen, M.E. et al. The effect of constitutive representations and structural constituents of ligaments on knee joint mechanics. Sci Rep 8, 2323 (2018). https://doi.org/10.1038/s41598-018-20739-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-20739-w
This article is cited by
-
Computational study of extrinsic factors affecting ACL strain during single-leg jump landing
BMC Musculoskeletal Disorders (2024)
-
Validation and evaluation of subject-specific finite element models of the pediatric knee
Scientific Reports (2023)
-
Adaptation of Fibril-Reinforced Poroviscoelastic Properties in Rabbit Collateral Ligaments 8 Weeks After Anterior Cruciate Ligament Transection
Annals of Biomedical Engineering (2023)
-
Contribution of Elastic and Collagen Fibers to the Mechanical Behavior of Bovine Nuchal Ligament
Annals of Biomedical Engineering (2023)
-
Sequential damage assessment of the posterolateral complex of the knee joint: a finite element study
Journal of Orthopaedic Surgery and Research (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.