Abstract
In this study, the low energy radiation responses of AlAs, GaAs and GaAs/AlAs superlattice are simulated and the radiation damage effects on their electronic structures are investigated. It is found that the threshold displacement energies for AlAs are generally larger than those for GaAs, i.e., the atoms in AlAs are more difficult to be displaced than those in GaAs under radiation environment. As for GaAs/AlAs superlattice, the Ga and Al atoms are more susceptible to the radiation than those in the bulk AlAs and GaAs, whereas the As atoms need comparable or much larger energies to be displaced than those in the bulk states. The created defects are generally Frenkel pairs, and a few antisite defects are also created in the superlattice structure. The created defects are found to have profound effects on the electronic properties of GaAs/AlAs superlattice, in which charge transfer, redistribution and even accumulation take place, and band gap narrowing and even metallicity are induced in some cases. This study shows that it is necessary to enhance the radiation tolerance of GaAs/AlAs superlattice to improve their performance under irradiation.
Similar content being viewed by others
Introduction
In the past decades, the development in micro-fabrication such as molecular beam epitaxy (MBE) and metal organic chemical vapor deposition (MOCVD) opens a new stage in science where artificial materials are designed for specific studies and applications1. It is noted that gallium arsenide (GaAs) and aluminum arsenide (AlAs) are perfectly lattice matched, and few difficulties are expected in the growth of (GaAs)m/(AlAs)n semiconductor superlattice (SL), which consists of m monolayers of GaAs alternating with n monolayers of AlAs. The artificial SL has been widely used in different applications like the optoelectronic devices with quantum cascade laser, high-frequency oscillators and thermoelectric devices2,3,4,5,6,7,8,9, due to the new physical phenomena such as quantum confinement, Brillouin-zone folding and the obtaining of a direct-gap superlattice from their indirect-gap constitutes10. In the application field of military and aerospace, the semiconductor materials are exposed to different radiation environments, which may result in defect generation, migration and aggregation, and ultimately may deteriorate their optical and electronic properties and influence their performance which may lead to permanent failure10,11,12,13,14,15. For example, Tanaka et al. reported that the photoluminescence intensity and the two-dimensional electron gas mobility of GaAs/AlGaAs heterostructures decreased obviously under electron irradiation14. Therefore, it is of great importance to study their phase stability and the radiation damage effects on the electronic properties of the semiconductor materials.
The radiation damage effects of GaAs and AlAs have been extensively studied16,17,18,19,20,21. Wesch et al. compared the radiation responses of GaAs and AlAs, and they found the AlAs behaves more robustly under Au+ ion irradiation18. Sayed et al. investigated the low energy displacement events of GaAs and AlAs employing the molecular dynamics (MD) method, who found that the threshold displacement energies (Eds) for Al atoms are significantly higher than those for Ga atoms along certain directions19. Nordlund et al. predicted that interstitials are dominant isolated defects in GaAs under He+ ion irradiation21. By contrast, the radiation responses of (GaAs)m/(AlAs)n SL have received relatively scant attentions22,23,24. Cullis et al. irradiated the AlAs/GaAs heterostructures with Si+ ions, and they suggested that the AlAs resisted ion damage accumulation far more strongly than the GaAs22. Jenčič et al. have studied the radiation responses of AlxGa1−xAs/GaAs (x = 0.2 and 0.85) samples to Kr+ and Xe+ irradiation and reported that the AlGaAs is more resistant to amorphization than GaAs and the resistance increases with the increasing Al content24. In spite of these experimental investigations, no theoretical simulation of dynamic process of radiation damage of GaAs/AlAs SL has been reported in the literature thus far. There still lacks an atomic-level understanding of the micro-structural evolution and the underlying mechanism for defect generation in the semiconductor superlattices.
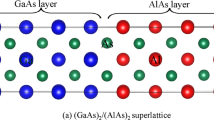
In recent years, the ab initio MD (AIMD) method has made it possible to simulate radiation damage of materials with the inclusion of motion of electrons, and has been extensively applied to simulate the displacement events in ceramic and semiconductors materials25,26,27,28,29,30,31,32,33. As compared with the classical MD method, the interatomic potentials are obtained from electronic structure calculations rather than empirical fitting of experimental results. Consequently, a lot of physical parameters like Eds can be determined with ab initio accuracy. Lucas and Pizzagalli have demonstrated that the average Eds for both C and Si sublattices in SiC determined from AIMD are in very close agreement to the experimental consensus and such an agreement has never been obtained with semi-empirical potentials or tight-binding methods30. Gao et al. carried out AIMD simulation of ion-solid interactions in SiC and revealed that during the dynamic process of displacement events a significant charge transfer occurs between atoms, and the charge transfer to and from recoiling atoms can alter the energy barriers and dynamics for stable defect formation34. Wang et al. investigated the radiation responses of pyrochlores to electron irradiation using the AIMD method and predicted a number of new mechanisms for defect generation and new defective states that are different from classical MD simulations33. These simulations have demonstrated that the AIMD method is a powerful tool in describing the ion-solid interactions in materials. In this study, the AIMD methods are employed to investigate the response behaviors of AlAs, GaAs and GaAs/AlAs SL under low energy irradiation. The geometrical configurations of AlAs, GaAs and GaAs/AlAs SL are illustrated in Fig. 1. The computational details are described in the Methods section. The threshold displacement energies have been determined, and the defect distribution and the pathway for defect generation have been provided. Meanwhile, the radiation damage effects on the electronic structures of these materials have also been investigated. The presented results provide a fundamental insight into the microscopic mechanism of displacement events in AlAs, GaAs and GaAs/AlAs SL, and advance the understanding of the electronic properties of these materials under radiation environment.
Results and Discussion
Lattice constants and cohesive energies for bulk AlAs and GaAs
The original point group of AlAs and GaAs crystal is the Td group of zinc blende35, as shown in Fig. 1(a). The lattice constants and cohesive energies for AlAs and GaAs are calculated and compared with the available results in Table 1. Our calculated lattice constant of 5.66 Å for AlAs is slightly smaller than the value of 5.71 Å for GaAs, which is in good agreement with the experimental results36 reported by Wyckoff and other theoretical results7,37,38. In this study, the lattice constant of GaAs/AlAs SL is set to be the intermediate value of 5.685 Å due to the small lattice mismatch between GaAs and AlAs.
The cohesive energy is the condensed-matter analog of molecular atomization energy and a measure of the inter-atomic bond strength, which is calculated by \({E}_{coh}(AB)=[n\times {E}_{iso}(A)+m\times {E}_{iso}(B)-{E}_{total}(AB)]/(n+m)\). Here, n and m denote the total number of A and B atoms in the unit cell, respectively, E toatl (AB) represents the energies of GaAs and AlAs, and E iso (A) and E iso (B) are the total energies of isolated A and B atoms, respectively. The cohesive energies of AlAs and GaAs are determined to be 3.74 and 3.21 eV/atom, respectively, which are in good agreement with the experimental results reported by Cohen et al.39 and the theoretical results reported by Ahmed et al.40. It is shown that our results are smaller than the calculated results of Ihm et al.41, which is resulted from the different computational details. In the study of Ihm et al., the nonlocal (angular-momentum-dependent) pseudopotentials were employed, and the exchange-correlation potential was described by the local-density approximation (LDA) within Winger parameterization41, while in our study norm-conserving Troullier-Matrins pseudopotentials are employed, and the LDA method within Ceperly-Alder parameterization is used to describe the exchange-correlation potential. We also find that the cohesive energy of AlAs is larger than that of GaAs, i.e, the <Al-As> bond is stronger than the <Ga-As> bond, which may be partially responsible for their different radiation tolerance.
Threshold displacement energies in AlAs, GaAs and GaAs/AlAs superlattice
The threshold displacement energy (Ed), which is defined as the minimum transferred kinetic energy for the primary knock-on atom (PKA) to be permanently displaced from its lattice site, is one of the critical physical parameters for estimating damage production rates and predicting the defect profile under electron, neutron and ion irradiation. In this study, the Eds for Al, Ga and As PKAs in bulk AlAs, GaAs and GaAs/AlAs SL are determined and summarized in Tables 2 and 3. For bulk AlAs and GaAs, the MD results reported by Sayed et al.19 are also included in Table 2 for comparison. Comparing our results with the MD results, we find that the Eds obtained by the AIMD method are much smaller in most cases, except for As[110], Al[001], Al[111] and Ga[001]. Previous AIMD simulation of ion-solid interactions in SiC revealed that the displacement event is actually a charge-transfer process and the charge transfer to and from recoiling atoms can alter the energy barriers and dynamics for stable defect formation34. The lower values of Ed found by AIMD compared to those determined by classical MD may be due to the fact that charge transfer that occurs during the recoil events is taken into account by the AIMD method, while in the classical MD simulation the charge of atoms is fixed.
For AlAs, the minimum Ed value is 13 eV for Al PKA along the [110] direction, and the As PKAs are more easily to be displaced along the [111], [123] and [001] directions, as indicated by the small values of 13 and 13.5 eV. Comparing the Ed values for Al and As atoms, we find that the As atoms are generally more easily to be displaced than Al atoms, except the case of [110] where the energy of 21.5 eV for As atom is 8.5 eV larger than that for Al atom. These results show that the As displacement may be dominant in the recoil events of AlAs.
For GaAs, the minimum Ed for Ga PKA is 8 eV along the \([\overline{1}\overline{1}\overline{1}]\) direction, which is comparable to the minimum value of 8.5 eV for As PKA along the [111] direction. Similar to AlAs, the As atoms are generally more easily to be displaced, since their Ed values are generally smaller than those for Ga PKAs, except the case of \([\overline{1}\overline{1}\overline{1}]\). Pons and Bourgoin found that the damaged defects in GaAs were generally caused by displacements of As atoms under electron irradiation17, which is consistent with our results. It is noted that for each recoil event the Ed values for AlAs are generally larger than those for GaAs, except for the cation recoils along the [112] direction. These results indicate that the lattice atoms in AlAs are generally more difficult to be displaced than those in GaAs under low energy irradiation, which may be caused by larger binding energies of AlAs. Sayed et al. investigated low energy displacement events in GaAs and AlAs employing the MD method, who found that the values of Eds for Al atoms are significantly higher than those for Ga atoms in certain directions19. Wesch et al. compared the damage formation of GaAs and AlAs under Au+ ion irradiation18. Their results showed that the backscattered yield in the region of GaAs increased slightly stronger with the ion fluences than AlAs, which is also in good agreement with our study.
As shown in Fig. 1(b), the GaAs/AlAs SL is terminated by the As layer and the Ga, Al and As atoms on the boundary of the As interface are selected as the PKA. As can be seen from Table 3, the maximum and minimum Ed values for the As PKAs are along the [111] and \([\overline{1}\overline{1}\overline{1}]\) directions, respectively, and the respective Ed values are 30 and 12 eV. In these two cases, the radiation damage end states show different character. For As[111], the As PKA moves away from its lattice site to eject its neighboring Al atom and occupies an interstitial site (Asint). The collided Al atom moves along the [111] direction and occupies another nearby As lattice site to form an antisite defect (AlAs). Then, the third ejected As atom occupies its neighboring Ga lattice site (AsGa), and the Ga atom forms an interstitial defect (Gaint). In the end, one pair of As FP, one Al vacancy (VAl), one AlAs antisite defect, one AsGa antisite defect and one Gaint defects are created. The associated defects in the case of As \([\overline{1}\overline{1}\overline{1}]\) are relatively simple, which consist of only one As vacancy (VAs) and one Asint. For Al PKAs, the maximum and minimum Ed values are determined to be 33 eV along the [001] direction and 10 eV along the [111] direction, respectively, and the pathway for defect generation are very different from each other. In the case of Al[001], besides the Al PKA, a number of neighboring Al and Ga atoms are also involved in the displacement events, which results in the formation of one pair of Al FP, one pair of Ga FP and two GaAl and AlGa antisite defects after recoil events. The displacement event in the case of Al[111] is much simpler, and only one pair of Al FP is created. Similarly, the Ga PKA is easy to be displaced along the [111] direction, as indicated by the minimum value of 9.5 eV. It is noted that the Ed values of Ga PKAs are generally smaller than those of the Al atoms, except the [013] direction, indicating that the Ga atoms are more easily to be displaced than Al atoms.
The average threshold displacement energies for PKAs in bulk GaAs and AlAs as well as GaAs/AlAs SL are plotted in Fig. 2. The average Eds over all the crystallographic directions considered in this study are calculated by \({E}_{ave}=({E}_{[100]}\times {n}_{1}+{E}_{[110]}\times {n}_{2}+{E}_{[111]}\times {n}_{3}+{E}_{[\overline{1}\overline{1}\overline{1}]}\times {n}_{4}\) + \({E}_{[013]}\times {n}_{5}+{E}_{[112]}\times {n}_{6}\) + \({E}_{[123]}\times {n}_{7})/\)\(({n}_{1}+{n}_{2}+{n}_{3}+{n}_{4}\) + n5 + n6 + n7 where n1, n2, n3, n4, n5, n6 and n7 are the number of equivalent directions for a specific direction. In bulk GaAs and AlAs, the average Ed values for cation recoils are obviously larger than that for As atoms, indicating that As displacement may be the dominant. We also find that the average value of 25.8 eV for Al PKAs is larger than the value of 20.3 eV for Ga PKAs. Although the Ga atom has larger atomic radius and mass than the As atom, the <Ga-As> bond is weaker than the <Al-As> bond, as indicated by the lower cohesive energy of GaAs in Table 1. On the other hand, the screening of the Coulomb force between the Ga PKA and its neighbors is more effective and the interaction between them is relatively smaller, which decreases the energy barrier for defect generation. Consequently, the Ga atoms are relatively more easily to be displaced than the Al atoms. Besides, we find that higher energies are needed for the As atoms in AlAs to be displaced than those for As atoms in GaAs. These results indicate that the AlAs may behave more robustly than the GaAs under radiation environment, agreeing well with theoretical19 and experimental18 findings. As for GaAs/AlAs SL, the average Ed values are determined to be 18.4, 15.0 and 18.7 eV for Al, Ga and As atoms, respectively. It is shown that the cations in the SL structure are more susceptible to the radiation than those in the bulk state, as indicated by the decreased average value of Eds. Under electron irradiation the maximum energy transferred to an atom can be expressed as \(T=2{E}_{e}({E}_{e}+2{m}_{e}{c}^{2})/M{c}^{2}\), where E e is the incident energy, m e is the electronic mass, M is the atomic mass and c is the velocity of light27. The Ed values of 20.3 and 15 eV for Ga recoil in bulk GaAs and SL correspond to 898 and 815 keV electron irradiation, respectively. As for Al recoil, the Ed values of 25.8 and 18.4 eV in bulk AlAs and SL correspond to 715 and 651 keV electron irradiation, respectively. It is noted that the cations in bulk state behave more robustly than those in the SL under electron irradiation. Bryant and Cox have irradiated the samples of CdS and CdTe employing the electron irradiation, and found that the CdS is more resistant to electron irradiation than the CdTe, due to the larger Ed value of ~9.6 eV for S atoms than the value of ~7.9 eV for Te atoms42. As for the As atoms in the SL structure, the Eds are comparable with those for As atoms in the bulk AlAs, while these values are much larger than those for As atoms in bulk GaAs. The similar average Eds for As atoms between bulk AlAs and the SL structure may due to the anisotropy of Ed, which leads to different contributions to the average value from directions with different Ed values. Obviously, the GaAs/AlAs SL exhibits different radiation tolerance from the bulk GaAs and AlAs. Comparing the two compositions in the SL structure, we find that the average Eds for GaAs are lower than those for AlAs, i.e., GaAs is more susceptible to low energy irradiation. Cullis et al. found that the GaAs layer of AlAs/GaAs epitaxial heterostructures was relatively easily amorphized under Si+ irradiation, whereas the AlAs layer was quite resistant to damage accumulation and remained its crystalline for the ion doses employed22, which agrees well with our results.
Defect distribution in AlAs, GaAs and GaAs/AlAs superlattice after recoil events
The created defects after each recoil event in bulk AlAs and GaAs are summarized in Tables 4 and 5, respectively. For Al PKAs, the damage end states are generally Al vacancy (VAl) and Al interstitial (Alint) except the case of Al[123], where the Al occupying the As lattice site (AlAs) and the As occupying the Al lattice site (AsAl) defects are created. Although the number of associated defects for Al PKAs is identical, the displacements of the PKA are very different from each other, due to the different defect generation mechanisms. As for the As PKAs in AlAs, the created defects are generally As vacancy (VAs) and As interstitial (Asint). It is noted that damage end states in the cases of [110], \([\overline{1}\overline{1}\overline{1}]\) and [123] show different character. For As[110], the As PKA moves 3.68 Å to replace its neighboring Al lattice site (AsAl), and the collided Al atom occupies the original site of As PKA (AlAs). In the recoil event of As[123], the As atom moves 1.89 Å away to eject its neighboring Al atom and occupies an interstitial site in the end. The collided Al atom also occupies an interstitial site, which is 1.67 Å away from its lattice site. Consequently, one pair of Al FP and one pair of As FP defects are created after the recoil event. The associated defects for As \([\overline{1}\overline{1}\overline{1}]\) are more complex, where two neighboring Al atoms are involved in the recoil events, and eventually one VAs defect, one AsAl antisite defect, two Alint defects and one VAl defect are formed. It is noted that the PKA displacements of 5.22 Å for As[001] and 5.20 Å for Al[001] are very close to each other. For the As and Al PKAs along the [001] direction, the first neighboring atoms are As and Al atoms, respectively, and the separating distances between the PKA and its first neighbor in both cases are 5.66 Å, i.e., the lattice constant of bulk AlAs. During the recoil events, the PKA moves along the [001] direction to collide with its first neighboring atom and replace it, which then moves back a little bit due to repulsive interaction. The similar displacements for As and Al PKAs may be due to their similar motion trajectory and similar atomic radii for As and Al, i.e., 1.19 Å for As atom and 1.21 Å for Al atom.
As shown in Table 5, although the created defects for Ga recoil events are generally Ga vacancy (VGa) and Ga interstitial (Gaint), the damage end states for Ga[110], Ga[111] and Ga[123] show different character. In the cases of Ga[110] and Ga[111], the Ga atom moves 4.19 and 2.08 Å away to replace its neighboring As lattice site (GaAs). In the end, the replaced As atom occupies the Ga PKA lattice site (AsGa) for Ga[110], while in the case of Ga[111] the rejected As atom forms the stable interstitial site (Asint). For Ga[123], one neighboring Ga atom and one As atom are also involved in the recoil events, and the created defects contain two pairs of Ga FP defects and one pair of As FP defect. As for As atoms in GaAs, the associated defects generally consist of VAs and Asint. For As[110], the As PKA leaves its lattice site and moves along the [110] direction. Eventually, it forms a stable interstitial defect, which is 4.09 Å away from its lattice site. The damage end states of the As[001], \([\overline{1}\overline{1}\overline{1}]\) and [013] recoils are somewhat different, where one neighboring Ga atom is involved in the displacement events. As for GaAs, although few antisite defects are created after displacement events, the associated defects are generally vacancies and interstitials. Nordlund et al. employed the MD simulations to investigate the atomic-level damage structures in GaAs under ion irradiation and found that a clear majority of the isolated defects produced by low-energy self-recoils and 6 MeV He ions were interstitials21.
The created defects after recoil events in GaAs/AlAs SL are summarized in Table 6. For Al atoms, the created defects generally contain VAl and Alint, which is similar to the cases of Al PKAs in bulk AlAs. The damage end states for Al[001] and Al \([\overline{1}\overline{1}\overline{1}]\) recoils are somewhat different. For Al \([\overline{1}\overline{1}\overline{1}]\), the Al PKA moves 4.87 Å away and collides its neighboring As atom, and one pair of Al FP and As FP are created in the end. In the case of Al[001], one pair of Al FP, one pair of Ga FP, one Ga occupying the Al lattice site (GaAl) and one Al occupying the Ga lattice site (AlGa) are formed, due to the fact that the other three neighboring atoms are involved in the displacement events. As for Ga atoms, most of the created defects are VGa and Gaint. The recoil events of Ga[001], [110] and \([\overline{1}\overline{1}\overline{1}]\) are found to show different character. In the case of [001], the Ga atom moves away from its lattice site to collide with its neighboring Al atom and occupies the Al lattice site. Then, the ejected Al atom forms an interstitial defect. As for Ga[110], the neighboring As atom is involved in the recoil event, and the radiation damage end states are GaAs and AsGa antisite defects. The associated defects for Ga \([\overline{1}\overline{1}\overline{1}]\) are more complex, as indicated by the created complex defects, i.e., one VGa defect, one GaAs defect, one Asint defect and one pair of Al FP. For the Al and Ga PKAs in GaAs/AlAs SL, the created defects are generally Al FP and Ga FP, respectively, which are similar to the cases of Al atoms in AlAs and Ga atoms in GaAs.
As for the As atoms, the damage end states are somewhat different from those for As PKAs in bulk AlAs and GaAs. The antisite defects are created in each recoil event, except the cases of \([\overline{1}\overline{1}\overline{1}]\) and [123], for which the generated defect is As FP. In the case of [001] and [110], the AsGa and GaAs antisite defects are created, with the PKA displacements of 2.49 and 4.17 Å, respectively, indicative of different defect mechanisms. The associated defects for three other cases are more complex, especially for As[111] recoil, where one pair of As FP, one VAl defect, one AlAs defect, one AsGa defect and one Asint defect are created. Comparing the defect distributions in AlAs, GaAs and GaAs/AlAs SL, we find that a number of antisite defects are created in GaAs/AlAs SL, whereas very few antisite defects are generated in bulk AlAs and GaAs. However, Frenkel pairs are dominant defects under low energy irradiation in both the bulk and SL structures, which is in good agreement with the results reported by Nordlund et al.21 and Pronko et al.23.
The radiation damage effects on the electronic properties of AlAs, GaAs and GaAs/AlAs superlattice
The (GaAs)m/(AlAs)n SLs with (m + n) ranging from 2 to 10 have been widely applied in luminescence and optical absorption, two-phonon absorption and Raman as well as infrared spectra due to their unusual properties12,43. Under radiation environment the defect creation, clustering and accumulation may have profound effects on their structural stability and electronic properties, and deteriorate their performance, which may lead to permanent failure. In order to further explore how the radiation damage influences the electronic properties of GaAs/AlAs SL, first-principles calculations based on density functional theory are carried out to investigate the electronic structures of some representative damaged states. The computations are based on a 2 × 2 × 2 supercell consisting of 64 atoms, with a 6 × 6 × 6 k-point sampling in reciprocal space and a cutoff energy of 500 eV.
For AlAs and GaAs, the considered defective states are illustrated in Fig. 3(a–c) and (d–f), respectively. The band structures for ideal and defective AlAs are shown in Fig. 4. In Figure 4(a), AlAs has an indirect gap at Χ point, and the energy gap is determined to be 1.31 eV. It is noted that the value of 1.31 eV is consistent with other LDA result of 1.33 eV5, whereas it is smaller than the experimental value of 2.16 eV44, due to the well-known discontinuity of exchange-correlation energy of the LDA. As one VAl and one Alint defects with separating distance of 4.68 Å are introduced in AlAs, defect levels are observed in the forbidden band region and the energy gap decreases to 0.34 eV, as shown in Fig. 4(b). In the case of Al[123], the Al PKA replaces the As lattice site (AlAs) and the ejected As atom occupies the PKA lattice site (AsAl). Figure 4(c) shows that the band gap of antisite-defect state for Al[123] decreases to 0.17 eV. As for As[001], one VAs and one Asint defects are created, which are separated by 5.22 Å from each other. Similarly, the band gap As-FP-defect state for As[001] is narrowed to 0.15 eV, as illustrated in Fig. 4(d).
Illustration of schematic view of defects created by PKA recoils in bulk AlAs and GaAs. (a) Al[110]; (b) Al[123]; (c) As[001] in bulk AlAs; (d) Ga[001]; (e) Ga[110] and (f) As [110] in bulk GaAs. The blue, red and green spheres represent the Ga, Al and As atoms, respectively. VX: X vacancy (X = Al, Ga or As); Xint: X interstitial (X = Al, Ga or As); XY: X occupying the Y lattice site (X, Y = Al, Ga or As). The yellow and pink spheres represent the vacancy and interstitial defects, respectively.
Figure 5 describes the band structures for ideal and defective GaAs. Different from AlAs, the energy gap for GaAs is direct with the value of 0.5 eV. This value is comparable with other LDA value of 0.41 eV15, while much smaller than the experimental value of 1.52 eV45. As show in Fig. 5(b), the defect levels are observed near the valence band maximum (VBM), and cross the Fermi level, indicative of metallic character of defective GaAs with one pair of Ga FP defect. For Ga[110], one pair of GaAs and AsGa antisite defects separated by 4.19 Å are created, and a number of electrons are distributed on the Fermi level, indicative of the metallic character (see Fig. 5(c)). In the case of As[110], the As PKA occupies the interstitial site, which is 4.09 Å away from the lattice site, and one pair of As Frenkel pair defects are created in the end. It is noted that the As[110] defective state also behaves metallic character.
For GaAs/AlAs SL, the damage end states are mainly Frenkel pair and antisite defects. The considered defective states are presented in Fig. 6. The density of state distribution and band structure for ideal and defective SL are illustrated in Figs 7 and 8, respectively. As shown in Fig. 7(a), the energy gap for ideal GaAs/AlAs SL is determined to be 1.14 eV, which is smaller than the experimental value of 2.09 eV44, whereas it is in agreement with the theoretical value of 1.16 eV5. What is more, the band structure for the ideal SL shows a direct gap at the Γ point, as illustrated in Fig. 8(a). Botti et al. have investigated the band structures of (GaAs)m/(AlAs)m SL using density functional theory and a semi-empirical method. They suggested that the energy gap for SL is direct at the Γ point when the number of monolayer is no less than 25, which is consistent with our results. In the case of Al[110], the band gap of GaAs/AlAs SL with one pair of Al FP is decreased by about 0.86 eV, as compared with the ideal SL. In Fig. 8(b), the defect levels are observed near the VBM and in the forbidden band region. The charge density difference contour of the SL containing the VAl and Alint defects is illustrated in Fig. 9(a). The Al interstitial forms new bonds with the nearest As atoms, as shown by the charge accumulation in the bonding regions. Figure 9(a) also clearly shows that VAl does not pair with its neighboring atoms, and the Al vacancy is negatively charged. For Al[112], the introduced defects are also Al FP, whereas defective SL behaves metallic character, as confirmed by the density of state distribution (see Fig. 7(c)) and the band structure (see Fig. 8(c)). As shown in Fig. 9(b), significant charge redistribution occurs and electrons are shared by the Al interstitial and its neighboring As atoms. In the case of Ga[111], the introduction of the VGa and Gaint defects induces the metallicity of GaAs/AlAs SL, due to the fact that the electrons occupy the Fermi level, as shown in the Figs 7(d) and 8(d). The Fig. 9(c) shows the charge density difference of GaAs/AlAs SL with the VGa and Gaint defects. The Ga interstitial donates electrons to its neighboring As atoms and forms new bonds with them, resulting in electron localization. In the case of As[110], the defect levels appear near the VBM and cross the Fermi level, as shown in Figs 7(e) and 8(e). Figure 9(d) clearly shows that the GaAs and AsGa antisite defects interact with each other and charge delocalization is induced. For the case of As[123], the defect configuration is unstable and the As interstitial recombines with the As vacancy upon structural relaxation. These results suggest that under irradiation the electronic structures of GaAs/AlAs SL are affected significantly, in which charge transfer, redistribution and even accumulation may occur, and band gap narrowing and even metallicity are induced. Consequently, the carrier concentration and mobility, as well as the electrical properties will be influenced. Therefore, it is necessary to enhance the radiation tolerance of GaAs/AlAs SL to improve its electrical performance under radiation environment.
Illustration of schematic view of defects created by PKA recoils in GaAs/AlAs superlattice. (a) Al[110]; (b) Al[112]; (c) Ga[111]; (d) As[110] and (e) As[123]. The blue, red and green spheres represent the Ga, Al and As atoms, respectively. VX: X vacancy (X = Al, Ga or As); Xint: X interstitial (X = Al, Ga or As); XY: X occupying the Y lattice site (X, Y = Al, Ga or As). The yellow and pink spheres represent the vacancy and interstitial defects, respectively.
Total density of state distribution for ideal and defective GaAs/AlAs superlattice. The Fermi level is at 0 eV. (a) Ideal state; (b) Al[110]; (c) Al[112]; (d) Ga [111]; (e) As[110] and (f) As[123]. Al[110]: Alint and VAl defective state; Al[112]: Alint and VAl defective state; Ga[111]: Gaint and VGa defective state; As[110]: AsGa and GaAs antisite defective state; As[123]: Asint and VAs defective state.
Band structures for ideal and defective GaAs/AlAs superlattice. (a) Ideal state; (b) Al[110]; (c) Al[112]; (d) Ga[111]; (e) As[110] and (f) As[123]. Al[110]: Alint and VAl defective state; Al[112]: Alint and VAl defective state; Ga[111]: Gaint and VGa defective state; As[110]: AsGa and GaAs antisite defective state; As[123]: Asint and VAs defective state.
Conclusions
In summary, low energy recoil events in AlAs, GaAs and GaAs/AlAs superlattice (SL) have been investigated by an ab initio molecular dynamics method. The radiation damage effects on the electronic structures of these materials are also studied. In bulk AlAs and GaAs, the threshold displacements energies (Eds) for As atoms are generally smaller than those for cations, indicating that the As displacements are dominant in the recoil events of bulk states. Besides, the Ed values for AlAs are generally larger than those for GaAs, suggesting that AlAs behaves more robustly under radiation environment. As compared with their bulk states, the cations in GaAs/AlAs SL structure are more susceptible to the radiation, whereas the As atoms are more difficult to be displaced, i.e., the GaAs/AlAs SL exhibits different radiation tolerance from their bulk states. The radiation damage states in bulk AlAs and GaAs are vacancy and interstitial defects. As for GaAs/AlAs SL, the created defects are generally Frenkel pairs (FP) and antisite defects. The band structures of defective GaAs/AlAs SL show that the introduction of FP and antisite defects generally induce metallicity except for the Al FP in the case of Al[110], in which the bandgap of SL decreases by about 0.86 eV, suggesting that the created defects have profound effects on the electronic structures. It is thus necessary to enhance the radiation tolerance of GaAs/AlAs SL to improve its electrical performance under radiation environment.
Methods
The low-energy displacement events of AlAs, GaAs and (GaAs)m/(AlAs)n SL are simulated by the Spanish Initiative for Electronic Simulations with Thousands of Atoms (SIESTA) code. The norm-conserving Troullier-Matrins pseudopotentials46 are employed to determine the interaction between ions and electrons, and the exchange-correlation potential is described by the local-density approximation (LDA) in Ceperly-Alder parameterization47. The valence wave functions are expanded by a basis set of localized atomic orbitals, and double-ζ basis sets plus polarization orbital (DZP) are employed, with a K-point sampling of 1 × 1 × 1 in the Brillouin zone and a cut-off energy of 60 Ry. The AIMD calculation is computationally expensive and is limited by the system size. However, if the system size is too small, the irradiated atoms will be knocked out of the box. In these cases, a (GaAs)2/(AlAs)2 superlattice, which consists of two monolayers of GaAs alternating with two monolayers of AlAs (see Fig. 1(b)) and totally 128 atoms, is considered in this work. A specific atom is selected as the primary knock-on atom (PKA), and it is given a kinetic energy to initiate a recoil event. If the PKA returns to its original position at the end of the recoil event, the simulation is restarted at higher recoil energy with an energy increment of 5 eV. Once the PKA is permanently displaced from its lattice site, additional runs are preformed to improve the precision to 0.5 eV. For each atom type, seven principal incidence directions are taken into account in the present study, as shown in Fig. 1(a). The simulations are conducted with an NVE ensemble and the maximum duration of each run is 1.2 ps to avoid the instability of the system.
References
Ferhat, M., Zaoui, A. & Certier, M. Electronic structure calculation for (GaAs)(1)(AlAs)(1) monolayer superlattice. Phys. Status Solidi B-Basic Res. 204, 673–678 (1997).
Daly, B. C., Maris, H. J., Imamura, K. & Tamura, S. Molecular dynamics calculation of the thermal conductivity of superlattices. Phys. Rev. B 66, 024301 (2002).
Barkissy, D. et al. Electronic Properties of GaAs/AlAs Nanostructure Superlattice for Near Infrared Devices at Low Temperatures. J. Low Temp. Phys. 182, 185–191 (2016).
Zhou, J. W. et al. Ab initio optimization of phonon drag effect for lower-temperature thermoelectric energy conversion. Proc. Natl. Acad. Sci. USA 112, 14777–14782 (2015).
Botti, S., Vast, N., Reining, L., Olevano, V. & Andreani, L. C. Ab initio and semiempirical dielectric response of superlattices. Phys. Rev. B 70, 045301 (2004).
Botti, S. & Andreani, L. C. Electronic states and optical properties of GaAs/AlAs and GaAs/vacuum superlattices by the linear combination of bulk bands method. Phys. Rev. B 63, 235313 (2001).
Ribeiro, M., Fonseca, L. R. C. & Ferreira, L. G. First-principles calculation of the AlAs/GaAs interface band structure using a self-energy-corrected local density approximation. Epl 94, 27001 (2011).
Minnich, A. J. et al. Modeling study of thermoelectric SiGe nanocomposites. Phys. Rev. B 80, 155327 (2009).
Luckyanova, M. N. et al. Coherent Phonon Heat Conduction in Superlattices. Science 338, 936–939 (2012).
Spasov, S. et al. Modifying the electronic properties of GaAs∕AlAs superlattices with low-density nitrogen doping. J. Appl. Phys. 100, 063718 (2006).
Fauzi, D. A. et al. In 5th International Conference on Mechatronics Vol. 53 IOP Conference Series-Materials Science and Engineering (eds A. A. Shafie, R. Khan, & M. Rashid) (2013).
Hakkarainen, T. et al. Optical properties of ion irradiated and annealed InGaAs/GaAs quantum wells and semiconductor saturable absorber mirrors. J. Phys. D-Appl. Phys. 38, 985–989 (2005).
Wang, Y. Y. et al. Radiation damage effects on double-junction GaInP2/GaAs solar cells. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. Atoms 330, 76–81 (2014).
Tanaka, N. & Ishikawa, T. Energy dependence and depth distribution of electron beam-induced damage in GaAs/AIGaAs heterostructures. J. Electron. Mater. 23, 341–346 (2013).
Kahaly, M. U., Nazir, S. & Schwingenschlogl, U. Band structure engineering and vacancy induced metallicity at the GaAs-AlAs interface. Appl. Phys. Lett. 99, 123501 (2011).
Grimshaw, J. A. & Banbury, P. C. The displacement energy in GaAs. Proceedings of the Physical Society 84, 151 (1964).
Pons, D. & Bourgoin, J. Anisotropic-Defect Introduction in GaAs by Electron Irradiation. Phys. Rev. Lett. 47, 1293–1296 (1981).
Wesch, W., Kamarou, A., Wendler, E. & Klaumünzer, S. 593MeV Au irradiation of InP, GaP, GaAs and AlAs. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. Atoms 242, 363–366 (2006).
Sayed, M., Jefferson, J. H., Walker, A. B. & Cullis, A. G. Computer simulation of atomic displacements in Si, GaAs, and AlAs. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. Atoms 102, 232–235 (1995).
Björkas, C. et al. Light and heavy ion effects on damage clustering in GaAs quantum wells. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. Atoms 257, 324–327 (2007).
Nordlund, K., Peltola, J., Nord, J., Keinonen, J. & Averback, R. S. Defect clustering during ion irradiation of GaAs: Insight from molecular dynamics simulations. J. Appl. Phys. 90, 1710–1717 (2001).
Cullis, A. G., Smith, P. W., Jacobson, D. C. & Poate, J. M. Differential ion damage and its annealing behavior in AlAs/GaAs heterostructures. J. Appl. Phys. 69, 1279–1286 (1991).
Pronko, P. P. et al. Ion Beam Mixing of GaAs/AlGaAs Superlattice and ITS Relationship to Amorphization. MRS Proceedings 147, 297–302 (2011).
Jenčič, I., Bench, M. W., Robertson, I. M. & Kirk, M. A. A comparison of the amorphization induced in AlxGa1−xAs and GaAs by heavy-ion irradiation. J. Appl. Phys. 69, 1287–1293 (1991).
Xiao, H. Y., Gao, F., Zu, X. T. & Weber, W. J. Threshold displacement energy in GaN: Ab initio molecular dynamics study. J. Appl. Phys. 105, 123527 (2009).
Xiao, H. Y., Weber, W. J., Zhang, Y., Zu, X. T. & Li, S. Electronic excitation induced amorphization in titanate pyrochlores: an ab initio molecular dynamics study. Sci Rep 5, 8265 (2015).
Jiang, M. et al. Ab initio molecular dynamics simulation of the effects of stacking faults on the radiation response of 3C-SiC. Sci Rep 6, 20669 (2016).
Jiang, M. et al. A comparative study of low energy radiation responses of SiC, TiC and ZrC. Acta Mater. 110, 192–199 (2016).
Yuan, Y. G. et al. Ab initio molecular dynamics simulation of low energy radiation responses of alpha-Al2O3. Sci Rep 7, 3621 (2017).
Lucas, G. & Pizzagalli, L. Ab initio molecular dynamics calculations of threshold displacement energies in silicon carbide. Phys. Rev. B 72, 161202 (2005).
Holmström, E., Kuronen, A. & Nordlund, K. Threshold defect production in silicon determined by density functional theory molecular dynamics simulations. Phys. Rev. B 78, 045202 (2008).
Liu, B., Xiao, H. Y., Zhang, Y., Aidhy, D. S. & Weber, W. J. Ab initio molecular dynamics simulations of threshold displacement energies in SrTiO3. J. Phys.-Condes. Matter 25, 485003 (2013).
Wang, X. J., Xiao, H. Y., Zu, X. T., Zhang, Y. & Weber, W. J. Ab initio molecular dynamics simulations of ion-solid interactions in Gd2Zr2O7 and Gd2Ti2O7. J. Mater. Chem. C 1, 1665–1673 (2013).
Gao, F., Xiao, H., Zu, X., Posselt, M. & Weber, W. J. Defect-Enhanced Charge Transfer by Ion-Solid Interactions in SiC using Large-Scale Ab Initio Molecular Dynamics Simulations. Phys. Rev. Lett. 103, 027405 (2009).
Konstantinos, T., Patrice, C., Jean-Yves, D. & Abdelhak, S. Thermal conductivity of GaAs/AlAs superlattices and the puzzle of interfaces. J. Phys.-Condes. Matter 22, 475001 (2010).
Wyckoff, R. W. G. Crystal Structures. Vol. 2 (Krieger, 1986).
Benyahia, N., Zaoui, A., Madouri, D. & Ferhat, M. Dynamic properties of III–V polytypes from density-functional theory. J. Appl. Phys. 121, 125701 (2017).
Zollo, G., Tarus, J. & Nieminen, R. M. Reliability of analytical potentials for point-defect simulation in GaAs. J. Phys.-Condes. Matter 16, 3923 (2004).
Cohen, M. L. & Chelikowsky, J. R. Electronic Structure and Optical Properties of Semiconductors. Vol. 8, page 79–139 (Springer-Verlag, 1988).
Ahmed, R., Hashemifar, S. J., Akbarzadeh, H. & Ahmed, M. & Fazal-e-Aleem. Ab initio study of structural and electronic properties of III-arsenide binary compounds. Comp. Mater. Sci. 39, 580–586 (2007).
Ihm, J. & Joannopoulos, J. D. Ground-state properties of GaAs and AlAs. Phys. Rev. B 24, 4191–4197 (1981).
Bryant, F. J. & Cox, A. F. J. Experimental and Calculated Atomic Displacement Threshold Energies for Binary Semiconductors. P. Roy. Soc. A-Math. Phy. 310, 319–339 (1969).
Luckyanova, M. N. et al. Anisotropy of the Thermal Conductivity in GaAs/AlAs Superlattices. Nano Lett. 13, 3973–3977 (2013).
Zhang, S. B., Hybertsen, M. S., Cohen, M. L., Louie, S. G. & Tomanek, D. Quasiparticle band gaps for ultrathin GaAs/AlAs(001) superlattices. Phys. Rev. Lett. 63, 1495–1498 (1989).
Vivaldo Leiria, C. Jr. & Matteo, C. Extended DFT + U + V method with on-site and inter-site electronic interactions. J. Phys.-Condes. Matter 22, 055602 (2010).
Troullier, N. & Martins, J. L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 43, 1993–2006 (1991).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Adachi, S. Properties of Group-IV, III-V and II-VI Semiconductors. Vol. 1, page 1-21 (John Wiley & Sons, Ltd, 2005).
Acknowledgements
H.Y. Xiao was supported by the NSAF Joint Foundation of China (Grant No.U1530129). Z.J. Liu was supported by National Natural Science Foundation of China (Grant No. 11464025) and the New Century Excellent Talents in University under Grant No. NECT-11–0906. The theoretical calculations were performed using the supercomputer resources at TianHe-1 located at National Supercomputer Center in Tianjin.
Author information
Authors and Affiliations
Contributions
H.X. and X.Z. designed the calculations. M.J. conducted the calculations and wrote the manuscript. S.P., G.Y. and Z.L. contributed the discussion and interpretation of the results. All authors discussed the results and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jiang, M., Xiao, H.Y., Peng, S.M. et al. A comparative study of low energy radiation response of AlAs, GaAs and GaAs/AlAs superlattice and the damage effects on their electronic structures. Sci Rep 8, 2012 (2018). https://doi.org/10.1038/s41598-018-20155-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-20155-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.