Abstract
The pursuit of mimicking complex multiscale systems has been a tireless effort with many successes but a daunting task ahead. A new perspective to engineer complex cross-linked meshes and branched/tree-like structures at different scales is presented here. Control over Saffman-Taylor instability which otherwise randomly rearranges viscous fluid in a ‘lifted Hele-Shaw cell’ is proposed for the same. The proposed control employs multiple-ports or source-holes in this cell, to spontaneously shape a stretched fluid film into a network of well defined webs/meshes and ordered multiscale tree-like patterns. Use of multiple ports enables exercising strong control to fabricate such structures, in a robust and repeated fashion, which otherwise are completely non-characteristic to viscous fingering process. The proposed technique is capable of fabricating spontaneously families of wide variety of structures over micro and very large scale in a period of few seconds. Thus the proposed method forms a solid foundation to new pathways for engineering multiscale structures for several scientific applications including efficient gas exchange, heat transport, tissue engineering, organ-on-chip, and so on. Proposal of multi-port Hele-Shaw cell also opens new avenues for investigation of complex multiple finger interactions resulting in interesting fluid patterns.
Similar content being viewed by others
Introduction
Plentiful existence of branched tree-like patterns in nature is an outcome of natural iterative process, over the millennia, towards the perfection of such designs. These branched structures therefore have been of interest to be used for various applications. Some examples include, microfluidic mixers and networks1,2, capillary pump3, synthetic leaf4, non-transparent solar electrodes5, and most importantly, heat exchangers6,7, mass transporters8,9, and vascular systems2,10,11,12. Tree-like structure with integrated source and sink segments have been demonstrated to be mechanically strong and at the same time energy efficient in flow and mass transport than any other design configuration13,14. Vascular systems also exhibit tree-like patterns at higher scales with extremely branched constructs that transform them into a web of interconnected micro capillaries15,16. These micro-capillaries are less in the form of tree-like and more as complex web of interconnected networks. In vitro models of such micro networks are of tremendous help to the field of artificial organ growth, response of tissues to various in-development treatment drug, curing diseases, cell sorting and many other tissue engineering applications17.
Among many techniques of fabricating such complex capillary-networks18, well-defined engineered micro arrays/channel-networks19,20 have shown momentous advancement in bio-applications21,22,23. Fabrication techniques presented in the literature are limited either in scalability23 or in time efficiency or controllability24. We propose a non-conventional, spontaneous, time-efficient, lithography-less method of shaping fluid into well-defined meshes and tree-like structures with source and sink segments by exercising control over Saffman-Taylor instability in a lifted Hele-Shaw cell. In Hele-Shaw cell25 a thin viscous fluid film, sandwitched between two parallel plates, when displaced by a less viscous fluid (normally air) develops Saffman-Taylor fingering instability26. In a “lifted Hele-Shaw cell” a variant of the same interface instability is induced by lifting apart the cell plates, sucking-in low viscous air as long air-columns/fingers from its peripheries27. Lifting of cell plates, done either angularly28 or parallely29,30, leaves a random and normally short-lived network of high-viscous fluid branches on both the cell plates. The pattern layout could substantially be altered by micro-patterning anisotropies on the cell slides27,31,32,33. We recently proposed use of yield-stress fluids in a lifted Hele-Shaw cell to retain the structures permanently34 and also the use of pits as anisotropies to control the Saffman-Taylor instability for shaping/fabricating fractal-like structures31.
In this paper, we first characterize the effect of a single hole (termed as source-hole) in lifted Hele-Shaw cell. We further propose to use multiple such sources-holes/ports as controlling units, for the first time to the best of our knowledge, to shape fluid in the desired patterns mentioned above. Our previous work31 demonstrated controlled shaping of fluid into branched patterns using control over fluid-air interface offered by blind pits that cross the interface. Additional control was exercised by manipulating depth of these pits. In contrast, in this paper, we use fundamentally different scientific principle of using multiple source-holes on the cell plate (forming what we term as multiport Hele-Shaw cell) inside stretched fluid interface. Thus the proposed control in this case is exercised by relative placement of these source-holes as against the limited control offered by depth of pits only at boundary in the previous case. Controlled branched patterns obtained in this paper, hence show distinct difference in terms of connected branch ends as against free branch ends in our previous work31. For example, we demonstrate in this paper shaping of fluid into ordered mesh patterns at two different scales and a replica of leaf venation. Thus, the proposed philosophy of using source-holes establishes solid foundation for shaping fluid into families of desired patterns at multiple scales. The shaping/fabrication process, irrespective of the structure scale, completes in a period of few seconds and the structures thus obtained are solidified followed by casting them into hollow channel-networks using an elastomer or a hydrogel as per the application requirement.
Results
Shaping of fluid into desired structures involve exercising control over highly noise sensitive viscous fingering process in a Hele-Shaw cell. Section-1.1 introduces fundamental concepts behind the proposed shaping of fluid by controlling viscous fingering and identifies process parameters. Section-1.2 discusses development of recipe for the desired shaping by using the results of characterization of process parameters. Structure fabrication/shaping, based on the control recipe thus evolved, is demonstrated in Section 1.3. Discussion in Section-2 summarizes the work, followed by methods in Section-3 explaining materials and experimental procedures used.
Proposed control using source-holes
Random pattern evolution in a lifted Hele-Shaw cell (Fig. 1(a)) is a two stage process-initiation (onset of Saffman-Taylor instability) and progression (shielding mechanism) of air finger. Initiation is the destabilization of stretched fluid film interface into a random waveform, when a low viscous air tends to rushes-in as soon as lifting commences. The length and width to which each wavelet/finger would grow, compared to others, depends on the relative inception (in terms of time and position) of each wavelet. This relative growth due to finger-finger interaction, known as shielding mechanism35, is what patterns the fluid into a highly disordered/random structure, graphically shown in Fig. 1(b). During cell lifting process, due to shielding mechanism, the number of fingers that supersede others reduce exponentially36 whereas their size in length and width continues to increase37.
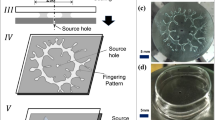
Schematic representation of (a) Lifted Hele-Shaw cell with parallel separation wherein the bottom plate squeezes the fluid against a top fixed plate to a final thickness of b 0 and radius R (position 1). Separation of plates is carried out while maintaining parallelity between the two cell plates (position 2). (b) Isometric representation of Hele-Shaw cell and the type of branched pattern that evolves, in the absence of controlling source-hole, on both cell plates as mirror images of each other. (c) Layout of ports/source-holes on one of the cell plate for fabricating a regular square arrayed structure with each cell size a × a. Enlarged section shows evolution of the interface (uniform interaction among the fingers) in lifting process giving rise to ordered structure branches. (d) Layout of source-holes on a cell plate and the type of controlled Cayley tree structure that would evolve from such a layout. Source-holes are placed at a radius of \({R}_{0},{R}_{1},\mathrm{...}{R}_{n}\) from the center wherein \({\delta }_{n}={R}_{n}-{R}_{0}\) with all the source-holes equally apart from each other by an angle θ. The inner most source-holes are at a radius of R 0 and the radius to which the fluid film interface is stretched is R. Non-uniformity (waveness) in circumferential ring is an exaggeration, of actually near-circular ring formed, so as to represent the source-hole positions at different \({R}_{n}^{^{\prime} }s\). In experiments, magnitude of δ n nedeed to shape the fluid into a tree-like pattern is very small (~μm).
We propose shaping of fluid using multiple-ports or source-holes in lifted Hele Shaw cell (LHSC) now termed as multiport lifted Hele Shaw cell (MLHSC). Introduction of multiple-ports/source-holes in a cell plate allows the controlled initiation of air fingers into the stretched film at many desired points. Such initiation of fingers is explored to completely transform the process for shaping fluid into well-defined mesh patterns as against random branched patterns formed in lifted Hele-Shaw cell. For obtaining well-defined mesh patterns, for example, source-holes are placed at the centroid of each cell-unit or each square as schematically shown in Fig. 1(c). Fingers emerging out of such multiple-ports are made to interact uniformly as schematically shown in Fig. 1(c). Uniform interaction is assured if all the fingers initiate simultaneously. To achieve simultaneous initiation of fingers, ports are sealed until separation begins to avoid liquid rise in ports. Controlled initiation should be followed by no tip-splitting/destabilization of fingers so as to avoid uncontrolled extra-branch formation and to have a uniform interaction. Finger-splitting/destabilization for a fluid with surface tension σ and viscosity τ 0 is a function of lifting velocity V and cell parameters b o and R. In what follow in Section 1.2, a modified non-dimensional number involving these parameters is proposed to carry out the characterization of finger splitting event. Although the pattern evolution process is explained here for uniformly spaced port arrays, it can be seen easily that the concepts can be extended to predict pattern evolution with non-uniform arrays of ports. Note here that because of multiple ports pressure inside film gets redistributed as against parabolic increase, from periphery towards cell center, in a cell without ports.
As another example to demonstrated effectiveness of proposed control method, we consider shaping of fluid into tree-like patterns. For controlled shaping of fluid into tree-like pattern source-holes are arranged along the circumferential region, just inside the stretched film interface as shown in Fig. 1(d), as an example. Fingers, as long air-columns, emerging out of these source-holes are made to undergo controlled non-uniform interaction by having source-holes placed at different distances (R n ) from the film center. Non-uniform interaction implies the unequal growth of fingers for shaping the fluid into an ordered tree-like pattern. Controlled non-uniform interaction via initiation-manipulation is again possible only for fingers which propagate while maintaining their stability i.e., which do not undergo tip-splitting mechanism27. To ensure this the lifting velocity, is always maintained below a threshold above which random tip-splitting events are observed.
Recipe for shaping fluid
Towards development of recipe for shaping fluid into desired arrayed structures, parameters influencing the process are identified and characterized first. As mentioned in Section 1.1 fabrication involves uniform interaction of fingers with no destabilization, the characterization of parametric dependencies of the finger destabilization process is thus presented in Fig. 2(a,b). Evolution of a single finger, emerging from a source-hole present at the center of a plate, with variation in parameters is shown in the figure. We plot the non-dimensional number μV/σ against cell parameters b 0/R and a curve is fitted to separate region with unstable evolution from that with stable. Validation of fitted curve is confirmed by studying the destabilization for two fluids (Fluid 1 and Fluid 2) with a contrasting difference in σ and τ 0. The fluids used are shear-thinning fluids which follow Herschel-Bulkley model (\(\tau ={\tau }_{0}+k{\gamma }^{n}\)) as shown in Supplementary Fig. 1(a). Although viscosity of the fluids vary with shear rate, it is equitable to consider the value of μ at γ ≤ 1 for calculating capillary number μV/σ as the velocity of stable fluid interface at the highest (V = 12.5 μm/s) is very very low (<1 mm/s) as shown in Supplementary Fig. 1(b). For a given V (say, bottom row in Fig. 2(b) where V = 2.5 μm/s) the number of branches formed (tip-splitting events) is less frequent and decreases as b 0 increases. For evolution without destabilization the fluid gets collected into a circular ring as can be seen in the last image of each row in Fig. 2(b). At low lifting velocity (V) it is found that both the outer and inner interface stabilizes at lesser b 0. All the arrayed patterns could be fabricated with interface-stability dependable parameters laying on or to the right of curve in Fig. 2(a,b)-stable region.
Source-hole characterization. (a) Stabilization of finger emerging from a single central source-holes is shown here for increasing V and b 0. Data is plotted between two non-dimensional quantities μ V/σ and b 0/R 0 and experiments were performed for two fluids with large difference in their rheological parameter (see Supplementary Fig. 1(a)). Radius R = 20 mm is kept constant for all cases. Inset image shows an intermediate lifting stage where a circular finger (air) penetrating from a single central source-hole displaces the fluid. The image also shows retreating of fluid from the outer interface. (b) Pictorial representation of how the finger destabilization process evolves before it reaches a stable point for different V and b 0 values. The pattern left on the cell plates, after the lifting process is complete, shows number of finger formations decrease as b 0 increases (left to right) until no finger destabilization happens thus shaping the fluid into a smooth circular ring (last image of all rows). Lifting velocity V was varied from 2.5 μm/sec to 12.5 μm/sec (step increase of 2.5 μm/sec) and minimum b 0 value was taken to be equal to \({50}^{\pm 2}\mu m\) (step increase of 25 μm). All images are from the experiments carried out for fluid-1 and the images for fluid-2 are shown in Supplementary Fig. 2.
Having mentioned characterization results and fundamental concepts in proposed control, the following simple recipe is proposed for fabrication of arrayed structures:
-
1.
Given arrayed pattern, determine the centroids of each unit cell as locations for source-hole anisotropies.
-
2.
For multiport Hele Shaw cell with anisotropies determined in step 1 use parameters in stable region of Fig. 2(a,b) to obtain the patterns.
For shaping of fluid into desired tree-like pattern, as shown schematically in Fig. 1(d), interaction of a single finger with two adjacent/outer-fingers is first characterized. Simulation results presented in35 demonstrated shielding of a finger by using numerically advanced initial positions to fingers adjacent to it. Further widening of these side fingers in a continuously decreasing area of spread, while progressing towards the center, completely stops/shields the central fingers to a certain length. Inspired by this and considering simultaneous finger initiation (as mentioned earlier) from all ports in our case, we propose relative placement of ports to affect shielding process. Specifically, we place ports for initiation of two outer fingers at a smaller radius R 0 relative to radius R 1 where port for initiation of central finger is placed (\({R}_{1}-{R}_{0}={\delta }_{1},{\delta }_{1}\mathrm{ > 0}\), see Fig. 3(a)). Variation of center finger length r 1 (see Fig. 3(a)) against angular distance (θ) between two adjacent source-holes for different \(\delta ^{\prime} s\) is shown in Fig. 3(b,c). In agreement with the simulation results35 the normalized finger length r 1/R follow a linear relation against θ given by r 1/R = Cθ + I, where C is slope and I the intercept. Graph in Fig. 3(b) show that with increase in δ 1, the value of C remains constant (=1.74) where as I decreases linearly. With r 1/R showing a reliance on both θ and δ 1 (represented by changing I), its variation against δ 1 is separately plotted in Supplementary Fig. 3. Note here that any finger length r n is measured as a distance traveled by that finger beyond the circumferential-line passing through source-holes placed at R 0 as shown in Figs 1(d) and 3(a).
Single finger-finger interaction. (a) Schematic diagram showing initiation and progression of two outer and one central finger from source-holes placed at a raduis of R 0 and R 1 respectively, where R 0 < R 1. Images i–vi are frames taken from a video-record of actual experiment showing the controlled non-uniform interaction. Corresponding to six stages (image i–vi) of the process, schematic diagram also represents six interface evolution stages. At time t = 4 sec all the fingers have grown to almost equal lengths (orange line) however outer fingers are ahead of central one as they had initiated from source-holes closer to the cell center (R 0). At time t > 4 outer fingers grow faster in size as they over-taken the central finger, getting more area to spread out, eventually shielding the center finger to a limited size. Fluid left between the fingers is shaped into long branches with a merging point (node) at the tip of central finger. Fluid, which had initially spread beyond the source-holes recollects itself into a circumferential branch. (b) The figure shows that with increase in θ, r 1 increases linearly with constant slope of 1.74 for all \(\delta ^{\prime} s\). Also as delta increases r 1 decreases for the same θ. (c) Pictorial representation, from actual structures fabricated, of variation in r 1/R against θ. Shapes formed here are form a Hele-Shaw cell with b 0 = 50 μm, R 0 = 15 mm, θ = 10° and δ 1 = 100 μm.
The characterization of single δ 1 can further be used to conceive recipe for several desired tree-like patterns. As an example we consider a Cayley-tree type structure38 with co-ordination number 3 and upto three generations as shown in Fig. 1(d) as a desired structure. Here the source-holes 2,4,6 and 8 are placed at maximum radius R 3 so that fingers initiate from them travel smallest length r 1. Source-hole 3 and 7, which give rise to 2nd generation fingers, travel a distance of r 2 while shielding all 1st generation fingers are thus placed at R 2 such that R 2 < R 3. Finger from source-hole 5 terminates at r 3 before shielding 1st and 2nd generation fingers along its way thus setting a position for source-hole 5 at R 1 such that R 1 < R 2. Finally finger 1 and 9 have to be ahead of all other fingers so that they can supersede all other fingers before shielding finger 5 at r 3 and are therefore places at a minimum distance of R 0. The recipe can be generalized as: In order to obtain an nth order Cayley tree with coordination number 3, source-holes generating fingers \({r}_{1},{r}_{2},{r}_{3}\mathrm{...}{r}_{n}\) should be placed in such a way so that \({R}_{0} < {R}_{1} < {R}_{2}\mathrm{... < }{R}_{n}\) where \({R}_{n}-{R}_{0}={\delta }_{n}\). Similar recipes can be developed for other tree-like patterns (using same principles).
Shaping of fluid into desired patterns
Well defined meshes
Having developed recipes for arrayed mesh and tree like patterns with corresponding characterization of parameters, we next demonstrate experimentally the effectiveness of the proposed fabrication at micro and higher scales. Although we demonstrated fabrication of structures with overall feature dimensions of 8 mm and 900 μm and Cayley tree structures (with co-ordination number 3) upto three generations, the control strategy can be extended to fabricate even higher generations and over much larger areas. Multiport Hele-Shaw cell is used to fabricate mesh’s with different linkage configurations viz. square, triangular and hexagonal. Micro structures with branch dimensions in micro domain and on other hand same structures with much bigger branch dimensions were considered for fabrication. To fabricate a structure, say square mesh shown schematically in Fig. 1(c), all source-holes need to be placed at the center of each structure unit (say, square) so that fluid is equally displaced by a penetrating finger shaping the fluid into a square mesh. Finger from a single port interacting uniformly with other surrounding fingers thus shaping the fluid into a square layout is shown in Fig. 4(a). To fabricate a mesh with some other branch configuration (say a triangular or hexagonal mesh), source-holes are to be placed at the center of each geometric unit. To demonstrate the potential of fabricating at micro and higher scales Fig. 4(b) shows structures on a single scale (i, iii and v) and on a magnified view (ii, iv and vi). Branch length and height in case of micro structures (ii, iv and vi) are 900 and 35–40 μm where as in macro structures (i, iii and v) is 8 and 0.5 mm respectively. The proposed method can not only fabricate arrayed symmetric structures (Fig. 4(b)) but also mimick relatively random patterns for example leaf venation (Fig. 4(b)(vii)). Source-holes were placed at the centroid of each polygon formed by the venation pattern. Fabricated and actual pattern is superimposed to match the two venation patterns.
Mesh patterns. (a) Evolution of fingers initiating at almost the same time and uniform interaction of central finger equally with fingers from all four sides as the time progresses (image i–vi) is shown here. Fingers initiate with a circular shape (image ii & iii) and gradually transform into rectangular shapes (image iv–vi) as the interaction effect comes into play. Shadow of source-holes created due to light source incorrectly displays a deformed view of expanding finges in image ii & iii. Parameters set were b 0 = 50 μm, a = 5 mm, and V = 4 μm/s. (b) Triangular, square, and hexagonal structures mimicking complex vascular systems are fabricated at two different scales. Image i, iii, and v show the geometrical patterns fabricated at a much higher scale wherein each branch is about 8 mm in length. These macro pattern were fabricated with b 0 = 125±10 μm. Micro-meshes with the same layout as macro structures are also shown in these figures to demonstrate the fabrication at two different scales. Image ii, iv, and vi show magnified micro-patterns with each branch length less then 1 mm and b 0 = 50±5 μm. Images in vii show a leaf venationn39 and its grayscale-form to highlight the venations pattern as a set of polygons. Enclosed part is fabricated to mimic the venation pattern in its exact form by having source-hole layout determined by locating the centroid of each polygon.
Tree-like pattern
Recipe proposed in Section 1.2 is now used to fabricate and further characterize tree-like structures with all end branches connected by a circumferential ring thus forming an integrated source and sink system. Any of the three source-holes (say source-hole 1, 2 and 3 in Fig. 1(d)) could be considered for fabrication of first generation structures. Normalized finger distance r 1/R of only first generation structure fabricated, as explained in Fig. 3(b,c), follows a linear relation with θ. Slope C = 4 from simulation35 differ hugely form the experimental value of C = 1.74 whereas intercept I = 0 is very close to the value of \(I=-0.08\simeq 0\) form experiments when δ 1 = 100 μm. This huge variation in C is attributed to the assumptions made in the simulations about the non-existence of σ and weak finger-finger interaction set-in by providing extra amplitude to two end fingers in the form of numerical noise. A strong finger-finger interaction is set in all the experiments by choosing a high value of δ 1.
Similar to the first generation r 1/R plots, normalized curves r 2/R and r 3/R for second and third generation structures were obtained from the experiments and plotted over the actual structures shown in Fig. 5(a) and (b) respectively. Structures shown here are obtained by controlled shaping of a section of the stretched fluid film with increasing θ. Any of the five source-holes (1–5 or 5–9) and all the 9 source-holes form Fig. 1(d) could be considered for fabrication of second and third generation structures respectively. Controlled shaping of first, second, and third generation structures over the entire interface of 360° shown in Fig. 5(c) demonstrates a completely controlled non-uniform interaction using sealed source-holes. Multiscale nature of controlled structures fabrication is demonstrated in Supplementary Fig. 4. Placement of source-holes to shape the fluid into mesh and tree-like structures discussed separately so far could be combined together to fabricate an integrated structure as demonstrated in Supplementary Fig. 5. Video record of experiments of controlled non-uniform interaction for fabrication of third generation structure over the entire 360° interface and uniform interaction of fingers to shape the fluid into a mesh structure is shown in Supplementary Video 1.
Tree-like patterns. Pictorial representation of increase in node distance (r n ) with increasing θ for (a) second generation structure where \({\delta }_{1}=200\,\mu m,\) and δ 2 = 400 μm (b) third generation structure with \({\delta }_{1}\mathrm{=200}\,\mu m\), \({\delta }_{2}=300\,\mu m,\) and \({\delta }_{3}=400\,\mu m\). (c) Images show a controlled non-uniform interaction of fingers initiating over the entire interface. Image-i show only the controlled first generation structures i.e, branches emerging out of the shaded circular portion (reference circle) divide only once before they merge with the circumferential ring. Image-ii shows second and image-iii shows third generation structures over 360° interface. All the fingers in image-iii are made to under go controlled interaction for their entire lengths thus producing a cayley-tree structure in its actual/ideal form. Parameters set for shaping these structures are, b 0 = 50 μm, R = 15 mm θ = 7.5° and V = 4 μm/s.
Discussion
This paper presented simple yet elegant control over Saffman-Taylor instability leading towards development of time and cost effective recipes that shape viscous fluids into patterns widely observed in the nature at multiple scales. Specifically two distinct classes of patterns were demonstrated: a mesh patterns with desired layouts and an ordered branched pattern with smoothly varying branch thicknesses (Supplementary Fig. 4). Use of multiport Hele-Shaw cell was an epiphany to shape fluids into layouts which are radically unlike those in conventional Hele-Shaw cell. Fabrication of highly ordered mesh structures (square, triangular and hexagonal layouts) demonstrates a very high degree of control over the Saffman-Taylor instability otherwise known to produce uncontrolled branched patterns. Fabrication of layouts precisely mimicking, with very ease and robustness, the flow transporting structures in plant leaves and other such systems redefines this process as exemplary method to bio-mimic structures. Apart from controlling robustly the finger-finger interactions, shaping of fluid into a Cayley-tree type structures with an important feature of connected end branches was demonstrated. Cayley-tree type structures characterized upto order three, have branch ratios (\({r}_{n}/{r}_{n+1}\)) in ranges that bear likeness to various structures exiting in nature. With appropriate fluid selection the minimum branch thickness (first generation branches) in these controlled structures can go down to few microns. Homogeneity of fluid used, source-hole and cell plate roughness, precision in plate separation are however the factors affecting the controlled fabrication at exceedingly smaller film thicknesses. At higher film thicknesses the process is relatively less affected by these factors and thus controlled fabrication can be carried out at larger scale. Fabricated structures when cast into channels networks find many application such as: in tissue growth, as efficient heat exchangers, mass transportation, capillary pumps, cell sorting and migration, artificial vasculature ans so on.
The proposed control, leading to robust repeatable fabrication would help establish otherwise difficult to obtain, correlation between simulated and experimental patterns in this domain. Proposal of multi-port Hele-Shaw cell also opens new avenues for investigation of complex multiple finger interactions resulting in interesting fluid patterns. Although we considered only one type of fluid (ceramic suspension with small yield stress) in the present paper, investigation using proposed ideas with different fluids (for example viscoelastic) can further open up interesting fluid dynamics and applications.
Methods
Experimental setups
A setups to work as parallely lifted Hele-Shaw cell, shown in Supplementry Fig. 6, was designed to operate at high precision. As the fingering process is highly sensitive to the existence of minuscule gradient in plate parallelity, a self-paralleling mechanism was used to restrict the gradient within few microns. To provide the squeeze and lifting force, motorized translation stage (MTS-90115–1–01, from Holmarc) operated via micro positioning controller (HO-MPC-3L, from Holmarc) was used. Position of lower cell plate, while squeeze and lifting process, was monitored using a linear position encoder (RGH25F, from Renishaw). A dSPACE’data acquisition card’ (ds1104) was used to interface linear position encoder with operating PC.
Fluid preparation
A fluid with a small yield stress property is prepared from a monomer HDDA (1, 6 Hexanediol diacrylate, by Sigma Aldrich) added with alumina (Almatis, CT3000, Mean particle size 0.5 microns, refractive index 1.7), 4wt.% Benzoin ethyl ether (BEE, as photo-initiator) and 2.5 wt.% Phosphate ester (PE, as surfactant). Alumina powder is incrementally added while the ceria stabilized zirconia balls were used to homogenize the fluid on a pot mill. The prepared fluid is a photo-resist ceramic suspension with viscosity, surface tension, and yield stress values dependent on the volume fraction of alumina added. Modular compact rheometer (Anton paar Physica MCR301) and Wilhelmy plate method was used to measure the fluid viscosity-profile and surface tension, respectively.
Controlling source-holes
Using a CNC-micro drilling machine source-holes were drilled on one of the cell plate for fabricating the structures. Diameter of source-holes in the present study is kept equal to 0.5 mm for all the experiments.
Design of experiment
A measured quantity of the fluid at the center cell plate is first compressed to required thickness (b 0) and radius (R). Source-holes, machined using the CNC machine, are sealed in advance form one side to prevent the penetration of fluid into them while squeezing the fluid. Before the separation process begins the sealing is removed to let the source-holes act as sources of low-viscous fluid. For tree-like pattern fabrication, compressed fluid film is allowed to spread radially beyond the source-holes by a maximum distance of around 1.5 mm. A delay of 30 seconds is introduced to stabilize the fluid film, followed by plate separation at constant velocity of 4 μm/s. Constant separation velocities in mesh structure fabrication case varies from 2.5 to 12.5 μm/s for different experiments. Complete experimental process is recorded by a camera (18 MP NIKON S9400) at 30 fps. Structure features like the finger lengths \({r}_{1},{r}_{2},\mathrm{...}{r}_{n}\) are measured using Image-J software and 3D profile of individual branches is mapped by white light interferometry (WLI) technique (MSA 500, Polytech, Germany).
References
Bahadorimehr, A. R., Damghanian, M. & Majlis, B. Y. A static micromixer inspired from fractal-like natural flow systems. In Advanced Materials Research, vol. 254, 25–28 (Trans Tech Publ, 2011).
Lim, D., Kamotani, Y., Cho, B., Mazumder, J. & Takayama, S. Fabrication of microfluidic mixers and artificial vasculatures using a high-brightness diode-pumped nd: Yag laser direct write method. Lab on a Chip 3, 318–323 (2003).
Gervais, L. & Delamarche, E. Toward one-step point-of-care immunodiagnostics using capillary-driven microfluidics and pdms substrates. Lab on a Chip 9, 3330–3337 (2009).
Wu, W. et al. Direct-write assembly of biomimetic microvascular networks for efficient fluid transport. Soft Matter 6, 739–742 (2010).
Han, B. et al. Bio-inspired networks for optoelectronic applications. Nature communications 5 (2014).
Heymann, D., Pence, D. & Narayanan, V. Optimization of fractal-like branching microchannel heat sinks for single-phase flows. International journal of thermal sciences 49, 1383–1393 (2010).
Xu, S., Li, Y., Hu, X. & Yang, L. Characteristics of heat transfer and fluid flow in a fractal multilayer silicon microchannel. International Communications in Heat and Mass Transfer 71, 86–95 (2016).
Pence, D. The simplicity of fractal-like flow networks for effective heat and mass transport. Experimental Thermal and Fluid Science 34, 474–486 (2010).
Wheeler, T. D. & Stroock, A. D. The transpiration of water at negative pressures in a synthetic tree. Nature 455, 208–212 (2008).
Borenstein, J. T. et al. Microfabrication technology for vascularized tissue engineering. Biomedical Microdevices 4, 167–175 (2002).
Nguyen, T. Q. & Park, W.-T. Rapid, low-cost fabrication of circular microchannels by air expansion into partially cured polymer. Sensors and Actuators B: Chemical 235, 302–308 (2016).
He, J. et al. Fabrication of circular microfluidic network in enzymatically-crosslinked gelatin hydrogel. Materials Science and Engineering: C 59, 53–60 (2016).
Bejan, A. & Lorente, S. Constructal tree-shaped flow structures. Applied Thermal Engineering 27, 755–761 (2007).
da Silva, A. K., Lorente, S. & Bejan, A. Constructal multi-scale tree-shaped heat exchangers. Journal of applied physics 96, 1709–1718 (2004).
Rhodin, J. A. Architecture of the vessel wall. Comprehensive Physiology (2011).
Mulvany, M. & Aalkjaer, C. Structure and function of small arteries. Physiological reviews 70, 921–961 (1990).
Lanza, R., Langer, R. & Vacanti, J. P. Principles of tissue engineering (Academic press, 2011).
Hasan, A. et al. Microfluidic techniques for development of 3d vascularized tissue. Biomaterials 35, 7308–7325 (2014).
Folch, A. & Toner, M. Cellular micropatterns on biocompatible materials. Biotechnology progress 14, 388–392 (1998).
Kaihara, S. et al. Silicon micromachining to tissue engineer branched vascular channels for liver fabrication. Tissue engineering 6, 105–117 (2000).
Khademhosseini, A., Langer, R., Borenstein, J. & Vacanti, J. P. Microscale technologies for tissue engineering and biology. Proceedings of the National Academy of Sciences of the United States of America 103, 2480–2487 (2006).
Tseng, P., Kunze, A., Kittur, H. & Di Carlo, D. Research highlights: microtechnologies for engineering the cellular environment. Lab on a Chip 14, 1226–1229 (2014).
Lee, K.-H., Lee, J. & Lee, S.-H. et al. 3d liver models on a microplatform: well-defined culture, engineering of liver tissue and liver-on-a-chip. Lab on a Chip 15, 3822–3837 (2015).
Kumar, P., Islam, T. U., Majumder, M. & Gandhi, P. S. A scalable, lithography-less fabrication process for generating a bio-inspired, multi-scale channel network in polymers (2017).
Hele-Shaw, H. S. On the motion of a viscous fluid between two parallel plates. In Nature 58, 34–36 (1898).
Saffman, P. G. & Taylor, G. The penetration of a fluid into a porous medium or hele-shaw cell containing a more viscous liquid. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 245, 312–329 (The Royal Society, 1958).
Ben-Jacob, E. et al. Experimental demonstration of the role of anisotropy in interfacial pattern formation. Physical review letters 55, 1315 (1985).
Zhang, S.-Z., Louis, E., Pla, O. & Guinea, F. Linear stability analysis of the hele-shaw cell with lifting plates. The European Physical Journal B-Condensed Matter and Complex Systems 1, 123–127 (1998).
Shelley, M. J., Tian, F.-R. & Wlodarski, K. Hele-shaw flow and pattern formation in a time-dependent gap. Nonlinearity 10, 1471 (1997).
Fontana, J. V. & Miranda, J. A. Finger competition in lifting hele-shaw flows with a yield stress fluid. Physical Review E 88, 023001 (2013).
ul Islam, T. & Gandhi, P. S. Fabrication of multscale fractal-like structures by controlling fluid interface instability. Scientific Reports 6 (2016).
Sinha, S., Kabiraj, S. K., Dutta, T. & Tarafdar, S. Radially interrupted viscous fingers in a lifting hele-shaw cell. The European Physical Journal B-Condensed Matter and Complex Systems 36, 297–300 (2003).
Tarafdar, S., Sinha, S., Nag, S. & Dutta, T. Fingering and pressure distribution in lifting hele-shaw cells with grooves: A computer simulation study. Physical Review E 80, 026–315 (2009).
ul Islam, T. & Gandhi, P. S. Spontaneous fabrication of three-dimensional multiscale fractal structures using hele-shaw cell. Journal of Manufacturing Science and Engineering 139, 031007 (2017).
Thamida, S., Takhistov, P. & Chang, H.-C. Fractal dewetting of a viscous adhesive film between separating parallel plates. Physics of Fluids (1994-present) 13, 2190–2200 (2001).
Amar, M. B. & Bonn, D. Fingering instabilities in adhesive failure. Physica D: Nonlinear Phenomena 209, 1–16 (2005).
Derks, D., Lindner, A., Creton, C. & Bonn, D. Cohesive failure of thin layers of soft model adhesives under tension. Journal of applied physics 93, 1557–1566 (2003).
Ostilli, M. Cayley trees and bethe lattices: A concise analysis for mathematicians and physicists. Physica A: Statistical Mechanics and its Applications 391, 3417–3423 (2012).
Corson, F., Adda-Bedia, M. & Boudaoud, A. In silico leaf venation networks: growth and reorganization driven by mechanical forces. Journal of theoretical biology 259, 440–448 (2009).
Acknowledgements
Authors thank Mr Raj Mashruwala for his generous donations for setting up the facility of “Suman Mashruwala Advanced Microengineering Laboratory” in the Department of Mechanical Engineering, IIT Bombay where this research was carried out. Authors also thank Prof. P. Bhargava for allowing use of Pot mill facility in Particulate Materials Laboratory in the Department of Metallurgical Engineering and Material Science where the fluid sample was prepared.
Author information
Authors and Affiliations
Contributions
The idea of using source-holes was conceived jointly and furthered by T.I. towards mesh pattern fabrication. T.I. carried out all the experiments, prepared all figures and wrote the main manuscript text in discussion with P.S.G. Experimental work was supervised by P.S.G. Both authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The proposed work borrows a part from a pending patent with international Application No. PCT/IN2016/000111 on the fabrication process technology filed by Indian Institute of Technology, Bombay. The two authors T.I and P.S.G are named as inventors in the application.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Islam, T.u., Gandhi, P.S. Viscous Fingering in Multiport Hele Shaw Cell for Controlled Shaping of Fluids. Sci Rep 7, 16602 (2017). https://doi.org/10.1038/s41598-017-16830-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16830-3
This article is cited by
-
Spontaneous re-arrangement of evaporating suspension into mesh-patterns towards concentration gradient generation on a chip
Sādhanā (2024)
-
Controlled viscous fingering in volatile fluid towards spontaneous evolution of ordered 3D patterns
Scientific Reports (2023)
-
Machine learning approach to predict viscous fingering in Hele-Shaw cells
International Journal on Interactive Design and Manufacturing (IJIDeM) (2023)
-
Geometrical operating parameter’s analysis used in flexural cartridges
International Journal on Interactive Design and Manufacturing (IJIDeM) (2023)
-
A practical approach towards utilisation of the net-shaped micro-structures developed in the lifting plate Hele–Shaw cell for micro-mixing
International Journal on Interactive Design and Manufacturing (IJIDeM) (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.