Abstract
Density functional supercell calculations of the Schottky barrier heights (SBH) of metal germanides and silicides on Si or Ge find that these vary with the facet, unlike those of elemental metals. In addition, silicides and germanides show a stronger dependence of their SBHs on the work function than those of elemental metals, as seen experimentally. Both effects are beyond the standard metal induced gap states model. NiSi2 is found to have a much lower SBH on n-Si(100) than on n-Si(111), as seen experimentally. It is shown how such results can be used to design lower SBH contacts for n-Ge, which are needed technologically. The SBHs of the better behaved Si/silicide interfaces can be used to benchmark the behavior of the less well behaved Ge-germanide interfaces for this purpose. The dependence of the SBH of epitaxial Pb-Si(111) on its reconstruction is also covered.
Similar content being viewed by others
Introduction
For both conventional semiconductors and layered semiconductors, the performance of their devices is often limited by their contact resistances1. This is due to the Schottky barriers at the contacts. A standard way to minimize the Schottky barrier heights (SBH) is to vary the contact metal, as the SBH will vary with the metal work function. However, this is difficult for many semiconductors as they suffer from Fermi level pinning, in which the SBH varies only weakly with the work function. This is expressed in terms of the Fermi level pinning factor S = ∂ϕn/∂ΦM being very small, where ϕn is the n-type barrier height and ΦM is the work function of the contact metal. For Si, the Fermi level pinning problem and a large SBH can be circumvented by heavily doping the Si, so that carriers can tunnel through the depletion layer, but this is less easy for other semiconductors where dopants are less soluble or not always shallow.
For example, germanium has higher electron and hole mobilities than Si and it is one of the more promising candidates for a next generation channel material. However, for Ge the n-type SBH is very large because the Fermi level is pinned close to its valence band edge2,3. Many approaches have been tried to overcome this problem, such as introducing ultra-thin oxide layers4, or delta-doping with As, S or Cl5. Another method is to use germanides or silicides6,7,8,9,10,11,12 which appear to have weaker Fermi level pinning13.
Schottky barrier behaviors are often classified as being limited by intrinsic properties14,15,16,17 or by extrinsic effects such as interfacial defects18. Generally, in Si or Ge the intrinsic effects tend to dominate. The intrinsic states include the metal induced gap states (MIGS)14. The MIGS are extensions of the travelling wave states of the metal continued into the band gap of the semiconductor and are drawn from the valence and conduction states of the bulk semiconductor14,17. As such, in a cubic semiconductor, the pinning factor S should be a function only of the semiconductor itself and independent of the type of metal, while the pinning energy or charge neutrality level (CNL) should be independent of the crystal face. Generally, if extrinsic effects are present, such as the interfacial defects at the contacts on MoS2, these tend to reduce S below the intrinsic MIGS value19,20,21 and so they are viewed as a negative factor.
However, there is a second type of ‘extrinsic factor’ in which varying the type of metal and the face can also be used to vary the Schottky barrier height. If this extrinsic quality can be accessed in a suitable way, it might be used to reduce the SBH of n-Ge.
It was previously noted that the SBHs of silicides on Si were much more weakly pinned than those of elemental metals13 – that is, S is much larger. Recently Nishimura et al.22 found that the SBH of germanides on Ge were also more weakly pinned than for elemental metals. They also found that their SBHs on Ge were face-dependent, whereas the SBHs of elemental metals were independent of face3. This is reminiscent of the behavior of NiSi2 where some years ago Tung23 found that the Si/NiSi2(111) interface had very different SBHs for its A and B orientations. Thus, here we carry out a detailed study of the face dependence of Schottky barrier heights of different metals.
Results
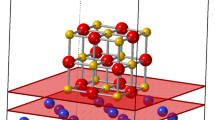
We first consider the disilicides. For silicide metals of higher work function, we use the cubic NiSi2 structure as a representative structure, as this has a high symmetry and is lattice-matched to Si. The Si/NiSi2 interface is interesting because the covalent bonding of the Si continues across the interface into the silicide. In NiSi2, the Ni sites are 8-fold coordinated by Si, and Si sites are 4-fold coordinated by Ni23,24. The bonds in NiSi2 themselves are only weakly polar13. At the interface, the NiSi2 lattice terminates in 7-fold Ni sites, which can be viewed as Ni ‘dangling bonds’, while the Si sites all remain 4-fold bonded across the interface24, Fig. 1(a). The Ni can be replaced by other transition metals to form their silicides. This NiSi2 structure is used for Ti, Cr, Fe, Ru, Co, Ni and Pt.
The (100) interface of NiSi2 has been much less studied than (111). Its structure was first modeled as containing 6-fold coordinated Ni sites25, but it was then noticed that it possessed a 2 × 1 reconstruction26. On the basis of total energy calculations, Yu et al.27 proposed an unusual 2 × 1 structure (Fig. 1(b)) which was later confirmed by Falke et al.28 using high resolution STEM. The 2 × 1 reconstructed interface has 5-fold Si sites and lateral Si-Si bonds on the Si side.
For silicides of metals of larger atomic radius, we use the YSi2 structure. This has a hexagonal unit cell which is lattice-matched to the √3 × √3(111) face of Si11, Fig. 2(a). Here, the silicons lie in a plane and the Y’s form layers above and below the silicons. The bonding in this lattice is very polar. The Si-terminated (0001) face of YSi2 bonds to Si(111). While YSi2 is hexagonal, its a and c lattice constants are quite similar. This allows us to construct a pseudo-(100)Si/YSi2 interface by rotating the YSi2 lattice to give the structure shown in Fig. 2(b). This structure is used for the silicides of Yb, Y, La and Zr. Thus, using NiSi2 and YSi2 lattices, we have the ability to study silicide/germanide interfaces from Yb to Pt, covering the widest range of metal work functions.
The structure of the (110)Si:NiSi2 interface is unknown, but a simple coherent interface model shown in Fig. 1(c) is used to represent this interface. We also built a (110) interface of YSi2 using the lattice matched interface shown in Fig. 2(b). However, this model has too large a lateral size and leaves too many dangling bonds on the Si side, and thus has a large interfacial energy. Instead, we took a slab of (110)YSi2 and disordered it by a molecular dynamics quench. This was then attached to the (110) face of Si and structurally relaxed. The resulting interface is shown in Fig. 2(c). It has no Si dangling bonds. This allowed us to study (110)Si/MSi2 interfaces for the full range of silicides using a combination of the NiSi2 and YSi2 structures. The resulting SBHs for the two types showed a continuous line of SBH values and reasonably well-behaved barrier heights.
The φn values for each face are plotted against the silicide work function in Fig. 3. This work function is estimated from the work function of the parent metal29 using a Miedema average6, WF = (ΦMΦSi 2)1/3. We see that the calculated φn values in Fig. 3 lie on separate lines for the (100) and (111) faces. We note the continuity of data points for NiSi2 and YSi2 lattices indicates that the φn values depend on work function and not the precise crystal structure. The (100) values are offset upwards from the (111) points. The calculated slope is S = 0.35 for (100) faces, and S = 0.51 for (111) faces. The slope for the most complicated interface (110) is found to be 0.41.
On average, the slopes are large, of order S~0.4, compared to those of elemental metals which are very small (S~ 0.05). This shows that silicide SBHs have much weaker Fermi level pinning than the SBHs of elemental metals. The calculated slopes for silicides are consistent with the experimental data6,10.
A similar set of calculations were carried out for germanides on Ge. Due to the narrower band gap of Ge, and the band gap under-estimation of local density formalism, it is more difficult to locate the band edges of Ge, and there is greater uncertainty in the SBH values for Ge systems. Nevertheless, we see that there is a similar behavior for the Ge systems. A slope of 0.24 is found for the (100) face of germanides and a slope of 0.35 for the (111) faces, Fig. 4. This means that the barrier heights of germanides also show weaker Fermi level pinning, like the silicides. This gives rise to smaller SBH values for the electropositive germanides on n-type Ge, as in experiment17.
It is this large slope factor which allows the dependence of SBH on face to occur for silicides and germanides. They are both an ‘extrinsic effect’. Our calculations13 accounted for the well-known change in SBH from the Si/NiSi2(111)A to (111)B interface orientation seen by Tung23. They now explain the less well- known but much larger (0.4 eV) reduction in n-type SBH from Si/NiSi2 (111)A to (100) also seen by Tung30,31.
Our calculated barrier heights for (100) facets lie above those for (111) for both Si and Ge. This is very clear if we normalise the Ge band gap and φn values to those of Si, as is done in Fig. 5. Our calculated results agree with experiment for Si/silicides, whose interfaces are abrupt, well-controlled and well characterised. However they are mostly opposite to experiment for Ge, where (111) SBH values often lie above (100) values as seen the experimental points in Fig. 5 for Nishimura22, Yamane32, Nishimura33 and Deng34. This suggests that Ge/germanide interfaces might be a problem, being disordered, non-abrupt or multi-faceted.
Experimentally it is more difficult to grow epitaxial germanides on Ge32,33,34,35,36. This is partly because of missing phases in the phase diagrams of bulk germanides35 and partly because of poor texture control and micro-crystallinity, which makes their Schottky barriers inhomogeneous and shifts the barrier size. Thus there are fewer well behaved epitaxial Ge/germanide systems for growth33,34.
Comparing experimental data with our calculated values in Fig. 5, we see that experimentally the (111) SBHs lie above the (100) values for the Ge/MnGex system33, for the range of germanides studied by Nishmura and Toriumi22 and for Fe3Si on Ge32. In some cases, one facet has an epitaxial layer on it while the other has a polycrystalline layer. On the other hand, there is the useful case of laser-processed NiGe2 where φn for the (100) facet is only 0.37 eV, compared to 0.6 eV for NiGe itself36. This case is consistent with our calculations. This is a reasonable starting point to create low ϕn SBHs for Ge. Thus, theory can help resolve some problems in these new channel materials.
What is the cause of the different behavior of elemental metals and silicides? At the Si surface, there are Si dangling bonds. When this Si surface makes an interface with an elemental metal, these dangling bond (DB) states hybridize with the metal states and form the MIGS. These MIGS spread out in energy across the whole bonding-antibonding gap of the Si15. The average energy of the MIGS or the CNL energy is therefore that of the Si DB states from which they originated, Fig. 6. Thus, all the properties of these MIGS are intrinsic to the semiconductor.
Now, at a Si/silicide interface, and taking the Si/NiSi2 interface as an example, the Si-Si bonds continue across the interface. There are no Si DBs on the Si side pointing into the metal region, the dangling bonds are on Ni atoms on the silicide side. Indeed, the state at EF for NiSi2(111) interface causing the SBH shift was shown to have Ni DB character by Lin13. When the interface forms, these metal DB states spread out in energy across the Ni-Si bonding-antibonding energy gap to form the MIGS, Fig. 7. The average energy of these MIGS is now the average energy of the Ni-Si energy gap, or Ex = ½(EM + ESi) in general, where these energies are the work functions of the metal and Si respectively. Hence when the silicide’s metal changes, the average energy of the MIGS also changes, by ½ the rate of EM. The slope factor S to zeroth order will therefore be ~0.5, as indeed it is.
We finally consider the Pb/Si epitaxial system where a structure-dependent SBH was found experimentally37,38. In this case Pb is an elemental metal. In this case, room-temperature deposited Pb on the 7 × 7(111)Si face39,40 shows a smaller 0.7 eV SBH on n-Si. When this is annealed, the interface changes to a rotated √3 × √3 lattice matching. This has a larger 0.93 eV SBH on n-Si experimentally. We have calculated the SBHs from supercells of these structures. The SBHs extracted from the Si band edges of the partial density of states at bulk Si layers referenced to EF in Fig. 8 show a similar shift to experiment, with a larger n-type SBH for the √3 × √3 phase. It has been remarked that the √3 × √3 system has an unusually large n-type SBH37, well below the trend of other elemental metals on Si. We see that the calculated SBHs for the √3 × √3(111) and √3 × √3(100) are similar.
(a) Si(111)7 × 7 structure with different layer heights colored. (b) Positioning of Pb atoms over the Si sites for the first Pb layer. (Pb = small grey balls). (c) Calculated local density of states near the band gap, vertical lines showing the band edges, for the two (111) interfaces and the (100) interface with √3 × √3 Pb layer.
Summary
In summary, the barrier heights of a wide range of metal disilicides and metal digermanides have been calculated using supercell models of the interfaces, for the three higher symmetry faces, (100), (111) and (110). The barrier heights show that the SBHs have a dependence of crystal facet, and much weaker Fermi level pinning than for elemental metals, which goes beyond MIGS theory. The dependence on facet is consistent with data for the (111) and (100) interfaces of NiSi2 and can be used to help understand the more complicated behavior of the facet dependence of germanides on Ge. These effects can be used to tune the SBHs for n-type contacts on Ge, which is presently a significant impediment to the use of Ge high mobility substrates in future CMOS devices.
Methods
We have calculated the SBHs of metal silicides and germanides on Si or Ge for metals of a wide range of work functions, using supercell models of the semiconductor and the silicide or germanide. The calculations are carried out using the plane wave density functional code CASTEP41,42. We use the generalized gradient approximation for the electron exchange-correlation functional, and norm-conserving pseudopotentials with a cutoff energy of 750 eV. The density of states calculations for Ge used a different pseudopotential which gives a band gap even in GGA, generated by OPIUM code. The convergence is carried out to an energy below 10−5 eV per atom, and with forces below 10−3 eV/Ǻ. A k-point mesh of 4 × 4 × 2 is used for Brillouin zone integrations. The calculations are carried out on supercells of 5 layers of silicide and 9 layers of Si (and no vacuum layer). The lattice geometry is relaxed in GGA. When there is a lattice mismatch between the Si and the silicide, the x, y lattice constants of the silicide are kept fixed to those of the Si and the vertical z distances are allowed to relax. This roughly conserves the silicide volume. The work function of a metal depends mostly on its atomic volume.
For the Si/Pb calculations, ultra-soft pseudopotentials were used with a 260 eV plane wave cutoff energy. There are 6 (double) layers of Si and 3(6) layers of Pb for Si 111 (100/110) interface. The Si (111) surface is built from the experimental structure reported in RefXX. A 5 × 5 supercell is used for (100) interface and a 3 × 3 supercell is used for (110) with a rotation of 45°. The lattice mismatch is less than 3% in all interface models. Only Γ point is used for reciprocal space integration in (111) model while 5 × 5 and 9 × 9 MP grid point is used for (100) and (110) respectively. The other side of Si slab is passivated with H. A 30 Ǻ vacuum is inserted in the model, which is confirmed by calculating the electrostatic potential to be thick enough to cut off the image interaction introduced by the periodical boundary condition.
The GGA functional is known to under-estimate the semiconductor band gap, thus it will also under-estimate the Schottky barrier height, as has been known for some years43. Here we can correct this effect by also calculating the density of states using the screened exchange (sX) hybrid density functional42. Generally though, we are interested in changes in SBH due to the face or rates of change of SBH with work function, which are not affected by the absolute band gap.
References
Allain, A., Kang, J., Banerjee, K. & Kis, A. Electrical contacts to two-dimensional semiconductors. Nature Mater. 14, 1195–1205 (2015).
Dimoulas, A., Tsipas, P., Sotiropoulos, A. & Evangelou, E. K. Fermi-level pinning and charge neutrality level in germanium. Appl. Phys. Lett. 89, 252110 (2006).
Nishimura, T., Kita, K. & Toriumi, A. Evidence for strong Fermi-level pinning due to metal-induced gap states at metal/germanium interface. Appl. Phys. Lett. 91, 123123 (2007).
Nishimura, T., Kita, K. & Toriumi, A. Significant shift of Schottky barrier heights at strongly pinned metal/germanium interface by inserting an ultra-thin insulating film. Appl Phys Express 1, 051406 (2008).
Ikeda, K. et al. Modulation of NiGe/Ge Schottky barrier height by sulphur segregation during Ni germanidation. App Phys Lett 88, 152115 (2006).
Freeouf, J. L. Silicide Schottky barriers: an elemental description. Solid State Commun. 33, 1059–1061 (1980).
Tu, K. N., Thompson, R. D. & Tsaur, B. Y. Low Schottky-barrier of rare earth silicide on n-Si. Appl. Phys. Lett. 38, 626–628 (1981).
Chen, L. J. & Tu, K. N. Epitaxial growth of transition metal silicides on silicon. Mater. Sci. Reports 6, 53–140 (1991).
Joo, M. S. et al. Interface configuration and Fermi-level pinning of fully silicided gate and high-K dielectric stack. J. Vac. Sci. Technol. B 24, 1341–1343 (2006).
Bucher, E. & Schulz, S. et al. Work function and barrier heights of transition-metal silicides. Appl. Phys. A 40, 71 (1986).
Vandre, S., Kalka, T., Preinesberger, C. & Dahne-Prietsch, M. Flat band conditions observed for lanthanide-silicide monolayers on n-type Si(111). Phys. Rev. Lett. 82, 1927–1930 (1999).
Tung, R. T. The physics and chemistry of the Schottky barrier height. App. Phys. Rev. 1, 011304 (2014).
Lin, L., Guo, Y. & Robertson, J. Metal silicide Schottky barriers on Si and Ge show weaker Fermi level pinning. Appl. Phys. Lett. 101, 052110 (2012).
Tersoff, J. Schottky barrier heights and the continuum of gap states. Phys. Rev. Lett. 52, 465–468 (1984).
Monch, W. Role of virtual gap states and defect in metal-semiconductor contacts. Phys. Rev. Lett. 58, 1260–1263 (1986).
Robertson, J. Band alignment at metal-semiconductor and metal-oxide interfaces. Phys. Stat. Solidi. A 207, 261–269 (2010).
Robertson, J. Band offsets of wide-gap oxides and implications for future electronic devices. J. Vac. Sci. Technol. B 18, 1785–1791 (2000).
Spicer, W. E., Lindau, I., Skeath, P., Su, C. Y. & Chye, P. Unified mechanism for Schott-ky barrier formation and III-V oxide interface states. Phys. Rev. Lett. 44, 420–423 (1980).
Das, S., Chen, H. Y., Penumatcha, A. V. & Apenzeller, J. High performance multilayer MoS2 transistors with Sc contacts. Nano Letts 13, 100–105 (2013).
Guo, Y., Liu, D. & Robertson, J. 3D behaviour of Schottky barriers of 2D Transition metal dichalcogenides. ACS Appl Mater Interfaces 7, 25709–25715 (2015).
Liu, D., Guo, Y., Fang, L. & Robertson, J. Sulfur vacancies in monolayer MoS2 and its electrical contacts. App Phys Lett 103, 183113 (2013).
Nishimura, T., Yajima, T. & Toriumi, A. Re-examination of Fermi level pinning for controlling Schottky barrier height at metal/Ge interface. Appl. Phys. Exp. 9, 081201 (2016).
Tung, R. T. Schottky-barrier formation at single-crystal metal-semiconductor interfaces. Phys. Rev. Lett. 52, 461–464 (1984).
Cherns, D., Anstis, D. R., Hutchinson, J. H. & Spence, J. C. H. Atomic structure of the NiSi2/Si(111) interface. Philos. Mag. A46, 849 (1982).
Cherns, D., Hetherington, C. J. D. & Humphreys, C. J. The atomic structure of the NiSi2-(001) Si interface. Philos. Mag. A 49, 165 (1984).
Loretto, D., Gibson, J. M. & Yalisove, J. M. Evidence for a dimer reconstruction at a metal-silicon interface. Phys. Rev. Lett. 63, 298–301 (1989).
Yu, B. D. et al. Structural and electronic properties of metal silicide/silicon interfaces: A first-principles study. J. Vac. Sci. Technol. B 19, 1180 (2001).
Falke, U., Bleloch, A., Falke, M. & Teichert, S. Atomic structure of a (2x1). Reconstructed NiSi2/Si(001). Interface. Phys. Rev. Lett. 92, 116103 (2004).
Michaelson, M. B. The work function of the elements and its periodicity. J. Appl. Phys. 48, 4729 (1977).
Tung, R. T. Schottky barrier height – do we really understand what we measure? J. Vac. Sci. Technol. B 11, 1546 (1993).
Tung, R. T. et al. Schottky-barrier inhomogeneity at epitaxial NSi2 interfaces on Si(001). Phys. Rev. Lett. 66, 72–75 (1991).
Yamane, K. et al. Effect of atomically controlled interfaces on Fermi-level pinning at metal/Ge interfaces. Appl. Phys. Lett. 96, 162104 (2010).
Nishimura, T. et al. Crystalline orientation dependence of electrical properties of Mn Germanide/Ge(111) and (001). Schottky contacts. Microelec. Eng. 88, 605 (2011).
Deng, Y. et al. Epitaxial formation and electrical properties of Ni germanide/Ge contacts. Thin Solid Films 557, 84–89 (2014).
DeSchutter, B., DeKeyser, K., Lavoie, C. & Detavernier, C. Texture in thin film silicides and germanides: a review. Appl. Phys. Rev. 3, 031302 (2016).
Lim, P. S. H., Chi, D. Z., Wang, X. C. & Yeo, Y. C. Fermi-level de-pinning at the metal-germanium interface by the formation of epitaxial nickel germanide NiGe2 using pulsed laser anneal. Appl. Phys. Lett. 101, 172103 (2012).
Heslinga, D. R., Weitering, H. H., van der Werf, D. P., Klapwijk, T. M. & Hibma, T. Atomic-structure dependent Schottky barrier at epitaxial Pb/Si(111). interfaces. Phys. Rev. Lett. 64, 1589–1592 (1990).
Weitering, H. H., Ettema, A. R. H. F. & Hibma, T. Surface States and Fermi-level pinning at epitaxial Pb/Si(111) surfaces. Phys. Rev. B 45, 9126–9135 (1992).
Takayanagi, K. et al. Structural analysis of Si(111)7 × 7 reconstructed surface by transmission electron diffraction. Surf Sci 164, 367–392 (1985).
Brommer, K. D., Needels, M., Larson, B. E. & Joannopoulos, J. D. Ab-initio theory of the Si(111) 7 × 7 surface reconstruction. Phys Rev Lett 68, 1355 (1992).
Clark, S. J. et al. First-principles methods using CASTEP. Z. Kristall. 220, 567 (2005).
Clark, S. J. & Robertson, J. ‘Screened exchange hybrid functional applied to solids. Phys. Rev. B 82, 085208 (2010).
Das, G. P. et al. Electronic Structure and Schottky Barrier Heights of (111) NiSi2/Si A- and B- type Interfaces. Phys Rev Lett 63, 1168 (1989).
Acknowledgements
We thank EPSRC grant EP/P005152/1 for funding.
Author information
Authors and Affiliations
Contributions
Y.G. and H.L. carried out the calculations, while J.R. wrote the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, H., Guo, Y. & Robertson, J. Face Dependence of Schottky Barriers Heights of Silicides and Germanides on Si and Ge. Sci Rep 7, 16669 (2017). https://doi.org/10.1038/s41598-017-16803-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16803-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.