Abstract
The magnetism of Fe2MnAl and Mn2FeAl compounds are studied by first principles. Evolutions of magnetic moment of Fe2MnAl display distinct variation trends under pressure, showing three different slopes at different pressure intervals, 0~100 GPa, 100~250 GPa, 250–400 GPa, respectively, and the moment collapses finally at 450 GPa. The magnetic moment of Mn2FeAl shows an increasing tendency below 40 GPa and decreases subsequently with pressure, and collapses ultimately at about 175 GPa. Such non-continuing decrease of Fe2MnAl originates from the unusual charge transfer of Fe and Mn and bond populations rearrangement of Fe-Fe and Mn-Fe, whereas the distinct moment evolution of Mn2FeAl is attributed to the complicated distributions of bond populations. The half-metallicity of the compounds can be maintained at low pressure, below about 100 GPa in Fe2MnAl and 50 GPa in Mn2FeAl. The magnetic moment collapse process didn’t induce volume and bond length anomalies in the two compounds, the unique anomaly is the elastic softening behaviour in elastic constant c 44 and shear (G) and Young’s (E) moduli of Fe2MnAl at 270 GPa, where the second moment collapse occurs.
Similar content being viewed by others
Introduction
The presence of nanotechnology requires more novel materials with extraordinary physical properties. Half-metallic heusler magnetic compounds can play a key role in the field of microdevice as it shows metallic properties in one of its spin orientations while an evident energy gap is formed in the other spin orientation. The number of heusler family is more than 1000 members and nearly all of them crystalline similar to that of binary semiconductors1. The general chemical formula can be classified into two different styles, half- (semi-) or full-heusler structures.
Recently, half-metallic (XYZ) characteristic has been reported in full-Heusler (X2YZ) alloys, including Co2YZ, Mn2YZ, Fe2YZ, Cr2YZ, and V2YZ2,3,4,5, where X and Y are transition metal elements and Z is a sp element, in which Fe-(Mn-)containing compounds attract much attention due to the complicated magnetic behavior of Fe and Mn element. Fe2MnAl exhibits Cu2MnAl-type structure (\(Fm\bar{3}m\), 225#) and Mn2FeAl has the Hg2CuTi-type structure (\(F\bar{4}3m\), 216#). However, the detailed magnetic moment evolution under pressure for the typical Fe-(Mn-)containing compounds are still unknown, in particular for the key role of the on-site coulomb term in this kind of compounds.
In this paper, two representative compounds Fe2MnAl and Mn2FeAl are deeply studied under pressure by first principles. Our comprehensive calculations confirmed the crucial role of on-site coulomb term in the investigation of electronic structures, whereas such influence is not sensitive in the macroproperty calculations. In addition, we also systematically simulated the magnetic moment evolution with volume variations and found the distinctly non-continuing decrease of moment in Fe2MnAl. Meanwhile, the abnormally magnetic moment increase with pressure is also observed in Mn2FeAl.
Computational Methods
Spin-polarized geometric and electronic relaxations are performed by the projector augmented wave method6. The exchange correlation is calculated using generalized gradient approximation perdew-burke-ernzerh function (GGA-PBE)7. The k meshes8 9 × 9 × 9 is used for the first Brillouin zone integration. Energy cutoff 450 eV is set for plane wave basis. The on-site Coulomb term U is selected for Fe (U = 2.0 eV) and Mn (U = 0.8 eV). The exchange integral J = 1.1 eV is also carefully selected. The self-consistent convergence of the energy is at 5.0 × 10−7 eV/atom.
Results and Discussion
Structural properties
The coordinates of the two compounds are shown in Fig. 1. The calculated volume-energy relationship determines the ferromagnetic (FM) states as the ground states of the Fe2MnAl and Mn2FeAl. The calculated equilibrium lattice constants are 5.673 and 5.781 Å for Fe2MnAl and Mn2FeAl, respectively, in good agreement with previous results 5.649, 5.68310, 5.6711, 5.8512, 5.81613 and 5.7610, 5.72514, 5.7415, respectively. All of the bonds in Mn2FeAl are longer than their counterparts in Fe2MnAl, such as the lengths of Mn(A)-Fe and Mn(B)-Fe are longer than those of Fe-Fe and Mn-Fe, respectively. There are two different kinds of bonds in each compound, the respective lengths are 2.8368 and 2.4568 Å in Fe2MnAl, slightly shorter than those of 2.8904 and 2.5032 Å in Mn2FeAl, respectively.
(a) The atomic coordinates are (0, 0, 0), (0.5, 0.5, 0.5), and (0.25, 0.25, 0.25) for Al, Mn, and Fe, respectively in Fe2MnAl. (b) Mn atoms site at A (0, 0, 0,) and B (0.25, 0.25, 0.25) denoted by Mn(A) and Mn(B), Fe and Al atoms site at (0.5, 0.5, 0.5) and Al (0.75, 0.75, 0.75) in Mn2FeAl, respectively.
Elastic constants
We obtain the three independent elastic constants, namely c 11, c 12 and c 44, with respective values of 290.3, 197.9, 113.9 GPa for Fe2MnAl, and 272.3, 126.7, 91.6 GPa for Mn2FeAl. Clearly, the respective values of Fe2MnAl are larger than those of Mn2FeAl. The calculated Young’s (E) and shear (G) moduli of Fe2MnAl (129.9, 79.3 GPa) are substantially smaller than those of Mn2FeAl (191.7, 83.5 GPa), whereas this is not true in bulk modulus (B), with values of 228.7 GPa in Fe2MnAl and 175.2 GPa in Mn2FeAl, both agreeing well with respective literatures 215.99, 200.910, 210.116 GPa and 150.210 GPa, respectively. The anisotropy factor A = 2c 44/(c 11-c 12) is 2.46 for Fe2MnAl, agreeing well with the available data 2.344, suggesting the present elastic constants are reliable. The calculated elastic constants satisfy the stability criteria17(c 11-c 12 > 0, c 11 > 0, c 44 > 0, c 11 + 2c 12 > 0, c 12 < B < c 11) in a wide pressure range, as shown in Fig. 2. To test this result, we simulate the phonon dispersion curves at 270 and 400 GPa by the finite displacement methodology with a supercell volume of eight times larger than the unit cell (128 atoms in total), as shown in Fig. 3. Clearly, the softening behaviors of shear (c 33, G) and Young’s (E) moduli of Fe2MnAl at 270 GPa failed to induce the structural instability at such critical point.
The magnitude of B/G ratio18 greater than 1.75 meaning the crystal is brittle, otherwise it means ductile behavior. Our computed B/G ratios are 2.882 and 2.097 for Fe2MnAl and Mn2FeAl, respectively. The simulated Poisson’s ratios (σ), 0.345 for Fe2MnAl and 0.294 for Mn2FeAl, indicate that Fe2MnAl displays stronger metallic bonding character. The relationship between bulk (B) and shear (G) moduli are G = 1.1B and G = 0.6B for covalent and ionic materials, respectively. Our simulated G/B ratios are 0.347 and 0.477 for Fe2MnAl and Mn2FeAl, respectively, indicating the weak ionic bonding feature.
Electronic properties
Our thorough test found that it is necessary to introduce the on-site coulomb term U and J during the calculation of electronic properties, otherwise the band structures at spin-down orientation will cross the Fermi level, as is shown in Fig. 4, in which the left panel is the density of states (DOS) but the right one is the energy band at G point of the Brillouin zone of Fe2MnAl near Fermi level in the spin-down orientation. According to the definition of spin polarization given19 by P = [N ↑(E F ) − N ↓(E F )]/N ↑(E F ) + N ↓(E F )], where N ↑(E F ) and N ↓(E F ) correspond to the spin-up and spin-down DOS at Fermi level, respectively. Considering the largest spin polarization nature10 and the largest energy gap between conduction band bottom and valence band top, and the best agreement of the calculated magnetic moment with the available calculations, the optimal combinations should be J = 1.1 eV and U = 2.0 and 0.8 eV for Fe and Mn, respectively. The calculated gaps are 0.55 and 0.4 eV for Fe2MnAl and Mn2FeAl, respectively, differing with the results10 0.465 (Fe2MnAl) and 0.544 eV (Mn2FeAl) by ignoring the influence of the on-site coulomb term. Neglect of the influence of on-site coulomb term11 couldn’t obtain the half-metallic character for Fe2MnAl and Fe2MnP.
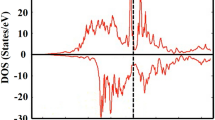
To further illustrate the nature of electronic structures, we simulate the total and atomic DOS, as are shown in Figs 5 and 6. Deep analysis to the DOS for the two compounds found that d states of Fe and Mn distributed mainly at the both sides of Fermi level, with an energy range of −4.5~5 eV, in which Mn displays stronger magnetism than Fe owing to its less overlap between spin-up and spin-down channels. The DOS profile also clearly reflects the strong magnetism of Mn and weak magnetism of Fe. Furthermore, both the two compounds formed potential valleys at Fermi level, implying the extreme stability of the compounds, as is reflected in the moment collapse process.
The two different kinds of Mn atoms in Mn2FeAl, named Mn(A) and Mn(B), presenting almost opposite charge probability distributions in the whole space, namely, charges located at spin-up channel distribute mainly at Fermi level, whereas charges located at spin-down channel distribute mainly at low-energy zone in Mn(A), which is just opposite in Mn(B) atom. The substantial discrepancy of spin-up and spin-down charge location is the origin of the higher magnetism collapse pressure. Mn(B) bonds with more Al and thus accumulates more charges at lower energy zone, which is obviously larger than that of Mn(A) in Mn2FeAl, as are also the cases for their Fermi-level values. In particular, Mn(A) exhibits a peak at Fermi level but Mn(B) and Fe locate at the steep hill, both of which make the charge transfer easier with respect to that of Fe2MnAl, consisting with the fact of its lower magnetism collapse pressure. Cr ion moment collapse process has been deeply discussed in Cr2TiAlC2 20, in which the contrary charge shift direction causes the moment collapse, whereas the present moment collapse of Fe and Mn show only certain shift under pressure. The DOS profiles of Fe2MnAl and Mn2FeAl consists well with their energy band profiles, as shown in Figs 7 and 8. The two bands of spin-up and spin-down channels of Mn2FeAl are extremely difficult to be totally merged even at 400 GPa due mainly to the subtle difference of conduction band profiles of Mn(A) and Mn(B).
Spin-polarized band structures of Mn2FeAl, same definition is used with that of Fig. 7.
Magnetic properties
The total magnetic moments are 2.010,16,21 and 1.014,15 for Fe2MnAl and Mn2FeAl, respectively, consisting with the other calculations, as seen from Figs 9 and 10. The calculated results agree with the Slater-Pauling rule22,23. Calculated unit cell volume of Mn2FeAl is 193.1 Å3, which is 10.82 Å3 larger than that of Fe2MnAl, but the volume discrepancy is quickly reduced under compression and the volume of Mn2FeAl is always larger than that of Fe2MnAl at any pressure. However the volume shrinkage of Mn2FeAl is obviously faster than that of Fe2MnAl in the pressure range of 0–400 GPa.
The calculated zero-pressure moments are 2.25 and −0.125 μ B for Mn and Fe in Fe2MnAl, respectively, in consistent with the other calculations (2.62, −0.31)21, (2.32, −0.15)10, (2.06, −0.06)16, (2.35, −0.16)24 in turn. The calculated moments are −1.66, 2.52, 0.16 μ B for Mn (A), Mn (B), and Fe in Mn2FeAl, respectively, agreeing well with the other calculations (−2.5414, −1.8515), (3.422, 2.8115), (0.0614, 0.0515) in turn. The values of Al are nearly zero and therefore could be ignored reasonably. Only one literature used U for Fe2MnAl21 but no one literature used it for Mn2FeAl.
The calculated moment collapse pressure is 450 GPa by GGA in Fe2MnAl. GGA results behave ladder-like decrease, existing three abrupt reductions at about 100, 250, 400 GPa, respectively. These three different slopes reveal the fast shift of spin-up and spin-down d state of Mn atom. The sudden collapse of Mn magnetism at 450 GPa indicates the instantaneous phase transition from ferromagnetic to nonmagnetic phases of Fe2MnAl, during which the cell volume and bond length didn’t occur any anomaly in Fe2MnAl, as are also the cases for Mn2FeAl, as shown in Figs 11 and 12. In addition, the compressibilities of the two different kinds of bonds are totally same, indicating the normal shrinkage of the geometry structure. Transition from high-spin to low-spin in MnO25,26 and MnGe27 are observed under pressure, in which moment collapse in MnGe27 is detected at about 5 GPa with the absence of abnormal moment enhancement behavior within 0–10 GPa. The mulliken charges and their bond populations of Fe and Mn behave critical phenomena at about 100 GPa, where the total moments of Fe2MnAl shows a sudden reduction. The charge transfer from Mn to Fe (and Al) slowdowns above about 100 GPa, above which the opposite charge transfer trend of Fe atom occurs, furthermore, the second collapse of total moment occurs at about 250 GPa, both of which are dominated by Mn atom. Accordingly, the two abrupt collapses originate mainly from the anomalous charge transfer under pressure. The rapid and giant collapse at about 400 GPa originates mainly from the energy band profile variation, which presents same variations with that of DOS. Within 0–100 GPa, the DOS of Fe decreases with pressure at Fermi level and keeps almost unchanged even at higher pressure in the spin-up channel, whereas the values of Mn increase with pressure and stabilize in a wide pressure range and increase again after the moment collapse. The DOS profiles of Fe and Mn clearly reflected their individually magnetic contributions to the total crystal structure. Both Fe d states, comprising of spin-up and spin-down components, distribute mainly at higher energy level, whereas Mn spin-up d states contribute mainly at lower energy level. Generally, both Fe d states shift towards lower energy level side under pressure, as is also the case in Mn. In fact, both Fe d states present highly delocalized features at 100 GPa below Fermi level, whereas this is not true in Mn, indicating that Mn also plays a key role to the total magnetism at high pressure.
The moment direction of Fe is changed at about 25 GPa in Fe2MnAl, and its magnitude keeps almost unchanged between 50 GPa and 400 GPa, with a value of about 0.15 μ B . The magnetism collapse process is highly correlated with the mulliken charge and bond population distributions, through which many evident evidences can be clearly seen, such as a strong indicator of charge transfer tendency is seen at the first collapse pressure 100 GPa, as are also the cases of 250 and 400 GPa, respectively.
The total moment curve of Mn2FeAl shows a peak at about 40 GPa, which is similar with the variation tendency of Mn(A)-Fe bond population. In addition, Mn(A/B)-Al also changed their curve slopes at 40 GPa. Moreover, opposite bond population trends in Mn(A)-Mn(B) and Mn(B)-Fe are formed at 100 GPa, suggesting the strong correlation of the bond population and the moment.
Generally, the magnetism characters of Mn and Fe consist with their respective DOS features. Moreover, the total DOS profile agrees with the energy band, namely, the energy gap of spin-down channel is closed at 50 GPa in Mn2FeAl and 100 GPa in Fe2MnAl. Fe d states occupy higher energy level sites and Mn d states distribute mainly at lower sites in Fe2MnAl. The DOS curves of Mn in both compounds consist with its magnetic direction. Under pressure, Mn(A) and Mn(B) display contrary magnitude variations at Fermi level at spin-up channel in Mn2FeAl, whereas Mn(B) varies larger than that of Mn(A) at spin-down channel.
Conclusions
The present investigation demonstrates that the Fe2MnAl and Mn2FeAl are highly stable under pressure, suggesting the impossibility of structural phase under pressure at least up to 400 GPa in Fe2MnAl and Mn2FeAl. The unusual moment evolution under pressure reveals the unusual charge transfer and bond population rearrangement. There are three moment collapses in Fe2MnAl and one abnormal moment increase in Mn2FeAl under pressure. These noncontinuous and continuous variations in Fe2MnAl and Mn2FeAl mean the spin state transition under pressure. The atomic density of states of Fe2MnAl and Mn2FeAl shifts towards lower energy side under pressure. The magnitudes of total density of states of Fe2MnAl and Mn2FeAl keep almost unchanged at Fermi level in a wide pressure range at spin-up channel.
References
Graf, T., Felser, C. & Parkin, S. S. P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 39, 1–50 (2011).
Abada, A., Amara, K., Hiadsi, S. & Amrani, B. First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe. J. Magn. Magn. Mater. 388, 59–67 (2015).
Kourova, N. I. et al. Specific features of the properties of half-metallic ferromagnetic Heusler alloys Fe2MnAl, Fe2MnSi, and Co2MnAl. Phys. Solid State 57, 700–708 (2015).
Adebambo, P. O., Adetunji, B. I., Olowofela, J. A., Oguntuase, J. A. & Adebayo, G. A. Prediction of metallic and half-metallic structure and elastic properties of Fe2Ti1-xMnxAl Heusler alloys. Physica B 485, 103–109 (2016).
Arikan, N. et al. Electronic and phonon properties of the full-Heusler alloys × 2YAl (X = Co, Fe and Y = Cr, Sc): a density functional theory study. J. Mater. Sci. 49, 4180–4190 (2014).
Blochl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Dahmane, F. et al. Structural, electronic and magnetic properties of Fe2-based full Heusler alloys: A first principle study. J. Magn. Magn. Mater. 407, 167–174 (2016).
Azar, S. M., Hamad, B. A. & Khalifeh, J. M. Structural, electronic and magnetic properties of Fe3-xMnxZ (Z = Al, Ge, Sb) Heusler alloys. J. Magn. Magn. Mater 324, 1776–1785 (2012).
Fujii, S., Ishida, S. & Asano, S. A Half-Metallic Band Structure and Fe2MnZ (Z = Al, Si, P). J. Phys. Soc. Jpn 64, 185–191 (1995).
Vinesh, A., Bhargava, H., Lakshmi, N. & Venugopalan, K. J. Appl. Phys. 105, 07A309–307A311 (2009).
Paduani, C. et al. A study of Fe2+xMn1-xAl alloys: Structural and magnetic properties. Physica B 398, 60–64 (2007).
Luo, H. Z. et al. Half-metallic properties for the Mn2FeZ (Z = Al, Ga, Si, Ge, Sb) Heusler alloys: A first-principles st. udy. J. Appl. Phys 103, 083908–083914 (2008).
Skaftouros, S., Ozdogan, K., Sasioglu, E. & Galanakis, I. Generalized Slater-Pauling rule for the inverse Heusler compounds. Phys. Rev. B 87, 024420–024424 (2013).
Belkhouane, M. et al. First-principles study of the electronic and magnetic properties of Fe2MnAl, Fe2MnSi and Fe2MnSi0.5Al0.5. J. Magn. Magn. Mater. 377, 211–214 (2015).
Born, M. & Huang, K. Dynamical theory of crystal lattices. (Clarendon Press, 1954).
Pugh, S. F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 45, 823–843 (1954).
Soulen, R. J. et al. Measuring the spin polarization of a metal with a superconducting point contact. Science 282, 85–88 (1998).
Yang, Z. J. et al. Magnetic moment collapse induced axial alternative compressibility of Cr2TiAlC2 at 420 GPa from first principle. Sci. Rep 6, 34092 (2016).
Kandpal, H. C., Fecher, G. H. & Felser, C. Calculated electronic and magnetic properties of the half-metallic, transition metal based Heusler compounds. J. Phys. D: Appl. Phys 40, 1507–1523 (2007).
Slater, J. C. The ferromagnetism of nickel. Phys. Rev 49, 537–545 (1936).
Pauling, L. The Nature of the Interatomic Forces in Metals. Phys. Rev 54, 899–904 (1938).
Plogmann, S. et al. Local moments in Mn-based Heusler alloys and their electronic structures. Phys. Rev. B 60, 6428–6438 (1999).
Kunes, J., Lukoyanov, A., Anisimov, V. I., Scalettar, R. T. & Pickett, E. Collapse of magnetic moment drives the Mott transition in MnO. Nature Materials 7, 198–202 (2008).
Kasinathan, D., Koepernik, K. & Pickett, W. E. Pressure-driven magnetic moment collapse in the ground state of MnO. New J. Phys. 9, 235–246 (2007).
Deutsch, M. et al. Two-step pressure-induced collapse of magnetic order in the MnGe chiral magnet. Phys. Rev. B 89, 180407–180411 (2014).
Acknowledgements
Yang Ze-Jin acknowledges the financial support from China Scholarship Council and the hospitality of Ames Lab at Department of Energy and Iowa State University of United States. Projects supported by the Natural Science Foundation of China (NSFC, Grant Nos: 11347220, 11547164, 21703206, and 11404287), NSF of Zhejiang Province, China (Grant Nos: LY16A040013, LY17B030008, LQ14A040003 and LY18E010007), and Science and Technology Foundation from Ministry of Education of Liaoning Province (Grant No: L2015333). A Project Supported by Scientific Research Fund of SiChuan Provincial Education Department in China (No. 14ZA0267).
Author information
Authors and Affiliations
Contributions
Y.Z.-J. organized the research and wrote the paper, G.Q.-H. did the calculations, Y.Z.-J., G.Q.-H., X.H.-N., S.J.-X., W.X.-W. and X.Z.-J. analyzed the data. These authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ze-Jin, Y., Qing-He, G., Heng-Na, X. et al. Pressure-induced magnetic moment abnormal increase in Mn2FeAl and non-continuing decrease in Fe2MnAl via first principles. Sci Rep 7, 16522 (2017). https://doi.org/10.1038/s41598-017-16735-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16735-1
This article is cited by
-
Electronic Structure, Elastic, Magnetic, and Optical Properties of Fe2MnZ (Z = Si, Ge, and Sn) Full Heusler Alloys: First-Principle Calculations
Journal of Superconductivity and Novel Magnetism (2019)
-
Density functional investigation of structural, electronic, optical and thermodynamic properties of Zn1−xBexO semiconductor
Applied Physics A (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.