Abstract
The magnetocaloric effect (MCE) is described by the change in temperature of a material by magnetic field variation and is a crucial subject in magnetism; it is motivated by the desire to enhance energy-efficient magnetic refrigeration for clean technology. Despite the recent discovery of the giant cryogenic MCE in double perovskites, the role of magnetic anisotropy has not yet been clearly discussed, because of the averaging effect of polycrystalline samples. Here, we investigated the anisotropic MCE in the single-crystal double perovskite Gd2CoMnO6. In addition to the ferromagnetic order of the Co2+ and Mn4+ moments, the large Gd3+ moments align below T Gd = 21 K, exhibiting an isotropic nature. Because of the intricate temperature development of magnetically hysteretic behaviour and metamagnetism, the change in magnetic entropy along the c-axis appears to be relatively small. On the contrary, the smaller but almost reversible magnetization perpendicular to the c-axis leads to a large MCE with a maximum entropy change of 25.4 J/kg·K. The anisotropic MCE generates a giant rotational MCE, estimated as 16.6 J/kg·K. Our results demonstrate the importance of magnetic anisotropy for understanding the MCE and reveal essential clues for exploring suitable magnetic refrigerant compounds aiming at magnetic functional applications.
Similar content being viewed by others
Introduction
Magnetic materials exhibiting the giant magnetocaloric effect (MCE) have been widely investigated1,2,3, and it would be advantageous to replace conventional refrigeration based on vapor compression and realize energy-efficient magnetic refrigeration for clean technology. It is desirable to design and discover new compounds that exhibit the giant MCE for more feasible applications. The giant and/or reversible MCE near room temperature has recently been found in several alloy systems such as Gd5(Si x Ge1−x )4, MnFeP0.45As0.55 5 (magnetic entropy change ΔS M = 18.0 J/kg·K for ΔH = 0–5 T), Ni–Mn–In6,7 (adiabatic temperature change ΔT ad = 6.2 K for ΔH = 0–1.9 T), and La(Fe,Si)13 8 (ΔS M = 16 kJ/m3·K for ΔH = 0–2 T), which offer potential refrigeration techniques for domestic usage and microelectronic devices. Cryogenic magnetic refrigeration is also essential for obtaining sub-Kelvin temperatures as a substitute for 3He/4He dilution refrigeration, whose cost continues to increase, and for hydrogen gas liquefaction, which is utilized as an alternative fuel. The MCE has been explored in many insulating oxides9,10,11,12,13, which can be easily manufactured on account of the chemical stability along with the avoidance of the refrigeration inefficiency driven by eddy current losses. Recently, the giant cryogenic MCE was discovered in several transition metal oxides such as Dy2CoMnO6 10 (ΔS M = 9.3 J/kg·K for ΔH = 0–7 T), HoMnO3 11 (ΔS M = 13.1 J/kg·K for ΔH = 0–7 T)., GdCrO4 12 (ΔS M = 29.0 J/kg·K for ΔH = 0–9 T), and HoCrO4 13 (ΔS M = 31.0 J/kg·K for ΔH = 0–8 T). However, most of the studies were performed on polycrystalline forms, preventing detailed characterization of the intrinsic properties of the giant MCE associated with magnetic and crystalline anisotropy.
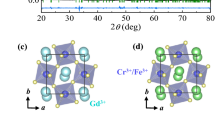
To investigate the influence of the anisotropic characteristics on the giant MCE in one of the transition metal oxides, we have synthesized single crystals of the double perovskite Gd2CoMnO6 (GCMO) using the conventional flux method14. Double perovskite R2CoMnO6 (R = La, …, Lu) compounds, where Co2+ and Mn4+ ions are alternately located in corner-shared octahedral environments, exhibit assorted physical properties such as metamagnetism15,16,17, exchange bias18,19, the re-entrant spin-glass state20,21, and multiferroicity16,22,23,24 because of the intricate magnetic interactions and ionic valence/antisite disorders between mixed-valence magnetic ions. The ferromagnetic order originates from the dominant Co2+ and Mn4+ superexchange interactions, and its transition temperature varies linearly from 204 K for La2CoMnO6 25 to 48 K for Lu2CoMnO6 26 as the size of the rare earth ions decreases. GCMO crystallizes in a monoclinic P2 1 /n double-perovskite structure with a unit cell of a = 5.3158 Å, b = 5.6050 Å, c = 7.5759 Å, and β = 89.9541°. The crystal structures viewed from the a- and c-axes are depicted in Fig. 1(a) and (b), respectively. The oxygen octahedral cages are considerably distorted due to the comparatively small radius of the Gd3+ ion. In a previous study, the polycrystalline form of GCMO revealed a large maximum entropy change of ΔS M ≈ 24 J/kg·K27, attributed to the large magnetic moments of Gd3+ ions.
From our examination of the anisotropic MCE in GCMO single crystals, we only found a ΔS M value of half that in the polycrystalline specimen along the magnetic easy c-axis despite the large magnetization (M) at an applied magnetic field (H). The significant reduction in MCE was caused by the strong temperature (T) dependence of the magnetic hysteresis and metamagnetic transition. Instead, the isothermal M perpendicular to the c-axis exhibited almost reversible hysteretic behaviour, which contributed to the giant MCE associated with the magnetic entropy change ΔS M = 25.4 J/kg·K and adiabatic temperature change ΔT ad = 7.3 K in ΔH = 0–9 T. As a result, the highly-anisotropic ΔS M produced a giant rotational MCE, estimated as 16.6 J/kg·K at 4 K. These results clearly suggest that a meticulous understanding of strongly anisotropic characteristics is crucial for finding improved functional properties in double-perovskite compounds.
Results and Discussion
The anisotropic magnetic properties of GCMO single crystals were examined parallel (H//c) and perpendicular to the c-axis (H⊥c). The T dependence of the magnetic susceptibility, χ = M/H, was measured upon warming at μ 0 H = 0.2 T after zero-H-cooling (ZFC χ) and upon cooling at the same field (FC χ), as shown in Fig. 2(a) and (b), respectively. As T decreases, χ increases smoothly until exhibiting a sharp rise at T C = 112 K, ascribed to the ferromagnetic order of the Co2+ (S = 3/2) and Mn4+ (S = 3/2) moments. The ferromagnetic behaviour was characterized by the positive Curie T determined by the Curie-Weiss law. T C was determined by the T derivative of χ and by the sharp anomaly in the T dependence curve of the heat capacity divided by the temperature (C/T) at zero magnetic field (Fig. 2(c)). Reducing T C further, FC χ reaches an approximate plateau. In contrast, ZFC χ decreases at the beginning of the warming from 2 K and the slope of χ changes at around T Gd = 21 K, below which C/T exhibits an abrupt increase, indicating the ordering of the Gd3+ moments. Above T Gd, the χ increases gradually due to the thermally activated domain wall motions. Just below T C, the ZFC χ shows a distinct peak, which signifies an additional domain wall de-pinning process. At μ 0 H = 2 T, ZFC and FC χ’s exhibit conventional ferromagnetic behaviour without any sharp anomaly near T C. The T at which the ZFC χ and FC χ curves start to split is observed, indicating the onset of magnetic irreversibility. The thermally hysteretic behaviour of the χ around T C indicates the first-order nature of the transition. The χ for the two different orientations at μ 0 H = 0.2 T exhibiting a strong magnetic anisotropy near T C indicates that the Co2+ and Mn4+ spins are mainly aligned along the c-axis.
Characterization of temperature-dependent physical properties in a GCMO crystal. (a,b) Temperature dependence of the magnetic susceptibility, χ = M/H, of double perovskite GCMO single crystal parallel (H//c, μ 0 H = 0.2 T and 2 T) and perpendicular (H⊥c, μ 0 H = 0.2 T) to the c-axis, respectively, measured upon warming from 2 to 300 K after zero-field-cooling and upon cooling at the same field. The vertical dashed line indicates the ferromagnetic transition temperature, T C = 112 K. (c) Temperature dependence of specific heat divided by temperature, C/T, measured at zero magnetic field. The inset shows a comparison of C/T up to 100 K between GCMO and Eu2CoMnO6 measured at zero magnetic field. The vertical dashed line denotes the ordering temperature of Gd3+ moments as T Gd = 21 K.
To estimate the entropy change based solely on the spin order of Gd3+ ions, ΔS Gd , the C/T for Eu2CoMnO6, which includes nonmagnetic Eu3+ ions with a similar ionic radius to Gd3+ ions, was measured, as shown in the inset of Fig. 2(c). The ΔS Gd below T Gd was obtained by integrating C/T by T (2–21 K) for GCMO after subtracting the data from Eu2CoMnO6. The calculated ΔS Gd was 17.3 J/mole·K, which is 50% of the expected value of the fully saturated Gd3+ moments, i.e., 2R ln(2J+1) = 34.6 J/mole·K, where R is the gas constant and J is the total angular momentum (J = 7/2 for the Gd3+ ion).
Figure 3(a) and (b) display the isothermal M for the two different orientations, measured up to μ 0 H = 9 T at 2 K. The initial M curve at H//c exhibits a gradual increase as H increases before a sudden jump at 6.2 T. The M at the maximum H of 9 T is found to be 15.7 μ B/f.u., which is 72% of the completely saturated moments by considering the effective magnetic moment of a Gd3+ ion as μ Gd = 7.98 μ B. The consecutive sweeping of H between +9 and −9 T leads to the sharp double-step metamagnetic transitions at H = ±3.9 and ±6.2 T. Consequently, the full curve exhibits narrow hysteretic behaviour with the remanent M as M r = 2.1 μ B/f.u. and the coercive field as H c = 0.9 T. In contrast, the M at H⊥c varies smoothly without any magnetic hysteresis. Regardless of the hard magnetic axis for the ferromagnetic Co2+ and Mn4+ sublattice, the large magnetic moment of 11.6 μ B/f.u. at 9 T implies the somewhat isotropic nature of the Gd3+ spins associated with the half-filled 4 f electronic configuration. In other words, the difference of the M values at 9 T between the two orientations is caused by the Co2+ and Mn4+ spins mainly aligned along the c-axis.
The plausible cause for the features of the metamagnetic transitions18,28 found in the fully hysteretic M curve at H//c (Fig. 3(a)) can be determined from the distinctive magnetic anisotropy between Gd3+ and Co2+/Mn4+ moments. After ZFC, the Co2+ and Mn4+ moments are mostly in a parallel or antiparallel arrangement along the c-axis, while the Gd3+ moments are oriented in random directions reflecting the isotropic character. Upon increasing H, the continuous increase of M up to 10.4 μ B/f.u. is mainly caused by the alignment of Gd3+ moments along with the flipping of only the partial Co2+ and Mn4+ spins due to the large magnetic anisotropic energy. At 6.2 T, the abrupt jump of M occurs because the Zeeman energy of the Co2+/Mn4+ sublattice overcomes the anisotropic energy. The gradual decrease in H from +9 T indicates the reduction of M until it encounters the two consecutive metamagnetic transitions, originating from the flipping of the Gd3+ spins and then the Co2+ and Mn4+ spins, respectively. This assumption is compatible with the magnetically anisotropic energy of the Co2+ and Mn4+ spins being larger than that of the Gd3+ spins. Although the postulation of rather isotropic nature of Gd3+ moments gives moderate interpretation for isothermal M at 2 K, the narrow hysteretic behaviour with a small M r may indicate small degree of interaction between Gd3+ and ferromagnetic Co2+/Mn4+ sublattices. Upon decreasing H from +9 T, the negative exchange coupling between Gd3+ and Co2+/Mn4+ spins accompanied by a smaller magnetocrystalline anisotropy energy and larger moment of Gd3+ ions leads to the progressive decrease in the net Gd3+ moments, followed by the considerable reduction of M r.
Figure 4 presents the full anisotropic curves of M up to 9 T at various T (T = 5, 10, 40, and 100 K). At 5 K and H//c, the double-step metamagnetic transitions broaden, while the remanent M and coercive field appear to be enhanced as M r = 2.4 μ B/f.u. and H c = 1.1 T. At 10 K, the area inside the magnetic hysteresis loop along H//c is considerably reduced with the shift in the metamagnetic transitions to lower H, but M r and H c are almost maintained. At H⊥c, a very narrow but large magnetic hysteresis loop is observed, presumably because of a weakened magnetic anisotropy due to thermal energy. As T increases further, the area of the magnetic hysteresis loop rapidly shrinks and M r and H c also decrease. At 100 K, a slight hysteretic behaviour remains but the metamagnetic transitions almost vanish.
Based on the distinctive magnetic properties for the two different orientations, an anisotropic MCE in the GCMO was obtained by measuring the initial M curves with dense T steps ranging from 2 to 180 K in Fig. 5. In contrast to the typical reduction of M values with the increase in T, the initial M curves at H//c develops in a complicated manner. The sharp steps of the metamagnetic transitions at 2 K move progressively to lower H and become broader as T increases. For this reason, the M value in a given H regime is lower than that at higher T. In the inset of Fig. 5(a), the isothermal M values measured at 5, 10, and 15 K are magnified. The green shaded areas represent specific examples of the reversed order of magnitude for the M values. As T is further increased, the occurrence of the reversed order shifts gradually to the lower H regime. At H⊥c, a small but broad transition feature also occurs at some temperature regime while moving to lower H as T is further increased, however, the overall magnitude of M is reduced in most of the regime of H with increasing T, as shown in the inset of Fig. 5(b).
Initial magnetization curves in a wide range of temperatures. (a) Initial curves of isothermal magnetization at H//c and various temperatures varying from 2 to 180 K. The inset shows the magnified region of magnetization for T = 5, 10, and 15 K. The green shaded ellipses indicate the reversed order of magnetization magnitudes due to the shift in metamagnetic transitions according to T. (b) Initial curves of isothermal magnetization at H⊥c and various temperatures varying from 2 to 180 K. The inset shows the magnified region of magnetization for T = 5, 10, and 15 K.
At a given T, the isothermal magnetic entropy change, ΔS M , can be obtained from the initial M curves using the Maxwell relation:
where μ 0 is the magnetic permeability in vacuum, H f is the end point of H for the integral (H f = 3, 5, 7, and 9 T), and the T gradient of M, \(\frac{\partial M(T,H)}{\partial T}\), was calculated approximately from the slope of two adjacent data points. The T dependence of the estimated entropy changes, ΔS M (T), are plotted in Fig. 6(a) and (b), respectively for H//c and H ⊥c with the H regimes of ΔH = 0–3, 0–5, 0–7, and 0–9 T. The ΔS M values for both orientations exhibit broad peaks at T C, where the ΔS M values are found to be 6.2 and 2.7 J/kg·K for H//c and H ⊥c, respectively. The much larger magnitude of ΔS M at T C for H//c describes the magnetic easy c-axis with respect to the ferromagnetic order of Co2+ and Mn4+ moments. At H//c, even with the large M at 2 K, the intercrossed isothermal M values due to the T development of metamagnetic transitions, as depicted in Fig. 5(a), results in a substantial cancellation of ΔS M . Consequently, a complicated T dependence of ΔS M is observed below T Gd for ΔH = 0–3 and 0–5 T, and even negative values of ΔS M are revealed for T = 20–90 K. The maximum ΔS M of 12.1 J/kg·K, found at 8 K for ΔH = 0–9 T, is smaller than the magnitude from the recent observation in the polycrystalline specimen. At H ⊥c, the near-absence of the estimated loss for ΔS M generates a large magnitude of ΔS M , shown as a peak at low T, followed by a steep decrease in ΔS M . The maximum MCE at 5 K for ΔH = 0–9 T is estimated as ΔS M = 25.4 J/kg·K.
Anisotropic magnetocaloric effect in GCMO. Temperature dependence of magnetic entropy change, ΔS M , obtained by integrating the temperature gradient of the initial magnetization curves in Fig. 4 for (a) H//c and (b) H⊥c with magnetic field regimes of ΔH = 0–3 T (yellow), 0–5 T (green), 0–7 T (red), and 0–9 T (blue).
By taking advantage of the strong magnetic anisotropy due to the distinctive characteristics of the double perovskite GCMO compound, the rotating MCE was measured by the angular dependence of ΔS M , denoted as ΔS θ , where θ is the angle deviating from the c-axis, i.e., θ = 0° for H//c and θ = 90° for H ⊥c (Inset of Fig. 7). Figure 7 shows ΔS θ obtained at 4 and 8 K for ΔH = 0–9 T. As there is a different T dependence of ΔS M between H//c and H ⊥c, the angle-dependent modulation of ΔS θ varies strongly with T. At 8 K, ΔS θ negligibly changes with the rotation of θ to 30° and increases linearly above 30°. The maximum ΔS θ was evaluated as only 7.8 J/kg·K. At 4 K, on the contrary, the continued variation of ΔS θ by θ rotation generates a giant rotational MCE as the maximum change of 16.6 J/kg·K, which would be beneficial for rotary magnetic refrigerator technology. The maximum difference of ΔS θ in the GCMO is comparable to the other rotating magnetic refrigerants such as HoMn2O5 29 (12.4 J/kg·K for ΔH = 0–7 T) and DyNiSi30 (17.6 J/kg·K for ΔH = 0–5 T).
A more feasible aspect of MCE can be attained as the adiabatic T change, ΔT ad , from the following equation:
where C(T, H) is the heat capacity at a given T and H. In many cases, C appears to be independent of the applied H, thus, it can be considered as a constant for the integral. However, in GCMO, the T dependence of C/T clearly varies depending on the magnitude of the applied H, as shown in Fig. 8(a) and (b) for H//c and H ⊥c, respectively, measured at H = 0, 3, 5, 7, and 9 T. At H//c, the C/T at very low temperatures decreases with H along with the emergence of a broad peak shifting to higher T. As T increases further, C/T decreases more slowly as H gradually increases. Therefore, the order of magnitude of C/T with respect to H is reversed at about 4 K. The C/T for H ⊥c exhibits similar T and H dependences as H//c. The C/T exhibits a greater reduction as H increases at the very low T regime with a further shift of the peak to higher T. ΔS Gd is also estimated from C/T taken at 9 T for H//c. ΔS Gd = 23.7 J/mole·K, which is about 69% of the value, assuming full saturation of Gd3+ moments, consistent with the measured magnetization at 9 T (Fig. 3(a)). Figure 8(c) and (d) display the T dependence of ΔT ad , estimated for H//c and H ⊥c, respectively, with ΔH = 0–3, 0–5, 0–7, and 0–9 T. At H//c, the T dependence of ΔT ad behaves similarly to that of ΔS M . For ΔH = 0–9 T, starting from ΔT ad = 1.3 K at 2 K, ΔT ad increases with T and reaches 8.3 K at the peak position as T = 17.0 K. However, the estimated T dependence of ΔT ad for H ⊥c was strongly influenced by the reciprocal of C/T during the calculation of the integral. Interestingly, the ΔT ad for ΔH = 0–9 T maintains its magnitude between 6.5 and 7.3 K up to T = 17.0 K, suggesting that the MCE steadily covers the wide range of the low T regime for H ⊥c.
Adiabatic temperature changes in GCMO. (a,b) Temperature dependence of C/T, measured at (a) H//c and (b) H⊥c with various magnetic fields, H = 0, 3, 5, 7, and 9 T, shown at T = 2–70 K. (c,d) Temperature dependence of adiabatic temperature change, ΔT ad , estimated from integrating the temperature gradient of the initial magnetization curves multiplied by the corresponding reciprocal of C/T for (c) H//c and (d) H⊥c with magnetic field regimes of ΔH = 0–3 T (yellow), 0–5 T (green), 0–7 T (red), and 0–9 T (blue).
In summary, we explored the anisotropy of the magnetic and magnetocaloric properties of single-crystal double perovskite GCMO. Contrary to the anticipated large MCE along the magnetic easy c-axis, we attained a maximum entropy change of only half the magnitude of that found in the polycrystalline specimen. This substantial reduction is attributed to the intricate temperature evolution of metamagnetic transitions. Alternatively, an almost reversible hysteretic behaviour of isothermal magnetization perpendicular to the c-axis results in a large entropy change of ΔS M = 25.4 J/kg·K, and thus the giant rotational MCE is taken as ΔS θ = 16.6 J/kg·K at 4 K. The strongly anisotropic magnetic properties of the double-perovskite compound offer essential clues for the fundamental and applied research on magnetic materials, aiming to enhance the functional properties.
Methods
Rod-shaped single crystals of GCMO were grown using the conventional flux method with Bi2O3 flux in air. The stoichiometric ratio of Gd2O3, Co3O4, and MnO2 powders was mixed and ground in a mortar, followed by pelletizing and calcining at 1000 °C for 12 h. The calcined pellet was reground and sintered at 1100 °C for 24 h. The same sintering procedure after regrinding was performed at 1200 °C for 48 h. A mixture of pre-sintered polycrystalline powder and Bi2O3 flux at a 1:12 ratio was heated to 1300 °C in a Pt crucible. It was melted at the soaking temperature for 5 h, slowly cooled to 985 °C at a rate of 2 °C/h, and cooled to room temperature at a rate of 250 °C/h. The temperature and magnetic field dependences of the DC magnetization, M, were examined by a vibrating sample magnetometer at T = 2–300 K and H = −9-9 T using a Physical Properties Measurement System (PPMS, Quantum Design, Inc.). The temperature dependence of specific heat, C, at various magnetic fields was measured with the standard relaxation method using the PPMS.
References
Pecharsky, V. K. & Gschneidner, K. A. Jr Magnetocaloric effect and magnetic refrigeration. Journal of Magnetism and Magnetic Materials 200, 44–56, https://doi.org/10.1016/S0304-8853(99)00397-2 (1999).
GschneidnerJr, K. A., Pecharsky, V. K. & Tsokol, A. O. Recent developments in magnetocaloric materials. Reports on Progress in Physics 68, 1479 (2005).
Yu, B. F., Gao, Q., Zhang, B., Meng, X. Z. & Chen, Z. Review on research of room temperature magnetic refrigeration. International Journal of Refrigeration 26, 622–636, https://doi.org/10.1016/S0140-7007(03)00048-3 (2003).
Pecharsky, V. K. & Gschneidner, J. K. A. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Physical Review Letters 78, 4494–4497 (1997).
Tegus, O., Bruck, E., Buschow, K. H. J. & de Boer, F. R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 415, 150–152 (2002).
Manosa, L. et al. Giant solid-state barocaloric effect in the Ni-Mn-In magnetic shape-memory alloy. Nat Mater 9, 478–481 (2010).
Liu, J., Gottschall, T., Skokov, K. P., Moore, J. D. & Gutfleisch, O. Giant magnetocaloric effect driven by structural transitions. Nat Mater 11, 620–626, http://www.nature.com/nmat/journal/v11/n7/abs/nmat3334.html#supplementary-information (2012).
Lyubina, J., Schäfer, R., Martin, N., Schultz, L. & Gutfleisch, O. Novel Design of La(Fe,Si)13 Alloys Towards High Magnetic Refrigeration Performance. Advanced Materials 22, 3735–3739, https://doi.org/10.1002/adma.201000177 (2010).
Phan, M.-H. & Yu, S.-C. Review of the magnetocaloric effect in manganite materials. Journal of Magnetism and Magnetic Materials 308, 325–340, https://doi.org/10.1016/j.jmmm.2006.07.025 (2007).
Ganeshraj, C., Pradheesh, R. & Santhosh, P. N. Structural, magnetic, transport and magnetocaloric properties of metamagnetic DyMn0.5Co0.5O3. Journal of Applied Physics 111, 07A914, https://doi.org/10.1063/1.3672067 (2012).
Midya, A. et al. Magnetocaloric effect in HoMnO3 crystal. Applied Physics Letters 96, 142514, https://doi.org/10.1063/1.3386541 (2010).
Palacios, E. et al. Effect of Gd polarization on the large magnetocaloric effect of GdCrO4 in a broad temperature range. Physical Review B 93, 064420 (2016).
Midya, A., Khan, N., Bhoi, D. & Mandal, P. 3d-4f spin interaction induced giant magnetocaloric effect in zircon-type DyCrO4 and HoCrO4 compounds. Applied Physics Letters 103, 092402, https://doi.org/10.1063/1.4819768 (2013).
Kim, M. K. et al. Investigation of the magnetic properties in double perovskite R2CoMnO6 single crystals (R = rare earth: La to Lu). Journal of Physics: Condensed Matter 27, 426002 (2015).
Blasco, J. et al. Evidence of large magneto-dielectric effect coupled to a metamagnetic transition in Yb2CoMnO6. Applied Physics Letters 107, 012902, https://doi.org/10.1063/1.4926403 (2015).
Wang, L. et al. Effect of metamagnetism on multiferroic property in double perovskite Sm2CoMnO6. Journal of Applied Physics 117, 17D914, https://doi.org/10.1063/1.4917517 (2015).
Su, J. et al. Magnetic and dielectric properties of metamagnetic TbCo0.5Mn0.5O3.07 ceramics. Journal of Materials Science 49, 3681–3686, https://doi.org/10.1007/s10853-014-8076-8 (2014).
Murthy, J. K. & Venimadhav, A. 4f-3d exchange coupling induced exchange bias and field induced Hopkinson peak effects in Gd2CoMnO6. Journal of Alloys and Compounds 719, 341–346, https://doi.org/10.1016/j.jallcom.2017.05.203 (2017).
Liu, W. et al. Griffiths phase, spin-phonon coupling, and exchange bias effect in double perovskite Pr2CoMnO6. Journal of Applied Physics 116, 193901, https://doi.org/10.1063/1.4902078 (2014).
Wang, X. L. et al. Structure and spin glass behaviour in non-metallic Yb2CoMnO6 perovskite manganite. Journal of Magnetism and Magnetic Materials 246, 86–92, https://doi.org/10.1016/S0304-8853(02)00033-1 (2002).
Sazonov, A. P., Troyanchuk, I. O., Sikolenko, V. V., Szymczak, H. & Bärner, K. Effect of the oxygen nonstoichiometry on the structure and magnetic properties of Nd2CoMnO6+δ double perovskites. physica status solidi (b) 244, 3367–3376, https://doi.org/10.1002/pssb.200642481 (2007).
Yáñez-Vilar, S. et al. Multiferroic behavior in the double-perovskite Lu2MnCoO6. Physical Review B 84, 134427 (2011).
Choi, H., Moon, J., Kim, J., Choi, Y. & Lee, N. Single Crystal Growth of Multiferroic Double Perovskites: Yb2CoMnO6 and Lu2CoMnO6. Crystals 7, 67 (2017).
Chikara, S. et al. Electric polarization observed in single crystals of multiferroic Lu2MnCoO6. Physical Review B 93, 180405 (2016).
Kim, M. K. et al. Effects of different annealing atmospheres on magnetic properties in La2CoMnO6 single crystals. Current Applied Physics 15, 776–779, https://doi.org/10.1016/j.cap.2015.04.009 (2015).
Lee, N. et al. Strong ferromagnetic-dielectric coupling in multiferroic Lu2CoMnO6 single crystals. Applied Physics Letters 104, 112907, https://doi.org/10.1063/1.4869479 (2014).
Murthy, J. K., Chandrasekhar, K. D., Sudipta, M., Topwal, D. & Venimadhav, A. Giant magnetocaloric effect in Gd2NiMnO6 and Gd2CoMnO6 ferromagnetic insulators. Journal of Physics D: Applied Physics 48, 355001 (2015).
Marsh, A. & Clark, C. C. Metamagnetism in the perovskite compound Gd2CoMnO6. Philosophical Magazine 19, 449–463, https://doi.org/10.1080/14786436908216304 (1969).
Balli, M., Jandl, S., Fournier, P. & Gospodinov, M. M. Anisotropy-enhanced giant reversible rotating magnetocaloric effect in HoMn2O5 single crystals. Applied Physics Letters 104, 232402, https://doi.org/10.1063/1.4880818 (2014).
Zhang, H. et al. Giant rotating magnetocaloric effect induced by highly texturing in polycrystalline DyNiSi compound. 5, 11929, https://doi.org/10.1038/srep11929, https://www.nature.com/articles/srep11929#supplementary-information (2015).
Acknowledgements
This work was supported by the NRF Grant (NRF-2014S1A2A2028481, NRF-2015R1C1A1A02037744, NRF-2016R1C1B2013709, NRF-2017K2A9A2A08000278, and 2017R1A5A1014862 (SRC program: vdWMRC center)) and partially by the Yonsei University Future-leading Research Initiative of 2014 (2016-22-0099). J.Y.M. acknowledges the tuition support from the Hyundai Motor Chung Mong-Koo Foundation.
Author information
Authors and Affiliations
Contributions
Y.J.C. and N.L. designed the experiments. J.Y.M. and M.K.K. carried out the growth of single crystals and performed magnetic and heat capacity measurements. J.Y.M., Y.J.C., and N.L. analysed the data and prepared the manuscript. All authors have read and approved the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moon, J.Y., Kim, M.K., Choi, Y.J. et al. Giant Anisotropic Magnetocaloric Effect in Double-perovskite Gd2CoMnO6 Single Crystals. Sci Rep 7, 16099 (2017). https://doi.org/10.1038/s41598-017-16416-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16416-z
This article is cited by
-
Synthesis, Structure, Morphology, Dielectric, and Optical Properties of LaSrZrFeO6: A Novel A-Site and B-Site Disordered Double Perovskite
Journal of Inorganic and Organometallic Polymers and Materials (2024)
-
Giant and highly anisotropic magnetocaloric effects in single crystals of disordered-perovskite RCr0.5Fe0.5O3 (R = Gd, Er)
Scientific Reports (2023)
-
Magnetocaloric effect in PrGd1-xBaxMn2O6 (0.0 ≤ x ≤ 1.0) double perovskite manganite system
Journal of Materials Science: Materials in Electronics (2023)
-
Rotating magnetocaloric effect in highly anisotropic TbIII and DyIII single molecular magnets
Scientific Reports (2022)
-
Study of large rotating magnetocaloric effect in strongly anisotropic double perovskite Tb2CoMnO6
Indian Journal of Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.