Abstract
Switching magnetization in a perpendicular magnetic tunnel junction (pMTJ) via voltage controlled magnetic anisotropy (VCMA) has shown the potential to markedly reduce switching energy. However, the requirement of an external magnetic field poses a critical bottleneck for its practical applications. In this work, we propose an elliptical-shaped pMTJ to eliminate the requirement of providing an external field by an additional circuit. We demonstrate that a 10 nm thick in-plane magnetized bias layer (BL) separated by a metallic spacer of 3 nm from the free layer (FL) can be engineered within the MTJ stack to provide the 50 mT bias magnetic field for switching. By conducting macrospin simulation, we find that a fast switching in 0.38 ns with energy consumption as low as 0.3 fJ at a voltage of 1.6 V can be achieved. Furthermore, we study the phase diagram of switching probability, showing that a pulse duration margin of 0.15 ns is obtained and low-voltage operation (~1 V) is favored. Finally, the MTJ scalability is considered, and it is found that scaling down may not be appealing in terms of both the energy consumption and the switching time for precession based VCMA switching.
Similar content being viewed by others
Introduction
Spin transfer torque (STT) based magnetic random access memory (MRAM)1,2 because of its non-volatility, high access speed and CMOS (complementary metal oxide semiconductor) compatibility3 has matured into one of a leading candidate in recent years4 to fill memory gaps in the extant memory hierarchy. A bit-cell of STT-RAM comprises of a magnetic tunnel junction (MTJ) which has a pinned-layer (PL) and a free-layer (FL) with their magnetization in either parallel (P) or anti-parallel (AP) state with respect to (w.r.t.) each other, which corresponds to logic “1” or “0”. In STT-RAM, a free-layer is written by passing a current with density larger than critical current density through the MTJ. If the current is flowing from FL towards PL, a spin-flux with vector parallel to the magnetization of PL (M PL ) acts on the FL to align the magnetization of FL (M FL ) with M PL , whereas if the current direction is reversed a reverse spin-flux with vector anti-parallel to M PL acts on the FL to orient it in the AP state. This current based magnetization switching, however, requires a large current density which ranges from 5 × 1010 A-m−2 for 35 ns to 1 × 1011 A-m−2 for 2 ns write-time1,2 to generate enough spins to toggle all magnetic moments of the FL. Inevitably, a large current results in considerable Joule heating in the MTJ. This results in self-heating5,6,7 induced degradation of the MTJ characteristics, e.g. the spin-polarization of spin-flux degrades thereby degrading the STT efficiency at higher temperatures. In addition, electromigration8,9 becomes prominent because of large current densities, and the dielectric may also break10 at voltages required to sustain required current densities. Furthermore, to provide a large enough current a bulky access transistor, i.e. with a large channel width-to-length ratio for bulk-MOSFET or with a large number of fins for FinFET (Fin Field Effect Transistor), is required. This implies that STT-RAM suffers from high energy consumption, reliability issues and a huge cell area11,12.
To reduce the operating current which would subsequently reduce both the energy consumption and the size of driving transistor, voltage control of magnetic anisotropy (VCMA)13 has been promulgated as an alternative to the STT14,15. There are several possible physical origins for VCMA effect. Among them, the redox reaction and the electromigration can result in a VCMA efficiency of 1000 fJ-V−1-m−1 16. However, the low reacting speed makes it unfeasible for memory application. Therefore, to design a memory cell, the most possible mechanism for VCMA effect is that electric field modulates the charge occupancy at the interface. First principles studies have shown that the modification of magnetic anisotropy by an electric field is contributed to the change of 3d-orbitals occupancies via spin-orbit interaction17. Since the VCMA based device relies on a voltage rather than a current to write, the current in this case can be greatly reduced by designing a MTJ with large enough resistance. Furthermore, the VCMA based precessional switching enables the FL to toggle in sub-nanosecond13,18. Therefore, the energy consumption can be substantially reduced by markedly reducing both the power-dissipation and the dissipation-time. Demonstrations18,19,20 hitherto have been on circular pMTJs. These demonstrations require an external in-plane magnetic field to enable the switching. This, however, is not a viable solution for integrated MRAM w.r.t. both the provision of an external field source and the field uniformity21,22. Consequently, the requirement of an external bias field poses a critical bottleneck for realizing practical VCMA memory.
In this work, therefore, we propose an elliptical pMTJ to eliminate the requirement of an external magnetic field source. Because of the elliptical structure, via shape anisotropy, an in-plane magnetized bias-layer (BL) separated from the FL by a metallic spacer can be directly engineered within the MTJ stack23. This in-plane BL, hence, provides a sufficient bias field for VCMA based precessional switching. We comprehensively appraise the effects of electronic, magnetic and physical design constraints on the FL switching dynamics to expound the device physics and an optimal operation window in the proposed design. Our results show that the required bias magnetic field can be contrived within the MTJ stack by an in-plane magnetized BL. For instance, a 10 nm thick BL separated by a 3 nm thick metallic spacer can provide an in-plane exchange field of 50 mT to bias the FL. Furthermore, we show that the FL can toggle in just 0.38 ns consuming only 0.3 fJ at a voltage of 1.6 V across the MTJ, which is attractive for memory applications. Our results also indicate that the pMTJ driven by precession based VCMA favors a low-voltage operation (~1 V) with a sufficient margin (0.15 ns) for the applied voltage pulse duration.
Methods
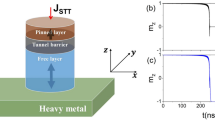
Figure 1(a) shows a schematic of an elliptical MTJ with perpendicular magnetic anisotropy (PMA), with major-axis (minor-axis) along x-axis (y-axis). A 1.2 nm thick Co20Fe60B20 24 PL and a 1.7 nm thick Co20Fe60B20 FL sandwich a MgO insulator of thickness tMgO. In this work, tMgO ranges from 1.2 nm to 2.8 nm, while the MTJ cross-section ranges from 150 × 50 nm2 to 114 × 38 nm2 with a fixed aspect-ratio (AR) of 3. Macrospin simulation, which has been shown to be valid in purview of dimensions considered in this work13,18,25,26, is developed to investigate the magnetization dynamics. The dynamics is described by the Landau-Lifshitz-Gilbert (LLG) equation27,28 as,
where γ is the gyromagnetic ratio, μ 0 is the vacuum permeability, α = 0.0128 is the Gilbert damping coefficient for Co20Fe60B20, and p PL (p BL ) is a unit-vector anti-parallel (parallel) to the magnetization of PL (BL). The magnetization unit-vector of FL m is [mx my mz], which is [0 0 ± 1] in stable states, with mx, my and mz being the projections on respective axis. H Eff is the effective magnetic field experienced by the FL. It is the vector sum of uniaxial anisotropy field H K , demagnetizing field H D , thermal fluctuation field H Therm , and external bias field H Bias , which are expressed as,
where KU is the anisotropy energy density with contributions from bulk anisotropy, KU_Bulk, and interfacial anisotropy KI. The latter is computed as KI0 − ξ ⋅ Ez. As implied from equation (2), the interfacial anisotropy is assumed to be linearly modified by the perpendicular component Ez of the electric-field E at the MgO-FL interface, at a rate determined by the VCMA coefficient ξ 24,29, where equation (2) assumes a positive value of Ez for the field direction shown in Fig. 1(a). For the voltage applied across the MTJ VMTJ, the magnitude of Ez is assumed to be VMTJ/tMgO 18,20. The CoFeB and the CoFeB/MgO interface parameters like saturated magnetization MS = 1.257 × 106 A-m−1, KU_Bulk = 2.245 × 105 J-m−3, KI0 = 1.286 × 10−3 J-m−2 24 and ξ = 50 fJ-V−1-m−1 30 are empirical parameters from experimental papers. The value of ξ at the CoFeB/MgO interface in literature is in the range of 20–100 fJ-V−1-m−1 30,31,32,33. More efficient VCMA effect, i.e. larger ξ, would result in even better performance of the proposed device than that predicted in this work.
(a) Schematic of an elliptical pMTJ with the major axis along the x-axis. A bias layer (BL) separated by a metal is engineered to provide the exchange field for the FL. The top and bottom water-blue layers are electrodes. (b) Applied voltage pulse with tRise = tFall = 50 ps and tOFF of 10 ns, which is long enough to ensure that the magnetization is completely relaxed. Positive voltage is defined for the electric field pointing from the PL to the FL.
In equation (3), Nx, Ny and Nz are the demagnetizing factors along x, y and z directions, which are determined by the shape and the size of magnet (shape anisotropy)34,35. The dipole field from the PL has been neglected assuming that this dipole field can be cancelled out by synthetic ferrimagnetic reference layers36. Thermal fluctuation is described by equation (4), where KB, V and Δt are the Boltzmann constant, the FL volume and the calculation time step of 5 ps, respectively. The stochastic partial differential equation (SPDE) described by equation (1) is integrated via fourth order Runge-Kutta method37,38,39. The device is assumed to operate at room temperature (T = 300 K), and self-heating effects due to Joule heating have been ignored because the VCMA devices operate at much lower current densities than traditional STT devices. G(1,0) with superscript along respective axis are independent random numbers computed at every time-step and each has a Gaussian distribution with zero mean and unit standard deviation40. H Bias (c.f. Fig. 1(a)) is provided by an in-plane magnetized BL (Co/Pt multilayers) via its dipole field, which is calculated by micromagnetics simulation using MuMax3 simulator41 with the simulation cell size of 1 nm along all three dimensions. Since H Bias is along x-axis in this study, subsequently, it is represented by Hx. The damping-like torque (DLT) with linear dependence on VMTJ, and the field-like torque (FLT) with quadratic dependence on VMTJ are respectively obtained as,
where \(\hslash \) is the reduced Planck constant, e is the electron charge, RMTJ is the MTJ resistance, ηMTJ(SV) is the STT efficiency, and ν = 2.97/7.82 V−1 is the ratio between the two torques42. Analysis of RMTJ includes the voltage dependence of tunneling magnetoresistance (TMR) and the dynamic angle θ between FL and PL as,
where VHalf = 0.4 V20,43, is the voltage across MTJ at which TMR becomes half of its value at zero-bias i.e. TMR0/2. RP is the MTJ resistance when both magnets are exactly parallel to each other and assumed to remain invariant to VMTJ 42,44, while RAP0 is the MTJ resistance when the MTJ is in AP state at zero bias. Since in recent years Slonczewski expression27 for spin-torque efficiency has been extended to account for multiple reflections of the spin-flux in spin valves45,46,47, the STT effect by the BL in this study is based on multi-reflection model. Hence, the STT efficiencies for the PL-MgO-FL MTJ (ηMTJ) and the FL-Metal-BL spin valve (ηSV) are computed as46,48,
where P1 is obtained from Julliere’s formula for equal polarization of FL and PL49 and P2 = 0.3550.
Data Availability
Correspondence and requests for materials should be addressed to G.G. (gauravdce07@gmail.com) or G.L. (elelg@nus.edu.sg).
Results and Discussion
Operation Principle
Since in a VCMA based MTJ, the interfacial anisotropy energy can be tuned by an applied voltage, the competition between the uniaxial anisotropy and the demagnetizing field, which determines the easy axis direction, can be controlled by voltage. Specifically, considering the bulk and the interface PMA with the demagnetization simultaneously, the net anisotropy energy density becomes,
When KU_Eff > 0, FL has a perpendicular magnetization i.e. it has easy-axis along z-axis. If KU_Eff < 0, the magnet has easy-axis along the major-axis of the elliptical FL i.e. x-axis in this work. Among the parameters in equation (2) and equation (8), tFL and Nz depend on the physical dimensions and remain fixed once the MTJ is fabricated, while Ez can be modified by controlling VMTJ. For precession based VCMA switching of the pMTJ devices18,20, these physical and electrical controls are designed such that in the absence of VMTJ, KU which equals KU_Bulk + KI0/tFL is large enough for KU_Eff to be positive. Howbeit, VMTJ is designed to have a sufficient Ez that can render KU_Eff to a computationally negative value. Physically, this implies that the FL destabilizes along z-axis and its easy-axis now aligns along x-axis, thereby forcing m to tend towards the new stable state. Conversely, if a negative voltage pulse is applied, as evident from equation (2) and equation (8), KU_Eff becomes more strongly positive because the interface anisotropy is enhanced. Categorically, this has been suggested as a scheme to read MTJ with increased reliability51. VC and EzC, respectively, symbolize the critical values, at which KU_Eff is zero and thus the easy-axis orientation changes, of VMTJ and Ez for given tFL. Moreover, Ez should not exceed the dielectric breakdown field EBreak which is slightly over 2 V-nm−1 10, i.e. EzC < V0/tMgO < EBreak. The design is furthermore constrained by a maximum permissible voltage in the system which is not discussed in this study because it is subjective to the targeted application and the desired stability factor Δ of FL. Δ is computed in the absence of VMTJ and described as52,
If the FL is permanently biased as in this work, the stability can be reduced quadratically, whereas if Hx is applied only during the write operation53, Δ can be substantially increased to equal Δ0. The scheme suggested in ref.53 depends on the Oersted field generated around the current carrying wire in the adjacent cells. Consequently, for a substantial Hx firstly it becomes power intensive and secondly this acts as a stray field and disturbs other bit-cells thereby limiting the memory density. Therefore, an alternative scheme of increasing Δ without compromising with VMTJ or reducing Hx would be an important future direction.
For precession based VCMA switching, a VMTJ as a trapezoidal pulse of duration tPulse is applied to toggle the FL, as shown in Fig. 1(b). A finite rise and fall time, tRise and tFall, respectively, of 50 ps is assumed to consider a non-ideal input. A full-scale voltage V0 is applied for time tHigh duration to temporarily change easy-axis from z- to x-axis. This induces the precession of m around the shifted H Eff . A sufficiently large Hx allows the FL mz to swing from +1 to −1 and vice versa as illustrated in Fig. 2(a)–(c) for the FL of thickness tFL 1.7 nm, cross-section 150 × 50 nm2, tMgO of 2 nm, V0 of 1.6 V and μ 0Hx of 50 mT. As shown in Fig. 2(a)–(c), by designing tON to be odd or even multiples of the half-precession period (tHalf = 0.35 ns for the shown cases), mz toggles or comes back to the original state, respectively. A large enough tOFF ensures that m relaxes to z-axis. Consequently, the final state of m strongly depends on tON since it determines if m is above or below the x-y plane when VMTJ goes to zero and easy-axis is switched back along z-axis. This implies that pulse duration should be controlled in a certain range for deterministic switching.
FL switching for a voltage pulse with tON in integer multiples of the half precession periods (tHalf): tON is (a) 0.35 ns, (b) 0.7 ns and (c) 1.05 ns while tHalf is 0.35 ns. For the odd multiples the FL toggles while for the even cases it restores to the original state and remains unaltered. Insets show a full three dimensional (3D) FL dynamics for the respective cases, where the red dash arrow, green arrow and blue line is the initial m state, final m state and its trajectory, respectively. (d) Bias field acting on the FL along x-axis generated by the BL for different metal spacer thicknesses tM and BL thicknesses tBL. This large enough exchange field, e.g. 50 mT for tBL of 10 nm and tM of 3 nm, can bias the FL for precession based VCMA switching.
Pessimistically, the deterministic switching based on precise control of precession cycles requires a bias magnetic field. To simplify the design of generating Hx, an elliptical pMTJ is used, which allows an in-plane magnetized BL separated by a metal spacer to be fabricated within the MTJ stack (c.f. Fig. 1a). The dipole field provided by the BL is shown in Fig. 2(d). It shows that, typically as expected, a thinner metal spacer results in a stronger bias field because a dipole field strengthens as the distance from the magnet decreases. Intuitively, thickening the BL, whereas ensuring that a single domain is maintained, would have more magnetic moments along the x-axis, which then would lead to a larger bias field for the same tM. Hence, the tM and the tBL can be custom designed to obtain the required Hx. In this work, the μ 0Hx applied on the MTJ is approximately 50 mT. As shown in Fig. 2(d), this large Hx can be provided via a 10 nm thick BL with the metal spacer of tM 3 nm, implying that an elliptical MTJ stack can function without an additional external system to provide the bias field.
VMTJ Dependence
First we investigate the electronic control of the device. To probe the effects of V0 on the precession based VCMA switching in an elliptical pMTJ, a representative FL of size 150 × 50 × 1.7 nm3 is chosen. The MTJ has tMgO of 2 nm, resistance-area (RA) product of 1820 Ω-μm2 and TMR0 of 144%20. A 50 mT bias field along x-axis Hx is applied to assist the switching. This in-plane field reduces the FL thermal stability from 138 to 28 as calculated from equation (9). However, because of the ultra-low power sub-nanosecond writing in this design, and the stability which suffices the requirements for embedded non-volatile cache memory51,54,55, the promulgated precessional VCMA based MRAM may be a promising replacement for power-intensive volatile static random-access memory (SRAM) in the cache. Furthermore, this stability also suffices for the MTJ based non-volatile logic (NVL)56.
The phase diagrams of the switching probability for switching from P-to-AP (P10) and from AP-to-P (P01) are shown in Fig. 3(a) and (b), respectively. For sweeping tON, tHigh is swept while tRise and tFall are held constant at 50 ps each. Each colour point is determined by simulating the device 100 times under the identical conditions while considering thermal fluctuation. Red regions (operation windows), which are directly related to the precession period, signify a deterministic toggling, i.e. 100% probability of switching, while the dark-blue regions denote an unaltered m state i.e. 100% probability that the original magnetic-state is retained. For given V0, the probability oscillates between 0 (the dark-blue regions) and 1 (the red regions) with tON because for the odd and even multiples of tHalf, the FL toggles and gets restored to the original state, respectively. However, at small V0 and large tON, the switching is nondeterministic and the probability is approximately 50%, as also observed experimentally in ref.13. This is because at low V0 and large tON, the VCMA effect is relatively weak and tHigh is comparable with the relaxation time, thus failing to keep the precession around x-axis for a long time and resulting in an uncertain final state in the presence of thermal fluctuation. Comparing Fig. 3(a) with 3(b) shows that there is no significant difference in the phase diagram for P10 and P01, which implies that there is symmetry in the switching from P-to-AP and AP-to-P, indicating that the STT effect, which always favours AP state in this work, is negligible. Next, the black curve with bars indicates deterministic switching without thermal fluctuation to explicitly illustrate the effect of thermal fluctuations for the fastest tON scenario. This tON equals tHalf. As shown in Fig. 3(a) and (b), the operation window shrinks, as expected, when thermal fluctuation is considered, implying that for precession based VCMA switching it perturbs the deterministic toggling. Moreover, the operation window expands as V0 diminishes. This is because the reduced V0 weakens the VCMA effect, resulting in a stronger interfacial anisotropy field along z-axis as evident from equation (2). This tends to increase mz and reduce mx thus subduing shape anisotropy field along x-axis, resulting in the reduction of the x-component of H Eff . The m still precesses around x-axis, although its trajectory is now not totally symmetrical about the x-y plane. Because the precessional period is inversely proportional to the magnetic field along the precession-axis, which is nearly along x-axis, with a reduced field along x-axis the precession period increases. As a result, the operation window, which is closely related to the precession period, increases as V0 decreases. A larger operation window implies more tolerance in variation for tHigh, and hence, a more reliable write-operation, indicating that the low-voltage operation is achievable for this studied device.
Phase diagram of switching probability from (a) parallel (P) to anti-parallel (AP) state (P10) and from (b) AP-to-P (P01) as a function of tON and V0 at tMgO of 2 nm and μ 0Hx of 50 mT (with thermal fluctuation). The black bars show the t ON operation windows without considering thermal fluctuation. The increasing operation window as V0 decreases indicates that the device favors a low-voltage operation. (c) Current density and (d) energy consumption per switch vs. V0. (e) Switching probability from P-to-AP ‘AND’ AP-to-P (P10 ⋅ P01) as a function of t ON and V0. Red regions indicate deterministic switching, i.e. 100% certainty of toggling. (f) Retention probability, i.e. (1-P10) ⋅ (1-P01) as a function of tON and V0. Red regions show with 100% probability that pre-configured data would not be altered.
The V0 dependence of current density J through the MTJ and energy consumption E is shown in Fig. 3(c) and (d), respectively, for both P-to-AP and AP-to-P switching of a unit probability with tON equal to a respective tHalf. As expected, J increases linearly as V0 increases, and remains in the order of 108 A-m−2 because of a thick enough (2 nm) MgO layer. This low current density then ensures a relatively low switching energy as seen in Fig. 3(d). The switching energy has two components,
where εMgO = 9.757 is the relative permittivity of MgO, ε0 is the vacuum permittivity, and A is the MTJ cross-sectional area. The first term in equation (10) is the Joule heating EJ, and second term is the charging energy EC consumed by the MTJ capacitance. The capacitance has been assumed to be independent of the relative magnetization of PL and FL because of the sub-μm2 MTJ cross-section58. EC ranges from 0.046 fJ to 1.138 fJ for V0 from 0.6 V to 3 V, which is 9% to 14% of E (0.5 fJ to 8.1 fJ), respectively. Because the current density stays lower than 2 × 109 A-m−2, a low switching energy (<10 fJ/switch) is achieved (c.f. Table I of ref.56. for a general comparison with other non-volatile memory technologies). Moreover, Fig. 3(e) exhibits the switching probability from P-to-AP ‘AND’ AP-to-P as a function of tON and V0. Red regions denote a deterministic switching, i.e. 100% certainty of toggling. At V0 = 1 V, the corresponding operation window of tON is from 0.31 ns to 0.46 ns i.e. 0.15 ns, a decent margin for tHigh to vary without affecting the reliable operation. On the other hand, Fig. 3(f) presents the retention probability as a function of tON and V0. Red regions show with 100% probability that pre-configured data is not disturbed. As a consequence, the red regions can be used for reading, e.g. as long as the read voltage is below 0.4 V, the FL magnetic state will always remain unaltered, which implies that an absolutely disturb-free read operation can be achieved for the MRAM application.
MgO Thickness Dependence
As demonstrated in the previous section, the device prefers a low-voltage operation for a decent pulse duration margin unto a value at which further decreasing V0 may fail the switching. Hence, to study the tMgO dependence on the switching, V0 is fixed to be 1.6 V in this section. This V0 allows a sufficient tMgO variation range to achieve low energy consumption as expounded later. RA-products, TMRs and VHalf for different MgO thicknesses are extracted from the experimental paper20. For a fixed V0 as the tMgO decreases, principally, both VCMA and STT effect become stronger. The former becomes stronger because Ez at the MgO-FL interface becomes stronger (see equation (2)). Simultaneously, the RA-product decreases exponentially as tMgO decreases. Since J is inversely proportional to the RA-product, J thus increases exponentially from 107 A-m−2 to 1010 A-m−2 for decreasing tMgO, as shown in Fig. 4(a), which makes the STT increasingly stronger. Figure 4(b) shows that at large tMgO, the two curves of tON, which is chosen to equal to tHalf, overlap, indicating that the VCMA effect dominates over the STT effect. Besides, a linear relation is observed on account of the fact that tON is inversely proportional to the precession frequency which in turn is almost proportional to H Eff . The H Eff varies linearly with H K , and H K is inversely proportional to tMgO (see equation (2)) because of the VCMA effect. For small tMgO, there is a divergence in tON between P-to-AP (black solid circles) and AP-to-P (red triangles) switching trends, implying that STT effect is substantial which can be understood as follows. Beyond the critical electric field which changes the easy axis from z- to x-axis, further strengthening of VCMA effect is inessential and has no significant additional contribution in the switching. However, STT effect has no such upper threshold in this case and starts to dictate the switching dynamics. Since the electron flow direction is from FL to PL, for P-to-AP switching, due to STT effect, the FL receives spin-flux anti-parallel to M PL . As a result, STT effect assists VCMA effect to attain an AP state and accelerates the switching process. In contrast, for AP-to-P switching, STT effect still endeavors to maintain the FL in the AP state while VCMA effect strives to toggle the FL into a P-state. The two effects thus jostle to toggle the FL. This decelerates the toggling, which results in a larger tON.
Effects of tMgO on (a) current density, (b) tON (optimal values used to switch, i.e. tHalf) and (c) energy consumption per switching operation at 1.6 V V0 and 50 mT μ 0Hx. Red lines with open triangles show the process from AP-to-P. Black lines with solid circles correspond to the process from P-to-AP. The smallest switching energy achieved is 0.3 fJ. Phase diagram for switching probability from (d) P-to-AP and (e) AP-to-P vs. tON and tMgO.
As discussed in the previous section, EC is a fraction of the Joule heating. When STT effect is substantial, the E shown in Fig. 4(c) nearly follows the declining trend of J in Fig. 4(a) since the switching time variation is relatively small. Nevertheless, when tMgO becomes thicker than 2.2 nm, EC becomes comparable to EJ because of the exponential decline in J and the corresponding Joule heating. Thus, for large tMgO, VCMA effect dominates, and the E slope tapers down with E approaching 0.3 fJ, which is also the minimum energy achieved in this work. Figure 4(d) and (e), respectively, show the phase diagrams of switching probability from P-to-AP (P10) and from AP-to-P (P01) as a function of tON and tMgO. An obvious oscillatory dependence on tON is observed. At large tMgO and for long pulse duration, the oscillations disappear because of weak VCMA effect. Interestingly in Fig. 4(d), there is a sharp decrease in the tON operation window for the first half precession cycle for small tMgO (the red region on the left-bottom around tMgO = 1.6 nm). This happens because in the said region a strong STT effect compliments the VCMA effect for P-to-AP switching, and greatly accelerates the switching process. This sharply reduces the precession period and the scope for tolerating variations in tHigh. For larger tMgO, a wider operation window indicates that the device can tolerate more variations in tHigh. It can be found that it is more favorable to design the device with a large MgO thickness for given V0, because both a larger margin in the pulse variation for deterministic switching and a lower write-energy can be achieved.
MTJ Scalability and Bias Magnetic Field
As noted earlier, the external bias field required in the switching has been a critical bottleneck in advancing it for memory applications and therefore in this work, the elliptical pMTJs have been presented so that Hx can be engineered within the stack and provided by a BL. Besides the thickness of BL discussed earlier, it is the MTJ cross-section that determines the number of magnetic moments in the BL to provide a bias field through the FL. Furthermore, the demagnetizing field scales with the cross-section thereby modifying the switching time, required bias field and energy landscape. Therefore, the MTJ cross-section is an important physical constraint to investigate and comprehend the device physics in our proposed VCMA device.
The effect of Hx on the switching probability is shown in Fig. 5(a) and (b). For a pMTJ with FL of 150 × 50 × 1.7 nm3 dimensions, tMgO of 2 nm and V0 of 1.6 V, there is a limited functional region in the range of 38–58 mT for μ 0Hx. This range can be shifted for different conditions. As seen from Fig. 5(a) and (b), increasing the bias field Hx shrinks the red region, i.e. the operation window, which is similar to the case exhibited in Fig. 3(a) and (b). When μ 0Hx increases to more than 58 mT, an excessively strong H Eff results in overly fastened precession, thus sharply reducing the relaxation time, which is too fast to allow deterministic switching. Conversely, if μ 0Hx is insufficient, i.e. less than 38 mT, deterministic switching around x-axis would not be supported. Hence, a probabilistic final state is attained by virtue of thermal fluctuation. To reduce the required Hx for switching, one possible way is to design tFL even closer to the critical thickness but this would further sacrifice Δ. This adjustment has three effects: it would weaken both the interfacial anisotropy and the demagnetizing field along z-axis, and enhance the demagnetizing field along x-axis. All of these would enable the operation at smaller VC. In consequence, a stronger VCMA effect is obtained at the same V0, which then relieves the requirement for larger μ 0Hx.
Phase diagram for switching probability of (a) P-to-AP and (b) AP-to-P as a function of tON and bias magnetic field μ 0Hx. Hx is the magnitude of H Bias projecting along x-axis. Optimal tON used to switch (tHalf) in (c) and energy consumption in (d) as a function of the MTJ width. The AR and FL thickness are held constant at 3 and 1.7 nm respectively, e.g. for width of 40 nm, the MTJ cross-section is 40 × 120 nm2.The black and red bars indicate the tON operation regions during which switching probability is 100%. The inset shows the critical voltage VC vs. the MTJ width.
Scalability of the pMTJ is next investigated in Fig. 5(c) and (d). The AR is held at 3, tFL at 1.7 nm, tMgO at 1.5 nm and V0 at 1.6 V, while the MTJ length and width are swept. The bars in Fig. 5(c) represent the operation windows, within which switching happens with 100% certainty. Figure 5(c) also shows that when the MTJ cross-section (represented as MTJ width) is scaled down, the optimal tON (the data-markers on the curve), which equals respective tHalf, increases. This happens because on scaling down the MTJ, Nz decreases which thus increases KU_Eff. As a result, VC (c.f. the inset), where KU_Eff = 0, as seen from equation (2) and equation (8), becomes larger. In consequence, it is more difficult to switch. Hence, it takes larger tON or the switching may even fail altogether. It is found that a considerable operation window is achieved for the MTJ cross-section between 39 × 117 nm2 and 45 × 135 nm2.
For the designs in Fig. 5(c), the respective energy consumption is shown in Fig. 5(d). At first a descending and then an ascending trend is observed when scaling down on account of the competition between tON and the MTJ resistance as evinced in equation (10). The former increases as observed in Fig. 5(c), while the latter also increases because for given RA-product, the MTJ resistance increases as the MTJ cross-section reduces. These two have opposite contributions to the Joule heating; therefore, the trends exhibit a local minima. These trends also imply that unduly scaling down the MTJ cross-section may not be attractive in terms of energy consumption.
Conclusion
We propose and appraise the elliptical pMTJs for voltage controlled precessional switching. The VMTJ, tMgO, STT, bias magnetic field and MTJ scalability effects on the pMTJ properties are investigated. We show that an in-plane magnetized BL designed within the MTJ stack can bias the FL to eliminate the need of providing a uniform in-plane magnetic field for the FL by an additional circuit. The pMTJ can be switched for as low as 0.3 fJ in just 0.38 ns at 1.6 V. Furthermore, it is shown that Joule heating can be adequately suppressed by increasing tMgO. We also find that the design favors to operate at low voltage (~1 V) and large MgO thickness. There is also a sufficient margin for the variation in tHigh without affecting the reliable operation. This should be encouraging for a practical disposition of the VCMA based MRAM. The advantages like fast switching, ultra-low energy consumption and non-volatility are very attractive for VCMA based MRAM application in cache memories.
References
Khvalkovskiy, A. et al. Basic principles of stt-mram cell operation in memory arrays. Journal of Physics D: Applied Physics 46, 074001 (2013).
Apalkov, D., Dieny, B. & Slaughter, J. Magnetoresistive random access memory. Proceedings of the IEEE 104, 1796–1830 (2016).
Hanyu, T. et al. Magnetic back-end technology. In Bernard, D., Ronald, B. G. & Kyung-Jin, L. (eds) Introduction to Magnetic Random-Access Memory, 165–198 (John Wiley & Sons, Inc., 2017).
Ohno, H., Endoh, T., Hanyu, T., Ando, Y. & Ikeda, S. Spin-transfer-torque magnetoresistive random access memory (stt-mram) technology. In Yoshio, N. (ed.) Advances in non-volatile memory and storage technology, 455–494 (Elsevier, 2014).
Choi, C.-M. et al. Temperature dependence of reliability characteristics for magnetic tunnel junctions with a thin mgo dielectric film. Semicond. Sci. Technol 31, 075004 (2016).
Oliver, B., Tuttle, G., He, Q., Tang, X. & Nowak, J. Two breakdown mechanisms in ultrathin alumina barrier magnetic tunnel junctions. Journal of Applied Physics 95, 1315–1322 (2004).
Hosotani, K. et al. Effect of self-heating on time-dependent dielectric breakdown in ultrathin mgo magnetic tunnel junctions for spin torque transfer switching magnetic random access memory. Japanese Journal of Applied Physics 49, 04DD15 (2010).
Ventura, J., Sousa, J., Liu, Y., Zhang, Z. & Freitas, P. Electromigration in thin tunnel junctions with ferromagnetic/nonmagnetic electrodes: Nanoconstrictions, local heating, and direct and wind forces. Physical Review B 72, 094432 (2005).
Schäfers, M. et al. Electric breakdown in ultrathin mgo tunnel barrier junctions for spin-transfer torque switching. Applied Physics Letters 95, 232119 (2009).
Dimitrov, D. et al. Dielectric breakdown of mgo magnetic tunnel junctions. Applied Physics Letters 94, 123110 (2009).
Fong, X. et al. Spin-transfer torque memories: Devices, circuits, and systems. Proceedings of the IEEE 104, 1449–1488 (2016).
Gupta, S. K., Park, S. P., Mojumder, N. N. & Roy, K. Layout-aware optimization of stt mrams. In Proceedings of the Conference on Design, Automation and Test in Europe, 1455–1458 (EDA Consortium, 2012).
Shiota, Y. et al. Induction of coherent magnetization switching in a few atomic layers of feco using voltage pulses. Nature Materials 11, 39 (2012).
Wang, K., Alzate, J. & Amiri, P. K. Low-power non-volatile spintronic memory: Stt-ram and beyond. Journal of Physics D: Applied Physics 46, 074003 (2013).
Yuasa, S. et al. Future prospects of mram technologies. In Electron Devices Meeting (IEDM), IEEE International, 3–1 (IEEE, 2013).
Nozaki, T. et al. Large voltage-induced changes in the perpendicular magnetic anisotropy of an mgo-based tunnel junction with an ultrathin fe layer. Physical Review Applied 5, 044006 (2016).
He, K., Chen, J. & Feng, Y. First principles study of the electric field effect on magnetization and magnetic anisotropy of feco/mgo (001) thin film. Applied Physics Letters 99, 072503 (2011).
Grezes, C. et al. Ultra-low switching energy and scaling in electric-field-controlled nanoscale magnetic tunnel junctions with high resistance-area product. Applied Physics Letters 108, 012403 (2016).
Kanai, S. et al. Electric field-induced magnetization reversal in a perpendicular-anisotropy cofeb-mgo magnetic tunnel junction. Applied Physics Letters 101, 122403 (2012).
Kanai, S., Matsukura, F. & Ohno, H. Electric-field-induced magnetization switching in cofeb/mgo magnetic tunnel junctions with high junction resistance. Applied Physics Letters 108, 192406 (2016).
Wilson, B. W. et al. Design and fabrication of well confined uniform magnetic field exposure systems. Bioelectromagnetics 15, 563–577 (1994).
Kreissig, M. et al. Vortex spin-torque oscillator stabilized by phase locked loop using integrated circuits. AIP Advances 7, 056653 (2017).
Lacoste, B. et al. Control of sub-nanosecond precessional magnetic switching in stt-mram cells for sram applications. In Memory Workshop (IMW), IEEE 8th International, 1–4 (IEEE, 2016).
Ikeda, S. et al. A perpendicular-anisotropy cofeb–mgo magnetic tunnel junction. Nature Materials 9, 721–724 (2010).
Heindl, R., Rippard, W. H., Russek, S. E., Pufall, M. R. & Kos, A. B. Validity of the thermal activation model for spin-transfer torque switching in magnetic tunnel junctions. Journal of Applied Physics 109, 073910 (2011).
Jaiswal, A., Fong, X. & Roy, K. Comprehensive scaling analysis of current induced switching in magnetic memories based on in-plane and perpendicular anisotropies. IEEE Journal on Emerging and Selected Topics in Circuits and Systems 6, 120–133 (2016).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. Journal of Magnetism and Magnetic Materials 159, L1–L7 (1996).
Timopheev, A., Sousa, R., Chshiev, M., Buda-Prejbeanu, L. & Dieny, B. Respective influence of in-plane and out-of-plane spin-transfer torques in magnetization switching of perpendicular magnetic tunnel junctions. Physical Review B 92, 104430 (2015).
Chien, D. et al. Enhanced voltage-controlled magnetic anisotropy in magnetic tunnel junctions with an mgo/pzt/mgo tunnel barrier. Applied Physics Letters 108, 112402 (2016).
Wang, W.-G., Li, M., Hageman, S. & Chien, C. Electric-field-assisted switching in magnetic tunnel junctions. Nature Materials 11, 64 (2012).
Li, X. et al. Thermally stable voltage-controlled perpendicular magnetic anisotropy in mo— cofeb— mgo structures. Applied Physics Letters 107, 142403 (2015).
Skowron′ski, W. et al. Underlayer material influence on electric-field controlled perpendicular magnetic anisotropy in cofeb/mgo magnetic tunnel junctions. Physical Review B 91, 184410 (2015).
Skowron′ski, W. et al. Perpendicular magnetic anisotropy of ir/cofeb/mgo trilayer system tuned by electric fields. Applied Physics Express 8, 053003 (2015).
Beleggia, M., De Graef, M., Millev, Y., Goode, D. & Rowlands, G. Demagnetization factors for elliptic cylinders. Journal of Physics D: Applied Physics 38, 3333 (2005).
Beleggia, M., De Graef, M. & Millev, Y. The equivalent ellipsoid of a magnetized body. Journal of Physics D: Applied Physics 39, 891 (2006).
Sato, H. et al. Co/pt multilayer based reference layers in magnetic tunnel junctions for nonvolatile spintronics vlsis. Japanese Journal of Applied Physics 53, 04EM02 (2014).
Franchin, M. Multiphysics simulations of magnetic nanostructures. Ph.D. thesis, University of Southampton (2009).
Skowron′ski, W. et al. Backhopping effect in magnetic tunnel junctions: Comparison between theory and experiment. Journal of Applied Physics 114, 233905 (2013).
Sharma, S., Muralidharan, B. & Tulapurkar, A. Proposal for a domain wall nano-oscillator driven by non-uniform spin currents. Scientific Reports 5, 14647 (2015).
Akimoto, H., Kanai, H., Uehara, Y., Ishizuka, T. & Kameyama, S. Analysis of thermal magnetic noise in spin-valve gmr heads by using micromagnetic simulation. Journal of Applied Physics 97, 10N705 (2005).
Vansteenkiste, A. et al. The design and verification of mumax3. AIP Advances 4, 107133 (2014).
Kubota, H. et al. Quantitative measurement of voltage dependence of spin-transfer torque in mgo-based magnetic tunnel junctions. Nature Physics 4, 37 (2008).
Kugler, Z. et al. Temperature and bias voltage dependence of co/pd multilayer-based magnetic tunnel junctions with perpendicular magnetic anisotropy. Journal of Magnetism and Magnetic Materials 323, 198–201 (2011).
Sankey, J. C. et al. Measurement of the spin-transfer-torque vector in magnetic tunnel junctions. Nature Physics 4, 67–71 (2008).
Hernández, S. & Victora, R. Calculation of spin transfer torque in partially polarized spin valves including multiple reflections. Applied Physics Letters 97, 062506 (2010).
Zhu, W., Zhang, Z., Zhang, J. & Liu, Y. Multiple reflection effect on spin-transfer torque dynamics in spin valves with a single or dual polarizer. Spin 5, 1550003 (2015).
Bell, R., Hu, J. & Victora, R. Dual referenced composite free layer design for improved switching efficiency of spin-transfer torque random access memory. IEEE Electron Device Letters 37, 1108–1111 (2016).
Slonczewski, J. Currents, torques, and polarization factors in magnetic tunnel junctions. Physical Review B 71, 024411 (2005).
Julliere, M. Tunneling between ferromagnetic films. Physics Letters A 54, 225–226 (1975).
Mangin, S. et al. Current-induced magnetization reversal in nanopillars with perpendicular anisotropy. Nature Materials 5, 210–215 (2006).
Noguchi, H. et al. Novel voltage controlled mram (vcm) with fast read/write circuits for ultra large last level cache. In Electron Devices Meeting (IEDM), IEEE International, 27–5 (IEEE, 2016).
Shiota, Y. et al. Evaluation of write error rate for voltage-driven dynamic magnetization switching in magnetic tunnel junctions with perpendicular magnetization. Applied Physics Express 9, 013001 (2015).
Han, G. et al. Perspectives of electric field controlled switching in perpendicular magnetic random access. IEEE Transactions on Magnetics 51, 1–9 (2015).
Smullen, C. W., Mohan, V., Nigam, A., Gurumurthi, S. & Stan, M. R. Relaxing non-volatility for fast and energy-efficient stt-ram caches. In High Performance Computer Architecture (HPCA), IEEE 17th International Symposium on, 50–61 (IEEE, 2011).
Saida, D. et al. Sub-3 ns pulse with sub-100 μ a switching of 1x–2x nm perpendicular mtj for high-performance embedded stt-mram towards sub-20 nm cmos. In VLSI Technology, IEEE Symposium on, 1–2 (IEEE, 2016).
Wang, K. & Amiri, P. K. Nonvolatile spintronics: perspectives on instant-on nonvolatile nanoelectronic systems. Spin 2, 1250009 (2012).
Mazierska, J., Ledenyov, D., Jacob, M. V. & Krupka, J. Precise microwave characterization of mgo substrates for hts circuits with superconducting post dielectric resonator. Superconductor Science and Technology 18, 18 (2004).
Ingvarsson, S., Arikan, M., Carter, M., Shen, W. & Xiao, G. Impedance spectroscopy of micron sized magnetic tunnel junctions with mgo tunnel barrier. Applied Physics Letters 96, 232506 (2010).
Acknowledgements
This work at the National University of Singapore was supported by CRP award no. NRF-CRP12-2013-01 and MOE2013-T2-2-125. The authors gratefully acknowledge the discussions with Xuanyao Fong, and the funding support from the National Research Foundation, Prime Minister Office, Singapore, under its Medium Sized Centre Programme.
Author information
Authors and Affiliations
Contributions
G.G. conceived and designed this project. G.G. and G.L. supervised the study. J.D. performed the computations and wrote the manuscript. All authors critically analyzed the data and modified the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deng, J., Liang, G. & Gupta, G. Ultrafast and low-energy switching in voltage-controlled elliptical pMTJ. Sci Rep 7, 16562 (2017). https://doi.org/10.1038/s41598-017-16292-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16292-7
This article is cited by
-
Route towards efficient magnetization reversal driven by voltage control of magnetic anisotropy
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.