Abstract
The conformations of polycarboxylate ether (PCE) type superplasticizer polymers adsorbed on the surface of MgO in cement pore solution are simulated by molecular dynamics (MD). Three types of PCEs commonly applied to concrete are simulated, namely a methacrylate type PCE (PCEM-P), an allyl ether type PCE (PCEA-P), and an isoprenyl ether type PCE (PCEI-P) with ethylene oxide (EO) unit numbers (P) of 25, 34 and 25, respectively. It is observed that the adsorbed layer thickness is inversely proportional to the experimentally measured adsorbed amount at the initial paste flow of 26 ± 0.5 cm. Simulation results indicate that the adsorbed layer thickness is sensitive to the initial polymer orientations against the model MgO surface. I.e., polymer molecules initially placed parallel/perpendicularly against the MgO surface gradually forms a train shaped or a loop and tail adsorption profile, respectively. As a result, the loop and tail shaped conformation gives a higher layer thickness.
Similar content being viewed by others
Introduction
Polycarboxylate ether-based superplasticizers (PCEs) adsorb onto the cement surface electrostatically with their negatively charged carboxylic acids in a polymer backbone while the polyethyleneglycol (PEG) side chains stretch toward the water phase, resulting in an excellent cement-dispersing effect1.
PEG molecules are surrounded by a large layer of structured water resulting from hydrogen bonds2,3. Accordingly, PEG side chains of PCEs that adsorb on cement would turn the surface of cement particles hydrophilic, making the agglomerated cement particles to be dispersed by steric repulsion of the PEG chains. For instance, it is well known that PEG stabilizes hydrophobic colloid acting as a protective agent4,5,6. Later, de Gennes7,8 established quantitatively that the steric repulsion generated by the grafted chains correlates with the adsorbed layer thickness (ALT) of the adsorbed polymer. It has been demonstrated by a variety of work that the steric repulsion of PCEs increases with increasing ALT1,9,10,11,12,13,14,15. There is very roughly linear trend between the ALT value and the PEG side chain length or the polymer’s hydrodynamic radius.
However, the PCE polymer structures used for these early studies were limited and sometimes unknown. The PCE dosage varies for different types of PEG macromonomers used at the preparation of a mortar or concrete with the settled initial fluidity. The reasons for that remain unsolved. Therefore, understanding the correlation of a PCE molecular structure with the cement dispersing effect would promote the development of more efficient superplasticizers to enhance concrete performance.
Recently, molecular dynamics (MD) simulations have been applied to the PCEs to elucidate its working mechanism16,17,18,19,20. However, the molecular size of these model PCEs was much smaller than those typically used for industrial applications in order to reduce computation cost, furthermore, only pure water was used, or only Na+, Ca2+ and Cl− were additionally added to mimic a cement pore solution.
In a previous work, we simulated the polymer conformations of the PCEs with the actual Mw used in experiments21. We considered different polymer backbones in water and in a synthetic cement pore solution. The PCEs used were common types utilized in the concrete industry, namely a methoxy polyethyleneglycol mono methacrylate–sodium methacrylate copolymer (PCEM-P), a methoxy polyethyleneglycol mono allyl ether–sodium maleate copolymer (PCEA-P) and a polyethyleneglycol mono (3-methyl-3-butenyl) ether–sodium acrylate copolymer (PCEI-P) with ethylene oxide (EO) unit numbers (P) of 25, 34 and 25 respectively. PCEA is an alternating copolymer formed from allyl ether and maleic anhydride monomers which alternate along the polymer backbone. In contrast, PCEM is a random copolymer22 while PCEI is a block copolymer with ABA, ABAA and AA blocks as evidenced by13C NMR spectroscopy23, where A and B refer to the monomer units containing the carboxylic acid group and PEG side chains, respectively.
It was found that the backbones of those PCEs are considerably stretched in water due to electrostatic repulsion between negatively charged carboxylic acid groups, whereas in synthetic cement pore solution the backbones are significantly distorted and shrunken due to the aggregation of the hydrophobic PEGs as well as the salting-out effect on the backbone21.
In this paper, we follow this preliminary effort and use MD simulations to investigate the conformations of the same three PCEs polymers adsorbed on an MgO surface in a synthetic cement pore solution. In addition, we also performed mini slump tests and compared results of simulated adsorbed polymer conformations against experiment to gain insights into possible correlation.
Schematically, this paper is organized as follows: First, our results are reported and discussed regarding the working mechanism of the PCE samples, and our findings are compared with those from works of other groups previously published. Then, we give a short conclusion. Lastly, we present our experimental and simulation methodology.
Results and Discussion
Dispersing performance of PCEs
To obtain an initial cement paste flow of 26 ± 0.5 cm, the PCE dosages measured are 1.35 mg/g (PCEM-25), 1.40 mg/g (PCEA-34) and 1.00 mg/g (PCEI-25). This result indicates that PCE polymer PCEI-25 has the highest dispersing ability among all the polymers tested.
PCE adsorption on cement
As exhibited in Fig. 1, the adsorption isotherms have a Langmuir shape, which was in line with those previously reported for monolayer adsorption between polar solutes and substrates24,25. The adsorbed amount increases sharply at low dosage, then reaches a plateau where PCE covers all surface by a monolayer. Such adsorption isotherms have also been reported earlier for PCEs26. In which saturated adsorption amounts are found as: 2.35 mg/g (PCEM-25) > 1.50 mg/g (PCEA-34) > 1.15 mg/g (PCEI-25). In contrast, the adsorbed amounts at the dosage required for a 26 ± 0.5 cm cement paste spread value (hereinafter, “the standard adsorbed amounts”) are 1.25 mg/g (PCEM-25) > 1.00 mg/g (PCEA-34) > 0.70 mg/g (PCEI-25), indicating that full coverage of the cement surface is not needed and coverage with 53–67% is enough to obtain the targeted flow. The difference in the standard adsorbed amounts of the PCEs seems to suggest the existence of different polymer conformations during adsorption. Later we will discuss about it on the basis of the adsorbed polymer conformation on MgO surface.
Estimation of the proton density on the MgO surface by zeta potential and MD simulation of short PCE polymer chains
The positive charge density (proton density) present on the MgO surface in cement pore solution is estimated based on the experimental data for the zeta potential of MgO and the use of the Grahame equation, indicating that 1 to 2 atoms in about 25 atoms/nm2 on MgO surface should be protonated (Fig. 2A). However, the real value of the proton density on the MgO surface is considered to be much larger because the Zeta potential is defined at the slipping plane and does not indicate the actual surface charge. Accordingly, in order to evaluate the best proton density using a modest computational time, a scaled down test is performed in synthetic cement pore solution using PCEI-10, which has a short side chain length of P = 10, lower M w of 18,100 and a grafting molar ratio τ = 20 mol%. A three layer MgO slab with the surface protonated in the wide range between 1 to 18 protons/nm2 is used. MD simulations are performed for 150 ns until relaxed polymer configurations in synthetic cement pore solution are obtained. Successively, the PCEI-10 molecule is placed at the centre of a system with an MgO surface and the adsorption is investigated by running additional 10–20 ns. The results are exhibited in Fig. 2B with the ALT values that are obtained by averaging the values from last 20% of each MD trajectory. It was observed that once the backbone was adsorbed on the surface, the resulting adsorption sites adhere to the surface and they are never desorbed. The ALT values demonstrate that the surface with 12 and 18 protons/nm2 makes a PCE backbone to adsorb very intensively (4.1 nm and 3.6 nm), resulting in a completely flat conformation of the backbone, with no observed mobility. The simulations also indicate that a strong adsorption is able to deform the MgO surface, slightly warping it. On the contrary, a density of 1 proton/nm2 generates a partial attraction of the PCEI-10 molecule (7.3 nm). As a result, the moderate proton densities of 2, 3, and 6 protons/nm2 produce stable layer thicknesses of 4.4, 5.0 and 5.2 nm, respectively. Therefore, we have selected 6 protons/nm2 throughout the result of studies for PCEs with doubled chain length because that value offers a balance between a fast adsorption process and preservation of the expected polymer features in the final adsorbed conformations, such as loops and tails.
Estimation of the proton density on the MgO surface in cement pore solution. (A) Calculation based on the zeta potential of MgO and the use of the Grahame equation. (B) Final conformation of PCEI-10 adsorbed on MgO surface for different proton densities (proton/nm2): (a) 1, (b) 2, (c) 3, (d) 6, (e) 12 and (f) 18, and their ALT (nm) are: (a) 7.3, (b) 4.4, (c) 5.0, (d) 5.2, (e) 4.1 and (f) 3.6.
Adsorbed conformation on the MgO surface in synthetic cement pore solution by MD simulations
The simulations of polymer conformation in synthetic cement pore solution are carried out until the values of calculated properties indicate a steady state with oscillation around a given value, due to thermal fluctuations. In the previous work21, we have demonstrated that whole PCE polymers require MD simulations as long as 200–350 ns and the PEG side chains 10–100 ns to reach a steady state until the initial energy is minimized and the thermal and pressure equilibrations are achieved. The final confirmation of PCEs show generation of PEG clusters, which arguably occurs due to the hydrophobic association of PEGs (i.e. salting-out effect) which is induced in the presence of inorganic ions or high pH values27. PEG molecules are known to easily aggregate with each other by hydrogen bonds28,29. Relaxed PCE backbones are significantly distorted and shrunken due to the salting-out effect as well.
Successively, the PCE molecules that had been stabilized in cement pore solution are placed at a location with their centre-of-mass coordinates about 10 nm apart from the MgO surface in two distinct orientations: one parallel and one perpendicular to the MgO surface. Figure 3A illustrates: (a) the initial structures of PCEM-25, PCEA-34, and PCEI-25 that are stabilized in synthetic cement pore solution mentioned above; (b) the final conformations of those samples on MgO surface after MD simulations of about 250 ns; and (c) the surface view of the final conformations, respectively. The simulation time of 250 ns for adsorption is sufficient to allow all properties to be converged to steady state values. All the PCE samples adsorbed on MgO surface other than PCEI-25 that is placed in parallel position. The reason is discussed later.
Adsorption properties predicted by simulations for initial parallel and perpendicular orientations. (A): Adsorbed conformation of the PCE samples. (a) Initial structure; (b) after 250 ns of dynamic evolution viewed from side and (c) viewed from top. (B): Adsorption properties. (B-1) R g(sim), (B-2) The R h(sim)/R g(sim) ratio, (B-3) ALT, (C): (C-1) Relationship between the saturated surface area and the R h(sim)/R g(sim) ratio that is averaged parallel one and perpendicular one. The saturated surface area is calculated by πR 2 g(sim) × {Ad saturated/(1000 × M w)} × (N A/1014), where Ad saturated is the saturated adsorption amount presented in Fig. 1, N A is the Avogadro constant. (C-2) Standard adsorbed amount vs. predicted ALT.
The adsorption conformation depends on the orientation that a stabilized PCE molecule is placed around the centre of the systems. Namely, the parallel placement against the MgO surface introduces adsorption conformation with PCE shape close to train while the perpendicular placement offers adsorption conformations pertaining loop or tail, leading to higher layer thicknesses. Figure 3B shows the adsorption properties of radii of gyration (R g(sim)), the hydrodynamic radii (R h(sim))/R g(sim) ratio and the ALT values calculated from the simulations.
The saturated surface areas that are calculated from PCEA-34 and PCEI-25 adsorption simulation results (6000 and 7300 cm2/g, respectively) are about two times or more than the specific surface area of 3299 cm2/g. It is consistent with a previous report30 that the surface area of cement increases by 2 to 2.5 times larger just after water contact. However, PCEM-25 covers about eight times the specific surface area. That can be explained in terms of the R h(sim)/Rg(sim) ratio (Fig. 3C-1). This ratio acts as an indicator of polymer conformation31, suggesting that the adsorbed conformation of PCEM-25, PCEI-25 and PCEA-34 changes from closer to linear to that closer to spherical in this order. Accordingly, the linear shaped PCEM-25 molecule can be considered to overlap the R g region of neighbouring molecules in solution in contrast with the spherical ones like PCEA-34 or PCEI-25 molecules.
It is assumed that ALT values more than 6 nm are required for superior superplasticizers such as PCEM, PCEA and PCEI (Fig. 3B-3) displaying a lower standard dosage that is required to obtain the initial paste flow of 26 ± 0.5 cm. Figure 3C-2 shows that ALT is inversely proportional, as expected, to the standard adsorbed amount at the initial paste flow of 26 ± 0.5 cm. Here, the ALT values are obtained by averaging the heights for the initial parallel and perpendicular placement simulations. However, the difference of the ALT is only 1.2 nm between PCEM-25 (the lowest one) and PCEI-25 (the highest one), and only 0.1 nm between PCEA-34 and PCEI-25. Here, it should be noted that, due to the high computational cost, only one ALT value is calculated for each orientation. The results show that, the deviation of the ALT in each PCE is comparatively large. Therefore, additional simulations should be performed to provide statistically meaningful values. Ideally, random initial orientations of molecule should be considered as well as different sequence of monomers for PCEI-25 and PCEM-25.
In addition, it is probably reasonable to assume that other factors beyond the ALT may affect the dispersion of the cement particles. Indeed, previous reports have deduced, for instance, that the non-adsorbed PCE supplements the cement-dispersing effect of the adsorbed PCE, acting as lubricants32,33 and that the hydrophilic PCE molecule shows superior effect of cement-dispersing to hydrophobic one34. The influence of adsorbed PCE molecules on the morphology of the hydrated grains may be considered as well.
We should discuss the reason why PCEI-25 is not adsorbed on MgO surface when it is placed at a parallel initial position. At first, it is conceived that the carboxylic acid groups on a PCEI-25 backbone do not work as the adsorption sites because of a perfect coverage with the PEG side chains, but PCEA-34 with a larger grafting ratio adsorbs. Hence, the conformation change of PCEI-25 and PCEA-34 has been carefully compared at the parallel placement. The simulation results are shown in Fig. 4A-1 (PCEI-25) and A-2 (PCEA-34). In Fig. 4A-1, we can see many stretched PEG chains are pointing to the MgO surface during a full trajectory of 200 ns where PCEI-25 backbone is about 3 nm away from the MgO surface. These PEG side chains can induce steric hindrance effect to prevent further downwards movement of the PCE backbone. Therefore, these stretched PEG side chains play somehow “shielding” role owing to such steric hindrance effect. In comparison, PCEA-34 adsorbs by pulling the aggregated PEG lump onto the backbone probably due to an easy rotation of maleic acid moiety toward a positively charged MgO surface even at the initial stage (Fig. 4A-2). Such conformation is obviously beneficial to the further adsorption of PCE backbone onto the MgO surface. In contrast, when a PCEI-25 molecule is placed at a perpendicular position (Fig. 4B-1), it can adsorb on MgO surface through the carboxylic acids at the end of the backbone. Those carboxylic acids less covered with PEG side chains can easily attack a positively charged MgO surface.
Snapshots of side views of PCEs samples adsorbing conformation (with (A) parallel initial orientation and (B) perpendicular initial orientation) on MgO surface with proton density of 6/nm2. PEG side chains in PCEs are colored in green to gain better contrast against the backbone atoms. (A-1) PCEI-25. The snapshots are taken from MD simulations from 154 to 164 ns of a trajectory with total length of 250 ns. (A-2) PCEA-34. The snapshots are taken from initial stage of MD simulations from 0 to 300 ps of a trajectory with total length of 250 ns. (B-1) PCEI-25. The snapshots are taken from initial stage of MD simulations from 0 to 50 ps of a trajectory with total length of 250 ns.
Many researchers obtained ALT values within 1–5 nm, which are smaller than the values in this paper, for PCEM type superplasticizers by the atomic force microscope (AFM) measurements in a KCl, NaCl or synthetic cement pore solution9,10,11,35. The ALT values predicted by the mean-field model9,36,37 are 3.0 nm, 3.1 nm and 4.0 nm for PCEM-25, PCEI-25 and PCEA-34, respectively. However, a general concern has been expressed about values for ALT obtained by AFM measurements as the AFM tip might compress the adsorbed polymer and thus lead to ALT lower than the actual values32, which would explain the contrast with our direct values obtained from analysis of atomic positions from simulations. In addition, the mean-field model disregards the aggregation of PEG side chains, which our simulation has shown to be significant. Indeed, Sakai et al.14 showed the significantly large layer thickness of 4.54–11.51 nm in allyl ether−maleic acid−styrene copolymer by measuring the amount of water passing through an alumina filter with minute holes of 100–200 nm in which PCE molecules are adsorbed.
Conclusions
The adsorption behaviour of three types of common PCE concrete superplasticizers (PCEM, PCEA and PCEI) on MgO surface in synthetic cement pore solution was studied by full atomistic MD simulations. Results indicate that polymer molecules placed initially parallel or perpendicularly against an MgO surface leads to adsorption in shape closer train or that pertaining loop and tail, respectively. A loop and tail shape produces a higher layer thickness. The predicted layer thickness is inversely proportional to the amount of adsorbed polymer at the initial paste flow. A PCE with the adsorbed layer thickness higher than 6 nm is a necessary condition for an excellent superplasticizer such as PCEM, PCEA and PCEI with a lower standard dosage. Nonetheless, it is suggested that other factors beyond the adsorbed layer thickness should be taken into consideration as well.
Materials
Cement
The cement used in this study was an ordinary Portland cement (CEM I 52.5 N Milke®classic from Heidelberg Cement, Geseke plant, Germany). Its phase composition as determined by quantitative X-ray diffraction (Bruker D8 advance instrument, software Topas 4.0) is presented in Table 1. The specific surface area of 3299 cm2/g is measured using a Blaine instrument (Toni Technik, Berlin/Germany). An average particle size (d 50 value) of 12.02 µm is determined by laser granulometry CILAS 1064 (Cilas, Marseille, France), and the density measured by a Helium pycnometer (Quantachrome, Odelzhausen, Germany) is 3.16 g/cm3.
PCE copolymers
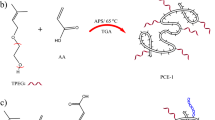
The chemical structure of the PCE samples investigated, PCEM-25, PCEI-25, and PCEA-34 are shown in Fig. 5. These structures are the same as those used in our previous work21. Their individual synthesis methods have been described previously38,39,40. The properties of the synthesized polymers are summarized in Table 2.
Chemical structures of the PCE samples studied. It is reproduced from authors’ own work21 published with ICE Publishing.
The M w , the polymer content (monomer conversion) and the polydispersity index (PDI) were determined by size exclusion chromatography (SEC, Waters Alliance 2695 from Waters, Eschborn, Germany) equipped with refractive index (RI) detector 2414 (Waters, Eschborn, Germany) and a three-angle dynamic light-scattering detector (mini Dawn from Wyatt Technologies, Santa Barbara, CA, USA): prior to application on the columns, the polymer solutions were filtered through a 0.2 μm filter. The polymers were separated on an Ultrahydrogel precolumn and three Ultrahydrogel (120, 250 and 500) columns (Waters, Eschborn, Germany) using 0.1 M aqueous sodium nitrate (NaNO3) solution (adjusted to pH 12.0 with sodium hydroxide (NaOH)) as an eluent at a flow rate of 1.0 mL/min. The value of refraction index increment (dn/dc) used to calculate M w and M n for all polymers is 0.135 mL/g (value for polyethylene oxide)41.
The SEC spectra of the PCE samples are shown in our previous work21. The polymer content (percentage of monomers converted to polymer) was determined by the area (%) of the polymer profile in the RI diagram.
The initial structure of the PCEs before geometric optimization is also shown in our previous work21. All polymer models are constructed using the polymer builder function of the Materials Studio package. It is emphasized that the PCEA side chains line up much more densely along the backbone than in PCEM and PCEI because of the alternating copolymer structure.
In all three PCE samples, PCEM-25, PCEI-25 and PCEA-34, the weight ratio of PEG macromonomer/carboxylic monomer is optimized for best dispersion. For example, the weight ratio of the monomers in PCEM-25 was 75/25 (PEG monomer/acid monomer) which is in good agreement with the value which has been suggested in previous work42. In this paper, the dosages applied in the cement paste tests are all converted to the values for the pure polymers without residual monomers to compare the effects of the polymers themselves.
Experimental and simulation procedures
Performance test with cement using ‘mini slump’ test
For the determination of the paste flow, a ‘mini slump’ test was utilised and carried out as follows. First, a constant water-to-cement (w/c) ratio of 0.3 was chosen. At this w/c ratio, the dosages of the polymers required to reach a spread of 26 ± 0.5 cm are determined. Generally, the polymer is dissolved in the required amount of mixing water placed in a porcelain cup. The amount of water contained in the polymer solution is subtracted from the amount of mixing water. Next, within 5 s, 350 g of cement are added to the mixing water and agitated manually for 1 min, then rested for 1 min without stirring. This is followed by intensive stirring for another 2 min. The cement paste is immediately poured into a Vicat cone (height 40 mm, top diameter 70 mm, bottom diameter 80 mm), then placed on a glass plate and the cone is vertically lifted. The resulting spread of the paste is measured twice, the second measurement being at a 90° angle to the first one, and averaged to give the spread value. All tests were carried out at 22 °C.
Adsorption measurement
The PCE adsorption on cement is measured using the depletion method. The non-adsorbed portion of polymer remaining in solution at equilibrium condition is determined by analyzing the total organic carbon (TOC) content of the solution. In a typical experiment, 50 g of cement, 15 g of water and the amount of PCE to be tested are filled into a 50 mL centrifuge tube, shaken in a wobbler (VWR International, Darmstadt/Germany) for 4 minutes at 2400 rpm and then centrifuged for 15 minutes at 8500 rpm. The supernatant is diluted with deionized water. The TOC content of the solution is determined by combustion at 890 °C on a High TOC II instrument (Elementar Analysensysteme, Hanau/Germany). From the difference between the TOC content of the polymer reference sample and the TOC content of the supernatant, the adsorbed amount of PCE is calculated.
Molecular Dynamics Simulations
MD simulations are performed using the GROMACS package43,44,45,46,47 version 5.1.2. Simulations are performed using the NVT canonical ensemble (constant temperature, volume, and number of atoms) at room temperature (300 K) with a time step of 2 fs. The LINCS algorithm48 and its parallel version P‐LINCS49 are applied to constrain bonds involving light atoms such as hydrogen. The visual molecular dynamics (VMD) visualization package50 is used to the analyze radius of gyration and hydrodynamic radius for the whole polymer based on MD trajectories saved every 5000 steps (10 ps) and averaged in the last 30 ns of the simulations. Prior to each NVT run, geometry optimization and a 5 ns MD relaxation process under the isothermal-isobaric ensemble (NPT) with pressure P = 1 bar and temperature (300 K) is applied.
The duration of each NVT run is adjusted based on the convergence of the properties. For the models considered that is expected to be from 150 to 500 ns. For the adsorbed models, ALT is calculated and used as a convergence criterion.
Model considerations
Initial conformations of PCEs for adsorption study in this work are obtained from those relaxed conformations in our previous work21. The previous simulations on the PCE conformations in solution21 are performed using the standard MD procedure using a periodic simulation box. However, the simulations of adsorption require slab geometry with 2D xy periodic boundary conditions and an artificial confinement in the z direction (perpendicular to the slab surface). Here, we use a confinement of the system within a z layer and Gromacs special features for this kind of simulation. Those features included wall setup scheme, xy periodic boundary conditions, and the use of the Ewald-zfac method to minimize unphysical interactions of atoms with periodic images in the z direction.
PCEs mainly adsorb on positively charged hydrates of cement phases such as C3A, C4AF and especially on ettringite crystallizing on hydrating cement grains51,52,53. However, the cement surface is unclear due to the hydrates changing with hydration time, with an inherent complexity54. Therefore, inert MgO is used as a model representing a complex cement particle10,11,55,56,57.
The synthetic cement pore solution used in the simulations is generated using the following amount of salts: 1.72 g/l gypsum (CaSO4 2H2O), 6.959 g/l sodium sulfate (Na2SO4), 4.757 g/l potassium sulfate (K2SO4), and 7.12 g/l potassium hydroxide (KOH) (pH = 13.1). The salts are assumed to be completely dissociated in water. Based on this assumption the exact molar concentrations of Ca2+, SO4 2−, Na+, K+, and OH− are calculated to be: Ca2+: 0.010 M, Na+: 0.098 M, K+: 0.181 M, SO4 2−: 0.086 M and OH−: 0.127 M. For simulation purposes, the molar concentrations are converted to volumetric concentrations: Ca2+: 6.087 × 10−3/nm3, Na+: 5.901 × 10−2/nm3, K+: 0.109/nm3, SO4 2−: 5.203 × 10−2/nm3, and OH−: 7.642 × 10−2/nm3.
Force Field Model for Polymer, MgO and ions
The ‘optimised potentials for liquid simulations’ (OPLS) all atom58,59,60,61,62 force field is employed to describe the interatomic forces for the model of all PCE polymers, the MgO substrate, and ions including Ca2+, Na+, K+, Cl−. Force field parameters for OH− and SO4 2− are taken from the ‘chemistry at Harvard macromolecular mechanics’ (CHARMM) force field63.
References
Uchikawa, H., Hanehara, S. & Sawaki, D. The role of steric repulsive force in the dispersion of cement particles in fresh paste prepared with organic admixture. Cement and Concrete Research 27, 37–50 (1997).
Hauet, T. & Eugene, M. A. New approach in organ preservation: potential role of new polymer. Kidney International 74, 998–1003 (2008).
Shikata, T., Okuzono, M. & Sugimoto, N. Temperature-dependent hydration/dehydration behavior of poly(ethylene oxide)s in aqueous solution. Macromolecules 46, 1956–1961 (2013).
Evans, R. & Napper, D. H. Kolloide, Steric stabilization II. Kolloid-Z. u. Z. Polymere 251, 329–336 (1973).
Evans, R. & Napper, D. H. Kolloide, Steric stabilization I. Kolloid-Z. u. Z. Polymere 251, 409–414 (1973).
Napper, D. H. Steric stabilization and the Hofmeister Series. Journal of Colloid and Interface Science 33, 384–392 (1970).
de Gennes, P. G. Conformations of polymers attached to an interface. Macromolecules 13, 1069–1075 (1980).
de Gennes, P. G. Polymers at an interface; a simplified view. Advances in Colloid and Interface Science 27, 189–209 (1987).
Flatt, R. J., Schober, I., Raphael, E., Plassard, C. & Lesniewska, E. Conformation of adsorbed comb copolymer dispersants. Langmuir 25, 845–855 (2009).
Houst, Y. F. et al. Design and function of novel superplasticizers for more durable high performance concrete (superplast project). Cement and Concrete Research 38, 1197–1209 (2008).
Kauppi, A., Andersson, K. M. & Bergström, L. Probing the effect of superplasticizer adsorption on the surface forces using the colloidal probe AFM technique. Cement and Concrete Research 35, 133–140 (2005).
Kleshchanok, D. & Lang, P. R. Steric repulsion by adsorbed polymer layers studied with total internal reflection microscopy. Langmuir 23, 4332–4339 (2007).
Nawa, T. Effect of chemical structure on steric stabilization of polycarboxylate-based superplasticizer. Journal of Advanced Concrete Technology 44, 225–232 (2006).
Sakai, E. & Daimon, M. Dispersion mechanisms of alite stabilized by superplasticizers containing polyethylene oxide graft chains. Proceedings of the 5 th CANMET / ACI International Conference on Superplasticizers and Other Chemical Admixtures in Concrete (Malhotra VM (ed)). American Concrete Institute, Farmington Hill, MI, USA, SP-173, 187–201 (1997).
Yoshioka, K., Sakai, E., Daimon, M. & Kitahara, A. Role of steric hindrance in the performance of superplasticizers for concrete. Journal of the American Ceramic Society 80, 2667–2671 (1997).
Mishra, R. K., Heinz, H., Zimmermann, J., Müller, T. & Flatt, R. J. Understanding the Effectiveness of Polycarboxylates as Grinding Aids. Proceedings of the 10 th CANMET/ACI International Conference on Superplasticizers and Other Chemical Admixtures in Concrete (Malhotra VM (ed)). American Concrete Institute, Farmington Hills, MI, USA, SP-288, 235–249 (2012).
Mohan, R., Jadhav, V., Ahmed, A., Rivas, J. & Kelkar, A. Effect of Plasticizer Additives on the Mechanical Properties of Cement Composite – A Molecular Dynamics Analysis. International Journal of Chemical, Molecular, Nuclear, Materials and Metallurgical Engineering 8, 84–88 (2014).
Ran, Q. et al. Molecular dynamics study of the effects of calcium ions on the conformational properties of comb-like poly(acrylic acid-co-methyl allyl polyoxyethylene ether). Computational Materials Science 109, 90–96 (2015).
Shu, X. et al. Tailoring the solution conformation of polycarboxylate superplasticizer toward the improvement of dispersing performance in cement paste. Construction and Building Materials 116, 289–298 (2016).
Zhang, Q. et al. pH-induced conformational changes of comb-like polycarboxylate investigated by experiment and simulation. Colloid and Polymer Science 294, 1705–1715 (2016).
Hirata, T. et al. Atomistic dynamics simulation to solve conformation of model PCE superplasticisers in water and cement pore solution. Advances in Cement Research 29(10), 418–428 (2017).
Pickelmann, J., Li, H., Baumann, R. & Plank, J. A 13C NMR Spectroscopic Study on the Repartition of Acid and Ester Groups in MPEG Type PCEs Prepared via Radical Copolymerization and Grafting Techniques. Proceedings of the 11 th CANMET/ACI Conference on Superplasticizers and Other Chemical Admixtures in Concrete (Malhotra VM, Gupta PR, Holland TC (eds)). American Concrete Institute, Farmington Hills, MI, USA, SP-302, 25–37 (2015).
Plank, J. et al. A microstructural analysis of isoprenol ether-based polycarboxylates and the impact of structural motifs on the dispersing effectiveness. Cement and Concrete Research 84, 20–29 (2016).
Calvet, R. Adsorption of organic chemicals in soils. Environmental health perspectives 83, 145–177 (1989).
Giles, C. H., MacEwan, T. H., Nakhwa, S. N. & Smith, D. Studies in adsorption. Part XI. A system of classification of solution adsorption isotherms, and its use in diagnosis of adsorption mechanisms and in measurement of specific surface areas of solids. Journal of the Chemical Society 3, 3973–3993 (1960).
Sakai, E., Yamada, K. & Ohta, A. Molecular structure and dispersion-adsorption mechanisms of comb-type superplasticizers used in Japan. Journal of Advanced Concrete Technology 1, 16–25 (2003).
Bailey, F. E. Jr. & Callard, R. W. Some properties of poly(ethylene oxide) in aqueous solution. Journal of applied polymer science 1, 56–62 (1959).
Begum, R. & Matsuura, H. Conformational properties of short poly(oxyethylene) chains in water studied by IR spectroscopy. Journal of the Chemical Society. Faraday Transaction 93, 3839–3848 (1997).
Linegar, K. L., Adeniran, A. E., Kostko, A. F. & Anisimov, M. A. Hydrodynamic radius of polyethylene glycol in solution obtained by dynamic light scattering. Colloid Journal 72, 279–281 (2010).
Uchikawa, H., Uchida, S., Ogawa, K. & Hanehara, S. Influence of CaSO4-2H2O, CaSO4-1/2H2O and CaSO4 on the initial hydration of clinker having different burning degree. Cement and Concrete Research 14, 645–656 (1984).
Roovers, J. & Martin, J. E. The hard-sphere model for linear and regular star polybutadienes. Journal of Polymer Science: Part B: Polymer Physics 27, 2513–2524 (1989).
Lange, A. & Plank, J. Contribution of non-adsorbing polymers to cement dispersion. Cement and Concrete Research 79, 131–136 (2016).
Sakai, E., Kakinuma, Y., Yamamoto, K. & Daimon, M. Relation between the shape of silica fume and the fluidity of cement paste at low water to powder ratio. Journal of Advanced Concrete Technology 7, 13–20 (2009).
Lange, A., Hirata, T. & Plank, J. Influence of the HLB value of polycarboxylate superplasticizers on the flow behaviour of mortar and concrete. Cement and Concrete Research 60, 45–50 (2014).
Banfill, P. F. G. et al. Improved superplasticizers for high performance concrete: the SUPERPLAST project. Proceedings of the 12 th International Congress on the Chemistry of Cement. ICCC, Montreal, Canada (2007).
Borget, P., Galmiche, L., Meins, J. F. L. & Lafuma, F. Microstructural characterisation and behaviour in different salt solutions of sodium polymethacrylate-g-PEO comb copolymers. Colloids and Surfaces A: Physicochemical and Engineering Aspects 260, 173–182 (2005).
Gay, C. & Raphaël, E. Comb-like polymers inside nanoscale pores. Advances in Colloid and Interface Science 94, 229–236 (2001).
Hirata, T., Yuasa, T. & Nagare, K. Cement admixture and cement composition. US Patent 6166112, Dec. assigned to Nippon Shokubai (2000).
Lange, A., Hirata, T. & Plank, J. The role of non-adsorbed PCE molecules in cement dispersion: experimental evidence for a new dispersion mechanism. Proceedings of the 10 th CANMET/ACI International Conference on Superplasticizers and Other Chemical Admixtures in Concrete (Malhotra VM (ed)). American Concrete Institute, Farmington Hills, MI, USA, SP-288, 435–449 (2012).
Yamamoto, M. et al. Copolymer for cement admixtures and its production process and use. US Patent 6727315, Apr. assigned to Nippon Shokubai (2004).
Teresa, M. et al. Polymer characterization by size-exclusion chromatography with multiple detection. Journal of Chromatography A 919, 13–19 (2001).
Winnefeld, F., Becker, S., Pakusch, J. & Götz, T. Effects of the molecular architecture of comb-shaped superplasticizers on their performance in cementitious systems. Cement and Concrete Composites 29, 251–262 (2007).
Berendsen, H. J. C., Spoel, D. V. D. & Drunen, R. V. GROMACS: A message-passing parallel molecular dynamics implementation. Computer Physics Communications 91, 43–56 (1995).
Hess, B., Kutzner, C., Spoel, D. V. D. & Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. Journal of Chemical Theory and Computation 4, 435–447 (2008).
Lindahl, E., Hess, B. & Spoel, D. V. D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. Journal of Molecular Modeling 7, 306–317 (2001).
Pronk, S. et al. Gromacs 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 29, 845–854 (2013).
Spoel, D. V. D. et al. GROMACS: Fast, flexible, and free. Journal of Computational Chemistry 26, 1701–1718 (2005).
Hess, B., Bekker, H., Berendsen, H. J. C. & Fraaije, J. G. E. M. LINCS: A linear constraint solver for molecular simulations. Journal of Computational Chemistry 18, 1463–1472 (1997).
Hess, B. P-LINCS: A parallel linear constraint solver for molecular simulation. Journal of Chemical Theory and Computation 4, 116–122 (2008).
Humphrey, W., Dalke, A. & Schulten, K. VMD: Visual molecular dynamics. Journal of Molecular Graphics 14, 33–38 (1996).
Plank, J. & Hirsch, C. Impact of zeta potential of early cement hydration phases on superplasticizer adsorption. Cement and Concrete Research 37, 537–542 (2007).
Yoshioka, K., Tazawa, E., Kawai, K. & Enohara, T. Adsorption characteristics of superplasticizers on cement component minerals. Cement and Concrete Research 32, 1507–1513 (2002).
Zingg, A. et al. Adsorption of polyelectrolytes and its influence on the rheology, zeta potential, and microstructure of various cement and hydrate phases. Journal of Colloid and Interface Science 323, 301–312 (2008).
Mindess, S., Young, J. F. & Darwin, D. Concrete 2 nd ed. Prentice Hall. NJ. USA (2003).
Flatt, R. J. et al. Interaction of superplasticizers with model powders in a highly alkaline medium. Proceedings of the 5th CANMET/ACI International Conference on Superplasticizers and Other Chemical Admixtures in Concrete (Malhotra VM (ed)). American Concrete Institute, Farmington Hill, MI, USA, SP-173, 743–762 (1997).
Ferrari, L., Kaufmann, J., Winnefeld, F. & Plank, J. Interaction of cement model systems with superplasticizers investigated by atomic force microscopy, zeta potential, and adsorption measurements. Journal of Colloid and Interface Science 347, 15–24 (2010).
Houst, Y. F., Bowen, P. & Perche, F. Adsorption of superplasticizers on a model powder. Proceedings of the 12th International Congress on the Chemistry of Cement (Beaudoin JJ, Makar JM, Raki L (eds)). EPFL, Montréal, Canada (2007).
Jorgensen, W. L., Maxwell, D. S. & Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. Journal of the American Chemical Society 118, 11225–11236 (1996).
Jorgensen, W. L. & McDonald, N. A. Development of an all-atom force field for heterocycles. Properties of liquid pyridine and diazenes. Journal of Molecular Structure: THEOCHEM 424, 145–155 (1998).
Kaminski, G. A., Friesner, R. A., Tirado-Rives, J. & Jorgensen, W. L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. The Journal of Physical Chemistry B 105, 6474–6487 (2001).
Price, M. L. P., Ostrovsky, D. & Jorgensen, W. L. Gas-phase and liquid-state properties of esters, nitriles, and nitro compounds with the OPLS-AA force field. Journal of Computational Chemistry 22, 1340–1352 (2001).
Rizzo, R. C. & Jorgensen, W. L. OPLS All-atom model for amines: resolution of the amine hydration problem. Journal of the American Chemical Society 121, 4827–4836 (1999).
Klauda, J. B. et al. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. The Journal of Physical Chemistry B 114, 7830–7843 (2010).
Acknowledgements
Dr. Hirata wishes to express his deep gratitude to the “Institute for Advanced Study” for financing his research and stay at TU München under a Rudolf Diesel fellowship. Dr. Branicio, Dr. Ye, Dr. Zheng and Dr. Sullivan acknowledge the support of the A*STAR Computational Resource Centre through the use of its high performance computing facilities.
Author information
Authors and Affiliations
Contributions
T.H. designed and organized. J.Y., P.B., J.Z. and A.L. performed the experiments. T.H., J.Y., P.B., J.Z., A.L. and J.P. wrote the manuscript. J.P. and J.Z. provided technical support and conceptual advice. M.S. supervised the research. All authors discussed and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hirata, T., Ye, J., Branicio, P. et al. Adsorbed Conformations of PCE Superplasticizers in Cement Pore Solution Unraveled by Molecular Dynamics Simulations. Sci Rep 7, 16599 (2017). https://doi.org/10.1038/s41598-017-16048-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16048-3
This article is cited by
-
Effect of sodium gluconate on molecular conformation of polycarboxylate superplasticizer studied by the molecular dynamics simulation
Journal of Molecular Modeling (2020)
-
Binding of calcium cations with three different types of oxygen-based functional groups of superplasticizers studied by atomistic simulations
Journal of Molecular Modeling (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.