Abstract
We describe a novel method of kinetic analysis of radioligand binding to neuroreceptors in brain in vivo, here applied to noradrenaline receptors in rat brain. The method uses positron emission tomography (PET) of [11C]yohimbine binding in brain to quantify the density and affinity of α2 adrenoceptors under condition of changing radioligand binding to plasma proteins. We obtained dynamic PET recordings from brain of Spraque Dawley rats at baseline, followed by pharmacological challenge with unlabeled yohimbine (0.3 mg/kg). The challenge with unlabeled ligand failed to diminish radioligand accumulation in brain tissue, due to the blocking of radioligand binding to plasma proteins that elevated the free fractions of the radioligand in plasma. We devised a method that graphically resolved the masking of unlabeled ligand binding by the increase of radioligand free fractions in plasma. The Extended Inhibition Plot introduced here yielded an estimate of the volume of distribution of non-displaceable ligand in brain tissue that increased with the increase of the free fraction of the radioligand in plasma. The resulting binding potentials of the radioligand declined by 50–60% in the presence of unlabeled ligand. The kinetic unmasking of inhibited binding reflected in the increase of the reference volume of distribution yielded estimates of receptor saturation consistent with the binding of unlabeled ligand.
Similar content being viewed by others
Introduction
Deficient noradrenergic neurotransmission is implicated in a spectrum of brain disorders, including neurodegenerative and psychiatric disorders. Locus coeruleus is the major source of neuronal terminals engaged in noradrenaline synthesis, and pathological protein deposition together with loss of neurons at this site has been described in Alzheimer’s disease1. Similarly, attenuated levels of noradrenaline have been reported in Parkinson’s disease2. Attenuated noradrenergic activity is implicated in major depression, as indicated by findings of depleted noradrenaline in depressed patients with rapidly worsening symptoms3. Thus, multiple post-mortem studies have revealed elevated α2 adrenoceptor expression in suicide victims with a retrospective diagnosis of major depression, with upregulation of the α2A adrenoceptor subtype noted particularly in the frontal and prefrontal cortices4,5,6.
Increased α2 adrenoceptor density is believed to compensate for attenuated noradrenaline release when experimental depletion of brain noradrenaline in rats led to upregulated cortical l α2 adrenoceptors7. In brains of patients who suffered from bipolar disorder, lower tyrosine hydroxylase immunoreactivity was found in locus coeruleus, consistent with deficient noradrenaline synthesis8. In support of low noradrenaline, a more recent PET study showed lower occupancy of noradrenaline transporters in locus coeruleus in patients with bipolar disorder or major depression, compared to healthy controls9. In attention-deficit/hyperactivity disorder (ADHD), impulsive behavior was associated directly with low noradrenergic tone10.
Central noradrenaline is known to modulate cognitive functions, such as arousal, mood, learning and memory (reviewed by Sara et al.11). To understand the neurobiology underlying brain disorders in the living brain, non-invasive PET using selective ligands can be used to monitor the activity of neurotransmission as a sign of disease severity and response to pharmacological therapy. The labeling of yohimbine with carbon-11 provided new opportunities to measure noradrenergic transmission in pathological conditions. [11C]yohimbine so far has been applied to image α2 adrenoceptor in vivo in different species, including humans12, pigs13,14, and rats15,16,17. However, the wide anatomical distribution of noradrenergic receptors complicates the quantification of receptor occupancy and receptor density.
The aims of the present study are twofold: First, we use yohimbine to obtain an estimate of the reference distribution volume of the radioligand in the absence of a true anatomical reference region. Second, we use kinetics to resolve the masking of ligand binding competition by pharmacological challenge that raises the plasma-free fraction of the radioligand.
Protein binding of drugs in plasma are of special interest in pharmacological studies because only the drug that is unbound to plasma proteins (i.e., is “free”) has access to target tissue and hence is biological active18. PET imaging of the brain with radiolabeleld ligands faces the same issue because the blood-brain barrier (BBB) permeability of the drug depends on the free-fraction of the ligand among many other factors. The CSF/plasma albumin ratio is 0.006, indicating that only a negligible fraction of albumin passes the BBB19. In vitro, the free drug concentration depends on factors such as protein quantity, drug affinity, and total drug concentration, while in vivo, factors such as metabolism, excretion and membrane transport, all influence the free drug concentration.
Quantification of neuroreceptor density with PET requires the determination of receptor availability at two or more different levels. The number of receptors available for radioligand binding can be modulated by agents that induce release or depletion of endogenous neurotransmitters, or by introduction of exogenous molecules that either bind to the receptors or affect the mechanism of binding of the endogenous ligands. Thus, pharmacological modulation changes the availability of sites for radioligand binding. Commonly, modulation of occupancy is achieved with unlabeled exogenous ligands that compete at the binding site. Receptor occupancy and density are then calculated from the fractional change of the receptor availability (also known as binding potential) after the pharmacologcial challenge.
To determine the binding potential, it is necessary to know the total volume of distribution of all labeled molecules in the tissue, VT, and the volume of distribution of molecules that cannot be displaced from binding (i.e., the volume of distribution indicative of “non-displaceable” binding), represented as VND20,21. For radioligands that bind to some regions only (as in the case of dopaminergic radioligands), estimates of VND are the volumes of distribution in brain regions with no specific binding (reference regions). In contrast, for radioligands distributed in the entire brain, a reference volume must be estimated from regional values of VT at two different different degrees of receptor occupancy, as described in Methods below.
Changes of free fractions of tracer in plasma, fP , do not perturb the calculation of binding potentials in the presence of a non-binding reference region, because the value of VND is obtained from the degree of non-displaceble binding in the reference region, which scales with the freely distributed ligand in plasma. In the absence of a non-binding reference region, changes of fP influence the magnitudes of VT and VND estimates and hence may mask the competition from a blocking agent.
Here, we demonstrate a novel solution to issue of elevation of the magnitude of fP in response to pharmacological challenge that may occur in vivo. The mathematical approach is designed to resolve the masking of competition attributable to the decreased protein binding of the tracer in plasma. As an example, we quantified the binding of [11C]yohimbine to widely distributed α2 adrenoceptors in the rat brain by an analysis that is not limited to α2 adrenoceptors but can be applied to radioligands of other receptors that lack a non-binding reference region.
Results
Tracer Accumulation as a Function of Time
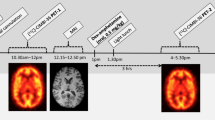
To evaluate the pattern of [11C]yohimbine binding to α2 adrenoceptors, we examined the binding at two levels of receptor occupancy, at baseline and at challenge with unlabeled yohimbine (0.3 mg/kg) administered as an i.v. bolus. The average time-activity curves (TACs) in plasma and brain regions show the kinetic behavior of [11C]yohimbine as it accumulates in the tissue (Fig. 1B). The clearance of the radioligand from the circulation occurred rapidly within the first 10 min after intravenous bolus injection. The uptake in cerebellum peaked at 10 min post-injection, while the accumulation peaked later in other brain regions at 20 min. TAC of the unlabeled yohimbine challenge revealed prominently elevated early uptake compared to baseline, showing that the effect of the challenge is not apparent exclusively from the TACs.
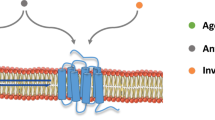
Tracer Accumulation as a Function of Time. Panel (A) illustrates the one-tissue compartment model used for data analysis. In this model, K1 represents the clearance from plasma to brain tissue while \({k}_{2}^{{\prime} }\) represents the fractional clearance of ligand from brain to plasma. Here, the free amount of ligand in plasma reflects the exchangeable compartment when only the unbound ligand crosses the BBB and enters brain tissue. The magnitude of K1 depends on the free concentration in plasma, cerebral blood flow, and the permeability surface area as well as the association and dissociation constants for plasma protein binding (depicted here as kpr,on and kpr,off). The magnitude of \({k}_{2}^{{\prime} }\) depends on the concentration of ligand in brain tissue and the association and disassociation constants for receptor binding (shown as grey arrows on the right hand side). Initial evaluation of tracer accumulation in panel (B) demonstrates that average plasma input curves are of similar magnitude, indicating that the challenge condition did not significantly alter the baseline input function. The solid curves represent the average time-activities of individual curves divided by the integral of the respective plasma input to normalize for variations attributed to differences of injected radioactive dose, body weight and other bioavailability factors. Baseline is shown in black, yohimbine challenge in blue, and the shaded areas indicate the standard error of the mean. The time-activity curves (TACs) at challenge condition were markedly higher compared to baseline across all regions, suggesting that the inhibition effect is not immediate visible.
Increased K 1 May Indicate Displacement of Plasma Protein Binding
As for the trends of TACs, the magnitude of unidirectional clearance from plasma to brain tissue, represented by K1, was markedly elevated in the challenge condition. The value of K1 at the challenge rose initially and maintained higher values during the time of acquisition than in the baseline (Fig. 2A). The magnitude of the fractional clearance from brain to plasma, symbolized by \({k}_{2}^{{\prime} }\), likewise was higher in the challenge than in the baseline condition, to the same relative extent as the value of K1 (Fig. 2B). The ratio of the the estimates of K1 and \({k}_{2}^{{\prime} }\) remained similar throughout the acquisition in both conditions (Fig. 2C). The increased values of K1 and \({k}_{2}^{{\prime} }\) in response to yohimbine challenge are the results of two opposite effects, one the blocking at α adrenoceptor sites by unlabeled yohimbine that underlies the elevated value of \({k}_{2}^{{\prime} }\), and the other the decreased protein binding reflected in the increased estimate of fP that accounts for the elevated value of K1.
K1 and \({k}_{2}^{{\prime} }\) as Functions of Time and Plasma Free Fractions Determined in Separate Groups. The clearance from plasma to brain, K1 (panel (A)), and the fractional clearance from brain to plasma, \({k}_{2}^{{\prime} }\) (panel (B)), were calculated as functions of time using iterative analysis where each point represents a time duration of 14.5 minutes. Estimates of K1 and \({k}_{2}^{{\prime} }\) from were plotted against the time of the last frame of linearization, baseline in black,and yohimbine challenge in blue, with the shaded areas indicating the standard error of the mean. Both K1 and \({k}_{2}^{{\prime} }\) estimates were markedly higher in the challenge than in the baseline condition. Elevated \({k}_{2}^{{\prime} }\) in the challenge condition indicates displacement on α2 adrenoceptor sites due to competition with unlabeled yohimbine, whereas increased K1 suggest that more free ligand crosses BBB in the challenge condition due to displacement of plasma protein binding. Because of two simultaneous opposite effects, the ratio of K1/\({k}_{2}^{{\prime} }\) at challenge condition (C) was at the same magnitude as baseline. This supports that yohimbine challenge was masked by elevated fP . To confirm this notion, we measured fP by means of plasma ultrafiltration (D) in a separate group of animals. In the ex vivo setup (D middle), 0.3 mg/kg yohimbine administered i.v. resulted in a significant increase of fP by 30% as compared to baseline (P < 0.05). In the in vitro study, plasma was drawn before amphetamine or yohimbine were added to the samples. This showed that amphetamine did not change fP , whereas yohimbine challenge produced a dose-dependent increase. Both low dose and high dose challenge increased fP significantly as compared to baseline (****P < 0.0001). The thick line in D (middle) represents the group average, and the thin lines show estimates in individual animals, which connect estimates at baseline and challenge in the same animals.
The early peak of VT curves (Fig. 1C) together with the elevated K1 (Fig. 2A) suggest that the increased values of fP reflect the effects of protein binding blocked by an unlabeled competitor. More than 80% of yohimbine in the circulation is bound to plasma proteins22 that renders [11C]yohimbine prone to self-displacement at plasma protein sites with increased value of fP . The higher fP of [11C]yohimbine in turn masks the competition from unlabeled yohimbine in the brain tissue.
To determine the degree of masking, we measured the free fractions of [11C]yohimbine at baseline and challenge conditions by means of plasma ultrafiltration in a separate group of animals. We determined the values of fP by administration of 0.3 mg/kg yohimbine. The challenge with unlabeled ligand ex vivo significantly raised the value of fP by 30% on average compared to baseline (P < 0.05) (Fig. 2D middle panel). To exclude the possibility that the elevation of fP is due to competition from hepatic metabolism or renal elimination, we repeated the experiment in vitro (Fig. 2D right panel). In vitro, the experiments confirmed no change of the value of fP with amphetamine challenge. As expected, the magnitude of fP increased significantly (P < 0.001) in response to challenge with unlabeled yohimbine, in proportion to the yohimbine dose.
Extended Inhibition Plots and Binding Potentials
On the basis of the substantial change of the value of fP shown ex vivo and in vitro, we applied the Extended Inhibition Plot to resolve the volume of distribution of non-displaceable radioligand at inhibition, VND(i). In the analysis, the volume of distribution of non-displaceable radioligand at baseline, VND(b), is required to determine the magnitude of VND(i) at the challenge.
Previously, in the same strain of animals with same PET protocol, we confirmed that the values of VND(b) and fP did not change when [11C]yohimbine binding was challenged with amphetamine (2 mg/kg)16, using the plasma input function. The plasma input was not metabolite corrected because data from two rats revealed no radioactive metabolites, as for radioactive metabolites in pigs14. Because the value of fP remained the same with amphetamine challenge, we used the Inhibition Plot to obtain a value of VND(b) of 0.286 ml cm−3. The similar experiments and analyses of the previous study allowed us to apply the value of VND(b) of the previous study to the present study.
The graphical analysis yielded an estimate of VND(i) at 0.599 ml cm−3 (Fig. 3A), and the degree of saturation, s, revealed that 56% of available receptors were blocked by unlabeled yohimbine, as shown in Fig. 3B.
Extended Inhibition Plot. Due to significantly increased fP in response to challenge, the Extended Inhibition Plot (eq. 36) (A) was applied to solve VND(i). In the Extended Inhibition Plot, regional estimates of VT at challenge condition are plotted versus the estimates at baseline. VND(b) was set to 0.286 ml cm−3, because this value was previously assessed in an identical strain of rats16. The solid lines illustrate the regression in individual animals and the stippled line illustrates the line of identity. The plots were constrained to produce one population-wise VND(i) value, which yielded 0.599 ml cm−3. The saturation, s, obtained by the Extended Inhibition Plot is presented for individual animals in (B). This revealed that 0.3 mg/kg yohimbine challenge blocked in average 56% of the available receptors. Panel (C) shows the MRI atlas, which the parametric images were superimposed on. Parametric images of VT in panel (D) show that yohimbine challenge did not change [11C]yohimbine VT compared to baseline due to a masked effect. The real inhibition effect of yohimbine challenge was revealed when BPND was calculated using VND(i) at 0.599 ml cm−3 (panel (E)). Correspondingly, the quantification of VT and BPND at steady-state in panels (F,G) are consistent with the parametric maps. The thin lines in (F) connect VT at baseline and challenge in the same animal, and the thick line shows the average of the population. VT was increased upon challenge with unlabelled yohimbine. The calculation of the BPND in (G) revealed a significant inhibition effect in response to challenge with unlabelled yohimbine (****P < 0.0001). The regional estimates of VT and BPND are listed for individual animals in Table 1. THAL thalamus, CP caudate putamen, HIPP hippocampus, PFC prefrontal cortex, SSC somatosensory cortex, MC motor cortex, HYP hypothalamus, CEREB cerebellum, OLF olfactory bulb.
The quantification of VT at the challenge condition revealed the masked effect reflected in the elevated value of fP , as illustrated both by the parametric images (Fig. 3D) and by regional VT estimates (Fig. 3F). To determine the real pharmacological displacement of [11C]yohimbine binding, we estimated the value of the binding potential, BPND, from the estimates of VT and the volumes of distribution of non-displaceable ligand, VND(i) and VND(b), respectively. As presented in Fig. 3E,G, calculations of BPND (by eq. 37 in Methods) revealed a significant decrease of BPND by the unlabeled ligand challenge. From the regionally differential estimates of BPND, we found the highest BPND in thalamus, caudate putamen, hippocampus and cortical regions, with cerebellum and olfactory bulb at the lowest binding. The estimates of BPND decreased significantly by 50–60% on average in response to the unlabeled ligand challenge, with a consistent reduction in all animals. The estimates of VT and BPND are listed in detail in Table 1.
Receptor Density
The values of BPND enabled us to determine the α2 adrenoceptor density in vivo. As presented in Fig. 4A, we estimated values of receptor density, Bmax, and receptor affinity (1/K D ) by means of Eadie-Hofstee plots. We calculated the bound quantity according to eq. 2, based on the information of the BPND and specific activity. We found the greatest receptor densities in thalamus, caudate putamen, and cortical areas, with the lowest densities in cerebellum and olfactory bulb as presented in Fig. 4B. The regional receptor densities are listed in detail in Table 2 and specific activity in Table 3.
Eadie-Hofstee Plot. Eadie-Hofstee Plot (eq. 1 in Methods) presented in (A) solves the receptor density (Bmax) and affinity (1/KD) from a linear relationship between the bound quantity and binding potentials. The bound quantity was calculated using specific activity and BPND (eq. 2 in Methods). Receptor densities was obtained from the Y-intercept and the half-saturation constant, KD, as the slope. Each bar represents the mean, the error bars correspond to the S.E.M. The highest densities of α2 adrenoceptors were found in thalamus, hippocampus, caudate putamen and prefrontal cortex, whereas lowest densities were found in cerebellum and olfactory bulb ((B) left). KD was at a similiar level in all examined regions at approximately 0.5 mM ((B) right) The regional receptor densities and KD are also listed in Table 2, and the specific activities that were used for calculation of bound quantity are listed in detail in Table 3. THAL thalamus, CP caudate putamen, HIPP hippocampus, PFC prefrontal cortex, SSC somatosensory cortex, MC motor cortex, HYP hypothalamus, CEREB cerebellum, OLF olfactory bulb.
Discussion
We characterized the binding profiles of [11C]yohimbine to α2 adrenoceptors in rat brain, using non-invasive PET. We quantified the binding potentials and regional receptor densities by means of competition analysis. The results of the study demonstrate a significant increase in fP in response to challenge with unlabeled yohimbine at the dose of 0.3 mg/kg. We argue that the elevation of fP was caused by displacement of radioligand from plasma proteins, which ultimately masked the effect of the pharmacological inhibition in the brain. The masked effect is evident from estimates of VT that reflect the total concentration in brain relative to the concentration in plasma. Furthermore, the challenge condition displayed consistently higher values of K1 in comparison to baseline, supporting the attribution of greater clearance of [11C]yohimbine and increased magnitude of fP due to decreased protein binding. When the magnitude of K1 is influenced by specific biological variables, including BBB permeability, cerebral blood flow (CBF) and fP , it is important to consider the changes of CBF a potential confound. In the challenge condition, the magnitude of K1 may be influenced by pharmacological action of yohimbine in the cardiovascular system. In humans and pigs, yohimbine is known to reduce CBF and increase blood pressure and heart rate14,23. Jakobsen et al.14 showed that CBF was unaffected by a low dose of yohimbine (0.07 mg/kg), while the higher dose (1.6 mg/kg) globally lowered CBF by 30%. In contrast, challenge with RX821002 had the opposite effect on CBF. In rats, yohimbine is known to raise blood pressure and heart rate24, while the effect on CBF is unknown.
The estimate of K1 was 0.2 ml/cm3/min, corresponding to a rate of escape of 0.167 s−1 for a vascular volume of 0.02 of 0.02 ml/cm3 25. Because there are two connected processes (escape from plasma protein binding and exchange across BBB), it is important to note that blood-brain transfer can be affected by the dynamics of protein binding (here symbolized by kPr,on and kPr,off). When the rate of relaxation from the plasma protein binding is greater than the exchange of tracer across the BBB, the loss of ligand bound to plasma proteins is likely to keep pace with the transfer of the tracer to brain tissue. If so, the transfer across BBB must depend on the original fraction of unbound ligand in plasma, including the unlabeled challenger. The kinetics of yohimbine relaxation from albumin is not known, but the relaxation of bilirubin from plasma proteins was estimated to occur at the rate of 0.6 s−1 26. If we assume that yohimbine leaves plasma protein binding at a rate similar to that of bilirubin, the free and bound yohimbine pools in brain vasculature are likely to maintain a constant ratio.
Another consideration is the perturbation of hepatic enzymatic clearance of [11C]yohimbine in the presence of unlabeled yohimbine at the challenge dose. However, inhibited elimination by peripheral organs is an unlikely explanation for the rise of the value of fP , when the in vitro assay eliminates effects of peripheral organs. The widespread expression of α2 adrenoceptors in the periphery may be another contributor to elevation of fP by displacement of radioligand from sites in heart, pancreas27, smooth muscles in blood vessels28,29, kidneys30, and platelets31.
Elevated fP may have influenced the findings by Jakobsen and colleagues14 of a lack of dose-dependent reduction of labeled yohimbine accumulation with unlabeled yohimbine challenge in pigs. Competition with a low dose (0.07 mg/kg) yohimbine reduced the value of VT of [11C]yohimbine in porcine brain by approximately 30%. However, pre-treatment with a 24-fold higher dose (1.7 mg/kg) failed to decrease VT further. Another selective ligand of α2 adrenoceptors, RX821002, was used to challenge [11C]yohimbine binding in porcine brain, where the low dose of 0.15 mg/kg caused greater decline of the value of VT than the higher dose of 0.7 mg/kg. Although values of fP were not determined in the study by Jakobsen and colleagues14, increase of the value of fP is a likely explanation, evident from findings in vitro that binding of yohimbine engages in dose-dependent competition with tritium-labeled yohimbine32 and with RX82100233.
In similar experiments by Smith et al.34, [11C]mirtazepin binding in porcine brain was sensitive to yohimbine competition in a dose-dependent manner, where challenge with 0.3 and 3.0 mg/kg yohimbine reduced [11C]mirtazepin binding by 23% and 43%, respectively. In contrast, challenge with RX821002 at dose of 0.1 mg/kg reduced [11C]mirtazepin binding by 35%, while a dose of 1 mg/kg failed to inhibit the binding further. It is unknown if the RX821002 challenge displaced plasma protein binding, but it is likely that RX821002 displaces binding to α2 adrenoceptor sites in peripheral organs that potentially contributes to a higher value of fP .
Pharmacological challenge by means of PET is a common test of the reversibility of radioligand binding. However, a number of studies have reported unaltered or increased occupancy of receptors after pharmacological challenge: A study of baboon brains showed that occupancy of 5-HT2A receptors by [18F]altanserin, administered as constant infusion, was unaltered in the presence of extracellular levels of serotonin, elevated with fenfluramine, a selective serotonin reuptake inhibitor35. The binding of [18F]altanserin is known to be sensitive to challenge with the 5-HT2A receptor antagonist, SR 46349 in baboons35 and also to non-radiolabeled altanserin in rodent brain36. Similarly, a PET study of neuroinflammation revealed increased [11C] PBR28 binding to the translocator protein (TSPO) in baboon brain in response to i.v. injection of 0.1 mg/kg LPS (lipopolysaccharide)37. The increases of binding at 1 and 4 hours post-administration were accompanied by increase of pro-inflammatory cytokines, causing the authors to propose that systemic inflammation by LPS can lead to increased TPSO expression. However, studies with infrared spectroscopy have shown that LPS binds to plasma albumin with the ratio 10:1, which changed the secondary structure of albumin38. Therefore, it cannot be excluded that increased [11C] PBR28 binding after LPS administration is confounded by increase of fP due to structural changes of albumin exerted by LPS. This possibility was confirmed recently by Hilmer et al.39 who showed that a low dose of LPS (0.1 ng/kg) administered i.v. to rhesus macaque monkeys increased [11C] PBR28 fP by 38%, as VT increased by 39%. Increased fP was also found to be elevated in response to pharmacological challenge in a study of α7 nicotinic acetylcholine receptors with [18F] DBT-1040, where the challenge with a dose of the antagonist ASEM at 1.24 mg/kg produced a two-fold increase of fP. The authors quantified VT/fP as an outcome parameter in order to determine the net effect of pharmacological blocking. Taken together, the examples illustrate that changes of fP are held to occur commonly in PET studies and knowledge of changes of fP will be necessary to determine the true effect of pharmacological challenge. Therefore, lack of inhibition or evidence of increased binding in future studies must raise the concern of changes to fP , measured with plasma ultrafiltration or equilibrium dialysis.
The direct relationship between increased fP and masked effects of challenge on VT must be interpreted with caution when fP and VT are determined in separate groups of animals, as in the present study. Another limitation of the Extended Inhibition Plot is the source of the baseline value of VND (estimated in a condition where fP remains constant). Ideally, estimation of two VND values requires at least three PET acquisitions. Instead, it may be possible to use a population-based value of VND(b) to estimate VND(i), as demonstrated in the present study. This approach requires homogeneity of the study populations, with the added limitation that biological variability affects the accuracy of the VND estimates. We note that the value of fP determined by plasma ultrafiltration is a steady-state estimate, whereas the exchange in vivo is a dynamic process, as discussed above, making it difficult to numerically extrapolate changes in fP to changes in VT. We suggest that fP should be quantified solely to determine whether criteria are met to employ the original plot, without the extension. If there is significant change of the magnitude of fP , the criteria may be met for the application of the Extended version of Inhibition Plot. As the plot operates with steady-state variables, the dynamic origin of fP will not influence the outcome.
The findings of the present study show that the α2 adrenoceptors are distributed throughout the brain. Regions with the greatest Bmax estimates included thalamus, hippocampus, and caudate-putamen, where the densities ranged between 2.4 and 2.5 pmol/cm3. The receptor density of caudate-putamen at 2.2 pmol/cm3 (corresponds to 220 fmol/mg protein) agrees with in vitro receptor binding results from rat caudate-putamen with [3H]rauwolscine, a stereoisomer of yohimbine that yielded an estimate of 197 fmol/mg protein41.
To enable comparison with other studies, we converted the values of Bmax per unit wet weight to values per unit dry weight of protein. Assuming that brain tissue contains 10% protein and dry weight therefore is one tenth of wet weight42, the range of values of Bmax in prefrontal cortex in this study is 216 fmol/mg protein, and the value of KD is 0.5 nM. To compare, we listed values of Bmax and KD from cortical areas of rat brain in Table 4. The table shows that comparison with results of in vitro binding assays is not simple, because of the great variability of findings of Bmax and KD among in vitro studies, depending on the method used.
The values of Bmax in prefrontal cortex in the present study are closest to the result of [3H]yohimbine binding assays by Rout et al.32 at 260 fmol/mg protein in the condition of no added magnesium in the assay. The authors demonstrated that [3H]yohimbine binding depends on many physiological factors such as pH, temperature, and Mg2+ concentration. We argue that the estimate by Rout et al.32 in absence of Mg2+ is closer to the physiological condition and therefore more directly comparable to the present results than the condition with 10 mM Mg2+ present, considering the physiological level of Mg2+ in brain tissue of 230 μM43. While the Bmax values are in range, the estimates of KD are 20-fold higher than the present estimates. The discrepant values of KD may relate to the method used to block non-specific binding. In the present study, the non-specific binding is computed as reflected in the value of VND, while the concentrations of competitors delivered to the binding sites in vitro often are in doubt because of the non-physiological delivery necessitated by the in vitro condition. Rout and colleagues used 100 μM noradrenaline to block non-specific binding, which may lead to an overestimation of KD because noradrenaline and [3H]yohimbine compete at the specific binding sites of α2 adrenoceptor.
In comparison to the results from [3H]yohimbine membrane binding studies by Brown et al.44,45, values of Bmax in the present study are 1.5-fold higher, while values of KD are 10-fold lower. The variability of estimates of Bmax and KD therefore may be attributed by differences in the methods of blocking neccesary to determine non-specific binding. Brown and colleagues used 10 μM phentolamine that is known to antagonize α1 and α2 adrenoceptors with higher selectivity to α1 adrenoceptor46. Thus, due to the affinity to α1 and α2 adrenoceptor, use of phentolamine may underestimate values of Bmax and overestimate values of KD, as α1 and some α2 adrenergic sites both may be blocked. The same blocking method was applied in the study by Boyajian et al.41 to block [3H]RX821002 binding to α2 adrenoceptor, the results of which are in agreement with the findings of Ribas and colleagues7 with estimates of [3H]RX821002 Bmax and KD in the same range. Estimates of Bmax generally are higher when determined with [11C]yohimbine than with [3H]RX821002, possibly due to differential affinities to α2 adrenoceptor subtypes. Yohimbine does not distinguish between the subtypes, whereas RX8201002 has a higher affinity to α2A and α2C than to α2B33. Therefore, use of RX8201002 may underestimate the desnity of α2 adrenoceptor sites. Altogether, more in vivo studies are essential to examine α2 adrenoceptors in health and disease when physiological variables strongly influence α2 adrenoceptor binding and are difficult to reproduce in vitro.
We estimated values of Bmax and KD with the Eadie-Hofstee plot from only two magnitudes of receptor occupancy, which may lower the accuracy. Ideally, more levels of occupancy yield more accurate regressions. However, due to the limited blood volume in rats, we did not perform additional PET acquisitions that would result in greater loss of blood that in turn would initiate compensatory physiological changes (increased heart rate and vasoconstriction) that affect radioligand delivery to the brain. The method presented here can be applied to larger mammals with greater blood volumes that enable estimates of Bmax and KD with higher accuracy. We acknowledge that receptor density and affinity estimated in vivo may not necessary reflect the ultimate estimates determined in vitro, because in vivo experiments often are performed in animals anesthetized with gas anesthetics known to elevate noradrenaline47.
In conclusion, we demonstrated the use of the Extended Inhibition Plot to quantify the binding potentials of [11C]yohimbine and density of α2 adrenoceptors in the living brain with PET. The method enables the analysis of future investigations of the noradrenergic and other transmission systems with wide distributions in brain, such as the nicotinic cholinergic system48.
Methods
Novel Quantitative Analysis of Specific Binding to Brain Receptors
We derived the present method from well-known principles of kinetics. We identified the following six steps to the determination of binding parameters of radioligands that achieve receptor occupancy. The binding parameters are constants in the fundamental equation that underlies the Eadie-Hofstee plot49,50,
where Bmax is the maximum binding capacity and 1/KD the affinity of the receptors. The variable B is the bound quantity of the ligand, and BPND is the binding potential of the radioligand at the specific degree of occupancy. To solve the equation of the Eadie-Hofstee plot for the two parameters, it is necessary to know the bound quantities of the ligand and the binding potentials in at least two conditions of different occupancy. The bound quantity is related to the binding potential by the relationship,
where M is the total mass of the ligand per unit volume of brain tissue, calculated from the known specific activity of the radioligand. The binding potential in turn is the ratio between the quantities of specifically (and hence displaceably) bound ligand and the unbound (and hence non-displaceable) ligand, equal to the ratio of the volumes of distribution of displaceable and non-displaceable ligand quantities,
where VT is the apparent volume of distribution of all tracer in the tissue, and VND is the apparent volume of distribution of unbound and hence non-displaceable tracer in the tissue, relative to the concentration in arterial plasma at steady-state.
Integral uptake equation
The first step is the kinetic analysis of tracer accumulation. The simplest mathematical description of the pharmacokinetic behavior of radiotracers in brain is the one-tissue compartment model (Fig. 1A) that assumes approach to a secular steady-state across the blood-brain barrier,
and
where the total tracer quantities in the vascular system (both free and bound to plasma proteins), m1, are distributed in the vascular volume, V0, and ca(t) reflects the concentration in that volume. Although, m1 reflects the total quantity of ligand in plasma, only the free amount is exchangable across the BBB (Fig. 1A).
The term m2 refers to tracer in brain tissue that reflects the clearance K1 from the circulation and the fractional clearance k′2 from the tissue. Linearized solutions yield the constants K1 and \({k}_{2}^{{\prime} }\), as previously summarized by Nahimi et al.12 and Phan et al.16. Briefly, at steady-state, VT equals the ratio \({K}_{1}/{k}_{2}^{{\prime} }\) where K1 is a function of blood flow, F, free plasma fraction, fP , and the permeability- surface area of the vascular bed, PS,
and \({k}_{2}^{{\prime} }\) is,
where k2 is the rate of efflux from VND, and BPND is the binding potential. Therefore, at steady-state, the values of K1 (eq. 6) and \({k}_{2}^{{\prime} }\) (eq. 7) yield,
At steady-state, the K1/\({k}_{2}^{{\prime} }\) ratio defines the total volume of distribution in tissue (VT) as determined by the total concentration in brain relative to plasma,
Equations 4 and 5 together define the exchange of tracer in the brain tissue as a whole,
from which the total quantity of tracer, m, is the sum of the solutions to the differential equations,
As m2, is unknown, eq. 11 is solved by substitution of the expression, m(1 − m1/m),
but when steady-state is approached, the m1/m ratio becomes negligible and eq. 12 reduces to,
Volumes of distribution from linearized graphical analysis of tracer kinetics
The second step is the choice of any one of several graphical solutions to eq. 13 based on dynamic measurements of any two of three kinetic variables that include the apparent volume of distribution, Vapp, [ml cm−3]
the apparent clearance of radioligand from plasma to brain, Kapp, [ml cm−3 min−1],
and the apparent residence time in the brain [min],
Six linearizations previously derived to obtain estimates of K1 and \({k}_{2}^{{\prime} }\) from steady-state solutions of eq. 13 used combinations of two out of the three dynamic variables (eqs 14, 15 and 16), including two regressions with negative slopes (‘N1’ and ‘N2’), and four regressions with positive slopes (‘P1-P4’). The ‘N1’ graph plotted the apparent clearance as a function of the apparent volume of distribution as derived by Gjedde et al.51 and Cumming et al.52 by dividing eq. 13 by \({\int }_{0}^{T}\,{c}_{{\rm{a}}}(t)dt\),
where K1 and \({k}_{2}^{{\prime} }\) represent y-intercept and slope, respectively. The ‘N2’ plot was derived by Gjedde et al.53 as the mirror of ‘N1’,
where VT is the y-intercept and \({k}_{2}^{{\prime} }\) is the reciprocal value of the slope. Division of eq. 13 by m(T) and k2′ yields the ‘P1’ plot with a positive slope of the linear relationship between the reciprocal value of Kapp(T) and Θ(T)51,
where VT is the reciprocal value of the slope, and K1 is the reciprocal value of the y-intercept. Logan and colleagues54 derived the ‘P2’ plot as the mirror of ‘P1’,
where VT is the slope of the line. The ‘P3’ plot was introduced by Reith et al.55 by division of eq. 13 with \({\int }_{0}^{T}\,m(t)\,dt\),
where K1 is the slope and \({k}_{2}^{{\prime} }\) the y-intercept. Nahimi et al.12 described the mirror version, ‘P4’,
where K1 is the reciprocal of the slope and VT is the reciprocal of the y-intercept. All six plots yielded similar estimates of K1, \({k}_{2}^{{\prime} }\), and VT when the parameters were estimated in the same time frames at steady-state. We applied all six plots because they have different sensitivities to linearity. We note that the Logan plot (‘P2’) and it’s mirror version, ‘P1’ plot, readily but deceptively approached linear relationships that remained linear throughout acquisition time, whereas the alternative plots (‘N1’, ‘N2’, ‘P3’, ‘P4’) lost linearity when steady-state was disrupted (Supplemental Fig. S2). Because the value of VT strictly is defined only at steady-state and because the later analysis steps are sensitive to the accuracy of values of VT, we applied all six plots to know when steady-state is present. The time frames of steady-state were objectively chosen based on the goodness of fit from iterative analysis (as described in details in Data Analysis).
Reference Volume of Distribution from Inhibition Plots
The third step is to estimate the volume of distribution of non-displaceable tracer, VND, most simply from a brain region with no specific binding of the ligand. If no such region exists, VND can be estimated by pharmacological blocking of specific binding, graphically solved with one of three plots, the so-called Inhibition, Saturation, and Occupancy plots. The Saturation Plot was first derived by Lassen and colleagues56,
where ΔVT, the difference of distribution volumes between baseline and response to pharmacological challenge, is plotted as a function of the volume of distribution at baseline, VT(b). The symbol s denotes the degree of saturation as the fraction of occupied receptors, and VND is the estimate of the y-intercept. Cunningham et al.57 derived the Occupancy Plot as the mirror of the Saturation plot,
while the Inhibition Plot previously was introduced by Gjedde and Wong58 and Gjedde et al.53, with the distribution volume in the challenge condition VT(i) plotted directly as a function of VT(b),
where VND is the intercept of the Inhibition Plot with the line of identity.
The three plots were derived from a common expression of the relative receptor availability at inhibition, BPND(i), and baseline, BPND(b),
where 1 − s denotes the fraction of available receptors in the presence of a competitor. The BPND equals,
and
where VND(i) and VND(b) denote the distribution volumes of non-displaceable tracer at inhibition and baseline, respectively. When the volumes are constant at the two conditions, (VND(i) = VND(b) = VND), eqs 26, 27 and 28 yield the expression of relative receptor availability in terms of volumes of distribution,
where rearrangement of eq. 29 yields the Inhibition Plot (eq. 25), Saturation (eq. 23), and Occupancy (eq. 24) plots.
A requirement of application of any plot is that fP , the free fraction of radioligand in plasma, must remain unchanged at baseline and challenge. At steady-state, the VND value is the ratio of the total concentrations of radioligand in blood, Ca, and brain, CND,
where VD is the volume in which CND is the concentration. The concentrations Ca and CND also are the concentrations of freely dissolved ligands in plasma CFP and tissue water, CFT,
and
such that the combination of eqs 30, 31 and 32 yields,
where VND is a product of a physical volume, V D , and two unitless ratios. The fP to fND ratio depends on the non-specific binding in plasma and brain tissue, while the CFT to CFP ratio depends on properties of the blood-brain barrier (BBB). Assuming that the radioligand enters the brain tissue by passive diffusion, and free concentrations at steady-state the of ligand across BBB are equal, eq. 33 reduces to,
such that a rise of fP would change the magnitude of VND.
Variable reference volumes of distribution from Extended Inhibition Plot
The fourth step is the correction for a change of the reference volume of distribution when plasma free fractions, fP , have changed in response to pharmacologcial challenge. In this case, eq. 29 can be applied in its unreduced form,
where VND(b) and VND(i) are the magnitudes at baseline and at inhibition. Isolation of VT(i) in eq. 35 yields the Extended Inhibition Plot,
takes the changes of fP and VND into account. The value of VND(b) must be known to solve for VND(i) in eq. 36, for example with reference to a pharmacological challenge that affects the receptor binding without altering fP , by modulating the release or depletion of endogenous transmitter. In contrast, challenge with a unlabeled ligand may raise fP , when the challenge with unlabeled ligand displaces ligand bound to plasma proteins. Challenge with unlabeled yohimbine may reduce the protein binding of the radioligand when as much as 82% of labeled yohimbine is bound to plasma proteins22.
Calculation of binding potentials from total and reference volumes
The fifth step is the calculation of binding potentials from volumes of distribution. The binding potential, BPND, is the ratio of specifically bound to non-displaceable ligand quantities in the tissue20,21. The BPND is determined from the total volume of distribution in the tissue, VT, and the volume of distribution of non-displaceable ligand, VND, determined at the respective conditions of variable occupancy,
where VND is obtained from a reference region devoid of specific receptors. In the case of yohimbine, α2 adrenoceptors are widely distributed in the brain, with no suitable reference region.
Determination of B max and K D estimates from Eadie-Hofstee Plot
The sixth and final step was the graphical solution to the Eadie-Hofstee Plot of eq. (1) (Eadie 1952, Hofstee 1952), where B is the bound quantity and BPND is the binding potential of ligands. We calculated the bound quantity from the relationship described by eq. 2.
Animals
Animal experiments were conducted according to the protocol approved by the Danish Animal Experiments Inspectorate in compliance with the law regulated by the Danish Ministry of Food, Agriculture and Fisheries. Five female Sprague Dawley rats (weighing 250–300 g) were housed two per cage with access to food and water ad libitum under 12/12 hours light/dark cycle conditions. The animals had two consecutive 90-minute PET acquisitions on the same day. Anesthesia was induced in a chamber with 5% isoflurane, maintained by mask with 2% isoflurane until the end of PET recording. To raise the delivery of yohimbine to the brain by limiting the reaction of yohimbine with p-glycoprotein at the BBB59, we gave animals cyclosporine i.v. 50 mg/kg 30 minutes before the baseline PET. With a half-life longer than 10 hours at doses exceeding 30 mg/kg60, only one dose was needed. We administered unlabeled yohimbine 5–10 min before the second acquisition at an IV dose of 0.3 mg/kg.
PET acquisitions and image processing
Animals were imaged in a tomograph designed for rodents (microPET R4, CTI Concorde Microsystems, Knoxville, TN, USA), with a spatial resolution at the center of the field of view at 3.69 mm3 61. PET images were processed with MINC software of McConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University. We reconstructed the photon attenuation correction of dynamic recordings by 3D-filtered back projection, resulting in a 128 × 128 × 63 matrix. Summed emission recordings were coregistered to a digital MRI atlas of the rat brain, using the program Register of MINC software. The dynamic emission recordings were resampled to the same 3D-space of the MRI rat brain atlas. We used masks of volumes of interest (VOIs) developed by Schiffer et al.62, which we resampled to MRI space. The masks were then used to extract time-activity curves from the resampled dynamic data sets.
Data analysis
We developed the user-friendly, open-source graphical user interface Kinetic Windows (KiWi) in MATLAB to aid robust and effective kinetic analysis. KiWi enables users to import time-activity curves, to plot dynamic PET parameters as functions of time (eqs 14–16), and ultimately to simultaneously plot data with the N1–N2 or P1–P4 plots. The uptake phase with the optimal dynamic data fit is objectively chosen in KiWi, identified as the frames with the r-squared precision closest to unity. The software is available on Github63 and MATLAB file exchange64. Time-activity curves for each region were analyzed together with the corresponding plasma activity curve as input. Here, we chose estimates of VT obtained graphically from N2 plot (eq. 18) derived by Gjedde et al.53. Parametric maps of BPND were constructed by means of eqs 27 and 28.
Plasma Ultrafiltration
To test the change of fP incurred by unlabeled yohimbine challenge relative to baseline, plasma ultrafiltration was performed as previously described by Gandelman et al.65 and plasma free fractions quantified both ex vivo and in vitro (the method is illustrated in Fig. 2D left). In the ex vivo experiment, a separate group of six female Sprague Dawley rats were subjected to plasma ultrafiltration and treated identically to animals that underwent PET acquisition. We administered cyclosporine (50 mg/kg) i.v., and we sampled arterial blood by catheter in the femoral artery. Samples from the baseline condition were collected 30 min after the cyclosporine treatment. To obtain blood from the unlabeled ligand challenge condition, we administered unlabeled yohimbine (0.3 mg/kg i.v.) and collected blood samples after 30 min. We centrifuged the blood samples in heparinized tubes for 20 min at 4 °C to generate plasma and stored the samples at −50 °C.
In the in vitro experiments, blood was drawn and yohimbine or amphetamine were added to the plasma samples later. The amounts of yohimbine and amphetamine added to the samples were calculated from the linear relationship between blood volume and body weight in rats66. The calculation assumed that plasma comprises 50% of the blood volume in rats and that the drug initially is distributed throughout plasma. The calculated amounts of drug were added to individual plasma samples. Thus 5 μg corresponded to a low yohimbine dose of 0.3 mg/kg and 25 μg to a higher dose of 1.5 mg/kg.
To measure fP , we used the Centrifree centrifugal filter device (Millipore, Bedford, MA) with a molecular cutoff of 30 kDa for all samples. This pore size was chosen to ensure filtration of the yohimbine fraction bound to albumin with a molecular weight of approximately 65 kD in rats67. On the day of fP determination, the plasma samples were thawed in room temperature in 20 min. Each sample unit of 1000 μl plasma was spiked with 50 μl [11C]yohimbine. After 10 minutes incubation at room temperature, aliquots of 50 μl of this solution were used to measure the total activity (unfiltered plasma). For triplicate measurements of the filtered plasma, the remaining volume was divided into three ultrafiltration devices and centrifuged for 20 min using a centrifuge with a fixed angle rotor at 1000 g. After filtration, we removed aliquots of 50 μl to assess the activity in protein-free plasma. The activity of filtered plasma was determined in triplicates. All samples were counted in a gamma device (Packard Cobra Gamma Counter, Model D5003). Non-specific binding of the tracer to the ultrafiltration device was recovered by performing the same procedure on a phosphate-buffered solution. The correction factor, r, was determined as the ratio of the activity in the phosphate buffer before filtration, Abuffer(total), to the filtered buffer, Abuffer(ultrafiltrate),
from which the plasma-free fraction, fP , was calculated as the ratio of the activity of the filtered plasma, Aplasma(ultrafiltrate), to the unfiltered plasma, Aplama(total), multiplied by the correction factor, r, for recovery,
Statistics
To determine fP elevation in response to unlabeled yohimbine challenge, we applied a non-parametric two-tailed test for the ex vivo assay. For the in vitro assay, we applied two-way ANOVA followed by Tukey’s post-hoc analysis. To examine whether yohimbine challenge changed VT and BPND compared to baseline, two-way ANOVA followed and Tukey’s post-hoc analysis was applied. For all tests, a probability of less than 0.05 was considered significant. Statistical analyses were carried out in GraphPad Prism v7.
Change history
16 April 2018
A correction to this article has been published and is linked from the HTML and PDF versions of this paper. The error has been fixed in the paper.
References
Braak, H. & Del Tredici, K. The pathological process underlying alzheimer’s disease in individuals under thirty. Acta neuropathologica 121, 171–181 (2011).
Sitte, H. H. et al. Dopamine and noradrenaline, but not serotonin, in the human claustrum are greatly reduced in patients with parkinson’s disease: possible functional implications. Eur. J. Neurosci. 45, 192–197 (2017).
Delgado, P. & Moreno, F. Antidepressants and the brain. Int. Clin. Psychopharmacol. 14, S9–S16 (1999).
Gonzalez-Maeso, J., Rodriguez-Puertas, R., Meana, J., Garcia-Sevilla, J. & Guimon, J. Neurotransmitter receptor-mediated activation of g-proteins in brains of suicide victims with mood disorders: selective supersensitivity of [alpha] 2A-adrenoceptors. Mol. psychiatry 7, 755 (2002).
Garca-Sevilla, J. A. et al. Up-regulation of immunolabeled α2A-adrenoceptors, gi coupling proteins, and regulatory receptor kinases in the prefrontal cortex of depressed suicides. J. neurochemistry 72, 282–291 (1999).
Meana, J. J., Barturen, F. & Garcia-Sevilla, J. A. α2-adrenoceptors in the brain of suicide victims: increased receptor density associated with major depression. Biol. psychiatry 31, 471–490 (1992).
Ribas, C., Miralles, A., Busquets, X. & Garca-Sevilla, J. A. Brain α2-adrenoceptors in monoamine-depleted rats: increased receptor density, g coupling proteins, receptor turnover and receptor mrna. Br. journal pharmacology 132, 1467–1476 (2001).
Wiste, A. K., Arango, V., Ellis, S. P., Mann, J. J. & Underwood, M. D. Norepinephrine and serotonin imbalance in the locus coeruleus in bipolar disorder. Bipolar disorders 10, 349–359 (2008).
Yatham, L. N. et al. A positron emission tomography study of norepinephrine transporter occupancy and its correlation with symptom response in depressed patients treated with quetiapine xr. Int. J. Neuropsychopharmacol. (2017).
Hesse, S. et al. The association between in vivo central noradrenaline transporter availability and trait impulsivity. Psychiatry Res. Neuroimaging 267, 9–14 (2017).
Sara, S. J. & Bouret, S. Orienting and reorienting: the locus coeruleus mediates cognition through arousal. Neuron 76, 130–141 (2012).
Nahimi, A. et al. Mapping α2 adrenoceptors of the human brain with 11C-yohimbine. J. Nucl. Medicine 56, 392–398 (2015).
Landau, A. M., Doudet, D. J. & Jakobsen, S. Amphetamine challenge decreases yohimbine binding to α2 adrenoceptors in landrace pig brain. Psychopharmacol 222, 155–163 (2012).
Jakobsen, S. et al. Detection of α2-adrenergic receptors in brain of living pig with 11C-yohimbine. J. Nucl. Medicine 47, 2008–2015 (2006).
Thomsen, M. B. et al. Neonatal domoic acid alters in vivo binding of [11C] yohimbine to α2-adrenoceptors in adult rat brain. Psychopharmacol 233, 3779–3785 (2016).
Phan, J.-A. et al. Quantification of [11C] yohimbine binding to α2 adrenoceptors in rat brain in vivo. J. Cereb. Blood Flow & Metab 35, 501–511 (2015).
Landau, A. M. et al. Decreased in vivo α2 adrenoceptor binding in the flinders sensitive line rat model of depression. Neuropharmacol 91, 97–102 (2015).
Muller, P. Y. & Milton, M. N. The determination and interpretation of the therapeutic index in drug development. Nat. reviews. Drug discovery 11, 751 (2012).
Pisani, V. et al. Increased blood-cerebrospinal fluid transfer of albumin in advanced parkinson’s disease. J. neuroinflammation 9, 188 (2012).
Gjedde, A., Wong, D. F., Rosa-Neto, P. & Cumming, P. Mapping neuroreceptors at work: on the definition and interpretation of binding potentials after 20 years of progress. Int. review neurobiology 63, 1–20 (2005).
Innis, R. B. et al. Consensus nomenclature for in vivo imaging of reversibly binding radioligands. J. Cereb. Blood Flow & Metab. 27, 1533–1539 (2007).
Berlan, M., Verge, R. L., Galitzky, J. & Corre, P. L. α2-adrenoceptor antagonist potencies of two hydroxylated metabolites of yohimbine. Br. journal pharmacology 108, 927–932 (1993).
Cameron, O. G., Zubieta, J. K., Grunhaus, L. & Minoshima, S. Effects of yohimbine on cerebral blood flow, symptoms, and physiological functions in humans. Psychosom. Medicine 62, 549–559 (2000).
Zaretsky, D. V., Zaretskaia, M. V., DiMicco, J. A. & Rusyniak, D. E. Yohimbine is a 5-HT 1A agonist in rats in doses exceeding 1 mg/kg. Neurosci. letters 606, 215–219 (2015).
Duong, T. Q. & Kim, S.-G. In vivo MR measurements of regional arterial and venous blood volume fractions in intact rat brain. Magn. resonance medicine 43, 393–402 (2000).
Zucker, S. D., Goessling, W. & Gollan, J. L. Kinetics of bilirubin transfer between serum albumin and membrane vesicles insight into the mechanism of organic anion delivery to the hepatocyte plasma membrane. J. Biol. Chem. 270, 1074–1081 (1995).
Saito, M., Saitoh, T. & Inoue, S. Alpha 2-adrenergic modulation of pancreatic glucagon secretion in rats. Physiol. & behavior 51, 1165–1171 (1992).
MacMillan, L. B., Hein, L., Smith, M. S., Piascik, M. T. & Limbird, L. E. Central hypotensive effects of the alpha2a-adrenergic receptor subtype. Science 273, 801 (1996).
Gavin, K., Colgan, M.-P., Moore, D., Shanik, G. & Docherty, J. α2C-adrenoceptors mediate contractile responses to noradrenaline in the human saphenous vein. Naunyn-Schmiedeberg’s archives of pharmacology 355, 406–411 (1997).
Hein, L., Altman, J. D. & Kobilka, B. K. Two functionally distinct alpha2-adrenergic receptors regulate sympathetic neurotransmission. Nat. 402, 181 (1999).
Požgajová, M., Sachs, U. J., Hein, L. & Nieswandt, B. Reduced thrombus stability in mice lacking the α2A-adrenergic receptor. Blood 108, 510–514 (2006).
Rouot, B., Quennedey, M. & Schwartz, J. Characteristics of the [3H]-yohimbine binding on rat brain α2. Naunyn-Schmiedeberg’s archives of pharmacology 321, 253–259 (1982).
O’Rourke, M., Blaxall, H., Iversen, L. & Bylund, D. Characterization of [3H]RX821002 binding to alpha-2 adrenergic receptor subtypes. J. Pharmacol. Exp. Ther. 268, 1362–1367 (1994).
Smith, D. F. et al. Inhibition of [11C]mirtazapine binding by α2-adrenoceptor antagonists studied by positron emission tomography in living porcine brain. Synap 59, 463–471 (2006).
Staley, J. K. et al. Comparison of [18F]altanserin and [18F]deuteroaltanserin for PET imaging of serotonin 2a receptors in baboon brain: pharmacological studies. Nucl. medicine biology 28, 271–279 (2001).
Riss, P. J. et al. Validation and quantification of [18F]altanserin binding in the rat brain using blood input and reference tissue modeling. J. Cereb. Blood Flow & Metab. 31, 2334–2342 (2011).
Hannestad, J. et al. Endotoxin-induced systemic inflammation activates microglia: [11C]PBR28 positron emission tomography in nonhuman primates. Neuroimage 63, 232–239 (2012).
Jürgens, G. et al. Investigation into the interaction of recombinant human serum albumin with Re-lipopolysaccharide and lipid a. J. endotoxin research 8, 115–126 (2002).
Hillmer, A. T. et al. Microglial depletion and activation: A [11C]PBR28 PET study in nonhuman primates. EJNMMI research 7, 59 (2017).
Hillmer, A. T. et al. PET imaging evaluation of [18F]DBT-10, a novel radioligand specific to α7 nicotinic acetylcholine receptors, in nonhuman primates. Eur. journal nuclear medicine molecular imaging 43, 537–547 (2016).
Boyajian, C., Loughlin, S. & Leslie, F. Anatomical evidence for alpha-2 adrenoceptor heterogeneity: differential autoradiographic distributions of [3H]rauwolscine and [3H]idazoxan in rat brain. J. Pharmacol. Exp. Ther. 241, 1079–1091 (1987).
Ericsson, C., Peredo, I. & Nistér, M. Optimized protein extraction from cryopreserved brain tissue samples. Acta Oncol. 46, 10–20 (2007).
Zhang, Z., Zhao, L., Lin, Y., Yu, P. & Mao, L. Online electrochemical measurements of ca2+ and mg2+ in rat brain based on divalent cation enhancement toward electrocatalytic nadh oxidation. Anal. chemistry 82, 9885–9891 (2010).
Brown, C., MacKinnon, A., McGrath, J., Spedding, M. & Kilpatrick, A. α2-adrenoceptor subtypes and imidazoline-like binding sites in the rat brain. Br. journal pharmacology 99, 803–809 (1990).
Brown, C., MacKinnon, A., McGrath, J., Spedding, M. & Kilpatrick, A. Heterogeneity of α2-adrenoceptors in rat cortex but not human platelets can be defined by 8-OH-DPAT, RU24969 and methysergide. Br. journal pharmacology 99, 481–486 (1990).
Hong, S.-S. et al. Bioisosteric phentolamine analogs as potent α-adrenergic antagonists. Bioorganic & medicinal chemistry letters 15, 4691–4695 (2005).
Anzawa, N. et al. Increased noradrenaline release from rat preoptic area during and after sevoflurane and isoflurane anesthesia. Can. J. Anesth. canadien d’anesthésie 48, 462–465 (2001).
Wong, D. F. et al. Human brain imaging of α7 nAChR with [18F]ASEM: a new PET radiotracer for neuropsychiatry and determination of drug occupancy. Mol. Imaging Biol. 16, 730–738 (2014).
Eadie, G. On the evaluation of the constants vm and km in enzyme reactions. Science 116, 688 (1952).
Hofstee, B. On the evaluation of the constants vm and km in enzyme reactions. S cience 116, 329–331 (1952).
Gjedde, A. Calculation of cerebral glucose phosphorylation from brain uptake of glucose analogs in vivo: a re-examination. Brain Res. Rev. 4, 237–274 (1982).
Cumming, P., Léger, G. C., Kuwabara, H. & Gjedde, A. Pharmacokinetics of plasma 6-[18F] fluoro-L-3, 4-dihydroxyphenylalanine ([18F]F-DOPA) in humans. J. Cereb. Blood Flow & Metab. 13, 668–675 (1993).
Gjedde, A., Gee, A. & Smith, D. Basic cns drug transport and binding kinetics in vivo. Blood-brain Barrier Drug Deliv To CNS 225–242 (2000).
Logan, J. et al. Graphical analysis of reversible radioligand binding from time-activity measurements applied to [N-11C-methyl]-(-)-cocaine PET studies in human subjects. J. Cereb. Blood Flow & Metab. 10, 740–747 (1990).
Reith, J. et al. Blood—brain transfer and metabolism of 6-[18F] fluoro-L-DOPA in rat. J. Cereb. Blood Flow & Metab. 10, 707–719 (1990).
Lassen, N. et al. Benzodiazepine receptor quantification in vivo in humans using [11C] flumazenil and PET: application of the steady-state principle. J. Cereb. Blood Flow & Metab. 15, 152–165 (1995).
Cunningham, V. J., Rabiner, E. A., Slifstein, M., Laruelle, M. & Gunn, R. N. Measuring drug occupancy in the absence of a reference region: the Lassen plot re-visited. J. Cereb. Blood Flow & Metab. 30, 46–50 (2010).
Gjedde, A. & Wong, D. F. Receptor occupancy in absence of reference region. Neuroimage 11, 6, S48 (2000).
Pearce, H. et al. Essential features of the P-glycoprotein pharmacophore as defined by a series of reserpine analogs that modulate multidrug resistance. Proc. Natl. Acad. Sci. 86, 5128–5132 (1989).
Tanaka, C., Kawai, R. & Rowland, M. Dose-dependent pharmacokinetics of cyclosporin A in rats: events in tissues. Drug metabolism disposition 28, 582–589 (2000).
Laforest, R., Longford, D., Siegel, S., Newport, D. F. & Yap, J. Performance evaluation of the microPET®-focus-f120. IEEE Transactions on Nucl. Sci 54, 42–49 (2007).
Schiffer, W. K. et al. Serial microPET measures of the metabolic reaction to a microdialysis probe implant. J. neuroscience methods 155, 272–284 (2006).
Phan, J.-A. Kiwi kinetic windows. https://github.com/jennyannphan/KiWi (2017).
Phan, J.-A. Kiwi kinetic windows. https://se.mathworks.com/matlabcentral/fileexchange/64128-jennyannphan-kiwi (2017).
Gandelman, M. S., Baldwin, R. M., Zoghbi, S. S., Zea-Ponce, Y. & Innis, R. B. Evaluation of ultrafiltration for the free-fraction determination of single photon emission computed tomography (spect) radiotracers: β-CIT, IBF, and iomazenil. J. pharmaceutical sciences 83, 1014–1019 (1994).
Lee, H. & Blaufox, M. Blood volume in the rat. J. Nucl. Medicine 26, 72–76 (1985).
Charlwood, P. Ultracentrifugal studies of rat, rabbit and guinea-pig serum albumins. Biochem. J. 78, 163 (1961).
Ribas, C., Miralles, A. & Garca-Sevilla, J. A. Acceleration by chronic treatment with clorgyline of the turnover of brain α2-adrenoceptors in normotensive but not in spontaneously hypertensive rats. Br. journal pharmacology 110, 99–106 (1993).
Acknowledgements
The authors thank Professor Doris Doudet for constructive scientific discussions and suggestions. We thank Mette Simonsen for technical assistance with PET acquisitions and blood sampling. Jenny-Ann Phan is a recipient of an MD-PhD fellowship from Aarhus University. The experiments were funded by Department of Nuclear Medicine and PET Centre, Aarhus University Hospital and by grants from the Council of Independent Research, Denmark. All authors declare no conflicts of interest, including relevant financial interests, activities, relationships, and affiliations. DFW acknowledges PHS NIH grant 2 R01 MH107197.
Author information
Authors and Affiliations
Contributions
J.A.P. designed, planned, and performed the experiments, analyzed data, and wrote scripts for the graphical user interface in MATLAB. A.M.L. contributed to study design, planning and assistance with image quantification. S.J. was responsible of radioligand production. D.F.W contributed to the content of the paper and interpretation of results of the study. A.G. conceived the study, designed the kinetic analyses, and supervised the work throughout the study. J.A.P. and A.G. wrote the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Phan, JA., Landau, A.M., Jakobsen, S. et al. Radioligand binding analysis of α2 adrenoceptors with [11C]yohimbine in brain in vivo: Extended Inhibition Plot correction for plasma protein binding. Sci Rep 7, 15979 (2017). https://doi.org/10.1038/s41598-017-16020-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16020-1
This article is cited by
-
Quantitative Rodent Brain Receptor Imaging
Molecular Imaging and Biology (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.