Abstract
As the “Asian Water Tower”, the Tibetan Plateau (TP) provides water resources for more than 1.4 billion people, but suffers from climatic and environmental changes, followed by the changes in water balance components. We used state-of-the-art satellite-based products to estimate spatial and temporal variations and trends in annual precipitation, evapotranspiration and total water storage change across eastern TP, which were then used to reconstruct an annual runoff variability series for 2003–2014. The basin-scale reconstructed streamflow variability matched well with gauge observations for five large rivers. Annual runoff increased strongly in dry part because of increases in precipitation, but decreased in wet part because of decreases in precipitation, aggravated by noticeable increases in evapotranspiration in the north of wet part. Although precipitation primarily governed temporal-spatial pattern of runoff, total water storage change contributed greatly to runoff variation in regions with wide-spread permanent snow/ice or permafrost. Our study indicates that the contrasting runoff trends between the dry and wet parts of eastern TP requires a change in water security strategy, and attention should be paid to the negative water resources impacts detected for southwestern part which has undergone vast glacier retreat and decreasing precipitation.
Similar content being viewed by others

Introduction
As the highest plateau in the world, the TP plays an important role in the climate and hydrology of eastern and southern Asia1,2,3. Many large rivers, including Yangtze, Yellow, Brahmaputra, Indus, Ganges, Mekong and Salween rivers, originate from the TP and adjacent mountains, and these rivers sustain the lives of more than 1.4 billion people4,5. Over the past decades, the TP has been experiencing significant climatic and environmental changes, such as warming6, wetting7, drying3, dimming3, greening8, glacier retreat9, wind stilling10,11, permafrost degradation12, desertification13 and land use change14. These changes are characterized by pronounced regional disparities. Over the last 30–35 years southern and eastern TP which are impacted by South and East Asian monsoon have received decreased precipitation, whereas in contrast central and northern TP have experienced increased convective precipitation due to warming3. Glaciers in western TP, which are under the dominance of westerlies, show positive mass balance, while the glaciers in other parts of the TP show extensive shrinkage and negative mass balance9. Understanding the water resources availability response to these changes is fundamentally important for food security and regional sustainable development2,14,15.
Although hydrological models are very useful in understanding climatic and anthropogenic impacts on runoff (Q)2,16,17, it is not easy to model inter-annual variation of Q over the TP because of its unique climatic, topographic and hydrological features. Adapting hydrological models to simulate hydroclimate processes over the TP is challenging given that some hydrological processes (such as snow melt and refreeze, glacier retreat, permafrost degradation, soil moisture movement) are still poorly understood18,19,20,21. This is compounded by lack of streamflow gauges and meteorological stations (especially over high altitudes) to develop understanding of the key processes22,23,24, to elucidate hydroclimate changes over time, and to parameterize hydrological models.
We show that spatial and temporal variations of Q in eastern TP, where four large rivers (Yangtze, Yellow, Mekong, and Salween) originate from, can be reasonably estimated from individual water balance components derived solely from state-of-the-art satellite-based products (precipitation (P)25, actual evapotranspiration (ET)26,27,28,29 and change in total water storage (ΔTWS)30). We then analyze predominant features of the hydroclimate, and explain trends and variances in the water balance components, and uncertainties involved in the modelled Q.
Results and Discussion
Model validation
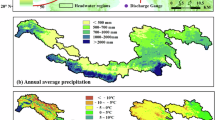
We first compared the modelled (estimated from satellite products of P, ET and ΔTWS) and observed annual Q anomaly series from 2003 (Oct 2002 to Sep 2003) to 2014 (Oct 2013 to Sep 2014) and the linear trends in the 12 years of modelled and observed Q anomaly series at basin scale (Fig. 1). Mean values over 2004–2009 were used as reference for anomalies calculation, which is consistent with the mascon TWS product30. The modelled or satellite-data reconstructed annual Q anomaly series from the five basins agreed reasonably well with the observed annual Q anomaly series with linear correlation coefficients of 0.73 to 0.80. Furthermore, trends in the modelled and observed annual Q anomaly series were in the same directions though their magnitudes were noticeably different at three gauges. Trends in the observed Q at the five gauges varied within −14.8–+7.3 mm year−2, while trends in the reconstructed annual Q had a narrower range of −6.4–+4.6 mm year−2, with uncertainties of about 0.3–1.3 mm year−2.
Comparison of observed and estimated Q anomaly time-series at the five gauges. Error bars are standard error generated from the four ET products. Luning basin is short of one year due to data missing. Blue lines are the river network. Red dots are the five streamflow gauges. Two gauges are for the Yangtze River (purple represents the Yangtze River basin) and one gauge is for each of the other three rivers (blue denotes the Yellow river basin, yellow represents the Mekong river basin, and orange the Salween river basin). Coloured area is the extent of eastern TP in this study. The map was generated using Google Earth (v 7.1.7.2606, https://www.google.com/earth/), Image Landsat/Copernicus.
Explaining the variation in annual Q
Figure 2 shows that proportion of variance in annual Q can be explained by the three water balance components P, ET and ΔTWS. In practically the entire region, except for small parts in north and south-west, P explained more than 70% of variance in annual Q. ET had a relatively minor role in controlling the inter-annual variability of Q, whereas ΔTWS significantly enhanced the explained variance of annual Q in north and south-west. This is partly because ET was more stable than ΔTWS. Our results indicate that ET variance accounted for 6.1–7.6% of P variance, but this number rose to 13.1–16.4% for ΔTWS variance. Another reason was that ΔTWS reflected permafrost-induced hydrological changes in northern part31,32,33 and melting water amount from permanent snow/ice in southwestern part34,35.
Contributions of water balance components to Q annual variation for eastern TP region shown in Fig. 1 for 2003–2014. (a), the coefficient of determination (R2) when only P is used to estimate Q variation. (b), additional R2 when ET together with P is used for estimating Q variation. (c), additional R2 when ΔTWS together with P is used for estimating Q variation. The maps were generated using ENVI (v 4.5, https://www.harris.com/solution/envi) © 2017 Harris Corporation.
Spatial pattern of trends
We further demonstrate spatial pattern of trends in P, ET, ΔTWS and Q over the recent 12 years (Fig. 3a–d). For interpretation purpose, we also show trends in TWS and distribution of multi-annual mean P (Fig. 3e,f). As expected, Q trends showed similar spatial pattern to P trends but had lower values because Q trends were moderated by slight changes or positive trends in ET and/or ΔTWS. P and Q increased clearly (+5–+23 mm year−2) in northwestern and eastern parts, decreased dramatically (−40–−10 mm year−2) in northern and southern parts. In middle and eastern parts, ET increased at +2–+7 mm year−2. For ΔTWS, increased trends were observed across most parts of the region, but the magnitudes were quite small (usually less than +2–+4 mm year−2). The TWS increased moderately (+6–+20 mm year−1) in northern part, but decreased substantially (−30–−50 mm year−1) in southwestern part, which is quite different from trends in ΔTWS because TWS is a state variable (with a unit of mm) while ΔTWS is a flux variable (with a unit of mm year−1).
Spatial pattern of trends in P, ET, ΔTWS, Q, TWS and mean P values for eastern TP region shown in Fig. 1 for 2003–2014. The maps were generated using ENVI (v 4.5, https://www.harris.com/solution/envi) © 2017 Harris Corporation.
Northern and southeastern parts, which are distinguished by dry and wet climates respectively (Fig. 3f), have undergone different changes that resulted in opposing Q trends. Increased trends in Q in the dry northern part were dominantly determined by increased trends in P. This is indicated by the aggregated trend in Q from regions with P less than 400 mm year−1 being +4.33 mm year−2, derived from trend in P being +6.40 mm year−2, compensated by trends in ET and ΔTWS being +0.17 mm year−2 and +1.90 mm year−2, respectively. In wet southeast, overall decreased trends in Q were similar to those in P trends, but in northern part of southeast, noticeable increased trends in ET (+4–+7 mm year−2) aggravated the decreased trends in Q. As a result, trend in aggregated Q from regions with P above 650 mm year−1 was −2.17 mm year−2, resultant from the trends in P, ET and ΔTWS being +0.58 mm year−2, +2.43 mm year−2, and +0.32 mm year−2, respectively.
Contribution of ΔTWS
As expected, ΔTWS responds mainly to P, especially in dry regions (see Supplementary Information, Fig. S2). The reason that ΔTWS contributed greatly in explaining the inter-annual variation of Q in north and south-west is probably because ΔTWS can reflect cryosphere hydrological dynamics. In northern part, trends in both TWS and ΔTWS were clearly positive; respectively these indicate that total water storage increased and the rate of change increased too. To be more specific, we took Zhimenda basin located in north as an example. The whole 12 years were divided into two six-year periods. For the first six years (2003–2008), mean annual P and ΔTWS were 392 mm year−1 and +2.07 mm year−1, respectively. For the second six years (2009–2014), mean annual P and ΔTWS were 452 mm year−1 andn +7.33 mm year−1, respectively. The results clearly show that the total water stored in Zhimenda basin had a surplus since ΔTWS was positive over 2003–2014; and both P and ΔTWS increased over the two periods, but ΔTWS increased more quickly. This can be attributed to permafrost degradation12, which includes the process of overall permafrost thaw and/or active layer deepening36. From this recently activated store, more water could leak deep into subsurface, leading to a substantial increase of groundwater storage. This phenomena has been demonstrated in other studies37,38. Owing to a large proportion of P converted into groundwater storage, water available for runoff generation was reduced39. Trend in Q was largely determined by trend in P-ΔTWS.
In southwestern part, TWS trend was negative, contrasted by positive trend in ΔTWS, which means total water storage decreased but the rate has slowed or even reversed. This region has a high percentage of permanent snow/ice, and change in the mass of snow/ice can be reflected by ΔTWS 9,32 (see Supplementary Information, Fig. S3). Taking Jiayuqiao basin located in this area as an example, substantial decrease in TWS occurred over 2003–2006 when mean annual ΔTWS and P were −23.2 mm year−1 and 671 mm year−1, respectively. Over 2007–2014 mean annual ΔTWS and P were +0.31 mm year−1 and 677 mm year−1, respectively. It means that there existed previously a huge loss in snow/ice mass caused by warming (P hardly changed), and meltwater accounted for a large proportion of Q. Afterward, the remaining snow/ice didn’t change greatly (ΔTWS was approaching to 0), providing limited amount of meltwater. The fact that meltwater has stopped increasing after vast snow/ice shrinkage largely contributed to the decreased Q trend observed in Jiaoyuqiao basin.
Contribution of ET
Globally ET is the second largest term in the terrestrial water balance after precipitation40. Compared to ΔTWS which is often assumed to be zero over a long period of time and a large region41, ET has more noticeable trends but with less intense fluctuations26. The small inter-annual variability of ET means that ET only provides a minor contribution in explaining Q variation, but its noticeable trends are indispensable in reconstructing Q trends. If the trends in ET were not considered, the Q trends would be severely over-estimated, especially for those basins with humid climates (Fig. 3). In other words, rapidly increased trend in ET in middle-south parts posed a threat to water resources availability, and this effect was more pronounced when P increased slightly or even decreased. Warming should be the main reason for the increasing trend in ET since ET of these wet regions are energy-limited3,6. Greening effect under the influence of CO2 fertilization could also play a role in enhancing ET 26,42,43.
Uncertainty analysis
The water balance method was first validated at basin scale by comparing satellite estimated Q against gauge observations, and then applied to eastern TP for temporal-spatial analysis. An uncertainty may arise in this extrapolation process because the drainage areas upstream of the five gauges don’t fully cover the entire eastern TP. However, such uncertainty should be small because the five validated basins account for 59% of the research domain.
As P is the primary factor governing long-term Q and its variability, it is very important that our P data is as accurate as it can be. There was a good agreement in trends and Coefficients of Variation (CV) between Tropical Rainfall Measuring Mission satellite (TRMM) P data and local observations at 87 gauges located within the research domain (see Supplementary Information, Fig. S5a and S5c). With respect to inter-annual variations in P, observations show strong correlations with TRMM P data for most gauges (see Supplementary Information, Fig. S5b). Moreover, inter-annual variation in observed Q from the five gauges can be best explained with the TRMM P data, compared to those obtained from west0144, MSWEP45, nearest interpolation results of the monthly gauge-observed P, and thin-plate regression interpolation46 results using TRMM as a covariate (see Supplementary Information, Table S4). Therefore, we directly used raw TRMM P data without further processing.
GRACE mascon TWS data has a spatial sampling of 0.5 degree, but the native resolution of a single mascon are 3 degrees in both latitude and longitude, which explains why TWS or ΔTWS shows abrupt boundaries (Figs 2c, 3b,e and 4b). The course resolution can lead to high leakage errors for small catchments because surrounding signals are mistaken as the information from the catchment itself. It can be observed from Fig. 1 that the most inaccurate Q trend estimation occurred at the smallest catchment Changdu (52,600 km2) and its surrounding is rich in glaciers. Applying gain factors is a way to decrease leakage error47. However, no improvements in Q trend estimates were found after ΔTWS data were up-scaled to 0.5 degree using gain factors (see Supplementary Information, Fig. S4a). Moreover, the gain factors, which were derived from Community Land Model (CLM) and should be close to 1, show unreasonable values for some grids (see Supplementary Information, Fig. S4b). Therefore, these optional gain factors were not applied here. In addition to leakage error, another source of uncertainty is the inversion error of mascon TWS data. We found this error accounted for 3–20% of annual amplitude in TWS, resulting in an uncertainty of less than 0.09 mm year−2 in ΔTWS trends (see Fig. 4b), which negligibly affected the reconstructed Q trends.
Uncertainties in ET trends, ΔTWS trends, and Q trends for eastern TP region shown in Fig. 1. (a), uncertainties in ET trends by considering the standard deviations of four ET products. (b), uncertainties in ΔTWS trends by considering the inversion error of mascon TWS. (c), uncertainties in reconstructed Q trends. Please note that uncertainties in ΔTWS trends are much smaller than the uncertainties in ET trends or in Q trends. Q trends are less uncertain than ET trends because Q trends are dominated by P trends. The maps were generated using ENVI (v 4.5, https://www.harris.com/solution/envi) © 2017 Harris Corporation.
Uncertainties in ET trends are usually less than 2 mm year−2, but for many grids of our study region, the values could be as high as 3–5 mm year−2. Trends in ET are much more uncertain than trends in ΔTWS, suggesting tremendous differences among the four ET products. The disparities could be caused by two factors: imperfectness or over-simplification of the ET model and low quality of input data (i.e., satellite data over eastern TP is usually of low quality because of cloud contamination and/or complicated terrain). The uncertainty in input data can be propagated into the ET estimates, leading to large inconsistencies among the models that are based on different concepts (see Supplementary Information, Fig. S1).
There was a strong resemblance in spatial pattern between uncertainties in ET trends and uncertainties in Q trends, indicating that the former largely influenced the latter. However, the latter were generally lower since Q trends were mainly controlled by P trends and significant P trends can supress the effect of uncertainties in ET trends. It can be seen from the Fig. 4c that Q trends had low uncertainties in dry northwestern and eastern regions and high uncertainties in the regions with annual mean P of 400–600 mm year−1, indicating that Q trends were more uncertain in moderate climate than in extreme (wet or dry) climate.
Summary
This study focused on spatial representation of Q trends and its drivers over eastern TP solely using satellite-based products. Results indicated that P was the most important factor in determining Q trends and explained a major part of annual variation in Q. ΔTWS variations played an important role in regions undergoing distinct cryosphere dynamics, and ET trends were indispensable in determining Q trends in wet regions. Northern dry regions showed increased Q trends, whereas wet southern regions showed decreased Q trends, demanding for appropriate adjustments to future water resources management. This study also indicated that permafrost-induced hydrological change and glaciers melting are of great importance for Q modelling over the TP, suggesting that there still exists significant room for improving the current hydrological models.
Methods
Water balance equation
The annual water balance at each grid cell can be described as:
where Q is annual runoff, P is annual precipitation, ET is annual actual evapotranspiration, and ΔTWS is change in Total Water Storage over the year. TWS is vertically integrated water stored, including groundwater, soil moisture, surface water, snow and ice, vegetation water, etc. The water year is defined as October to September to minimize effects of snowfall and glaciers on yearly water balances48. All variables have units of mm year−1. The baseline averages over 2004 to 2009 were used to calculate anomalies of water balance components.
Data
All the above data were obtained from satellite-based products. Monthly precipitation data were sourced from the TRMM (3B43) precipitation product from Mirador at the NASA Goddard Earth Sciences Data and Information Services Center (GES DISC)25, which estimates 0.25o gridded precipitation by merging 3B-42 and gauged precipitation data. Monthly ET data from Jan 2002 to Sep 2014 were obtained from four state-of-the-art diagnostic ET products: PML26, GLEAM27, MOD1628, P-LSH29. The median of ET anomalies from the four ET products were used for the analyses. The anomaly, rather than the actual value, was used to overcome systematic bias in the different ET products (see Supplementary Information Table S3 and Fig. S1). Monthly streamflow data for the five basins from Jan 2002 to Sep 2014, recorded by the Tibetan and Qinghai Hydrological Bureaus, were obtained from the hydrological annuals compiled by the Chinese Ministry of Water Resources. Monthly TWS data from Apr 2002 to Mar 2016 came from the Jet Propulsion Laboratory (JPL)-RL05M Mascon (mass concentration) Version 2. The mascon data is essentially another form of gravity field basis functions and is superior to the standard spherical harmonic approach due to implementation of prior geophysical constraints and less dependence on gain factors30. ΔTWS is calculated as TWS at the end of a water year minus TWS at the beginning of a water year.
Statistical analysis
12 water years of data, from 2003 (Oct 2002 to Sep 2003) to 2014 (Oct 2013 to Sep 2014), were used for the analysis. First, basin-scale modelled annual Q anomaly series were assessed against the Q observations. Weighting averaging was used to obtain basin-average P, ET, and ΔTWS values, in which a grid’s weight is the ratio of this grid’s area inside the basin boundary (please note that the basin is the drainage area upstream of each gauge). Then, the annual series of Q anomaly were calculated for all 0.25o grids across the region using Equation (1). The percentage of variance in Q that can be explained by P, by both P and ET, and by both P and ΔTWS was estimated as the coefficient of determination (R2) of the linear regression of Q versus P, Q versus P and ET, and Q versus P and ΔTWS, respectively. The trends in Q, P, ET and ΔTWS over the 12 years were calculated using the non-parametric Mann-Kendall test49. The uncertainties in ET trends were derived from the differences between trends in ET + sd ET and trends in ET−sd ET . The uncertainty in ET (denoted as sd ET ) is the standard deviations of the four ET anomalies. The uncertainties in ΔTWS trends were derived from the differences between trends in ΔTWS + sdΔ TWS and trends in ΔTWS−sdΔ TWS . The uncertainty in ΔTWS (denoted as sdΔ TWS ) is the squared mean of uncertainties of TWS 30 at the beginning and the end of a water year.
References
Xu, X., Lu, C., Shi, X. & Gao, S. World water tower: An atmospheric perspective. Geophysical Research Letter 35, 1–5 (2008).
Lutz, A. F., Immerzeel, W. W., Shrestha, A. B. & Bierkens., M. F. P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nature Climate Change 6, 587–592 (2014).
Yang, K. et al. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Global and Planetary Change 112, 79–91 (2014).
Immerzeel, W. W., van Beek, L. P. H. & Bierkens, M. F. P. Climate Change Will Affect the Asian Water Towers. Science 328(5984), 1382–1385 (2010).
Immerzeel, W. W. & Bierkens, M. F. P. Asia’s water balance. Nature Geoscience 5, 841–842 (2012).
Duan, A. M. & Xiao, Z, X. Does the climate warming hiatus exist over the Tibetan Plateau? Scientific Reports. doi:https://doi.org/10.1038/srep13711 (2015).
Xu, Z. X., Gong, T. L. & Li, J. Y. Decadal trend of climate in the Tibetan Plateau—regional temperature and precipitation. Hydrological Process 22, 3056–3065 (2008).
Piao, S. et al. Changes in satellite-derived vegetation growth trend in temperate and boreal Eurasia from 1982 to 2006. Global Chang Biology 17, 3228–3239 (2011).
Yao, T. D. et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nature Climate Change 2, 663–667 (2012).
Zhang, Y. Q., Liu, C. M., Tang, Y. H. & Yang, Y. H. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau. Journal of Geophysical Research – Atmospheres 112, D12110, https://doi.org/10.1029/2006/2006JD008161 (2007).
You, Q. L. et al. Decreasing wind speed and weakening latitudinal surface pressure gradients in the Tibetan Plateau. Climate Research 42, 57–64 (2010).
Liu, J., Kang, S., Gong, T. & Lu, A. Growth of a high-elevation large inland lake associated with climate change and permafrost degradation in Tibet. Hydrology and Earth System Sciences 14, 481–489 (2010).
Xue, X., Guo, J., Han, B. S., Sun, Q. W. & Liu, L. C. The effect of climate warming and permafrost thaw on desertification in the Qinghai-Tibetan Plateau. Geomorphology 108, 182–190 (2009).
Cui, X. & Graf, H. F. Recent land cover changes on the Tibetan Plateau: A review. Climate Change 94, 47–61 (2009).
Gain, A. K. & Wada, Y. Assessment of Future Water Scarcity at Different Spatial and Temporal Scales of the Brahmaputra River Basin. Water Resource Management 28, 999–1012, https://doi.org/10.1007/s11269-014-0530-5 (2014).
Li, Z. et al. Multiscale Hydrologic Applications of the Latest Satellite Precipitation Products in the Yangtze River Basin using a Distributed Hydrologic Model. Journal of Hydrometeorology 16, 407–426, https://doi.org/10.1175/JHM-D-14-0105.1 (2015).
Cong, Z., Yang, D., Gao, B., Yang, H. & Hu, H. Hydrological trend analysis in the Yellow River basin using a distributed hydrological model. Water Resources Research 45, 335–345, https://doi.org/10.1029/2008WR006852 (2009).
Zhang, Y. S., Ohata, T. & Kadota, T. Land-surface hydrological processes in the permafrost region of the eastern Tibetan Plateau. Journal of Hydrology 283, 41–56 (2003).
Qiu, J. Thawing permafrost reduces river runoff. Nature, doi:https://doi.org/10.1038/nature.2012.9749 (2012).
Immerzeel, W. W., Petersen, L., Ragettli, S. & Pellicciotti, F. The importance of observed gradients of air temperature and precipitation for modeling runoff from a glacierized watershed in the Nepalese Himalayas. Water Resources Research 50, 2212–2226, https://doi.org/10.1002/2013WR014506 (2014).
Li, S. H., Yao, T. D., Yang, W., Yu, W. S. & Zhu, M. L. Melt season hydrological characteristics of the Parlung No. 4 Glacier, in Gangrigabu Mountains, south-east Tibetan Plateau. Hydrological Processes 30, 1171–1191 (2016).
Immerzeel, W. W., Wanders, N., Lutz, A. F., Shea, J. M. & Bierkens, M. F. P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrology and Earth System Sciences 19(11), 4673–4687 (2015).
Mishra, V. Climatic uncertainty in Himalayan Water Towers. Journal of Geophysical Research Atmospheres 120, 2689–2705, https://doi.org/10.1002/2014JD022650 (2015).
Palazzi, E., von Hardenberg, J. & Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. Journal of Geophysical Research Atmospheres 118, 85–100, https://doi.org/10.1029/2012JD018697 (2013).
Huffman, G. J. et al. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. Journal of Hydrometeorology 8, 38–55, https://doi.org/10.1175/JHM560.1 (2007).
Zhang, Y. Q. et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Scientific Reports 6, 19124, https://doi.org/10.1038/srep19124 (2016).
Miralles, D. G. et al. El Niño–La Niña cycle and recent trends in continental evaporation. Nature Climate Change 4, 122–126, https://doi.org/10.1038/NCLIMATE2068 (2014).
Mu, Q., Zhao, M. & Running, S. W. Improvements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sensing of Environment 115, 1781–1800, https://doi.org/10.1016/j.rse.2011.02.019 (2011).
Zhang, K., Kimball, J. S., Nemani, R. & Running, S. W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resources Research 46, W09522 (2010).
Watkins, M. M., Wiese, D. N., Yuan, D. N., Boening, C. & Landerer, F. W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. Journal of Geophysical Research: Solid Earth 120, 2648–2671, https://doi.org/10.1002/2014JB011547 (2015).
Xu, M., Kang, S. C., Zhao, Q. D., & Li, J. Z. Terrestrial Water Storage Changes of Permafrost in the Three-River Source Region of the Tibetan Plateau, China. Advances in Meteorology, doi:https://doi.org/10.1155/2016/4364738 (2016).
Gardelle, J., Berthier, E., Arnaud, Y. & Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. The Cryosphere 7, 1263–1286, https://doi.org/10.5194/tc-7-1263-2013 (2013).
Cheng, G. & Wu, T. Response of permafrost to climate change and their environmental significance, Qinghai-Tibet Plateau. Journal of Geophysical Research 112, F02S03, https://doi.org/10.1029/2006JF000631 (2007).
Moiwo, J. P., Yang, Y. H., Tao, F. L., Lu, W. X. & Han, S. M. Water storage change in the Himalayas from the Gravity Recovery and Climate Experiment (GRACE) and an empirical climate model. Water Resources Research 47, W07521, https://doi.org/10.1029/2010WR010157 (2011).
Song, C. Q., Ke, L. H., Huang, B. & Richards, K. S. Can mountain glacier melting explains the GRACE-observed mass loss in the southeast Tibetan Plateau: From a climate perspective? Global and Planetary Change 124, 1–9 (2015).
Cheng, W., Zhao, S., Zhou, C. & Chen, X. Simulation of the decadal permafrost distribution on the Qinghai-Tibet Plateau (China) over the past 50 years. Permafrost and Periglacial Processes 23, 292–300 (2012).
Jiao, J. J., Zhang, X. T., Liu, Y. & Kuang, X. X. Increased Water Storage in the Qaidam Basin, the North Tibet Plateau from GRACE Gravity Data. PLoS ONE 10, e0141442, https://doi.org/10.1371/journal.pone.0141442 (2015).
Xiang, L. W. et al. Groundwater storage changes in the Tibetan Plateau and adjacent areas revealed from GRACE satellite gravity data. Earth and Planetary Science Letters 449, 228–239 (2016).
Yi, S. H., Wang, X. Y., Qin, Y., Xiang, B. & Ding, Y. J. Responses of alpine grassland on Qinghai–Tibetan plateau to climate warming and permafrost degradation: a modeling perspective. Environmental Research Letters 9, 074014, https://doi.org/10.1088/1748-9326/9/7/074014 (2014).
Leuning, R., Zhang, Y. Q., Rajaud, A., Cleugh, H. & Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resource Research 44, W10419, https://doi.org/10.1029/2007WR006562 (2008).
Donohue, R. J., Roderick, M. L. & McVicar, T. R. On the importance of including vegetation dynamics in Budyko’s hydrological model. Hydrology and Earth System Sciences 11(2), 983–995 (2007).
Donohue, R. J., Roderick, M. L., McVicar, T. R. & Yang, Y. T. A simple hypothesis of how leaf and canopy-level transpiration and assimilation respond to elevated CO2 reveals distinct response patterns between disturbed and undisturbed vegetation. Journal of Geophysical Research – Biogeosciences. 122(1), 168–184 (2017).
Milly P. C. D. & Dunne K. A. Potential evapotranspiration and continental drying. Nature Climate Change 6, doi:https://doi.org/10.1038/NCLIMATE3046 (2016).
He, J. & Yang, K. China Meteorological Forcing Dataset. Cold and Arid Regions Science Data Center at Lanzhou, doi:https://doi.org/10.3972/westdc.002.2014.db (2011).
Beck, H. E. et al. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrology and Earth System Sciences 21(1), 589–615 (2017).
Wood, S. N. Generalized Additive Models: An Introduction With R; Chapman & Hall/CRC: Boca Raton, FL, USA (2006).
Wiese, D. N., Landerer, F. W. & Watkins, M. M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resources Research 52, 7490–7502, https://doi.org/10.1002/2016WR019344 (2016).
Dai, A. G., Qian, T. T. & Trenberth, K. E. Changes in Continental Freshwater Discharge from 1948 to 2004. Journal of Climate 22, 2773–2792 (2009).
Hamed, K. H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. Journal of Hydrology 349, 350–363 (2008).
Acknowledgements
We thank the NASA Goddard Earth Sciences Data and Information Services Center for providing TRMM precipitation data and the Jet Propulsion Laboratory for providing GRACE total water storage data and GLDAS land water storage data. Our thanks are extended to Diego Miralles, Qiaozhen Mu, and Ke Zhang for sharing us GLEAM, MOD16, P-LSH land surface evapotranspiration datasets, respectively. Yuanyuan Wang was finically supported by the Chinese Scholarship Council.
Author information
Authors and Affiliations
Contributions
Y.Q.Z. conceived this study. Y.Y.W. performed the data analysis and plotting. Y.Q.Z., Y.Y.W., H.X.L., G.H.Q. collected data. Y.Y.W., Y.Q.Z. and F.H.S.C. drafted the paper. Y.Y.W., Y.Q.Z., F.H.S.C., T.R.M. and L.Z. contributed interpretation of the results and to the text.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Zhang, Y., Chiew, F.H.S. et al. Contrasting runoff trends between dry and wet parts of eastern Tibetan Plateau. Sci Rep 7, 15458 (2017). https://doi.org/10.1038/s41598-017-15678-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15678-x
This article is cited by
-
Atmospheric dynamic constraints on Tibetan Plateau freshwater under Paris climate targets
Nature Climate Change (2021)
-
The change of hydrological variables and its effects on vegetation in Central Asia
Theoretical and Applied Climatology (2021)
-
Understanding the spatial differences in terrestrial water storage variations in the Tibetan Plateau from 2002 to 2016
Climatic Change (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.