Abstract
The porosity of clay aggregates is an important property governing chemical reactions and fluid flow in low-permeability geologic formations and clay-based engineered barrier systems. Pore spaces in clays include interlayer and interparticle pores. Under compaction and dewatering, the size and geometry of such pore spaces may vary significantly (sub-nanometer to microns) depending on ambient physical and chemical conditions. Here we report a molecular dynamics simulation method to construct a complex and realistic clay-like nanoparticle aggregate with interparticle pores and grain boundaries. The model structure is then used to investigate the effect of dewatering and water content on micro-porosity of the aggregates. The results suggest that slow dewatering would create more compact aggregates compared to fast dewatering. Furthermore, the amount of water present in the aggregates strongly affects the particle-particle interactions and hence the aggregate structure. Detailed analyses of particle-particle and water-particle interactions provide a molecular-scale view of porosity and texture development of the aggregates. The simulation method developed here may also aid in modeling the synthesis of nanostructured materials through self-assembly of nanoparticles.
Similar content being viewed by others
Introduction
The structure of clay aggregates (i.e., porosity, pore geometry, and pore size distribution) under subsurface conditions is one of the important factors controlling gas/oil in place, ion exchange capacity, hydrologic conductivity, and mechanical strength of low-permeability geologic formations1. Clay minerals are composed of sheets of metal ions either tetrahedrally (T) or octahedrally (O) coordinated by framework oxygen ions or hydroxyl groups. Pore spaces in clay-bearing rocks include interlayer [i.e., space internal to the particle between clay layers (i.e., TOT layers)] and interparticle (i.e., space between clay particles or platelets) pores2,3. Interparticle porosity decreases under low and moderate compaction, while interlayer porosity only decreases under large compression and depends on the amount of water present in the interlayer pores (i.e., 1 or 2 water layers)4. The exchange of chemical species including water, gases and ions between interlayer and interparticle pores is vital to understanding clay swelling5,6, the migration of radionuclides away from a nuclear waste disposal site7, and the potential release of CO2 through shale caprocks in a subsurface carbon storage facility8,9. The migration of fluids in interparticle pores particularly affects oil and gas extraction. For example, in shale plays, gas flows from the shale matrix dominated by micropores to an interconnected fracture system10.
The variation of water content (i.e., dry, partially saturated, and saturated) in clay pores determines in part the partitioning of ions between the bulk aqueous solution in larger pores and the adsorbed species on clay basal and edge surfaces11,12. The amount of water in clay aggregate also influences the adsorption of industrially important gases such as CH4 and CO2 13. Dewatering of clays during sedimentation also affects mudstone porosity: the more rapidly deposited the clay platelets, the less time the interparticle pores have to dewater, and therefore the water content remains high14. While the effects of water on interlayer properties and clay swelling are well studied15, the effects of dewatering on clay aggregate structure at the nanoscale under sedimentation are largely unexplored16. Here we investigate the change in micro-porosity of clay-like nanoparticle aggregates under relevant sedimentation/diagenesis conditions using molecular modeling techniques.
From a classical molecular dynamics (MD) simulation perspective, designing clay aggregates for modeling is challenging. The first challenge is the system size, particularly how to use nanoparticles to provide a reasonable representation of actual clay particles found in nature, with particle sizes (e.g., microns) beyond the existing computational capability. The second challenge for modeling clay particles is that the structure of edge surfaces of clay particles under varying pH conditions is not well understood17. Numerous quantum mechanical simulations tried to address this issue by studying the stability17,18 and acid-base properties of clay edge surfaces19,20,21,22. At the molecular level, one of the most widely used force fields to describe water-clay mineral systems (i.e., ClayFF23) was initially developed to simulate the interaction of water with unreactive basal surfaces and interlayers of layered minerals, but the applicability of ClayFF to edge surfaces has only recently been investigated24,25,26. Consequently, the majority of MD simulation studies of clay-water systems have been carried out using a simple slit-shape pore without considering edge effects13,15,17,27,28,29,30,31,32. Lammers et al.29 attempted to simulate clay particles and observed the detachment of OH groups from particle edges. Two studies have simulated ion and water transport between interparticle and interlayer regions of smectite particles including the edge surfaces, but only orthogonal-shaped pores were included along with fully rigid clay layers2,33. Although interesting results were obtained from these studies, a complex and realistic clay aggregate model with interlayer and interparticle pores, and interparticle boundaries at the atomistic scale is required to fully investigate the exchange of water and ions between interlayer and interparticle pores34. Simulations of increasingly complex pore sizes and geometries can be used to study, for example, the relative significance of ion adsorption onto the basal versus edge surfaces of clay minerals, the effect of nanoscale fluid flow on the metamorphism of the continental crust35, and properties of nanoporous organic matter in shale36.
In this paper, we develop a methodology to create nanoscale models of multi-particle, dual porosity clay aggregates based on the endmember layered mineral gibbsite, Al(OH)3, in order to simulate more “rock-like” systems and to be able to characterize the coupling of transport and chemistry in these systems. This work represents a breakthrough in the preparation of simulation models of nanoporous materials in which the pore structure depends on the compaction and dewatering processes. Such models can then be used to simulate nanopore properties in both natural and engineered materials. Our example is based on nanoparticles comprised of a layered mineral, but the methodology could be applied to virtually any type of nanoparticle composition or geometry.
Results
Impact of dewatering rate on the stacking of clay-like nanoparticles
In Fig. 1 we present the results to demonstrate the effects of dewatering on the particle-particle interaction and particle alignment. The micro-porosity and texture of nanoparticle aggregates largely depend on the manner that clay-like particle organized. Starting with the hydrated gibbsite aggregate shown in Fig. 1A (see Method for details generating this system), water molecules were randomly removed from the simulation cell while the system was compressed (P = 100 MPa, T = 300 K) until the system reached an equilibrium state (i.e., constant volume). For ‘fast’ dewatering, all water molecules were completely removed at the beginning of the simulation. For ‘intermediate’ dewatering rate (results not shown in Fig. 1), 100 water molecules were withdrawn from the cell every 100 time steps (no waters remained in the simulation box after 55 ps). For ‘slow’ dewatering, 10 water molecules were randomly deleted every 100 steps (no waters remained in the simulation box after 550 ps). Visual inspection of the simulation snapshots indicates that particles formed during ‘slow’ dewatering processes (Fig. 1C) form large stacks with close contacts between basal surfaces (i.e., bulk-like) to form a more compact system compared to ‘fast’ dewatering (Fig. 1B). During ‘fast’ dewatering (Fig. 1B), less stacking of nanoparticles results in larger pores. To quantify this observation we calculated the orientation of particles (Fig. 1D) and the number of particles that form stacks of 2, 3, or 4 particles for fast and slow dewatering (Fig. 1E). In Fig. 1D, θ is the angle between the vector normal to the basal surface of each particle and the z direction of the simulation box. In general, the results in Fig. 1D indicate the preferred orientation of nanoparticles (i.e., parallel to each other), which agrees with experimental data16,37. For ‘slow’ dewatering, there is higher possibility that the particles are aligned parallel to the xy-plane compared to ‘fast’ dewatering. As more particles are oriented nonparallel to the xy-plane, the porosity increases. As shown in Fig. 1E, for ‘fast’ dewatering approximately 22 out of 54 nanoparticles do not stack on top of another particle. These delaminated particles are responsible for the high porosity in the aggregates. During ‘slow’ dewatering, aggregates of 3 or 4 nanoparticles form (see inset ii) but during ‘fast’ dewatering the largest aggregates contain only 3 nanoparticles.
Simulation snapshot representing the hydrated clay-like nanoparticle aggregates that we used as a starting system to study the effects of dewatering and water content on aggregate structure (A). Simulation snapshots showing the effect of ‘fast’ (B) and ‘slow’ (C) dewatering rate on dry aggregate structures. Comparison of particle orientations (D) and the stacking of particles (E) under different dewatering rate. Insets (i) and (ii) illustrate stacks of 3 and 4 nanoparticles, respectively.
Impacts of dewatering rate and water content on nano-structural properties of aggregates
In Fig. 2A we summarize the effect of dewatering rate on the pore size distribution (PSD) calculated for clay-like nanoparticle aggregates. The PSD was calculated by using the method proposed by Gubbins et al.38. The results indicate that the PSD varies significantly depending on the dewatering process. ‘Fast’ dewatering (black line-Fig. 2A) yields a wider PSD with larger pores developed, compared to slower dewatering. For ‘fast’ dewatering, the pores in the aggregate include micropores (<2 nm39) and mesopores (2–50 nm39); for the ‘intermediate’ and ‘slow’ dewatering processes, only micropores are formed. One possible explanation for this difference is that under fast dewatering and compaction, nanoparticles do not have enough time to rearrange themselves into a large stack, which would result in larger pores in the aggregate structure.
To study the effect of water content on the clay-like nano-aggregate, from the configuration of Fig. 1A different nanoparticle-water systems with various amounts of water were created. In the first system, all water molecules farther than 3 Å away from any nanoparticle were removed at the beginning of the simulation. This method created a nanoparticle-water system in which each particle is surrounded by a 3 Å water film (‘1 W’), and the total water content is 22.5 wt%. In the second system, each particle is surrounded by a 6 Å water film (‘2 W’), and the water content is 37.2 wt%. These systems were then compressed at P = 100 MPa, T = 300 K until an equilibrium state (i.e., constant volume) was achieved. The ‘1 W’ and ‘2 W’ cases represent the closed systems where water exchange with the surrounding environment does not occur. To explore the possibility that water can be expelled from the system during compression37, in a third system all water molecules that moved into a predefined region during the simulation of the ‘2 W’ system were extracted from the system (Method). Note that water molecules can only move into the predefined region if they can desorb from the nanoparticle surfaces and if there is pore connectivity. This extraction method was described in more detail in our previous study of methane release in kerogen nanopores40. This simulation was conducted for 89 ns, during which the water content was reduced from 37.2 wt% (i.e., that of ‘2 W’ system) to 6 wt%. The results obtained for this system are labeled as ‘2W_dewatering’. Note that after 89 ns, water molecules were still able to move to the predefined region but at a very slow rate (i.e., for the last 1 ns, only 13 water molecules were deleted). Assuming that all water molecules would eventually be expelled from the system, we deleted the remaining water molecules and continued compressing the simulation box. The results reported for this system are labeled as ‘2 W_dry’.
As shown in Fig. 2B, water content in the aggregates also affects the PSD. For example, in the ‘2W’ system, pore diameters can be as large as 26 Å. Lower water content leads to smaller pore sizes in the aggregates. In the‘1 W’ system, only pores smaller than 20 Å are observed. In addition, the maximum in the pore size distribution profile is found from 12 to 16 Å for the‘2 W’ system while for other systems (i.e., ‘1 W’, ‘2W_dewatering’, ‘2W_dry’) the maximum is observed from 4 to 8 Å. This indicates that the pore structure and pore size in the clay aggregates vary depending on the abundance of water. Pores in the hydrated nanoparticle aggregates are larger than those in the dry aggregates (‘2W_dewatering’, ‘2W_dry’). Note that pore spaces in the‘1 W’ and ‘2 W’ systems are completely filled by water.
Our results also suggest that early dewatering and compression might play a dominant role in the pore size distribution of the gibbsite aggregates. A similar pore size distribution was found in the ‘slow’ system in Fig. 2A and the ‘2W-dry’ system in Fig. 2B (both systems are dry and obtained at different dewatering rates, it takes 0.55 ns for the ‘slow’ system, and more than 89 ns for the ‘2W-dry’ system to be dried). This indicates that late dewatering and compression (e.g., after 0.55 ns in our simulations) does not significantly affect the pore structure of nanoparticle aggregates. Both early compression and dewatering (less than 0.55 ns) significantly affect pore structures.
In Fig. 3 we illustrate the effects of dewatering rate and water content on the total porosity and pore surface area (SA) of the nanoparticle aggregates. The porosity and surface area were calculated using Materials Studio software41,42. Note that the SA reported in Fig. 3B is larger than that observed for gibbsite (i.e., 418 m2/g)43 and typical clays (i.e., ~30 m2/g)10 because of the small particle size in our simulations. The results suggest that decreasing the dewatering rate and water content reduces the porosity of nanoparticle aggregates. The reason for this observation can be explained via the SA data presented in Fig. 3B. When the accessible SA decreases, the number of particle-particle contacts increases, and therefore the porosity decreases. The large accessible SA obtained for ‘fast’ dewatering indicates that particle-particle contact is not preferred, compared to slower dewatering systems. This is because particles do not have enough time to arrange and organize to maximize their contact area. When particles are surrounded by thin water films (i.e., ‘2 W’ and ‘1 W’ systems) there is almost no direct particle-particle contact (i.e., surface area for ‘2 W’ and ‘1 W’ is comparable with the surface area when there is no contact between particles). When the amount of water is reduced, the number of particle-particle contacts increases, leading to a decrease in porosity.
Water structure at the nanoparticle surfaces is strongly dependent on water content. Fig. 4A and C illustrate the density profiles of water oxygen atoms near nanoparticle surface atoms for the ‘1 W’ and ‘2 W’ systems. For the ‘2 W’ system, the density profile (black line) indicates that water oxygen atoms (Ow) form a first peak around 2 Å with a shoulder at approximately 1.75 Å from the particle atoms. A second peak is found at 2.75 Å. Detailed analysis indicates that the shoulder peak at 1.75 Å is a result of the interaction between Ow atoms and H atoms of the gibbsite particles (i.e., the shoulder peak for Ow-all aligns with the first peak in the Ow-H density profile). Simulation snapshots in Fig. 4B show that these hydrogen atoms are mainly the hydrogen atoms of OH groups that point away from the surface (denoted OH-1 on Fig. 4B) and possibly the OH groups at the edge (not shown). The peak at 2.0 Å is associated with the accumulation of coordinating water molecules (Fig. 4B) near (5-coordinated) Al atoms at the edge (i.e., this peak is aligned with the first peak on the density profile of Ow-Al(Edge)). The adsorption of a water molecule to form a complete octahedral (6-coordinated) shell about each edge Al atom is expected24. The second peak at 2.75 Å is associated with the interaction of Ow with the surface hydroxyl O and H atoms denoted OH-2 in Fig. 4B (note that the OH-2 groups are almost parallel to the gibbsite surface). Similar peak positions were observed at lower water content (Fig. 4 C). However, because of the change in the porosity and pore size distribution when water content was reduced from ‘2 W’ to ‘1 W’, the majority of water in the ‘1 W’ system is interfacial water (i.e., the peak intensities for the ‘1 W’ system are higher than for the ‘2 W’ system). In addition, a significant fraction of water molecules in the ‘2 W’ system can be considered bulk-like since they are located between 8 to 10 Å from the nanoparticle surface (see Fig. 4A).
Relative position of water O atom (Ow) with respect to gibbsite nanoparticle atoms for 2 W (A) and 1 W (C) systems. Simulation snapshots demonstrate the interaction of water with different sites on gibbsite basal and edge surfaces (B). Red, pink, and cyan spheres represent for O, Al, and H atoms of gibbsite, respectively. Red and white spheres represent water O and H atoms, respectively. In (A) and (C), red, green, and blue lines represent the closest distance of Ow atoms to O, H, and edge-Al atoms of the nanoparticles in the aggregate, respectively, while the black line represents the closest distance of Ow atoms to particle atoms.
Discussion
In this work, we have built a model gibbsite nanoparticle and have used MD simulations to study the structure and texture of aggregates formed by the nanoparticles. We found that dewatering and water content affect the porosity and structure of aggregates formed during compaction. Fast dewatering yields larger pores and a wider pore size distribution, compared to slower dewatering. When water is abundant in the system, gibbsite nanoparticles were surrounded by water that prevented direct particle-particle contact, resulting in a higher porosity. The particle-particle and water-particle interactions are responsible for the origin of aggregate porosity during compression. If particles orient and arrange to maximize the interactions between gibbsite basal surfaces, the aggregate will have lower porosity. Porosity from our simulations agree with available experimental data despite the fact that our model nanoparticle is much smaller than those formed in nature or by synthesis.
Our work provides insight into aggregate micro-porosity based on layered Al(OH)3 (gibbsite) nanoparticles, including the effects of compaction and dewatering processes. Subsequent MD simulations will probe the structural and dynamic properties of hydrated clay mineral aggregates under much more diverse pore environments than is usually reported. Additionally, we establish a methodology for creating more realistic and complex nanoparticle systems of varying porosity, which can be extended to other types of nanoparticles created from bulk structures. For example, the simulation method developed here may also help model the synthesis of nanostructured materials through self-assembly of nanoparticles44. Finally, the aggregate in this work is created with individual particles of the same size and shape. Future work will need to investigate the effects of particle polydispersity and size/shape distribution on the final pore size distribution and compaction of clay aggregates45,46.
Method
We first describe our method for constructing a gibbsite nanoparticle with an explicit representation of basal and edge surfaces. Then we describe our approach to build nanoparticle aggregates.
Single nanoparticle
We selected gibbsite [Al(OH)3] as a good starting point for developing multi-particle simulation models because its structure consists of stacked sheets of linked octahedra of aluminum hydroxide. These neutral aluminum hydroxide sheets are similar to the octahedral sheets bonded to silicate sheets in clay minerals such as kaolinite, illite and smectite. Our choice of gibbsite permits us to design particle aggregates similar in shape to clay particles and with interparticle porosity only; the complexity associated with interlayer porosity in clay platelet aggregates will be addressed in future work.
Each gibbsite layer consists of a sheet of octahedral Al atoms coordinated by 3 hydroxyl O atoms each above and below the Al sheet. Gibbsite grows well along the lateral (‘a’ and ‘b’) directions that include the octahedral sheets, resulting in thin hexagonal nanoparticles43,47,48,49. In our approach, a hexagonal gibbsite particle was cleaved from a slab of 3 layers of gibbsite along the (1 0 0) and (1 1 0) directions as shown in Fig. 5A. The (1 0 0) and (1 1 0) faces were selected since they are the most common for particles with a pseudo-hexagonal shape50, and these faces are also observed experimentally for gibbsite nanoparticles48. Additional OH groups were added to coordinate edge Al atoms, resulting in five-fold coordination of edge Al atoms. On the basal (0 0 1) surface there are only bridging OH groups (i.e., OH group bonded to 2 Al atoms), but on the edge surfaces there are both singly-coordinated (i.e., OH group bonded to 1 Al atom) and bridging OH groups. The structure of the basal and edge surfaces in our model is consistent with experimental data48.
Gibbsite nanoparticle construction. Red, white, and pink spheres represent oxygen, hydrogen, and aluminum atoms, respectively. (A) Basal gibbsite surface with pre-defined cutting directions (black). Atoms colored blue at the center and corners of the hexagon guide the cleavage. (B) Hexagonal gibbsite nanoparticle and its dimensions. (C) Three layers of gibbsite nanoparticle. (D) All Al-O-Al angles at the particle perimeter were defined in our simulations in addition to the ClayFF force field.
Each hexagonal nanoparticle has 2016 atoms including 288 Al, 864 O, and 864 H atoms, 2.1 nm edges (Fig. 5B), and a thickness of 1.34 nm (3 gibbsite layers, Fig. 5C). This particle is much smaller than those synthesized in the laboratory or found in the nature43,47,48,49. However, this work focuses on the micro-porosity of nanoparticle aggregates, and in consideration of computational resources and simulation time, our particle size selection is a reasonable choice. Coarse grained techniques51 can be used to simulate larger particles and system sizes, but the interfacial chemistry is not well described at this level of theory.
The total potential energy of the gibbsite nanoparticle is described using ClayFF, in which interatomic interaction energies are described by nonbonded Lennard Jones and electrostatic energy terms23. Partial charges of +1.575 e, −0.95 e, and +0.425 e are assigned to the Al, O, and H atoms, respectively, which results in a charge-neutral particle. The only bonded energy term used in ClayFF for the mineral phase is the OH bond stretch. ClayFF was first developed to simulate clay mineral basal surfaces with periodic boundary condition (i.e., no edges). Recent efforts further developed ClayFF by defining harmonic Mg-O-H and Al-O-H angle bending terms to simulate specific edges of brucite and gibbsite, respectively24,25. Although the (1 0 0) edge can be successfully simulated using the new Al-O-H angle bending term, a hexagonal gibbsite particle with (1 0 0), (1 1 0), and (0 0 1) surfaces was not numerically stable. To overcome this issue, an Al-O-Al angle bending term was explicitly defined using a harmonic potential for the Al-O-Al angles at the edge surfaces (Fig. 5D). In our simulations, equilibrium values for Al-O-H and Al-O-Al angles are 110° and 100°, respectively. Because particle-particle interactions and collisions in our multi-particle simulations discussed below are quite strong, we used k = 800 kcal.mol−1.rad−2 to maintain the nanoparticle edge structure. Note that the use of a large k value will affect the calculated vibrational properties, but it is unlikely to affect the structural properties of nanoparticle aggregates reported in this work.
Nanoparticle aggregates
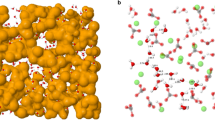
To construct nanoparticle aggregates, 54 gibbsite nanoparticles were initially placed in a simulation box of 30 × 30 × 30 nm3 (Fig. 6A) followed by the addition of 55,008 water molecules. Initial water-water and water-nanoparticle distances were 7 Å and 8 Å, respectively (Fig. 6A). This system was equilibrated for 0.3 ns in the NVT ensemble (constant number of particles, volume, and temperature T = 300 K) using LAMMPS52. During this simulation, long-range electrostatic interactions were calculated using PPPM (particle-particle-particles-mesh) solver53 with a time step of 1 fs. The simulation temperature was kept constant by applying a Nosé-Hoover thermostat54. The rigid SPC55 model was used for water, along with the SHAKE algorithm56. The use of rigid SPC55 or flexible SPC57 water model will not affect the structural properties presented herein. However, when studying spectroscopic and other dynamic properties that vary with changes in molecular geometry, the flexible SPC water model should be implemented58. Interactions among unlike atom types were calculated using an arithmetic mixing rule. After initial equilibration as described above, the system (Fig. 6B) was compressed using an NPT ensemble (constant number of particles, pressure 100 MPa, and temperature 300 K) simulation until the simulation cell volume reached a constant value (Fig. 6C). During this initial NPT simulation, long-range electrostatic interactions were turned off. A cut-off distance of 10 Å was used for all the non-bonded interactions. The final configuration illustrated in Fig. 6C is the system that we used to study the effects of dewatering and water content on the structure and porosity of nanoparticle aggregates. For all subsequent dewatering simulations, long-range electrostatic interactions were once again calculated with PPPM.
Snapshots represent configurations at different stages of simulations as described in the text: initial configuration of nanoparticles and water (A), after initial NVT simulation (B), and after initial NPT simulation (C). Water molecules are presented by red-white wireframes. Nanoparticles are illustrated by different isosurfaces representing the van der Waals radii of perimeter atoms. A schematic shows a slab region (blue) of 10 Å thickness in the z direction that we used to study the water expulsion from the simulated system during compression (D).
Effect of dewatering rate on aggregate volume and texture
Starting with the hydrated gibbsite aggregate shown in Fig. 6C, three new simulations were performed to investigate the impact of evaporation or dewatering rate on the aggregate structure and porosity. In each simulation, water molecules were randomly removed from the simulation cell while the system was compressed under NPT conditions (P = 100 MPa, T = 300 K) until the system reached an equilibrium state (i.e., constant volume). In the first system, all water molecules were completely deleted at the beginning of the simulation. In the second system, 100 water molecules were withdrawn from the cell every 100 time steps (no waters remained in the simulation box after 55 ps). In the third system, 10 water molecules were deleted every 100 steps (no waters remained in the simulation box after 550 ps). The results reported for the first, second, and third systems are labeled as ‘fast’, ‘intermediate’, and ‘slow’, respectively. The range of dewatering rates in this work is arbitrarily selected because of the unknown dewatering rate in the process of sedimentation. However, the method could be applied for a much slower rate using enhanced simulation techniques, but our initial results presented herein already demonstrate the effect on aggregate structure with only minor changes to the dewatering rate.
Effect of water content on aggregate volume and texture
From the configuration of Fig. 6C different nanoparticle-water systems with various amounts of water were created. In the first system, all water molecules farther than 3 Å away from any nanoparticle were removed at the beginning of the simulation. This method created a nanoparticle-water system in which each particle is surrounded by a 3 Å water film (‘1 W’), and the total water content is 22.5 wt%. In the second system, each particle is surrounded by a 6 Å water film (‘2 W’), and the water content is 37.2 wt%. These systems were then compressed under NPT conditions (P = 100 MPa, T = 300 K) until an equilibrium state (i.e., constant volume) was achieved.
In the ‘1 W’ and ‘2 W’ systems, the water content was fixed during the NPT simulations. They therefore represent closed systems where water exchange with the surrounding environment does not occur. There is the potential for water to be expelled from the system during compression37. To explore this possibility, we designed a third system (Fig. 6D) where a slab region 10 Å thick was defined in the z direction that spans the entire simulation box in the x and y directions of the final configuration of the ‘2 W’ system. All water molecules that moved into this region during the simulation were extracted from the system by deletion. Note that water molecules can only move into this region if they can desorb from the nanoparticle surfaces and if there is pore connectivity. This extraction method was described in more detail in our previous study of methane release in kerogen nanopores40. This simulation was conducted for 89 ns, during which the water content was reduced from 37.2 wt% (i.e., that of ‘2 W’ system) to 6 wt%. The results obtained for this system are labeled as ‘2W_dewatering’. Note that after 89 ns, water molecules were still able to move to the deletion region but at a very slow rate (i.e., for the last 1 ns, only 13 water molecules were deleted). Assuming that all water molecules would eventually be expelled from the system, we deleted the remaining water molecules and continued compressing the simulation box. The results reported for this system are labeled as ‘2W_dry’.
References
Bergaya, F. & Lagaly, G. Handbook of Clay Science. 2nd edn, Vol. 5 (Elsevier, 2013).
Rotenberg, B., Marry, V., Malikova, N. & Turq, P. Molecular Simulation of Aqueous Solutions at Clay Surfaces. Journal of Physics: Condensed Matter 22 (2010).
Likos, W. J. & Lu, N. Pore-scale Analysis of Bulk Volume Change from Crystalline Interlayer Swelling in Na - and Ca -smectite. Clays and Clay Minerals 54, 515–528 (2006).
Van Loon, L. R., Glaus, M. A. & Müller, W. Anion Exclusion Effects in Compacted Bentonites: Towards a Better Understanding of Anion Diffusion. Applied Geochemistry 22, 2536–2552 (2007).
Hensen, E. J. M. & Smit, B. Why Clays Swell. The Journal of Physical Chemistry B 106, 12664–12667 (2002).
Anderson, R. L. et al. Clay Swelling - A Challenge in The Oilfield. Earth-Science Reviews 98, 201–216, https://doi.org/10.1016/j.earscirev.2009.11.003 (2010).
Madsen, F. T. Clay Mineralogical Investigations Related to Nuclear Waste Disposal. Clay Minerals 33, 109–129 (1998).
Loring, J. S. et al. In Situ Molecular Spectroscopic Evidence for CO Intercalation into Montmorillonite in Supercritical Carbon Dioxide. Langmuir 28, 7125–7128 (2012).
Michels, L. et al. Intercalation and Retention of Carbon Dioxide in a Smectite Clay promoted by Interlayer Cations. Scientific Reports 5 (2015).
Kuila, U. & Prasad, M. Specific Surface Area and Pore-size Distribution in Clays and Shales. Geophysical Prospecting 61, 341–362 (2013).
Fuller, A. J. et al. Caesium Incorporation and Retention in Illite Interlayers. Applied Clay Science 108, 128–134 (2015).
Wang, Y. F. Nanogeochemistry: Nanostructures, Emergent Properties and Their Control on Geochemical Reactions and Mass Transfers. Chemical Geology 378, 1–23 (2014).
Jin, Z. H. & Firoozabadi, A. Effect of Water on Methane and Carbon Dioxide Sorption in Clay Minerals by Monte Carlo Simulations. Fluid Phase Equilibria 382, 10–20 (2014).
Meade, R. H. Factors Influencing the Early Stages of the Compaction of Clays and Sands: Review. Journal of Sedimentary Research 36, 1085–1101, https://doi.org/10.1306/74d71604-2b21-11d7-8648000102c1865d (1966).
Cygan, R. T., Greathouse, J. A., Heinz, H. & Kalinichev, A. G. Molecular Models and Simulations of Layered Materials. Journal of Materials Chemistry 19, 2470–2481 (2009).
Knudsen, K. D., Fossum, J. O., Helgesen, G. & Haakestad, M. W. Small-angle Neutron Scattering from a Nano-layered Synthetic Silicate. Physica B: Condensed Matter 352, 247–258 (2004).
Lavikainen, L. P., Hirvi, J. T., Kasa, S., Schatz, T. & Pakkanen, T. A. Stability of Dioctahedral 2:1 Phyllosilicate Edge Structures based on Pyrophyllite Models. Theoretical Chemistry Accounts 134 (2015).
Kwon, K. D. & Newton, A. G. Structure and Stability of Pyrophyllite Edge Surfaces: Effect of Temperature and Water Chemical Potential. Geochimica et Cosmochimica Acta 190, 100–114, https://doi.org/10.1016/j.gca.2016.06.021 (2016).
Tournassat, C., Davis, J. A., Chiaberge, C., Grangeon, S. & Bourg, I. C. Modeling the Acid-Base Properties of Montmorillonite Edge Surfaces. Environmental Science & Technology 50, 13436–13445, https://doi.org/10.1021/acs.est.6b04677 (2016).
Liu, X. D., Cheng, J., Sprik, M., Lu, X. C. & Wang, R. C. Interfacial Structures and Acidity of Edge Surfaces of Ferruginous Smectites. Geochimica et Cosmochimica Acta 168, 293–301, https://doi.org/10.1016/j.gca.2015.07.015 (2015).
Liu, X. D., Lu, X. C., Cheng, J., Sprik, M. & Wang, R. C. Temperature Dependence of Interfacial Structures and Acidity of Clay Edge Surfaces. Geochimica et Cosmochimica Acta 160, 91–99, https://doi.org/10.1016/j.gca.2015.04.005 (2015).
Tazi, S., Rotenberg, B., Salanne, M., Sprik, M. & Sulpizi, M. Absolute Acidity of Clay Edge Sites from Abinitio Simulations. Geochimica et Cosmochimica Acta 94, 1–11, https://doi.org/10.1016/j.gca.2012.07.010 (2012).
Cygan, R. T., Liang, J. J. & Kalinichev, A. G. Molecular Models of Hydroxide, Oxyhydroxide, and Clay Phases and the Development of a General Force Field. The Journal of Physical Chemistry B 108, 1255–1266 (2004).
Pouvreau, M., Greathouse, J. A., Cygan, R. T. & Kalinichev, A. G. Structure of Hydrated Gibbsite and Brucite Edge Surfaces: DFT Results and Further Development of the ClayFF Classical Force Field with Metal-O-H Angle Bending Terms. The Journal of Physical Chemistry C 121, 14757–14771 (2017).
Zeitler, T. R., Greathouse, J. A., Gale, J. D. & Cygan, R. T. Vibrational Analysis of Brucite Surfaces and the Development of an Improved Force Field for Molecular Simulation of Interfaces. The Journal of Physical Chemistry C 118, 7946–7953, https://doi.org/10.1021/jp411092b (2014).
Newton, A. G., Kwon, K. D. & Cheong, D. K. Edge Structure of Montmorillonite from Atomistic Simulations. Minerals (2016).
Ho, T. A. & Striolo, A. Water and Methane in Shale Rocks: Flow Pattern Effects on Fluid Transport and Pore Structure. AICHE J. 61, 2993–2999 (2015).
Cygan, R. T., Romanov, V. N. & Myshakin, E. M. Molecular Simulation of Carbon Dioxide Capture by Montmorillonite Using an Accurate and Flexible Force Field. The Journal of Physical Chemistry C 116, 13079–13091 (2012).
Lammers, L. N. et al. Molecular Dynamics Simulations of Cesium Adsorption on Illite Nanoparticles. Journal of Colloid and Interface Science 490, 608–620 (2017).
Botan, A., Rotenberg, B., Marry, V., Turq, P. & Noetinger, B. Hydrodynamics in Clay Nanopores. The Journal of Physical Chemistry C 115, 16109–16115 (2011).
Rao, Q. & Leng, Y. S. Methane Aqueous Fluids in Montmorillonite Clay Interlayer under Near-Surface Geological Conditions: A Grand Canonical Monte Carlo and Molecular Dynamics Simulation Study. The Journal of Physical Chemistry B 118, 10956–10965 (2014).
Greathouse, J. A., Hart, D. B., Bowers, G. M., Kirkpatrick, R. J. & Cygan, R. T. Molecular Simulation of Structure and Diffusion at Smectite-Water Interfaces: Using Expanded Clay Interlayers as Model Nanopores. The Journal of Physical Chemistry C 119, 17126–17136, https://doi.org/10.1021/acs.jpcc.5b03314 (2015).
Churakov, S. V. Mobility of Na and Cs on Montmorillonite Surface under Partially Saturated Conditions. Environmental Science & Technology 47, 9816–9823, https://doi.org/10.1021/es401530n (2013).
Bourg, I. C. & Ajo-Franklin, J. B. Clay, Water, and Salt: Controls on the Permeability of Fine-Grained Sedimentary Rocks. Accounts of Chemical Research 50, 2067–2074, https://doi.org/10.1021/acs.accounts.7b00261 (2017).
Plumper, O. et al. Fluid-driven Metamorphism of the Continental Crust Governed by Nanoscale Fluid Flow. Nature Geoscience 10, 685–690, https://doi.org/10.1038/ngeo3009 (2017).
Bousige, C. et al. Realistic Molecular Model of kerogen’s Nanostructure. Nature Materials 15, 576, https://doi.org/10.1038/Nmat4541 (2016).
Meheust, Y., Dagois-Bohy, S., Knudsen, K. D. & Fossum, J. O. Mesoscopic Structure of Dry-pressed Clay Samples from Small-angle X-ray Scattering Measurements. Journal of Applied Crystallography 40, s286–s291, https://doi.org/10.1107/S0021889807008552 (2007).
Bhattacharya, S. & Gubbins, K. E. Fast Method for Computing Pore Size Distributions of Model Materials. Langmuir 22, 7726–7731, https://doi.org/10.1021/la052651k (2006).
Sing, K. S. W. et al. IUPAC Recommendations. Pure and Applied Chemistry 57, 603–619 (1985).
Ho, T. A., Criscenti, L. J. & Wang, Y. F. Nanostructural Control of Methane Release in Kerogen and Its Implications to Wellbore Production Decline. Scientific Reports 6, 28053, https://doi.org/10.1038/srep28053 (2016).
Accelyrs. Materials Studio, Release 5.5. Accelrys Software Inc., San Diego, CA (2010).
Connolly, M. L. Solvent-Accessible Surfaces of Proteins and Nucleic-Acids. Science 221, 709–713, https://doi.org/10.1126/science.6879170 (1983).
Louaer, S., Wang, Y. & Guo, L. Fast Synthesis and Size Control of Gibbsite Nanoplatelets, Their Pseudomorphic Dehydroxylation, and Efficient Dye Adsorption. ACS Applied Materials & Interfaces 5, 9648–9655 (2013).
Li, M. & Schnablegger, H. & Mann, S. Coupled Synthesis and Self-assembly of Nanoparticles to Give Structures with Controlled Organization. Nature 402, 393–395 (1999).
Ebrahimi, D., Whittle, A. J. & Pellenq, R. J. M. Effect of Polydispersity of Clay Platelets on the Aggregation and Mechanical Properties of Clay at the Mesoscale. Clays and Clay Minerals 64, 425–437, https://doi.org/10.1346/Ccmn.2016.0640407 (2016).
Churakov, S. V. & Gimmi, T. Up-Scaling of Molecular Diffusion Coefficients in Clays: A Two-Step Approach. The Journal of Physical Chemistry C 115, 6703–6714, https://doi.org/10.1021/jp112325n (2011).
Kumara, C. K., Ng, W. J., Bandara, A. & Weerasooriya, R. Nanogibbsite: Synthesis and Characterization. Journal of Colloid and Interface Science 352, 252–258 (2010).
Rosenqvist, J., Persson, P. & Sjoberg, S. Protonation and Charging of Nanosized Gibbsite (alpha-Al(OH)) Particles in Aqueous Suspension. Langmuir 18, 4598–4604 (2002).
Hiemstra, T., Vanriemsdijk, W. H. & Bruggenwert, M. G. M. Proton Adsorption Mechanism at the Gibbsite and Aluminum-Oxide Solid-Solution Interface. Netherlands Journal of Agricultural Science 35, 281–293 (1987).
Martins, D. M. S., Molinari, M., Gonçalves, M. A., Mirão, J. P. & Parker, S. C. Toward Modeling Clay Mineral Nanoparticles: The Edge Surfaces of Pyrophyllite and Their Interaction with Water. The Journal of Physical Chemistry C 118, 27308–27317, https://doi.org/10.1021/jp5070853 (2014).
Ebrahimi, D., Whittle, A. J. & Pellenq, R. J.-M. Mesoscale Properties of Clay Aggregates from Potential of Mean Force Representation of Interactions Between Nanoplatelets. The Journal of Chemical Physics 140, 154309, https://doi.org/10.1063/1.4870932 (2014).
Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular-Dynamics. Journal of Computational Physics 117, 1–19, https://doi.org/10.1006/jcph.1995.1039 (1995).
Hockney, R. W. & Eastwood, J. W. Computer simulation using particles. (Taylor & Francis Group, LLC., 1988).
Nose, S. A Molecular-Dynamics Method for Simulations in the Canonical Ensemble. Molecular Physics 52, 255–268, https://doi.org/10.1080/00268978400101201 (1984).
Pullman, B. Intermolecular Forces (Springer, 1981).
Ryckaert, J. P., Ciccotti, G. & Berendsen, H. J. C. Numerical-Integration of Cartesian Equations of Motion of a System with Constraints - Molecular-Dynamics of N-Alkanes. Journal of Computational Physics 23, 327–341, https://doi.org/10.1016/0021-9991(77)90098-5 (1977).
Amira, S., Spangberg, D. & Hermansson, K. Derivation and Evaluation of a Flexible SPC Model for Liquid Water. Chemical Physics 303, 327–334, https://doi.org/10.1016/j.chemphys.2004.04.024 (2004).
Mizan, T. I., Savage, P. E. & Ziff, R. M. Molecular Dynamics of Supercritical Water Using a Flexible SPC Model. The Journal of Physical Chemistry 98, 13067–13076, https://doi.org/10.1021/j100100a042 (1994).
Acknowledgements
Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This material is based upon work supported by the U.S. Department of Energy, National Energy Technology Laboratory and Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division.
Author information
Authors and Affiliations
Contributions
All authors designed the research. T.A.H. performed simulations and prepared first draft. Y.W., J.A.G., and L.J.C. wrote part of the paper.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ho, T.A., Greathouse, J.A., Wang, Y. et al. Atomistic Structure of Mineral Nano-aggregates from Simulated Compaction and Dewatering. Sci Rep 7, 15286 (2017). https://doi.org/10.1038/s41598-017-15639-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15639-4
This article is cited by
-
Resolving intermediates during the growth of aluminum deuteroxide (Hydroxide) polymorphs in high chemical potential solutions
Communications Chemistry (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.