Abstract
Growth of X-enes, such as silicene, germanene and stanene, requires passivated substrates to ensure the survival of their exotic properties. Using first-principles methods, we study as-grown graphene on polar SiC surfaces as suitable substrates. Trilayer combinations with coincidence lattices with large hexagonal unit cells allow for strain-free group-IV monolayers. In contrast to the Si-terminated SiC surface, van der Waals-bonded honeycomb X-ene/graphene bilayers on top of the C-terminated SiC substrate are stable. Folded band structures show Dirac cones of the overlayers with small gaps of about 0.1 eV in between. The topological invariants of the peeled-off X-ene/graphene bilayers indicate the presence of topological character and the existence of a quantum spin Hall phase.
Similar content being viewed by others
Introduction
Graphene-like group-IV, such as silicene1,2,3, germanene1,4,5, and stanene6,7, with two-dimensional (2D) honeycomb geometry have attracted much attention in recent years due to their exotic properties8,9,10,11. Their low-buckled geometries with a mixing of \(s{p}^{2}\) and \(s{p}^{3}\) hybrids but the same lateral symmetry as graphene (Gr) are responsible for extraordinary electronic and optical properties1,8, e.g., the appearance of Dirac cones near the K corner points of the hexagonal Brillouin zone (BZ). The almost zero gap, together with vanishing effective masses, indicate high room-temperature carrier mobility. The first realization of a silicene field effect transistor operating at room temperature has been reported12. Suggestions that silicene may join graphene as a wonder material13 or stanene as the next supermaterial for chip interconnects14 can be found in literature. The linearly dispersive bands of the Dirac cones give rise to a constant optical absorbance, determined by the Sommerfeld finestructure constant15. The spin-orbit interaction opens a fundamental gap in the 2D honeycomb group-IV materials15,16,17,18. They are quantum spin Hall (QSH) insulators6,16,17,18,19 with a quantized spin Hall conductivity18.
Silicene, germanene, and stanene, referred to as X-enes, are not found in nature, even not corresponding graphite-like layered materials. Therefore, X-enes have to be synthesized. There were trials to grow 2D group-IV materials on metallic and semimetallic substrates8,9,20, which however hinder a proper decoupling of the key electronic states from the underlying substrate9. A van der Waals (vdW) epitaxy of weakly interacting monolayer films on passivated or self-passivated substrates has been predicted21. Graphite-like materials with hexagonal atomic arrangements are expected to be promising substrate candidates22. Indeed, first experimental studies, e.g. on MoS2 surfaces or 2D crystals4,23, have been made, in line with theoretical investigations24. Studies also suggest graphene25,26,27, or hexagonal boron nitride (hBN)28,29, as substrates. By means of ab initio calculations, the possibility of a vdW epitaxy of silicene or stanene on insulator surfaces, e.g. CaF2(111)30, Al2O3(0001)31, and SiC(0001)32, has been investigated. In the case of the topological insulator Bi2Te3(111)7 and non-passivated SiC(0001)33 surfaces, however, the hybridization between Sn overlayer and substrate is too strong.
The graphene/SiC systems have been widely studied to demonstrate epitaxial growth of graphene34,35,36,37. The passivation of SiC substrates due to the graphene overlayers may open a venue towards X-enes on a substrate available from the well-known graphene-on-SiC technology. Indeed, deposition of Sb2Te3 films on monolayer epitaxial graphene and quasi freestanding bilayer graphene was already achieved38. In this letter, we combine the ideas of deposition of silicene, germanene, and stanene on 2D hexagonal atomic arrangements and passivated wide-gap insulators. We investigate geometries and electronic structures of honeycomb group-IV crystals on graphene/4H-SiC(0001) and graphene/4H-SiC(000 \(\bar{1}\)) substrates. The topological character of the X-ene/Gr bilayers and the existence of a quantum spin Hall phase are investigated as well.
Results and Discussion
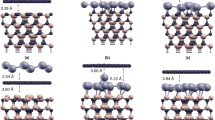
The repeated slab method39 is applied to simulate the substrate covered by the overlayers. The individual slabs are separated by a vacuum region of more than 15 Å thickness. One slab is illustrated in Fig. 1. The SiC(000 \(\bar{1}\)) substrate is represented by four Si-C bilayers, whose bottom side is passivated by hydrogen atoms (see32). On top of the uppermost Si atomic layer, a graphene layer is deposited in an optimized distance \({d}_{\text{SiC}/\text{Gr}}\). The Gr/SiC(000 \(\bar{1}\)) substrate is then decorated by a X-ene crystal in a optimized distance \({d}_{\mathrm{Gr}/{\rm{X}}-{\rm{ene}}}\). The lattice mismatch between silicene (germanene, stanene), Gr, and SiC is given by the lateral lattice constants a = 3.87 (4.06, 4.67) Å, 2.47 Å, and 3.8 Å.
In order to have almost vanishing in-plane strains, one has to extend and rotate the 2D hexagonal cells of the three materials. The stacking of the two honeycomb crystals over the hexagonal SiC surface was explicitly obtained by the coincidence lattice method40. The non-primitive unit cells of the adapted 2D lattices are listed in Table 1 together with the resulting biaxial strains.
Energetics and Geometry
The cell size of the SiC(0001) surfaces is somewhat smaller than the favored (\(6\sqrt{3}\) × \(6\sqrt{3})\) R30° reconstruction, but larger than the favored 2 × 2 translational symmetry for graphene formation on SiC(000 \(\bar{1}\)) surfaces41. However, for the C-terminated surface, the formation of high-quality graphene islands has been also reported with a \(\sqrt{3}\) × \(\sqrt{3}\) reconstruction of the interface34. Here, because of the constraint due to the third X-ene layer, we study SiC surface cells with reasonable numbers of atoms between 12 and 19. In the case of stanene we use a 4 × 4 translational symmetry, which covers four 2 × 2 cells of the SiC(000 \(\bar{1}\)) surface identified for growth of graphene. The starting geometries are relaxed. Thereby the lateral unit cell of the SiC slab is conserved, while the atomic positions are allowed to move free. The distance \({d}_{\text{SiC}/\text{Gr}}\) of the Gr overlayer is found by varying the vdW gap between the two systems, Gr and SiC. On top of the bilayer substrate, the X-ene layer is added and a similar procedure is adopted to investigate its geometry and energetics.
The Gr layers deposited on C-terminated SiC(000 \(\bar{1}\)) surfaces remain unbuckled (see Supplementary Fig. S1). The distances \({d}_{\mathrm{SiC}/\mathrm{Gr}}=3.03-3.06\) Å indicate vdW interaction. They are equal to the characteristic values for vdW bonded layers21,30,42. In contrast, on Si-terminated SiC(0001) the smaller distances \({d}_{\mathrm{SiC}/\mathrm{Gr}}=1.81-1.93\) Å are due to vertical, partially covalent Si-C bonds as displayed in Fig. 1. A vdW bonding of X-ene only happens at the Gr/SiC(000 \(\bar{1}\)) system. The X-ene/Gr distances correspond to characteristic lengths found for freestanding double layers25. The buckling amplitudes of the X-ene layer are practically the same as in the freestanding crystals43. The reasons for the different behavior of graphene grown on C- and Si-terminated, polar SiC surfaces have been discussed elsewhere44. The energetics and the structural results given in Supplementary Table S1 clearly indicate the favorization of group-IV honeycomb crystal growth on graphene that is deposited on the C-terminated SiC(000 \(\bar{1}\)) substrate, instead of the Si-terminated surface.
Quasiparticle Band Structures of X-ene/Gr/SiC(000\(\bar{1}\))
For the most stable configurations, quasiparticle band structures versus the small joint 2D BZ of the trilayers are displayed in Fig. 2. Band states are projected onto atomic sites. The band structures of X-ene/Gr/SiC(0001) in Supplementary Fig. S2 show that folded linear bands of graphene and X-ene cannot be clearly identified. Due to the formation of covalent bonds between the monolayer and the substrate, SiC surface levels are mixed with graphene bands, giving rise to new substrate energy levels. A similar hybridization also happens for the X-ene overlayer, especially for silicene, the monolayer most strongly bound to the Gr layer. For germanene, structural distortions and interlayer bonding affect the monolayer electronic properties more slightly than silicene, but the modification of its conduction band dispersion is still found at K (see Supplementary Fig. S2). In addition, a competitive indirect gap from K to \({\rm{\Gamma }}\) is also observed for the bands projected onto the first BZ.
We focus on the geometries on SiC(000 \(\bar{1}\)) surfaces, where the properties of the honeycomb graphene and X-ene layers are almost kept unchanged. In this case, contributions of the three layers can be identified in Fig. 2 by applying the folding arguments onto the BZs, which are related to the large lateral unit cells described in Table 1. In the graphene case, the Dirac cones at corner points K of the 1 × 1 BZ are again folded onto K points of the smaller BZs in all cases. For X-ene this is only true for germanene and stanene. In the silicene case, according to the coincidence lattice given in Table 1, linear bands around K are folded onto the \({\rm{\Gamma }}\) point. Folded bulk states of SiC do only appear below \(-0.6\) eV. The flat green bands, which pin the Fermi level at zero energy, are due to the unsaturated C-dangling bonds of the SiC(000 \(\bar{1}\)) surface, which are partly filled by a small electron transfer from the X-ene/graphene overlayer (see Fig. 2). They may behave as the dangling bond band at the unreconstructed 1 × 1 surface in a spin-polarized calculation, and open a gap dominated by strong electron-correlation effects45, which cannot be described by a semilocal XC functional. Nevertheless, the electron transfer moves down the Fermi level. Correspondingly, the band states around the Dirac nodes of graphene and X-ene become empty. However, because the different band fillings the Dirac points of X-enes are slight above in energy compared to that of graphene. The vdW interaction in the X-ene layers opens small gaps, between the Dirac cones, of 96 meV at Γ (silicene), 116 meV at K (germanene), and 146 meV at K (stanene), similar as for other vdW depositions of X-enes21,25,30. The gap values are only slightly larger than those obtained for freestanding bilayers25. The exceptional case of germanene is illustrated by the hybridization of germanene- and graphene-derived states near the Dirac points. The orbital and element projections in Figs. S3 and S4 suggest that the hybridization involves Cp z and Gep z states, i.e., different atoms but the same orbital symmetry.
Topological Properties
The survival of the X-ene Dirac cones with small gaps in Fig. 2 suggests to check rigorously the topological nature of the overlayers. Because of the surface dangling bonds of the SiC substrate, we determine the Z 2 invariants46 only for the X-ene/graphene bilayers peeled off the SiC(000 \(\bar{1}\)) surface. In this case, for example, the band structure of the germanene/graphene overlayer with substrate in Fig. 2(b) shows the Dirac cones of both honeycomb materials at K slightly below the Fermi level. Because of the absence of inversion symmetry, we apply the method of Yu et al.47 based on the evolution of the charge centers of the Wannier functions (WCC) between two time-reversal invariant momenta (TRIM) of the BZ46,48 and implemented in the VASP code18,49. The topological invariant Z 2 is determined by the crossings of an arbitrary reference line modulo 2 connecting two TRIM points within the WCC phase evolution \({\rm{\Theta }}\) along the k y line47.
When the SiC(000 \(\bar{1}\)) substrate is peeled off, the surface dangling bonds represented in Fig. 2 as valence band top disappear and the Fermi level is pinned by the Dirac-like bands of X-enes (see Fig. 3 and Supplementary Fig. S5). The weak vdW interaction between the X-enes and graphene is not strong enough to open a graphene gap, resulting in a half-metallic system due charge transfer from X-enes to graphene. Similar processes occur when the SiC(000 \(\bar{1}\)) substrate is present. In this case, however, charge is transferred from the overlayers to the dangling bond bands of the surface, making the Dirac cones of X-enes and graphene almost unoccupied. The topological behavior present in the freestanding X-enes is affected by the interaction with graphene. For silicene, this effect is strong enough to destroy the topological character of the system, as indicated by only horizontal lines in Supplementary Fig. S6. For germanene there is a very small charge transfer to graphene, as can be seen by the coincidence position of the Dirac cones of both overlayers in Fig. 3. As a result the topological properties of germanene are preserved, as indicated by the Kramers pair switchings by the interconnected curved lines in the WCC evolution in Fig. 4. These pair switchings are illustrated by zooms in energy and k-space in the part (b) of the figure. It makes clear that gaps do not appear in the part (a). They only seemingly appear due to the low k-point density presented there.
In the stanene case (see Supplementary Fig. S6), strong charge transfer to graphene also occurs. The topological properties are strongly affected. Although some lines in the WCC evolution appear to interconnect, the topological behavior is not clear. For germanene/graphene the presence of pair switchings simply give a topological invariant \({Z}_{2}=1\), which suggests that this system is a QSH phase18,46,49.
Summary and Conclusions
In summary, based on first-principles calculations including vdW interaction in the ground state and quasiparticle effects in the electronic structure, we demonstrated that C-terminated SiC(000 \(\bar{1}\)) slabs passivated by graphene may serve as substrates for a vdW epitaxy of graphene-like group-IV layers with low-buckled honeycomb geometry. Due to the reduced overlayer-substrate interaction Dirac cones almost survive in the folded band structures, although small fundamental gaps are opened. The resulting germanene/graphene bilayer is a topological system. Its topological invariant indicates the realization of a QSH phase. The silicene/graphene bilayer clearly becomes a trivial system while the topology of stanene/graphene system is unclear. Our results suggest to use graphene-covered SiC(000 \(\bar{1}\)) substrates for the deposition of silicene, germanene or stanene. Common intercalation may result in X-ene/graphene bilayer structures with topological character.
Methods
Ab initio studies of the energetic stability and the equilibrium geometries of the X-enes on graphene covered SiC substrates are performed within the density functional theory (DFT) by using the projector-augmented wave (PAW) method for generation of wave functions and pseudopotentials50, as implemented in the Vienna ab-initio simulation package (VASP)51. Exchange and correlation (XC) are described within the Perdew-Burke-Ernzerhof (PBE) functional52. To account explicitly for vdW interaction, the optB86b functional53 is employed. The plane-wave expansion is restricted by a kinetic energy cutoff of 400 eV, while the BZ integrations are carried out with a 3 × 3 × 1 Γ-centered Monkhorst-Pack k-point mesh.
Equilibrium geometries are found by minimizing the total energy with a stopping criterion of 0.01 meV/atom. Atomic positions are then relaxed until the Hellmann-Feynman forces become smaller than 10 meV/Å. Band structures require quasiparticle studies to account for the excitation aspect. A computation of the quasiparticle self-energies for all atomic arrangements needed is computationally too time-consuming. Moreover, spin-orbit interaction has to be taken into account. We apply the approximate DFT-1/2 method54. Its characteristic CUT parameters, the radii to model the XC self-energy for a constituting atom, have been described elsewhere32,43. For instance, for the excited holes in C2p states it is calculated to be 2.89 bohr. As a result, for SiC we compute an indirect gap \({E}_{g}\mathrm{=3.01}\) eV, which is very close to the experimental value of 3.2 eV.
References
Cahangirov, S., Topsakal, M., Aktürk, E., Sahin, H. & Ciraci, S. Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium. Phys. Rev. Lett. 102, 236804, https://doi.org/10.1103/PhysRevLett.102.236804 (2009).
Feng, B. et al. Evidence of Silicene in Honeycomb Structures of Silicon on Ag(111). Nano Lett. 12, 3507–3511, https://doi.org/10.1021/nl301047g (2012).
Xu, X. et al. Effects of Oxygen Adsorption on the Surface State of Epitaxial Silicene on Ag(111). Sci. Rep. 4, 7543 https://doi.org/10.1038/srep07543 (2014).
Zhang, L. et al. Structural and Electronic Properties of Germanene on MoS2. Phys. Rev. Lett. 116, 256804, https://doi.org/10.1103/PhysRevLett.116.256804 (2016).
Dávila, M. E. & Le Lay, G. Few layer epitaxial germanene: a novel two-dimensional Dirac material. Sci. Rep. 6, 20714 https://doi.org/10.1038/srep20714 (2016).
Xu, Y. et al. Large-Gap Quantum Spin Hall Insulators in Tin Films. Phys. Rev. Lett. 111, 136804, https://doi.org/10.1103/PhysRevLett.111.136804 (2013).
Zhu, F. et al. Epitaxial growth of two-dimensional stanene. Nat. Mater. 14, 1020–1025, https://doi.org/10.1038/nmat4384 (2015).
Zhao, J. et al. Rise of silicene: A competitive 2D material. Prog. Mater. Sci. 83, 24–151, https://doi.org/10.1016/j.pmatsci.2016.04.001 (2016).
Grazianetti, C., Cinquanta, E. & Molle, A. Two-dimensional silicon: the advent of silicene. 2D Mater. 3, 012001, http://stacks.iop.org/2053-1583/3/i=1/a=012001?key=crossref.e5002d600974292af32b7f784241927a. https://doi.org/10.1088/2053-1583/3/1/012001 (2016).
Acun, A. et al. Germanene: the germanium analogue of graphene. J. Phys. Condens. Matter 27, 443002, http://stacks.iop.org/0953-8984/27/i=44/a=443002?key=crossref.a0ef4847cc20303dcbe68e889d63844c, https://doi.org/10.1088/0953-8984/27/44/443002 (2015).
Fang, Y. et al. Quantum Spin Hall States in Stanene/Ge(111). Sci. Rep. 5, 14196, https://doi.org/10.1038/srep14196 (2015).
Tao, L. et al. Silicene field-effect transistors operating at room temperature. Nat. Nanotechnol. 10, 227–231, https://doi.org/10.1038/nnano.2014.325 (2015).
Brumfiel, G. Sticky problem snares wonder material. Nat. 495, 152–153, https://doi.org/10.1038/495152a (2013).
Choi, C. Q. Could Atomically Thin Tin Transform Electronics? Sci. Am. December, http://www.scientificamerican.com/article/could-atomically-thin-tin-transform-electronics/ (2013).
Matthes, L., Pulci, O. & Bechstedt, F. Massive Dirac quasiparticles in the optical absorbance of graphene, silicene, germanene, and tinene. J. Phys. Condens. Matter 25, 395305, http://www.ncbi.nlm.nih.gov/pubmed/24002054 http://stacks.iop.org/0953-8984/25/i=39/a=395305?key=crossref.b698cb518156faea9c5f1ab0f29ee341, https://doi.org/10.1088/0953-8984/25/39/395305 (2013).
Liu, C. C., Feng, W. & Yao, Y. Quantum spin Hall effect in silicene and two-dimensional germanium. Phys. Rev. Lett. 107, 1–4, https://doi.org/10.1103/PhysRevLett.107.076802 (2011).
Liu, C.-C., Jiang, H. & Yao, Y. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin. Phys. Rev. B 84, 195430, https://doi.org/10.1103/PhysRevB.84.195430 (2011).
Matthes, L., Küfner, S., Furthmüller, J. & Bechstedt, F. Quantization and topological states in the spin Hall conductivity of low-dimensional systems: An ab initio study. Phys. Rev. B 93, 121106, https://doi.org/10.1103/PhysRevB.93.121106 (2016).
Chang, C.-Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477, https://doi.org/10.1038/nmat4204 (2015).
Resta, A. et al. Atomic Structures of Silicene Layers Grown on Ag(111): Scanning Tunneling Microscopy and Noncontact Atomic Force Microscopy Observations. Sci. Rep. 3, 2399, https://doi.org/10.1038/srep02399 (2013).
Kokott, S., Matthes, L. & Bechstedt, F. Silicene on hydrogen-passivated Si(111) and Ge(111) substrates. Phys. Status Solidi - Rapid Res. Lett. 7, 538–541, https://doi.org/10.1002/pssr.201307215 (2013).
Gao, G. et al. Artificially stacked atomic layers: Toward new van der waals solids. Nano Lett. 12, 3518–3525, https://doi.org/10.1021/nl301061b (2012).
Chiappe, D. et al. Two-dimensional Si nanosheets with local hexagonal structure on a MoS 2 surface. Adv. Mater. 26, 2096–2101, https://doi.org/10.1002/adma.201304783 (2014).
Scalise, E. et al. Engineering the electronic properties of silicene by tuning the composition of MoX 2 and GaX (X=S,Se,Te) chalchogenide templates. 2D Mater. 1, 011010, http://stacks.iop.org/2053-1583/1/i=1/a=011010 http://stacks.iop.org/2053-1583/1/i=1/a=011010?key=crossref.c10caa25a3cd6e4c2224b01662268a23, https://doi.org/10.1088/2053-1583/1/1/011010 (2014).
Cai, Y., Chuu, C.-P., Wei, C. M. & Chou, M. Y. Stability and electronic properties of two-dimensional silicene and germanene on graphene. Phys. Rev. B 88, 245408, https://doi.org/10.1103/PhysRevB.88.245408 (2013).
De Crescenzi, M. et al. Formation of Silicene Nanosheets on Graphite. ACS Nano 10, 11163–11171, https://doi.org/10.1021/acsnano.6b06198 (2016).
Zuo, Z. et al. In-situ epitaxial growth of graphene/h-BN van der Waals heterostructures by molecular beam epitaxy. Sci. Rep. 5, 14760 https://doi.org/10.1038/srep14760 (2015).
Wang, M., Liu, L., Liu, C. C. & Yao, Y. Van der Waals heterostructures of germanene, stanene, and silicene with hexagonal boron nitride and their topological domain walls. Phys. Rev. B - Condens. Matter Mater. Phys. 93, 1–8, https://doi.org/10.1103/PhysRevB.93.155412 (2016).
Tang, S. et al. Precisely aligned graphene grown on hexagonal boron nitride by catalyst free chemical vapor deposition. Sci. Rep. 3, 2666, https://doi.org/10.1038/srep02666 (2013).
Kokott, S., Pflugradt, P., Matthes, L. & Bechstedt, F. Nonmetallic substrates for growth of silicene: an ab initio prediction. J. Phys. Condens. Matter 26, 185002, http://www.ncbi.nlm.nih.gov/pubmed/24728001 http://www.ncbi.nlm.nih.gov/pubmed/24728001%5Cnhttp://stacks.iop.org/0953-8984/26/i=18/a=185002?key=crossref.cb377c64ffb5917d473f0f255a1956fd, https://doi.org/10.1088/0953-8984/26/18/185002 (2014).
Chen, M. X., Zhong, Z. & Weinert, M. Designing substrates for silicene and germanene: First-principles calculations. Phys. Rev. B 94, 075409, https://doi.org/10.1103/PhysRevB.94.075409 (2016).
Matusalem, F., Bechstedt, F., Marques, M. & Teles, L. K. Quantum spin Hall phase in stanene-derived overlayers on passivated SiC substrates. Phys. Rev. B 94, 241403, https://doi.org/10.1103/PhysRevB.94.241403 (2016).
Glass, S. et al. Triangular Spin-Orbit-Coupled Lattice with Strong Coulomb Correlations: Sn Atoms on a SiC(0001) Substrate. Phys. Rev. Lett. 114, 247602, https://doi.org/10.1103/PhysRevLett.114.247602 (2015).
Berger, C. et al. Electronic Confinement and Coherence in Patterned Epitaxial Graphene. Science (80-.). 312, 1191–1196, https://doi.org/10.1126/science.1125925 (2006).
Emtsev, K. V. et al. Towards wafer-size graphene layers by atmospheric pressure graphitization of silicon carbide. Nat. Mater. 8, 203–207, https://doi.org/10.1038/nmat2382 (2009).
Qi, Y., Rhim, S. H., Sun, G. F., Weinert, M. & Li, L. Epitaxial graphene on SiC(0001): More than just honeycombs. Phys. Rev. Lett. 105, 3–6, https://doi.org/10.1103/PhysRevLett.105.085502 (2010).
Sforzini, J. et al. Approaching Truly Freestanding Graphene: The Structure of Hydrogen-Intercalated Graphene on 6H-SiC(0001). Phys. Rev. Lett. 114, 106804, https://doi.org/10.1103/PhysRevLett.114.106804 (2015).
Boschker, J. E. et al. Coincident-site lattice matching during van der Waals epitaxy. Sci. Rep. 5, 18079, https://doi.org/10.1038/srep18079 (2015).
Bechstedt, F. Principles of Surface Physics. Advanced Texts in Physics http://link.springer.com/ https://doi.org/10.1007/978-3-642-55466-7 (Springer, Berlin, Heidelberg, 2003).
Koda, D. S., Bechstedt, F., Marques, M. & Teles, L. K. Coincidence Lattices of 2D Crystals: Heterostructure Predictions and Applications. J. Phys. Chem. C 120, 10895–10908, https://doi.org/10.1021/acs.jpcc.6b01496 (2016).
Forbeaux, I., Themlin, J.-M. & Debever, J.-M. Heteroepitaxial graphite on 6H-SiC(0001): Interface formation through conduction-band electronic structure. Phys. Rev. B 58, 16396–16406, https://doi.org/10.1103/PhysRevB.58.16396 (1998).
Björkman, T., Gulans, A., Krasheninnikov, A. V. & Nieminen, R. M. Van der Waals bonding in layered compounds from advanced density-functional first-principles calculations. Phys. Rev. Lett. 108, 1–5, https://doi.org/10.1103/PhysRevLett.108.235502 (2012).
Matusalem, F., Marques, M., Teles, L. K. & Bechstedt, F. Stability and electronic structure of two-dimensional allotropes of group-IV materials. Phys. Rev. B 92, 045436, https://doi.org/10.1103/PhysRevB.92.045436 (2015).
Varchon, F. et al. Electronic Structure of Epitaxial Graphene Layers on SiC: Effect of the Substrate. Phys. Rev. Lett. 99, 126805, https://doi.org/10.1103/PhysRevLett.99.126805 (2007).
Bechstedt, F. & Furthmüller, J. Electron correlation effects on SiC(111) and SiC(0001) surfaces. J. Phys. Condens. Matter 16, S1721–S1732, http://stacks.iop.org/0953-8984/16/i=17/a=014?key=crossref.eb36290c6d234fcc9b6941df65d1f628. https://doi.org/10.1088/0953-8984/16/17/014 (2004).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302, https://doi.org/10.1103/PhysRevB.76.045302 (2007).
Yu, R., Qi, X. L., Bernevig, A., Fang, Z. & Dai, X. Equivalent expression of Z$_2$ topological invariant for band insulators using the non-Abelian Berry connection. Phys. Rev. B 84, 075119, https://doi.org/10.1103/PhysRevB.84.075119 (2011).
Fu, L., Kane, C. L. & Mele, E. J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 98, 106803, https://doi.org/10.1103/PhysRevLett.98.106803 (2007).
Matthes, L., Küfner, S., Furthmüller, J. & Bechstedt, F. Intrinsic spin Hall conductivity in one-, two-, and three-dimensional trivial and topological systems. Phys. Rev. B 94, 085410, https://doi.org/10.1103/PhysRevB.94.085410 (2016).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775, https://doi.org/10.1103/PhysRevB.59.1758 (1999).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186, https://doi.org/10.1103/PhysRevB.54.11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868, https://doi.org/10.1103/PhysRevLett.77.3865 (1996).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131, https://doi.org/10.1103/PhysRevB.83.195131 (2011).
Ferreira, L. G., Marques, M. & Teles, L. K. Approximation to density functional theory for the calculation of band gaps of semiconductors. Phys. Rev. B 78, 125116, https://doi.org/10.1103/PhysRevB.78.125116 (2008).
Acknowledgements
This work was supported by the Brazilian funding agencies CNPq (grants. No. 305405/2014-4 and No. 308742/2016-8), CAPES (grants No. 23038.005810/2014-34, No. 88881.068355/2014-01 within the PVE/CsF program and scholarship grant), together with São Paulo Research Foundation (FAPESP) (grants No. 2012/507383-3 and No. 2014/13907-7). The authors also acknowledge the National Laboratory for Scientific Computing (LNCC/MCTI, Brazil) for providing HPC resources of SDumont supercomputer.
Author information
Authors and Affiliations
Contributions
F.B. conceived the project, F.M. and D.S.K. did the calculations, all authors analysed the results. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Matusalem, F., Koda, D.S., Bechstedt, F. et al. Deposition of topological silicene, germanene and stanene on graphene-covered SiC substrates. Sci Rep 7, 15700 (2017). https://doi.org/10.1038/s41598-017-15610-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15610-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.