Abstract
Quantum coherence is one of the old but always important concepts in quantum mechanics, and now it has been regarded as a necessary resource for quantum information processing and quantum metrology. However, the question of how to quantify the quantum coherence has just been paid the attention recently (see, e.g., Baumgratz et al. PRL, 113. 140401 (2014)). In this paper we verify that the well-known quantum Fisher information (QFI) can be utilized to quantify the quantum coherence, as it satisfies the monotonicity under the typical incoherent operations and the convexity under the mixing of the quantum states. Differing from most of the pure axiomatic methods, quantifying quantum coherence by QFI could be experimentally testable, as the bound of the QFI is practically measurable. The validity of our proposal is specifically demonstrated with the typical phase-damping and depolarizing evolution processes of a generic single-qubit state, and also by comparing it with the other quantifying methods proposed previously.
Similar content being viewed by others
Introduction
Originally, the concept of coherence was introduced to describe the interference phenomenon among waves. In recent years, quantum coherence has been paid much attention, as it is a necessary resource for various quantum engineerings, e.g., quantum key distributions1, quantum computation2, and quantum metrology3, etc. Indeed, the basic advantage of the quantum information processing over the classical counterpart is based on the utilizations of quantum coherence.
Quantum coherence is a fundamental phenomenon in quantum physics. However, as one of the important physical resources, its measurement is not easy to be defined. In fact, in recent years various functions such as the fidelity based distance measurement4, trace distance5, relative entropy6, quantum correlation7,8, and the skew information9,10 etc., have been suggested to quantify the quantum coherence. With these measurements, certain properties of quantum coherence, typically, e.g., the distillation of coherence11,12 and the nonclassical correlations7,8,13, have been described. Note that the quantum correlation has been well measured by quantum discord14 and other distance functions15,16. Furthermore, quantum entanglement, as a specifical representation of the quantum correlation in various multipartite quantum systems, has been quantified both pure axiomatically and experimentally17,18,19,20. The former is achieved by introducing some mathematical functions, such as the entanglement entropy17, entanglement of distillation12, and entanglement cost19, etc. While, the latter one was implemented by measuring the violations of the Bell-type inequalities, although certain exceptional cases wherein the non-locality vanishes but entanglement persists, still exist21.
A basic question is, how to generically quantify the quantum coherence carried by an arbitrary quantum state of a quantum system4,6,9,22? Interestingly, Baumgratz et al 6. pointed out that, any quantity \(C(\rho )\) for effectively measuring the amount of quantum coherence in a quantum state \(\rho \) should satisfy the following conditions:
(C1) It should be non-negative and vanishes if and only if the state is incoherent, i.e. \(C(\rho )\ge 0\) and \(C(\rho )=0\) iff \(\rho \in \) \(\Pi \) with \(\Pi \) being the set of incoherent states.
(C2a) It should be non-increasing under any incoherent completely positive and trace preserving (ICPTP) operation, i.e., \(C(\rho )\ge {C}_{ICPTP}(\rho )\); or (C2b) More strictly, it should be monotonic for average under subselection based on the measurement outcomes, i.e., \(C(\rho )\ge \sum {p}_{n}C({A}_{n}\rho {A}_{n}^{\dagger }/{p}_{n})\); and
(C3) It should be convex, i.e., contractive under mixing of quantum states; \(\sum {p}_{n}C({\rho }_{n})\ge C(\sum {p}_{n}{\rho }_{n})\) for any ensemble \(\{{p}_{n},{\rho }_{n}\}\).
In what follows, these conditions will be called as Baumgratz et al.’s criticism for simplicity. It is easy to verify that, once the conditions (C2b) and (C3) are satisfied simultaneously, the condition (C2a) is satisfied naturally. Above, the ICPTP operation maps an incoherent state to another incoherent state. It is defined as follows. Generally, any quantum operation \({\rm{\Phi }}(\rho )\) performed on the quantum state \(\rho \) can be written as
in the Kraus representation, wherein \(\{{A}_{\mu }:\,\,{\sum }_{\mu }{A}_{\mu }^{\dagger }{A}_{\mu }=I\}\) are the complete-positive-trace-preserving operators. Also, any incoherent state can always be expressed as \(\delta ={\sum }_{i\mathrm{=1}}^{d}{p}_{i}|i\rangle \langle i|\), with the zero off-diagonal elements. Furthermore, if the operation \({A}_{\mu }\) satisfies the condition6: \({A}_{\mu }\hat{\delta }{A}_{\mu }^{\dagger }\in \) \({\rm{\Pi }}\), with \({\rm{\Pi }}\) denoting the set of incoherent states for an arbitrary \(\hat{\delta }\in \) \({\rm{\Pi }}\) and \(\mu \), then \({A}_{\mu }\) is an ICPTP and reads23: \({A}_{\mu }={\sum }_{k,l}^{n}{a}_{kl}|k\rangle \langle l|\), wherein every \(k\le n\) occurs at most once. Obviously, the operator \({A}_{\mu }\) maps a diagonal matrix to another diagonal one. In this sense, the usual dephasing, depolarizing, phase-damping and amplitude-damping processes can be treated as the incoherent operations, respectively.
Besides various measurements proposed previously, in this paper we introduce another quantity, i.e., the quantum Fisher information (QFI), to generically quantify the quantum coherence. As every ICPTP operation can be obtained from a partial trace on an extended system under certain unitary transformations24, we specifically show that, the QFI satisfies the Baumgratz et al.’s criticism. Since QFI is also mathematically related to some other functions proposed previously, such as the relative entropy25, fidelity based on the distance measurement26, and the skew information27 etc., for quantifying the quantum coherence, it is logically reasonable28 by using the QFI to quantify the quantum coherence. However, differing from most of the pure axiomatic functions proposed previously, the present proposal by using the QFI to quantify quantum coherence is experimentally testable, as the lower- and upper bounds of the QFI are practically measurable. The validity of our proposal will be demonstrated specifically with the evolutions of a generic one-qubit state under the typical phase-damping and depolarizing processes, respectively.
Quantum Fisher information and its Properties
For completeness, we briefly review QFI and some of its properties29, which will be utilized below to prove our arguments.
As we know that some of physical quantities are not directly accessible but can only be indirectly estimated from the measurement outcomes of the other observable(s). The quantum estimation theory has been developed to focus the relevant parameter estimation problems. Typically, the well-known Cramér-Rao inequality26 states that the lower bound of the variance of the estimated quantity \(\theta \) should be limited by
with \({F}_{Q}({\rho }_{\theta })\) being the QFI of the quantum state \({\rho }_{\theta }\). Therefore, the QFI plays a very important role in quantum metrology and determines the reachable accuracy of the estimated quantity. Historically, there are several definitions of the QFI from different perspectives, see, e.g.,27. In quantum metrology, in term of the selfadjoint operator symmetric logarithmic derivative (SLD) \({L}_{\theta }\) 29, defined by
for a quantum state \({\rho }_{\theta }\) with a parameter \(\theta \) being estimated, the QFI is generically defined as
Note that the equation (3) is a Lyapunov matrix equation, whose generic solution can be written as
By writing \({\rho }_{\theta }\) in its eigenbasis, i.e., \({\rho }_{\theta }={\sum }_{i}{\mu }_{i}|{\mu }_{i}\rangle \langle {\mu }_{i}|\), such a generic solution can be specifically expressed as
As a consequence, with Eq. (4) the QFI is given by
Physically30,31, the parameter \(\theta \) expected to be estimated coincides with a global phase. It can be encoded by applying a unitary transformation: \({U}_{\theta }=\exp (-i\theta H)\), to a quantum state, i.e.,
Here, \(H\) is the Hamiltonian of the quantum system with the initial state \(\rho \). Typically, \(H\) is assumed to be independent from \(\theta \). As a consequence, Eq. (7) becomes26:
with \(\{{\lambda }_{i},|{\lambda }_{i}\rangle \}\) being the eigenvalues and the corresponding eigenvectors of the density operator \(\rho \), respectively.
It is proven that the QFI possesses some important properties. First, it is additive under tensoring32, i.e.,
for a composite system \(A+B\). Next, it is unchanged under any unitary transformation \(U\) commuting with the Hamiltonian \(H\) 32, i.e.,
Axiomatically, the QFI links the fidelity of the distance measurement for two quantum states \(\rho (t)\) and \(\rho (t+{\rm{\Delta }}t)\) as26:
with \({D}_{B}^{2}({\rho }_{1},{\rho }_{2})=\mathrm{4(1}-\sqrt{{F}_{B}({\rho }_{1},{\rho }_{2})})\) being the Bures distance, and \({F}_{B}({\rho }_{1},{\rho }_{2})=(Tr\sqrt{\sqrt{{\rho }_{1}}{\rho }_{2}\sqrt{{\rho }_{1}}})\) the Uhlmann fidelity. Here, \({\rho }_{1}=\rho (t)\) and \({\rho }_{2}=\rho (t+{\rm{\Delta }}t)\).
More interestingly, one can always explicitly construct a pure-state ensemble of a given mixed state \(\rho ={\sum }_{k}{p}_{k}|{{\rm{\Psi }}}_{k}\rangle \langle {{\rm{\Psi }}}_{k}|\) in the basis \(\{|{{\rm{\Psi }}}_{k}\rangle \}\), wherein the QFI in Eq. (9) can be rewritten specifically as33,34
Here, \({({\rm{\Delta }}H)}_{|{{\rm{\Psi }}}_{k}\rangle }^{2}=\langle {{\rm{\Psi }}}_{k}|{H}^{2}|{{\rm{\Psi }}}_{k}\rangle -{\langle {{\rm{\Psi }}}_{k}|H|{{\rm{\Psi }}}_{k}\rangle }^{2}\) is the variance of the observable \(H\) for the pure state \(|{{\rm{\Psi }}}_{k}\rangle \), and its relevant standard variance reads \({({\rm{\Delta }}H)}_{\rho }^{2}={sup}_{\{{p}_{k},|{\rm{\Psi }}\rangle \}}{p}_{k}{({\rm{\Delta }}H)}_{|{{\rm{\Psi }}}_{k}\rangle }^{2}\). Consequently33, we have the following inequality chain:
where the equality chain holds only for the pure states. Obviously, this inequality chain implies that the upper bound of the QFI is \(\mathrm{4(}{\rm{\Delta }}H{)}_{\rho }^{2}\), while the above Cramér-Rao inequality indicates that the lower bound of the QFI is \(\mathrm{1/(}{\rm{\Delta }}\theta {)}^{2}\). Given both the lower- and upper bounds of the QFI are observable, quantifying the quantum coherence by the QFI should be physically measurable, at least theoretically.
Results
We now prove that the QFI satisfies the Baumgratz et al.’s criticism and thus can be used to quantify the quantum coherence.
Verification of condition (C1)
It is easy to prove that the QFI satisfies the condition (C1). In fact, if the density matrix of the state \(\rho ={\sum }_{k}{p}_{k}|k\rangle \langle k|\) is diagonal in the eigenvectors \(\{|k\rangle \}\) of \(H\), then the minimum average of variance of the observable \(H\) is \({\sum }_{k}{p}_{k}{({\rm{\Delta }}H)}_{|k\rangle }^{2}=0\), as \({({\rm{\Delta }}H)}_{|k\rangle }^{2}=0\). On the other hand, if the density matrix is not diagonal, then for any decomposition of \(\rho \): \(\rho ={\sum }_{k}{p}_{k}|{{\rm{\Psi }}}_{k}\rangle \langle {{\rm{\Psi }}}_{k}|\), one can always find a state \(|{{\rm{\Psi }}}_{n}\rangle \notin \{|k\rangle \}\) in which \({({\rm{\Delta }}H)}_{|{{\rm{\Psi }}}_{n}\rangle }^{2} > 0\). As a consequence,
is always satisfied. Therefore, with the Eq. (13) the QFI vanishes if and only if the quantum system is in an incoherent state. This indicates that QFI satisfies the condition (C1) satisfactorily.
Verification of condition (C3)
The convexity of the QFI can be generically expressed as
with \({p}_{k}\ge 0\), \(\sum {p}_{k}\mathrm{=1}\), and \({F}_{Q}^{R}(\tilde{\rho },H)\) being the reduced QFI (to distinguish from the QFI \({F}_{Q}(\rho ,H)\)). To verify such a feature, we consider a typical quantum state: \(\rho =p{\rho }_{1}+\mathrm{(1}-p){\rho }_{2}\). Obviously, if the decompositions: \({\rho }_{1}={\sum }_{k}{\alpha }_{k}|{\alpha }_{k}\rangle \langle {\alpha }_{k}|\) and \({\rho }_{2}={\sum }_{k}{\beta }_{k}|{\beta }_{k}\rangle \langle {\beta }_{k}|\) satisfy the Eq. (13), then we have \({F}_{Q}({\rho }_{1},H)=4{\sum }_{k}{\alpha }_{k}{({\rm{\Delta }}H)}_{|{\alpha }_{k}\rangle }^{2}\) and \({F}_{Q}({\rho }_{2},H)=4{\sum }_{k}{\beta }_{k}{({\rm{\Delta }}H)}_{|{\beta }_{k}\rangle }^{2}\), respectively. Note that \(\rho ={\sum }_{k}p{\alpha }_{k}|{\alpha }_{k}\rangle \langle {\alpha }_{k}|+{\sum }_{k}\mathrm{(1}-p){\beta }_{k}|{\beta }_{k}\rangle \langle {\beta }_{k}|\) is also an effective decomposition of \(\rho \), thus
Thus, the QFI is really convex32.
Verification of condition (C2a)
To demonstrate that the QFI satisfies the condition C(2a), i.e., it decreases monotonously under the mixing of density matrix induced by ICPTP operation, we generically introduce a positive linear mapping \({{\mathbb{J}}}_{\rho }^{f}:{{\bf{M}}}_{n}\to {{\bf{M}}}_{n}\). Here, \({{\mathbb{J}}}_{\rho }^{f}=f({{\mathbb{L}}}_{\rho }{{\mathbb{R}}}_{\rho }^{-1}){{\mathbb{R}}}_{\rho }\) with the function \(f:{{\mathbb{R}}}^{+}\to {{\mathbb{R}}}^{+}\) being a standard operator monotone function27 and \({{\mathbb{L}}}_{\rho }(A)=\rho A\), \({{\mathbb{R}}}_{\rho }(A)=A\rho \). Following the ref.27, a \(f\)-dependent QFI function
is obtained. Here, \({({{\mathbb{J}}}_{\rho }^{f})}^{-1}\) satisfies the following monotonic relation27,35: \({{\rm{\Phi }}}^{\ast }{({{\mathbb{J}}}_{{\rm{\Phi }}(\rho )}^{f})}^{-1}{\rm{\Phi }}\le {({{\mathbb{J}}}_{\rho }^{f})}^{-1}\), for any completely positive and trace preserving mapping \(\Phi \) defined by Eq. (1). It is proven that27
Thus, QFI is monotonic under the mixing of quantum states32. Based on quantum resource theory6,36, any function could be used to quantify the quantum coherence, if it satisfies the conditions (C1,C2a) and (C3), simultaneously. A typical example is the distance based on fidelity definition4. However, strictly speaking6, the function accurately quantifying the quantum coherence should satisfy the condition (C2b), besides the conditions (C1) and (C3). Therefore, the condition (C2b) is stricter than the condition (C2a), and thus is relatively harder to be verified. In the following, we provides such a verification for the QFI under certain assumptions.
Verification of condition (C2b)
To verify the monotonicity of the QFI, i.e.,
with \({F}_{Q}^{A}(\rho ,H)\) being the average QFI, let us consider a joint quantum system \(A+B\). The subsystem \(A\) is treated as the work one and the subsystem \(B\) the ancillary one, which can be generated by, e.g., the measuring apparatus or the environment of the subsystem \(A\). Suppose that \(A+B\) is closed and thus any dynamic process of such a joint quantum system can be described by a unitary evolution, i.e., \({\rho }_{AB}(t)=U{\rho }_{AB}\mathrm{(0)}{U}^{\dagger }\). By taking partial trace on the subsystem \(B\), then the reduced density matrix of the subsystem \(A\) at time \(t\) is given as \({\rho }_{A}(t)=T{r}_{B}[U{\rho }_{AB}\mathrm{(0)}{U}^{\dagger }]\). Typically, for the initial state of the joint system \({\rho }_{AB}\mathrm{(0)}={\rho }_{A}\mathrm{(0)}\otimes {\rho }_{B}\mathrm{(0)}\), the state of the subsystem \(A\) at the time \(t > 0\) takes consequently the form in Eq. (1), with \({A}_{\mu }^{\dagger }={A}_{ij}^{\dagger }=\sqrt{{\lambda }_{i}}\langle {\psi }_{i}|U|{\psi }_{j}\rangle \). Here, \(\{{\lambda }_{i},|{\psi }_{i}\rangle \}\) is a spectral decomposition of \({\rho }_{B}\mathrm{(0)}\), i.e., \({\rho }_{B}\mathrm{(0)}={\sum }_{i}{\lambda }_{i}|{\psi }_{i}\rangle \langle {\psi }_{i}|\). On the other hand, it has been proven that24,25, one can always construct an extended state \(\rho \mathrm{(0)}={\rho }_{A}\otimes |\psi {\rangle }_{B}\langle \psi |\) and a unitary transformation \(U\) to satisfy the dynamical map Eq. (1). Here, \(|\psi {\rangle }_{B}\) is fixed for any state \({\rho }_{A}\) of the subsystem \(A\), and \({A}_{\mu }{=}_{B}{\langle {\varphi }_{\mu }|U|\psi \rangle }_{B}\) with \({\{|{\varphi }_{\mu }\rangle }_{B}\}\) being the basis of the Hilbert space for the subsystem \(B\).
First, if the system is initially in a pure state \(|{\psi }_{i}\rangle =|\psi {\rangle }_{A}\otimes |\psi {\rangle }_{B}\), then under the unitary operation \(U\), it will evolve generically to \(|{\psi }_{f}\rangle ={\sum }_{kl}\varphi (k,l)|{\alpha }_{k}\rangle |{\beta }_{l}\rangle \) with \(|{\alpha }_{k}\rangle \) and \(|{\beta }_{l}\rangle \) being the orthogonal eigenvectors of Hamiltonian \({H}_{A}\) and \({H}_{B}\), respectively. This means that, the QFI in the pure state \(|\psi {\rangle }_{f}\) can be easily calculated as
where \(p(k,l)=|\varphi (k,l{)|}^{2}\) and \({{\rm{\Gamma }}}_{kl}={\alpha }_{k}+{\beta }_{l}\). Suppose that \({H}_{A}\otimes {I}_{B}+{I}_{A}\otimes {H}_{B}\) commutes with the unitary transformation \(U\), then from Eqs (10) and (11), we have \({F}_{Q}(|{\psi }_{f}\rangle ,{H}_{A}\otimes {I}_{B}+{I}_{A}\otimes {H}_{B})={F}_{Q}{(|\psi \rangle }_{A},{H}_{A})+{F}_{Q}{(|\psi \rangle }_{B},{H}_{B})\), and \({F}_{Q}{(|\psi \rangle }_{A},{H}_{A})=\mathrm{4\{}{\sum }_{kl}p(k,l){\alpha }_{k}^{2}-{[{\sum }_{kl}p(k,l){\alpha }_{k}]}^{2}\}\). This implies that, if one performs a measurement on the subsystem \(B\) and obtain the outcome \({\beta }_{l}\), then the joint quantum system will collapse into the state
with \(p(l)={\sum }_{k}|\varphi (k,l{)|}^{2}\). As the probability to find the subsystem \(B\) in state \(|{\beta }_{l}\rangle \) is \(p(l)\), the average QFI of the joint system \(A+B\) after the subselection, related to the measurement outcome, can be calculated as \({F}_{Q}(H)={\sum }_{l}p(l){F}_{Q}(|{\psi }_{f}(l)\rangle ,H)\) with \({F}_{Q}(|{\psi }_{f}(l)\rangle ,H)=\mathrm{4(}\Delta H{)}_{|{\psi }_{f}(l)\rangle }^{2}\) being the QFI of the state \(|{\psi }_{f}(l)\rangle \). Furthermore, with the help of Eqs (21) and (22), we have \({F}_{Q}(H)=\mathrm{4[}{\sum }_{kl}p(k,l){\alpha }_{k}^{2}-{\sum }_{l}{({\sum }_{k}p(k,l){\alpha }_{k})}^{2}]/p(l)\). After a straightforward derivation, one can verify that37
This indicates that the QFI is really nonincreasing, as \({F}_{Q}(H)\) is actually just the statistical average of \({F}_{Q}({\rho }_{l},{H}_{A})\), i.e., \({F}_{Q}({\rho }_{l},{H}_{A})={\sum }_{l}{p}_{l}{F}_{Q}({\rho }_{l},{H}_{A})\) with \({\rho }_{l}={A}_{l}|\psi {\rangle }_{A}\langle \psi |{A}_{l}^{\dagger }/{p}_{l}\) and \({A}_{l}={}_{B}{\langle {\beta }_{l}|U|\psi \rangle }_{B}\). Therefore, the monotonicity of the QFI
is verified.
Next, for a more generic initial state, e.g., \({\rho }_{A}\times |\psi {\rangle }_{BB}\langle \psi |\) with the subsystem \(A\) being in a mixture one: \({\rho }_{A}={\sum }_{k}{w}_{k}|{w}_{k}\rangle \langle {w}_{k}|\), we have \({F}_{Q}({\rho }_{A},{H}_{A})={\sum }_{k}{w}_{k}{F}_{Q}(|{w}_{k}\rangle ,{H}_{A})\), as the decomposition \(\{{w}_{k},|{w}_{k}\rangle \}\) fulfills the Eq. (13). Furthermore, with Eq. (24), we have
Finally, from the convexity of the QFI verified above, one can prove that
This indicates that the QFI satisfies the condition (C2b) specifically.
Numerical confirmations
The validity of the above verifications can be more clearly demonstrated with certain specific incoherent processes. Without loss of the generality, let us consider the QFI in a generic one-qubit state
with \(\overrightarrow{n}=(a,b,c)\) and \(\overrightarrow{\sigma }=({\sigma }_{x},{\sigma }_{y},{\sigma }_{z}{)}^{\dagger }\). Obviously, the eigenvalues of such a density operator can be easily obtained as \({\lambda }_{1}=\mathrm{(1}+|n\mathrm{|)/2,}\,\,|n|=\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}\) and \({\lambda }_{2}=\mathrm{(1}-|n\mathrm{|)/2}\), with the corresponding eigenvectors being \(|{\lambda }_{1}\rangle =(a+ib,|n|-c{)}^{\dagger }/\sqrt{\mathrm{2|}n{|}^{2}-2c}\) and \(|{\lambda }_{2}\rangle =(a+ib,-|n|-c{)}^{\dagger }/\sqrt{\mathrm{2|}n{|}^{2}+2c}\), respectively.
The convexity and monotonicity of the QFI, i.e., the Eqs (16) and (20)
First, let us consider a depolarizing process, which can be described equivalently by the following incoherent operation (with \(p\in \mathrm{[0,}\,\mathrm{1]}\)):
in the Kraus representation. One can easily prove that, for the mixture state (27) an ICPTP could be constructed by the following unitary transformation:
with \(|\psi {\rangle }_{B}=\mathrm{|0}{\rangle }_{B}\), \(|{\varphi }_{2}{\rangle }_{B}=i\mathrm{|2}{\rangle }_{B}\), \({\sigma }_{ij}^{A,B}=|i{\rangle }_{A,B}\langle j|\), and \(|{\varphi }_{\mu }{\rangle }_{B}=|\mu {\rangle }_{B},\mu =\mathrm{0,}\,\mathrm{1,}\,3\). Here, \(|i{\rangle }_{A}\) and \(|i{\rangle }_{B}\) are the basis of the Hilbert spaces for the subsystems A and B, respectively. Certainly, the above unitary transformation \({U}_{d}\), satisfying the relation \({A}_{\mu }\,={}_{B}{\langle {\varphi }_{\mu }|{U}_{d}|\psi \rangle }_{B}\), is not unique. By utilizing Eq. (9) one can easily check that
with \(H=\mathrm{|0}\rangle \langle \mathrm{0|}\). It is easy to prove that, \({\tilde{\rho }}_{\mu }={A}_{\mu }\tilde{\rho }{A}_{\mu }^{\dagger }/{p}_{\mu },\,\mu =\mathrm{0,}\,\mathrm{1,}\,\mathrm{2,}\,3\) with \({p}_{\mu }=Tr({A}_{\mu }\tilde{\rho }{A}_{\mu }^{\dagger })\) and \({\sum }_{\mu }{A}_{\mu }\tilde{\rho }{A}_{\mu }^{\dagger }=\) \((I+\mathrm{(1}-4p\mathrm{/3)}n\cdot \overrightarrow{\sigma })\). Thus, the average QFI in Eq. (26) and the reduced QFI in Eq. (16) for the present state (27) are easily calculated as
and
respectively.
Similarly, for the phase damping channel with the equivalent ICPTP
a unitary transformation:
with \(|\psi {\rangle }_{B}=|0{\rangle }_{B}\), \(|{\phi }_{\mu }{\rangle }_{B}=|\mu {\rangle }_{B}\), can be constructed. Correspondingly, we have \({\sum }_{\mu }{A}_{\mu }\tilde{\rho }{A}_{\mu }^{\dagger }=(I+\mathrm{(1}-p)\) \(a{\sigma }_{x}+\mathrm{(1}-p)b{\sigma }_{y}+c{\sigma }_{z}\mathrm{)/2}\). As a consequence, the average QFI in Eq. (26) and the reduced QFI in Eq. (16) read
and
respectively.
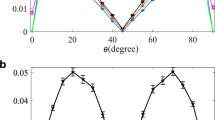
Figure 1 shows how the QFI, the average QFI, and the reduced QFI functions vary with the parameter \(a\) in the quantum state \(\tilde{\rho }\). It is seen that, for both the depolarizing- and the phase-damping processes described here, these functions are all monotonic and convex. Specifically, for any parameter \(a\), Eqs (16) and (20) are always established. This clearly indicates that the QFI satisfies the Baumgratz et al.’s criticism and thus can be utilized to quantify the quantum coherence, at least theoretically.
(Color online) The monotonicity and convexity of the QFI for the typical depolarizing- and phase-damping processes (versus the parameter \(a\) in the generic one-qubit state with \(b=0\), \(c=\sqrt{1-{a}^{2}}\) and \(p=0.1\)): the QFI function \({F}_{Q}(\tilde{\rho },H)\) (red solid), the average QFI function \({F}_{Q}^{A}(\tilde{\rho },H)\) (green plus sign) in Eq. (26) and the reduced QFI function \({F}_{Q}^{R}(\tilde{\rho },H)\) (blue dashed-dotted) in Eq. (16).
Comparisons with the other measure methods
To further check the validity of our proposal, we compare the QFI with the other functions proposed previously for quantifying quantum coherence. Specifically, for a common single-qubit quantum state (27) with \({a}^{2}+{b}^{2}+{c}^{2}\le 1\), the relative entropy6 are calculated as
Analogously, the fidelity based on distance measurement defined by4 \({C}_{f}(\tilde{\rho })=1-\sqrt{{{\rm{\max }}}_{\delta \in I}F(\tilde{\rho },\delta )}\) with \(F(\tilde{\rho },\delta )=[tr\sqrt{{\tilde{\rho }}^{\mathrm{1/2}}\delta {\tilde{\rho }}^{\mathrm{1/2}}}]\) can be expressed as
and the \({l}_{1}\,norms\) function reads
It is seen from the Fig. 2 that, all of these functions really measure the quantum coherence; different coherent suppositions (with different parameters \(a\)) correspond to different values of the quantifying functions. When \(a\) equals \(0\) (which corresponds to a completely-mixed state), the values of these functions equal to \(0\); While, for the typical supposition pure state \(\mathrm{(|0}\rangle +\mathrm{|1}\rangle )/\sqrt{2}\), they all reach a common normalized maximum value \(1\).
(Color online) Quantum coherence in a typical one-qubit state (27) quantified by different functions; the QFI (red solid), relative entropy (green dashed), fidelity (blue dotted) and \({l}_{1}\,norm\) \({C}_{{l}_{1}}\) (yellow dashed-dotted). Here, for simplicity the parameter \(a\) in (27) is changed from \(0\) to \(1\), \(b\) is fixed as \(0\), and \(c=\sqrt{1-{a}^{2}}\). For comparison, all the values of these functions are normalized by divided their achievable maximum.
Conclusion
In summary, we have verified that the QFI could satisfy the Baumgratz et al.’s criticism and thus can also be utilized to quantify the quantum coherence. Given most of the other coherence measurements proposed previously, e.g., the relative entropy, fidelity, and \({l}_{1}\,norms\) etc., are basically axiomatic, the QFI quantification of the quantum coherence seems more experimental, as its lower- and upper bounds are both related to certain measurable quantities.
References
Pirandola, S. Quantum discord as a resource for quantum cryptography. Sci. Rep. 4, 6956 (2014).
Knill, E. & Laflamme, R. Power of one bit of quantum information. Phys. Rev. Lett. 81, 5672–5 (1998).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nature Photonics 96, 222–229 (2011).
Shao, L. H., Xi, Z., Fan, H. & Li, Y. The fidelity and trace norm distances for quantifying coherence. Physical Review A 91 (2014).
Rana, S., Parashar, P. & Lewenstein, M. Trace distance measure of coherence. Physical Review A 93 (2016).
Baumgratz, T., Cramer, M. & Plenio, M. B. Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014).
Ma, J., Yadin, B., Girolami, D., Vedral, V. & Gu, M. Converting Coherence to Quantum Correlations. Physical Review Letters 116, 160407 (2016).
Streltsov, A., Singh, U., Dhar, H. S., Bera, M. N. & Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015).
Pires, D. P. Céleri, L. C. & Soarespinto, D. O. Geometric lower bound for quantum coherence measure. Physical Review A 91, 042330 (2015).
Girolami, D. Observable measure of quantum coherence in finite dimensional systems. Phys. Rev. Lett. 113, 170401 (2014).
Winter, A. & Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404 (2016).
Chitambar, E. et al. Assisted distillation of quantum coherence. Phys. Rev. Lett. 116, 070402 (2015).
Xi, Z., Li, Y. & Fan, H. Quantum coherence and correlations in quantum system. Sci. Rep. 5 (2015).
Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. Physical Review Letters 88, 017901 (2002).
Roga, W., Giampaolo, S. M. & Illuminati, F. Discord of response. Journal of Physics A Mathematical & Theoretical 47, 628–640 (2014).
Farace, A., Pasquale, A. D., Rigovacca, L. & Giovannetti, V. Discriminating strength: a bona fide measure of non-classical correlations. New Journal of Physics 16 (2014).
Vedral, V., Plenio, M. B., Rippin, M. A. & Knight, P. L. Quantifying entanglement. Phys. Rev. Lett. 78, 2275–2279 (1997).
Plbnio, M. B. & Virmani, S. An introduction to entanglement measures. Quantum Information & Computation 7, 1–51 (2005).
Hayden, P. M., Terhal, B. M. & Horodecki, M. The asymptotic entanglement cost of preparing a quantum state. Journal of Physics A General Physics 34, 6891–6898 (2000).
Li, N. & Luo, S. Entanglement detection via quantum fisher information. Phys. Rev. A 88, 014301 (2013).
Liu, B. et al. Time-invariant entanglement and sudden death of non-locality. Physical Review A 94, 062107 (2016).
Oi, D. K. & Aberg, J. Fidelity and coherence measures from interference. Physical Review Letters 97, 220404 (2006).
Yuan, X., Zhou, H., Cao, Z. & Ma, X. Intrinsic randomness as a measure of quantum coherence. Physical Review A 92 (2017).
Ángel R & Huelga, S. F. Open quantum systems. an introduction. Physics 24 (2012).
Frieden, B. R. & Binder, P. M. Physics from Fisher Information: A Unification (Cambridge University Press, 2004).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439 (1994).
Petz, D. & Ghinea, C. Introduction to quantum fisher information. Quantum Probability & Related Topics 261–281 (2014).
Luis, A. Fisher information as a generalized measure of coherence in classical and quantum optics. Opt. Exp 20, 24686–24698 (2012).
Paris, M. G. A. Quantum estimation for quantum technology. International Journal of Quantum Information 07, 125–137 (2008).
Escher, B. M., Filho, R. L. D. M. & Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nature Physics 7, 406–411 (2011).
Pasquale, A. D., Rossini, D., Facchi, P. & Giovannetti, V. Quantum parameter estimation affected by unitary disturbance. Physical Review A 88, 29073–29082 (2013).
Tóth, I. G. & Apellaniz. Quantum metrology from a quantum information science perspective. J. Phys. A: Math. Theor. 47, 424006 (2014).
Tóth, G. & Petz, D. Extremal properties of the variance and the quantum Fisher information. Phy. Rev. A 87, 032324 (2013).
Yu, S. Quantum fisher information as the convex roof of variance. Eprint Arxiv (2013).
Petz, D. Covariance and fisher information in quantum mechanics. J. Phys. A: Math. Gen. 35, 929 (2002).
Gour, G. & Spekkens, R. W. The resource theory of quantum reference frames: manipulations and monotones. New Journal of Physics 10, 1218–1221 (2008).
Mehra, J. Philosophical Reflections and Syntheses (Springer Berlin Heidelberg, 1995).
Acknowledgements
This work was supported in part by the NSFC grant Nos 11174373 and U1330201.
Author information
Authors and Affiliations
Contributions
L.F. Wei proposed the model, X.N. Feng performs the calculations. Both of them analyzed the results and co-wrote the paper. All authors have contributed to the information and material submitted for publication, and all authors have read and approved the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feng, X.N., Wei, L.F. Quantifying quantum coherence with quantum Fisher information. Sci Rep 7, 15492 (2017). https://doi.org/10.1038/s41598-017-15323-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15323-7
This article is cited by
-
Coherence resource power of isocoherent states
Scientific Reports (2022)
-
Quantifying the Quantumness of an Ensemble of Quantum States
International Journal of Theoretical Physics (2022)
-
Protecting Quantum Coherence and Quantum Fisher Information in Ohmic Reservoir
International Journal of Theoretical Physics (2020)
-
Multiparameter estimation, lower bound on quantum Fisher information, and non-Markovianity witnesses of noisy two-qubit systems
Quantum Information Processing (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.