Abstract
Quantum random number generation attracts considerable attention, since its randomness inherently originates in quantum mechanics, but not mathematical assumptions. Randomness certification, e.g. entropy estimation, becomes a key issue in the context of quantum random number generation protocol. We study a self-testing protocol based on dimension witness, with the assumption of independent devices. It addresses the random number extraction problem in a practical prepare-and-measure scenario with uncharacterized devices. However, the lower bound of min-entropy as a function of dimension witness is not tight in existing works. We present a tighter bound of analytic form, by introducing the Lagrangian multiplier method to closely analyze the optimization problem on average guessing probability. Through simulation, it turns out that a significantly higher random number generation rate can be achieved in practice.
Similar content being viewed by others
Introduction
Random numbers are widely used in modern science and technology, or even everyone’s daily life. Whether random numbers are of high quality or not depend on what kind of application we use them in. Some applications only require the random sequence to perform well in statistical tests, such as Monte Carlo simulation. Knuth has presented the most commonly used statistical test methods in his famous book “The Art of Computing Programming”, and standard testing suit has been developed by NIST1. However, random numbers used in cryptography not only require good statistical properties, but also require security, or unpredictability2,3. That is, an attacker who knows part of the random sequence still have no information on other bits, he can only guess with a probability no more than one-half. Both classical cryptography and quantum cryptography require a secure random source4,5,6. A common and convenient way is to generate random sequence by a computer algorithm starting from a seed string, which is reffered to as pseudorandom number generator (PRNG). PRNG cannot be truly random, while security based on algorithm complexity make it not real unpredictable3. True random number generator (TRNG) collects unpredictable data from physical process. Specifically, this paper only concerns the quantum random number generation (QRNG)7, in which entropy gathering proceeds essentially based on the inherent randomness of quantum mechanics.
Many established methods of quantum optics may be used in QRNG3,8, where inherent randomness can be gathered by different quantum parameters of light, such as branching path9, time of arrival10,11,12, attenuated pulse13, photon counting14,15, vacuum fluctuations16,17,18, phase noise19,20,21, and amplified spontaneous emission22,23. Randomness certification of these methods may be foiled when the devices are untrusted or far from the theoretical model. It turns out that the device-independent (DI) QRNG24,25,26,27,28 offers a solution to the aforementioned problem. By exploiting the quantum violation of Bell inequalities, certified randomness can be achieved without any assumption about the physical implementation. Unfortunately, the observation of a Bell inequality violation without loophole may be extremely challenging, since it requires an unrealistically high detection efficiency to eliminate the detection loophole28. Under such a circumstance, compromise solutions termed semi-device-independent QRNG29,30 were proposed to explore the tradeoff between loophole-free and implementation. These schemes outperform DI-QRNG by easier implementation and higher performance, with general assumptions such as trusted preparation or measurement devices31,32,33, and a bounded dimension34,35,36,37,38.
This paper addresses a semi-device-independent randomness certification problem in the prepare-and-measure scenario. Bowles et al.34 proposed the so-called dimension witness to bound the quantumness of a prepare-and-measure scenario could behave, with the assumption that the state preparation and measurement devices share no correlations. Based on the aforementioned witness, Lunghi et al.35 proposed a self-testing QRNG protocol (BQB14 for short)36 with a bounded dimension constraint, in which devices had no need to be characterized. The BQB14 derived a lower bound of the min-entropy as a function of dimension witness, and was capable of monitoring the randomness in real time. However, this min-entropy bound was not tight due to the relaxation in derivation procedures, with the domain of dimension witness. As a result, the extracted rate of random bits had a certain gap with the optimal one. We introduce the Lagrangian multiplier method to closely analyze the optimization problem on average guessing probability, and thus a tighter bound of analytic form is presented. As a result, lower guessing probability bound and higher min-entropy can be achieved. We compare the certified randomness between this paper and BQB14 by simulation analysis, it turns out that set-up with the proposed tighter bound achieves a significantly higher certified randomness rate in a practical self-testing QRNG.
Results
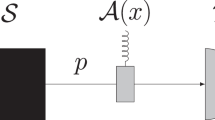
The prepare-and-measure scenario of QRNG is illustrated in Fig. 1, where a self-testing protocol is performed with uncharacterized devices on both sides. This paper follows the assumptions in BQB1435, where imperfection of preparation and measurement devices are modeled by internal random variable λ and μ. Specifically, it is assumed that devices share no correlations, where p(λ, μ) = q λ ⋅ r μ and ∑ λ q λ = ∑ μ r μ = 1. The random inputs of preparations and measurements are denoted by x ∈ {0, 1, 2, 3} and y ∈ {0, 1}, and a binary outcome is b =±1. In each round of the experiment, a qubit state \({\rho }_{x}^{\lambda }\) is prepared according to random input x and internal random variable λ, and a similar measurement \({M}_{y}^{\mu }\) is performed then.
Self-testing QRNG protocol consists of three stages. Data collection: prepare-and-measure experiments are performed with uncharacterized devices, and events {x, y, b} are collected to evaluate the observed probabilities p(b|x, y). Entropy monitoring: dimension witness W is evaluated by the table of p(b|x, y), then the min-entropy can be bounded by an analytic function of variable W. Randomness extraction: random numbers are extracted according to the min-entropy in postprocessing.
In the stage of data collection, events {x, y, b} are collected to evaluate the observed probabilities p(b|x, y). Since the observer has no information on the variables λ and μ, he will observe
where
The observed states and measurements are denoted by \({\overrightarrow{S}}_{x}\) and \({\overrightarrow{T}}_{y}\) on the Bloch sphere with Pauli vector \(\overrightarrow{\sigma }\) = (σ 1, σ 2, σ 3). According to the purification principle of quantum state, \({\overrightarrow{S}}_{x}\) and \({\overrightarrow{T}}_{y}\) can be decomposed on the Bloch sphere by
where \({\overrightarrow{S}}_{x}^{\lambda }\) and \({\overrightarrow{T}}_{y}^{\mu }\,(|{\overrightarrow{S}}_{x}^{\lambda }|=|{\overrightarrow{T}}_{y}^{\mu }|=\mathrm{1)}\) are on the surface of the sphere.
In the stage of entropy monitoring, dimension witness W is evaluated by the table of p(b|x, y)34,
The witness W indicates that how quantum is the combination of preparations and measurements, while classical events yield W = 0 and quantum events give 0 ≤ |W| ≤ 134. To certify the randomness, we derive an upper bound f ′ (W) of the guessing probability p g as an analytic function of W, where 0 ≤ W ≤ 1. Assuming the choices of preparations and measurements are uniformly distributed, we have the average guessing probability
where f ′ (W) is tighter than the previous result f (W)35, and the derivation process will be given in next section. Thus, the min-entropy has a tighter lower bound as an analytic function of W
In the stage of randomness extraction, random numbers are extracted from the raw data. The lower bound \(-{\mathrm{log}}_{2}f^{\prime} (W)\) of H min is the parameter to determine how many random bits can be extracted in postprocessing.
Derivation of tighter bound
For given inputs x, y and local randomness λ, μ, the guessing probability is given by
To certify the randomness, we need to derive an upper bound of the average guessing probability p g in (7). Instead of relaxation by inequalities in precious work35, we closely maximize the guessing probability with the witness constraint, which is considered to be the reason for the advantage of this paper. Assuming uniformly distributed x and y, we have
where p(b = 1|x, y) are denoted in (1), (4) and (5).
It is hard to directly derive an analytic solution of the initial problem in (10). Thus, we first focus on a sub-problem of (10) and derive an upper bound on the average guessing probability over the inputs only, where \({p}_{\lambda \mu }^{g}\) is maximized with the witness constraint W λμ :
As presented in previous work34, we have \({\overrightarrow{S}}_{xx^{\prime} }^{\lambda }=({\overrightarrow{S}}_{x}^{\lambda }-{\overrightarrow{S}}_{x^{\prime} }^{\lambda })/2\). Note that \({\overrightarrow{S}}_{x}^{\lambda }\) must be on the plane spanned by the measurement vectors \({\overrightarrow{T}}_{y}^{\mu }\), so as to maximize the objective function. The angles of \({\overrightarrow{S}}_{x}^{\lambda }\) and \({\overrightarrow{T}}_{y}^{\mu }\) are denoted by {θ 0, θ 1, θ 2, θ 3, ϕ 0, ϕ 1} on this plane. Using the symmetrical nature of the problem, without loss of generality, we set ϕ 0 = 0, ϕ 1 ∈ \([0,\,\frac{\pi }{2}]\), θ 0 ∈ [ϕ 0, ϕ 1], θ 1 = θ 0 + π, θ 2 ∈ \([{\theta }_{0},\,{\theta }_{0},\,\frac{\pi }{2}]\), θ 3 = θ 2 + π. Thus, problem in (11) can be reduced as:
where \({p}_{\lambda \mu }^{g}\) can be simplified as \({p}_{\lambda \mu }^{g}({\theta }_{0},{\theta }_{2},{\varphi }_{1})=\frac{1}{2}+\frac{1}{8}(|\cos ({\theta }_{0})|+|\cos ({\theta }_{0}-{\varphi }_{1})|+|\cos ({\theta }_{2})|+|\cos ({\theta }_{2}-{\varphi }_{1})|)\).
The Lagrange function of problem in (12) is given by
where υ denotes the Lagrange multiplier. The optimal solution \(({\theta }_{0}^{\ast },{\theta }_{2}^{\ast },{\varphi }_{1}^{\ast },{\upsilon }^{\ast })\) should satisfy the gradient equations39:
where \({\nabla }_{{\theta }_{0},{\theta }_{2},{\varphi }_{1},\upsilon }L=(\frac{\partial L}{\partial {\theta }_{0}},\frac{\partial L}{\partial {\theta }_{2}},\frac{\partial L}{\partial {\varphi }_{1}},\frac{\partial L}{\partial \upsilon })\). Combining (12) and (14), we get
The inequality in (15) holds due to \(2\sqrt{1-{W}_{\lambda \mu }}\le 1+\mathrm{(1}-{W}_{\lambda \mu })\) and 0 ≤ W λμ ≤ 1. The convexity of the witness has been proved in the supplemental material of previous work35
Thus, the average guessing probability p g can be bounded by
The inequalities in (17) hold because f ′ is concave and decreasing. Finally, we get
To summarize, we first present an analytic solution of the sub-problem in (11), then derive an upper bound of the average guessing probability problem in (10) using the convexity and decrement of the function f ′ (W). As an analytic function of W, the bound f ′ (W) is tighter than f (W) in previous work35.
Simulations
In this section, we perform numerical simulations to compare the proposed method and the original one.
Figure 2(a) gives the comparison of theoretical bounds on average guessing probability. Curve I & II denote the upper bound \(f(W)=\frac{1}{2}(1+\sqrt{(1+\sqrt{1-{W}^{2}})\mathrm{/2}})\) in BQB14 and the proposed \(f^{\prime} (W)=\frac{1}{2}(1+\sqrt{\mathrm{(2}-W\mathrm{)/2}})\) in this paper, respectively. Curve III & IV indicate the intermediate results \(\{\frac{1}{4}(3+\sqrt{1-{W}_{\lambda \mu }}),\,\frac{1}{4}(2+\sqrt{1+{W}_{\lambda \mu }})\}\) in (15) as a solution of the sub-problem in (11). Curve II is derived from Curve III & IV according to the relationship between the initial guessing probability problem in (10) and the sub-problem in (11). As Fig. 2(a) shows, Curve II proposed by this paper is tighter than Curve I in BQB14.
Simulation analysis. (a) Comparison of theoretical bounds on average guessing probability. Curve I: upper bound f (W) in BQB14; Curve II: upper bound f ′ (W) in this paper; Curve III & IV: intermediate results in (15) as a solution of the sub-problem in (11). (b) Comparison of the certified randomness in a practical QRNG with off-the-shelf experimental parameters. Orange line: min-entropy using the bound f (W) in BQB14; Blue line: min-entropy using the bound f ′ (W) in this paper. Dashed line: dimension witness W corresponding to channel loss is presented on the right axis.
Figure 2(b) presents the comparison of the certified randomness in a practical QRNG with a prepare-and-measure set-up like BB8440. Off-the-shelf experimental parameters are set as follows: detection efficiency η d = 10%, dark count rate p d = 10 −5, detector misalignment d e = 1%. Thus the overall QBER e = (0.5(1 − 10− d/10)p d + η d d e )/(10−d/10 + (1 − 10−d/10)p d ). The observed probabilities are assumed as follows: p(1|0,0) = 1 − e, p(1|1,0) = e,p(1|2,0) = p(1|3,0) = 1/2,p(1|0,1) = p(1|1,1) = 1/2,p(1|2,1) = 1 − e,p(1|3,1) = e. In Fig. 2(b), Orange & Blue lines denote the min-entropy using the bound f (W) in BQB14 and f′ (W) in this paper, respectively. Note that the dimension witness W = 0.996 when loss is zero due to detector misalignment, and the certified randomness has a gap between BQB14 and this paper, even when W is close to 1.
Conclusion
We have presented an analytic bound as a function of dimension witness to estimate the certified randomness, in the prepare-and-measure QRNG with independent devices. Compared with previous works, our work enjoys the advantage of a tighter bound of min-entropy. Simulations have demonstrated that self-testing QRNG with the proposed tighter bound achieves a significantly higher random number generation rate. Benefiting from the better performance of this bound, the self-testing QRNG with similar assumption will accomplish a better balance between security and practicality. There are several issues to be addressed in future. First, the effects of finite-size random number and sampling should be considered. Second, how to guarantee the two-dimensional Hilbert space and independent devices assumptions are essential in practice.
References
Rukhin, A. et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications. NIST SP 800-22 Rev1a (2010).
Yao, A. C. Theory and application of trapdoor functions. In 23rd Annual Symposium on Foundations of Computer Science, 80–91 (1982).
Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Reviews of Modern Physics 89, 015004 (2017).
Zhang, C. et al. Decoy-state measurement-device-independent quantum key distribution with mismatched-basis statistics. Science China Physics Mechanics Astronomy 58, 590301 (2015).
Gao, F., Liu, B. & Wen, Q. Quantum position verification in bounded-attack-frequency model. Science China Physics Mechanics Astronomy 59, 110311 (2016).
Wang, Z. et al. Experimental verification of genuine multipartite entanglement without shared reference frames. Science Bulletin 61, 714–719 (2016).
Wang, P. X., Long, G. L. & Li, Y. S. Scheme for a quantum random number generator. Journal of Applied Physics 100, 056107 (2006).
Rarity, J., Owens, P. & Tapster, P. Quantum random-number generation and key sharing. Journal of Modern Optics 41, 2435–2444 (1994).
Jennewein, T., Achleitner, U., Weihs, G., Weinfurter, H. & Zeilinger, A. A fast and compact quantum random number generator. Review of Scientific Instruments 71, 1675–1680 (2000).
Stipčević, M. & Rogina, B. M. Quantum random number generator based on photonic emission in semiconductors. Review of Scientific Instruments 78, 045104 (2007).
Wayne, M. A., Jeffrey, E. R., Akselrod, G. M. & Kwiat, P. G. Photon arrival time quantum random number generation. Journal of Modern Optics 56, 516–522 (2009).
Wahl, M. et al. An ultrafast quantum random number generator with provably bounded output bias based on photon arrival time measurements. Applied Physics Letters 98, 171105 (2011).
Wei, W. & Guo, H. Bias-free true random-number generator. Optics Letters 34, 1876–1878 (2009).
Fürst, H. et al. High speed optical quantum random number generation. Optics express 18, 13029–13037 (2010).
Ren, M. et al. Quantum random-number generator based on a photon-number-resolving detector. Physical Review A 83, 023820 (2011).
Shen, Y., Tian, L. & Zou, H. Practical quantum random number generator based on measuring the shot noise of vacuum states. Physical Review A 81, 063814 (2010).
Gabriel, C. et al. A generator for unique quantum random numbers based on vacuum states. Nature Photonics 4, 711–715 (2010).
Symul, T., Assad, S. & Lam, P. K. Real time demonstration of high bitrate quantum random number generation with coherent laser light. Applied Physics Letters 98, 231103 (2011).
Guo, H., Tang, W., Liu, Y. & Wei, W. Truly random number generation based on measurement of phase noise of a laser. Physical Review E 81, 051137 (2010).
Qi, B., Chi, Y.-M., Lo, H.-K. & Qian, L. High-speed quantum random number generation by measuring phase noise of a single-mode laser. Optics Letters 35, 312–314 (2010).
Jofre, M. et al. True random numbers from amplified quantum vacuum. Optics Express 19, 20665–20672 (2011).
Williams, C. R., Salevan, J. C., Li, X., Roy, R. & Murphy, T. E. Fast physical random number generator using amplified spontaneous emission. Optics Express 18, 23584–23597 (2010).
Argyris, A., Pikasis, E., Deligiannidis, S. & Syvridis, D. Sub-tb/s physical random bit generators based on direct detection of amplified spontaneous emission signals. Journal of Lightwave Technology 30, 1329–1334 (2012).
Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021 (2010).
Nieto-Silleras, O., Pironio, S. & Silman, J. Using complete measurement statistics for optimal device-independent randomness evaluation. New Journal of Physics 16, 013035 (2014).
Bancal, J.-D., Sheridan, L. & Scarani, V. More randomness from the same data. New Journal of Physics 16, 033011 (2014).
Hensen, B. et al. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Acn, A. & Masanes, L. Certified randomness in quantum physics. Nature 540, 213–219 (2016).
Li, H.-W. et al. Semi-device-independent random-number expansion without entanglement. Physical Review A 84, 034301 (2011).
Pawłowski, M. & Brunner, N. Semi-device-independent security of one-way quantum key distribution. Physical Review A 84, 010302 (2011).
Cao, Z., Zhou, H. & Ma, X. Loss-tolerant measurement-device-independent quantum random number generation. New Journal of Physics 17, 125011 (2015).
Cao, Z., Zhou, H., Yuan, X. & Ma, X. Source-independent quantum random number generation. Physical Review X 6, 011020 (2016).
Marangon, D. G., Vallone, G. & Villoresi, P. Source-device-independent ultrafast quantum random number generation. Physical Review Letters 118, 060503 (2017).
Bowles, J., Quintino, M. T. & Brunner, N. Certifying the dimension of classical and quantum systems in a prepare-and-measure scenario with independent devices. Physical Review Letters 112, 140407 (2014).
Lunghi, T. et al. Self-testing quantum random number generator. Physical Review Letters 114, 150501 (2015).
Han, Y.-G. et al. More randomness from a prepare-and-measure scenario with independent devices. Physical Review A 93, 032332 (2016).
Brask, J. B. et al. Megahertz-rate semi-device-independent quantum random number generators based on unambiguous state discrimination. Physical Review Applied 7, 054018 (2017).
Xu, F., Shapiro, J. H. & Wong, F. N. Experimental fast quantum random number generation using high-dimensional entanglement with entropy monitoring. Optica 3, 1266–1269 (2016).
Boyd, S. & Vandenberghe, L. Convex optimization 215–249 (Cambridge university press, 2004).
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of IEEE International Conference on Computers Systems and Signal Processing, 175–179 (1984).
Acknowledgements
This work was supported by National Key Research and Development Program of China (2016YFA0302600), National Natural Science Foundation of China (NSFC) (61475148, 61575183, 61771439, 61702469), Foundation of Science and Technology on Communication Security Laboratory (Grant No. 6142103040105), and Strategic Priority Research Program (B) of the Chinese Academy of Sciences (CAS) (XDB01030100, XDB01030300).
Author information
Authors and Affiliations
Contributions
Z.-Q.Y., W.H., B.-J.X., G.-C.G. and Z.-F.H. conceived the project. X.-W.F. and Z.-Q.Y. proposed the theoretical method. X.-W.F., Z.-Q.Y. and Y.-G.H. analysed the results. X.-W.F. wrote the main manuscript text. S.W. and W.C. reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fei, XW., Yin, ZQ., Huang, W. et al. Tighter bound of quantum randomness certification for independent-devices scenario. Sci Rep 7, 14666 (2017). https://doi.org/10.1038/s41598-017-15318-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15318-4
This article is cited by
-
Practical decoy-state quantum random number generator with weak coherent sources
Quantum Information Processing (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.