Abstract
Previous experiments showed that Hf/Sb co-doping in ZrNiSn impressively improved the electrical conductivity (σ). To explore the physical reasons for this improvement, the electronic structures of HfxZr1−xNiSn1−ySby (x = 0, 0.25, 0.5; y = 0, 0.02) have been systematically investigated by using the first-principles method and semiclassical Boltzmann transport theory. 50% Hf doping at Zr site in ZrNiSn simultaneously increases the degeneracy and dispersion of energy bands near the conduction band edge, which are helpful to optimizing Seebeck coefficient and slightly improving σ. Furthermore, 2% Sb co-doping at Sn site in Hf0.5Zr0.5NiSn not only increases total density of states near the Fermi energy but also retains high mobility, and N v reaches eleven at the conduction band minimum, thereby inducing a large improvement in σ. Additionally, the Bader charge analysis shows the reason why Sb co-doping supplies more electrons. It is most likely derived from that Sb loses more electrons and Sb-Ni has a stronger hybridization than Sn-Ni. Moreover, we predict that the ZT of Hf0.5Zr0.5NiSn0.98Sb0.02 at 1000 K can reach 1.37 with the carrier concentration of 7.56 × 1018 cm−3, indicating that Hf/Sb co-doping may be an effective approach in optimizing thermoelectric properties of ZrNiSn alloy compounds.
Similar content being viewed by others
Introduction
Exploration of sustainable new clean energies has become a global consistent viewpoint, due to the depletion of fossil fuels and the resulting in environmental pollution1. Thermoelectric (TE) materials can perform directly converting waste heat into electricity using in all-solid-state by a temperature difference to induce carriers to flow in a semiconductor, which are helpful to resolving today’s energy crisis2,3,4. Although the TE devices are very reliable and compact, the relatively low efficiency limits their widespread applications. The conversion efficiency of a TE material can be characterized by the dimensionless figure of merit ZT, defined as ZT = S 2 σT/(κ e + κ l ), where S, σ, T, κ e , and κ l are the Seebeck coefficient, electrical conductivity, absolute temperature, electrical thermal conductivity, and lattice thermal conductivity, respectively5,6,7. An excellent TE material should have a large S, a high σ, and a low κ l , comparatively speaking a high κ e is not a problem8,9,10.
For metals or degenerate semiconductors11, S, density-of-states effective mass (\({m}_{{\rm{DOS}}}^{\ast }\)), σ, and carrier mobility (μ) are given by5,12:
where \({m}_{{\rm{b}}}^{\ast }\) is the band effective mass and n is the carrier concentration. From the above formulas, we can clearly see that S and σ have an inverse dependence on n. A large \({m}_{{\rm{b}}}^{\ast }\) is favorable to enlarge S by increasing the \({m}_{{\rm{DOS}}}^{\ast }\) while it will in turn lead to a significant reduction in σ via μ 13,14. Therefore, it is imperative to achieve the balance between σ and S via optimizing n and adjusting \({m}_{{\rm{b}}}^{\ast }\) to maximize power factor (S 2 σ). For this purpose, it is valuable to find an appropriate extrinsic dopant to provide a high n with a low deformation potential (Ξ) and a low alloy scattering potential15,16,17. A low Ξ and a low alloy scattering potential, which signify a weak electron-phonon interaction, are favorable for obtaining a high μ. Considering low scattering is not conducive to suppressing κ l , therefore an appropriate dopant inducing multiscale scattering centers is also vital by making a compromise between μ and κ l for attaining high TE performance.
Obeying 18-valence-electron rule, ZrNiSn has a cubic structure and a narrow band gap (E g ~ 0.5 eV) with relatively large S (~213 V K−1 at 800 K) and high structural stability even at high temperature18. However, the κ of pure ZrNiSn is high and its σ is small (~5.85 × 104 Ω−1 m −1 at 800 K), which lead to its low ZT value. The nanostructuring strategy has been employed to reduce κ l by enhancing phonon scattering at the grain boundaries, but it will deteriorate μ, which especially limits the improvement of ZT. To overcome this limitation, the isoelectronic substitution of Hf at Zr site in ZrNiSn has been proved to be highly effective to reduce κ l and optimize electrical properties19,20. Previous experiments showed that 50% than 25% Hf doping in ZrNiSn could more efficiently enhance TE performance, which not only increased S (~252 μV K−1 at 800 K), but also slightly increased σ (~5.9 × 104 Ω−1 m −1 at 800 K)21,22,23,24. Those experimental works have detailedly discussed the supression of κ l , however, there is no specific analysis of the reasons for the increasing of power factor (PF) of HfxZr1−xNiSn (x = 0.25, 0.5). Therefore, it is necessary to devote more effort to analyzing the physical reason of improved PF. Although Hf doping increases S, there is a little increase in σ. Hence, it is necessary to further optimize σ for higher TE properties. Yu et al.22 reported that the κ l of HfxZr1−xNiSn0.98Sb0.02 (x = 0.5, 0.6) samples reduced to 3.1 W m−1 K−1 and 3.3 W m−1 K−1 at room temperature, respectively, and n-type 2% Sb doping at Sn site in Hf0.5Zr0.5NiSn has shown to be an effective approach to further remarkably enhance σ (~14.8 × 104 Ω−1 m −1 at 800 K) by optimizing n. Nevertheless, they also did not explain why Sb co-doping in Hf0.5Zr0.5NiSn could further efficiently improve TE properties.
In this work, to explore the influences of Hf/Sb co-doping, we substituted Zr sites with various Hf doping contents and co-doping Sb at Sn site in ZrNiSn, and systematically investigated the electronic structures and transport properties of HfxZr1−xNiSn1−y Sby (x = 0, 0.25, 0.5; y = 0, 0.02) by using the first-principles calculations and semiclassical Boltzmann transport theory. Our calculation results show that 50% Hf doping in ZrNiSn simultaneously increases the degeneracy (N v ) at the bottom of conduction band (CB) and the dispersion of energy-band near the CB edge, which are helpful to increasing S and slightly enhanceing σ. Meanwhile, we elucidate that why 2% Sb co-doping further largely improves σ. It increases total density of states near the Fermi energy (E F) and leads to the convergence of the light and heavy bands and valley degeneracy. N v reaches eleven at the Γ point of the bottom of conduction band. Besides, our work also demonstrates that Hf0.5Zr0.5NiSn0.98Sb0.02still maintains high μ in spite of \({m}_{{\rm{b}}}^{\ast }\) increasing. Therefore, a great improvement in σ occurs. The ZT (~1.37) of Hf0.5Zr0.5NiSn0.98Sb0.02 with the n of 7.56 × 1018 cm−3 at 1000 K is predicted.
Results and Discussion
Crystal structure and bonding properties of pure and Hf/Sb co-doped ZrNiSn
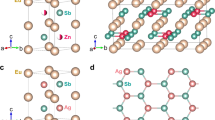
The C1 b -type structure of ZrNiSn (space group: F \(\bar{4}3\,m\), no. 216)25 is crystallized by three interpenetrating facecentered cubic (fcc) sublattices26, as depicted in Fig. 1(a). Each unit cell contains four Zr atoms, four Ni atoms, and four Sn atoms. The electronegativity values of Zr, Ni, and Sn are 1.33, 1.91, and 1.96, respectively. The most electropositive element Zr donates all of its valence electrons to the more electronegative elements Ni and Sn, as a result, ZrNiSn can be described as Zr4+ (NiSn)4− 27. This system is filled by the substructures which are similar to ZnS lattice. These substructures are formed by Ni atoms with Sn or Zr in the centers of the tetrahedron, as shown in Fig. 1(b,c). Figure 1(d,e) present the local structures of 50% Hf substitutions at Zr sites in a 2 × 2 × 3 ZrNiSn supercell and 2% Sb co-doping at Sn48 site in a 144-atoms cell of Hf0.5Zr0.5NiSn.
Using the equation of state (EOS) to fit the E-V curve, where E is the total energy of one unit cell (with the unit of Ry), V is the volume of one unit cell (with the unit of a.u.3), we firstly acquire the most stable ZrNiSn structure. Its lattice constant (a) is ~6.141 Å which is consistent with the experimental value (a ~ 6.110 Å), proving the reliability of our theoretical method. For well understanding of the electron distribution and bonding properties of ZrNiSn, we calculated the electron localization function (ELF)28. Figure 2(b) reveals that ELF is evenly distributed around Zr atoms, this means that Zr donates its valence electrons to the [NiSn]4−, which coincides with the above analysis that, in ZrNiSn, Zr atoms tend to lose electrons, while Ni and Sn atoms tend to gain electrons owing to their larger electronegativity. Whereas the ELF between the Zr and Ni atoms mainly localizes around Ni, and a certain number of charges appear in center position between Sn and Ni, indicating Zr and Ni atoms incline to form an ionic bond, while there is a distinct covalent bond characteristics between Ni and Sn atoms.
Electronic structure analysis of HfxZr1−xNiSn1−ySby
Regarding the transport properties are predominantly affected by the electronic states at the vicinity of the valence band maximum (VBM) and the conduction band minimum (CBM), we only concern with the electronic states near the E F. Usually good TE materials are narrow-band-gap semiconductors and precise E g is very vital to estimating the TE performance. One important feature of the electronic structure is its band structure which is closely related to the TE properties of the materials. Figure 3(a,b) plots the band structure and partial density of states (PDOS) of ZrNiSn. With modified mBJ method by DFT, we calculated the band structure of ZrNiSn. The calculated E g of ZrNiSn is about 0.52 eV which is similar to that with PBE-GGA (0.51 eV), and it is also good agreement with previously calculated value (~0.50 eV)29,30. The band gap can be estimated using experimental data from the temperature reliance on σ by31:
where σ 0 is a pre-exponential factor. Muta et al.32 estimated that the E g of ZrNiSn is about 0.20 eV corresponding to the prior experimental value (~0.186 eV)33,34. It is extremely unexpected because DFT usually underestimates, not overestimates, E g. The E g of experimental value is smaller than calculated value, which may originate from the formation of impurity band in the gap, due to the presence of Ni interstitial atoms with its d orbitals when Ni atoms excess (>25%), namely Frenkel pairs35. Despite a drastically reduced E g due to Ni interstitial band36, the n-type ZrNiSn is not over-whelmed by bipolar effect, because the holes in ZrNiSn have low μ 37, leading to a low hole electrical conductivity (σ p ). As a result of the total S for multiple carriers is weighted by the individual σ 38:
This is one possible reason why ZrNiSn normally has a relatively large S. The N v at the Γ point of the top of valence band (VB) is six, this relatively high N v is the other possible reason for having a relatively large S. It is well known that ZT inversely depends on κ. Therefore, the optimal dopants not only can substantially improve PF, but also can significantly suppress κ.
Previous experiments reported that Hf substitution at Zr site in ZrNiSn could significantly suppresse κ l and improve electron transport simultaneously19,20. To clearly analyze the reason for this increase of PF, we also calculated the band structures of HfNiSn and HfxZr1−xNiSn (x = 0.25, 0.5). The band structure of HfNiSn was ploted in Supplemental Fig. S1. What is worth mentioning that all our calculations include the spin-orbital coupling (SOC). As has been reported that SOC is only a small effect on the band structure of ZrNiSn, while there is a distinct effect on the band structure of HfNiSn if SOC is included. That is why SOC is considered here. According to Eq. (2) we know, a high N v will increase \({m}_{{\rm{DOS}}}^{\ast }\) and thus enlarges S, because which is proportional to \({m}_{{\rm{DOS}}}^{\ast }\). N v contains the orbital degeneracy (N v at one extrema point) and valley degeneracy (separate pockets at the same or similar energy). As shown in Fig. 4(a), the N v of ZrNiSn at the X point of the bottom of CB is 2. While we can note from Fig. 4(b) that 25% Hf doping in ZrNiSn makes six orbital degeneracy at the Γ point of the bottom of CB, which may increase its S. Figure 4(c) depicts that 50% Hf doping induces six effective electron-pockets with the difference in energy between them is 0.013 eV at the M point (N v = 4) and Γ point (N v = 2) of the bottom of CB. This means that the energy bands of M and Γ points of the bottom of CB simultaneously participate in transport, which may be responsible for the improvement of S of Hf0.5Zr0.5NiSn. Yu et al. reported that the n-type 2% Sb co-doping at Sn site in Hf0.5Zr0.5NiSn could further greatly improve σ 22. To explore physical reason for such improvement, we calculated the band structure of Hf0.5Zr0.5NiSn0.98Sb0.02. N v increases when the difference in energy of their band extrema within a few k B T, and σ enhances. Because in a system, the total electrical conductivity (σ total ) can be expressed as:
when it contains two valence (or conduction) bands. Here, subscripts 1 and 2 refer to the transport properties of carriers in the individual band39. As seen in Fig. 5, there are eleven approximately degenerated bands (N v = 11) at the Γ point of the bottom of CB, which are conducive to improving σ total . This also makes S not fall too much via enlarging \({m}_{{\rm{DOS}}}^{\ast }\) as governed by Eq. (2), this is one of the possible reasons why σ has been impressively enhanced without reduction S too much. Apart from the CBM, there are two other conduction band extremums (CBEs) with little difference in energy, one occurs at the X point, and another lies in the Z point. These conduction valleys have almost equal energies, as shown in Table 1, therefore increasing valley degeneracy. The \({m}_{{\rm{DOS}}}^{\ast }\) can be re-written as40:
where N 1, N 2 and N 3 are the valley degeneracies for the CBM and two CBEs, respectively. According to Eq. (7), the higher valley degeneracy of the CBM and CBEs are favorable for higher σ total and larger \({m}_{{\rm{DOS}}}^{\ast }\). This is another possible reason for impressively enhacing σ and no too much reduction of S. Meanwhile, at the Γ point, the light band with small \({m}_{{\rm{b}}}^{\ast }\) (~0.63 m e) at the vicinity of the E F is beneficial to enhancing σ and the heavy band with large \({m}_{{\rm{b}}}^{\ast }\) (~4.23 m e) close to the CBM is conducive to S. The coexistence of light and heavy bands, accompanying by an increase in the number of effective electron-pocket near the E F, may strongly increase σ of Hf0.5Zr0.5NiSn0.98Sb0.02 without too much decreasing S. The remarkable advantage of this band structure is the band convergence induced by 2% Sb doping, which increases ZT value in the whole temperature range. Figure 5 presents that n-type 2% Sb co-doping makes Hf0.5Zr0.5NiSn0.98Sb0.02 become a degenerate semiconductor with E F moving into CB by 0.12 eV. The large n and the appearance of light band near the E F may remarkably enhance σ, in the meantime, it also probably decreases S. While the heavy band and high N v are favorable for increasing S, which will overwhelm detriment from increasing n, thus that’s why σ dramatically increases without too much decreasing S.
To clearly understand the states near the E F, we calculated the PDOS of ZrNiSn. In Fig. 3(b), the band edge is mainly contributed by the Zr-t2g, and the bottom of the CB partly comes from Ni-eg. Thus, the substitution on the Zr site can effectively adjust the band structure near the band edge. Doping often results in reduction of S, however, Hf doping increases S. More particularly, 50% Hf doping simultaneously increases S and σ. To analyze the reasons for enhanced PF by Hf doping, we calculated the total density of states (TDOS) of HfxZr1−xNiSn (x = 0, 0.25, 0.5) as shown in Fig. 6(a). Hf doping increases the TDOS near the E F, in fact, an enhanced TDOS near the E F contributes to forming a high σ due to σ(E F) ∝ TDOS\({|}_{E={E}_{{\rm{F}}}}\). It is also found that the TDOS of x = 0.25 is larger than that of x = 0.5 near the band edge. While the larger \({m}_{{\rm{b}}}^{\ast }\) (~1.97 me) of x = 0.25, as depicted in the Table 2, will reduce the μ than of x = 0.5, which may counteract the increase of σ by a larger TDOS. Moreover, 50% Hf doping also increases the dispersion of energy bands near the CB edge, and its smaller \({m}_{{\rm{b}}}^{\ast }\) (~1.18 m e) than x = 0.25 gives obvious evidence to this, which is also helpful to improving σ. As a consequence, 50% Hf doping can increase PF through simultaneously increasing S and slightly optimizing σ.
To further analyze the reasons for enhanced more PF by 50% Hf doping, we also calculated the partial DOS (Fig. 6(b)) and band decomposition charge density (Fig. 6(c)) of CBM and VBM of Hf0.5Zr0.5NiSn system. Figure 6(b) indicates that the contributions to energy band edge of both CB and VB are mainly comprised of d orbitals of Ni, Zr and Hf, and the corresponding \({m}_{{\rm{b}}}^{\ast }\) is large due to localizing 3d states. This fact is beneficial to electrical transport with increasing \({m}_{{\rm{DOS}}}^{\ast }\). Therefore, Hf0.5Zr0.5NiSn has a relatively large S. From Fig. 6(c), we can see that the charges accumulate around the Ni, Hf, and Zr atoms, while charges around Sn1 and Sn2 atoms are few at the CBM. Thereby Sb doping at Sn site may effectively increase the TDOS near the E F. Previous experiments showed that Sb doping at Sn site would further remarkably enhance σ without significantly reducing S 22. This motivates our great interest to investigate the reason for such improved TE properties. As seen in Fig. 6(d) that Sb doping leads to an increase in the TDOS near the CB edge, which are why σ remarkably improves.
Enhancement of electrical transport properties by Hf/Sb co-doping in ZrNiSn
As mentioned above, a promising TE material requires a large S, a high σ, and a low κ. Experiments have shown that Hf substitution at Zr site in ZrNiSn can effectively reduce κ l by isoelectronic substitution creating multiscale scattering centers and alloy scattering of phonons due to the mass and size differences between dopant atoms and host atoms19,20. Prior experiments demonstrated that Hf doping also enhanced PF and Sb doping in Hf0.5Zr0.5NiSn further primarily improved σ 22. To deeply understand the influences of Hf/Sb co-doping, herein various doping concentrations were simulated and the transport properties of HfxZr1−xNiSn1−ySby (x = 0, 0.25, 0.5; y = 0, 0.02) were calculated as a function of n at 300 K, 700 K, and 1000 K within the framework of the semiclassical Boltzmann transport theory. The strategy previously used by Ong et al.41 was adopted with available experimental data18,19,20,22 to roughly estimate relaxation time (τ). Accordingly, the standard electron-phonon dependence on T and n for τ is: τ = C 0 T −1 n −1/3 with τ in s, T in K and n in cm−3. For comparision the doping effect of Hf at different concentrations, we firstly calculated the electrical transport properties of HfxZr1−xNiSn (x = 0, 0.25, 0.5), as ploted in Fig. 7. Compared with pure phase of ZrNiSn (ZT ~ 0.24 with the optimal n of 7.745 × 1019 cm−3 at 1000 K) (Fig. 7(a)), 25% Hf doping increases S and almost unchanges σ, hence increasing the ZT (~0.74 with the optimal n of 3.162 × 1020 cm−3 at 1000 K) (Fig. 7(b)). Fascinatingly, 50% than 25% Hf doping can more effectively enhance the ZT (~1.07 with the optimal n of 1.710 × 1020 cm−3 at 1000 K) by synergistically enhancing S and σ (Fig. 7(c)). Herein, the κ l of experimental value was employed for evaluating ZT 18,19,22,42. The calculated results also show that the TE properties of n-type HfxZr1−xNiSn (x = 0, 0.25, 0.5) compounds are better than those of p-type ones. This can be well explained by a large electronegativity difference (Δχ) between Hf4+ and (NiSn)4−, which gives rise to a higher formation energy of cation antisite defects (E AS) and a lower formation energy of anion vacancies (E v )8.
To further research the effect of Sb co-doping, we calculated the electrical transport properties of Hf0.5Zr0.5NiSn0.98Sb0.02 by combining the semiclassical Boltzmann transport theory under constant τ approximation. As shown in Fig. 8, the peak ZT can reach 1.37 by achieving strikingly improvement of σ and no too much reduction of S with the n of 7.56 × 1018 cm−3 at 1000 K. It should be noted that the experiment workers only measured the κ before 800 K22. While calculating κ of large doping systems are usually difficult. Here, the κ of Hf0.5Zr0.5NiSn0.985Sb0.015 20, which probably has a similar crystal structure to Hf0.5Zr0.5NiSn0.98Sb0.02 and thereby has analogous κ, was adopted to predict the ZT of Hf0.5Zr0.5NiSn0.98Sb0.02 at 1000 K. From Fig. 8(a), we can see that S is affected by bipolar effect decreasing at high temperature. This reduction can be attributed to the convergence of light and heavy bands at the bottom of CB. The bipolar effect may be caused by the small direct E g (~0.44 eV) as displayed in Fig. 5, in which the excitation of electron-hole pairs and the opposing contribution to S total from the two types of carriers23. To our knowledge, the bipolar effect will decrease the TE performance, thus it is valuable to seek method for decreasing bipolar effect.
Figure 8(b) manifests that σ remarkably enhances, which may originate from the increment of n and/or μ. To verify this viewpoint, we calculated the temperature dependence of n of Hf0.5Zr0.5NiSn1−ySby (y = 0, 0.02). μ was obtained from the calculated σ and n by using the expression μ = σ/ne. As seen in Fig. 9, 2% Sb doping really greatly increases n, and high μ basically remain sametime. Thereby, increasing of n may be the main reason for large increase in σ. While our calculated μ is higher than the experimental value, which may results from two factors. First, our calculated n (~4.29 × 1020 cm−3) is smaller than that of Zhu et al.22 reported (~5.24 × 1020 cm−3) at room temperature. High n in the experiment may be caused by interstitial Ni atoms. Another potential reason is that the calculated m * (~2.31 m e ) is smaller than experimental one (~2.64 m e ) in ref.22.
To understand the large increase in n, the Bader charge analysis of Hf0.5Zr0.5NiSn and Hf0.5Zr0.5NiSn0.98Sb0.02 were calculated by using VASP. The calculated results show that the total number of losing electrons from Sb are 8.87|e| in a unit supercell, and thus n is greatly increased. This means that Sb atom loses more electrons than Sn atom, it is one possible reason why Sb doping more effectively increases n. Besides, each nearest neighbor Ni atom of Sb averagely obtains more 2.22 e from the Sb atom than that from Sn, manifesting Sb-Ni has a stronger interaction than Sn-Ni. In fact, the stronger hybridization between Sb and Ni atoms will more conduces to increasing the DOS near the CB edge, which is corroborated by Fig. 6(d). This may be another possible reason why Sb doping supplies more electrons. Hence, σ remarkably enhances. With increasing n, the E F shifts deeper in the CB and the differential conductivity turns into more symmetric regarding the Fermi level. In contrast to the dramatical increase of σ, S reduces. Hf/Sb co-doping reduces S from 213 μV K−1 (of ZrNiSn) to 153 μV K−1 (of Hf0.5Zr0.5NiSn0.98Sb0.02) at 800 K, this no explicitly decreasing is most likely due to the N v increasing which is the key parameters for making a compromise between n and S.
Calculation results show that Hf0.5Zr0.5NiSn0.98Sb0.02 still maintains high μ especially above 500 K as revealed in Fig. 9(a) despite the \({m}_{{\rm{b}}}^{\ast }\) increases, which is majorly ascribed to two reasons. For one thing, in general, high μ and small \({m}_{{\rm{b}}}^{\ast }\) are found in materials with small Δχ (e.g. IrSb3 μ = 1320 cm2 V−1 s−1, \({m}_{{\rm{b}}}^{\ast }\) = 0.17 m e at 300 K), and low μ and large \({m}_{{\rm{b}}}^{\ast }\) are found in ionic materials (e.g. FexCr3−xSe4 μ = 0.1 cm2 V−1 s−1, \({m}_{{\rm{b}}}^{\ast }\) = 4 m e at 300 K)43,44,45,46,47. While, HH compounds, which frequently exhibit both ionic and covalent bonding, bridge these extremes. Thus, Hf0.5Zr0.5NiSn0.98Sb0.02 still maintains relatively high μ (26.3 cm2 V−1 s−1) with relatively large \({m}_{{\rm{b}}}^{\ast }\) (2.64 m e) at 300 K. Another, a low Ξ and a low alloy scattering potential with the weak coupling between phonons and electrons are conducive to compensating for the decrease of μ due to the large \({m}_{{\rm{b}}}^{\ast }\). This is also a reason for Hf0.5Zr0.5NiSn0.98Sb0.02 still maintaining a high μ, which has been experimentally confirmed15,16,17. Therefore, the tradeoff between μ and \({m}_{{\rm{b}}}^{\ast }\) is achieved, and then maximizing PF through the balance of σ and S is realized by Eqs (1) and (3). However, the μ has a slight reduction below 500 K. This slight reduction can be mainly attributed to the the reduction of κ l of Hf0.5Zr0.5NiSn0.98Sb0.02 with high n (~4.29 × 1020 cm−3 at room temperature) and large \({m}_{{\rm{b}}}^{\ast }\) (~2.31 m e). As is reported15,48,49, acoustic phonon scattering is the dominant scattering mechanism with high n and large \({m}_{{\rm{b}}}^{\ast }\) at low temperature. Because when an acoustic phonon wave crosses through the lattice, it induces a local strain in the crystal, resulting in a perturbation of the band and carriers scatterings. The high μ retention is due to that the compromise between μ and κ l which is made by minimizing the influence of the acoustic phonon scattering with a small Ξ and a low alloy scattering potential as already mentioned. Thereby, a high TE performance is attained with ~28% enhancement of the highest ZT of Hf0.5Zr0.5NiSn0.98Sb0.02 compared with Hf0.5Zr0.5NiSn.
Conclusions
In summary, the electronic structures and TE transport properties of Hf/Sb co-doping in ZrNiSn have been systematically investigated by using the first-principle calculations and semiclassical Boltzmann theory. We elucidate the possible origins for the improvement of TE properties of ZrNiSn by Hf/Sb co-doping. 50% Hf doping not only increases the N v with the Γ and M points simultaneously participating in transportation at the bottom of CB but also increases the dispersion of energy bands near the CB edge. These are helpful to increasing S and sligtly enhancing σ at the same time. Then, 2% Sb co-doping increases total density of states near the E F and remains high μ, and leads to converging of light and heavy bands. N v reaches eleven at the conduction band minimum, therefore resulting in a striking improvement in σ. Moreover, from the Bader analysis, we also find the reason that why Sb co-doping could provide higher n. It results from that Sb loses more electrons and Sb-Ni has a stronger hybridization than Sn-Ni. Our calculation results demonstrate that the ZT of Hf0.5Zr0.5NiSn0.98Sb0.02 can reach 1.37 with the n of 7.56 × 1018 cm−3 at 1000 K. Thus, Hf/Sb co-doping can be an effective strategy in tuning band structure and enhancing TE properties of ZrNiSn alloy compounds.
Computational Details
The lattice structures of HfxZr1−xNiSn1−ySby (x = 0, 0.25, 0.5; y = 0, 0.02) were optimized with the plane-wave cutoff energy of 500 eV and the energy convergence of 10−6 eV by the Vienna ab initio simulation package (VASP) based on the density functional theory (DFT)50,51. The Perdew-Burke-Ernzerh of (PBE) parameterization of generalized- gradient approximation (GGA) was used for the exchange-correlation potential52. The full-potential linearized augmented plane wave (FLAPW) method53 was applied to calculate the electronic structures of HfxZr1−xNiSn1−ySby (x = 0, 0.25, 0.5; y = 0, 0.02), which was implemented in WIEN2k54,55,56. Modified Becke-Johnson (mBJ) semi-local exchange potential was employed for improving the accuracy of band gap57,58.
Here, the SOC of elements (Hf, Zr, Ni, Sn, and Sb) and the relativistic effect of heavy element Hf were considered. The TE transport properties were evaluated with BoltzTraP code which was based on semiclassical Boltzmann transport theory59,60,61. We used R mt × K max = 7 (K max was the magnitude of the largest k vector) as the cutoff parameter. While, R mt , the smallest muffin-tin radius of Ni, Zr, Sn, Hf, and Sb atoms, were set to be 2.45 a.u., 2.42 a.u., 2.47 a.u., 2.46 a.u., and 2.45 a.u., respectively. The rigid band approach (RBA) and the constant scattering time approximation were utilized to evaluate the TE transport properties. When doping, the RBA is supposed to be without changing the band structure of the compound but to shift the Fermi level up or down. The constant scattering time approximation, which is based on a smoothed Fourier interpolation of the bands, is usually implemented for metals and degenerately doped semiconductors. These approximations also have been extensively imposed in the calculation for study many TE materials62,63,64,65,66. For HfxZr1−xNiSn alloys (x = 0.25, 0.5), the substitution of Hf atoms at Zr sites was performed in a 12-atoms cell. For Hf0.5Zr0.5NiSn0.98Sb0.02 alloy compound, we constructed a 2 × 2 × 3 ZrNiSn supercell, and then replaced Zr atoms with Hf atoms and substituted Sn atom with Sb atom in a 144-atoms cell. To accurately understand the effect of Hf/Sb co-doping on the electronic structures and transport properties of HfxZr1−xNiSn1−ySby alloy compounds (x = 0, 0.25, 0.5; y = 0, 0.02), we took all kinds of situations as much as possible and the shortest distances among the doping atoms should be as large as possible. The most stable doping site was obtained through optimizing the structures by using the VASP.
References
Wang, S. et al. High thermoelectric performance in Te-free (Bi,Sb)2Se3 via structural transition induced band convergence and chemical bond softening. Energ. Environ. Sci. 9, 3436–3447 (2016).
Feng, Z. et al. Ag-Mg antisite defect induced high thermoelectric performance of α-MgAgSb. Sci. Rep. 7, 2572 (2017).
Shi, X. et al. Multiple-Filled Skutterudites: High Thermoelectric Figure of Merit through Separately Optimizing Electrical and Thermal Transports. J. Am. Chem. Soc. 133, 7837–7846 (2011).
Tritt, T. Holey and Unholey Semiconductors. Science 283, 804–805 (1999).
Snyder, G. & Toberer, E. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008).
Shi, X., Chen, L. & Uher, C. Recent advances in high-performance bulk thermoelectric materials. Int. Mater. Rev. 61, 379–415 (2016).
Shen, J., Wu, L. & Zhang, Y. First-principles studies of the TE properties of [110]-Ge/Si core/shell nanowires with different surface structures. J. Mater. Chem. A 2, 2538–2543 (2014).
Zhu, T. et al. Compromise and Synergy in High-Efficiency Thermoelectric Materials. Adv. Mater. 29, 1605884 (2017).
Luo, D., Wang, Y., Yan, Y., Yang, G. & Yang, J. The high thermopower of the Zintl compound Sr5Sn2As6 over a wide temperature range: first-principles calculations. J. Mater. Chem. A 2, 15159–15167 (2014).
Ye, L. et al. Electronic structure and thermoelectric properties of the Zintl compounds SrAlSb and CaAlSb: first-principles study. RSC Adv. 5, 50720–50728 (2015).
Cutler, M., Leavy, J. & Fitzpatrick, R. Electronic transport in semimetallic cerium sulfide. Phys. Rev. 133, A1143 (1964).
Feng, Z. et al. Origin of different thermoelectric properties between Zintl compounds Ba3Al3P5 and Ba3Ga3P5: A first-principles study. J. Alloys Compd. 636, 387–394 (2015).
Goldsmid, H. Thermoelectric Refrigeration. Plenum Press, New York (1964).
Pei, Y., Lalonde, A., Wang, H. & Snyder, G. Low effective mass leading to high thermoelectric performance. Energ. Environ. Sci. 5, 7963–7969 (2012).
Xie, H. H. et al. Beneficial Contribution of Alloy Disorder to Electron and Phonon Transport in Half-Heusler Thermoelectric Materials. Adv. Funct. Mater. 23, 5123–5130 (2013).
Liu, Z. et al. Lithium doping to enhance thermoelectric performance of MgAgSb with weak electron-phonon coupling. Adv. Energy. Mater. 6, 1502269 (2016).
Liu, X. et al. Low Electron Scattering Potentials in High Performance Mg2Si0.45Sn0.55 Based Thermoelectric Solid Solutions with Band Convergence. Adv. Energy. Mater. 3, 1238–1244 (2014).
Xie, H. et al. Interrelation between atomic switching disorder and thermoelectric properties of ZrNiSn half-Heusler compounds. Crystengcomm 14, 4467–4471 (2012).
Kimura, Y., Ueno, H. & Mishima, Y. Thermoelectric Properties of Directionally Solidified Half-Heusler (M0.5 a, M0.5 b)NiSn (Ma, Mb = Hf, Zr, Ti) Alloys. J. Electron. Mater. 38, 934–939 (2009).
Liu, Y. et al. Demonstration of phonon-glass electron-crystal strategy in (Hf,Zr)NiSn half-Heusler thermoelectric materials by alloying. J. Mater. Chem. A 3, 22716–22722 (2015).
Sakurada, S. & Shutoh, N. Effect of Ti substitution on the thermoelectric properties of (Zr,Hf)NiSn half-Heusler compounds. Appl. Phys. Lett. 86, 3159 (2005).
Yu, C. et al. High-performance half-Heusler thermoelectric materials Hf1−xZrxNiSn1−ySby prepared by levitation melting and spark plasma sintering. Acta. Mater. 57, 2757–2764 (2009).
Shen, Q. et al. Effects of partial substitution of Ni by Pd on the thermoelectric properties of ZrNiSn-based half-Heusler compounds. Appl. Phys. Lett. 79, 4165–4167 (2001).
Zhang, H. et al. Thermoelectric properties of n-type half-Heusler compounds (Hf0.25Zr0.75)1−xNbxNiSn. Acta Mater. 113, 41–47 (2016).
Mihaela, X., Bojin, D. & Hoffmann, R. The RE M E Phases. Helv. Chim. Acta 86, 1653–1682 (2003).
Graf, T., Felser, C. & Parkin, S. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 39, 1–50 (2011).
Zeier, W. et al. Engineering half-Heusler thermoelectric materials using Zintl chemistry. Nat. Rev. Mater. 1, 16032 (2016).
Savin et al. ELF: The electron localization function. Angew. Chem. Int. Ed. 36, 1808–1832 (1997).
Rai, D. et al. Study of electronic and an enhanced thermoelectric properties of ZrxHf1−x−yTayNiSn: A first principles study. RSC Adv. 6, 95353–95359 (2015).
Zou, D., Xie, S., Liu, Y., Lin, J. & Li, J. Electronic structure and thermoelectric properties of half-Heusler Zr0.5Hf0.5NiSn by first-principles calculations. J. Appl. Phys. 113, 193705 (2013).
Gazka, K. et al. Improved thermoelectric performance of (Zr0.3Hf0.7)NiSn half-Heusler compounds by Ta substitution. J. Appl. Phys. 115, 105 (2014).
Muta, H., Kanemitsu, T., Kurosaki, K. & Yamanaka, S. Substitution Effect on Thermoelectric Properties of ZrNiSn Based Half-Heusler Compounds. Mater. Trans. 47, 1453–1457 (2006).
Aliev, F. et al. Gap at the Fermi level in the intermetallic vacancy system RBiSn (R = Ti, Zr, Hf). Z. Phys. B: Condens. Matter 75, 167–171 (1989).
Aliev, F., Kozyrkov, V., Moshchalkov, V., Scolozdra, R. & Durczewski, K. Narrow band in the intermetallic compounds MNiSn (M = Ti, Zr, Hf). Z. Phys. B: Condens. Matter 80, 353–357 (1990).
Romaka, V. et al. Peculiarities of structural disorder in Zr- and Hf-containing Heusler and half-Heusler stannides. Intermetallics 35, 45–52 (2013).
Yu, Y., Zhang, X. & Zunger, A. Natural off-stoichiometry causes carrier doping in half-Heusler filled tetrahedral structures. Phys. Rev. B 95, 085201 (2017).
Wang, S. et al. Conductivity-limiting bipolar thermal conductivity in semiconductors. Sci. Rep. 5, 10136 (2015).
Wood, C. Materials for thermoelectric energy conversion. Rep. Prog. Phys. 51, 459–539 (1999).
Pei, Y. et al. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 473, 66–69 (2011).
Fan, D. et al. Understanding the electronic and phonon transport properties of a thermoelectric material BiCuSeO: a first-principles study. Phys. Chem. Chem. Phys. 19, 12913–12920 (2017).
Ong, K., Singh, D. & Wu, P. Analysis of the thermoelectric properties of n-type ZnO. Phys. Rev. B 83, 115110 (2011).
Kimura, Y. & Chai, Y. Ordered Structures and Thermoelectric Properties of MNiSn (M = Ti, Zr, Hf)-Based Half-Heusler Compounds Affected by Close Relationship with Heusler Compounds. JOM 67, 233–245 (2015).
Toberer, E., May, A. & Snyder, G. Zintl chemistry for designing high efficiency thermoelectric materials. Chem. Mater. 22, 624–634 (2009).
Hsu, K. et al. Cubic AgPbmSbTe2+m: Bulk Thermoelectric Materials with High Figure of Merit. Science 303, 818–821 (2004).
Rowe, D. CRC handbook of thermoelectrics. CRC Press, Lonon (1995).
Slack, G. & Tsoukala, V. Some properties of semiconducting IrSb3. J. Appl. Phys. 76, 1665–1671 (1994).
Snyder, G., Caillat, T. & Fleurial, J. Thermoelectric, transport, and magnetic properties of the polaron semiconductor FexCr3−xSe4. Phys. Rev. B 62, 10185–10193 (2000).
Anno, H., Matsubara, K., Motohara, Y., Sakakibara, T. & Tashiro, H. Effects of doping on the transport properties of CoSb3. J. Appl. Phys. 86, 3780–3786 (1999).
Yang, J. et al. Influence of electron-phonon interaction on the lattice thermal conductivity of Co1−xNixSb3. Phys. Rev. B 24, 678–686 (2002).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys.: Condens. Matter 6, 8245 (1994).
Fu, X. et al. Generalized gradient approximation made simple. Appl. Phys. Lett. 125, 89–96 (2015).
Singh, D. J. & Nordstrom, L. Planewaves, Pseudopotentials, and the LAPW method. Springer, New York (2006).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864 (1964).
Koelling, D. & Harmon, B. A technique for relativistic spin-polarised calculations. J. Phys. C 10, 3107–3114 (1977).
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2k: An Augmented Plane Wave plus Local Orbitals Program for Calculating Crystal Properties. J. Endocrinol. 196, 123–130 (2010).
Tran, F. & Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 102, 226401 (2009).
Engel, E. & Vosko, S. Exact exchange-only potentials and the virial relation as microscopic criteria for generalized gradient approximations. Phys. Rev. B 47, 13164 (1993).
Ziman, J. Electrons and phonons: the theory of transport phenomena in solids. Oxford, Oxford (1960).
Madsen, G., Schwarz, K., Blaha, P. & Singh, D. Electronic structure and transport in type-I and type-VIII clathrates containing strontium, barium, and europium. Phys. Rev. B 68, 125212 (2003).
Madsen, G., Singh, D. & David, J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71 (2006).
Zhang, X. et al. Origin of high thermoelectric performance of FeNb1−xZr/HfxSb1−ySny alloys: A first-principles study. Sci. Rep. 6, 33120 (2016).
Luo, D. & Wang, Y. The driving force for forming As-As bonding and its effect on the electronic structures and the thermoelectric properties of Zintl Ca5M2As6 (M = Sn, Ga). RSC Adv. 7, 14262–14271 (2017).
Jin, Y., Feng, Z., Ye, L., Yan, Y. & Wang, Y. Mg2Sn: a potential mid-temperature thermoelectric material. RSC Adv. 6, 48728–48736 (2016).
Feng, Z. et al. An impurity intermediate band due to Pb doping induced promising thermoelectric performance of Ca5In2Sb6. Phys. Chem. Chem. Phys. 17, 15156–15164 (2015).
Zhang, X., Wang, C. & Wang, Y. Influence of the elements (Pn = As, Sb, Bi) on the transport properties of p-type Zintl compounds Ba2ZnPn2. Comp. Mater. Sci. 127, 8–14 (2017).
Acknowledgements
This research was sponsored by the National Natural Science Foundation of China (Nos 51371076, 11674083, and 51571083), Excellent Youth Foundation of Henan Province (No. 154100510013).
Author information
Authors and Affiliations
Contributions
J.Z. carried out the calculations under the guidances of Y.W. and X.Z., and drafted the manuscript. All authors took part in the discussion and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J., Zhang, X. & Wang, Y. Hf/Sb co-doping induced a high thermoelectric performance of ZrNiSn: First-principles calculation. Sci Rep 7, 14590 (2017). https://doi.org/10.1038/s41598-017-15205-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-15205-y
This article is cited by
-
Enhanced thermoelectric performance of Zr1−xNiSnTax half-Heusler alloys: a first-principle study
Journal of Computational Electronics (2024)
-
Enhanced thermoelectric performance of Hf-doped ZrNiSn: a first principle study
Journal of Molecular Modeling (2024)
-
Theoretical Study of Mechanical Stability and Physical Properties of Co2V1−xZrxGa
Journal of Superconductivity and Novel Magnetism (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.