Abstract
We investigated the effect of vacancy formation on brittle (D022) to ductile (L12-like) transition in Al3Ti using DFT calculations. The well-known pseudogap on the density of states of Al3Ti migrates towards its Fermi level from far above, via a W − M co-doping strategy, where M is Si, Ge, Sn or Pb respectively. In particular, by a W − M co-doping the underline electronic structure of the pseudogap approaches an octahedral (L12: t2g, eg) from the tetragonal (D022: eg, b2g, a1g, b1g) crystal field. Our calculations demonstrated that (1) a W-doping is responsible for the close up of the energy gap between a1g and b1g so that they tend to merge into an eg symmetry, and (2) all M-doping lead to a narrower gap between eg and b2g (moving towards a t2g symmetry). Thus, a brittle to ductile transition in Al3Ti is possible by adopting this W − M co-doping strategy. We further recommend the use of W-Pb co-doped Al3Ti to replace the less anodic Al electrode in Al-battery, due to its improved ductility and high Al diffusivity. Finally this study opens a new field in physics to tailor mechanical properties by manipulating electron energy level(s) towards higher symmetry via vacancy optimization.
Similar content being viewed by others
Introduction
Brittle to ductile transition is of interest to a wide range of fundamental research and applications1,2,3,4,5,6. In particular, effects of either intrinsic vacancy7,8, extra-electron9, or dopants10,12 on brittle-ductile transition in Nb5Si3, NiSc, Al12W-type and L12-Al3Sc are reported. TiAl-based intermetallic compounds are desirable candidates for high temperature structural applications due to many attractive properties. Among the Al-Ti alloys, Al3Ti has received particular interests for its high specific strength, elastic moduli13, low density (~3.3 g/cm3), good thermal conductivity and high melting point (~1400 °C). However, the stable but brittle tetragonal D022-Al3Ti is less favored in real applications. Many investigations are conducted aiming to improve the ductility of D022-Al3Ti. Hong12 calculated the density of states (DOS) of the brittle D022-Al3Ti and the ductile L12-Al3Ti phases, and proposed a strategy to simultaneously stabilize the ductile L12 and destabilized the brittle D022 phase by ternary alloy additions. He further pointed out that by adding in lower-valence elements, the pseudogap (on DOS) migrates from above to below the Fermi level, thus, diminishing simultaneously the antibonding for the ductile L12 and the bonding states for the brittle D022 phases. But Hong did not take into consideration the formation of either intrinsic or extrinsic defects into his model. On the other hand, Niu9 proposed to promote ductile to brittle transitions in Al12W-type intermetallic by an extra-electron doping, which is on the opposite direction of the current work. The underline electronic structures of pseudogap in both D022 and L12 Al3Ti phases are reported recently by Chen14. Crystal field splitting as shown in Fig. 1 is found responsible for the formation of the pseudogaps, i.e., an octahedral crystal field of eg (d2 x−y, d2 z) and t2g (dxy, dxz, dyz) for the ductile L12 phase, and a tetragonal one of b1g (d2 x−y), a1g (d2 z), b2g (dxy) and eg (dxy, dyz) for the brittle D022 phase. It is interesting to notice that the main difference between the octahedral and tetragonal crystal field splitting is the elongation in tetragonal along the z-axis, which relaxes the electron density along the z-axis and moves (1) the d2 z energy downwards apart from the d2 x−y and (2) the dxz and dyz lower than the dxy level. An effective unit area as shown in Fig. 2a is defined as S = lx × ly, where lx and ly is respectively the shortest atomic distance along the x and y axis. By shrinking the unit cell (or d in Fig. 2a) along the z-axis or expanding in the xy-plane indicated by S, a tetragonal crystal structure may return to and approach an octahedral-like structure. Thus, by reducing the ratio r (Å−1) (r = d/S), a brittle-ductile transition may be facilitated. From first-principles calculations, we test this new strategy to achieve the designed reduction of r by adopting a W − M co-doping strategy. Key challenges in this approach are (1) to generate sufficient Al vacancies in D022-Al3Ti to make the brittle structure more deformable and (2) to manipulate specific electron energy levels to transfer the low symmetry tetragonal to a high symmetry octahedral-like crystal field.
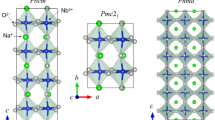
Comparison of the lattice and electronic structures between D022-Al3Ti and L12-Al3Ti. The schematic diagram between the two structures shows that for the tetragonal D022-Al3Ti, the 3d-orbital splits into b1g (d2 x−y), a1g (d2 z), b2g (dxy) and eg (dxy, dyz), while for the octahedral L12-Al3Ti, the 3d-orbital splits into eg (d2 x−y, d2 z) and t2g (dxy, dxz, dyz).
(a) Crystal structure of the W − M co-doping Al3Ti (Note that the unit cell length (d) along the z-axis and the effective unit area (S) are highlighted, where lx is the length between M and Ti and ly is the length between Al and W). (b) The calculated ratio r (Å−1) (r = d/S) in pure D022-Al3Ti and W − M co-doping systems with an Al vacancy at the V1 site.
Moreover, due to the decrease in Gibbs free energy, Al3Ti may also be used as the anode material to replace Al in Al-battery. Recently, electronic structure of pure D022-Al3Ti12,14 and Al diffusion mechanisms of D022-Al3Sc11 are reported. However, like many brittle intermetallics, short cycling life of a native D022-Al3Ti electrode is expected due to the structure damages during the charge and discharge processes. In addition, high Al diffusivity is essential to Al-battery, which requires an easy formation of Al vacancy based on Shi’s11 findings that Al vacancies facilitate the Al diffusion in Al3Sc. Therefore, the current study on the formation of Al vacancies may provide practical solutions to enhance both the mechanical and electrochemical properties of Al3Ti for Al-battery applications.
Results
Crystal structure
Crystal structures of both the ductile (L12) and brittle (D022) phases are shown in the Fig. 1. A L12-Al3Ti crystallizes in the Pm \(\bar{3}\) m space group, in which the Al atoms are located at the face centers of the cubic lattice and the Ti atoms are located at the vertices. And a D022-Al3Ti crystallizes in the I4/mmm. The conventional D022 cell contains two Al atoms at the Wyckoff site 2b (defined as Al1), four Al atoms at the 4d site (defined as Al2) and two Ti atoms at the 2a site. In this study, the lattice parameters are fixed at the values of a = b = 0.3851 nm and c = 0.8611 nm, for c/a = 2.236, which are in satisfactory agreement with other experimental and calculation results15,16.
To conduct a systematic study, the site preference of W in D022-Al3Ti was investigated first by using a 2 × 2 × 1 supercell including 32 atoms. The first-principles calculations have been performed to calculated the total energies E tot for the pure D022-Al3Ti supercell and E dope for [(Al23W)Ti8] and [Al24(Ti7W)] structures. To determine the site preference of W, the substitution energy E sub is defined as:
where μ i (i = Al, Ti and W) is the chemical potential of these atoms in their stable bulk phases. In this study, the stable phases are considered as Ti in hcp structure17, Al in the fcc structure18. After occupying Al1, Al2 and Ti site by a W-atom, the substitution energies of the three structures are −1.089 eV, −0.969 eV and 0.005 eV, respectively. It is clearly seen that the ternary W-atom strongly favors the Al site over the Ti site in the D022-Al3Ti. Therefore, we default to substitute W-atom at the Al1 site in the following work, as the blue sphere shown in Fig. 2a.
Then the IV-group elements M (M = C, Si, Ge, Sn and Pb) were introduced into the D022-Al3Ti/W system and occupied the Ti site to form a W − M cluster, as the green sphere shown in Fig. 2a. The substitution energies of single M-atom doping at the Ti site in D022-Al3Ti can be written as:
where E M is the total energy of single M-atom occupying Ti site. While the substitution energies of W − M clusters can be written as:
where E w−M is the total energy of W − M co-doping system. ΔE is defined as:
The results are showed in Table 1. ΔE are positive which means that the co-doping systems have much lower substitution energies than the single doping systems. It indicates that introducing W in pure D022-Al3Ti structure will conduce to the substitution of Ti by M.
Vacancy formation energy
The crystal model with an Al vacancy were created by removing an individual Al-atom from W − M co-doping supercell. In order to reduce the computation loads, we focus on the first-nearest neighbors, thus, the two possible Al vacancies are at V1 and V2 sites considering the system symmetry, shown as yellow spheres in Fig. 2a. The stability of the defected structures were studied by vacancy formation energy calculation after the atomic defects are relaxed completely. The formation energy of a neutral aluminum vacancy (hereafter simply referred to as an aluminum vacancy) (\({E}_{V}\)) is estimated by the following equation (5):
where E V(M) is the vacancy formation energy, E def is the total energy of D022-Al3Ti/W supercell containing one M-atom and one Al vacancy simultaneously and E W−M is the total energy of W − M co-doping supercell. The last term represents the difference in the number of atoms from the W − M co-doping system, where \({n}_{i}\) denotes the number of atoms to be taken from or inserted into the supercell in order to take account of point defect generation. If a corresponding atom is inserted into the supercell, \({n}_{i}\) is negative and if such an atom is taken away from the supercell, \({n}_{i}\) is positive. \({\mu }_{i}\) is the chemical potential of these atoms in their stable bulk phases. The calculated defect formation energies are tabulated in Table 2.
From Table 2, it can be easily observed that the vacancy formation energies of Al at V1 site are higher than that at V2 site. For a W − M co-doping system, when the Al vacancy occurs at V2 site, the vacancy formation energies are negative under both Al-rich environment and Ti-rich environment, which indicates V2 defects can be formed spontaneously during the fabrication of the alloy. In addition, both V1 and V2 defects are spontaneously formed by a W-Pb co-doping under either Al-rich or Ti-rich environment. The results attribute to the fact that the W − M co-doping cluster plays a vital role in the formation of Al vacancies.
Electronic states of defected structure
The calculated DOS are given in Fig. 3a for the pure D022-Al3Ti, and in Fig. 3b–f for W-C, W-Si, W-Ge, W-Sn and W-Pb co-doping Al3Ti with an Al vacancy at the V1 site, respectively. Δn is introduced to indicate the valley of psuedogap. The value of Δn is the energy of the lowest position on the calculated DOS curve. Thus, the positive value means the psuedogap is higher than the Fermi level. The result is shown in Table 3. A clear pseudogap is observed in the D022-Al3Ti (circled part in Fig. 3a), which indicates the strong bonding-antibonding separation. The result shows a strong hybridization existing in the D022 structure as well as a strong directionality in bonding. Therefore, it is difficult to form the slip system in the tetragonal D022 structure and leads to brittleness. The partial DOS of D022-Al3Ti around the pseudogap was investigated, shown in Fig. 3g. From the edges of the gap, the splitting 3d orbitals could be observed clearly, thus, b1g (d2 x−y) energy is higher than a1g (d2 z) on the right edge, while b2g (dxy) energy is higher than eg (dxy, dyz) on the left edge, which appears a typical tetragonal crystal field.
The calculated (DOS) of (a) pure D022-Al3Ti, (b–f) W − M co-doping Al3Ti with an Al vacancy at V1 site, W = C, Si, Ge, Sn and Pb, respectively. The calculated partial DOS of (g) pure D022-Al3Ti, (h) W-Pb co-doping Al3Ti (Note only 3d orbitals are presented here). All arrows indicate the psuedogap position.
From Fig. 3b–f, by adding different M elements and forming a W − M co-doping cluster with an Al vacancy at V1 simultaneously, the pseudogap migrates from far above towards the Fermi level, indicated by the red arrows. The results show that there are less bonding states which may favor a D022 to L12-like transition. To carry out a more in-depth and detailed study, partial DOS crossing the pseudogap of the W-Pb co-doping system was calculated and shown in Fig. 3h. Contributions from W and Pb to bonding electrons were investigated separately. On the right edge of the pseudogap, it is observed that W-atom contributes a lot to form strong hybridization between the d2 z and d2 x−y levels. Similarly on the left edge of the pseudogap, the Pb-atom has a strong influence on rising the dxz energy and dyz energy towards the dxy level (or a strong hybridization among these 3d orbitals). Therefore, the vacancy-induced 3d-orbital-splitting tend to facilitate a ductile L12-like structure, thus, eg (d2 x−y, d2 z) and t2g (dxy, dxz, dyz).
To obtain the brittle to ductile transition, the tetragonal D022 structure is expected to transform into an octahedral-like structure, which could be realized by either a shrinking along z-axis or an expanding on the xy-plane or both. By representing the ratio r of z-axis d to the xy-plane S, the change in structures are quantified, as shown in Fig. 2b. Taking pure D022-Al3Ti as the standard, it can be concluded that r decreased with the formation of Al vacancy at V1 site, which indicates that the tetragonal crystal field tends to transform into an octahedral-like crystal field. As a result, the stable phase change from D022 to L12–like ductile structures. When an Al vacancy forms at the V2 site, S remains nearly a constant except for the W-C co-doping. The larger S in the W-C co-doping system is due to the small size of C. Among all M elements in Table 4, C is the only dopant whose size is smaller than that of Al (0.39 Å for Al3+). More details will be outlined in Session 3 below.
Discussion
In order to enable a brittle to ductile transition, we proposed and validated a W − M co-doping mechanism to (1) generate sufficient Al vacancies in D022-Al3Ti, and (2) simultaneously to manipulate specific electron energy levels to approach the high symmetry octahedral-like electronic structures. In particular, an equation for the lattice energy of W − M co-dopants is derived based on the EW−M (eV) given in Table 1:
where R M is the ionic radius of M.
The calculated EW−M based on equation (6) is −170.1, −168.7, −167.6, −165.8, −164.6 eV for M = C, Si, Ge, Sn and Pb respectively, which is very close to the DFT calculations, thus, −169.9, −168.7, −167.9, −165.8, −164.6 eV. Therefore, EW−M is in proportional to the cross-session of an M-ion (\({{\rm{R}}}_{{\rm{M}}}^{2}\)), or EW−M is 2-dimensional size (or xy-plane) dependent only. This is a good indicator that a W − M co-doping may only manipulate the xy-plane while leaving out the z-direction untouched.
Similarly, an equation for the formation energy of V2-W − M co-dopants is derived based on the \({{\rm{E}}}_{{{\rm{V}}}_{2}}\) (eV) data given in Table 2:
Both equations (7) and (8) reasonably reproduce DFT calculations shown in Table 2. We derived V2-W − M equations only since they are stable (or having negative formation energy) for all the M elements. Like equation (6), both equations (7) and (8) are in proportional to the cross-session changes of a substitutional M-ion and an Al vacancy (R M−0.39)2. Once again, a V2-W − M co-doping may only manipulate the xy-plane while leaving out the z-direction untouched. This 2-D manipulation function of W − M co-doping is the basis that enables a brittle (D022) to ductile (L12-like) transition, which can be applied not only for Al3Ti but all intermetallics in general.
Finally, we have systematically investigated a series of W − M co-doping D022-Al3Ti (M = C, Si, Ge, Sn and Pb) intermetallics using first-principles calculation method. The site preference of W in pure D022-Al3Ti was first studied, it shows W (a d element) has a clear preference to substitute Al1 (a sp element) site due to the strong crystal field. Then, we confirmed the [(Al23W)Ti8] system is conductive to the subsequent doping of M-atom. Meanwhile, a M substitution of Ti reduces the stability of [(Al23W)Ti8], which might benefit the intercalation and deintercalation of Al-ion during charge-discharge cycling in rechargeable Al-battery. The two possible Al vacancies were also investigated. In comparison to the vacancy formation energies of Li-ion in Li3N19 (−0.14 ~ 0.52 eV), the Al vacancies in W − M co-doped Al3Ti have much lower formation energies, therefore, high Al diffusivity is expected.
The DOS of W − M co-doping Al3Ti with an Al vacancy at the V1 site were investigated. The results show the pseudogap migrates towards the Fermi level from far above, indicating a tendency to transform into ductile L12-like structure. By analyzing the partial DOS around the pseudogap, we found that W and Pb have almost independent contributions to the transition, thus, W mainly influents d2 x−y and d2 z while Pb have a strong effect on dxy, dxz and dyz. It shows the crystal splitting effect on the 3d orbitals plays a decisive role not only on the formation but also the transformation of pseudogap. Therefore, this study contributes to the formation of a new field in physics to design mechanical properties from electronic structures via vacancy optimization.
Methods
Calculations were carried out within the framework of density functional theory (DFT)20, using the projector-augmented wave (PAW) method21 and the Perdew-Burke-Ernserhof (PBE)22 for the exchange-correlation energy functional, via the Vienna ab initio Simulation Package (VASP)23. We first calculated the equilibrium lattice parameters of the Al3Ti using plane-wave cutoff energy of 340 eV and a 7 × 7 × 7 k-point mesh in the Monkhorst-Pack scheme13 by using the 2 × 2 × 1 supercell including 32 atoms. In all calculations, self-consistency was achieved with a tolerance in the total energy of 0.01 meV, and the atom were relaxed until the forces were less than 0.01 eV/Å. The crystal structures were fully optimized by independently modifying lattice parameters and internal atomic coordinates.
Data availability statement
All data generated or analyzed during this study are included in this published article.
References
Jang, D. C. & Greer, J. R. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nature Mater 9(3), 215–219 (2016).
Peterlik, H. et al. From brittle to ductile fracture of bone. Nature Mater 5(1), 52–55 (2006).
Ramos, L. et al. Structural signature of a brittle-to-ductile transition in self-assembled networks. Phys. Rev. Lett. 107(14) (2011).
Tallinen, T. & Mahadevan, L. Forced tearing of ductile and brittle thin sheets. Phys. Rev. Lett. 107(24) (2011).
Yuan, C. C. et al. NMR Signature of evolution of ductile-to-brittle transition in bulk metallic glasses. Phys. Rev. Lett. 107(23) (2011).
Wu, P. & Wu, T. Temperature-dependent modulus of resilience in metallic solids – calculated from strain-electron-phonon interactions. J. Alloys Compd. 705, 269–272 (2017).
Pan, Y. et al. Vacancy induced brittle-to-ductile transition of Nb5Si3 alloy from first-principles. Mater. Des. 86, 259–265 (2015).
Yuan, Z. P., Cui, H. B. & Guo, X. F. First-principle calculation on mechanical and thermal properties of B2-NiSc with point defects. J. Semicond. 38(1), 5 (2017).
Niu, H. Y. et al. Extra-electron induced covalent strengthening and generalization of intrinsic ductile-to-brittle criterion. Sci. Rep, 2 (2012).
Pan, Y. et al. Influence of vacancy on structural and elastic properties of NbSi2 from first-principles calculations. Mater. Des. 108, 13–18 (2016).
Shi, T. T. et al. Atomic diffusion mediated by vacancy defects in pure and transition element (TM)-doped (TM = Ti, Y, Zr or Hf) L1(2) Al3Sc. Mater. Des. 108, 529–537 (2016).
Hong, T. et al. Crystal-structure, phase-stability, and electronic-structure of Ti-Al intermetallics-TiAl3. Phys. Rev. B. 41(18), 12462–12467 (1990).
Milman, Y. V. et al. Mechanical behaviour of Al3Ti intermetallic and L12 phases on its basis. Intermetallics 9(9), 839–845 (2001).
Chen, Z. L. et al. Chemical bonding and pseudogap formation in D0(22) and L1(2) structure (V, Ti)Al3. J. Phys. Chem. Solids. 71(7), 946–951 (2010).
Frazier, W. E. & Benci, J. E. Crystal structure and phase relationships in as-cast and melt spun Al3Ti and Al3Ti plus copper. Scripta. Mater. 25(10), 2267–2272 (1991).
Ghosh, G. et al. Stability and elastic properties of L12-(Al,Cu)3(Ti,Zr) phases: Ab initio calculations and experiments. Intermetallics 15(1), 44–54 (2007).
Wei, X. P. et al. The electronic and magnetic properties of defects on half-metallic Ti2NiIn alloy. J. Solid State Chem. 233, 221–228 (2015).
Li, J. et al. First-principles study of Al/Al3Ti heterogeneous nucleation interface. Appl. Surf. Sci. 307, 593–600 (2014).
Wu, S., Dong, Z. & Wu, P. Effect of transition metal (M = Co, Ni, Cu) substitution on electronic structure and vacancy formation of Li3N. J. Mater. Chem. 21(1), 165–170 (2010).
Loo, F. J. J. & Rieck, G. D. Diffusion in the titanium-aluminum system inter-diffusion between solid Al and Ti or Ti-Al alloys. Acta. Metall. 21(1), 61–71 (1973).
Srinivasan, S., Desch, P. B. & Schwarz, R. B. Metastable phases in the Al3X (X = Ti, Zr, and Hf) intermetallic system. Scripta Mater. 25(11), 2513–2516 (1991).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140(4A), A1133–A1138 (1965).
Sridharan, S. & Nowotny, H. Studies in the ternary system Ti-Ta-Al and in the quaternary system Ti-Ta-Al-C. Z. Metallkd. 74, 468–472 (1983).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. 32(5), 751–767 (1976).
Allred, A. L. & Rochow, E. G. Electronegativities of carbon, silicon, germanium, tin and lead. J. Inorg. Nucl. Chem. 5(4), 269–288 (1958).
Acknowledgements
The authors acknowledge the computational resources from the National Supercomputing Center in Tianjin (TH-1A system). P. Wu’s work on mechanical modeling is partially supported by the National Research Foundation, Prime Minister’s Office, Singapore, under its Marine Science Research & Development Programme (Award Number MSRDP-P28).
Author information
Authors and Affiliations
Contributions
M.K.Z., P.W., X.B. and Q.L.L. designed and coordinated the overall study. M.K.Z. and P.W. wrote the manuscript. Z.M.K. performed theoretical calculations with the help from P.W., X.B. and Q.L.L. All contributed to the discussions of the results.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhu, M., Wu, P., Li, Q. et al. Vacancy-induced brittle to ductile transition of W-M co-doped Al3Ti (M=Si, Ge, Sn and Pb). Sci Rep 7, 13964 (2017). https://doi.org/10.1038/s41598-017-14398-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-14398-6
This article is cited by
-
Multi-Doping Effect on Ductility of TiAl3: A DFT Study
Metals and Materials International (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.