Abstract
Transmutation of long-lived fission products (LLFPs: 79Se, 93Zr, 99Tc, 107Pd, 129I, and 135Cs) into short-lived or non-radioactive nuclides by fast neutron spectrum reactors without isotope separation has been proposed as a solution to the problem of radioactive wastes disposal. Despite investigation of many methods, such transmutation remains technologically difficult. To establish an effective and efficient transmutation system, we propose a novel neutron moderator material, yttrium deuteride (YD2), to soften the neutron spectrum leaking from the reactor core. Neutron energy spectra and effective half-lives of LLFPs, transmutation rates, and support ratios were evaluated with the continuous-energy Monte Carlo code MVP-II/MVP-BURN and the JENDL–4.0 cross section library. With the YD2 moderator in the radial blanket and shield regions, effective half-lives drastically decreased from 106 to 102 years and the support ratios reached 1.0 for all six LLFPs. This successful development and implementation of a transmutation system for LLFPs without isotope separation contributes to a the ability of fast spectrum reactors to reduce radioactive waste by consuming their own LLFPs.
Similar content being viewed by others
Introduction
Nuclear energy provides 16% of the world’s electricity production1. Although nuclear energy does not release greenhouse gases, it does produce highly radioactive spent nuclear fuel (SNF)2. After recovering U and Pu from SNF by conventional reprocessing, such as the PUREX process, the disposal of high-level radioactive wastes is a major concern in many countries. Most of the radioactive hazard remaining in high-level radioactive wastes after thousands of years comes from minor actinides (MAs; isotopes of Np, Am, and Cm) and some long-lived fission products (LLFPs; 79Se, 93Zr, 99Tc, 107Pd, 129I, and 135Cs)3. The disposal of such SNF in stable deep geological repository has been considered, however, it has not been fully implemented.
The partitioning and transmutation (P&T) strategy has been proposed and research and development have begun in several countries to reduce the inventory of radioactive wastes to be stored and the long-term hazard for future generations4,5,6,7,8,9,10,11,12,13,14. The P&T strategy consists of two major techniques, elemental separation of MAs and LLFPs from high-level radioactive wastes by a chemical process (partitioning) and nuclear reactions of these nuclides into short-lived or non-radioactive nuclides (trasmutation) in nuclear reactors or accelerator-driven transmutation systems(ADS). The P&T strategy has been well studied for MAs12,15,16,17,18,19,20, while little attention has been paid to LLFPs especially for transmutation of LLFPs. After the amount of MAs is reduced by transmutation, LLFPs become the main source of the hazard. It is because they are associated with radioactive release from geological repositories owing to their high solubility in water and mobility in the geosphere15,21,22.
There are two technical difficulties that make transmutation of LLFPs less efficient: (1) the isotopic compositions and (2) small neutron capture cross sections of LLFPs23,24,25. The transmutation of LLFPs is a neutron-consuming process and it requires high neutron flux and excess of neutrons in principle. After partitioning, the isotopic compositions of the LLFPs are not monoisotopic, but are a mixture of stable and radioactive isotopes including LLFP. The consumption of neutrons to transmute the LLFPs is much larger than when isotope separation is applied because isotopes other than the LLFPs also capture neutrons. Only 129I and 99Tc have been considered that can be transmuted because of their relatively large neutron capture cross sections and large isotopic abundance26,27. Therefore, in most studies, the transmutation of LLFPs involves isotope separation14,28,29,30. However, no isotope separation system for elements related to LLFPs is technologically and economically feasible at an industrial scale31,32.
There are some studies on transmutations of LLFPs by reactor systems to address these two technical difficulties. The feasibility of reactor systems depends on the neutron balance. All LLFPs and the fuel are neutron consumers. Even with isotopic separation, it needs at least 0.3 neutron/fission for LLFP-transmutation33. The transmutations of LLFPs in common light water reactors has been known to be difficult mainly because of lack of excess neutrons34,35. The subcritical ADS or also called hybrid systems, which produce energy and to transmute radioactive wastes, appear to be a possible alternative to critical reactors14,16,28,30,36. Although numerous programs have conducted to evaluate the ADS availability, the high-power accelerator technology is a complex system and any ADS system had not yet been demonstrated.
In this context, fast neutron spectrum reactor is the most attractive solution in the existing system with respect to the neutron balance, because of their high neutron flux and excess of neutrons29,37,38,39. Since most LLFPs have large neutron capture cross sections in the 1 to 103 eV region, the neutron spectrum must be softened to use the fast reactor system for transmuting LLFPs via resonance absorption. Metal hydrides (e.g., ZrH2) have been frequently proposed as neutron moderator materials for fast reactor systems because of the good neutron moderating ability of 1H and the high density of the materials40,41. However, a fission of fissile nuclide (e.g. 235U 239Pu) and the neutron capture reaction of stable 92Zr both produce 93Zr, which is one of the LLFPs. Moreover, metal hydrides sometimes induce a thermal spike by elastic collisions due to over-moderated neutrons near the core, causing the dissociation of hydrogen at high temperatures. Therefore, alternative moderator materials are required to develop a more effective transmutation system for LLFPs41.
In this study, we propose yttrium deuteride (YD2) as a moderator material for the transmutation of LLFPs in a fast spectrum reactor. Yttrium is a possible alternative to Zr because Y has a small neutron capture cross section over a wide neutron energy range and produces no radioactive isotopes with long half-lives. The bulk density of YH2 is smaller than that of ZrH2 and the dissociation temperature of YH2 is 1200 °C, which is 300 °C higher than that of ZrH2. These physical and chemical properties may help to avoid thermal spikes42,43. Furthermore, we have revealed that the thermal spike observed for ZrH2 can be suppressed by using the deuteride (ZrD2) instead of the hydride44. Based on these findings and the fact that YD2 is expected to have similar physical and chemical properties as YH2, YD2 is a promising material as a neutron moderator for fast spectrum reactors to transmute LLFPs.
To accomplish effective transmutation of LLFPs in reactor systems, the effective half-life, which is the half-life of a nuclide resulting from the transmutation, must be decreased. In addition, the transmutation rate (TR) of LLFP must be larger than the production rate of LLFP in the core. The ratio of the TR to the production rate is called the support ratio (SR), and it is an important parameter to evaluate the efficiency of transmutation systems26,41. A transmutation system with SR > 1.0 in any reactor system will prevent the increase of LLFPs from its waste. However, it has not been achieved to transmute all LLFPs with SR > 1.0 without isotope separation.
This paper demonstrates a transmutation method for LLFPs that does not require isotope separations. In this method, the LLFPs can be transmuted to stable or short-lived radioactive isotopes by introducing a novel moderator material, YD2, to the fast neutron spectrum reactor. We studied the effects of the moderator on the associated neutron energy spectra, the effective half-lives of LLFPs, transmutation rates (TRs), and SRs by simulations with the continuous-energy Monte Carlo code MVP-II and the burn-up simulation code MVP-BURN with JENDL-4.0 nuclear data library45,46.
Results and Discussion
Implementation of the concept at a fast reactor
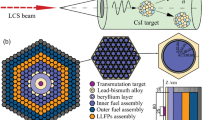
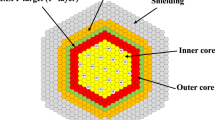
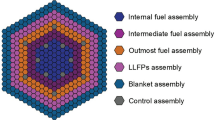
Figure 1 shows layout of the fast reactor core, the assembly configuration, and the pin array based on the Japanese fast breeder reactor MONJU (see Supplementary Table 1 for details of the core description). The radial blanket and shield regions where fast neutrons leak from the core are used for transmuting LLFPs. The LLFP assembly is an assembly that are loaded in the radial blanket or shield regions with pins containing pellets of a mixture of LLFPs and moderator. The composition of the SNF depends on the fuel, core type, and irradiation history. The initial isotopic compositions (%) of the elements, including LLFPs, are determined from the burn-up simulation of mixed oxide (MOX) fuel in the fast reactor by MVP-II and MVP-BURN45,46. The initial isotopic compositions used in this study are listed in Table 1. In the simulations, the LLFP pellets are assumed as homogeneous mixtures of the metallic or chemical forms of the target LLFP and YD2 in various ratios (see Method section for details).
Core layout of the fast spectrum reactor for LLFP transmutation. Plan view and side view of the core layout of the fast spectrum reactor with numbers and lengths of assemblies and pins in the core and radial blanket region. For the transmutations of Cs and Zr, the pellets were loaded along the full length of the radial blanket assembly, whereas the pellets were loaded at the core height of the radial blanket assembly for Se, Tc, Pd, and I. The shield region was used for the transmutations of Cs and Zr, but they were loaded only at the core height of the shield assembly. Unless the shield region is used for the transmutation, the shielding assemblies surround the core and radial blanket assemblies to shield neutrons and gamma rays from the reactor vessel.
Neutron spectra at different positions in the reactor
The effect of the proposed YD2 moderator material on the neutron spectra leaking from the core was examined. Figure 2 shows the 110-group (110 energy bins) neutron energy spectrum of inner- and outer-cores, the first row in the radial blanket region, and the fourth row in the shield regions. The neutron spectra at the inner- and outer-cores are hard. The neutron spectra at the radial blanket and shield regions broaden and are soften resulting from the introduction of YD2 moderator material. The spectrum from the first row of the radial blanket region loaded with depleted UO2 pellets (without LLFP and moderator) shows a flux (n cm−2s−1lethargy−1) on the order of 1012 at 10–100 eV, whereas the spectrum with LLFP and moderator (Cs 70% + YD2 30%) shows a flux approximately one order of magnitude higher in the energy region below 100 eV. This softened spectrum is effective for transmuting LLFPs. It is also confirmed that the integrals of the microscopic capture reaction rates compared with those without the YD2 moderator are greater for all LLFPs (Supplementary Table 3).
Comparison of neutron spectra at various locations in the reactor. Simulated energy dependence of the neutron flux at the inner- (red), outer- (magenta), first row at the radial blanket with the depleted UO2 pellet (blue), first row at the radial blanket with Cs 70% + YD2 30% (bold blue), and outermost row of the shield region with Cs 90% + YD2 10%.
Transmutation of 79Se, 93Zr, 99Tc, 107Pd, 129I, and 135Cs
The masses of transmuted LLFPs over 20 years of continuous irradiation were simulated and calculated. Figure 3 shows that all LLFPs decrease approximately linearly with increasing irradiation time. For 79Se, 99Tc, 107Pd, and 129I, reductions are more than 25%, whereas reductions are less than 10% over 20 years of irradiation for 93Zr and 135Cs. This results are due to the considerably smaller neutron capture cross sections of 93Zr and 135Cs compared to those of other LLFPs. However, the results imply that the neutron capture cross section of averaged thermal and resonance region does not seems to govern the order of transmutation efficiency. The amounts of the other isotopes also vary linearly over 20 years of irradiation (see Supplementary Figures 2–7).
Transmutation analyses
The approximately linearly decreases of LLFPs (Fig. 3) used to evaluate the effective half-lives, and the TR and SR values for LLFPs were obtained by linear fitting of numerical data of the simulations. Table 2 shows only maximum values and Table 4 in supplementary information shows the maximum, minimum and average rates of transmuted LLFPs. The maximums are calculated from the first irradiation period (0 to 2 years), and the minimums are from the final period (18–20 years). As shown in Table 2, the effective half-lives of the LLFPs decreases substantially to 102 years from natural half-life, which are much shorter than their natural half-lives. The radioactivities of the LLFPs persist with the total radioactivity for over 105 years (see Supplementary Figure 8). The decreases in effective half-lives indicate that the radioactivities of LLFPs will be reduced the time scale to 102 years. These radioactivities will be reduced the time scale to 102 years as the effective half-lives indicated.
The TRs seems to be smaller than other proposed systems. The relatively low TRs are acceptable because the key objective of this system is to develop a method to achieve SR > 1.0 for all LLFPs (see Method section for details).
The SRs were calculated from the ratio of the transmuted LLFP mass to the produced LLFP mass in the core fuel. As shown in Table 2, the SRs for 79Se, 99Tc, 107Pd, and 129I are sufficiently large (SR > 1) with the conditions that they are loaded in 54 assemblies in the innermost row of the radial blanket region. The SRs for these LLFPs are higher because of their relatively large neutron capture cross sections and small fission yields. In contrast, the SRs for 93Zr and 135Cs are barely more than 1.0, even though they were loaded in a total 498 assemblies in the radial blanket region (full length) and the radial shield region (core height).
The computational simulations were performed separately for each LLFP, although the simultaneous transmutation of all LLFPs is necessary in practice. The minimum number of assemblies (N min ) required to achieve SR > 1.0 were estimated from the number of loaded assemblies (N loaded ) divided by SR (N min = N loaded /SR) (Table 2). For instance, 79Se is loaded in 54 assemblies in the simulation, but the number of assemblies required to achieve SR > 1.0 for the simultaneous transmutation is only 1. For 93Zr and 135Cs, much more assemblies are required to achieve SR > 1.0 for the simultaneous transmutation of all LLFPs. When the total number of required assemblies is less than the total number of assemblies (498 assemblies), it is possible that SR > 1.0 for the simultaneous transmutation of all LLFPs. Nevertheless, the total number of assemblies required for the simultaneous transmutation exceeded 530. To improve the overall system efficiency, we focus on Cs in the next section because Cs is the most difficult LLFP to transmute.
Non-continuous transmutation of 135Cs
The irradiation and cooling method (see Method section for more details) was used to study a more suitable Cs transmutation scheme. Figure 4 shows the transmutation of Cs isotopes by the “irradiation and cooling method”. The initial compositions of Cs isotopes contain approximately equal amounts of 133Cs as 135Cs (Table 1). In the reaction chain of Cs isotopes (Supplementary information Figure 9), 133Cs produces 134Cs by the neutron capture reaction, and then 134Cs produces 135Cs. Considering the half-life of 134Cs (2.0648 years), the irradiation and cooling method, which consists of 2 years of irradiation and 6 years of cooling, was proposed to suppress the production of 134Cs, which is a source of 135Cs32. In this method, the weight of 135Cs gradually decreases, meaning that the method would take longer time than continuous irradiation. Nevertheless, when the “irradiation and cooling method” is applied, SRs are >1.0 for all LLFPs and the resulting total number of assemblies required for simultaneous transmutation is comparable with the total number of assemblies considered.
The target nuclides are converted into stable or non-radioactive nuclides during transmutation, and the compositions of nuclides in the target pellets change. Therefore, LLFPs from irradiated pellets under real irradiation must be recycled. In this study, pellet recycling is not considered, although recycling will improve efficiency. Additionally, optimizing the pin and blanket configurations and the LLFP and YD2 mixing ratio will also improve the efficiency of the proposed transmutation system.
Conclusion
We demonstrated that using YD2 as a moderator may improve transmutations of LLFPs in the fast spectrum reactor and can be achieved SR > 1.0 for all LLFPs. Neutron spectra in various positions in the reactor were analyzed and the LLFP transmutation capability defined by the effective half-lives, SRs and TRs of LLFPs were evaluated by the Monte Carlo code MVP-II and the burn-up simulation code MVP-BURN with JENDL-4.0 nuclear data library.
YD2 was shown to be an effective moderator material for softening the neutron spectrum leaking from the core. This soft spectrum allowed LLFP transmutation in the radial blanket and shield regions. Each LLFP was loaded without isotope separation but with the initial compositions contained all isotopes. The calculations and analyses showed that the half-lives of LLFPs decreased drastically from more than 105 years to less than 102 years. The TRs for LLFPs were relatively small compared to other systems because we focused on improving the SRs. The SRs for all LLFPs were >1.0, including 135Cs, which is difficult to transmute effectively. Although the simulations were performed with assuming each LLFP was loaded separately, the proposed system achieved SR > 1.0 for all LLFPs within a total of 481 assemblies when the irradiation and cooling method of Cs transmutation was applied. The number was smaller than the 498 assemblies, which is the maximum number of assemblies by the core specification.
We established an effective, efficient transmutation method for LLFPs to increase transmutation efficiency and improve SRs without isotope separations. If the core region is composed of transuranic or long-life MA nuclides and they can be burned as fuel materials, all the long-lived radioactive elements can be consumed by using the proposed system. In future work, we will examine the simultaneous transmutations of all LLFPs with SR > 1.0. Furthermore, such computational simulation study strongly depends on the nuclear data library regarding nuclear fission and reaction, such as cross section of nuclide, fission product yield, decay chain47. We thus also address the improvements of these data by various way of physical descriptions48,49.
Methods
Computational model and method
The core characteristics was evaluated with a continuous-neutron energy Monte Carlo Code MVP-II/MVP Burn46 with JENDL-4.045 cross-section library. The number of history of neutrons was 10,000batch, the number of skipped batches was 100 for accurate source distribution, and the number of effective batches was 1,000. From this Monte Carlo simulation, the neutron spectrum and the reaction rates of LLFPs in various regions in the fast spectrum reactor were obtained. The typical statistical error of the multiplication factor (k eff ) was about 0.015% in 1 \(\sigma \) error. The statistical error for reaction rates for all LLFPs at the most inner row of radial blanket are also sufficiently low between 0.1–0.5%, and that at the most outer row of shield region for Cs and Zr are below 1.0%. The burn-up simulations were performed using MVP-BURN code with ChainJ40 burn-up chain data handling actinides from Th to Cm and 193 FPs46. The fission product yield data was also derived from JENDL-4.0.
Reactor core description
The fast reactor core used in this study is a sodium-cooled fast breeder reactor. Figure 1 shows the core layout, assembly configuration, and pin array. Some of the parameters are summarized in Supplementary Table 1. The reactor is simulated to produce a thermal power of about 710 MWt. The core consists of 198 fuel assemblies, 19 control rods, 174 radial blanket assemblies, and 384 radial shielding assemblies in a core height of 930 mm and diameter of 1800 mm. The core fuel assembly contains 169 core fuel pins that are composed of uranium-plutonium MOX fuel pellets covered by stainless steel cladding. The radial blanket is composed of three rows, and the number of assemblies in the innermost (first row), middle (second row), and the outermost (third row) are 54, 60, and 60, respectively. The radial blanket assembly incorporates 61 pins. The primary feature of the radial blanket assembly is to convert fertile fuel (depleted UO2) into fissile material by neutron capture reactions. In this system, the radial blanket assemblies are replaced by the assemblies with pins containing the pellets of the mixture of LLFPs and moderator as an alternative for depleted UO2 pellets. In the simulations, refueling could not be simulated for the fuel assemblies and LLFPs. Therefore, the core fuel volume was virtually magnified 100-fold to obtain the constant neutron flux from the core for 20 years.
Selection of LLFPs
In general, the major LLFPs are 79Se, 93Zr, 99Tc, 107Pd, 126Sn, 129I, and 135Cs. These nuclides will probably dominate the long-term radioactivity of the geological disposal of SNF (Supplementary Figure 1). Because the total amount of 126Sn is small, we have focused on 79Se, 93Zr, 99Tc, 107Pd, 129I, and 135Cs. Transmutation scheme for target LLFPs are as follows:
The chemical forms of the LLFPs are an important factor to consider. The material design and fabrication of the irradiation target containing LLFPs and moderator material involve considerations of a wide range of phenomena that affect pellet performance, such as thermal tolerance, swelling, irradiation damage, cracking, radioactive isotope production, and gas evolution. It is difficult to treat LLFPs as the same chemical substance because they have different physical and chemical properties. Assessing a pellet as a function of temperature and irradiation history is a minimum performance standard. The metallic form is the best choice because it generally has high melting point and the space volume for loading can be minimized50. Thus, we have chose metallic forms for 79Se, 93Zr, 99Tc and 107Pd. The pellets containing these metals were simulated as a homogeneous mixture with the moderator material, YD2. For I, our previous study showed that BaI2 is the most suitable compound because of its chemical stability and easy manufacturing50. For Cs, many Cs compounds have been proposed51. In this study, cesium carbonate (Cs2CO3) was chosen because it has a higher melting point (610 °C) and chemical stability at the ordinary temperature of the fast reactor. We will address the fabrication of LLFP pellets with YD2 in a future study.
To transmute LLFPs efficiently and effectively, the LLFPs should be dispersed homogeneously in the pellet42. In a previous study, we fabricated Zr-based pellets containing thin Tc metal wires and simulated the homogeneous dispersion of immiscible materials42. To simplify and reduce the calculation cost, various ratios with metallic or chemical forms of the target LLFPs were investigated with homogeneous dispersion in YD2. The mixing ratios of LLFP/YD2 were varied based on the position of the radial blanket or radial shielding assemblies (Supplemental Table 1). These ratios were determined based on our previous studies52 although they have not been optimized yet.
The composition of LLFPs obtained from the burn-up simulations of MOX fuel by fast breeder reactor core at 80 GWd/t for 2 years are listed in Table 1. The isotopic compositions in Table 1 were used as the initial composition for LLFPs in the pellet. The transmutations of LLFPs were computationally simulated without isotope separation.
Assembly configuration design for LLFPs transmutation
The transmutation capability strongly depends on the neutron capture cross sections of the LLFPs. The neutron capture cross sections in the electronvolt to kiloelectronvolt region of LLFPs (Supplementary Figure 2) allow the transmutation of the LLFPs by softened neutron spectra in the blanket and shield regions. The amounts of LLFPs that need to be transmuted are different for each element. Two types of arrangement of the radial blanket assembly were used depending on their transmutation capability. The overall length of the assembly consists of the fuel length (core height), the upper and lower blankets, the fission gas plenum, and other structural objects. The full length includes the total length of the fuel length and the upper and lower blankets. For Se, Tc, Pd, and I (Type-1), LLFPs were loaded in 54 of the radial blanket assemblies in the innermost row (core height). For Zr and Cs (Type-2), LLFPs were loaded in 498 assemblies in the radial blanket (full length) and shield region (core level). The total irradiation period was determined by the life-time of the LLFP assemblies, which was evaluated as 20 years. However, 20 years of irradiation is an unrealistic scenario for a real nuclear reactor owing to the irradiation damage to the constituent materials. However, our simulation is the worst-case scenario for the pellets containing LLFPs. The isotope composition in the pellets changes during irradiation. The pellets will be recycled so that the other elements produced by transmutation are removed.
Transmutation of cesium
Cesium has the stable isotope 133Cs, short-lived 134Cs and 136Cs, and long-lived 135Cs and 137Cs (Supplementary Figure 9). 133Cs produces 134Cs by the neutron capture reaction, and then 134Cs produces 135Cs in the same way. Consequently, at the beginning of the irradiation, the loaded 133Cs produces 134Cs, which becomes the source of 135Cs. We developed the irradiation and cooling method based on this sequence31. After 2 years of irradiation, 133Cs is transmuted into 134Cs, which decays with a half-life of 2.0648 years. A cooling interval 6 years after irradiation allows 134Cs to decay into stable 134Ba. After 134Cs decays out, irradiation of 135Cs is followed by decay into stable 136Ba. Cs transmutation is achieved by repeating 2 years of irradiation and 6 years of cooling. In this study, the production and neutron capture of 134Ba, 136Ba, and 137Ba (produced by the decay of 137Cs) were neglected because they decrease the SRs slightly.
Effective half-life, transmutation ratio and support ratio
The effective half-life is an important parameter for evaluating the efficiency of transmutation. The effective half-life is the half-life when transmutation is considered. For a single target nuclide, the effective half-life can be defined as
where \(\lambda \), \(\sigma \), and \(\phi \) are the decay constant of the target LLFP, the effective neutron capture cross section, and the neutron flux, respectively. If the \(\lambda \) values of LLFPs are small, linear expression can be applied. In this system,
Other two important parameters of the transmutation system are Transmutation Rate (TR) and Support Ratio (SR). TR is defined as the ratio of the amount of initial loaded LLFPs to the amount of transmuted LLFPs in the target assembly (per unit time) as
where N(0) and T are the number of initial atoms of a LLFP in the target assemblies and the irradiation period, respectively. If the burn-up chain of a LLFP only has a capture reaction,
and if the value of \(\sigma \phi \) T is small enough,
In this system, TR of LLFPs except for 135Cs can be approximately expressed by Eq. 5.
SR is defined as the ratio of the amount of transmuted LLFPs to the amount of LLFPs produced in the core fuel over the same period of time in a reactor,
where \(\gamma \) and M are the LLFP yield per fission of fuel materials and the total fission rate of the core, respectively. If the burn-up chain of a LLFP only has a capture reaction,
and if the value of \(\sigma \phi \) T is small enough,
In this system, SR except for 135Cs can be approximated by Eq. 8. The easiest way to increase SR is to increase the amount of initially loaded LLFPs. However, when N(0) is increased, \(\sigma \phi \) is decreased by the neutron self-shielding effect in the target. The diluted LLFP targets increase the TRs due to smaller neutron flux depression, thus the two effects oppose each other. This is why the fast spectrum reactor systems in many previous studies could not transmute LLFPs simultaneously with SR > 1.0. If SR > 1.0 can be achieved, the self-produced LLFPs could be transmuted during electric power generation.
Change history
05 December 2017
A correction to this article has been published and is linked from the HTML version of this paper. The error has been fixed in the paper.
References
Lior, N. Energy resources and use: The present situation and possible paths to the future. Energy 33, 842–857 (2008).
Ewing, R. C. Long-term storage of spent nuclear fuel. Nature Materials 14, 252–257 (2015).
OECD-NEA. Advanced Nuclear Fuel Cycles and Radioactive Waste Management (2006).
IAEA. Evaluation of actinide partitioning and transmutation, vol. 214 (1982).
Ramspott, L. D. et al. Impacts of new developments in partitioning and transmutation on the disposal of high-level nuclear waste in a mined geologic repository (1992).
Rubbia, C., Aleixandre, J., Andriamonje, S. et al. A european roadmap for developing accelerator driven systems (ADS) for nuclear waste incineration. ENEA Report 88 (2001).
OECD-NEA. Actinide and fission product partitioning and transmutation Status and assessment report (1999).
Mukaiyama, T. et al. Review of research and development of accelerator-driven system in Japan for transmutation of long-lived nuclides. Progress in Nuclear Energy 38, 107–134 (2001).
Salvatores, M. Nuclear fuel cycle strategies including partitioning and transmutation. Nucl. Eng. Des. 235, 805–816 (2005).
Wigeland, R. A., Bauer, T. H., Fanning, T. H. & Morris, E. E. Separations and transmutation criteria to improve utilization of a geologic repository. Nuclear Technology 154, 95–106 (2006).
Warin, D. Status of the french research on partitioning and transmutation. In MRS Proceedings (2006).
OECD-NEA. Potential Benefits and Impacts of Advanced Nuclear Fuel Cycles with Actinide Partitioning and Transmutation (2011).
González-Romero, E. Impact of partitioning and transmutation on the high level waste management. Nuclear Engineering and Design 241, 3436–3444 (2011).
Hwang, I. et al. The concept of proliferation-resistant, environment-friendly, accident-tolerant, continual and economical reactor (PEACER). Progress in Nuclear Energy 37, 217–222 (2000).
Salvatores, M., Slessarev, I., Uematsu, M. & Tchistiakov, A. The neutronic potential of nuclear power for long-term radioactivity risk reduction. Progress in Nuclear Energy 32, 471–475 (1998).
OECD-NEA. Accelerator-driven systems (ADS) and fast reactors (FR) in advanced nuclear fuel cycles - a comparative study (2003).
Messaoudi, N. & Tommasi, J. Fast burner reactor devoted to minor actinide incineration. Nuclear Technology 137, 84–96 (2002).
Liu, B. et al. Transmutation of minor actinides in the pressurized water reactors. Annals of Nuclear Energy 64, 86–92 (2014).
Walker, C. & Nicolaou, G. Transmutation of neptunium and americium in a fast neutron flux: EPMA results and KORIGEN predictions for the superfact fuels. Journal of Nuclear Materials 218, 129–138 (1995).
Bowman, C. et al. Nuclear energy generation and waste transmutation using an accelerator-driven intense thermal neutron source. Nuclear Instruments and Methods in Physics Research Section A 320, 336–367 (1992).
OECD-NEA. Regulating the long-term safety of geological disposal Towards a common understanding of the main objectives and bases of safety criteria (2007).
JAEA. Technical reliability of geological disposal for high-level radioactive wastes in Japan, vol. 3 (1999). JNC-TN–1400-99–020.
Wakabayashi, T. & Higano, N. Study on MA and FP transmutation in fast reactors. Progress in Nuclear Energy 32, 555–562 (1998).
Gray, W. J. Fission product transmutation effects on high-level radioactive waste forms. Nature 296, 547–549 (1982).
Wakabayashi, T. Transmutation characteristics of MA and LLFP in a fast reactor. Progress in Nuclear Energy 40, 457–463 (2002).
Kloosterman, J. L. & Li, J. Transmutation of Tc-99 and I-129 in fission reactors. A calculational study. In Netherlands Energy Research Foundation (ECN), Petten (Netherlands). Funding organisation: Commission of the European Communities, Brussels (Belgium) (1995).
Aoyama, T., Maeda, S., Maeda, Y. & Suzuki, S. Transmutation of technetium in the experimental fast reactor JOYO. Journal of Nuclear and Radiochemical Sciences 6, 279–282 (2005).
Nifenecker, H., David, S., Loiseaux, J. & Meplan, O. Basics of accelerator driven subcritical reactors. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 463, 428–467 (2001). Accelerator driven systems.
Suzuki, M., Ezoubtchenko, A., Akatsuka, H., Matsuura, H. & Takagi, R. Isotope separation required in SCNES and future subjects. Progress in Nuclear Energy 40, 561–568 (2002).
Malambu, E., Haeck, W., Sobolev, V. & Abderrahim, H. MA and LLFP transmutation performance assessment in the MYRRHA experimental ADS. In Proceedings of the Eighth Information Exchange Meeting on Actinide and Fission Product Partitioning and Transmutation, Las Vegas, Nevada, 9–11 November (2004).
Ohki, S. & Takaki, N. Transmutation of cesium-135 with fast reactors. In Proceedings of Seventh Information Exchange Meeting on Actinide and Fission Product Partitioning and Transmutation , Jeju, Korea, 14–16 (2002).
Lu, H., Ishiwatari, Y. & Oka, Y. Study on the llfps transmutation in a super-critical water-cooled fast reactor. Nuclear Engineering and Design 241, 395–401 (2011).
Salvatores, M., Slessarev, I. & Uematsu, M. A global physics approach to transmutation of radioactive nuclei. Nuclear Science and Engineering 116, 1–18 (1994).
OECD-NEA. Physics and Safety of Transmutation Systems, A Status Report (2006).
Tommasi, J., Delpech, M., Grouiller, J.-P. & Zaetta, A. Long-lived waste transmutation in reactors. Nuclear Technology 111, 133–148 (1995).
Yang, W. S. & Khalil, H. S. Blanket design studies of a lead-bismuth eutectic-cooled accelerator transmutation of waste system. Nuclear Technology 135, 162–182 (2001).
Takaki, N. & Mizuno, T. Design study on sodium-cooled fast reactor core loaded with LLFP transmutation sub-assemblies. In Proceedings of GENES4/ANP2003 (2003).
Yokoyama, T., Wakabayashi, T., Tachi, Y., Takaki, N. & Matsuyama, S. New target concepts for increase in transmutation rate of llfps in FBR recycle system. In Proceedings of International Conference on the Nuclear Fuel Cycle (2009).
Ezoubtchenko, A., Akatsuka, H. & Suzuki, M. Isotope separation methods for self-consistent nuclear energy system. Progress in Nuclear Energy 32, 729–735 (1998).
Wakabayashi, T. Improvement of core performance by introduction of moderators in a blanket region of fast reactors. Science and Technology of Nuclear Installations 2013 (2013).
Tachi, Y., Wakabayashi, T. & Yokoyama, T. Study on target fabrication for LLFP transmutation by fast reactors. In Proceedings of Global 2009, Paris (2009).
Anderson, J. L., Mayo, W. & Lantz, E. Reactivity control of fast-spectrum reactors by reversible hydriding of yttrium zones. NASA Technical note (1968). NASA-TN-D-4615.
Vetrano, J. Hydrides as neutron moderator and reflector materials. Nuclear Engineering and Design 14, 390–412 (1971).
Yokoyama, T., Wakabayashi, T., Tachi, Y. & Nagata, A. Optimizing pin layout in transmutation rate of long-life FP with deuteride moderator for fast reactors. In Proceedings of GLOBAL 2011, Makuhari, Japan (2011).
Shibata, K. et al. JENDL-4.0: a new library for nuclear science and engineering. Journal of Nuclear Science and Technology 48, 1–30 (2011).
Okumura, K., Mori, T., Nakagawa, M. & Kaneko, K. Validation of a continuous-energy Monte Carlo burn-up code MVP-BURN and its application to analysis of post irradiation experiment. Journal of Nuclear Science and Technology 37, 128–138 (2000).
Aliberti, G., Palmiotti, G., Salvatores, M. & Stenberg, C. G. Impact of nuclear data uncertainties on transmutation of actinides in accelerator-driven assemblies. Nuclear Science and Engineering 146, 13–50 (2004).
Usang, M. D., Ivanyuk, F. A., Ishizuka, C. & Chiba, S. Effects of microscopic transport coefficients on fission observables calculated by the Langevin equation. Physical Review C 94, 044602 (2016).
Iwamoto, O. et al. JENDL actinoid file 2008. Journal of Nuclear Science and Technology 46, 510–528 (2009).
Osaka, M. et al. Research and development of minor actinide-containing fuel and target in a future integrated closed cycle system. Journal of Nuclear Science and Technology 44, 309–316 (2007).
Kase, T., Konashi, K., Takahashi, H. & Hirao, Y. Transmutation of cesium-137 using proton accelerator. Journal of Nuclear Science and Technology 30, 911–918 (1993).
Mori, T. & Nakagawa, M. Mvp/gmvp: general purpose Monte Carlo codes for neutron and photon transport calculations based on continuous energy and multigroup methods. JAERI Data/Code (1994). JAERI-Data/Code–94–007.
Acknowledgements
We would like to thank T. Yokoyama from Toshiba Nuclear Engineering Services Corp. and A. Hara from Toshiba Corp. for their assistance with carrying out computational simulations, helpful suggestions, and valuable discussions. This study comprises the results of “Research and development of an innovative transmutation system of LLFP by fast reactors”, entrusted to the Tokyo Institute of Technology by the Ministry of Education, Culture, Sports, Science and Technology of Japan (MEXT).
Author information
Authors and Affiliations
Contributions
S.C., T.W., Y.T., and N.T. conceived the study. S.C., T.W., and N.T. designed the transmutation system and computational simulations. Y.T. assisted with materials and fabrication. T.W., N.T., and A.T. carried out computational simulations and analyses. S.C., A.T., S.O., and T.Y. co-wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Change History: A correction to this article has been published and is linked from the HTML version of this paper. The error has been fixed in the paper.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A correction to this article is available online at https://doi.org/10.1038/s41598-017-17100-y.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chiba, S., Wakabayashi, T., Tachi, Y. et al. Method to Reduce Long-lived Fission Products by Nuclear Transmutations with Fast Spectrum Reactors. Sci Rep 7, 13961 (2017). https://doi.org/10.1038/s41598-017-14319-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-14319-7
This article is cited by
-
Gamma-ray irradiation behavior of a hexagonal Ti–6Ta alloy applied in spent nuclear fuel reprocessing
Journal of Materials Science (2022)
-
Concept of a fast breeder reactor to transmute MAs and LLFPs
Scientific Reports (2021)
-
A comprehensive review on radioactive waste cycle from generation to disposal
Journal of Radioanalytical and Nuclear Chemistry (2021)
-
Study on method to achieve high transmutation of LLFP using fast reactor
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.