Abstract
The BCR constitutively transmits a “tonic” survival signal in the absence of exogenous antigen-binding. However, the strength of tonic BCR signal and its relationship with antigen-triggered survival signal are poorly understood. We found that primary B cells expressing high levels of BCR had elevated BCR tonic signal and increased survival compared with those expressing low levels of BCR. In addition, we found that crosslinking BCR with low doses of F(ab′)2 α-IgM antibodies did not enhance, but rather decreased, B cell survival and that only when most of the BCR were occupied by F(ab′)2 α-IgM antibodies was B cell survival enhanced. Based on these experimental results, we present a mathematical model integrating tonic and antigen-triggered BCR signals. Our model indicates that the signal generated from crosslinked BCR is 4.3 times as strong as the tonic signal generated from free BCR and that the threshold of B cell activation corresponds to the signal generated by crosslinking 61% of the surface BCR. This model also allows the prediction of the survival probability of a B cell based on its initial BCR level and the strength and duration of antigen stimulation, and fits with the mechanism of B cell tolerance.
Similar content being viewed by others
Introduction
The B cell receptor (BCR) is a heterotrimeric complex consisting of antigen (Ag) binding immunoglobulins and the signal-transducing Igα/Igβ heterodimers. In mature B cells, Ag binding to the BCR initiates a cascade of signaling events that eventually lead to the activation of transcription factors such as NF-κB, NFAT and AP-1, which regulates the expression of genes involved in B cell survival, activation and differentiation1,2,3. Dysregulated BCR signaling results in altered survival and activation of B cells and B cell-mediated immune responses, leading to primary immunodeficiencies4,5, autoimmune diseases6,7,8,9 and even B cell malignancies10,11. It is therefore important to understand the mechanisms by which the exogenous Ag stimulation is converted to the survival and activation signals. Studies thus far have revealed many tyrosine kinases and adaptor molecules that participate in BCR signal transduction triggered by BCR stimulation12. Both negative13 and positive14 feedback mechanisms that regulate BCR signaling have been identified. Whereas the negative feedback system functions to prevent excessive signals, the positive feedback mechanism can result in a steep dose response to Ag stimulation and can thus function as an on/off switch of signal transduction. An intriguing feature of BCR signaling is that there is an activation threshold14,15,16. In other words, while B cells do not respond to low doses of Ag stimulation, a robust response can be induced when the Ag dose reaches a certain level. The existence of such a threshold can be explained in part by a positive feedback mechanism in the regulation of NF-κB activation14. The presence of a threshold in Ag-triggered BCR signaling functions to prevent B cell activation by self Ag, which binds to autologous B cells only weakly, and is an important mechanism for maintaining peripheral B cell tolerance.
Although BCR signal transduction has been extensively studied thus far, most studies have focused on exogenous Ag-triggered BCR signaling events. It is now clear that, even in the absence of Ag binding, BCR constitutively transmits a tonic survival signal. The requirement of tonic BCR signal for B cell survival has been demonstrated by the finding that in vivo ablation of BCR expression in mice causes rapid death of B cells17. The tonic BCR survival signal is transmitted through Igα and Igβ heterodimers18 and the B cell death due to the lack of tonic BCR signal can be rescued by PI3 kinase signaling19. These results provide compelling evidence that BCR transmits a tonic signal in the absence of Ag stimulation though Igα and Igβ heterodimers and activates the downstream PI3 kinase to maintain B cell survival. Further studies have revealed that tonic BCR signal is also important for the survival of malignant B cells20 even though these B cells have oncogenic mutations that lead to their uncontrolled proliferation. Despite the biological significance of tonic BCR signal, it is difficult to analyze its signaling events in detail using conventional biochemical or immunological approaches. The strength of the intrinsic tonic BCR signal and its relationship with the extrinsic Ag-triggered survival signal remain largely unknown.
We decided to address the regulation of tonic signal by analyzing the kinetics of B cell survival during in vitro culture in the absence of exogenous Ag stimulation. In addition, to investigate the possible interactions between tonic and Ag-triggered BCR signal, we have analyzed the kinetics of B cell survival in response to a wide range of doses of F(ab′)2 α-IgM antibodies (Abs), which mimic Ag stimulation. We found that B cell survival in the absence of Ag stimulation positively correlated with BCR levels. In addition, we found that F(ab′)2 α-IgM Abs enhanced B cell survival only when most of the cell surface BCR were crosslinked by these Abs. Based on these and additional experimental results, we provide a mathematical model integrating the tonic BCR signal and Ag-triggered survival signal. This model reveals the relative strength of the tonic signal generated from free BCR and the signal generated from crosslinked BCR. This model also allows us to predict the survival probability of a primary B cell cultured under various conditions and provides new insights into the mechanisms of B cell tolerance.
Materials and Methods
Mice
C57BL/6 mice were purchased from Shanghai Slac Laboratory Animal Corporation and maintained in specific pathogen free conditions. All animal experiments were approved by Fudan University Animal Committee. In addition, all methods were performed in accordance with the guidelines and regulations of Fudan University.
B cell culture and survival assay
Primary B cells were purified from the spleen of C57BL/6 mice using a mouse B lymphocyte enrichment set (Cat# 557792, BD Biosciences). Briefly, splenocytes in single cell suspension were first incubated with a cocktail of biotinylated antibodies (α-CD4, α-CD43 and α-TER119) that recognize T cells, developing B cells, B-1 cells, activated B cells, antibody secreting plasma cells and erythrocytes, but not resting, mature B cells. After washing, the cells were incubated with the streptavidin particles and the labeled cells were removed by a Cell Separation Magnet. The purity of B cells was >95% as judged by their B220 expression (Supplementary Figure S1A). The majority of the purified B cells were CD23+ follicular B (Supplementary Figure S1B) and AA4− mature B cells (Supplementary Figure S1C). Purified primary B cells were cultured in 96 well flat bottom plates (5 × 105/ml, 200μl/well) in triplicate for various time period in medium (RPMI1640 supplemented with 10% FBS, 5 × 10−5 M 2-mercaptoethanol, and 100 U of penicillin and streptomycin) alone or in the presence of different concentrations of F(ab′)2 α-IgM Abs (Cat# 16-5092, eBioscience). The cells were stained with 7-amino-actinomycin D (7-AAD) and the percentages of viable (7-AADlow FSChigh) and dead (7-AADhigh FSClow) cells were analyzed by a FACSVerse flow cytometer (BD Biosciences). Ibrutinib, an inhibitor of the Bruton’s tyrosine kinase (BTK), was purchased from Cosmo Bio (Cat# S2680), Japan, and dissolved in DMSO.
Analysis of BCR levels
B cells (105) were incubated with PE-conjugated rat α-mouse IgM monoclonal Ab (Cat# 553521, BD Biosciences) on ice and mixed once during the incubation. The cells were then washed twice with 200 µl of FACS buffer (PBS containing 2% FBS and 0.02% sodium azide), suspended in 200 µl of FACS buffer and analyzed with a FACSVerse flow cytometer. The Geo mean fluorescence intensity (MFI) of BCR was used as an index of BCR levels.
Intracellular staining of phosphorylated SYK (pSYK), ERK (pERK) and AKT (pAKT)
Splenocytes (106) were first incubated on ice for 15 min in 50 µl of FACS buffer (1 x PBS, 2% FBS and 0.02% sodium azide) containing 5 µg/ml of Rat anti-mouse CD16/CD32 (Cat# 553142, BD Biosciences) to block the Fc receptor. The cells were then washed and stained with FITC- or PE-conjugated anti-mouse IgM (Cat# 553408 and Cat# 553521, BD Biosciences). After washing, the cells were fixed and permeabilized with a fixation/permeabilization kit (Cat# 554714, BD Biosciences) according to the manufacturer’s protocol. The cells were then stained with PE-conjugated anti-pSYK (pY348), or Alexa Fluor 647-conjugated anti-pERK1/2 (pT202/pY204) or anti-pAKT (pS473) (BD Biosciences). The levels of pSYK, pERK and pAKT were analyzed in gated IgMhigh and IgMlow population by a FACSVerse flow cytometer as outlined in Supplementary Figure S2.
Mathematical modeling of the tonic BCR survival signal in B cells
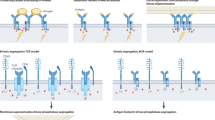
A scheme for BCR level in each cell is illustrated in Fig. 1A. MFI of BCR decreased during culture due to a decrease of BCR level in each B cell. The BCR level in each B cell is different and could be converted to a value between 0 and 1. Therefore, BCR level in individual B cell is shown by the following equation:
where d 1 is the rate of BCR degradation. Our experimental results indicated that the strength of tonic BCR survival signal correlated with BCR levels (MFI). In other words, BCR functioned as if it is an enzyme that catalyzed a chemical reaction to create a tonic survival signal. Accordingly, tonic BCR signal can be expressed by the following reaction:
This chemical reaction means that in the absence of surface BCR expression there is no survival signal generated and the above reaction only proceeds to the left direction (Signal off ). The existence of surface BCR constitutively generates a survival signal (Signal on ) dependent on BCR levels at a rate constant of k 1. On the other hand, certain amount of the tonic signal is constitutively consumed (signal consumption) at a rate of d 2 to maintain B cell viability. The sum of Signal on and Signal off is set to 1. Thus the tonic signal generated from BCR can be expressed as the following equations:
In the above equations, if dSignal on /dt is smaller than 0, the amount of tonic signal will keep decreasing. We think that when the amount of tonic signal decreased to a certain level (which we call deadline), a B cell will die.
Modeling of Ag-triggered survival signal
A scheme for F(ab′)2 α-IgM Abs binding to and release from the surface BCR is illustrated in Fig. 1B and can be expressed as the following equilibrium:
where k 2 and k 3 are the rate constant of BCR-anti-IgM binding and disassociation, respectively. BCR free and BCR Anti-IgM represent BCR that are not bound or bound by F(ab′)2 α-IgM Abs, respectively, and the sum of BCR free and BCR Anti-IgM is equivalent to BCR level . When the above reaction reaches an equilibrium, the proportion of the crosslinked BCR (BCR bound by the F(ab′)2 α-IgM Abs) among the total BCR can be expressed by the following equation:
The unit of F(ab′)2 α-IgM Abs is μg/ml. Based on the equation (4), the changes in the crosslinked BCR (BCR Anti-IgM ) are therefore expressed by the following equations:
The above differential equation and the equation (1) lead to the following equation showing the relationship of the concentrations of F(ab′)2 α-IgM Abs, time (h) in culture and the proportion of the crosslinked BCR:
The strength of the survival signals (Signal on ) correlated with the amount of crosslinked BCR and can be expressed as the following chemical reaction:
where k 4 is the rate constant of Signal on generated by crosslinked BCR and d 2 again is the rate constant of signal consumption required for maintaining the viability of a B cell. Therefore, the survival signal is expressed by the following differential equation:
A Model integrating the tonic and Ag-triggered survival signals
In combining the tonic BCR signal and Ag-triggered signal, we considered two points. First, binding of F(ab′)2 α-IgM Abs to BCR induces conformational changes of BCR complex to initiate a cascade of signaling events1,2, which we think will simultaneously disrupt the tonic survival signal. Ag-triggered survival signal is thus generated at the expense of tonic signal. Therefore, we assume that the total survival signal (tonic + Ag-triggered − signal consumption) in the presence of BCR crosslinking is expressed by the following differential equation:
However, the above equation does not take into consideration that there is an activation threshold or offset in Ag-triggered BCR signaling, i.e., if the strength of Ag-triggered signal is below the offset, such a signal will not be converted to an effective survival signal but instead lost15,16. We found that crosslinking up to 72% of the total surface BCR did not induce increased B cell survival. More precisely, crosslinking up to 61% of the surface BCR failed to generate a survival signal, and crosslinking 61–72% of the total surface BCR did generate a survival signal but its amount was not greater than the amount of the tonic survival signal lost due to BCR crosslinking, resulting in no increase in B cell survival. Therefore, we assume that the 61% is the true offset for Ag-triggered survival signal and the total survival signal (tonic + [offset Ag-triggered] − signal consumption) can be expressed by the following revised equation:
where (BCR Anti-IgM – BCR level · offset) should be set to 0 if BCR Anti-IgM is smaller than BCR level · offset. The final scheme showing both the intrinsic tonic and extrinsic Ag-triggered signals is illustrated in Fig. 1C.
Parameter optimization using weighted least squares method
The d 1, k 2 and k 3 variables were determined using the weighted least squares method to allow the model to best fit with the experimental results. Although the least squares method is normally used for such a modeling, we defined the error value based on the following equation to reduce the influence of the data with large SD and to increase the influence of the data with small SD.
In the above equation, J is the error value (sum of the weighted squared difference), n is the number of experiments, y is the experimental data, σ is the SD of the data. The variables of the model (f) were determined to obtain the smallest value of J.
Parameter optimization using genetic algorithm (GA)
GA is a commonly used method for optimizing variables. We used Unimodal Normal Distribution Crossover (UNDX) and Minimal Gap Generation (MGG) methods21,22,23 to calculate the values of parameters k 1, k 4, d 2, offset and deadline, which cannot be directly determined from the experimental data. To determine k 1, d 2, and deadline, we used GA to allow th9 model to best fit with the survival data obtained at 0, 18, 48 and 72 h of culture (a total of 4 data points). First, one hundred individuals with different set of parameters were created as the first generation. Each individual has a randomly created value (0~0.2) for k 1, d 2 and deadline, and values of d 1, k 2 and k 3 were determined from experimental data. The n + 1 generation was created from n generation as outlined in Supplementary Figure S3). The survival rate was calculated for each individual in the n + 1 generation and the GA was terminated when the mean value of the sum squared difference of all the individuals was almost the same as that found in an individual with the smallest value of the sum squared difference. The variables of the individual with the smallest value of the sum squared difference was considered to be optimum.
To determine k 4 and offset, GA was carried out to allow the modeling to best fit with the actual survival data of 0, 0.3, 3 and 10 µg/mL of F(ab′)2 α-IgM Abs at 0, 18, 48 and 72 h (a total of 16 data points). Here again 100 individuals with different parameters were used as the first generation. Each individual was initialized based on the values of d1, k 2 and k 3 determined from the experimental data and the values for k 1, d 2, and deadline were allowed to change between 50~150% of the previous values, k 4 between 0~0.2 and offset between 0~1. GA was then carried out as described in the previous paragraph to search for optimum set of parameters. We generated random numbers using Mersenne Twister method24 that can rapidly create high quality pseudorandom numbers. We also carried out GA side by side using 10 different random number seeds and confirmed that very similar optimum parameters were obtained. The parameters calculated from the experimental data and the GA-derived optimum parameters are shown in Table 1.
Computer simulation of B cell viability
Based on the differential equations obtained for the tonic and Ag-triggered survival signals, we calculated the changes of the following 3 variables in each cell: BCR level , BCR Anti-IgM , Signal on using the highly accurate fourth-order Runge–Kutta method. The initial value of each variable was defined as in the following: initial BCR level (MFI) was converted to a value between 0–1 and BCR Anti-IgM was set to 0. Since the strength of the survival signal before culture correlated with the initial BCR level, Signal on in each B cell was considered to be the same as the initial BCR level . Each of the 3 variables was calculated for every 0.01 h interval between time 0 to 72 h and a cell was predicted to die when the value of Signal on dropped below the value of the deadline. Simulation was carried out for 200 representative cells at each dose of the F(ab′)2-α-IgM Ab and the survival rate was determined based on the predicted fate of these 200 cells. For example, B cell viability was considered to be 40% if 80 out of the 200 cells were alive.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Results
The strength of tonic BCR signal correlates with BCR levels
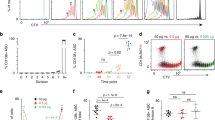
We purified spleen B cells and first analyzed the changes of their BCR levels during in vitro culture in the absence of extrinsic stimuli. As shown in Fig. 2A, BCR levels gradually decreased during culture. BCR levels are normally maintained by a dynamic equilibrium of at least the following 4 processes: the assembly and transport of newly synthesized BCR, internalization of the surface BCR, recycling of the internalized BCR back to the cell surface, and degradation of the internalized BCR25. In the absence of extrinsic stimuli that induce active gene transcription and protein translation, we think that the amount of the newly synthesized BCR is smaller than the amount degraded, leading to a gradual decrease of surface BCR levels. B cell viability concomitantly decreased during the culture, with some cells died at early time point whereas some cells survived even after 3 days (Fig. 2B). Interestingly, B cells expressing high levels of BCR (BCRhigh) had significantly elevated viability than BCRlow cells (Fig. 2C). Conversely, MFI of BCR in live cells was consistently >2-fold that in dead cells (Fig. 2D). These results suggested a positive correlation between BCR levels and B cell viability. Notably, BCR levels decreased only moderately from 18 h to 72 h (Fig. 2A), in contrast to a greater decrease in B cell viability during the same period (Fig. 2B). We think that there is a time lag between the reduction in BCR levels and the decrease in B cell viability.
B cell viability correlates with BCR levels. Purified spleen B cells were cultured in the absence of Ag stimulation as described in Materials and Methods and analyzed for their BCR levels and viability at different time points. BCR levels (A) and B cell viability (B) gradually decreased during culture. (C) B cells expressing higher levels of BCR had greatly elevated viability than BCRlow cells. B cell viability was analyzed in gated BCRhigh and BCRlow population and was set as 100 at time 0. (D) Live B cells had significantly higher BCR levels (shown as % MFI) than did dead B cells. Mean ± SD of 3 independent experiments are shown. *p < 0.05; **p < 0.01; ***p < 0.005 (paired t test).
To confirm the results shown in Fig. 2, we further gated B cells into 10 subpopulations based on their BCR levels (Fig. 3A) and analyzed their survival during culture. The results demonstrated that B cell viability positively correlated with BCR levels at each time point during culture (Fig. 3B). Moreover, we found that BCRhigh cells had elevated levels of the phosphorylated ERK (pERK) (Fig. 3C and D) and AKT (pAKT) (Fig. 3E and F) than BCRlow cells. In contrast, SYK phosphorylation was undetectable both in BCRhigh and BCRlow cells (Supplementary Figure S2). Notably, BCRhigh cells had a remarkable increase in the levels of pAKT over the background (isotype) but only showed a moderate increase in the levels of pERK. AKT Phosphorylation has been shown to mediate B cell survival by promoting FOXO1 degradation3,19. These results collectively indicate that BCRhigh cells have stronger tonic survival signals than do BCRlow cells.
B cells expressing higher levels of BCR have elevated viability and tonic signal than B cells expressing low levels of BCR. (A) B cells were gated into 10 population based on their BCR levels. Each population contained the same numbers of B cells. (B) Viability of each gated B cell population before culture (0 h) and at 18 h, 48 h and 72 h after culture in medium alone. Levels of phosphorylated ERK (pERK) (C and D) and pAKT (E and F) in gated BCRlow and BCRhigh population are shown. Representative FACS profiles (C and E) and mean ± SD of 3 independent experiments (D and F) are shown. Gating strategies are outlined in Supplementary Figure S2. *p < 0.05 (paired t test).
Tonic BCR signal contributes to the survival of B cells cultured in the absence of Ag stimulation
To verify that the survival of primary B cells cultured in the absence of Ag stimulation was dependent on tonic BCR signal, we compared the kinetics of B cell survival in the presence or absence of Ibrutinib, an inhibitor of BTK that plays a critical role in BCR signaling. As shown in Fig. 4, in the continuous presence of Ibrutinib (1 nM-100 nM), but not DMSO used to dissolve Ibrutinib, B cell viability decreased significantly during culture. Incubation of B cells with a higher dose of Ibrutinib (1000 nM) for only 1 h, followed by wash of B cells with the culture medium, also resulted in a significant decrease in B cell viability (Fig. 4). Furthermore, pAKT levels were significantly decreased in the presence of 100 nM of Ibrutinib (Supplementary Figure S4). These results indicate that the survival of B cells cultured in the absence of Ag stimulation is dependent on tonic BCR signal and inhibition of this tonic signal by a BTK inhibitor results in decreased survival.
Inhibition of BCR signaling results in decreased B cell survival. Purified spleen B cells were cultured in medium in the absence or presence of 1, 10 or 100 nM of Ibrutinib, an inhibitor of BTK. Alternatively, B cells were incubated with 1 µM of Ibrutinib for 1 h, washed twice to remove Ibrutinib, and then cultured in medium for various time periods. The cells were analyzed for their viability at different time points. Mean ± SEM of 3 independent experiments are shown. *p < 0.05; **p < 0.01; ***p < 0.005 (One-way Anova).
Low doses of F(ab′)2 α-IgM Abs do not enhance but rather reduce B cell survival
Crosslinking BCR on mature B cells with F(ab′)2 α-IgM Abs, which mimic Ag stimulation, initiates signal cascades that eventually lead to B cell survival and activation. It is unclear, however, how the Ag-induced survival signal and the tonic signal are integrated to allow appropriate B cell responses. We first analyzed B cell viability in the presence of different doses of F(ab′)2 α-IgM Abs. As shown in Fig. 5, F(ab′)2 α-IgM Abs at 10 and 30 μg/ml enhanced B cell viability as compared with B cells cultured in medium alone (0 μg/ml) at both 48 h or 72 h. These observations are consistent with the notion that crosslinking BCR on mature B cells triggers a survival and activation signal. Intriguingly, low doses of F(ab′)2 α-IgM Abs (0.1 to 3 μg/ml) did not enhance, but rather decreased, B cell viability, when compared with non-stimulated B cells (Fig. 5).
A 3D illustration showing that stimulation with low doses of F(ab′)2 α-IgM Abs resulted in decreased B cell viability compared with unstimulated cells. Purified spleen B cells were cultured in the absence or presence of various concentrations of F(ab′)2 α-IgM Abs and analyzed for their viability at different time points. Mean ± SD of 2 independent experiments are shown. *p < 0.05; ***p < 0.005; ****p < 0.001 (One-way Anova).
B cell survival is enhanced only when most of their BCR are occupied by the F(ab′)2 α-IgM Abs
We next investigated the mechanism underlying the nonlinear response in B cell survival induced by F(ab′)2 α-IgM Abs, as shown in Fig. 5. We hypothesized that the overall strength of signals induced by F(ab′)2 α-IgM Abs should correlate with the amount of cell surface BCR that are crosslinked by these Abs. We therefore stained B cells with different concentrations of PE-conjugated α-IgM Ab to estimate the proportion of the surface BCR that are bound by F(ab′)2 α-IgM Abs. We stained 105 cells in 200 μl of medium in a 96 well flat bottom plate, which was the same conditions as we used for cell culture, to correctly estimate the proportion of crosslinked BCR at different concentrations of F(ab′)2 α-IgM Abs. Since the molecular weight of the PE-conjugated α-IgM Ab (180–200-kDa) is roughly twice that of the F(ab′)2 α-IgM Abs (100-kDa) which lack the Fc portion of the IgG, we stained B cells with 0.2, 0.6, 2, 6, 20 and 60 μg/ml of PE-conjugated α-IgM Ab, which had roughly the same molar concentration as 0.1, 0.3, 1, 3, 10 and 30 μg/ml of the F(ab′)2 α-IgM Abs, respectively. As shown in Fig. 6A, the MFI almost reached a plateau at 20 and 60 μg/ml of PE-labeled α-IgM Ab (solid circles), which were defined as 100% of saturation. At 6 μg/ml or lower concentrations of PE-labeled α-IgM Ab, only up to 72% of the cell surface BCR were occupied (solid circles). These observations suggest that B cell survival can be enhanced only when most of their BCR were crosslinked by the F(ab′)2 α-IgM Abs.
Determination of the α-IgM Ab concentrations that saturate the surface BCR. (A) Purified spleen B cells were stained with different concentrations of a PE-conjugated α-IgM Ab and analyzed for MFI by FACS. MFI obtained with 60 µg/ml of PE-conjugated α-IgM Ab was set to 100. (B) Proportion of crosslinked BCR in the presence of 1 μg/ml of PE-conjugated α-IgM Ab. Solid circle, actual experimental data; Red line, simulation results. Mean ± SD of 2 independent experiments are shown.
Mathematical modeling of the tonic BCR survival signal in B cells
To better understand how the tonic signal and Ag-triggered signal are integrated to regulate B cell survival and activation, we first performed mathematical modeling of the tonic BCR signal in B cells cultured in the absence of F(ab′)2 α-IgM Abs. Our experimental results indicated that the strength of tonic signal positively correlated with BCR levels and therefore we simply used MFI of BCR as the generator of tonic signal. We assumed that the decreased MFI in cultured B cells was due to a decrease in the BCR level on each B cell and that the tonic signal in each B cell correlated with its BCR level. The distribution of BCR levels of 8342 cells before culture (0 h) (Supplementary Figure S5) indicated that BCR levels in primary B cells differed by more than 1000-fold. To determine d 1 in equation 1, BCR level at 0 h was set to 1 and based on the BCR levels at 18 h, 48 h and 72 h (Fig. 2A), d 1 was determined to be 0.01435 [/h] using the weighted least squares method. The simulation of the decrease in BCR levels is shown in Fig. 7A (red line), which indicated that BCR levels decreased from 1 at 0 h to 0.3558 at 72 h, equivalent to a 64% reduction.
Simulation of BCR levels and B cell viability. (A) Decrease in BCR levels during culture. The experimental data (same as Fig. 2A) and simulation are shown by black and red lines, respectively. (B) B cell viability in the absence of external stimuli. Actual data (same as Fig. 5, 0 µg/ml of F(ab′)2 α-IgM Abs) and simulation results are indicated by black and red lines, respectively. Dotted red line, simulation results when k 1 was set to ~40% of the original value.
We next used GA to calculate the values of k 1, d 2 and deadline in the absence of stimuli (equation 2) to allow the model to best fit with the actual survival data shown in Fig. 5 (0 µg/ml of F(ab′)2 α-IgM Abs). To facilitate the simulation of B cell survival, we selected 200 cells with their distribution of BCR levels similar to that of the parental 8342 cells. The highest fluorescence intensity of BCR (67558) was converted to 1, and the average and the median of BCR levels became 0.07460 and 0.04360, respectively. Optimum parameters obtained with 10 different seeds were averaged and k 1, d 2 and deadline were determined to be 0.02381 [/h], 0.1239 [/h] and 0.01034, respectively. The survival curve depicted from these parameters is shown in Fig. 7B (solid red line), which well matched the actual data (Fig. 7B, black line). If we set the value of k 1 (the parameter for tonic signal) to 0.009523 [/h] (equivalent to ~40% of the original value of k 1), the survival curve (Fig. 7B, dotted red line) appeared very similar to that obtained in the presence of 100 nM of the BTK inhibitor Ibrutinib (Fig. 4, light blue column), suggesting that the generation of tonic signal decreased by 60% in the presence of 100 nM of Ibrutinib.
Modeling of the survival signal generated by stimulation with F(ab′)2 α-IgM Abs
Based on the results shown in Fig. 6A (solid circles) and using weighted least squares method, the ratio of k 3/k 2 was determined to be 1.132. The result of simulation is shown in Fig. 6A (red line) where the proportion of the crosslinked BCR at 60 μg/ml of PE-conjugated Ab was set as 100%. To determine the values of k 3 and k 2, we analyzed the changes in the proportion of crosslinked BCR. An example is shown in Fig. 6B where the proportion of the crosslinked BCR reached a plateau in 1 h in the presence of 1 μg/ml of PE-conjugated α-IgM Ab. Based on the experimental data shown in Fig. 6B (solid circles), k 2 and k 3 was determined to be 2.779 [ml/μg/h] and 3.145 [/h], respectively, using the weighted least squares method. The values of k 2 and k 3 indicated that 95% of the BCR were saturated in 30 min in the presence of 1 μg/ml of the F(ab′)2 α-IgM Abs. Theoretically, only 82% of the BCR would be crosslinked in 30 min in the presence of 0.1 μg/ml of the F(ab′)2 α-IgM Abs whereas 99% of the BCR would be crosslinked in just 9 min in the presence of 10 μg/ml of the F(ab′)2 α-IgM Abs.
Integrating the tonic BCR signal and the survival signal generated by stimulation with F(ab′)2 α-IgM Abs
Crosslinking BCR with F(ab′)2 α-IgM Abs is known to trigger signal cascades that eventually lead to B cell survival and activation. The strength of the signal is determined by the concentration of F(ab′)2 α-IgM Abs. At 3 μg/ml or lower doses of F(ab′)2 α-IgM Abs (equivalent to <6 μg/ml of the PE-conjugated α-IgM Ab), only up to 72% of the BCR were crosslinked (Fig. 6A, solid circles) and in such cases a survival signal cannot be generated (Fig. 5). More precisely, crosslinking up to 61% of the surface BCR failed to generate a survival signal, and crosslinking 61–72% of the total surface BCR did generate a survival signal but its strength was not greater than the tonic survival signal lost due to BCR crosslinking, resulting in no increase in B cell survival. At 10 and 30 μg/ml of F(ab′)2 α-IgM Abs (equivalent to 20 and 60 μg/ml of PE-conjugated α-IgM Ab), almost all the BCR were crosslinked (Fig. 6A, solid circles), resulting in the generation of survival signals (Fig. 5). Next, we used GA to determine k 4 and offset in the presence of F(ab′)2 α-IgM stimulation based on equations 1, 6 and 11. We used the data of 0, 0.3, 3 and 10 µg/ml shown in Fig. 5 and obtained following results: k 1, 0.02980; d 2, 0.1543; deadline, 0.01032; k 4, 0.1294; offset, 0.6097 (Summarized in Table 1). Based on these parameters, we calculated viability of B cells cultured in the presence of different concentrations of F(ab′)2 α-IgM Abs for different times (Fig. 8, red line), which correlated well with the actual experimental data (Fig. 8, black line). These results suggest that our model successfully integrated the tonic and Ag-triggered signals and correctly predicted the survival probability of primary B cells. In particular, the reduced B cell survival at low doses of F(ab′)2 α-IgM Abs was very well recapitulated in the simulation.
A mathematical model integrating the tonic and Ag-triggered survival signals correctly predicts the viability of B cells cultured in the presence of different doses of F(ab′)2 α-IgM Abs for different time periods. Actual experimental data (adopted from Fig. 5, black) and simulation results (red) are shown.
Discussion
Although BCR constitutively transmits a tonic survival signal in the absence of Ag stimulation, it is difficult to analyze its nature using conventional biochemical approaches. To overcome this difficulty, we have combined actual experiments with mathematical modeling to investigate its strength, regulation and relationship with the Ag-triggered survival signal. In the present study, we have successfully built a mathematical model that integrates tonic BCR signal and signal induced by BCR crosslinking. Our model reveals that the rate constant for the generation of tonic signal (k 1) and Ag-triggered signal (k 4) is 0.02980 and 0.1294, respectively. In other words, crosslinking a BCR generates a signal that is 4.3 (0.1294/0.02980) times as strong as the tonic signal generated from a free BCR. To our knowledge, this is the first attempt to determine the strength of tonic BCR signal relative to the signal generated from crosslinked BCR. This model also allows us to predict the survival probability of a B cell based on its initial BCR level and the strength and duration of BCR crosslinking and fits very well with the mechanisms that regulate B cell tolerance.
Another intriguing finding in the present study is that a survival signal is not generated even when 61% of the surface BCR is crosslinked by F(ab′)2 α-IgM Abs. We think that the strength of the signal generated by crosslinking 61% of the surface BCR corresponds to the threshold (or offset) for Ag-triggered signaling. The existence of such a threshold is important for B cells not to respond to stimulation by self Ag. B cell development proceeds in an ordered fashion in the bone marrow (BM). Committed B cell progenitors rearrange their Ig heavy and then light chain genes to become IgM+ immature B cells. Immature B cells that react strongly with self Ag are deleted in BM, a mechanism termed central B cell tolerance1. Those that do not react with self Ag strongly are allowed to exit BM and migrate to the secondary lymphoid tissues such as spleen and lymph node where they become mature B cells. Therefore, mature B cells in general do not react strongly with self Ag. The existence of a threshold in BCR signaling can effectively prevent mature B cells from being activated by self Ag and allow a robust response of mature B cells against foreign Ag that can crosslink BCR with high affinity and/or high avidity.
It should be noted that this threshold applies only when BCR alone is stimulated. If a B cell simultaneously receives stimulation through other receptors such as CD40 or cytokine receptors, crosslinking most of the surface BCR is no longer a prerequisite for inducing a survival signal. Such a situation occurs when B cells are stimulated by foreign Ag. In this case, foreign Ag-specific T cells will provide help for B cells by upregulation of CD40 ligand that can bind to CD40 on B cells and by secretion of cytokines such as IL-4. Therefore, the existence of such a threshold does not inhibit B cell activation against foreign Ag but only prevents B cell response against self Ag in which case B cells cannot receive T cell help as self Ag-specific T cells are normally deleted in the thymus during T cell development. In the present study, we focused on the survival signal generated by BCR alone and in this case the existence of a high threshold for inducing B cell survival functions to prevent B cell activation by self Ag stimulation.
We found that BCRhigh cells had significantly elevated levels of pAKT compared with BCRlow cells. In contrast, both BCRhigh and BCRlow cells had similarly undetectable levels of pSYK. Using genetic approaches, Srinivasan et al. have elegantly demonstrated that tonic BCR survival signal is predominantly mediated by PI3 kinase, which targets AKT for phosphorylation22. AKT phosphorylation promotes B cell survival by inactivating transcription factor FOXO13. The elevated AKT phosphorylation in BCRhigh cells is therefore consistent with the increased survival of these cells. It has also been demonstrated that canonical NF-κB signaling, or MEK1 and Rac1 activation, fails to rescue the survival of B cells lacking BCR22. MEK is known to phosphorylate ERK3 and we found that BCRlow cells had barely detectable levels of pERK and BCRhigh cells only had a moderate increase of pERK over the background (isotype). The limited amount of pERK in BCRhigh cells is also in agreement with the previous finding that MEK-ERK MAP kinase pathway does not mediate B cell survival22. We think that the levels of surface BCR and intracellular pAKT are two important parameters reflecting the strength of tonic BCR signal.
We have used primary mature B cells purified from mouse spleen. More than 90% of the purified spleen B cells are follicular B cells and about 5–10% are marginal zone B cells (MZB). These MZB express higher levels of BCR than do follicular B cells and are thought to have a tendency to react with self Ag and differentiate into Ab secreting plasma cells26. It would therefore be interesting to analyze the survival of MZB in the absence or presence of different doses of F(ab′)2 α-IgM Abs and build a mathematical model predicting their fate. Another important B cell subpopulation are B-1 cells, which are localized in the peritoneal and plural cavities and secrete natural Abs even in the absence of BCR crosslinking27. It remains to be investigated how the tonic and Ag-triggered survival signals are regulated in B-1 cells. Development of mathematical models predicting the survival of these different B cell subsets should provide important insights in understanding their differential responses to foreign and self Ag stimulation. Moreover, memory B cells, which can be rapidly activated by Ag stimulation, normally express isotype-switched IgG-BCR. The IgG-BCR has unique structural and biological properties28 and it would greatly help understand memory B cell responses by establishing a mathematical model integrating tonic and Ag-triggered signals from IgG-BCR.
The tonic BCR signal is important for the survival of not only normal B cells but also B lymphoma cells. Although there are many subtypes of B lymphomas, an intriguing common feature is that all types of B lymphomas require BCR signals to gain advantages in their tumorigenesis in vivo 10,11 and the BTK inhibitor has demonstrated clinical benefit for several types of B cell lymphomas. It remains to be investigated how the relatively “weak” tonic BCR signal is critical for B cell malignancies. One possibility is that although B lymphoma cells have acquired oncogenic mutations that allow their uncontrolled proliferation, they still rely on BCR signals for their survival. The results of the current study suggest that inhibition of BCR expression might lead to decreased tonic BCR signal in B lymphomas. Mathematical modeling of the tonic BCR signal in normal and malignant human B cells should provide important clues for understanding the pathogenesis of B lymphomas and for developing effective therapies.
References
Kurosaki, T., Shinohara, H. & Baba, Y. B cell signaling and fate decision. Annu. Rev. Immunol. 28, 21–55 (2010).
DeFranco, A. L. The complexity of signaling pathways activated by the BCR. Curr. Opin. Immunol. 9, 296–308 (1997).
Mackay, F., Figgett, W. A., Saulep, D., Lepage, M. & Hibbs, M. L. B-cell stage and context-dependent requirements for survival signals from BAFF and the B-cell receptor. Immunol. Rev. 237, 205–225 (2010).
Khan, W. N. et al. Defective B cell development and function in Btk-deficient mice. Immunity 3, 283–299 (1995).
Kerner, J. D. et al. Impaired expansion of mouse B cell progenitors lacking Btk. Immunity 3, 301–312 (1995).
O’Keefe, T. L., Williams, G. T., Davies, S. L. & Neuberger, M. S. Hyperresponsive B cells in CD22-deficient mice. Science 274, 798–801 (1996).
Otipoby, K. L. et al. CD22 regulates thymus-independent responses and the lifespan of B cells. Nature 384, 634–637 (1996).
Bolland, S. & Ravetch, J. V. Spontaneous autoimmune disease in FcɣRIIB-deficient mice results from strain-specific epistasis. Immunity 13, 277–285 (2000).
Pao, L. I. et al. B cell-specific deletion of protein-tyrosine phosphatase Shp1 promotes B-1a cell development and causes systemic autoimmunity. Immunity 27, 35–48 (2007).
Dühren-von, M. M. et al. Chronic lymphocytic leukaemia is driven by antigen-independent cell-autonomous signalling. Nature 489, 309–312 (2012).
Young, R. M. et al. Survival of human lymphoma cells requires B-cell receptor engagement by self-antigens. Proc. Natl. Acad. Sci. USA 112, 13447–13454 (2015).
Kurosaki, T. & Hikida, M. Tyrosine kinases and their substrates in B lymphocytes. Immunol. Rev. 228, 132–148 (2009).
Shinohara, H., Inoue, K., Yumoto, N., Nagashima, T. & Okada-Hatakeyama, M. Stimulus-Dependent Inhibitor of Apoptosis Protein Expression Prolongs the Duration of B Cell Signalling. Sci. Rep. 6, 27706 (2016).
Shinohara, H. et al. Positive feedback within a kinase signaling complex functions as a switch mechanism for NF-κB activation. Science 344, 760–764 (2014).
Shinohara, H. & Kurosaki, T. Negative role of TAK1 in marginal zone B-cell development incidental to NF-κB noncanonical pathway activation. Immunol. Cell Biol. 94, 821–829 (2016).
Kil, L. P. et al. Btk levels set the threshold for B-cell activation and negative selection of autoreactive B cells in mice. Blood 119, 3744–3756 (2012).
Lam, K. P., Kühn, R. & Rajewsky, K. In vivo ablation of surface immunoglobulin on mature B cells by inducible gene targeting results in rapid cell death. Cell 90, 1073–1083 (1997).
Kraus, M., Alimzhanov, M. B., Rajewsky, N. & Rajewsky, K. Survival of resting mature B lymphocytes depends on BCR signaling via the Igα/β heterodimer. Cell 117, 787–800 (2004).
Srinivasan, L. et al. PI3 kinase signals BCR-dependent mature B cell survival. Cell 139, 573–586 (2009).
Szydlowski, M. et al. FOXO1 activation is an effector of SYK and AKT inhibition in tonic BCR signal-dependent diffuse large B-cell lymphomas. Blood 127, 739–748 (2016).
Ono, I., Yamamura, M. & Kobayashi, S. A Genetic Algorithm with Characteristic Preservation for Function Optimization. Proc. IIZUKA 96, 511–514 (1996).
Satoh, H., Yamamura, M. & Kobayashi, S. Minimal Generation Gap model for Gas Considering Both Exploration and Exploitation. Proc. IIZUKA 96, 494–497 (1996).
Kobayashi, S. The Frontiers of Real-Coded Genetic Algorithms. Trans. Jpn. Soc. Artif. Intell. 24, 147–162 (2009).
Matsumoto, M. & Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator. ACM Trans. Model. Comput. Simul. 8, 3–30 (1998).
Ouchida, R., Kurosaki, T. & Wang, J. Y. A role for lysosomal-associated protein transmembrane 5 in the negative regulation of surface B cell receptor levels and B cell activation. J. Immunol. 185, 294–301 (2010).
Pillai, S. & Cariappa, A. The follicular versus marginal zone B lymphocyte cell fate decision. Nat. Rev. Immunol. 9, 767–777 (2009).
Baumgarth, N. B-1 Cell Heterogeneity and the Regulation of Natural and Antigen-Induced IgM Production. Front. Immunol. 7, 324 (2016).
Xu, Y. et al. No receptor stands alone: IgG B-cell receptor intrinsic and extrinsic mechanisms contribute to antibody memory. Cell Res. 24, 651–664 (2014).
Acknowledgements
We thank Lumin Zhang for excellent technical support and the Animal Facility of Fudan University for maintaining the mice. This work was supported by the National Basic Research Program of China (2015CB943300 to J.Y.W.), the National Natural Science Foundation of China (81373129 and 81571529 to J.Y.W), and a Grant-in-Aid for JSPS Research Fellow (JP16J10309 to S.Y.).
Author information
Authors and Affiliations
Contributions
Y.Z. performed the experiments; S.Y. established the mathematical model; M.Y and Y.W. supervised the research; J.Y.W. designed the research and wrote the paper.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yasuda, S., Zhou, Y., Wang, Y. et al. A model integrating tonic and antigen-triggered BCR signals to predict the survival of primary B cells. Sci Rep 7, 14888 (2017). https://doi.org/10.1038/s41598-017-13993-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-13993-x
This article is cited by
-
A single donor is sufficient to produce a highly functional in vitro antibody library
Communications Biology (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.