Abstract
Electrically deformable surfaces based on dielectric elastomers have recently demonstrated controllable microscale roughness, ease of operation, fast response, and possibilities for programmable control. Potential applications include marine anti-biofouling, dynamic pattern generation, and voltage-controlled smart windows. Most of these systems, however, exhibit limited durability due to irreversible dielectric breakdown. Lowering device voltage to avoid this issue is hindered by an inadequate understanding of the electrically-induced wrinkling deformation as a function of the deformable elastic film thickness. Here we report responsive surfaces that overcome these shortcomings: we achieve fault-tolerant behavior based on the ability to self-insulate breakdown faults, and we enhance fundamental understanding of the system by quantifying the critical field necessary to induce wrinkles in films of different thickness and comparing to analytical models. We also observe new capabilities of these responsive surfaces, such as field amplification near local breakdown sites, which enable actuation and wrinkle pattern formation at lower applied voltages. We demonstrate the wide applicability of our responsive, fault-tolerant films by using our system for adjustable transparency films, tunable diffraction gratings, and a dynamic surface template/factory from which various static micropatterns can be molded on demand.
Similar content being viewed by others
Introduction
Dynamic control of surface topography and roughness is highly desired for its potential to accomplish what is difficult for traditional static surfaces to achieve, such as adjustable wettability1, smart adhesion2, antifouling abilities3, tunable light diffraction4, e-skin and stretchable devices5,6. Depending on the material’s mechanical properties, such surfaces can show a variety of topographies during deformation, including wrinkling (or buckling), formation of localized ridges, period-doubling, creasing, and delamination7,8. Several methods have been used to induce such surface deformation, such as in-plane mechanical compression9,10,11, relaxation after depositing thin films on pre-stretched substrates12,13,14,15,16,17, thermal expansion mismatch after cooling thin films deposited on hot substrates18,19,20,21,22, ion irradiation23,24, differential swelling of film layers2,25,26,27,28,29, and electric-field-induced deformation30,31,32.
Among these various approaches, electric-field-induced deformation is particularly attractive due to its ability to reversibly actuate at high frequency and its potential for miniaturization and programmable control33. This type of deformation relies on the concept of voltage-induced electromechanical instability34,35,36,37,38,39, a phenomenon frequently observed in dielectric elastomer actuators (DEAs)40,41,42,43,44,45. Wang and Zhao, for example, have produced creased/cratered/wrinkled structures by immobilizing a DEA on a rigid substrate32,46. This DEA-like system is composed of four layers from top to bottom: a conductive liquid (e.g. NaCl solution) as a top electrode, an elastic layer, a rigid layer, and a bottom electrode. When a high voltage is applied across the two electrodes, the elastic layer is squeezed and thus tends to expand laterally due to its incompressibility. Meanwhile, the rigid layer not only provides a higher breakdown strength, but it also confines the elastic layer and blocks its expansion. The resulting lateral compressive stresses induce instabilities which deform the surface structure. Designs such as these pave the way for more practical applications such as responsive anti-biofouling surfaces in marine environments3. van den Ende et al. have shown further application of these DEA-based systems by creating smart windows and mirrors based on wrinkling-induced light diffusion31.
In order to incorporate these DEAs into real-world applications, however, it will be necessary to address the issues with dielectric breakdown which limit the durability of these systems. Local inhomogeneity, defects, and large deformations during actuation in DEA-like systems may create some locally thinner areas (e.g. depressions of creases and wrinkles) which, at constant surface potential, create high local fields. These high fields drive the film to become even thinner in these locations, resulting in a positive feedback loop which leads to eventual dielectric breakdown and thus short circuiting40. This breakdown vulnerability is catastrophic and makes many DEA devices short-lived. Efforts to circumvent this breakdown issue by inducing wrinkling at lower voltages have been hindered by a limited understanding of the factors which affect the critical voltage for wrinkling, such as device thickness.
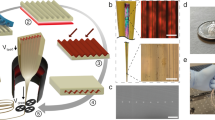
Here we report the fabrication and characterization of a fault-tolerant electrically responsive surface (Fig. 1a) that addresses these issues and introduces novel capabilities for a variety of applications. The fault-tolerance is due to self-insulation of localized breakdown, and presence of multiple defects does not prevent the actuation. Furthermore, targeted breakdown can be used to create patterned morphologies under lower voltages. We contribute to the fundamental understanding of these DEA-like systems by investigating how the critical voltage/field necessary to induce surface wrinkles varies with the elastic film thickness (from 9 µm to 83 µm). Finally, we demonstrate potential applications in tunable transparency films, dynamic diffraction gratings, and dynamic surface templates using commercially available materials for the rigid layer (Kapton tape), elastic layer (PDMS), and integrated top electrode (Au).
(a) Concept of DEA-like responsive surfaces. When voltage is applied, the PDMS layer and coated gold film deform due to the electric field (oriented normal to the surface). (b) Flat surface at 0–3 kV, as observed by optical profiler (left) and optical microscope (right). (c) Formation of craters at 4 kV. (d) Formation of wrinkles at 5 kV. HPDMS is 22 µm and HKapton is 50 µm for each of the samples shown in (b–d).
Results and Discussion
Dynamic Topography at Different Voltages: From Cratering to Wrinkling
One of the most common approaches to achieve large topographical changes is to wrinkle the surfaces of bilayer films, in which the top film is much stiffer than the bottom elastic layer. In this system, lateral (in-plane) compressive stress above a critical value will cause strain mismatch between the two layers and induce wrinkling9. Wrinkling of a surface can also be induced by applying an out-of-plane force, normal to an elastomeric coating47. This model is natural to apply to our DEA-like system, as the applied electric field generates an out-of-plane force. To make a device working with this out-of-plane model, we fabricate it with four layers from the top to the bottom (Fig. 1a): a thin gold film as the top electrode, an elastic dielectric layer made of polydimethylsiloxane (PDMS), a rigid layer (Kapton film), and a gold-coated glass slide as the bottom electrode. The top electrode can buckle with the compliance of the PDMS elastic dielectric layer underneath. PDMS is not directly coated on the bottom electrode since its dielectric strength (21 kV/mm) is much lower than the critical electric field required to induce wrinkling. Instead, PDMS is coated on a 50 µm thick Kapton film with dielectric strength of 197 kV/mm to prevent breakdown before the applied voltage reaches the critical wrinkling value.
When applying voltage, reversible wrinkles can be observed on the surface of the gold top electrode through both an optical profiler and optical microscope, as depicted in Fig. 1a. While the optical profiler shows a detailed height map of the surface profile, the optical microscope gives a quick two-dimensional view of the pattern structure. Figure 1b–d show images of the flat state (0 to 3 kV), and actuated states at 4 kV and 5 kV. It can be seen in Fig. 1b that when the voltage is below 3 kV, the surface is relatively smooth, since the force is not sufficient to deform the surface. When the voltage is 4 kV (Fig. 1c), some craters are observed on the surface. These craters can be attributed to defects due to voids, partial curing, or the intrinsic inhomogeneity of polymer, which may concentrate the local field or stress and make some small regions become thinner when the voltage is applied. Since it has been reported that charges tend to flow to thinner areas of dielectric elastomer actuator48, this process leads to charge localization and forms craters before the whole film is wrinkled. At 5 kV (Fig. 1d), the induced out-of-plane force reaches the critical value required to create wrinkles on the surface. We thus demonstrate that different surface patterns can be generated, namely craters at 4 kV and wrinkles at 5 kV, simply by applying different voltages to generate different amounts of out-of-plane force.
In addition to a detailed profile of the wrinkled structure, the optical profiler also measures surface roughness of larger areas. Measuring roughness (see Methods) as a function of applied voltage provides a facile means of determining the critical voltage and corresponding electric field that induces wrinkling. Figure 2a plots the root mean squared roughness, Rrms, of the surface at various applied voltages for different thicknesses of PDMS. The critical wrinkling voltage, Фc, for each thickness of PDMS is determined by fitting the data with an empirical exponential growth function: Rrms = R0 + 120 × exp (k (Φ−Φc)) nm, where R0 is the roughness when the applied voltage is zero and k is the exponential growth constant.
(a) Surface roughness at different applied voltages for PDMS thicknesses ranging from 9 to 83 µm. The critical voltage is determined by the empirical function Rrms = R0 + 120 × exp (k (Φ−Φc)) nm, where R0 is the roughness at Φ = 0. (b) Critical electric field for wrinkling of Au on different thicknesses of PDMS. As the PDMS thickness decreases, the curve deviates from the theoretical value (0.048 kV/µm), which assumes the top gold film to be infinitesimally thin.
To further relate the critical voltage to the critical field, the thickness of the dielectric layer needs to be incorporated in the above equation. Since a Kapton film is added underneath the PDMS to increase the breakdown voltage, the effective thickness of dielectric layer should be considered and the electric field in the PDMS film can be expressed as32:
where Φ denotes the applied voltage, H is the thickness of each layer and ε is its corresponding electrical permittivity. Here ɛPDMS/εKapton equals to 2.65⋅ε0/3.5⋅ε0 = 0.76. The derived critical wrinkling fields for different thicknesses of PDMS are shown in Fig. 2b. This experimental data is in reasonable agreement with that of the out-of-plane force-induced wrinkling model developed by Huang49, which predicts a critical wrinkling field of 0.048 kV/µm (shown as the dashed line in Fig. 2b). In this model, the critical field to induce wrinkling in PDMS can be expressed as:
where \({{\rm{Y}}}_{{PDMS}}\) is the Young’s modulus (83 kPa, see Method section) and ɛ is the dielectric constant (ɛPDMS = 2.65⋅ε0). ξc is a constant based on Poisson’s ratio. ξc = 2/3 when the Poisson’s ratio is 0.5 for PDMS31.
Note that our observed critical wrinkling field increases relative to the predicted value of equation (2) with decreasing PDMS film thickness. This discrepancy may be attributed to the fact that the model assumes the top electrode to be infinitesimally thin49, an assumption which can never be satisfied in reality. Thus, the measured critical field approaches the predicted value as the PDMS film thickness increases, when the top gold electrode is relatively thinner. This trend is consistent with a theoretical study of in-plane compression on similar systems which did not assume an infinitesimally thin top film50.
When designing a DEA-like device, a common strategy to reduce the working voltage is to decrease the film thickness so that the same field can be maintained at lower applied voltage. However, our trend in critical wrinkling field versus PDMS film thickness implies that decreasing PDMS thickness does not always lead to a proportional reduction of the working voltage. Further characterization on devices with very low PDMS thicknesses will be necessary to fully understand these systems.
Since we select commercially available materials (Kapton tape, PDMS, etc.) with low price for ease of fabrication, the working voltage shown here is relatively high (3 to 7 kV). We have demonstrated that using different materials for the elastic and rigid layers with the same design might reduce the voltage (Supplementary Fig. S2). For example, from equation (1) we know that an elastic layer with a low Young’s modulus and high dielectric constant can reduce the critical field for wrinkling, and from equation (2) the field can be amplified under the same applied voltage if choosing a material with thinner thickness or higher dielectric constant for the rigid layer.
Fault-Tolerant Surface and Defect-Amplified Electric Field
Many real-world applications of these electrically-actuated responsive surfaces require large-scale deformations, such as strong light diffusion in tunable optics or rough texture change for dynamic camouflage. Achieving these large topographical changes typically requires high actuation voltages. These high voltages, however, can cause dielectric breakdown of the DEA system that eliminates its ability to act as a responsive surface51,52. Therefore, most DEA-based responsive surfaces are restricted to relatively low voltage ranges, limiting their ability to achieve significant levels of deformation. This issue motivates an investigation into potential mechanisms for (1) achieving fault-tolerant behavior, in which the surface can still actuate after some degree of dielectric breakdown, and (2) lowering the applied voltage levels necessary to achieve large-scale surface deformation.
We explore the effects of dielectric breakdown on our system by applying voltages much higher than Φc (the critical voltage to induce wrinkling). For example, as we tuned the applied voltage from 0 to 8 kV across a 22 µm PDMS film, the wrinkles appear at Φc = 4.17 kV (green line in Fig. 2a) and create valleys on the surface. When the voltage is raised further, the surface roughness and wrinkle depth also increase, making the film at the bottom of these wrinkle valleys even thinner. For a constant applied voltage, locally thinner areas in the film experience much higher electric fields, and that is where breakdown occurs when the applied voltage is high enough. These high local electric fields across the film result in high leakage current flowing through the elastomer and cause Joule heating and higher local conductivity53, resulting in a positive feedback loop until the short circuit current is high enough to cause the breakdown and the burning of the conductive 16 nm Au material around the breakdown fault, leaving even the damaged dielectric insulated from further breakdown. Video SV1 in supporting information shows the formation of the local breakdown when the applied voltage reaches 8 kV, and Fig. 3a highlights the breakdown regions in red circles. The current generated from this process can be observed using the amperometer of the power supply, and it vanishes once the Au around the punctures has burned away, which leaves the electrodes disconnected. After removing the applied voltage, we observe punctures formed from these small burned regions on the surface (Fig. 3b). The number of these breakdown punctures saturates after several high voltage cycles, as shown in Fig. 3c. Note that because these regions of local breakdown are insulated from the rest of the surface, immediate large-scale breakdown of the device is prevented and the punctured film can still actuate for many times (Fig. 3d); similar self-clearing behavior has been observed in DEA artificial muscles under large deformation when single-walled carbon nanotubes are used as electrodes54. This fault-tolerant behavior in our DEA-like system prevents malfunction even under high voltage, which prolongs life of the system and simplifies the manufacturing process, since even slightly defective films can still actuate.
In addition to enabling fault-tolerant behavior, the local breakdown phenomena we observe in our DEA-like system can also be used to activate our surfaces at lower voltages in the presence of breakdown-induced punctures. Through optical profiler measurements, we observe that the voltage required to reach a roughness of about 900 nm has decreased from 5 kV to 3.5 kV, a reduction of 30%. We hypothesize that edge effects and charge accumulation around punctures in the film amplify local electric fields, as has been observed previously for capacitors55,56. This amplified field reduces the minimum voltage necessary to actuate the surface near the punctures. We thus present an unconventional method to decrease the need for high working voltages, which has always been a concern for DEA-like systems. As mentioned in the previous section (Fig. 2b), reducing the voltage by decreasing device thickness may also increase the minimum field necessary to induce wrinkling. The result here provides another strategy by locally enhancing the electric field near electrodes or puncture sites.
Applications
Tunable Transparency Film
One of the most promising applications of these DEA-like systems is in films or windows with tunable transparency57 (Video SV2 in supporting information). As the applied voltage is gradually increased and the surface topography changes, the transmittance through the film also changes due to optical diffusion. As shown in Fig. 4a, the transmittance drops slightly once craters appear on the surface, then further decreases near 5 kV when the wrinkles diffuse more light. When increasing the voltage to 6 kV, the amplitude of the wrinkles increases to yield even lower light transmittance. This tunable transparency phenomenon is reversible and stable for many cycles, as shown in Fig. 4b.
Note that the sharp drops in transmittance at 17 and 70 seconds in Fig. 4b are due to inductive voltage spikes which appear when switching on the power supply58. This voltage spikes come from inductive loads which can generate magnetic field when current flow through them at the moment the power supply is switched on/ off. The peak voltage induces large topographical changes, resulting in very low transmittance. The transmittance drops immediately from 39% to 11% and relaxes back to about 28% after a few seconds. However, the short-lived peak voltage does not cause dielectric breakdown in the system, as demonstrated by the fact that the device can work reproducibly for several cycles (Fig. 4b). It has been reported that working above the breakdown voltage for a short time period will not irreversibly damage DEA systems59.
Dynamic Diffraction Grating
Besides smart windows, this responsive surface can also achieve dynamic diffraction grating for applications such as wavelength selection, masks for photolithography, or astronomy and space instrument60. This application requires regularly-spaced, unidirectional wrinkles, rather than the randomly-oriented patterns described previously. We achieve these patterns by coupling the voltage-induced wrinkling process with mechanically-induced wrinkles, formed upon bending the structure (Fig. 5a). This process yields two sets of wrinkles: primary wrinkles, appearing at a certain critical stress, and secondary wrinkles, induced under higher stress10,61. In this experiment we induce the primary wrinkles by mechanical bending the film, inducing a stress lower than where secondary wrinkles would appear. It is not well known what the critical stress is in our system that induces the secondary wrinkles, but by using electrical voltage, we could alter the total stress applied and cross into the secondary wrinkle generation, which results in the ability to tune the wavelength of existing wrinkles for light grating. The wrinkle spacing can be characterized optically by diffraction:
where d is the separation of grating elements (spacing of wrinkles here), and can be calculated from the light wavelength λ (650 nm) and the angle between successive diffraction orders θ, and n is a non-zero integer.
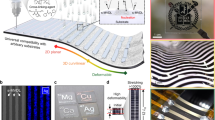
Applications in tunable diffraction gratings. (a) Setup for mechanically inducing wrinkles, the spacing of which can be electrically tuned. (b) Measured diffraction angle, calculated d value, and observed wrinkle spacing as a function of applied voltage. (c) Images of directional wrinkles at different voltages, and (d) the corresponding diffraction patterns.
The diffraction angle and calculated d, shown in Fig. 5b, are consistent with the wrinkle spacings directly observed by microscope. Figure 5c shows optical images of directional wrinkles under different applied voltages, and Fig. 5d shows the corresponding diffraction pattern. When no voltage is applied, primary wrinkles form due to mechanical bending alone. As the figure shows, primary wrinkles with a spacing of 5 µm can be clearly observed, whereas secondary wrinkles with larger spacing are relatively shallow and insignificant, so the formed diffraction pattern is mainly due to the primary wrinkles. When a voltage of 3.4 kV is applied, the additional electric force facilitates the formation of secondary wrinkles, which emerge and propagate from the existing shallow secondary wrinkles induced from mechanical bending. The larger spacing (41 µm) of these secondary wrinkles yields a correspondingly smaller diffraction pattern spacing. When the voltage increases to 4 kV, the spacing of the wrinkles further increases to 60 µm. This value is similar to the spacing achieved using pure electric compression without mechanical bending (Fig. 1d), indicating that electrically-induced wrinkling starts to dominate the overall wrinkling mechanism. At even higher voltages such as 5 kV, the isotropic electrically-induced wrinkling dominates the anisotropic mechanically-induced compression, such that the wrinkles tend to lose unidirectionality and the diffraction pattern blurs.
Dynamic Factory for Fabricating Permanent Patterns
The applicability of this DEA-like system can be extended even further by replicating and preserving our voltage-induced surface patterns, which we accomplish using molding. By pouring uncured epoxy on the responsive surface and applying voltage while the epoxy cures, we can obtain a copy of the surface craters or wrinkles, as depicted in Fig. 6. Removing the applied voltage and peeling off the epoxy results in a replicate of the wrinkled structure. In this process, the gold layer comprising the top electrode is transferred to the epoxy without damaging the underlying PDMS. Thus, after sputtering gold on the PDMS again, the immobilized DEA system can be reused to mold another pattern. We demonstrate several patterns made from the reusable pattern factory in Fig. 6a. This pattern replication operation is carried out at room temperature and requires only 30 minutes for epoxy curing and 5 minutes for re-deposition of the gold top electrode, enabling easy and fast fabrication for different replicated patterns.
(a) Process of dynamic micropattern fabrication, with images of replicated patterns created from the reusable DEA-like template (from left to right: 0 kV with mechanical bending, 3.4 kV with mechanical bending, and 5.5 kV without mechanical bending). (b) Demonstration of the fabrication of different patterns on the same film.
Furthermore, this technique can even be used to create multiple patterns on the same film, which is an advantage over traditional molding processes based on mechanically-induced wrinkles. This complex patterning is achieved by altering the design of the bottom electrode, as exemplified in Fig. 6b, in which only the left half of the film is supported by the gold bottom electrode underneath the Kapton tape. The sample is first mechanically bent (as in Fig. 5a) to obtain unidirectional wrinkles on the entirety of the film. Then, we apply 7 kV to create punctures on the left half of the surface as a pre-treatment and subsequently remove the voltage. When applying voltage again (4 kV), the portion with the gold bottom electrode will be affected by the field and show wrinkles around the punctures, while the other part will only maintain the small-scale, mechanically-induced wrinkles.
Conclusions
In summary, we demonstrate a simple method for fabricating fault-tolerant electrically-responsive surfaces based on commercially-available materials and standard metal evaporation technology. The DEA-like system can produce different surface topographies upon application of voltage and remains functional due to self-insulation even after multiple high voltage breakdown punctures. Targeted breakdown punctures can be used for amplification of local electric fields for actuation at lower working voltages. We find that the critical wrinkling field increases with decreasing thickness of the elastic layer, in quantitative agreement with the out-of-plane wrinkling model, with potential to assist in different device designs. Optical applications would benefit from using a high transmittance material as the rigid film to achieve a highly transparent off-state. Lowering the Young’s modulus of the elastic layer, decreasing the thickness of the rigid layer, and increasing the dielectric constant of both, would decrease the working voltage and enhance the performance of the demonstrated (changeable transparency films, dynamic light-grating filter, and a template/factory for static surface patterns) and other applications this versatile, low-cost technology.
Methods
Experimental Setup
A schematic of our DEA-like system is depicted in Fig. 1a. The bottom electrode was formed by sputter-coating (K550 sputter coater, Emitech, Inc.) a 16 nm thick layer of gold onto a glass slide. As the rigid layer for the device, a polyimide film (50 µm thick Kapton tape, DuPont, Young’s modulus 2.5 GPa) was adhered to the bottom electrode. The elastic dielectric layer of the devices was formed using PDMS (Sylgard 184, Dow Corning): a solution with 3 wt.% crosslinker in the matrix base was diluted in toluene (90%) and stirred for 5 hours to achieve homogeneity. The solution was then spin-coated (Laurell WS-650MZ-23NPP) on the Kapton film at speeds ranging from 500 to 5000 rpm to achieve layers of different thicknesses. The samples were then cured in an oven at 45 °C overnight to form solidified elastomer films with a Young’s modulus of approximately 83 kPa. A thin gold film (16 nm, Young’s modulus 36 GPa) was subsequently sputter-coated on the top of the PDMS to create the top electrode. For mechanically bent films, the bottom electrode was made flexible by coating the gold layer on an overhead projector transparency film (Nobo ACCO Brands). The films shown in Figs 5 and 6b are bent to a curvature of −0.38 cm−1. Electrically-induced deformation of the film surfaces was achieved using a HV Power Supply (Gamma High Voltage Research). For micropattern fabrication, an epoxy resin base (reaction product: bisphenol-a-(epichlorhydrin), epoxy resin with average molecular weight >700, butyl 2,3-epoxypropyl ether) and hardener (polyamide resin) were used and cured at room temperature for 30 minutes.
Measurement
The final film thicknesses were measured by a Dektak 6 M Stylus Profiler. An Olympus Reflected Fluorescence system BX51 with a charge-coupled device (CCD) (INFINITY3-3URM from Lumenera Corporation) was used to observe the surface patterns by optical microscope. 3D mapping profiles and surface roughness were measured using a Zygo Newview Interferometric Profilometer. The surface roughness, Rrms, is defined as the root mean square of the height differences between each point on the surface and the mean height. For measurements of Young’s modulus, mechanical testing was done with a Hounsfield Low Load Electric Screw Machine (5 kN) and a MTS Nanoindenter XP.
Data Availability Statement
All the details and parameters of the experiments are described in Methods Section and Supplementary Information.
References
Chung, J. Y., Youngblood, J. P. & Stafford, C. M. Anisotropic wetting on tunable micro-wrinkled surfaces. Soft Matter 3, 1163 (2007).
Chan, E. P., Smith, E. J., Hayward, R. C. & Crosby, A. J. Surface wrinkles for smart adhesion. Adv. Mater. 20, 711–716 (2008).
Shivapooja, P. et al. Bioinspired surfaces with dynamic topography for active control of biofouling. Adv. Mater. 25, 1430–1434 (2013).
Yu, C., O’Brien, K., Zhang, Y. H., Yu, H. & Jiang, H. Tunable optical gratings based on buckled nanoscale thin films on transparent elastomeric substrates. Appl. Phys. Lett. 96, 041111 (2010).
Qian, Y. et al. Stretchable Organic Semiconductor Devices. Adv. Mater. 28, 9243–9265 (2016).
Qian, Y. et al. Thin-film organic semiconductor devices: from flexibility to ultraflexibility. Sci. China Mater. 59, 589–608 (2016).
Vella, D., Bico, J., Boudaoud, A., Roman, B. & Reis, P. M. The macroscopic delamination of thin films from elastic substrates. Proc. Natl. Acad. Sci. USA 106, 10901–10906 (2009).
Wang, Q. & Zhao, X. A three-dimensional phase diagram of growth-induced surface instabilities. Sci. Rep. 5, 8887 (2015).
Stafford, C. M. et al. A buckling-based metrology for measuring the elastic moduli of polymeric thin films. Nat Mater 3, 545–550 (2004).
Efimenko, K. et al. Nested self-similar wrinkling patterns in skins. Nat. Mater. 4, 293–272 (2005).
Brau, F. et al. Multiple-length-scale elastic instability mimics parametric resonance of nonlinear oscillators. Nat. Phys. 7, 56–60 (2010).
Cai, S., Chen, D., Suo, Z. & Hayward, R. C. Creasing instability of elastomer films. Soft Matter 8, 1301–1304 (2012).
Chen, D., Cai, S., Suo, Z. & Hayward, R. C. Surface energy as a barrier to creasing of elastomer films: An elastic analogy to classical nucleation. Phys. Rev. Lett. 109, 038001 (2012).
Khang, D.-Y., Jiang, H., Huang, Y. & Rogers, J. A. A Stretchable Form of Single-Crystal. Science (80-.). 311, 208–212 (2006).
Yang, S., Khare, K. & Lin, P. C. Harnessing surface wrinkle patterns in soft matter. Adv. Funct. Mater. 20, 2550–2564 (2010).
Sun, Y., Choi, W. M., Jiang, H., Huang, Y. Y. & Rogers, J. A. Controlled buckling of semiconductor nanoribbons for stretchable electronics. Nat. Nanotechnol. 1, 201–207 (2006).
Jiang, H. et al. Finite width effect of thin-films buckling on compliant substrate: Experimental and theoretical studies. J. Mech. Phys. Solids 56, 2585–2598 (2008).
Bowden, N., Brittain, S., Evans, A. G., Hutchinson, J. W. & Whitesides, G. M. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 393, 146–149 (1998).
Chen, X. & Hutchinson, J. W. Herringbone Buckling Patterns of Compressed Thin Films on Compliant Substrates. J. Appl. Mech. 71, 597–603 (2004).
Mei, H., Huang, R., Chung, J. Y., Stafford, C. M. & Yu, H. H. Buckling modes of elastic thin films on elastic substrates. Appl. Phys. Lett. 90, 151902 (2007).
Cai, S., Breid, D., Crosby, A. J., Suo, Z. & Hutchinson, J. W. Periodic patterns and energy states of buckled films on compliant substrates. J. Mech. Phys. Solids 59, 1094–1114 (2011).
Gioia, G. & Ortiz, M. Delamination of compressed thin films. Adv. Appl. Mech. 33, 119–192 (1997).
Moon, M.-W. et al. Wrinkled hard skins on polymers created by focused ion beam. Proc. Natl. Acad. Sci. USA 104, 1130–1133 (2007).
Kim, P., Abkarian, M. & Stone, H. A. Hierarchical folding of elastic membranes under biaxial compressive stress. Nat. Mater. 10, 952–957 (2011).
Jin, L., Cai, S. & Suo, Z. Creases in soft tissues generated by growth. EPL (Europhysics Lett. 95, 64002 (2011).
Guvendiren, M. & Burdick, J. a. & Yang, S. Solvent induced transition from wrinkles to creases in thin film gels with depth-wise crosslinking gradients. Soft Matter 6, 5795–5801 (2010).
Li, B., Jia, F., Cao, Y. P., Feng, X. Q. & Gao, H. Surface wrinkling patterns on a core-shell soft sphere. Phys. Rev. Lett. 106, 234301 (2011).
Kang, M. K. & Huang, R. Swell-induced surface instability of confined hydrogel layers on substrates. J. Mech. Phys. Solids 58, 1582–1598 (2010).
Tanaka, T. et al. Mechanical instability of gels at the phase transition. Nat. 325, 796–798 (1987).
Shian, S. & Clarke, D. R. Electrically tunable window device. Opt. Lett. 41, 1289–1292 (2016).
Van Den Ende, D., Kamminga, J. D., Boersma, A., Andritsch, T. & Steeneken, P. G. Voltage-controlled surface wrinkling of elastomeric coatings. Adv. Mater. 25, 3438–3442 (2013).
Wang, Q., Tahir, M., Zhang, L. & Zhao, X. Electro-creasing instability in deformed polymers: experiment and theory. Soft Matter 7, 6583–6589 (2011).
Morales, D., Palleau, E., Dickey, M. D. & Velev, O. D. Electro-actuated hydrogel walkers with dual responsive legs. Soft Matter 10, 1337–1348 (2014).
Zhou, J., Hong, W., Zhao, X., Zhang, Z. & Suo, Z. Propagation of instability in dielectric elastomers. Int. J. Solids Struct. 45, 3739–3750 (2008).
Zhao, X. & Suo, Z. Method to analyze electromechanical stability of dielectric elastomers. Appl. Phys. Lett. 91, 061921 (2007).
Liu, Y., Liu, L., Zhang, Z., Shi, L. & Leng, J. Comment on ‘method to analyze electromechanical stability of dielectric elastomers’. [Appl. Phys. Lett. 91, 061921 (2007)]. Appl. Phys. Lett. 93, 106101 (2008).
Mao, G., Huang, X., Diab, M., Liu, J. & Qu, S. Controlling wrinkles on the surface of a dielectric elastomer balloon. Extrem. Mech. Lett. 9, 139–146 (2016).
Mao, G. et al. Nucleation and propagation of voltage-driven wrinkles in an inflated dielectric elastomer balloon. Soft Matter 11, 6569–6575 (2015).
Kollosche, M., Kofod, G., Suo, Z. & Zhu, J. Temporal evolution and instability in a viscoelastic dielectric elastomer. J. Mech. Phys. Solids 76, 47–64 (2015).
Brochu, P. & Pei, Q. Advances in dielectric elastomers for actuators and artificial muscles. Macromol. Rapid Commun. 31, 10–36 (2010).
Madden, J. D. W. et al. Artificial muscle technology:Physical principles and Naval prospects. IEEE J. Ocean. Eng 29, 706–728 (2004).
Mirfakhrai, T., Madden, J. D. W. & Baughman, R. H. Polymer artificial muscles. Mater. Today 10, 30–38 (2007).
Carpi, F. et al. Standards for dielectric elastomer transducers. Smart Mater. Struct. 24, 105025 (2015).
Liu, Y., Liu, L., Zhang, Z. & Leng, J. Dielectric elastomer film actuators: characterization, experiment and analysis. Smart Mater. Struct. 18, 095024 (2009).
Koh, S. J. A. et al. Mechanisms of large actuation strain in dielectric elastomers. J. Polym. Sci. Part B Polym. Phys. 49, 504–515 (2011).
Wang, Q. & Zhao, X. Creasing-wrinkling transition in elastomer films under electric fields. Phys. Rev. E 88, 042403 (2013).
Shenoy, V. & Sharma, A. Pattern formation in a thin solid film with interactions. Phys. Rev. Lett. 86, 119–122 (2001).
Lu, T., Keplinger, C., Arnold, N., Bauer, S. & Suo, Z. Charge localization instability in a highly deformable dielectric elastomer. Appl. Phys. Lett. 104, 022905 (2014).
Huang, R. Electrically induced surface instability of a conductive thin film on a dielectric substrate. Appl. Phys. Lett. 87, 151911 (2005).
Huang, Z. Y., Hong, W. & Suo, Z. Nonlinear analyses of wrinkles in a film bonded to a compliant substrate. J. Mech. Phys. Solids 53, 2101–2118 (2005).
Gatti, D. et al. The dielectric breakdown limit of silicone dielectric elastomer actuators. Appl. Phys. Lett. 104, 052905 (2014).
Plante, J.-S. & Dubowsky, S. Large-scale failure modes of dielectric elastomer actuators. Int. J. Solids Struct. 43, 7727–7751 (2006).
Gisby, T. A., Xie, S. Q., Calius, E. P. & Anderson, I. A. Leakage current as a predictor of failure in dielectric elastomer actuators. Proc. SPIE 7642, 764213 (2010).
Yuan, W. et al. Fault-tolerant dielectric elastomer actuators using single-walled carbon nanotube electrodes. Adv. Mater. 20, 621–625 (2008).
Catalan-Izquierdo, S., Bueno-Barrachina, J.-M., Cañas-Peñuelas, C.-S. & Cavallé-Sesé, F. Capacitance evaluation on parallel-plate capacitors by means of finite element analysis. Renew. Energies Power Qual. J. 1, 613–616 (2009).
Bansevicius, R. & Virbalis, J. A. Distribution of electric field in the round hole of plane capacitor. J. Electrostat. 64, 226–233 (2006).
Ohzono, T., Suzuki, K., Yamaguchi, T. & Fukuda, N. Tunable Optical Diffuser Based on Deformable Wrinkles. Adv. Opt. Mater. 1, 374–380 (2013).
Scherz, P. & Monk, S. Practical Electronics for Inventors Third Edition. (2013).
Kobayashi, T. & Smoukov, S. K. Pulsed actuation avoids failure in dielectric elastomer artificial muscles. Int. J. Smart Nano Mater. 5, 217–226 (2014).
Singh, S. Diffraction gratings: aberrations and applications. Opt. Laser Technol. 31, 195–218 (1999).
Park, J. et al. Controlled wavelength reduction in surface wrinkling of poly (dimethylsiloxane). Soft Matter 6, 677–684 (2010).
Acknowledgements
This work was funded by the European Research Council (ERC) grant to Stoyan Smoukov, EMATTER (# 280078). The authors are especially grateful to Dr. Michael Sutcliffe for training and suggestions in optical profiler measurement, to Giovanni Orlando in Department of Materials Science and Metallurgy in University of Cambridge for setting up high voltage operating stage on microscope, and to Kara Fong and Dr. Alexander Khaldi in University of Cambridge for proofreading and generous suggestions. T.W. and F.Z. acknowledge scholarship funding from the China Scholarship Council (CSC). T.W. also thanks the Engineering and Physical Sciences Research Council (EPSRC) Center for Doctoral Training in Sensor Technologies and Applications (grant number EP/L015889/1) for support.
Author information
Authors and Affiliations
Contributions
I.-T.L. and S.K.S. conceived the experiments, and I.-T.L. conducted the experiments with help from T.W. and F.Z. The data was analyzed by I.-T.L. and all authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lin, IT., Wang, T., Zhang, F. et al. Fault-Tolerant Electro-Responsive Surfaces for Dynamic Micropattern Molds and Tunable Optics. Sci Rep 7, 12481 (2017). https://doi.org/10.1038/s41598-017-12899-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-12899-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.