Abstract
The water quality index (WQI) has been used to identify threats to water quality and to support better water resource management. This study combines a machine learning algorithm, WQI, and remote sensing spectral indices (difference index, DI; ratio index, RI; and normalized difference index, NDI) through fractional derivatives methods and in turn establishes a model for estimating and assessing the WQI. The results show that the calculated WQI values range between 56.61 and 2,886.51. We also explore the relationship between reflectance data and the WQI. The number of bands with correlation coefficients passing a significance test at 0.01 first increases and then decreases with a peak appearing after 1.6 orders. WQI and DI as well as RI and NDI correlation coefficients between optimal band combinations of the peak also appear after 1.6 orders with R2 values of 0.92, 0.58 and 0.92. Finally, 22 WQI estimation models were established by POS-SVR to compare the predictive effects of these models. The models based on a spectral index of 1.6 were found to perform much better than the others, with an R2 of 0.92, an RMSE of 58.4, and an RPD of 2.81 and a slope of curve fitting of 0.97.
Similar content being viewed by others
Introduction
Water shortage problems in semi-arid areas have become more and more serious in recent years1,2,3,4. Recent studies show that a lack of water resources could affect nearly 5.5 billion people in 10 years5. Severe water shortages and large volumes of sewage render river and lake water pollution issues serious in arid areas6,7. The water quality of rivers and lakes is becoming central to human and economic development. Therefore, the evaluation and estimation of water quality levels is essential for societal and economic development8.
With advances in space information science and with an increasing use of computer applications in recent years, remote sensing has become a useful tool of surface parameter monitoring9,10. It allows one to monitor large scale water bodies that suffer from qualitative problems more effectively. Via remote sense, an optical reflectance sensor was used in this study. Optical sensor systems use sunlight as a source of light and are equipped with light-emitting components that provide radiation in specific band regions11,12. The optical sensors generate hyperspectral information on water quality levels in the visible and near-infrared ranges. Some studies have evaluated relationships between hyperspectral reflectance wavebands and water quality parameters.
Studies on surface water spectral features and modified model methods have shown that it is possible to perform water quality parameter monitoring by applying remote sensing technologies to more water quality variables with higher precision. Single water quality parameters such as chlorophyll-a, total suspended solids, turbidity levels, transparency levels, levels of dissolved organic matter, chemical oxygen demand, biological oxygen demand, etc., have been widely estimated through remote sensing technology monitoring10,13,14,15,16,17,18,19. Although estimated models of water quality parameters are relatively accurate, they generate uncertain results because water environments are complex and changeable. Therefore, a water body spectrum is shown for the entire water environment and is not a single water quality parameter. Many scholars have developed estimation models of a single water quality parameter based on water body spectrum data10,17,18. Thus, estimation models of a single water parameter introduce a certain level of uncertainty. From such analyses, a water quality index that reflects the entire water environment should be developed to evaluate the entire water environment.
Several methods for evaluating the water quality levels of rivers and lakes have been introduced20,21. Therefore, a good water quality assessment method should not only accurately reflect spatial variations in water quality, but should also conveniently to quickly monitor water quality levels. The water quality index (WQI)22,23,24,25,26 is used for the water quality assessment of drinking water source by the Ministry of Water Resources, Monitoring and Evaluation Center of Water Environment. The WQI was initially proposed by Horton27 and Brown et al.28. Since then, various methods for the calculation of the water quality index (WQI) have been designed by several authors29,30,31. WQI is a mathematical instrument used to transform large quantities of water characterization data into a single value that represents the water quality level and that reflects overall water quality levels32. However, while WQI methods can assess the water quality of a single sample, they are not easily able to identify spatial or temporal variations in water quality, which are vital to the comprehensive assessment and management of surface water quality. These difficulties associated with successive and integrated sampling have become a significant obstacle to the monitoring and management of water quality, and remote sensing technologies make up for shortcomings of spatial and temporal variations. The establishment of a water quality index that can be widely used for environmental management and that is easy to calculate, to master and to use to meet remote sensing monitoring requirements is explored in this study.
The main objectives of this study are (i) to create a water quality index (WQI) for surface water quality evaluation and classification in arid areas and to create a WQI map via GIS (ii) to extract sensitive wave bands and build a spectral index (RI, DI, NDI) that is significantly related to the water quality index, (iii) to establish an estimation model of the water quality index (WQI) based on the spectral index (RI, DI, NDI), to develop sensitive wave bands and a Support Vector Regression Model (SVR) for dry areas, and (iv) to estimate the accuracy of the model relative to WQI values. We not only assess water quality levels using the WQI for a semi-arid area, but we also develop a new algorithm that can estimate the WQI via remote sensing techniques.
Results and Analysis
Statistical analysis of the water quality index
A summary of water quality observations for Ebinur Lake Watershed surface water of the Boertala River, the Jing River, the Akeqisu-Kuitun River (A-KR) and artificial reservoirs (RES) for October of 2016 is presented in Table 1. At different water quality levels, (pH) levels varied considerably from 7.62–8.46 spanning one order of magnitude with a mean value of 7.97 and Coefficient of Variation of 12.29%. Concentrations of TDS also experienced varied considerably from 81.4 mg/L–9470 mg/L with a mean value of 728.88 mg/L and with a Coefficient of Variation of 19.2%. TDS values of the Ebinur Lake Watershed were found to be lower and strongly variable and most likely because upstream reservoirs of the Bolatala and Jing Rivers serve as a settling watershed. Ca levels of the four rivers were found to be similar and to range from low to moderate (42.8 mg/L–1082.16 mg/L) with an average value of 161.1 mg/L and a Coefficient of Variation of 144.02% and characterized by strong variations in the Ebinur Lake Watershed. (TN), (BOD5) and DO values were found to be similar in the Ebinur Lake Watershed with average values of 1.54 mg/L, 2.26 mg/L, and 29.12 mg/L respectively with a low Coefficient of Variation of (<100%) and less variation. Concentrations of NH3 +-N were also highly variable at 0.01 mg/L–9.21 mg/ with a mean value of 0.62 mg/L and a Coefficient of Variation of 316.79%. (COD) and TP values exhibit similar trends with Coefficient of Variation values of between 100% and 200%. For metal indicators, concentrations of (Iron), (Mg), (Na), (Copper), (Zinc) and (Volatile phenol) are similar with Coefficients of Variation varying considerably between 100% and 200%. In addition, the Coefficient of Variation for Mg was measured at 318.56. (HCO3 −) and varies considerably from 89.94–24324.13 spanning one order of magnitude with a mean value of 1,419.31 mg/L and with a Coefficient of Variation of 358.74% that is highly variable. Concentrations of SO4 2− also varied considerably from 4.8 mg/L–8424 mg/L with a mean value of 961.88 mg/L and a Coefficient of Variation of 172.28%. SO4 2− levels in the Ebinur Lake Watershed were found to be lower and strongly variable and most likely due to the presence of the Boertala and Jing River reservoirs upstream, which serve as a settling watershed. (PO4 3−) was found to vary considerably from 0–1.7, spanning one order of magnitude with a mean value of 0.2237 mg/L and highly variable Coefficient of Variation of 153.57%. (Cr) was found to vary considerably from 0.01–0.16, thus spanning one order of magnitude with a mean value of 0.0283 mg/L and a highly variable Coefficient of Variation of 102.47%. In short, the water quality index changes considerably in this watershed while pH, DO and TDS values change less. Water quality levels thus vary considerably in the watershed.
Assessment of water quality based on the WQI
In this study, the quality of the Ebinur Lake Watershed surface water was evaluated. To assess the water quality of the river, the WQI method was used. pH, HCO3 −, TP, TN, BOD, NH3 +-N, Iron, Copper, Zinc, Volatile phenol, DO, TDS, Cl−, SO4 2−, Na, Ca, Mg, COD, PO4 3− and Cr values were taken into account for the calculation of WQI values for each sampling location in the Ebinur Lake Watershed in October of 2016. Analysis results for all 48 sampling points were used for quality evaluations. Furthermore, World Health Organization33 limits were used for the calculations. Distribution maps of the water quality parameters (pH, HCO3 −, TP, TN, BOD, NH3 +-N, Iron, Copper, Zinc, Volatile phenol, DO, TDS, Cl−, SO4 2−, Na, Ca, Mg, COD, PO4 3− and Cr) and a WQI map for the river were prepared using Geographic Information System (GIS) techniques and are presented in Fig. 4 and Table 2.
Spatially, water quality index (WQI) levels are high for most areas of the Boertala River downstream from Ebinur Lake and (Fig. 1) and occupy the V category. This water is unsuitable for drinking. The highest value of 438 is observed for the Kuitun River. As this water body is located in the town of Tuotuo, the effects of human factors are severe, and water quality levels in this river are poor. Therefore, as water quality levels worsen, WQI levels increase. The best levels of water quality for the Ebinur Lake Watershed are found in the upper reaches of the Bortala River. Its WQI value is less than 100 (I grade water quality) and is suitable for drinking. Poor water quality levels are observed for midstream reaches of Boertala River of Wenquan County where the effects of human factors are severe and where water quality levels have resulted in mutations and in the development of water quality index anomalies. From an ecological perspective, the ecological environment of Ebinur Lake is the worst in the watershed. Rivers originate from mountains surrounding the watershed where the ecological environment is superior to that of Ebinur Lake.
Spatial characteristics of the WQI for the Ebinur Lake Watershed (Map by ArcGIS10.2.2 (http://www.esri.com/software/arcgis)).
Hyperspectral characteristics of surface water
Figure 2 (a) shows how on the basis of the river areas described above, 48 water samples were classified into 5 categories and spectral plots of each category were averaged as a representative spectral curve of this water quality level (Fig. 2a). Five spectral plots of similar shapes were identified with two pronounced absorption features located at approximately 700 and 950 nm. Of the five categories, sample site 31 exhibited lowest reflectance and a location slightly downstream exhibited the highest reflectance. Sample site 21 presented the highest reflectance value. This sample site is located in the downstream area of the river (into the lake). For each class, an average spectrum was calculated (Fig. 2a), and the plots show reflectance curves of two deep absorption regions at 750 and 980 nm and several weak absorption regions at approximately 452 nm, 703 nm, and 850 nm. It was easy to identify differences in water quality at roughly 700–720 nm and 1,070 nm of the peak. Average and standard values are shown in Fig. 2(b) with no outliers and a normal distribution.
Spectral curves of water in different rivers (Map by Origin 9.1 (http://www.originlab.com/software)).
Correlations between the water quality index and spectra
Sensitive wave band selection is central to constructing a water quality index (WQI) estimation model, and correlation coefficients for the water quality index (WQI) and spectral reflectance (single wave bands) are usually used to identify water quality index bands (sensitive wave bands). All correlation coefficients between the water quality index (WQI) and raw reflectance data treated based on fractional derivatives (0 order, 0.2 order, 0.4 order, 0.6 order, 0.8 order, 1.0 order, 1.2 order, 1.4 order, 1.6 order, 1.8 order, and 2.0 order) were tested with a significance level of 0.01 (|r| = 0.24 or above). Spectral curves of correlation coefficients of the raw reflectance and of raw reflectance data treated by fractional derivatives (0 order, 0.2 order, 0.4 order, 0.6 order, 0.8 order, 1.0 order, 1.2 order, 1.4 order, 1.6 order, 1.8 order, and 2.0 order) are plotted in Fig. 3. For the raw reflectance data, 45 bands passed the significance test at 0.01, but as the order of the derivative increases, correlation coefficients increase beyond the 0.01 level in some wavelength ranges. However, band values do not pass the significance test at 0.01. In addition, as the order declines from 1.0 to 2.0, band values increasingly pass the significance test at the 0.01. As correlation coefficients increase, when the order reaches 1.6, correlation coefficients reach 0.68 at 1,368 nm. On the whole, the curves fluctuate greatly, and thus more information cannot be derived from Fig. 3.
Correlation coefficients between the WQI and raw reflectance data treated by fractional derivatives (Map by Origin 9.1 (http://www.originlab.com/software)).
From Fig. 3 it is not clear how many bands of raw reflectance data treated by fractional derivatives passed the significance test at 0.01, and thus raw reflectance data and raw reflectance data treated by fractional derivatives are measured and corresponding trend lines and relationships between raw reflectance data and raw reflectance data treated by fractional derivatives and the water quality index (WQI) are shown in Fig. 4. For these 11 mathematical forms of reflectance, different numbers of bands passed the significance test. With an increase in derivative order, values first decreased and then increased, and all reached a minimum value at the 1.0 fractional orders and a maximum value at the 1.6 fractional orders. However, band numbers do not pass the significance test at 0.01. In addition, as the order declines from 1.0 to 2.0, band numbers increasingly pass significance testing at 0.01. As correlation coefficients increase, once the order reaches 1.6, the correlation coefficient is 0.68.
The number of bands passing the significance test and trend lines (Map by Origin 9.1 (http://www.originlab.com/software)).
Relationships between the water quality index (WQI) and the spectral indices
Contour maps of r values between the water quality index (WQI) and two-band spectral indices (DI, NDI and RI) are shown in Fig. 5. A strong correlation between the DI, NDI and RI and the water quality index (WQI) is largely found in the visible and near-infrared ranges (Fig. 5). While the performance of the three spectral indices as predictors of the water quality index (WQI) appears to vary by wavelength, constant forms are revealed. Wavelength combinations in the 350–1100 nm region for R2 spectra (Fig. 5) show a significant correlation between the RI and the water quality index (WQI).
Contour maps of correlation coefficients (r) between WQI values and normalized difference, ratio, and difference spectral indices based on raw reflectance data treated by fractional derivatives using two reflectance spectra at i and j nm (n = 48). (Map by MATLAB 2014a (https://www.mathworks.com/software)).
Wave bands of combinations (DI, RI and NDI) for the reflectivity of the raw spectrum curve and raw reflectance data treated by fractional derivatives and corresponding strong correlations with the water quality index (WQI) were mainly found to be concentrated in two zones (Fig. 5). The ratio index (RI) sensitivity region and normalization index sensitivity region were found to be nearly consistent. However, index sensitivity zones were found to differ. For the RI, good wavelength combinations were observed with R2 values of 0.40 and 0.92, respectively (Table 3). The correlation r is minimal in raw reflectivity wave bands of the combinations (R883/R934), and the maximum correlation coefficient value is found in raw reflectance data treated by 1.6 order derivatives located at R600 − R900. For the different index (DI), good wavelength combinations were observed with R2 values of 0.497 and 0.585, respectively (Table 3). The lowest correlation r is found in raw reflectivity wave bands of the combinations (R583 − R844), and the maximum correlation coefficient is found in raw reflectance data treated by 1.6 order derivatives for R500 to R900. For the normalized index (NDI), good wavelength combinations were found with R2 values of 0.764 and 0.914, respectively (Table 3). The weakest correlation r is found in raw reflectance data treated by 0.2 order derivatives of combinations ((R520 − R760)/(R520 + R760)), and the largest correlation coefficient is found in raw reflectance data treated by 1.6 order derivatives in the R452 and R703 zones. Raw observations show several weak absorption regions at close to 452 and 703 nm, and R452 and R703 zones of NDI wave bands of the combinations correlation coefficient are the highest. Therefore, the spectrum absorption valley is central to the study of water quality sensitivity levels. In addition, a reflectivity value of 964 nm is found in the most important area of the sensitive band. This analysis reveals the presence of a strong correlation between DI, RI, NDI and the different water quality indices. Strong correlations with water quality are mainly found as r values (Table 3).
Particle swarm optimization (PSO)-support vector regression model
Establishing a WQI estimation model based on a support vector regression model
MATLAB 2014a is applied to design a particle swarm optimization (PSO) support vector regression model. Hyperspectral parameters of sensitive wave bands and the spectral index and water quality index (WQI) of the Ebinur Lake wetlands are used to develop a particle swarm optimization - support vector regression model (POS-SVR). Data were randomly chosen and segregated into training and testing components at a 7:3 ration. After training the model (POS-SVR), it was tested using 30% of the data that differed from the training set. This was conducted to assess the generalization accuracy of the trained model and to ascertain its capacity to use the SVR learned pattern to predict target values for previously unseen datasets. This method is referred to as model validation and the performance assessment method used is only as good as the criteria set for this reason. Each input factor applies a different measurement unit. To eliminate dimension effects of these variables and to realize equivalent expression effects for each input factor, the non-dimensional method is applied for the data analysis to standardize various input factors and to compress the scope of change for each input factor to −1 to 1. The premnmx function is applied in MATLAB 2014a to normalize the input factors. When the nerve cell is satisfactorily accurate, the postmnmx function can be applied to recover the original magnitude of the normalized data. The different input parameters of the POS-SVR model for parameter comparison is as described in Table 4.
Verifying the estimation model of the water quality index
After modeling different water quality indices (WQIs), the accuracy of obtained models was examined for an independent dataset consisting of 11 samples. The corresponding validation results are shown in Figs 6, 7 and statistical results are summarized in Table 5. Scatter diagrams are presented for prediction and real values of the inversion model in Figs 6, 7. The coefficient of determination R2 between predicted and measured values for monitoring model accuracy is higher, the measured and predicted values are basically linear, and the RMSE is low while the slope of the fitting curve is closer to 1. Therefore, the related POS-SVR model exhibits a strong non-linear fitting capacity, denoting excellent effects of the hyperspectral spectral index on the monitoring water quality index (WQI). Figures 6, 7 and Table 5 show a scatter diagram for the measured real and predicted values.
Correlations between the measured verification values and the predicted values based on a sensitivity bandpass significance test conducted at the 0.01 level (Map by EXCEL (https://www.microsoft.com/software)).
Correlations between the measured verification values and predicted values based on the spectral index (RI, DI, and NDI) (Map by EXCEL (https://www.microsoft.com/software)).
Figures 6, 7 and Table 5 show that the predicted water quality index (WQI) value is very consistent with the measured water quality index value. The 15 water quality index estimation models were validated by the 22 water samples. In total, 22 models present acceptable results at RPD > 1.4 and with a slope of close to 1. The sensitive wave band estimation model is more accurate for the 1.6 order derivates. R2 is valued at 0.92; RMSE is valued at 58.40, RPD is valued at 2.71, and the slope is valued at 0.85. The spectral index estimation model is more accurate for the 1.6 derivates. R2 is valued at 0.92; RMSE is valued at 61.15, RPD is valued at 2.81, and the slope is valued at 0.97.
Compare the accuracy of the machine learning algorithm and geographically weighted regression (GWR)
R883/R934, R583 − R844, and (R520 − R760)/(R520 + R760) is the independent variable, the GWR model was used for regression analysis of WQI, AIC value is 402.69, R2 is 0.86, residual sum of squares value is 879.91. Test the model with a validation sample, R2 is 0.75, RMSE is 80.33, and RPD is 1.90. Scatter diagrams are presented for prediction and real values of the inversion model Fig. 8.
Scatter plot of measured and predicted WQI in GWR models (Map by EXCEL (https://www.microsoft.com/software)).
Compare the accuracy of the machine learning algorithm and geographically weighted regression (GWR), the spectral index estimation model is more accurate for the 1.6 derivates based on machine learning algorithm. R2 is valued at 0.92; RMSE is valued at 61.15, RPD is valued at 2.81, and the slope is valued at 0.97. Therefore, the water quality index (WQI) monitoring model based on machine learning algorithm is highly stable and presents a high level of predictive capacity. The Particle swarm optimization - support vector regression model can thus be used to generate water quality index estimations for the semi-arid central Asian zone of Xinjiang, China.
Discussion
Assessment of water quality and of the spatial variability of the water quality index (WQI).
In this study, the water quality of Ebinur Lake watershed surface water was evaluated. Rivers of the Ebinur Lake Watershed recharge Ebinur Lake. To evaluate the water quality levels of Ebinur Lake Watershed surface water, 48 sampling sites and 20 water quality parameters were selected for monitoring and analysis. Water quality parameters pH, HCO3 2−, TP, TN, BOD5, NH3 +-N, Iron, Copper, Zinc, Volatile phenol, DO, TDS, Cl−, SO4 2−, Na, Ca, Mg, COD, PO4 3− and Cr were used to calculate WQI values to evaluate river water quality levels. WQI values were found to range between 56.61 and 2886.52. The WQI classification shows that the Ebinur Lake Watershed presents varying levels of water quality. The downstream areas of the river present poor water quality levels, where the main pollutant sources include wastewater discharged from Wenquan County and the city of Bole, leather and marble factories downstream from the Boertala River Valley and agricultural activities in the oasis of the Ebinur Lake Watershed; the main pollutant sources include wastewater discharged from Jinghe County, the leather industry, saltwork and saline land downstream from the Jinghe River and agricultural and grazing activities in the oasis of the Ebinur Lake Watershed. The Kuitun-Akeqisu River is located in the southwestern area of the watershed. A large amount of salt is found on either side of the river, and water quality in the area is highly saline. Effects of water quality parameters on the WQI map were investigated. Consequently, environmental pollutants negatively affect all water surfaces of the Ebinur Lake Watershed. Therefore, necessary protection measures should be taken on the planned usage of river water.
Estimate water quality index (WQI) value based on hyperspectral remote sensing data
In this study, an estimated water quality index (WQI) value is established based on sensitive wave bands and a spectral index of hyperspectral data. Water quality levels are directly estimated and assessed via remote sensing techniques. Most previous studies18,34,35 have focused on single indices of water quality such as chlorophyll-a, TDS, and NTU. While single indices of water quality are monitored using remote sensing technologies, and while single water quality parameters of monitoring models are highly accurate, such results are uncertain. As water quality conditions are reflected by all water quality parameters, overall water quality conditions are monitored by remote sensing; spectral reflectance values reflect overall parameters. Therefore, single indices of water quality monitored using remote sensing technologies are uncertain. The water quality index (WQI) reflects overall water quality conditions. The evaluation and estimation of surface water quality based on the hyperspectral remote sensing is feasible. In this study the accuracy of the estimation model is improved through the use of new hyperspectral indices (DI, RI, and NDI) and via particle swarm optimization - support vector regression. Remote sensing techniques make it possible to develop a spatial and temporal understanding of surface water quality indices and to more effectively and efficiently monitor water surfaces. Such tools can also be used to estimate water quality distributions. Future studies must measure the applicability of satellite remote sensing data and of unmanned aerial vehicle (UAV) technologies for estimating WQI values. As the number of in situ samples continues to increase, a unique regression model that effectively measure the water quality parameters of different watersheds should be developed for arid regions.
Conclusions
The Ebinur Lake Watershed of the Xinjiang Autonomous Region, China, was used as a study area. We used optimal bands based on difference index, ratio index, and normalized difference index algorithms to assess the WQI using spectral eleven orders (interval 0.2) of fractional derivatives for remote sensing data, and we measured the performance of the proposed models using GA-SVR and the band difference algorithm. The results are as follows:
-
(1)
Water quality levels for drinking purposes were evaluated via the water quality index (WQI) method. The computed WQI values were found to range between 56.6133 and 2,886.5198. The prepared WQI map shows that the arid area generally presents low levels of water quality.
-
(2)
As the order increased, the number of bands with correlation coefficients passing a significance test at 0.01 first increased and then decreased with a peak appearing with the 1.6 order and with an R2 of 0.525. The WQI and derivative spectral data of DI, RI and NDI correlation coefficients among the optimal band combinations also show a peak with the 1.6 order and R2 values of 0.818, 0.8624 and 0.8297.
-
(3)
In total, 22 WQI estimation models were generated from a principal component single band and from RI, DI, and DNI values based on the 1.6 order derivative, the lowest RMSE, the highest R2 (0.92) and the RPD (2.59).
-
(4)
Comparisons of the predictive effects of the 22 water quality index estimation models calibrated by POS-SVR show that the model based on RI, DI, and NDI values of the 1.6 order is much better than the others while better predicting the water quality index of the study area (R2 (0.92), RMSE = 58.4, RPD (2.81) and a slope of curve fitting of 0.97).
This study not only estimates a water quality index using different techniques for the semi-arid area of central Asia but also develops a new algorithm that can be applied to this area and to other areas.
Materials and Methods
Study area
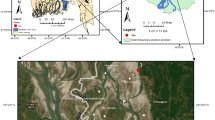
The Ebinur Lake Watershed (44°05′−45°08′N, 82°35′−83°16′E) (Fig. 9) is located on the northern slope of the Tien Shan Mountains southwest of the Junggar Basin. The watershed covers an area of 50,621 km2. It is surrounded by a mountainous region (24,317 km2; Alatau Mountains, Maliyi Mountains and Biezhentao Mountains) and by plains (Jinghe Oasis) (26,304 km2) to the north, west and south36. Artificial reservoirs (RES) are found southwest of the watershed. The area is characterized by a typical temperate arid continental climate with the mountain-oasis-desert system presenting typical temperate arid ecological characteristics. The study region is located inland (2,000 km from the Pacific and Indian Ocean and 3,000 km from the Arctic Ocean); moisture in the study area is derived from the Atlantic Ocean (7,000 km), but water vapor transport from maritime areas is limited36.
(a) Map of the study area with an inset map showing the location of the Xinjiang Autonomous Region within China; (b) satellite map of the study area; (c) Kuitui River, (e) Boertala River, (e) Jing River; photographs of the three selected sampling locations (photographed by Xiaoping Wang, Map by ArcGIS10.2.2 (http://www.esri.com/software/arcgis)).
The lake is a terminal lake fed by the Kuitun Mountains, Akeqisu River, Jing River, Tuotuo River, Sikeshu River, Boertala River, Akaer River and Daheyanzi River. Surface water levels of Ebinur Lake and the Tuotuo River are currently low and thus water ecological safety levels are threatened. Severe water shortage problems and the presence of large volumes of sewage have rendered river and lake water pollution levels high in the Ebinur Lake Watershed, a typical arid area of central Asia37.
Materials
Sample collection
Water samples were collected on October 5, 2016 from 48 locations within the Ebinur Lake Watershed (Fig. 9). Collected water quality samples were stored at low temperatures (under 2 °C) during transport before water quality measurements were carried out in a laboratory. Samples were transported in polyethylene plastic bottles previously rinsed with 10% HCI and cleaned with deionized water to minimize changes in water chemical characteristics. We used a handheld global positioning system (GPS) indicator to determine the central coordinates of each sample and used a digital camera to photograph the sampling area (see Fig. 9). Temperature and pH levels were recorded at the time of sampling along the shore. All other measurements were taken within a day following sample collection in the lab. Biochemical oxygen demand (BOD5), total nitrogen (TN), total phosphorus (TP), iron, copper, chemical oxygen demand (COD), zinc, volatile phenol (V.P.) ammonia nitrogen (NH3 +-N), Henderson-Hassebalch (HCO3 −), dissolved oxygen (DO), total dissolved solids (TDS), chloride (Cl−), sulphate ion (SO4 2− ), natriumion (Na), calcium (Ca), magnesium (Mg), phosphate (PO4 3−) and (Chromium VI) Cr concentrations collected over five days were determined according to corresponding methods as is shown in Table 6.
Hyperspectral data collection
The FieldSpec③3 ASD Spectroradiometer device is an optical sensor that uses detectors other than photographic film to measure the distribution of radiation in a particular wavelength region to measure the radiant energy level (radiance and irradiance). It was used to visualize spectral reflectance patterns of lake water corresponding to water content levels. Observation methods applied to water surfaces can be found in Supplementary Fig. S1.
To observe the water surfaces (Fig. S1), the spectral range of the spectrometer was set to 350–1050 nm with a 1 nm sampling interval. To avoid environment changes in illumination conditions, measurements between water the target, sky, and whiteboard were collected at each station. Sky conditions were also recorded at each station during spectral measurement.
All field spectrometer measurements were processed to remove sky and sun glare using a constant water body reflection coefficient38. Therefore, hyperspectral reflectance values, Rrs, were calculated using the following equation:
where L u is the total upwelling radiance, L s is the sky radiance, ρ is the water surface reflection efficiency level of 0.028, an d E d is the measured down welling solar irradiance.
Methods
Fractional Derivative Method
Fractional derivative methods have been widely used in certain fields because models described by the fractional derivative are more accurate and efficient than methods based on integer derivatives39,40. The most frequently used definitions are the following: Grunwald - Letnikov (G-L), Riemann - Liouville (R-L), and Caputo41. As it is less complex than the others, the G-L definition was employed in this study. Grunwald - Liouville is defined as follows42:
where a is the step length, where h is the order number, and where t and a are the respective upper and lower limits of the derivative. The Gamma formula is written as follows:
Based on our use of ASD spectrometer data, when the sampling interval is 1 nm, h = 1. f (X) is the fractional order derivative, which is defined as follows:
Therefore, (5) can be regarded as the numerical algorithm used to calculate the fractional derivative of hyperspectral data, and a zero order denotes that hyperspectral data are not treated by the derivative algorithm.
Determination of the best indices
In obtaining the most sensitive bands from water environment data, previous studies show that the combination of various bands can improve the sensitivity of hyperspectral reflectance data to water quality values43. Therefore, this method explores the relationships between water quality and the spectrum reflectance and then applies a 2D correlation diagram to study relationships between the difference index (DI), ratio index (RI), normalization index (NDI), and water quality index44. Optimal combination bands for the water quality index value are selected from 350 nm-1,050 nm and are entered into MATLAB 2014a (MathWorks, 2014).
Ri and Rj are random bands selected at 350 nm –1,050 nm while Ri and Rj denote the original reflectivity values of any two bands selected at 350 nm–1,050 nm.
Calculation of the Water Quality Index (WQI)
The Water Quality Index (WQI) is an extracted and estimated index that reflects the composite effects of all water quality parameters45. First, each water quality parameter was assigned a weight (Wi) from a scale of 1 (lowest effect on water quality parameters) to 5 (strongest effect on water quality parameters) based on perceived effects on primary health and according to its relative importance to the surface water environment46,47. PO4 3−, SO2 and Cr values were assigned the highest weight (8) due to their primary role in water quality assessments; a minimum weight of 1 was assigned to parameters Ca, Mg and Na due to their limited importance for water quality assessments48. The relative weight (Wi) is computed from the following equation:
where Wi is the relative weight, Wi is the weight of each parameter, and n is the number of parameters. Then, a quality rating (Qi) for each parameter is assigned by dividing its concentration in each water sample by its limit given in the WHO33 quality standards for surface water quality for the People’s Republic of China. This result is multiplied by 100;
where Qi is the quality rating, Ci is the concentration of each water quality parameter for each water sample, and Si is the surface water standard for each water quality parameter according to WHO guidelines33 (2008). To measure the WQI, the SIi value should be calculated first using the following equations;
where SIi is the water quality index of the ith parameter and Qi is the water quality level based on the ith water quality parameter49.
Estimate the WQI using a machine learning algorithm
Machine learning algorithms have become very popular in the era of big data. Machine learning is an artificial science. The field’s main objects of study are artifacts and specifically algorithms that improve performance with experience. The Support Vector Regression (SVR) Model is the main algorithm used for machine learning. We used the Support Vector Regression Model to estimate the WQI for the arid area50,51,52.
Given sample data (xi, yi), i = 1, 2, …, l where xi denotes the input vector,\({y}_{i}=f({x}_{i})\) is the estimated output measure. Estimated methods can be written as:\(f(x)=\omega \varphi (x)+b\) where \(\varphi (x)\) is a nonlinear model drawn from the input space to a high dimensional space; ω is a weight vector; and b is the offset.
The regression target identifies parameters \(\omega \) and b, which minimize the regression error function. The regression error function can be defined as:
where \(\Gamma (.)\) is a loss function and where Constant C > 0 is a fixed penalty parameter. The most commonly used loss function is the \(\varepsilon \)-insensitive loss function:
This shows that the loss is 0 when the difference between the measured and predicted value is less than a small positive number of \(\varepsilon \). To smooth the regression function, a minimum \(\omega \) must be found, and based on the fitting error, the regression function can be solved as a constrained optimization problem:
where \({\xi }_{i}\) i and \({{\xi }_{j}}^{\ast }\) are slack variables of upper and lower constraints on outputs of the system. The dual optimization problem illustrated in Equation (14) leads to a quadratic programming (QP) solution involving the Lagrange optimization method that can be expressed as:
where ai, ai* are Lagrange multipliers. After solving the optimization problem, denote the optimal solution as \(\overline{a}={(\overline{{a}_{1}},\overline{{a}_{2}},\overline{{a}_{3}},\mathrm{.....}\overline{{a}_{l}},\overline{{a}_{l}})}^{T},\overline{b}\) and obtain the regression result:
According to the Hilbert-Schmidt theorem, the inner product \(\phi ({x}_{i})\bullet \phi (x)\) can be replaced by a kernel function K(x i, x) that satisfies Mercer’s conditions53. Then, the outcome can be rewritten as:
the most commonly used kernel function is the radial basis kernel function (RBF) \(K(x,{x}_{i})=\exp (-{\Vert x-{x}_{i}\Vert }^{2}/{\sigma }^{2})\). Three parameters including the penalty coefficient C, the parameter of the kernel function \(\sigma \) and the width of the insensitive loss function \(\varepsilon \) constitute the model parameters and have a considerable impact on the performance of the SVR model. These parameters are often used by trial and error and are difficult to use to obtain the optimal value. The PSO can extract the optimal value fast in parallel with a complicated search space54, and we adopt it to select optimal parameters of the SVR model. The PSO uses particle populations corresponding to individuals in an evolutionary algorithm to explore the solution space of a problem55,56. A flowchart for the proposed PSO-SVR algorithm can be found in Supplementary Fig. S2.
Statistical analysis
Test data analyses were constructed using Origin8.0 (Origin Lab Corporation, America), and Matlab 2014a (Math Works Corporation, America) was applied to design the program environment. The significance of the statistical correlations was evaluated from P values and was compared to predicted and measured values from three indices, i.e., the estimate corresponds to high values of R2, to the root mean standard error (RMSE) and to the average standard error (SD)57 as follows:
In formulas (4), (5), (6), and (7), *(xi) is the predicted value; (yi) is the measured value; N is the total number of samples; \(\mathop{x}\limits^{-}\) is the average value of the sampled value, and \(\mathop{y}\limits^{-}\) is the average sample forecast value. SD is the standard deviation of the dataset, RMSE is the root mean square error, and when the RMSE is smaller the model’s predictive capacity is stable. As the R2 of the decision coefficient approaches a value of 1, the accuracy of the model improves. For a high RPD of the relative analysis error (RPD < 1.4), the model is not reliable. As 1.4 < RPD < 2, the model is moderately accurate, and RPD > 2, the model presents a high level of predictive ability.
Besides R 2, RMSE, SD and RPD, in order to acquire the accuracy of the estimate model of WQI based on machine learning algorithm, geographically weighted regression (GWR) (http://gwr4.software.informer. com/ download/) model is selected in this study. As highlighted in the literature58,59, the main contribution of the GWR technique is the ability to explore the spatial variation of explanatory variables in the model, where the coefficients of explanatory variables may vary significantly over geographical space. Compare and analyze the accuracy of the machine learning algorithm and geographically weighted regression (GWR) model. Verify the reliability of the machine learning algorithm model.
Water quality assessment standards
The calculated WQI values are classified into five categories as follows32. When the WQI value > 50, the water quality level is excellent and is suited for drinking, and values of 50 > and > 100 denote that water quality levels are good. Values of 100 > HIX > 200 denote poor water quality levels. When 200 > HIX > 300, water quality levels are very poor. A value of HIX < 300 denotes that water is unsuitable for drinking (see Table 7).
References
Coble, P. G., Green, S. A., Blough, N. V. & Gagosian, R. B. Characterization of dissolved organic matter in the Black Sea by fluorescence spectroscopy. Nature 348(6300), 432–435 (1990).
Gudasz, C. et al. Temperature-controlled organic carbon mineralization in lake sediments. Nature 466(7305), 478–81 (2010).
Finlay, J. C., Small, G. E. & Sterner, R. W. Human Influences on Nitrogen Removal in Lakes. Science 342, 247–250 (2013).
Li, J., Liu, Z., He, C., Yue, H. & Gou, S. Water shortages raised a legitimate concern over the sustainable development of the drylands of northern china: evidence from the water stress index. Science of the Total Environment. 590-591, 739–750 (2017).
Amitrano, D. et al. Sentinel-1 for Monitoring Reservoirs: A Performance Analysis. Remote Sens. 6, 10676–10693 (2014).
Lindberg, R. H., Östman, M., Olofsson, U., Grabic, R. & Fick, J. Occurrence and behaviour of 105 active pharmaceutical ingredients in sewage waters of a municipal sewer collection system. Water Res. 58(3), 221–229 (2014).
Zhou, H. B. et al. Simulation of water removal process and optimization of aeration strategy in sewage sludge composting. Bioresour. Technol. 171C, 452–460 (2014).
Li, R., Zou, Z. & An, Y. Water quality assessment in Qu River based on fuzzy water pollution index method. Journal of environmental sciences 50(12), 87–92 (2016).
Brando, V. et al. High-resolution satellite turbidity and sea surface temperature observations of river plume interactions during a significant flood event. Ocean Sci. 11, 909–920 (2015).
Gholizadeh, M. H., Melesse, A. M. & Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 16(8), 1298 (2016).
Kipp, S., Mistele, B. & Schmidhalter, U. The performance of active spectral reflectance sensors as influenced by measuring distance, device temperature and light intensity. Computers and Electronics in Agriculture 100, 24–33 (2014).
Song, K., Li, L., Li, S., Tedesco, L. & Hall, B. Hyperspectral remote sensing of total phosphorus (TP) in three central indiana water supply reservoirs. Water, Air, & Soil Pollution 223(4), 1481–1502 (2012).
Liu, N. T. et al. Development and validation of a machine learning algorithm and hybrid system to predict the need for life-saving interventions in trauma patients. Medical & Biological Engineering & Computing 52(2), 193–203 (2014).
Shareef, M. A., Khenchaf, A. & Toumi, A. Integration of passive and active microwave remote sensing to estimate water quality parameters. Radar Conference (1–4) (2016)
Xiao, R., Wang, G., Zhang, Q. & Zhang, Z. Multi-scale analysis of relationship between landscape pattern and urban river water quality in different seasons. Scientific Reports 6, 25250 (2016).
Fichot, C. G. et al. High-resolution remote sensing of water quality in the san francisco bay-delta estuary. Environmental Science & Technology 50(2), 573 (2016).
Kutser, T. et al. Remote sensing of black lakes and using 810 nm reflectance peak for retrieving water quality parameters of optically complex waters. Remote Sensing 8(6), 497 (2016).
Giardino, C. et al. Evaluation of multi-resolution satellite sensors for assessing water quality and bottom depth of lake garda. Sensors 14, 24116–24131 (2014).
Yang, Y., Gao, B., Hao, H., Zhou, H. & Lu, J. Nitrogen and phosphorus in sediments in china: a national-scale assessment and review. Science of the Total Environment 576, 840–849 (2017).
Giardino, C., Oggioni, A., Bresciani, M. & Yan, H. Remote sensing of suspended particulate matter in himalayan lakes. Mountain Research & Development 30(May 2010), 157–168 (2017).
Jena, V., Dixit, S. & Gupta, S. Assessment of water quality index of industrial area surface water samples. Int. J. Chem. Technol. 5(1), 278–283 (2013).
Misaghi, F., Delgosha, F., Razzaghmanesh, M. & Myers, B. Introducing a water quality index for assessing water for irrigation purposes: a case study of the ghezel ozan river. Science of the Total Environment 589, 107–116 (2017).
Yi, W. & Yu, Q. Discussion about water quality evaluation index method in drinking water source. Environ. Monit. China 19(5), 43–47 (2003).
Qiu, M. L., Liu, L. H., Zou, X. W. & Wu, L. X. Comparison of water quality evaluation standards and evaluation methods between at home and abroad. J. China Inst. Water Resour. Hydropower Res. 11(3), 176–182 (2013).
Xu, Y. et al. Seasonal patterns of water quality and phytoplankton dynamics in surface waters in guangzhou and foshan, china. Science of the Total Environment. 590–591, 361–369 (2017).
Anuar, N., Pauzi, A. M. & Bakar, A. A. A. Methodology of water quality index (WQI) development for filtrated water using irradiated basic filter elements. Mathematical Sciences and its Applications, 040010 (2017).
Howladar, M. F., Numanbakth, M. A. A. & Faruque, M. O. An application of Water Quality Index (WQI) and multivariate statistics to evaluate the water quality around Maddhapara Granite Mining Industrial Area, Dinajpur, Bangladesh. Environmental Systems Research 6(1), 13 (2018).
Brown, R. M., McClelland, N. I., Deininger, R. A. & Tozer, R. G. A water quality index – do we dare? Water Sew. Works 117, 339–343 (1970).
Debels, P., Fıgueroa, R., Urrutia, R., Barra, R. & Niell, X. Evaluation of water quality in the Chilla’n river (Central Chile) using physicochemical parameters and a modified water quality index. Environ. Monit. Assess. 110, 301–322 (2005).
Saeedi, M., Abessi, O., Sharifi, F. & Maraji, H. Development of groundwater quality index. Environ. Monit. Assess. 163(1–4), 327–335 (2009).
Lai, Y. C., Chien, C. C., Yang, Z. H., Surampalli, R. Y. & Kao, C. M. Developing an integrated modeling tool for river water quality index assessment. Water Environment Research A Research Publication of the Water Environment Federation 89(3), 260 (2017).
Şener, Ş., Şener, E. & Davraz, A. Evaluation of water quality using water quality index (WQI) method and gis in Aksu river (Sw-turkey).Science of the Total Environment, s 584–585, 131–144 (2017).
WHO. Guidelines for Drinking-Water Quality. World Health Organization, Geneva, Switzerland 2008.
Lim, J. & Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 187, 1–17 (2015).
Duan, W.; et al. Spatial and temporal trends in estimates of nutrient and suspended sediment loads in the ishikari river, Japan, 1985 to 2010. Sci. Total Environ 461, 499–508 (2013).
Wang, X. et al. Evaluation and estimation of surface water quality in an arid region based on EEM-parafac and 3D fluorescence spectral index: a case study of the Ebinur lake watershed, china. Catena 155, 62–74 (2017).
Zhang, F. et al. The influence of natural and human factors in the shrinking of the Ebinur lake, xinjiang, china, during the 1972–2013 period. Environmental Monitoring & Assessment 187(1), 4128 (2015a).
Tan, J., Cherkauer, K. & Chaubey, I. Developing a comprehensive spectral-biogeochemical database of midwestern rivers for water quality retrieval using remote sensing data: a case study of the wabash river and its tributary, indiana. Remote Sensing 8(6), 517 (2016).
Zhang, J. & Chen, K. Variational image registration by a total fractional-order variation model. Journal of Computational Physics 293, 442–461 (2015b).
Zhang, D. et al. Quantitative estimating salt content of saline soil using laboratory hyperspectral data treated by fractional derivative 1, 1–11 (2016).
Sierociuk, D. et al. Diffusion process modeling by using fractional-order models. Applied Mathematics & Computation 257, 2–11 (2015).
Xue, D. & Wang, D. A fractional-order adaptive regularization primal-dual algorithm for image denoising. Information Sciences 296, 147–159 (2015).
Shi, T., Liu, H., Chen, Y., Wang, J. & Wu, G. Estimation of arsenic in agricultural soils using hyperspectral vegetation indices of rice. Journal of Hazardous Materials 308, 243 (2016).
Jin, X., Du, J. & Liu, H. Remote estimation of soil organic matter content in the Sanjiang Plain, Northwest China: The optimal band algorithm versus the GRA-ANN model. Agricultural & Forest Meteorology 218-219, 250–260 (2016).
Sahu, P. & Sikdar, P. K. Hydrochemical framework of the aquifer in and around East Kolkata wetlands, West Bengal, India. Environ. Geol. 55, 823–835 (2008).
Yidana, S. M. & Yidana, A. Assessing water quality using water quality index and multivariate analysis. Environ. Earth Sci. 59, 1461–1573 (2010).
Varol, S. & Davraz, A. Evaluation of the groundwater quality with WQI (Water Quality Index) and multivariate analysis: a case study of the Tefenni plain (Burdur/Turkey). Environ. Earth Sci. 73, 1725–1744 (2015).
Ji, D., Shi, J., Xiong, C., Wang, T. & Zhang, Y. A total precipitable water retrieval method over land using the combination of passive microwave and optical remote sensing. Remote Sensing of Environment 191, 313–327 (2017).
Ramakrishnaiah, C. R., Sadashivaiah, C. & Ranganna, G. Assessment of water quality index for the groundwater in Tumkur Taluk, Karnataka tate, India. E-J. Chem. 6(2), 523–530 (2009).
Wiley, E. O., Mcnyset, K. M., Peterson, A. T., Robins, C. R. & Stewart, A. M. Niche modeling and geographic range predictions in the marine environment using a machine-learning algorithm. Oceanography 16(3), 120–127 (2003).
Marjanović, M., Kovačević, M., Bajat, B. & Voženílek, V. Landslide susceptibility assessment using svm machine learning algorithm. Engineering Geology 123(3), 225–234 (2011).
Liu, J., Zhang, Y., Yuan, D. & Song, X. Empirical estimation of total nitrogen and total phosphorus concentration of urban water bodies in china using high resolution ikonos multispectral imagery. Water 7(11), 6551–6573 (2015).
Chen, Y. et al. Short-term electrical load forecasting using the support vector regression (svr) model to calculate the demand response baseline for office buildings. Applied Energy 195, 659–670 (2017).
TAN, L, HE, B, LIU, W, PANG, D. Estimation of chlorophyll content of Eremurus chinensis based on optimization support vector regression machine. Chinese Journal of Ecology, 36(2), 555–562 (In Chinese) (2017).
Akande, K. O., Owolabi, T. O., Olatunji, S. O. & Abdulraheem, A. A. A hybrid particle swarm optimization and support vector regression model for modelling permeability prediction of hydrocarbon reservoir. Journal of Petroleum Science & Engineering. 150, 43–54 (2017).
Kumar, T. L. M. & Prajneshu. Nonlinear support vector regression model selection using particle swarm optimization algorithm.National Academy Science Letters, 1–7 (2016).
Harti, A., Lhissou, R. & Chokmani, K. Spatiotemporal monitoring of soil salinization in irrigated Tadla Plain (Morocco) using satellite spectral indices. International Journal of Applied Earth Observation and Geoinformation 50, 64–73 (2016).
Dziauddin, M. F., Powe, N. & Alvanides, S. Estimating the Effects of Light Rail Transit (LRT) System on Residential Property Values Using Geographically Weighted Regression (GWR). Applied Spatial Analysis & Policy 8(1), 1–25 (2015).
Chen, Q., Mei, K. & Dahlgren, R. A. et al. Impacts of land use and population density on seasonal surface water quality using a modified geographically weighted regression. Science of the Total Environment 572, 450 (2016).
Acknowledgements
The research was carried out with the financial support provided by the Scientific and technological talent training program of Xinjiang Uygur Autonomous Region (grant No. QN2016JQ0041), National Natural Science Foundation of China (grant No. 41361045), National Natural Science Foundation of China (Xinjiang Local Outstanding Young Talent Cultivation) (grant No. U1503302) and The Innovation Training Program Foundation for Graduate Education from the Xinjiang Uygur Autonomous Region (grant No. XJGRI2016014). The authors appreciate the very constructive suggestions and comments from anonymous reviewer.
Author information
Authors and Affiliations
Contributions
Xiaoping WANG led the idea conceptualization, analysis, figure generation, and writing. Xiaoping WANG and Fei ZHANG discussed idea conceptualization. Xiaoping WANG and Jianli DING contributed to editing and organization of the revised paper. All co-authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, X., Zhang, F. & Ding, J. Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake Watershed, China. Sci Rep 7, 12858 (2017). https://doi.org/10.1038/s41598-017-12853-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-12853-y
This article is cited by
-
Mapping reservoir water quality from Sentinel-2 satellite data based on a new approach of weighted averaging: Application of Bayesian maximum entropy
Scientific Reports (2024)
-
A Critical Review of Remote Sensing Methods for Inland Water Quality Monitoring: Progress, Limitations, and Future Perspectives
Water, Air, & Soil Pollution (2024)
-
A Hybrid Approach of Supervised Self-organizing Maps and Genetic Algorithms for Predictive Mapping of Arsenic Pollution in Groundwater Resources
Exposure and Health (2024)
-
Evaluation of groundwater quality for drinking purposes based on machine learning algorithms and GIS
Sustainable Water Resources Management (2024)
-
Assessment of Water Dynamics and Water Quality Parameters over Gobind Sagar Reservoir, India, Based on High-Resolution Remote Sensing Approach
Water Conservation Science and Engineering (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.