Abstract
Understanding the dynamics of open quantum systems is important and challenging in basic physics and applications for quantum devices and quantum computing. Semiconductor quantum dots offer a good platform to explore the physics of open quantum systems because we can tune parameters including the coupling to the environment or leads. Here, we apply the fast single-shot measurement techniques from spin qubit experiments to explore the spin and charge dynamics due to tunnel coupling to a lead in a quantum dot-lead hybrid system. We experimentally observe both spin and charge time evolution via first- and second-order tunneling processes, and reveal the dynamics of the spin-flip through the intermediate state. These results enable and stimulate the exploration of spin dynamics in dot-lead hybrid systems, and may offer useful resources for spin manipulation and simulation of open quantum systems.
Similar content being viewed by others
Introduction
Electronic properties of quantum dots (QDs) have been widely studied to explore the solid-state physics of confined, interacting electrons1,2,3,4,5 and in addition consider various applications to quantum effect devices, quantum models, quantum information technologies and so on6,7,8. The QDs used are mostly isolated from their environment, including the leads, as much as possible to minimize dissipation and decoherence9. On the other hand, QDs coupled to their environment provide novel systems with the coupling electrically tunable. The environment can be tailored by applying bias voltages or using specific states such as ferromagnets10, superconductors11, quantum Hall states12,13,14, and others. This variability gives rise to attractive science like Fano interference15,16,17, RKKY interactions18, and the general physics of open and nonequilibrium systems. The higher order tunneling process in the open system also creates interesting phenomena like Kondo effects19,20. The higher order process occurs via transitions to and from the virtural intermediate states because of the time energy uncertainty principle. When such transitions happen, they can induce a spin change but no charge change between the initial and the final states. This is not the case for the first order tunneling process which accompanies a charge change with a spin change21,22,23. The difference between the two processes sounds obvious in quantum mechanics, and indeed has often been assumed to account for the exotic spin-related phenomena like the Kondo effect. However, most of the experiments have been performed using steady-state charge transport measurement24,25 and no direct measurement of time-dependent spin and charge changes has been demonstrated yet. Resolving the dynamics of higher order tunneling processes will therefore strengthen our understanding of the underlying physics of exotic spin phenomena.
In this work, we apply techniques of fast manipulation and readout of charge and spin states in a quantum dot coupled to the lead to directly reveal the time-dependent charge and spin change in the first and the second order processes induced by the dot-lead tunneling. Our experimental system is an electrostatically defined double quantum dot (DQD) in GaAs. One QD stores the target single-electron and another ancillary QD is used for spin initialization and readout. We measured time-dependent spin and charge changes and demonstrate the spin change with no charge change through the intermediate state in the second order tunneling process.
Results
Device and measurement scheme
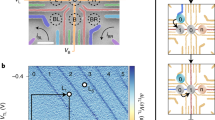
Figure 1(a) shows a scanning electron micrograph of the device. By applying negative voltages on the gate electrodes, a DQD and a QD charge sensor26 are formed at the lower and upper sides, respectively. The left QD in the DQD couples to a lead, and the coupling strength is tuned by the voltage V T applied on gate T. The QD charge sensor is connected to an RF resonator formed by the inductor L and the stray capacitance C p for RF reflectometry26,27,28. The number of electrons in each QD (n 1,n 2) is monitored by the intensity of the reflected RF signal V sensor .
(a) Scanning electron micrograph of the device and the schematic of the measurement setup. A DQD is formed at the lower side, and the charge states are monitored by the charge sensor QD at the upper side. The charge sensor is connected to resonators formed by the inductor L and the stray capacitance C p for RF reflectometry. The external magnetic field of 0.5 T is applied in plane along the z axis. (b) ΔV sensor as a function of V P2 andV P1. Charge states are identified by distinct levels in ΔV sensor . The number of electrons in each QD is given as (n 1, n 2). The triangle shows the region of the spin blockade. The positions corresponding to steps of pulse sequences (O i , I, M) are indicated. (c) Schematic of the measurement scheme. The spin state is initialized to a (0, 2) singlet at I. Next, we move into O i in (1, 1) where the spin couples to the lead. Finally, the spin state is measured using spin blockade at M.
The spin state is initialized using singlet formation in a single QD due to the tight confinement29,30. The charge state of single electrons in the dot can be detected in a fast and sensitive manner using the rf charge sensor. We combine the charge sensing with the effect of Pauli spin blockade31 to measure the spin change in the dot in a sufficiently short time scale.
Figure 1(b) shows the charge stability diagram of the DQD. The external magnetic field of 0.5 T is applied in plane along the z axis to create a large enough Zeeman splitting for the spin readout. We measure the sensor signal V sensor as a function of the plunger gate voltages of QD2 (V P2), and QD1 (V P1). We observe a change ΔV sensor each time the DQD charge configuration (n 1, n 2) changes. Depicted in Fig. 1(b), the values (n 1, n 2) are assigned by counting the number of charge transition lines from the fully depleted configuration (n 1, n 2) = (0,0). Around the charge state transition (1, 1) ↔ (0, 2), we observe a suppression of the (0,2) charge signal due to the Pauli spin blockade [in the region indicated by the triangle in Fig. 1(b)]. In this specific measurement of the stability diagram, unlike elsewhere, upon pulsing (0, 2) → (1, 1) we move through the singlet-triplet T + anti-crossing very slowly (adiabatically), to induce a sizable triplet component of the (1, 1) state even at a zero interaction time. Pulsing quickly back (1, 1) → (0, 2) results in a Pauli blocked signal inside the denoted triangular area. This shows us where we can utilize the Pauli spin blockade to readout the spin state in the following measurements, probing the dot spin and charge tunneling-induced dynamics. The operation scheme to measure the effect of the lead on the spin is depicted in Fig. 1(c). We initialize the state to a (0, 2) singlet by waiting at the initialization point I denoted in Fig. 1(b) and return back to the point M. Next, we move to the operation point O i . In this step, the electron in QD1 interacts with the lead and the dot state might be changed by electron tunneling. The tunneling rate can be modified by tuning V T, which changes the tunnel coupling, and the position of O i , which changes the dot potential with respect to the Fermi energy of the lead (O1: close to a charge transition, O2: deep in the Coulomb blockade). In this detuned condition at O i , the single-electron dynamics in QD1 dominates over two-electron effects. At the next step, the spin state is measured using spin blockade by pulsing the dot to the point denoted by M. If the spin state has not changed, we observe the (0, 2) singlet again. If the spin state has changed, a polarized triplet component (T ±) is measured as a blocked (1, 1) → (0, 2) charge transition. From the charge signal, we can therefore deduce the spin state.
Measurement around a charge transition
In this way, we first measure the spin relaxation using the operation point O1 close to a charge transition line, see Fig. 1(b), where the QD level is close to the Fermi level of the lead. The tunneling gate voltage is set to V T = −660 mV. The red circles in Fig. 2(a) show the measured singlet probability as a function of the interaction time at O1. We average over 512 measurement cycles to produce a single data point. Initially at 1, the singlet probability decreases upon increasing the interaction time from zero. This decrease indicates that a triplet component is formed by the interaction with the lead. Fitting with an exponential reveals a relaxation time of 3.0 μs. Note that this relaxation time is much smaller than the intrinsic spin relaxation time (several hundreds of μs, ms)29.
(a) Observed spin and charge signals (the singlet probability and the average of the sensor signal 〈V sensor 〉) as a function of the interaction time. Red circles show the spin signal (left axis). The blue trace shows the charge signal (right axis). The smooth lines are exponential fits resulting in the relaxation time of 3.0 μs for the spin, and 1.8 μs for the charge. (b) Statistics of the charge signal at the operation point. Histogram of observed values of the charge sensor V sensor (on the x axis), N(V sensor )/N tot is plotted as a function of the interaction time (y axis). The two peaks, at V sensor = −960 mV, and −780 mV, correspond to the (1,1) and the (0,1) charge states, respectively. The weight of the (0,1) component increases with the longer interaction time. (c) Schematic of the spin relaxation by a first-order tunneling process. An electron escapes from the QD, and the QD becomes empty. Another electron comes in after that.
Similarly to spin, we also measure the lifetime of charge in this configuration. In this measurement, we monitor the QD charge sensor while we are at O1. The blue trace in Fig. 2(a) shows V sensor over 16384 measurement cycles as a function of the interaction time. As seen there, 〈V sensor 〉 changes exponentially, with the fitted charge relaxation time of 1.8 μs. To examine the charge relaxation in more detail, we plot in Fig. 2b histograms of the values of V sensor (the x axis) for a varying interaction time (the y axis). The two peaks along a horizontal cut correspond to the (1,1) and the (0,1) charge states, respectively. At zero interaction time, only the (1,1) state signal is present, while the (0,1) state appears for finite interaction times.
In this configuration, the mechanism of the relaxation for both spin and charge is a first-order tunneling process32. Namely, the electron tunnels out of the QD1 into the lead, after which the dot is refilled from the lead, and the initial information is lost. The spin and charge relaxations: the information loss of the spin demonstrated in Fig. 2(a) and of the charge in Fig. 2(a,b), happen simultaneously. We note that though the relaxation timescales are similar, they are not identical. The difference comes from a difference in the rate dependence on the Fermi occupation of the lead (see Supplementary Information).
Measurement in Coulomb blockade
We now investigate the spin dynamics in a Coulomb blockaded dot. To this end, we repeat the previously described measurement using the operation point O2, deep in the (1,1) region, see Fig. 1(b). Here, the QD level is far below the Fermi level of the lead. To increase the speed of the lead-induced spin dynamics on the dot, we increase the dot-lead tunnel coupling by setting V T = −560 mV. As can be seen in Fig. 3(a), similarly to before, the spin state displays an exponential decay, with the relaxation time of 4.5 μs. (The saturation value of the spin signal is slightly different from that in Fig. 2(a). This will be caused by an imperfection in the readout of the T + state with increasing the dot-lead tunnel coupling.) However, now the charge signal barely changes, indicating that the charge state is not affected. (The slight change of the charge signal in Fig. 3(a) is caused by the distorted voltage pulses applied on P1 and P2. Due to a cross-talk between the plunger gates and the sensor, the pulse distortion slightly affects the observed charge signal.) This is confirmed by Fig. 3(b), where the histograms of the values of V sensor display a single peak corresponding to the (1,1) charge state. The spin therefore decays at a fixed QD charge configuration.
(a) The observed singlet probability and 〈V sensor 〉 as a function of the interaction time at O2 [see Fig. 1(b)]. Red circles show the spin signal (left axis). The blue trace shows the charge signal (right axis). The red smooth curve is an exponential fit resulting in the relaxation time of 4.5 μs. The charge signal shows no relaxation. (b) Histogram of observed values of the charge sensor voltage V sensor (on the x axis), N(V sensor )/N tot , is plotted as a function of the interaction time (y axis). The peak corresponds to the (1,1) charge state. (c) Schematic of the spin relaxation by a second-order tunneling process. An electron of the QD1 is swapped with one in the lead in a single step. The spin state is changed even though the charge state is stable.
We therefore interpret this as the observation of a spin relaxation induced by a second-order tunneling process24,25, where the electron in QD1 swaps with a random electron from the lead in a single step. Figure 4(a) shows the spin signal as we change the voltage applied on gate T, V T. Applying more negative voltage V T prolongs the spin relaxation time, by decreasing the tunnel coupling to the lead, as 0.7, 1.7 and 5.0 μs, for V T = −560, −565, −570 mV, respectively. (We note that the relaxation time at V T = −560 mV is different from the corresponding value of V T given in Fig. 3(a) due to a shift of the QD conditions between experiments.) In addition to V T, we can tune the spin decay timescale by the plunger gate voltages. Figure 4(b) shows the spin relaxation rate as we change the operation point from O2 toward O1, parametrizing the displacement by the voltage δ. Upon increasing δ (moving towards the charge transition line), the spin relaxation rate is enhanced. The measured dependence is well fitted by an analytical expression for an inelastic cotunneling rate, giving \(\propto {(\mathrm{1/(}\mu \mathrm{(2)}-{\mu }_{F})+\mathrm{1/(}{\mu }_{F}-\mu \mathrm{(1))})}^{2}\), with μ(N) and μ F being the electrochemical potential at the dot with N electrons29 and the Fermi energy of the lead, respectively (see Supplemental Information for details). This demonstrates the two handles on the speed of the lead-induced dynamics of the QD spin.
(a) The spin relaxation signal as a function of the interaction time at O2 for different values of the gate voltage applied on gate T, V T. Circles, triangles, and squares show the result at V T = −560, −565, −570 mV, respectively. The lines are exponential fits. (b) The spin relaxation rate as a function of δ. Circles show the experimental data and the line shows a theoretical curve considering the second-order tunneling process.
Discussion
To sum up the results observed in the Coulomb blockade regime, we state that the interaction with the lead influences only the dot spin and not its charge. The spin relaxation thus directly uncovers the second order tunneling processes. This interaction can be utilized for the spin initialization, measurement and manipulation if leads have special properties. We note that even though the timescale of the dot-lead interaction realized in this experiment was tuned to \(\sim \mu \)s, it is straightforward to enhance it by increasing the tunnel coupling, and/or utilizing the Kondo effect, which enhances the second-order tunneling at low temperatures.
In conclusion, we have measured spin dynamics in a QD-lead hybrid system. Close to a charge transition, we observe spin and charge relaxation signals corresponding to the first-order tunneling process. In the Coulomb blockade, we observe spin relaxation at a fixed charge configuration, corresponding to the second-order tunneling process. The demonstrated dot-lead spin exchange can be useful as a general resource for spin manipulations, and simulations of open systems under non-equilibrium conditions.
Methods
The device was fabricated from a GaAs/AlGaAs heterostructure wafer with an electron sheet carrier density of 2.0 × 1015 m−2 and a mobility of 110 m2/Vs at 4.2 K, measured by Hall-effect in the van der Pauw geometry. The two-dimensional electron gas is formed 90 nm under the wafer surface. We patterned a mesa by wet-etching and formed Ti/Au Schottky surface gates by metal deposition, which appear white in Fig. 1(a). All measurements were conducted in a dilution fridge cryostat at a temperature of 13 mK.
The RF resonator for RF reflectometry is formed by the inductor L = 270 nH and the stray capacitance C p = 1.06 pF. A change in the electrostatic environment around the sensing dot changes its conductance, which shifts the tank circuit resonance and modifies V sensor measured at f res = 297 MHz, the circuit resonance frequency.
References
Tarucha, S., Austing, D. G., Honda, T., van der Hage, R. J. & Kouwenhoven, L. P. Shell Filling and Spin Effects in a Few Electron Quantum Dot. Phys. Rev. Lett. 77, 3613–3616 (1996).
Kouwenhoven, L. P. et al. Excitation Spectra of Circular, Few-Electron Quantum Dots. Science 278, 1788–1792 (1997).
Ciorga, M. et al. Addition spectrum of a lateral dot from Coulomb and spin-blockade spectroscopy. Phys. Rev. B 61, R16315–R16318 (2000).
Kouwenhoven, L. P., Austing, D. G. & Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 64, 701 (2001).
van der Wiel, W. G. et al. Electron transport through double quantum dots. Rev. Mod. Phys. 75, 1–22 (2002).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum Spintronics: Engineering and Manipulating Atom-Like Spins in Semiconductors. Science 339, 1174–1179 (2013).
Weiss, U. Quantum Dissipative Systems (World Scientific, Singapore, 2008), 3rd ed.
Hamaya, K. et al. Spin transport through a single self-assembled InAs quantum dot with ferromagnetic leads. Appl. Phys. Lett. 90, 053108 (2007).
Deacon, R. S. et al. Tunneling Spectroscopy of Andreev Energy Levels in a Quantum Dot Coupled to a Superconductor. Phys. Rev. Lett. 104, 076805 (2010).
Feve, G. et al. An On-Demand Coherent Single-Electron Source. Science 316, 1169–1172 (2007).
Altimiras, C. et al. Non-equilibrium edge-channel spectroscopy in the integer quantum Hall regime. Nat. Phys. 6, 34–39 (2010).
le Sueur, H. et al. Energy Relaxation in the Integer Quantum Hall Regime. Phys. Rev. Lett. 105, 056803 (2010).
Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 124, 1866–1878 (1961).
Kobayashi, K., Aikawa, H., Katsumoto, S. & Iye, Y. Tuning of the Fano Effect through a Quantum Dot in an Aharonov-Bohm Interferometer. Phys. Rev. Lett. 88, 256806 (2002).
Otsuka, T. et al. Fano Effect in a Few-Electron Quantum Dot. J. Phys. Soc. Jpn. 76, 084706 (2007).
Craig, N. J. et al. Tunable Nonlocal Spin Control in a Coupled-Quantum Dot System. Science 304, 565–567 (2004).
Goldhaber-Gordon, D. et al. Kondo effect in a single-electron transistor. Nature 391, 156–159 (1998).
van der Wiel, W. G. et al. The Kondo Effect in the Unitary Limit. Science 289, 2105–2108 (2000).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Amasha, S. et al. Spin-dependent tunneling of single electrons into an empty quantum dot. Phys. Rev. B 78, 041306 (2008).
Simmons, C. B. et al. Tunable Spin Loading and T 1 of a Silicon Spin Qubit Measured by Single-Shot Readout. Phys. Rev. Lett. 106, 156804 (2011).
De Franceschi, S. et al. Electron Cotunneling in a Semiconductor Quantum Dot. Phys. Rev. Lett. 86, 878–881 (2001).
Schleser, R. et al. Cotunneling-Mediated Transport through Excited States in the Coulomb-Blockade Regime. Phys. Rev. Lett. 94, 206805 (2005).
Barthel, C. et al. Fast sensing of double-dot charge arrangement and spin state with a radio-frequency sensor quantum dot. Phys. Rev. B 81, 161308 (2010).
Schoelkopf, R. J. et al. The Radio-Frequency Single-Electron Transistor (RF-SET): A Fast and Ultrasensitive Electrometer. Science 280, 1238–1242 (1998).
Reilly, D. J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Fast single-charge sensing with a rf quantum point contact. Appl. Phys. Lett. 91, 162101 (2007).
Hanson, R. et al. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217 (2007).
Petta, J. R. et al. Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots. Science 309, 2180–2184 (2005).
Ono, K., Austing, D. G., Tokura, Y. & Tarucha, S. Current Rectification by Pauli Exclusion in a Weakly Coupled Double Quantum Dot System. Science 297, 1313–1317 (2002).
Biesinger, D. E. F. et al. Intrinsic Metastabilities in the Charge Configuration of a Double Quantum Dot. Phys. Rev. Lett. 115, 106804 (2015).
Acknowledgements
We thank J. Beil, J. Medford, F. Kuemmeth, C. M. Marcus, D. J. Reilly, K. Ono, RIKEN CEMS Emergent Matter Science Research Support Team and Microwave Research Group in Caltech for fruitful discussions and technical supports. Part of this work is supported by the Grant-in-Aid for Scientific Research (No. 26220710, 16H00817, 16K05411, 17H05187), CREST (JPMJCR15N2, JPMJCR1675), PRESTO (JPMJPR16N3), JST, ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan), RIKEN Incentive Research Project, Advanced Technology Institute Research Grant, the Murata Science Foundation Research Grant, Izumi Science and Technology Foundation Research Grant, TEPCO Memorial Foundation Research Grant, The Thermal & Electric Energy Technology Foundation Research Grant, The Telecommunications Advancement Foundation Research Grant, Futaba Electronics Memorial Foundation Research Grant, MST Foundation Research Grant, Kato Foundation for Promotion of Science Research Grant, DFG-TRR160, and the BMBF - Q.com-H 16KIS0109.
Author information
Authors and Affiliations
Contributions
T.O., T.N., M.D., S.A., J.Y., K.T., G.A. and S.T. planned the project; T.O., T.N., M.D., S.A., A.L. and A.D.W. performed device fabrication; T.O., T.N., M.D., S.A., J.Y., K.T., G.A., P.S., A.N., T.I., D.L. and S.T. conducted experiments and data analysis; all authors discussed the results; T.O., T.N., M.D., S.A., J.Y., K.T., G.A., P.S. and S.T. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Otsuka, T., Nakajima, T., Delbecq, M.R. et al. Higher-order spin and charge dynamics in a quantum dot-lead hybrid system. Sci Rep 7, 12201 (2017). https://doi.org/10.1038/s41598-017-12217-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-12217-6
This article is cited by
-
Scalable fabrication of graphene nanoribbon quantum dot devices with stable orbital-level spacing
Communications Materials (2022)
-
Formation of quantum dots in GaN/AlGaN FETs
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.