Abstract
A new, composite plasmonic waveguide based electromagnetic cloaking scheme is proposed with Si nano-spacer. Here we show, that the scattering fields of an object located on the cloak do not interact with the evanescent field, resulting in object’s invisibility. Finite difference time domain (FDTD) numerical calculations were performed to extract the modal distributions and surface intensities on a composite plasmonic waveguide with a metasurface overlayer. Spatially varying effective permittivity was analytically calculated using transformation optics. Cloaking was demonstrated for a cylindrical object with diameter of 70% from the waveguide width on a high index ridge waveguide structure with silicon nitride guiding layer on silica substrate. Our results open the door to new integrated photonic devices, harnessing from evanescent fields distortion on composite plasmonic waveguides and dielectric nano-spacers for the variety of applications from on-chip optical devices to all-optical processing.
Similar content being viewed by others
Introduction
The concept of an invisibility cloak with metamaterials has been a topic of interest over the last few centuries. Metamaterials are a man-made engineered materials composites with exotic electromagnetic properties achieved through subwavelength structuring1,2,3. However, obtaining effective material parameters for the metamaterials is not trivial due to their structural inhomogeneity and strong spatial dispersion4,5. The recent developments in metamaterial science6,7,8,9 and nanotechnology10,11 have enabled the possibility of cloaking an object to become a technological reality. One approach to achieve an invisibility cloak is transformation optics12,13. In this approach, based on the invariance of Maxwell’s equations to coordinate transformations, we can deform the wave paths in a specific manner. Instead of physically transforming the medium, the values of the chosen material parameters are modified, i.e., the relative permittivity and permeability tensors are changed14. This leads to a spatially varying medium parameters which, in essence, transform the coordinates of the electromagnetic fields, resulting in a concealed object.
Silicon photonics integrated circuits are considered to enable future computing systems with optical input-outputs co-packaged with CMOS chips to circumvent the limitations of electrical interfaces. Silicon based photonic integrated circuits are widely used in applications such as optical modulators15, optical interconnects16, biosensors17,18, and more. A metamaterial overlayer, or simply a metasurface, on an integrated photonic structure, allows for nurturing the device with novel functionalities. The introduction of metasurfaces simplifies the design of metamaterial structures due to its characteristic thickness, which typically much smaller than the wavelength. This essentially converts the design process to two dimensional. One of the most appealing applications of metasurfaces is achieving invisibility cloaks by tailoring evanescent fields. This can be allowed in a controllable manner using an integrated photonics platform.
Composite plasmonic waveguides19 incorporating dielectric and metallic films such as in ref.19, offer great potential for ultra-compact integrated photonic devices due to substantial increase of the propagation distance of the plasmon waves. Surface plasmons20,21 (SP) are a type of a surface waves extending along a metal-dielectric interface considering the momentum matching conditions. The SP benefits from spatial confinement and high local field intensity. One of the major limitations in the implementation of plasmonic circuits is their short propagation length. Composite plasmonic waveguides19 provide large confinement of light in sub-wavelength scale. They also allow for the control of the surface plasmons excited in the metal overlayer while substantially reducing inevitable ohmic losses of conventional plasmonic materials.
In this paper we present an analysis of the modal distribution and surface intensity in a channel photonic waveguides with a metasurface overlayer. The spatial distribution of the metasurface permittivity was analytically calculated based on the transformation optics principles. The spatial distribution was then imported into a commercial Maxwell solver (Lumerical) using finite-difference time-domain method (FDTD).
Theory and Design
Composite Plasmonic Waveguide Structure
Our theoretical analysis is based on the semi-analytical model of orthonormalization of complex eigenmodes at an abrupt step, developed for the investigation of the transmission and surface intensity in composite plasmonic waveguide structures19. Briefly, the monochromatic plane wave with λ 0 illuminates the waveguide endfacet and excites the fundamental guided mode E i0. At some distance from the waveguide input, there is an abrupt step introduced by the slab plasmonic film made of gold with length of L along the propagation direction z. This region is called a composite plasmonic waveguide structure since it includes the dielectric waveguide with plasmonic overlayer which excites three orthogonal hybrid plasmonic modes E γ1. The transmittance and surface intensity is obtained by thexpans mode matching at the abrupt steps and the explicit formulation of the eion coefficients which expand modes at abrupt steps.
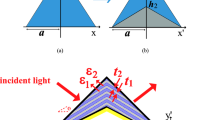
Consider a guided wave system as shown in Fig. 1. A plasmonic metasurface with length of L = 10 μm, height of d m = 40 nm is introduced on top of the silicon nitride22 (Si3N4) ridge waveguide to form a high index composite plasmonic waveguide structure on a silicon dioxide23 (SiO2) substrate. In order to confine the optical mode in vicinity with the metal-dielectric interface and for the efficient coupling to the surface plasmon modes, silicon24 (Si) nano-spacer is placed on top of the metasurface. The height of the Si nano-spacer is spatially varied in order to achieve control over the plasmonic wave. The composite plasmonic waveguide structure is confined in between the abrupt steps 1 and 2 and illuminated by the fundamental mode guided in the dielectric waveguide as shown in Fig. 1.
Illustration of the composite plasmonic waveguide structure and materials to study the invisibility cloaking scheme. Wavelength of λ 0 = 637 nm illuminates the dielectric waveguide exciting the fundamental mode guided in region 0. Region 1 is characterized by the metasurface and Si nano-spacer placed on the waveguide with length L in the propagation direction exciting three hybrid plasmonic modes. Region 2 is identical to the region 0 in terms of the optical properties and functionality. A scattering object with optical index of 1.3 is placed on the metasurface.
At the interface separating a dielectric with a permittivity ε d and a metal with a permittivity ε m , SPs are evanescently excited by the coupling between free carriers of the metal and the incident electromagnetic field under momentum matching conditions. In composite plasmonic waveguide structure, the guided fundamental mode couples to the multiple modes excited in region 1 starting from the discontinuity with metasurface overlayer.
The use of CMOS technology compatible ridge waveguide25 in a combination with the metasurface26,27,28,29 provides design flexibility in on-chip light manipulations with novel SP based photonic circuits. The dielectric nano-spacer adds the additional degree of freedom for light confinement for coupling into hybrid plasmonic modes.
Design of a Metamaterial Overlayer Using Transformation Optics
Although the general concepts of metamaterials were designed considering propogating waves, metasurfaces can be used to control waves in the near field regime, such as surface plasmons30,31,32,33,34. Here, we consider a transformation which maps rectangular region in the virtual system to an arbitrary region (the cloak) in the physical system.
As previously stated, the layer can potentially be electromagnetically transformed by changing the material properties of the medium. That means it is possible to change the coordinate system of the object, in order to obtain a new refractive index distribution which will present the same electromagnetic properties. Mathematically, this transformation can be realized by modifying the dielectric and magnetic properties of the materials described by the following relations:
where ε and μ are the dielectric and magnetic constants in the original space, and ε′ and μ′ are the same constants in the transformed one. A is the Jacobian transformation matrix which relates the coordinates between the physical and virtual systems and given by
Where (x, y, z) are the coordinates of the physical space and (x′, y′, z′) are of the virtual space. To simplify the design, we assume that μ′ = μ = 1 symmetry along the x axis and consider a 2 dimensional transformation in the x − z plane with no change along the y axis. If the mapping satisfies the Cauchy–Riemann conditions35 which for our case are given by
the transformed material becomes inhomogeneous and isotropic.
To generate the discrete coordinate transformation, the boundaries of the physical domain are first defined by
To satisfy (3), the bounded area is divided into a mesh with 235 × 9 blocks and mapped using quasi-conformal (QC) transformation scheme36. The grid is numerically generated using an iterative algorithm that solves the discrete partial ecliptic differential equations generated by substituting (3) into (2) using successive over-relaxation (SOR) method37. The resulting orthogonal domain is then replicated in the bottom half space (−0.4 ≤ x ≤ 0) and represented by the black mesh as shown in Fig. 2.
Since the mesh in Fig. 2 is orthogonal and satisfies (3), the permittivity tensor in (1) becomes a scalar matrix and the effective mode index is \({n}_{{\rm{e}}{\rm{f}}{\rm{f}}}=\sqrt{{\varepsilon }^{^{\prime} }}=\sqrt{\varepsilon }/det({\bf{A}})\), represented by the color-map in Fig. 2.
The proposed method can conceal an object of an arbitrary shape if object’s longest dimension is less than the white cloaking area shown in Fig. 2. In addition, we found that our concept is feasible for the objects made of different materials such as dielectrics or metals.
Results and Discussion
Modal Distribution
Figure 3 shows the dominant y-component of the electric field magnitude supported by the waveguide for Si nano-spacer height of 10 nm. Figure 3(a) and Fig. 3(e) show the field profile of the purely dielectric mode (DM) supported by the dielectric waveguide in the \(z < -L\mathrm{/2}\) and \(z > L\mathrm{/2}\) regions. Figure 3(b) anf Fig. 3(f) show the profile of the fundamental hybrid mode supported by the composite dielectric/plasmonic waveguide for \(-L\mathrm{/2}\, < \,z\, < \,L\mathrm{/2}\). HDM results as a combination of DM and a symmetric SPP mode supported by the adjacent thin metal ridge waveguide. Figure 3(c) and (g) show the profiles of the SPPs and Fig. 3(d,h) show the SPPa modes, supported by the thin metal ridge waveguide.
(Up) Calculated spatial distributions of y-component of the electric field magnitude \(|{ {\mathcal E} }_{y}(x,y)|\) supported by the waveguide. (Down) Calculated electric field magnitude cross-sections \(|{ {\mathcal E} }_{y}(x\,=\,\mathrm{0,}\,y)|\). (a) and (e) Show dielectric mode (DM), (b) and (f) show hybrid plasmonic/dielectric mode (HDM), (c) and (g) show SPP symmetric mode(SPPs); (d) and (h) show SPP asymmetric mode (SPPa).
The nature of the modes depends on the optical properties of a waveguide structure and materials. They are localized in different areas of the waveguide. The region 1 is illuminated by the DM mode, which is the fundamental guided mode supported by the waveguide. Between the steps of discontinuity shown in Fig. 1, a resonance occurs when the DM matches the SPPs, together they create the HDM. SPPa mode is a short range surface plasmon mode and compared to the symmetric mode, the asymmetric SPPa mode penetrates much deeper to the metal film.
Mechanism of the invisibility cloak with composite plasmonic waveguides
As was described earlier, we study the cloak structure with composite plasmonic waveguides. The fundamental dielectric mode illuminates the waveguide overlapped with a metasurface of the effective permittivity. To confirm the cloak operation we calculate the integrated total surface intensity I over a waveguide width and along the interaction length L in the propagation direction (5) as shown on Fig. 4 while I is:
\({ {\mathcal E} }_{\gamma 1}(x,y,z)\) are extracted complex vectorial electric and magnetic field components calculated using FDTD. With the surface intensity I integrated across the plasmonic overlayer along the length from \(z=-L\mathrm{/2}\) to \(z=L\mathrm{/2}\) and full width of the waveguide. \(i,j,m\) indicate guided modes which are HDM, SPPs and SPPa respectively as in19, \({c}_{i\mathrm{0,}\gamma 1}\) is the expansion coefficient and η is the electric field components in x, y, z directions.
Integrated surface intensity is an essential parameter to assess the effectiveness of evanescent invisibility cloak with a composite plasmonic waveguide. Figure 4 shows 3D colormaps of \(|{E}_{\eta }{|}^{2}\) for four different cases. Integrated surface intensity of the composite plasmonic waveguide with slab gold overlayer is shown on Fig. 4a. Figure 4b shows I distribution calculated on composite plasmonic waveguide with slab gold overlayer while an object of cylindrical shape and index of 1.3 is placed on it. The object boundaries are visible due to the scattering effect as a result of the interaction with evanescent fields. Around the object, HDM shows strong localization across the metamaterial overlayer which results in observed increased intensity. Here, we are aiming to prevent the field localization around an object. Waveguide with transformed metamaterial overlayer is shown on Fig. 4c and with transformed metamaterial overlayer together with the object on Fig. 4d. Due to the carefully designed invisibility cloak on a composite plasmonic waveguide, the scattering effect from the object is avoided and invisibility is demonstrated.
The current bottleneck of realization of an invisibility cloak is the implementation of the required parameters, especially at visible wavelengths. Here we propose to spatially change the effective mode index of HDM mode by changing the thickness of the Si nano-spacer instead of spatially modifying the refractive index of the gold film. Correlating the properties of the structure with the calculated gradient index distribution can be physically realized by using grey-scale lithography technique38,39. This technique enables to adiabatically tailor the topology of the dielectric layer, in our case the Si nano-spacer height, adjacent to the gold surface to demonstrate the cloaking effect.
The fabrication procedure of the proposed design is straightforward. The first step is manufacturing Si3N4 ridge waveguides on SiO2 substrate by etching a slab of Si3N4 to the required dimensions. Then, a Poly(methyl methacrylate) (PMMA) photoresist is spin coated on the Si3N4 ridge and the pattern is created using electron beam (e-beam) lithography. The gold is deposited on the area exposed to the e-beam and then the Si thin film is deposited on top of the gold. For the creation of the specific pattern required for the device, the varying thickness of the Si nano-spacer is achieved using lift-off process.
Here, the proposed structure consists of five layers with their corresponding dielectric constants and widths, respectively, as shown in Fig. 5. The wave equation has to be satisfied in each distinct region, solving it results in an implicit expression for the dispersion relation linking β and ω. The effective mode index of HDM mode, defined as \({n}_{{\rm{eff}}}=\beta /{k}_{0}\), is obtained by numerically solving the structure for different heights of the Si layer as shown in Fig. 5.
The proposed device directs the flow of light smoothly around the cloaked region and is effective for a wide range of refractive indices and materials. We explored the effectiveness of the cloak in terms of the optical properties of the object. We found that the concealing effect is preserved for variety of materials which agrees with the concepts of transformation optics.
To conclude, here we proposed the new composite plasmonic waveguide scheme with dielectic nano-spacer based on the transformation optics principles to manipulate with light and distort the evanescent fields in a controllable manner to conceal an object. The plasmonic metasurface is placed on the composite plasmonic waveguide with the nano-spacer. High dielectric nano-spacer made of Si has contributed to the light confinement in vicinity with the metasurface boundary and facilitated the coupling to the hybrid plasmonic modes. The light manipulation is realized due to the engineered effective permittivity which in turn avoids the scattering effect. Our calculated results demonstrate that the designed metasurface can deflect the evanescent wave into a predefined, analytically calculated pattern. Since plasmons are localized in the direction perpendicular to the metamaterial overlayer boundary and accompanied by the combination of the transverse and longitudinal electromagnetic fields, they have maximum intensity on the surface with the metamaterial overlayer. The gradient material properties of this layer enable the invisibility effect to take place. Our theoretical study of invisibility cloaking scheme with composite plasmonic waveguides and Si nano-spacer enables the understanding of the complex behavior of hybrid plasmonic modes for the light manipulation on-chip and further design of integrated on-chip devices.
Methods
Expression of the eigenmodes at an abrupt step for the calculations of the surface intensity
One can achieve the modes at the beginning of the gold-coated region (1) and the fundamental mode excited at the input region (0) to determine the entire composite waveguide by applying appropriate mode-matching conditions at the input (z = 0) and output (z = L) interfaces of the dielectric rib waveguide and the composite dielectric/metallic stripe waveguide. We assume guided pure dielectric mode, DM, in Fig. 3(a) designated by a subscript \(i0\) in the input: region 0 in Fig. 3 and output: Region 2 on Fig. 1 side (pure dielectric waveguide) of the first step and orthogonal guided modes \(\gamma 1\,=\,i\mathrm{1,}\,j1\) or m1 assigned to HDM in cross-sections in Fig. 3(b), SPPs in Fig. 3(c) and SPPa in Fig. 3(d) modes, respectively, in the output side (dielectric waveguide with plasmonic overlayer) of the first step as shown in Fig. 1(a) with quasi-transverse magnetic components. At \(z\,=\,0\), the general complex field distributions at the boundary between region 0 and region 1, ignoring the reflected and radiated modes, are:
Where \(\xi =x,y\) and \({\bf{E}}={E}_{x}\hat{x}+{E}_{y}\hat{y}+{E}_{z}\hat{z}\) and \({\bf{H}}={H}_{x}\hat{x}+{H}_{y}\hat{y}+{H}_{z}\hat{z}\). \(\hat{x}\), \(\hat{y}\) and \(\hat{z}\) are unit vectors in the x, y and z directions respectively. An expression for the expansion coefficient between input mode \(i1\) in region 0 and mode \(j1\) in region 1 is derived using the complex orthogonality principle:
Where \(\gamma 1=i\mathrm{1,}\,j\mathrm{1,}\,m1\). We now express a general complex electric and magnetic field distribution components:
and
Where \({\beta }_{\delta }\) is the propagation constant of mode \(\delta \). \({\bar{ {\mathcal E} }}_{\delta }(x,y,z)\) and \({\bar{ {\mathcal H} }}_{\delta }(x,y,z)\) are extracted complex vectorial electric and magnetic field components calculated using FEM and \(\bar{ {\mathcal E} }={ {\mathcal E} }_{x}\hat{x}+{ {\mathcal E} }_{y}\hat{y}+{ {\mathcal E} }_{z}\hat{z}\) and \(\bar{ {\mathcal H} }={ {\mathcal H} }_{x}\hat{x}+{ {\mathcal H} }_{y}\hat{y}+{ {\mathcal H} }_{z}\hat{z}\). \({a}_{\delta }={N}_{\delta }{A}_{\delta }={E}_{\delta }(x,y,z)/({ {\mathcal E} }_{\delta }(x,y)exp(-j{\beta }_{\delta }z))={H}_{\delta }(x,y,z)/({ {\mathcal E} }_{\delta }(x,y)exp(-j{\beta }_{\delta }z))\) and \({A}_{\delta }\) is complex, \({A}_{\delta }=|{A}_{\delta }|exp(-j{\phi }_{\delta })\) related to the power carried by the mode as: \({P}_{\delta }=|{A}_{\delta }{|}^{2}\). The normalization factor \({N}_{\delta }\) giving rise to each mode carrying unity power, \({P}_{\delta }\,=\,1\) is: \({N}_{\delta }\,=\,{\mathrm{(2/}\Re ({\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{({\bar{ {\mathcal E} }}_{\delta }\times {{\bar{ {\mathcal H} }}^{\ast }}_{\delta })}_{z}{\rm{dxdy}}))}^{\mathrm{1/2}}\). For z = 0 these are:
Power in any region is defined as:
A relation between eigenmodes at an abrupt step is detailed below.
By substituting (8) and (9) into (7) we obtain:
To obtain a relation between eigenmodes at an abrupt step:
and
Where:
\({N}_{\delta }\) can then be expressed as:
which is:
An expansion coefficient \({c}_{i\mathrm{0,}\gamma 1}\) expanding mode i1 from region 0 into mode γ1 in region 1 over the first abrupt step is:
At z = L, the expansion coefficients are derived in a similar manner to that detailed above resulting in:
Since,
or:
And the transmittance through the composite plasmonic waveguide is obtained as:
or:
Where \({C}_{\gamma 1}=({I}_{i\mathrm{0,}\gamma 1}+{I}_{\gamma \mathrm{1,}i0}{)}^{2}\mathrm{/(4}{I}_{i\mathrm{0,}i0}{I}_{\gamma \mathrm{1,}\gamma 1})\) and L is length of a gold overlayer.
The transmittance through the composite-plasmonic waveguide structure presented here, can be calculated using (22) (or (23)).
Simulation of invisibility cloak on a composite plasmonic waveguide
The effective permittivity was derived and implemented using MATLAB. The simulations were performed using the commercial software packages Lumerical FDTD. In calculations, the fundamental mode was used as a source to excite hybrid plasmonic modes. The guided modes were explored using mode monitor. The distribution of the surface intensity was explored using field monitor while recorded simultaneously. Perfectly matched layers (PMLs) were used as the boundary conditions at the z axis and symmetry boundary conditions were used along the y axis. The simulation mesh was set to the high accuracy with the mesh step of 0.01 μm. The mesh around the gold and silicon layers was set to finer mesh with steps of 0.0025 μm. Conformal mesh refinement was applied to all materials. Lumerical FDTD simulations and MATLAB calculations were performed on a workstation with the following components: Intel Xenon 3.5 GHz E5-1650 CPU with 32 GB of RAM.
References
Zheludev, N. I. The road ahead for metamaterials. Science 328, 582–583 (2010).
Soukoulis, C. M. & Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nature Photonics 5, 523–530 (2011).
Liu, Y. & Zhang, X. Metamaterials: a new frontier of science and technology. Chemical Society Reviews 40, 2494–2507 (2011).
Simovski, C. R. On electromagnetic characterization and homogenization of nanostructured metamaterials. Journal of Optics 13, 013001 (2010).
Chipouline, A., Simovski, C. & Tretyakov, S. Basics of averaging of the maxwell equations for bulk materials. Metamaterials 6, 77–120 (2012).
Ni, X., Wong, Z. J., Mrejen, M., Wang, Y. & Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 349, 1310–1314 (2015).
Gorodetski, Y. & Karabchevsky, A. Plasmonic rack-and-pinion gear with chiral metasurface. In SPIE Photonics Europe, 98830H–98830H (International Society for Optics and Photonics, 2016).
Liberal, I. & Engheta, N. Zero-index platforms: where light defies geometry. Opt. Photonics News 27, 26–33 (2016).
Alù, A. Metamaterials: Prime time. Nature Materials 15, 1229–1231 (2016).
Karabchevsky, A., Mosayyebi, A. & Kavokin, A. V. Tuning the chemiluminescence of a luminol flow using plasmonic nanoparticles. Light: Science & Applications 5, e16164 (2016).
Terekhov, P. D., Baryshnikova, K. V., Shalin, A. S., Karabchevsky, A. & Evlyukhin, A. B. Resonant forward scattering of light by high-refractive-index dielectric nanoparticles with toroidal dipole contribution. Optics Letters 42, 835–838 (2017).
Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006).
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Schurig, D., Pendry, J. & Smith, D. R. Calculation of material properties and ray tracing in transformation media. Optics Express 14, 9794–9804 (2006).
Reed, G. T., Mashanovich, G., Gardes, F. & Thomson, D. Silicon optical modulators. Nature Photonics 4, 518–526 (2010).
Alduino, A. & Paniccia, M. Interconnects: Wiring electronics with light. Nature Photonics 1, 153 (2007).
Karabchevsky, A. & Kavokin, A. V. Giant absorption of light by molecular vibrations on a chip. Scientific Reports 6 (2016).
Liu, Y. et al. Surface plasmon resonance biosensor based on smart phone platforms. Scientific Reports 5, 12864 (2015).
Karabchevsky, A., Wilkinson, J. S. & Zervas, M. N. Transmittance and surface intensity in 3d composite plasmonic waveguides. Optics express 23, 14407–14423 (2015).
Ritchie, R. Plasma losses by fast electrons in thin films. Physical Review 106, 874 (1957).
Barnes, W. L., Dereux, A. & Ebbesen, T. W. Surface plasmon subwavelength optics. Nature 424, 824–830 (2003).
Philipp, H. R. Optical properties of silicon nitride. Journal of the Electrochemical Society 120, 295–300 (1973).
Gao, L., Lemarchand, F. & Lequime, M. Refractive index determination of sio2 layer in the uv/vis/nir range: spectrophotometric reverse engineering on single and bi-layer designs. Journal of the European Optical Society-Rapid publications 8 (2013).
Aspnes, D. & Studna, A. Dielectric functions and optical parameters of si, ge, gap, gaas, gasb, inp, inas, and insb from 1.5 to 6.0 ev. Physical review B 27, 985 (1983).
Katiyi, A. & Karabchevsky, A. Figure of merit of all-dielectric waveguide structures for absorption overtone spectroscopy. Journal of Lightwave Technology 35, 2902–2908 (2015).
Raether, H. Surface plasmons on smooth surfaces (Springer, 1988).
Karabchevsky, A., Tsapovsky, L., Marks, R. S. & Abdulhalim, I. Study of immobilization procedure on silver nanolayers and detection of estrone with diverged beam surface plasmon resonance (spr) imaging. Biosensors 3, 157–170 (2013).
Karabchevsky, A., Auslender, M. & Abdulhalim, I. Dual-surface plasmon excitation with thin metallic nanoslits. Journal of Nanophotonics 5, 051821–051821 (2011).
Karabchevsky, A., Karabchevsky, S. & Abdulhalim, I. Fast surface plasmon resonance imaging sensor using radon transform. Sensors and Actuators B: Chemical 155, 361–365 (2011).
Genevet, P., Lin, J., Kats, M. A. & Capasso, F. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes. Nature Communications 3, 1278 (2012).
Sun, S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nature Materials 11, 426–431 (2012).
Huang, L. et al. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light: Science & Applications 2, e70 (2013).
Lin, J. et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 340, 331–334 (2013).
Liu, Y. & Zhang, X. Metasurfaces for manipulating surface plasmons. Applied Physics Letters 103, 141101 (2013).
Turpin, J. P., Massoud, A. T., Jiang, Z. H., Werner, P. L. & Werner, D. H. Conformal mappings to achieve simple material parameters for transformation optics devices. Optics Express 18, 244–252 (2010).
Li, J. & Pendry, J. Hiding under the carpet: a new strategy for cloaking. Physical review letters 101, 203901 (2008).
Thompson, J. F., Soni, B. K. & Weatherill, N. P. Handbook of grid generation (CRC press, 1998).
Zentgraf, T., Liu, Y., Mikkelsen, M. H., Valentine, J. & Zhang, X. Plasmonic luneburg and eaton lenses. Nature Nanotechnology 6, 151–155 (2011).
Gabrielli, L. H., Liu, D., Johnson, S. G. & Lipson, M. On-chip transformation optics for multimode waveguide bends. Nature Communications 3, 1217 (2012).
Acknowledgements
The research leading to these results was funded by the start-up grant of A.K.
Author information
Authors and Affiliations
Contributions
A.K. conceived the idea and conducted the research. Y.G. performed the calculations with input from E.F. and A.K. All authors analyzed the results and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Galutin, Y., Falek, E. & Karabchevsky, A. Invisibility Cloaking Scheme by Evanescent Fields Distortion on Composite Plasmonic Waveguides with Si Nano-Spacer. Sci Rep 7, 12076 (2017). https://doi.org/10.1038/s41598-017-10578-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-10578-6
This article is cited by
-
Plasmonic tweezers: for nanoscale optical trapping and beyond
Light: Science & Applications (2021)
-
Enhanced absorption in all-dielectric metasurfaces due to magnetic dipole excitation
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.