Abstract
To date, there is a gap in the data about the state and mass balance of glaciers in the climate-sensitive subtropical regions during the Little Ice Age (LIA). Here, based on an unprecedented tree-ring sampling coverage, we present the longest reconstructed mass balance record for the Western Himalayan glaciers, dating to 1615. Our results confirm that the later phase of LIA was substantially briefer and weaker in the Himalaya than in the Arctic and subarctic regions. Furthermore, analysis of the time-series of the mass-balance against other time-series shows clear evidence of the existence of (i) a significant glacial decay and a significantly weaker magnitude of glaciation during the latter half of the LIA; (ii) a weak regional mass balance dependence on either the El Niño-Southern Oscillation (ENSO) or the Total Solar Irradiance (TSI) taken in isolation, but a considerable combined influence of both of them during the LIA; and (iii) in addition to anthropogenic climate change, the strong effect from the increased yearly concurrence of extremely high TSI with El Niño over the past five decades, resulting in severe glacial mass loss. The generated mass balance time-series can serve as a source of reliable reconstructed data to the scientific community.
Similar content being viewed by others
Introduction
The youngest and highest Himalayan mountains sustain enormous fresh water reservoirs in the form of snow, glaciers, natural lakes, permafrost and wetlands, and support a population of ~1.3 billion1. In fact, the Hindu Kush-Himalaya (HKH) harbors ~50% (by area)1 of all the glaciers outside of the polar regions which are also vulnerable to minute changes in temperature and precipitation regimes due to their latitudinal positions1. The uncertainties in the understanding of the status of glaciers and climate change in the Himalayan region are high due to the scarce and fragmented glacio-meteorological records, owing to the difficult terrain and inclement weather conditions2, 3. The increased frequency of extreme weather events and glacial disasters in these high mountains warrants a glaciological database and chronology to better assess the past and present glacier-climate relationship, and the future hydrometeorological scenarios1, 4. The assessment of the retreating Himalayan glaciers5 has generated considerable concern regarding the changing climate and its widespread effects on the future natural resources6, 7.
The difference between snow/ice accumulation and loss, i.e., the mass balance of a glacier, is the most consistent and direct indicator of its health and response to the changing climate1, 8. However, existing glacier mass balance records display poor temporal and spatial coverage with a discreet and non-uniform global distribution that signifies the even poorer availability of glacial records for the climate-sensitive subtropical mountains such as the Himalaya1. The absence of precise historical or dendroglaciological records is the reason why we have the so little knowledge about the state of the Himalayan glaciers during the Little Ice Age (LIA)9. For the tropical and sub-tropical regions, the Little Ice Age is usually marked between 1500 CE and 1850 CE10,11,12. There are already several disagreements on the concept9, 13, driving factors14, 15, duration16, prevalence17, 18, synchronicity19,20,21, and climatological characteristics22 of the LIA. We certainly cannot generalize the LIA response of the Arctic and subarctic glaciers to the lower latitude Himalayan ones as glaciers can display dissimilar behavior even in similar regional climatic settings due to varying geometry and bed topography9. Reaching a global understanding of the LIA effects, at different latitudes and altitudes, is essential to comprehend the past and future implications of drastic transient climate fluctuations. In addition to investigating dendroglaciology at the local scale, the detection of regional scale climate signals also need proper exploration since the glacier mass balance shows high cross-correlations across regional scales8. However, in the Himalayan context, a reconstructed regional mass balance record based on tree-ring data or any other proxy is unavailable mainly due to the hardships of reliable field data collection in the difficult terrain. There were several exploratory attempts to investigate the relationship of tree-ring width with Himalayan hydroclimatology23,24,25,26,27,28 and recent glacier movements29,30,31.
Our research is the maiden attempt to reconstruct the longest regional scale glacier mass balance records for the Western Himalaya based on tree-ring sampling at an unprecedented scale. Another highlight of our study is that it presents valid evidence of the significant mass loss experienced by the Himalayan glaciers even during the LIA. A comparative analysis with the Arctic and subarctic glaciers reveals that the Himalayan glaciers behaved differently during the LIA, thus indicating that the LIA was substantially briefer and weaker in the Himalayan region. We demonstrate an improved understanding of the temporal-regional glacier-climate relationship with significant implications for El Niño and Total Solar Irradiance (TSI). The generated mass balance time-series can serve as a source of reliable reconstructed data to the scientific community.
Sampling and LIA trends
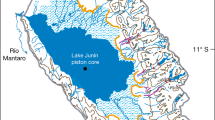
In this study, we have selected the study area based on the availability of all the glaciological mass balance measurements and the corresponding tree-ring sampling in the Indian Himalaya (Fig. 1). The study provides a representative mass balance time-series for ~10,000 glaciers within similar climate zones in the Western Himalaya within the red dotted ellipse in Fig. 1. A short introduction to the dendroglaciology is given in the materials and methods section, as is a detailed account of the data collection, statistical analysis, mass balance reconstructions, and validations. We have performed separate data collection and analysis for the glaciers in the three Indian Himalayan states which represent different climates and precipitation regimes and significantly contribute to the Indus and Ganges river systems (Fig. 1). The northernmost state of Jammu and Kashmir (J&K) displays the highest climatic variability, with a mixture of temperate continental, Mediterranean, temperate and humid subtropical towards the west and south-west and cold arid and semi-arid towards east and north-east32. The J&K glaciers under consideration here fall within the temperate continental climate zone and mostly gain ice mass through winter snowfall caused by the Western Disturbance (WD)33. This study does not include the Karakoram glaciers in eastern and north-eastern J&K because they represent completely different topographical and climatic controls and lack high altitude tree-line and measured glaciological mass balances. The Himalayan state south of J&K is Himachal Pradesh (HP) and the HP glaciers fall within the temperate and temperate continental climate zones32. These glaciers receive snowfall from both the WD in the winter and the Indian Summer Monsoon (ISM). The J&K and HP glaciers contribute to the Indus river system while the glaciers in the southernmost Himalayan state of Uttarakhand (UK) contribute to the Ganges river system. The UK glaciers fall mainly within the humid subtropical climate and receive snow mainly from ISM. Thus, although all of the Himalayan glaciers receive varied WD contributions to their mass budget34, 35, the J&K glaciers represent the monsoon shadow zone, the HP glaciers signify the monsoon transition zone, and the UK glaciers are monsoon dominated; accordingly, these western Himalayan glaciers warrant separate considerations for their mass balance reconstructions.
Study area. The study provides a representative mass balance time-series for ~10,000 glaciers within similar climate zones in the Western Himalaya (within red dotted ellipse). The data used to generate the broad climate categories were obtained from the supplementary material from Peel et al.32 and the information about the precipitation regimes was inferred from Burbank et al.33. The glacier outlines are taken from http://rds.icimod.org/Home/Data?group=15&&themekey=HKH&&page=1&&themekey=HKH. The background hillshade image was generated using a 90 m spatial resolution Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM) (http://rds.icimod.org/Home/DataDetail?metadataId = 8744). The inset map displays the location of the study area marked by the red rectangle. The map is created using ArcGIS Version 10.4 (http://desktop.arcgis.com/en/arcmap/latest/get-started/setup/arcgis-desktop-quick-start-guide.htm).
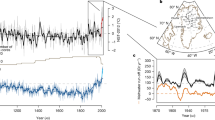
We present the regional mass balance reconstruction results in Fig. 2. The longest reconstructed time-series goes back to 1615 CE for the UK glaciers (Fig. 2a), followed by 1682 CE for J&K (Fig. 2b), and 1728 CE for the HP glaciers (Fig. 2c). Our first objective is to visualize the glacier mass balance scenarios during the latter half of the LIA which is marked by a considerable decrease in the solar activity particularly during 1645 CE – 1715 CE (Maunder minimum) and 1790 CE – 1830 CE (Dalton minimum)36. The gray shaded regions in Fig. 2 highlight the years with the highest positive mass balance and lowest Total Solar Irradiance (TSI) during the LIA. However, the violet ellipses within the gray shading in Fig. 2 also mark the years with extremely negative mass balances even during low solar activity in the LIA. These observations strikingly coincide with the long-term tree-ring-based spring temperature patterns in the western Himalaya37 (pink dotted curve in Fig. 2). The extremely negative mass balances in the gray shaded regions can easily be seen flanking the positive temperature anomaly years. If we go ahead in this time-series (~1880 CE – 1940 CE) in Fig. 2, we find several more years highlighted by black ellipses when although the TSI was lower, the mass balances were significantly negative due to the positive Niño 4 indices. This highlights a significant dependence of the UK (Fig. 2a) and southern HP (Fig. 2c) glaciers not only on the temperature conditions but also on the ISM precipitation. The reverse of this effect can be observed for the years marked by the green ellipses in Fig. 2, which show positive mass balances in the post LIA years with low TSI and negative Niño 4 indices. At the same time, the J&K glaciers (Fig. 2b), which are at the highest altitudes and the highest Himalayan latitudes are relatively far from industrial settlements and dense populations, and receive significant winter snowfall from the WD, show the least fluctuation in their mass balance profile due to their lack of dependence on the ISM and regional temperature instabilities. Thus, we believe that the episodes of significantly negative mass balances (violet ellipses) during the gray shaded phases in the LIA (Fig. 2) were the result of an enhanced El Niño affecting the ISM and increasing the temperatures, while the purple arrows (Fig. 2) further signify a more direct relationship between the high TSI and more negative mass balances during the LIA in the years with potentially weaker El Niño. These visual observations and inferences are well-supported by the results of the wavelet analysis (Fig. 3) described below. Wavelet decomposition studies are especially relevant to the analysis of non-stationary systems, i.e., systems with short-lived transient components, such as those observed in climate-related series, and the wavelet analysis permits the analysis of the relationships between two different signals.
Reconstructed specific mass balance for the Himalayan glaciers. (a) UK glaciers. (b) J&K glaciers. (c) HP glaciers. Gray shaded regions highlight the years with positive mass balance and the lowest TSI during the LIA. Violet ellipses within the gray shading highlight a few of the most negative mass balances during the lower solar activity in the LIA, probably due to an enhanced El Niño affecting ISM, as is evident in the latter years with high Niño 4 index (black ellipses). Purple arrows signify the direct relationship between high TSI and more negative mass balances during the LIA. Green ellipses show positive mass balances in the post LIA years with low TSI and negative Niño 4 index. Blue ellipses highlight the increased coincidences of El Niño with extremely high TSI since the 1970s. The reconstructed mean spring temperature departure time-series is taken from Yadav and Singh37, the TSI time-series is obtained from http://spot.colorado.edu/~koppg/TSI/TSI_TIM_Reconstruction.txt, and the Niño 4 index is derived from http://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Nino4/ ref. 38.
Wavelet power spectrum. (a) UK glaciers. (b) J&K glaciers. (c) HP glaciers. (d) Western Himalaya. Plots are prepared using an online tool (http://ion.exelisvis.com)40. The black contours are the 10% significance regions above the global wavelet spectrum (GWS). Netted region represents the cone of influence.
Figure 3 shows the results of an advanced time–frequency analysis that we performed by carefully considering the recommendations (detailed in the materials and methods section) given by the pioneer studies39, 40 describing wavelet transformations for climate time-series. The periodicities and oscillations of the regional mass balances derived from the robust wavelet analysis display a spectacular congruence with the observations made in Fig. 2. For the UK glaciers, the lowest reconstructed mass balance corresponds to 1631 CE (Fig. 2a), during the LIA. It follows a positive temperature anomaly in the preceding years, and the equivalent time-frequency graph in Fig. 3a suggests a periodicity of ~2–5 years corresponding to strong El Niño episodes in those years41. Similarly, the next significantly low mass balance in 1648 CE (Fig. 2a), can be attributed to another short but strong El Niño episode with a periodicity ~2–4 years (Fig. 3a). However, flanking these El Niño episodes, another significant periodicity of ~8–10 years during ~1640–1655 CE is noticeable (Fig. 3a) and can be attributed to the North Atlantic Oscillation (NAO) variability. The dropping temperatures and multiple positive mass balances during this period (Fig. 2a) are thus understandable as being related to the positive phase of the NAO and the warm phase of the El Niño-Southern Oscillation (ENSO) intensifying the WD and bringing precipitation to the Himalaya42. Interestingly, the entire period from ~1660–1720 CE has an ~32 year periodicity (Fig. 3a), a possible mark of the Atlantic Multi-decadal Oscillation (AMO)42,43,44, coupled with an NAO episode of ~8 year periodicity in between from 1685-1700 CE (Fig. 3a). This is the reason behind the absence of any ENSO periodicity during this interval, as the warm phase of the AMO is known to break the ENSO-NAO relationship and simultaneously results in higher than average temperatures (Fig. 2a) over the western Himalaya42. The NAO episode in the middle of this AMO periodicity can be responsible for the considerable spring precipitation in the Himalaya42 and thus for the positive mass balance during ~1685–1690 CE (Fig. 2a,b). In case of the J&K glaciers, the blank spaces in most of the time-series (Fig. 3b) indicate that, as mentioned above, due to their latitudinal and altitudinal setting, they receive significant winter snowfall from the WD and thus show the least fluctuation in their mass balance profile due to their lack of dependence on the ISM and regional temperature fluctuations. Their dependence on the strong WD events is the reason why they show the strongest power bands during the end of 17th and the start of 18th centuries (Fig. 3b). A significant part of this power spectrum during the early 18th century falls within the cone of influence and is not as well resolved as for rest of the Himalaya (Fig. 3b). The time-series for the HP glaciers are the shortest, with a significant span within the cone of influence (Fig. 3c). However, they also show some periodicities of ~2–8 years around ~1730–1760 CE as did the UK and J&K glaciers (Fig. 3c), with several occurrences of positive mass balances (Fig. 2c), thus indicating a prolonged response to the strong AMO episode at ~1660–1720 CE. Figure 3d displays an average picture of the glacier mass balance in the time-frequency domain for the entire western Himalaya. For a larger part of ~1800–1950 CE, any significant periodicity in the reconstructions is absent, as this is the period when the deforestation, population explosion, and industrialisation in these regions started at unprecedented scales. This fact, combined with weaker and sparser El Niño episodes and a significant cold phase of the AMO during ~1880–1930 CE42, led to widely mixed and aperiodic responses of the Western Himalayan glaciers to the climate during this period. Nevertheless, in the past 5 decades, several significant trends have been observed which are detailed in the next section.
Comparisons and recent trends
In Fig. 4, we show the variable responses of the Arctic, subarctic, and Himalayan glaciers to the LIA and post-LIA climate conditions. One thing to consider is that the mass balance for the Arctic45 and subarctic glaciers46 as shown in Fig. 4 is the net yearly mass balance while that of the Himalayan glaciers is the specific net yearly mass balance. Thus, although the magnitudes of the mass balances seem highly variable and incomparable, our main focus in this discussion will be on the positive or negative values and the trends of the mass balances. The gray shaded regions in Fig. 4 correspond to the years of lowest TSI during the LIA, and throughout these phases, we observe the highest consistency in the positive mass balances for the Arctic and subarctic glaciers (Fig. 4a). As already highlighted in the previous section and visible in Fig. 4, the Himalayan glaciers during these phases did not show many positive mass balances due to a combination of vital climatic scenarios which decide the regional glacial regime. In fact, our observations, given in Figs 2 and 4, are quite consistent with a recent study47 that compiled multiproxy records to infer that the glacial advance in the Himalaya occurred prominently up to 1600 CE during the LIA unlike the Canadian, European, and Icelandic glaciers which showed significant advances throughout the LIA. This study47 also establishes that the advancement of the glaciers during late-Holocene and LIA was significantly widespread at least in the Central Himalaya, i.e., for the UK glaciers47. A speleothem, which is another proxy for reconstructing past climate, collected from a cave at an elevation of ~1520 m in western Uttar Pradesh (south of the location of UK glaciers) showed cooler and wetter conditions during ~1450–1889 CE48 along with the confirmed presence of a warmer and drier climate flanking this period due to weak South Asian monsoon48. However, Rowan47 has clearly compiled several instances of glacier advances during this phase of the LIA from the region, thus confirming the importance of precipitation in addition to the lowered temperatures for the advances of glaciers in the Himalayan Ranges. Several studies48,49,50 have further confirmed the seasonal control of westerly winter precipitation in the southern latitudes of UK glaciers, which happens to be even greater in case of the HP and J&K glaciers. On the similar lines, the complex nature of precipitation (monsoon/westerly)-temperature regimes in these mountains have additionally been long-established51 by the fact that the recorded LIA glacier advances are negatively correlated with the hemispheric temperature records and thus, significantly driven by the patterns of westerlies47, 51. Due to the westerly influence, the LIA in the Western Himalaya was slightly delayed than the eastern part47. However, another study52 based on lacustrine sediments suggests the start of cold conditions since 1300 CE, lasting throughout the LIA. We also observed similar scenarios where the UK glaciers are the ones showing the largest mass balance variability, followed by the HP glaciers, and finally by the most consistent profile for the J&K glaciers (Fig. 2).
Mass balance comparisons between the Arctic, subarctic, and Himalayan glaciers. (a) Yearly mass balance time-series. (b) Decadal moving average mass balance time-series. The dashed black rectangle shows the recent period (1970–2010) of decreasing mass balance trend. The gray shaded regions correspond to the years with the lowest TSI during the LIA. The red shaded region highlights the start of strong solar cycles that in later years (since the 1970s) started showing substantial coupling with strong El Niño episodes and rising regional temperatures. The violet line represents the time when the Northern Hemisphere temperatures started experiencing a steep rise due to the cumulative effects of industrialisation. The mass balance data for Sweden are taken from Linderholm et al.45, and those of the Canadian Rockies are from Lewis and Smith46. The Northern Hemisphere temperatures are derived from Mann et al.20 and the mean spring temperature departure time-series for the western Himalaya is taken from Yadav and Singh37.
The differences in the LIA responses of these Northern Hemisphere glaciers from across varying latitudes are easily noticeable (Fig. 4). However, the main aim of this section is to highlight the more subtle responses post-LIA, particularly since the start of the second decade of the 20th century. The violet line in Fig. 4 shows the period when the Northern Hemisphere temperatures20 started experiencing a steep unidirectional rise. During the 1930s, the Northern Hemisphere temperature anomaly became positive, and, from this point onwards, the number of positive mass balance years in Arctic Sweden and subarctic Canada showed a significant decline (Fig. 4a). In the case of the Himalaya, the red shaded region in Fig. 4 highlights this phase of rising regional temperatures, and the start of the strong solar cycles that in later years (Since the 1970s), started showing substantial coupling with strong El Niño episodes. Figure 3a and d also shows mass balance periodicities of 9–12 years during ~1970–1990, a representation of the response to a few of the strongest consecutive solar cycles in past 400 years53. In fact, we see that ~50% of the years since 1970 experienced an exceptionally high TSI of >1361 Wm−2, ~40% of which also underwent warm phases of ENSO. These decades are also the ones which have seen unprecedented increase in regional populations, industrialisation, emissions, and deforestation. This makes the distinction between the different contributions from natural and anthropogenic drivers difficult to determine, as Fig. 4 (dashed black rectangle) shows the significantly decreasing mass balance per year since 1970 for the Himalayan glaciers. In fact, only 6 years in the past 5 decades have shown positive regional scale mass balances (Fig. 2). This significant trend of decreasing mass balance has never been so persistent for the western Himalaya (Fig. 4b). The current solar cycle and the subsequent ones are expected to be particularly weak and the mass balance response of the Himalayan glaciers in the coming decades can help us to clearly resolve the degrees of contribution from the natural and anthropogenic drivers. However, there is one more way to achieve this resolution up to a certain extent, as is shown in Fig. 5, i.e., by considering regional mass balance deterioration. While the decadal rates of decrease in mass balance for the UK and HP glaciers (Fig. 5) are ~6% and ~5%, respectively, with a significant yearly correlation in their declines, the decadal rate of decrease for the J&K glaciers (which are the farthest from anthropogenic influences54) is nearly stable (Fig. 5). The reason behind the moderate trend of mass loss in J&K can be attributed to the increasing precipitation55 and the lower rate of warming56 in the region. Although, the J&K glaciers have shown a moderate mass loss trend throughout their time-series, the recent trends for all three Himalayan subregions suggest that the anthropogenic drivers are certainly accentuating the glacier mass loss in the regions which are lower in latitude and altitude and are closer to the population.
Conclusions and future prospects
The present study aims to provide the first reconstruction of the longest Himalayan glacier mass balance time-series since 1615 CE. These data can be invaluable to the research community to make hydroclimatic inferences about the glaciated Himalayan terrain during the past 400 years. The results also establish that the temporal extent of the LIA was considerably shorter in terms of glacier advances in the Himalaya and that the Himalayan glaciers suffered significant mass losses even during the latter half of the globally accepted age of the LIA. This study further displays the complex climatic controls on the Himalayan glacier mass balances which make them behave in a considerably different manner than the glaciers in higher latitudes. Our results suggest that the Western Himalayan deglaciation started much earlier in the LIA. The tree-ring based spring-to-summer (March–April–May) temperature reconstruction of the UK Himalaya57 suggests that this region was relatively warmer during the LIA and did not indicate any centennial cold excursions. This indicates that the LIA was identified as a minor event at least in terms of the changes in spring temperatures, and that the period 1600–1700 CE was generally warm during springs57. Further, the tree samples collected from Lahaul-Spiti (HP)57 indicate that this region was also warm even during the period 1400–1500 CE, followed by a decrease in the summer temperatures to the coldest during 1700–1900 CE. Thus, we see that even between the adjoining states of UK and HP, the temperatures displayed significant spatio-temporal variability. This variability is even more pronounced if we compare the Eastern Himalaya with the western part. Krusic et al.58 reconstructed summer temperature variability over the Bhutanese Himalaya showing three prominent cold periods. Two of these periods were in the mid-fifteenth century, and the third one occurred in the late seventeenth century, followed by the warmest period in the first decade of the twenty first century coinciding with the timing of general glacier recession in the Eastern Himalaya58. The LIA in the Western Himalaya was not as conspicuous a phenomenon as in the higher latitudes of the Northern Hemisphere. Instead, in the Western Himalaya, LIA was indeed a disconnected phenomenon where periods of warmer episodes intruded the periods of cooler episodes. Our results also highlight the fact that glaciation and deglaciation are resultants of not only temperatures but also precipitation and this complex control of precipitation and temperature regimes is extremely prominent in the Himalaya. Our mass balance time-series suggests that even during several advances in the LIA47, there have been phases when significant deglaciation occurred within the Himalaya and the advances showed by some glaciers should not be generalised for the entire mountain range.
Although, the study acknowledges the contributions of anthropogenic drivers of climate change in the Himalayan region, it also highlights a strong effect from the increased yearly concurrence of extremely high TSI with El Niño in the past five decades, resulting in severe glacial mass loss. A global study by Solomina et al. (2016)59 also correlates the glacier advances with the increased volcanism and low solar irradiance and deglaciations with the anthropogenic activities, thus depicting the significance of external controlling factors on the glacier mass balances. While the instrumental records are inadequate to convincingly assess the extent of anthropogenic climate change, ~180 years of industrial-era warming has already resulted in rising surface temperatures above the preindustrial values, and natural background variability for several regions including the subtropical latitudes in which the Himalaya is situated60. Although, this external anthropogenic forcing can partly control the glacial regime in the Himalaya, the natural climate variability still emerges as the key deciding element governing the Himalayan glacier mass balances5. Similar to several other studies for the region30, 43, 54, our study also identifies ENSO, NAO, and AMO as the primary drivers of the regional mass balance variability. The fact that the past few decades have experienced intensified episodes of NAO, closely correlating with rising temperature61, 62 also suggests a robust natural climatic control over the Himalayan glaciers.
Glacier mass balance is a function of a combination of various climatic factors, and we never expected a direct correlation of our reconstructed mass balance time-series with any particular parameter over an extended temporal scale. Such individual controls can occur during their extremes with short spatio-temporal domains, and we have identified several such controls throughout the time-series using visual comparative analysis and wavelet transforms. In fact, the results that we obtained strongly point towards the diverse regional climatic scenarios, complex topographical controls, and an increasing population pressure on the Himalayan glaciers. These are also the main factors that govern the tree-ring growth in the highest tree-lines closest to the glaciers and this is the reason behind our successful glacier mass balance time-series reconstruction, which not only shows a fairly acceptable performance (explained in the validation section of the materials and methods section) but also correlates with the findings of other significant paleoclimatic studies for the region26, 37, 42, 47.
This study is a significant step in the direction of establishing glacial chronologies in the Himalayan region. The scope of our research is not to study the advances but to specifically focus on the deglaciation and our results show that the deglaciation in Himalaya in general, and in Western Himalaya in particular, started much before the global average start of deglaciation following the LIA. We agree that the time period between 1500 to 1850 CE denoted as the LIA10,11,12 is debatable in the Indian context. Our study covers major part of the LIA time span and for the initial LIA stages, we are in continuous effort to collect suitable dendrochronological records. We understand that there is still a need for considerable future work, in terms of expanding the sample sites across the Himalaya by including the Eastern Himalaya and Brahmaputra river basin glaciers. This proposed sampling must consist of both, the dendrochronology (tree-ring) samples from the proximity of the glaciers, and the observed glacier mass balances across the Himalayan mountain ranges at longer and consistent spatio-temporal scales. Another improvement for model development and the resolution of the uncertainties would account for the complex topographical differences by sampling multiple adjacent glaciers with different terrain characteristics.
Materials and Methods
To reconstruct the glacier mass balance records for past few centuries, several botanical proxies based on lichenometry63, 64, wood density65 and tree-ring width64, 66 have been used. However, the lichenometry results lack a necessity for reconstructing annual mass balances, which is an annual resolution67. Tree-ring chronologies from trees with strong climate signals are capable of providing this annual resolution66. The years with high winter snow accumulation and moderate summers favor positive glacier mass balance while providing unfavorable growing conditions for trees, thus resulting in narrow annual tree-rings, and vice-versa68, 69. This inverse relationship between the meteorological parameters controlling the glacier mass balance and the tree-ring width of climatically sensitive species provides a basis for reconstructing the mass balance in remote and inaccessible glacial environments. The first results of the relationship between tree-ring variability, meteorological parameters, and glacier ice volume were reported in the 1960s70 followed by subsequent developments31, 44, 68, 69, 71,72,73,74,75,76. Below we describe the methodological steps taken in order to obtain the results detailed in this paper.
Tree-ring data
Tree rings of many of the conifers growing in the diversified geographical regions of the Himalaya are found datable and suitable for the analysis of the changing climate72, 77. We collected tree-ring samples (increment cores) from conifers growing at the upper limits of the subalpine forests close to the snouts of the glaciers from three locations in the Central and Western Himalayan regions (Supplementary Fig. 1). The samples were taken from Abies spectabilis (from two sites 78 tree/112 cores and 28 tree/35 core, respectively) and Pinus wallichiana (83 tree/122 cores). We included an additional site from the North-West Himalaya (Fig. 1) for the tree-ring width data of Abies pindrow (9 tree/10 cores). These data were taken from the NOAA website (http://www.ncdc.noaa.gov/paleo/treering.html) and samples were collected from Sonmarg, Kashmir close to the Thazwas or Tajwah Glacier. These data were updated later by replication of the tree-ring width data of the same species collected in 2015 from the same region with an increased sample size of 14 tree/27cores. Each of these sampling sites is representative of a particular climate regime (Fig. 1). We selected the trees growing at the uppermost tree line zone due to their proximity to the glaciers. The katabatic winds blowing through the glaciers significantly regulate the growth of these nearby trees, thus providing sensitive tree-ring sequences comparable to the changing Equilibrium Line Altitudes (ELA) of the glacier, which responds to climatic variations. We dated the tree-ring sequence of these cores using visual matching of growth patterns using the “skeleton plot” method of cross-dating78. We measured the dated tree-ring widths using the LINTAB measuring system and TSAP-Win software79. The quality of the cross-dating of the tree-ring width series was further checked using the COFECHA program80. Tree-ring width data series were detrended using cubic smoothing splines with a 50% frequency response cutoff of 30 years to make the ring width indices using the ARSTAN program81. This also eliminated age-related growth trends and maximised the signal from common factors influencing tree growths. All of the tree-ring width indices were combined to form a tree-ring chronology. We used the residual tree chronology of the Central, Western and North western Himalayan regions to minimize the effect of autocorrelation (Supplementary Fig. 2). The suitability of these chronologies was assessed on the basis of their statistical parameters namely, mean sensitivity (MS), the average correlation between all series (Rbar), the expressed population signal (EPS), and the first-order autocorrelation of the series. The Rbar and EPS values were computed using a 30-year moving window with a 15-year overlap (Supplementary Fig. 3).
Tree-ring chronologies
The relation between mass balance and tree growth is a function of several climatic drivers. Trees growing closer to the snout are more sensitive to the local environment created by the nearby glaciers. A study of katabatic winds and their patterns in Rongbuk Valley82, north of Mount Everest suggests that these wind play a great role in changing the local circulation patterns. The katabatic winds are extremely strong, regular, and prominent in the high Himalaya. The reason for this is that even though the glaciated area in high mountains is not as large as the ice sheets, the larger high altitude glaciers which control the glacio-hydrology of the region prominently are capable of generating such wind patterns daily in the afternoon and the narrow valleys in these mountains further channelise and intensify the flow of these winds downslopes. Based on this premise of significant glacier control over nearby tree growth, we generated tree-ring index chronologies from four sites with three conifers, namely, Abies pindrow (Thazwas Glacier-J&K), Abies pindrow (Solang Valley-HP), Abies spectablis (Dokriani valley-UK), and Pinus wallichiana (Gangotri valley-UK) to reconstruct the mass balance. The tree-ring chronologies from the Dokriani valley and the Gangotri valley were found to be positively correlated to each other (r = 0.6, p < 0.001) and were merged to make a regional chronology representative for the entire UK. The residual ring-width index chronologies of these taxa along with the number of samples (cores) included in these chronologies is shown in Supplementary Fig. 2. The mean sensitivities for these chronologies are 0.26, 0.29, 0.18, and 0.17 with the mean correlations (Rbar) of 0.21, 0.17, 0.18, and 0.29 and the signal-to-noise ratios of 5.44, 6.50, 16.20, and 30.23 for Abies pindrow (Thazwas Glacier), Abies pindrow (Solang Valley), Abies spectablis (Dokriani valley), and Pinus wallichiana (Gangotri valley), respectively (Supplementary Table 1). The mean sensitivity values of these chronologies indicate that they have high inter-annual variability and display strong environmental signals.
Mass balance and climate data
We reconstructed the regional mass balance of the Central, Western and NW Himalaya on the basis of the correlations between the tree-ring width indices and the available glaciological mass balance data for the corresponding geographical regions. Supplementary Table 2 shows the details of the observed mass balance data of the glaciers in the region used for reconstruction and the period for which the mass balance data is available. The measured glaciological balance for the Himalayan glaciers is extremely scarce and here we have used all the available and published glaciological mass balance records in order to produce the best possible time-series.
Climate is the common factor influencing both mass balance and tree growth. We analysed the tree growth-climate connection (Supplementary Fig. 4) to validate the mass balance-tree-ring width relationship (Supplementary Fig. 5). This analysis also proved the sensitivities of the sampled tree species to the high altitude Himalayan climate. Observational temperature and precipitation data in the Himalayan region is scarce and fragmented1. In addition, the weather stations are located at distant locations from the sampling sites. Therefore, we have used a gridded dataset35 covering the sampling locations to ensure the better reliability of the correlation analysis. The temperature data from the National Center for Environmental Prediction and the National Center for Atmospheric Research (NCEP/NCAR)83 for 1948–2017 and the precipitation data from the Global Precipitation Climatology Project84 for 1901–2013 was used to analyze the correlation with tree-ring width indices (Supplementary Figure 4). We used the average monthly temperatures and the total monthly precipitation starting from October of preceding year to September of the current growth year for all the sites to correlate with the tree-ring indices.
The correlation analysis shows that the winter temperature (December to February) is directly related to tree growth in the case of the Abies spectabilis collected near Dokriani glacier and the Pinus wallichiana collected near the Gangotri Glacier in UK (Supplementary Figure 4a,b). This relationship indicates that the Himalayan fir and pine trees conduct a significant amount of photosynthesis during warm winters and that the resultant photosynthates are used as stored food in the ensuing growing season. A similar relationship was observed for Pinus wallichiana in previous studies in the Himalaya85, 86. The analysis also showed positive correlations with the precipitation in May in the case of both the Abies spectabilis and Pinus wallichiana sampled from near the Dokriani and the Gangotri glaciers, respectively. This relationship was found to be statistically significant only in the case of samples collected near the Dokriani glacier. A rather significant negative growth relationship with the temperature of October of the previous year was observed for the samples collected near the Gangotri glacier. At first look, the correlation analysis of the samples taken near the Dokriani glacier and the Gangotri glacier suggests that, in this region and for the sampled tree species, the temperature plays a more significant role in determining tree growth than the precipitation. However, another fact is that the precipitation data from the extremely limited number of meteorological stations in the Himalayan region, which are ultimately used to generate the gridded datasets, are often not representational of the tree-ring sampling sites, as the precipitation in these mountains is mostly controlled by orography and shows significant variations between neighboring valleys1.
Samples of Abies pindrow were collected near the Solang valley in HP and the Thazwas valley in J&K. The growth of Abies pindrow in HP shows a statistically significant negative correlation with the temperature of the preceding October, November and July. In addition, it shows a statistically significant positive correlation with the precipitation in the month of February. The tree growth of Abies pindrow in J&K shows a strong negatively correlation with the summer temperatures (May-September). Subsequently, it shows a significant positive correlation with the total precipitation during the months of May and June. The analysis suggests that the increased precipitation and reduced temperature during the summer months in these arid (HP) and WD dominated (J&K) mountains favor growth by reducing the water losses caused by evapotranspiration.
Mass balance reconstruction
The significant negative correlation between the tree-ring data and the Annual Specific Mass Balance (MB s ) suggests that the tree-ring width of these alpine silver fir and pine could be a useful indicator of the MB s variation. Correlations between the mass balance and tree-ring width index (RWI) chronologies for J&K, HP, and UK are −0.80 (p < 0.001), −0.81 (p < 0.001), −0.84 (p < 0.001), respectively. Based on these correlations, the following linear regression models (given as equations 1, 2, and 3) between the RWI and the MB s were developed for each site (Supplementary Figure 5).
The suitability of the tree-ring chronologies was assessed by using the threshold value of EPS 0.8587. The durations of 1931–2015, 1872–2013, 1861–2014, and 1903–2015 were used as the common period (Supplementary Table 1) for Abies pindrow (Thazwas Glacier), Abies pindrow (Solang Valley), Abies spectablis (Dokirini valley), and Pinus wallichiana (Gangotri valley), respectively for the statistical analysis of the chronology (Supplementary Fig. 3). Further, to ensure the reliability and stability of the regression model (Supplementary Fig. 5), various statistical tests are carried out and the associated errors are estimated (Supplementary Table 3) (Supplementary Fig. 6).
The coefficient of determination (R2) is interpreted as the proportion of the variability of the dependent variable explained by the model. An R2 that is closer to 1 is better for the model88, 89. The adjusted R2 is a correction to the R2 which takes into account the number of variables used in the model. It could be negative if the R2 is near zero. The variance explained by the regression model (Supplementary Fig. 5) accounted for 70.4%, 64% and 66% of the UK, JK and HP time-series, respectively. For the validation of the output of the regression model, various statistical tests have been used (Supplementary Table 3). The correlation coefficients for UK (−0.84), HP (−0.81), and J&K (−0.80) were found to be significant at the 99% confidence level. The root mean square error (RMSE) has been widely used as a validation parameter for the reliability of the tree-ring chronologies-based reconstructions90. The predicted residual error sum of squares (PRESS) RMSE is a form of cross-validation used to provide a summary measure of the fit of a model91, 92. In the present study, the RMSE ranged from 0.15 m w.e. to 0.85 m w.e., whereas the PRESS RMSE ranged from 0.17 m w.e. to 0.33 m w.e., thus indicating considerably small errors in the reconstructed values. The F-test was used to estimate the significance of the regression model93 and it also provided acceptable values for UK (47.75, p < 0.001), HP (48.14, p < 0.001), and J&K (42.24, p < 0.001). These values validate the statistical significance of the models. The Durbin-Watson statistical coefficient (DW) is the order one autocorrelation coefficient and is used to check that the residuals of the model are not autocorrelated94. The DW values were found to be between 1.44 and 2.49 for all models, indicating that the residuals of the model are not autocorrelated. The positive values of reduction of error (RE), and coefficient of efficiency (CE)88, 89 show significant skills in the reconstruction and acceptable model performances90.
Cyclic behavior and spatial correlation of the reconstructed mass balance data
Wavelet analysis is a commonly used method for analyzing local variations of power within a time-series. The method involves the decomposition of a time-series into time-frequency space, which enables the determination of both the dominant modes of variability and their temporal variations38. In the present study, we used wavelet spectral analysis to determine the time-frequency domain of the annual specific mass balance (AS-MB) using the Interactive Wavelet Plot tool (http://ion.exelisvis.com/). The wavelet transforms demonstrated dominant periodic signals that could be correlated with the prevailing weather events (WD, ENSO, AMO) in the Himalaya. These signals vary in amplitude in a time-series and give information about changes in frequency. We also correlated the reconstructed annual specific mass-balance with the NOAA annual snow cover data interpolated for the Himalayan region (http://www.cpc.noaa.gov/data/snow/, Supplementary Figure 7) for nearly four decades (1972–2009). Theoretically, more snow cover should be associated with a more positive mass balance. The analysis shows positive correlations between the reconstructed mass balances and the snow cover for the entire Himalayan region. The correlation is most significant for the Indian Summer Monsoon (ISM) dominated regions (r > 0.6) and lower but still significant in the WD dominated regions (r > 0.3).
Reliability of the reconstructed mass balance data
The published records of the field-estimated mass balance data for the Himalayan glaciers are very scarce and fragmented. Therefore, the reconstructed mass balance was compared with that of the mass balance estimated at regional scales using geodetic methods95,96,97,98 and degree-day method99, 100 (Supplementary Figure 8). In general, the mass balance reconstructed in the present study was found to be in agreement with the estimated regional geodetic mass balance and well within their error limits. Exceptions include a few cases involving the mass balance of only a single basin100 or a specific glacier99. It is interesting to note that the estimated mass balance of the Chhota Shigri glacier during 1986–200099 is significantly less than the reconstructed mass balance, while the estimated mass balances during 1969–1985 and 2001–2012 for the same glacier99 show excellent agreement with our region-wide reconstructed mass balance. Thus, the reconstructed mass balance is in better agreement with the regional or long-term mass balance observations than with the glacier-specific or short-term mass balance observations. Further, the validation by comparison with geochronological and moraines dates through absolute dating techniques, i.e., radiocarbon (14 C) and terrestrial cosmogenic nuclide (TCN), as compiled by Rowan47 is not preferable here. For example, the TCN ages of moraines are single ages or more commonly the average of several samples and due to the large temporal uncertainty going up to ~200 years, it is not wise to directly correlate such geochronological data with our yearly reconstructed mass balances. Several studies101,102,103,104 have reported the glacier advances based on tree-ring dating in Tibet during the similar time frame as our study (1750 ± 20 CE). The estimated mass balances of the Karakoram region96, 97 display the famous ‘Karakoram anomaly’105 and are positive and significantly different from the reconstructed mass balance of the both HP and J&K glaciers, and therefore have not been included for this comparison.
Data availability
The supporting datasets used for analyses during the current study are available as published literature and we have cited the source for accessing the data at appropriate places. The reconstructed mass balance dataset generated during the current study is available from the corresponding author on reasonable request. All data generated or analysed during this study are included in this published article (and its Supplementary Information files).
Ethical approval and informed consent
We confirm that this study does not involve any biological experiments, harm to any animal species, or anthropogenic data collection.
References
Singh, S. et al. Changing climate and glacio‐hydrology in Indian Himalayan Region: a review. Wiley Interdisciplinary Reviews: Climate Change 7(3), 393–410, doi:10.1002/wcc.393 (2016).
Sam, L., Bhardwaj, A., Singh, S. & Kumar, R. Remote sensing flow velocity of debris-covered glaciers using Landsat 8 data. Progress in physical geography. doi:10.1177/0309133315593894 (2015).
Snehmani Bhardwaj, A., Singh, M. K., Gupta, R. D., Joshi, P. K. & Ganju, A. Modelling the hypsometric seasonal snow cover using meteorological parameters. Journal of spatial science. 60(1), 51–64, doi:10.1080/14498596.2014.943310 (2015).
Goswami, B. N., Venugopal, V., Sengupta, D., Madhusoodanan, M. S. & Xavier, P. K. Increasing trend of extreme rain events over India in a warming environment. Science 314, 1442–1445, doi:10.1126/science.1132027 (2006).
Bolch, T. et al. The state and fate of Himalayan glaciers. Science 336, 310–314, doi:10.1126/science.1215828 (2012).
Immerzeel, W. W., Van Beek, L. P. H. & Bierkens, M. F. P. Climate change will affect the Asian water towers. Science, 328, 1382–1385, doi:10.1126/science.1183188 (2010).
IPCC. Summary for policymakers. In: Stocker, T. F. et al. (Eds), Climate Change 2013: The Physical Science Basis. Contribution of Working Group III to the Fifth Assessment Report of Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge and New York (2013).
Pelto, M. S. & Reidel, J. Spatial and temporal variations in annual balance of North Cascade glaciers, Washington 1984–2000: Hydrological Processes, 15, 3461–3472, doi:10.1002/hyp.1042 (2001).
Matthews, J. A. & Briffa, K. R. The ‘Little Ice Age’: re-evaluation of an evolving concept. Geografiska Annaler: Series A. Physical Geography 87, 17–36, doi:10.1111/j.0435-3676.2005.00242.x (2005).
Graham, N. E., Ammann, C. M., Fleitmann, D., Cobb, K. M. & Luterbacher, J. Support for global climate reorganization during the “Medieval Climate Anomaly”. Climate Dynamics 37, 1217–1245, doi:10.1007/s00382-010-0914-z (2011).
Grove, J. M. The Initiation of the "Little Ice Age" in regions round the North Atlantic. Climatic Change 48(1), 53–82 (2001).
Lamb, H. H. The early medieval warm epoch and its sequel. Palaeogeography, Palaeoclimatology, Palaeoecology 1, 13–37, doi:10.1016/0031-0182(65)90004-0 (1965).
Ogilvie, A. E. J. & Jonsson, T. ‘Little Ice Age’ research: a perspective from Iceland. Climatic Change 48, 9–52, doi:10.1023/A:1005625729889 (2001).
Lean, J., Beer, J. & Bradley, R. S. Reconstruction of Solar Irradiance since 1610: Implications for Climatic Change. Geophysical Research Letters 22, 3195–3198, doi:10.1029/95GL03093 (1995).
Mann, M. E., Bradley, R. S. & Hughes, M. K. Global-scale Temperature Patterns and Climate Forcing Over the Past Six Centuries. Nature 392, 779–787, doi:10.1038/33859 (1998).
Mann, M. E. et al. Global signatures and dynamical origins of the Little Ice Age and Medieval Climate Anomaly. Science 326(5957), 1253–1256, doi:10.1126/science.1177303 (2009).
Jones, P. D. & Mann, M. E. Climate over past millennia. Reviews of Geophysics 42, RG202, doi:10.1029/2003RG00 0143 (2004).
Liu, L. B., Yao, Z. and Thompson, L. G. A pollen record of Holocene climatic changes from the Dunde ice cap, Qinghai-Tibetan Plateau. Geology 26(2), 135–138 (1998).
Grove, J. M. Little Ice Ages: Ancient and Modem, 2, Routledge. London. 718 p (2004).
Mann, M. E., Bradley, R. S. & Hughes, M. K. Northern Hemisphere temperatures during the past millennium: Inferences, uncertainities, and limitations. Geophysical Research Letters 26(6), 759–762, doi:10.1029/1999GL900070 (1999).
Porter, S. C. Recent glacier variations and volcanic eruptions. Nature 291, 139–142, doi:10.1038/291139a0 (1981).
Nesje, A. & Dahl, S. O. The ‘Little Ice. Age’ - only temperature? The Holocene 13(1), 139–145, doi:10.1191/0959683603hl603fa (2003).
Bhattacharyya, A. & Chaudhary, V. Late-summer temperature reconstruction of the eastern Himalayan region based on tree-ring data of Abies densa. Arctic, Antarctic, and Alpine Research 35(2), 196–202 (2003).
Treydte, K. S. et al. The twentieth century was the wettest period in northern Pakistan over the past millennium. Nature 440(7088), 1179–1182, doi:10.1038/nature04743 (2006).
Cook, E. R. et al. Asian monsoon failure and megadrought during the last millennium. Science 328(5977), 486–489, doi:10.1126/science.1185188 (2010).
Yadav, R. R. & Bhutiyani, M. R. Tree‐ring‐based snowfall record for cold arid western Himalaya, India since AD 1460. Journal of Geophysical Research: Atmospheres 118(14), 7516–7522, doi:10.1002/jgrd.50583 (2013).
Shekhar, M. Application of Multi-proxy tree-ring parameters in the reconsutcion of climate vis-à-vis glacial fluctuation from the Eastern Himalaya. Ph.D thesis. Department of Botnay, University of Lucknow, Lucknow, Uttar Pradesh, India http://shodhganga.inflibnet.ac.in/bitstream/10603/43041/1/mayank_shekhar_ph_d_botany_2013.pdf (2014).
Shekhar, M. & Bhattacharyya, A. Reconstruction of January–April discharge of Zemu Chuu–A first stage of Teesta River North Sikkim Eastern Himalaya based on tree-ring data of fir. Journal of Hydrology: Regional Studies 4(B), 776–786, doi:10.1016/j.ejrh.2015.06.019 (2015).
Singh, J. & Yadav, R. R. Tree-ring indications of recent glacier fluctuations in Gangotri, western Himalaya, India. Current Science 79(11), 1598–1601 (2000).
Bhattacharyya, A. & Yadav, R. R. Dendrochronological reconnaissance of Pinus wallichiana to study glacial behaviour in the western Himalaya. Current Science 70(8), 739–743 (1996).
Borgaonkar, H. P., Ram, S. & Sikder, A. B. Assessment of tree-ring analysis of high-elevation Cedrus deodara D. Don from Western Himalaya (India) in relation to climate and glacier fluctuations. Dendrochronologia 27(1), 59–69, doi:10.1016/j.dendro.2008.09.002 (2009).
Peel, M. C., Finlayson, B. L. & McMahon, T. A. Updated world map of the Köppen-Geiger climate classification. Hydrology and Earth System Sciences 11, 1633–1644, doi:10.5194/hess-11-1633-2007 (2007).
Burbank, D. W., Bookhagen, B., Gabet, E. J. & Putkonen, J. Modern climate and erosion in the Himalaya. Comptes Rendus Geoscience 344(11–12), 610–626, doi:10.1016/j.crte.2012.10.010 (2012).
Dimri, A. P. et al. Western Disturbances: A review. Reviews of Geophysics 53(2), 225–246, doi:10.1002/2014RG000460 (2015).
Kumar, P. et al. Response of Karakoram-Himalayan glaciers to climate variability and climatic change: A regional climate model assessment. Geophysical Research Letters 42(6), 1818–1825, doi:10.1002/2015GL063392 (2015).
Zharkova, V. V., Shepherd, S. J., Popova, E. & Zharkov, S. I. Heartbeat of the Sun from Principal Component Analysis and prediction of solar activity on a millennium timescale. Scientific reports 5(15689), 1–11, doi:10.1038/srep15689 (2015).
Yadav, R. R. & Singh, J. Tree-ring-based spring temperature patterns over the past four centuries in western Himalaya. Quaternary Research 57(3), 299–305, doi:10.1006/qres.2002.2337 (2002).
Rayner, N. A. et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. Journal of Geophysical Research 108(D14), 4407, doi:10.1029/2002JD002670 (2003).
Lau, K. M. & Weng, H. Y. Climate signal detection using wavelet transform: How to make a time series sing. Bulletin of American Meteorological Society 76, 2391–2402, doi:10.1175/1520-0477(1995)076<2391:CSDUWT>2.0.CO;2 (1995).
Torrence, C. & Compo, G. P. A practical guide to wavelet analysis. Bulletin of the American Meteorological society 79(1), 61–78, doi:10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 (1998).
Trenberth, K. E. Spatial and temporal variations of the Southern Oscillation. Quarterly Journal of the Royal Meteorological Society 102(433), 639–653, doi:10.1002/qj.49710243310 (1976).
Yadav, R. R. Long-term hydroclimatic variability in monsoon shadow zone of western Himalaya, India. Climate Dynamics 36(7–8), 1453–1462, doi:10.1007/s00382-010-0800-8 (2011).
Hubeny, J. B., King, J. W. & Santos, A. Sudecadal to multidecadal cycles of late Holocene North Atlantic climate variability preserved by estuarine fossil pigments. Geology 34(7), 569–572, doi:10.1130/G22671.1 (2006).
Knight, J. R., Allan, R. J., Folland, C. K., Vellinga, C. K. & Mann, M. E. A signature of persistent natural thermohaline circulation cycles in observed climate. Geophysical Research Letters 32(20), L20708. doi:1029/2005GL024233 (2005).
Linderholm, H. W., Jansson, P. & Chen, D. A high-resolution reconstruction of Storglaciären mass balance back to 1780/81 using tree-ring data and circulation indices. Quaternary Research 67, 12–20, doi:10.1016/j.yqres.2006.08.005 (2007).
Lewis, D. & Smith, D. J. Dendrochronological mass balance reconstruction, Strathcona Provincial Park, Vancouver island, British Columbia, Canada. Arctic, Antarctic, and Alpine Research 36, 598–606 (2004).
Rowan, A. V. The ‘Little Ice Age’ in the Himalaya: A review of glacier advance driven by Northern Hemisphere temperature change. The Holocene 27(2), 292–308, doi:10.1177/0959683616658530 (2017).
Liang, F. et al. Panigarh cave stalagmite evidence of climate change in the Indian Central Himalaya since AD 1256: Monsoon breaks and winter southern jet depressions. Quaternary Science Reviews 124, 145–161, doi:10.1016/j.quascirev.2015.07.017 (2015).
Kotlia, B. S. et al. Climatic fluctuations during the LIA and post-LIA in the Kumaun Lesser Himalaya, India: Evidence from a 400 y old stalagmite record. Quaternary International 304, 183–192, doi:10.1016/j.quaint.2012.01.025 (2012).
Kotlia, B. S., Singh, A. K., Joshi, L. M. & Dhaila, B. S. Precipitation variability in the Indian Central Himalaya during last ca. 4,000 years inferred from a speleothem record: Impact of Indian Summer Monsoon (ISM) and Westerlies. Quaternary International. 371, 244–253, doi:10.1016/j.quaint.2014.10.066 (2015).
Murari, M. K. et al. Timing and climatic drivers for glaciation across monsoon-influenced regions of the Himalayan–Tibetan orogen. Quaternary Science Reviews 88, 159–182, doi:10.1016/j.quascirev.2014.01.013 (2014).
Rawat, S., Gupta, A. K., Sangode, S. J., Srivastava, P. & Nainwal, H. C. Late Pleistocene–Holocene vegetation and Indian summer monsoon record from the Lahaul, Northwest Himalaya, India. Quaternary Science Reviews, 114, 167–181, 10.1016/j.quascirev.2015.01.032.
Hrushesky, W. J. et al. Sunspot dynamics are reflected in human physiology and pathophysiology. Astrobiology 11(2), 93–103, doi:10.1089/ast.2010.0574 (2011).
Chadchan, J. & Shankar, R. An analysis of urban growth trends in the post-economic reforms period in India. International Journal of Sustainable Built Environment 1(1), 36–49, doi:10.1016/j.ijsbe.2012.05.001 (2012).
Archer, D. R. & Fowler, H. J. Spatial and temporal variations in precipitation in the Upper Indus Basin: global teleconnections and hydrological implications. Hydrology and Earth System Science 8, 47–61, doi:10.5194/hess-8-47-2004 (2004).
Fowler, H. J. & Archer, D. R. Conflicting signals of climatic change in the Upper Indus Basin. Journal of Climate 19, 4276–4293, doi:10.1175/JCLI3860.1 (2006).
Yadav, R. R., Park, W.-K. & Bhattacharyya, A. Spring-temperature variations in western Himalaya, India, as reconstructed from tree-rings: AD1390-1987. The Holocene 9(1), 85–90, doi:10.1191/095968399667529322 (1999).
Krusic, P. J. et al. Six hundred thirty eight years of summer temperature variability over the Bhutanese Himalaya. Geophysical Research Letters 42(8), 2988–2994, doi:10.1002/2015GL063566 (2015).
Solomina, O. N. et al. Glacier fluctuations during the past 2000 years. Quaternary Science Reviews 149, 61–90, doi:10.1016/j.quascirev.2016.04.008 (2016).
Abram, N. J. et al. Early onset of industrial-era warming across the oceans and continents. Nature. 536, 411–418, doi:10.1038/nature19082 (2016).
Hurrell, J. W. Influence of variations in extratropical wintertime teleconnections on Northern Hemisphere temperature. Geophysical Research Letters 23(6), 665–668, doi:10.1029/96GL00459 (1996).
Schulz, M. et al. Tracing climate variability; the search for climate dynamics on decadal to millennial time scales. In Climate Development and History of the North Atlantic Realm, Wefer, G., Berger, W. H., Behre, K. E. & Jansen, E. (eds). Springer-Verlag: Berlin; 125–148 (2002).
Rabatel, A., Jomelli, V., Naveau, P., Francou, B. & Grancher, D. Dating of Little Ice Age glacier fluctuations in the tropical Andes: Charquini glaciers, Bolivia, 16°S. Comptes Rendus Geoscience 337(15), 1311–1322, doi:10.1016/j.crte.2005.07.009 (2005).
Winchester, V., Harrison, S. & Warren, C. R. Recent retreat Glaciar Nef, Chilean Patagonia, dated by lichenometry and dendrochronology. Arctic, Antarctic, and Alpine Research 33(3), 266–273 (2001).
Wood, L. J., Smith, D. J. & Demuth, M. N. Extending the Place Glacier mass-balance record to AD 1585, using tree rings and wood density. Quaternary Research 76(3), 305–313, doi:10.1016/j.yqres.2011.07.003 (2011).
Nicolussi, K. & Patzelt, G. Reconstructing glacier history in Tyrol by means of tree-ring investigations. Zeitschrift für Gletscherkunde und Glazialgeologie 32, 207–215 (1996).
Winchester, V. & Harrison, S. Dendrochronology and lichenometry: colonization, growth rates and dating of geomorphological events on the east side of the North Patagonian Icefield, Chile. Geomorphology 34(3–4), 181–194, doi:10.1016/S0169-555X(00)00006-4 (2000).
LaMarche, V. C. & Fritts, H. C. Tree rings, glacial advance, and climate in the Alps. Zeitschrift fur Gletscherkunde und Glazialgeologie 7, 125–131 (1971).
Matthews, J. A. & Briffa, K. R. Glacier and climatic fluctuations inferred from tree growth variations over the last 250 years, central southern Norway. Boreas 6(1), 1–24, doi:10.1111/j.1502-3885.1977.tb00692.x (1977).
Bray, J. R. & Struik, G. J. Forest growth and glacial chronology in eastern British Columbia, and their relation to recent climatic trends. Canadian Journal of Botany 41(8), 1245–1271, doi:10.1139/b63-104 (1963).
Brauning, A. Tree-ring evidence of ‘Little Ice Age’ glacier advances in southern Tibet. The Holocene 16(3), 369–380, doi:10.1191/0959683606hl922rp (2006).
Bhattacharyya, A. & Shah, S. K. Tree-ring studies in India past appraisal, present status and future prospects. IAWA journal 30(4), 361–370, doi:10.1163/22941932-90000224 (2009).
Heikkinen, O. Dendrochronological evidence of variations of Coleman glacier, Mount Backer, Washington, USA. Arctic and Alpine Research 16(1), 53–64, doi:10.2307/1551172 (1984).
Larocque, S. and Smith, D.J. ‘Little Ice Age’ proxy glacier mass balance records reconstructed from tree rings in the Mt Waddington area, British Columbia Coast Mountains, Canada. The Holocene, 15(5), 748–757, doi:10.1191/0959683605hl848rp (2005).
Villalba, R., Leiva, J. C., Rubulls, S., Suarez, J. & Lenzano, L. Climate, tree-ring, and glacial fluctuations in the Rio Frias Valley, Rio Negro, Argentina. Arctic and Alpine Research 22(3), 215–232 (1990).
Watson, E. & Luckman, B. Tree-ring-based mass-balance estimates for the past 300 years at Peyto Glacier, Alberta, Canada. Quaternary Research 62(1), 9–18, doi:10.1016/j.yqres.2004.04.007 (2004).
Bhattacharyya, A., LaMarche, V. C. & Telewski, F. W. Dendrochronological reconnaissance of the conifers of northwest India. Tree-Ring Bulletin 48, 21–30 (1988).
Stokes, M. A. & Smiley, T. L. An Introduction to Tree-Ring Dating. The University of Chicago Press, Chicago, 73 (1968).
Rinn, F. TSAP-Win: time series analysis and presentation for dendrochronology and related applications. Frank Rinn, Heidelberg (2003).
Holmes, R. L. Computer-assisted quality control in tree-ring dating and measurement. Tree-ring bulletin 43(1), 69–78 (1983).
Cook, E. R. & Krusic, P. J. Program ARSTAN: a tree-ring standardization program based on detrending and autoregressive time series modeling, with interactive graphics. Lamont-Doherty Earth Observatory, Columbia University, Palisades, NY (2005).
Song, Y., Zhu, T., Cai, A., Lin, W. & Kang, L. Glacier winds in the Rongbuk Valley, north of Mount Everest: 1. Meteorological modeling with remote sensing data. Journal of Geophysical Research: Atmospheres 112(D11), 1–10, doi:10.1029/2006JD007867 (2007).
Kalnay, E. et al. The NCEP/NCAR 40-Year Reanalysis Project. Bulletin of American Meteorological Society 77(3), 437–471, doi: 10.1175/1520-0477 (1996).
Schneider, U. et al. GPCC Full Data Reanalysis Version 7.0 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges built on GTS-based and Historic. Data. doi:10.5676/DWD_GPCC/FD_M_V7_050 (2015).
Yadav, R. R. & Bhattacharyya, A. Climate and growth relationship in blue Pine (Pinus wallichiana) from the western Himalaya, India. The Korean. Journal of Ecology 20(2), 95–102 (1997).
Singh, J. & Yadav, R. R. Tree-ring indications of recent glacier fluctuations in Gangotri, western Himalaya, India. Current Science 79(11), 1598–1601 (1990).
Wigley, T. M. L., Briffa, K. R. & Jones, P. D. On the average value of correlated time series with applications in dendroclimatology and hydrometeorology. Journal of Climate and Applied Meteorology 8, 201–213, doi:10.1175/1520-0450 (1984).
Fritts, H.C. T Rings and Climate. Academic Press, New York, 567 (1976).
Cook, E. R., Meko, D. M., Stahle, D. W. & Cleaveland, M. K. Drought reconstructions for the continental United States. Journal of Climate 12(4), 1145–1162, doi: 10.1175/1520-0442 (1999).
Schofield, M. R., Barker, R. J., Gelman, A., Cook, E. R. & Briffa, K. R. A model-based approach to climate reconstruction using tree-ring data. Journal of the American Statistical Association 111(513), 93–106, doi:10.1080/01621459.2015.1110524 (2016).
Cook, E. R. & Kairiukstis, L. A. (Eds) Methods of Dendrochronology: Applications in the Environmental Sciences. Springer, 393 (1990).
Allen, E. B. et al. A tree‐ring based reconstruction of Logan River streamflow, northern Utah. Water Resources Research 49(12), 8579–8588, doi:10.1002/2013WR014273 (2013).
Mundo, I. A. et al. Multi-century tree-ring based reconstruction of the Neuquén River streamflow, northern Patagonia, Argentina. Climate of the Past 8, 815–829, doi:10.5194/cp-8-815-2012 (2012).
Duan, J., Wang, L., Li, L. & Sun, Y. Tree-ring-inferred glacier mass balance variation in southeastern Tibetan Plateau and its linkage with climate variability. Climate of the Past 9(6), 2451–2458, doi:10.5194/cp-9-2451-2013 (2013).
Berthier, E. et al. Remote sensing estimates of glacier mass balances in the Himachal Pradesh (Western Himalaya, India). Remote Sensing of Environment 108(3), 327–338, doi:10.1016/j.rse.2006.11.017 (2007).
Gardelle, J., Berthier, E., Arnaud, Y. & Kaab, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. The Cryosphere 7(6), 1885–1886, doi:10.5194/tc-7-1263-2013 (2013).
Kääb, A., Berthier, E., Nuth, C., Gardelle, J. & Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 488(7412), 495–498, doi:10.1038/nature11324 (2012).
Vincent, C. et al. Balanced conditions or slight mass gain of glaciers in the Lahaul and Spiti region (northern India, Himalaya) during the nineties preceded recent mass loss. The Cryosphere 7(2), 569–582, doi:10.5194/tc-7-569-2013 (2013).
Azam, M. F. et al. Reconstruction of the annual mass balance of Chhota Shigri glacier, Western Himalaya, India, since 1969. Annals of Glaciology 55(66), 69–80, doi:10.3189/2014AoG66A104 (2014).
Kumar, R. et al. Development of a glacio-hydrological model for discharge and mass balance reconstruction. Water Resources Management 30(10), 3475–3492, doi:10.1007/s11269-016-1364-0 (2015).
Bräuning, A. Tree-ring evidence of ‘Little Ice Age’ glacier advances in southern Tibet. The Holocene 16(3), 369–380, doi:10.1191/0959683606hl922rp (2006).
Loibl, D. M. & Lehmkuhl, F. Glaciers and equilibrium line altitudes of the eastern Nyainqêntanglha Range, SE Tibet. Journal of Maps 11(4), 575–588, doi:10.1080/17445647.2014.933451 (2015).
Xu, P., Zhu, H. F., Shao, X. M. & Yin, Z. Y. Tree ring-dated fluctuation history of Midui glacier since the little ice age in the southeastern Tibetan plateau. Science China Earth Sciences 55(4), 521–529, doi:10.1007/s11430-011-4338-3 (2012).
Zhu, H., Xu, P., Shao, X. & Luo, H. Little Ice Age glacier fluctuations reconstructed for the southeastern Tibetan Plateau using tree rings. Quaternary International 283, 134–138, doi:10.1016/j.quaint.2012.04.011 (2013).
Minora, U. et al. 2001–2010 glacier changes in the Central Karakoram National Park: a contribution to evaluate the magnitude and rate of the “Karakoram anomaly.”. The Cryosphere Discussions 7, 2891–2941, doi:10.5194/tcd-7-2891-2013 (2013).
Acknowledgements
We express our gratitude to Prof. Sunil Bajpai, Director, BSIP for providing official permission to publish (vide BSIP/RDCC/89/2016–2017) and necessary facilities to carry out this work. We also thank the PCCFs Uttarakhand, Himachal Pradesh and Jammu and Kashmir, and DFO Uttarkashi and other forest office staffs of the Indian Himalayan states for their help and providing necessary facilities during tree-ring sampling. We thank Mrs. Meenakshi Joshi (IFS) Uttarakhand for her insights on the topic and constructive suggestions. We thank Prof. Hans W. Linderholm and Prof. Dan J. Smith for sharing the mass balance time-series for Storglaciären (Sweden) and Canadian glaciers, respectively. M.S. acknowledges the financial support by the Department of Science and Technology, New Delhi vide SERB-DST Project No. SR/FTP/ES-127/2014 [Young Scientist Scheme]. P.S.R. extends his sincere acknowledgement to SERB–DST projects SR/DGH/44/2012 and SR/DGH/56/2013 for financial support to carry out this research work.
Author information
Authors and Affiliations
Contributions
M.S. conceptualised and designed the research and performed the tree-ring sampling. A.B., M.S. and S.S. performed statistical tests, and wrote the manuscript and materials and methods section with inputs from all the co-authors. M.S., A.K.P. and I.R. performed raw data generation and analysis. A.B., P.S.R., F.J.M.-T., and M.-P.Z. helped in analysing the results and correlating them with the climatic parameters.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shekhar, M., Bhardwaj, A., Singh, S. et al. Himalayan glaciers experienced significant mass loss during later phases of little ice age. Sci Rep 7, 10305 (2017). https://doi.org/10.1038/s41598-017-09212-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-09212-2
This article is cited by
-
Is climate change pushing gymnosperms against the wall in the northwestern Himalayas?
Regional Environmental Change (2023)
-
Habitat suitability, range dynamics, and threat assessment of Swertia petiolata D. Don: a Himalayan endemic medicinally important plant under climate change
Environmental Monitoring and Assessment (2023)
-
Tree ring derived summer temperature variability over the past millennium in the western Himalayas of northern Pakistan
Frontiers of Earth Science (2023)
-
Towards understanding various influences on mass balance of the Hoksar Glacier in the Upper Indus Basin using observations
Scientific Reports (2022)
-
Predicting habitat suitability and niche dynamics of Dactylorhiza hatagirea and Rheum webbianum in the Himalaya under projected climate change
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.