Abstract
A poor interface or defected interfacial segment may trigger interfacial cracking, loss of physical and mechanical functions, and eventual failure of entire material system. Here we show a novel method to diagnose local interphase boundary based on interfacial electron work function (EWF) and its gradient across the interface, which can be analyzed using a nano-Kelvin probe with atomic force microscope. It is demonstrated that a strong interface has its electron work function gradually changed across the interface, while a weaker one shows a steeper change in EWF across the interface. Both experimental and theoretical analyses show that the interfacial work function gradient is a measure of the interaction between two sides of the interface. The effectiveness of this method is demonstrated by analyzing sample metal-metal and metal-ceramic interfaces.
Similar content being viewed by others
Introduction
For functional and structural multiphase materials, composites and thin films, the interface between adjacent substances or phases plays a crucial role in affecting performance of the material systems. It is challenging to directly evaluate interfacial bonding strength. Although transmission electron microscopy is widely used to characterize interfacial structure and defects1, 2, it is difficult to simultaneously identify detrimental interfaces or interfacial segments as risk carriers, which may trigger global failure of thin films, multiphase and composite materials. Computational simulation provides valuable information on interfacial behavior3, 4. However, such computational analysis is feasible only for limited situations and insufficient for guiding material design. Although there are various methods for interfacial bonding evaluation, e.g., tension tests, peeling tests, local pushing tests, scratching tests, and quantification of interfacial fracture energy5,6,7,8,9,10,11,12,13 etc., these methods only provide information on average or overall interfacial bonding for films or coatings and composites. Thus, they are unable to capture local detrimental interfacial segments which could trigger global failure. Micro-indentation tests are often used to evaluate local interfacial failure from formed kinks on load-displacement curves or local cracking at interfaces13,14,15,16. However, cracking of hard brittle films or coatings themselves may also result in kinks on the indentation curves, and interfacial cracking could initiate from the hard/brittle coatings rather than at interface. Thus, alternative methods that can provide information on local interfacial failure are highly desired.
In principle, the interfacial bonding is largely determined by the electron behavior that determines atomic interactions at interface4, 17,18,19. The mechanical behavior of metals is correlated to their electron work function (EWF or φ)20,21,22,23, which is the minimum energy required to move electrons at Fermi level from inside a solid to its surface24. A higher EWF corresponds to a more stable electronic state, which is related to the stability of mechanical and electrochemical states of a solid or its resistance to mechanical and electrochemical attacks. A material with a higher EWF has stronger atomic bonds, higher elastic modulus and electrochemical resistance20,21,22,23,24,25. EWF can also be an indicator of interfacial strength. An early study shows that lower interfacial EWFs corresponds to weaker interfaces26. Compared to grains, grain boundaries have lower EWF27, leading to faster degradation when exposed to corrosive environments and lowered resistance to mechanical attacks such as creep28. However, interfaces do not always show low EWF. Electron localization may enhance the interfacial bonding for coherent interfaces29. In our studies, it is noticed that the gradient of EWF across an interface appears to reflect the interfacial bonding strength. An interfacial segment with a lower EWF gradient, dφ/dx, is stronger than one with a high gradient. This phenomenon is observed for both metal-metal and metal-ceramic interfaces. Thus, a further look into the correlation between EWF and interfacial strength could lead to new methodologies for interfacial evaluation.
In this article, we show a novel approach to diagnose local interphase boundary based on interfacial electron work function (EWF) and its gradient across the interface, which can be analyzed using a nano-Kelvin probe with atomic force microscope. The effectiveness of this method is demonstrated by analyzing sample metal-metal and metal-ceramic interfaces. First-principle analysis is also carried out to look into interfacial electronic configurations. Efforts are made to elucidate mechanisms responsible for the variation in EWF across the interface and its correlation with the interfacial bonding.
Samples materials for this study include conventional 2507 duplex stainless steel (DSS), Fe-45Cr-5C cast iron and TiC/Co composite. Specimens were wet ground with SiC paper up to 2000 grit, and then mechanically polished using a 1.5 µm-diamond paste. The steel sample was electrochemically polished using a solution of HNO3:H2O = 1:1 for 20 sec under an applied voltage of 1.2 V. The electrochemical polishing helped distinguish ferrite and austenite phases. All specimens were ultrasonically cleaned in ethanol and dried by a N2 gas flow. Experiments were performed using Bruker MultiMode AFM 8 with PeakForce KPFM capability. Bruker magnetic material coated probes (MESP) with 2.8 N/m force constant were used for the magnetic force microscopy (MFM) image and work function measurements, while Bruker ScanAsyst-Air probes with 0.4 N/m force constant and diamond probes with 350 N/m force constant were used to measure the modulus and deformation, respectively.
First-principles calculation was conducted using the Vienna Ab initio Simulation Package (VASP) with projector-augmented wave (PAW) potential30,31,32,33,34. The generalized gradient approximation (GGA) with the exchange-correlation functional of Perdew-Burke-Ernzerhof (PBE) was employed35. An cutoff energy of 400 eV and dense k-points sampling with a Methfessel-Paxton smearing of 0.2 eV were used to guarantee high numerical accuracy for both energy and stress optimization. The global break condition for the electronic self-consistency was chosen as 1.0 × 10–5 eV per supercell for all calculations. Due to the ferromagnetic nature of Fe, the spin-polarized set is necessary for our calculations. To investigate austenite/ferrite interfaces, we constructed 1 × 2 × 3 supercells of Fe-FCC (γ–Fe: a = 3.442 Å, b = 6.884 Å, c = 10.326 Å) on its primitive cell (a = b = c = 3.442 Å), and 1 × 2 × 4 supercells of Fe-BCC (α − Fe: a = 2.8664 Å, b = 5.7328 Å, c = 11.4656 Å) on its primitive cell (a = b = c = 2.8664 Å). (001) facet of the Fe-FCC supercell was connected to (001) and (021) facets of the Fe-BCC supercells to build (001)γ||(001)α and (001)γ||(021)α interfaces, respectively. For the calculation of work function, the vacuum layers of 15 Å were inserted in these interfacial models. It should be mentioned that thickness of the γ−Fe cell and that of α − Fe cell are 10.326 Å and 11.4656 Å, respectively. Thus, total thickness of the interface model with the additional vacuum layer of 15 Å is equal to about 36.7916 Å. Such a size should be large enough for calculating the system’s properties under study. For sufficient convergence, the tolerance value in the geometry optimization is 1.0 × 10−5 eV/atom, which is small enough to ensure accuracy of conducted calculations.
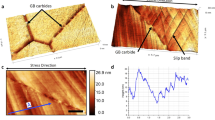
Ferrite/austenite interface in a duplex stainless steel (DSS) was investigated as an example of metal-metal interfaces. Figure 1(a) presents a MFM image (Magnetic Force Microscopy) of the steel, confirming that it consists of ferromagnetic ferrite (α) and paramagnetic austenite (γ). Corresponding maps of work function, elastic modulus and deformation are given in Fig. 1(b–d). Line profiles of the properties are also provided. As shown, the austenite has a higher work function than the ferrite, accompanied with larger modulus and smaller deformation magnitude than those of the ferrite. Average values of the properties are given in Table 1. As shown in Fig. 1(b), the EWF line profile cresses two F/A interface locations, which changes gradually at location 1 while rapidly at location 2. At interface, the modulus decreases along with a larger deformation magnitude. The modulus is dependent on the atomic bond strength and lattice configuration. A deeper interatomic potential well corresponds to higher bond stability, rendering the atomic bonding stronger. This is also applied to interfacial zone with disordered structure but the interatomic potential is the same. In general, the higher the interfacial modulus, the stronger is the interface36, 37. As demonstrated, the interface with smaller dφ/dx at location 1 is stronger than the one at location 2. We examined more α/γ interfacial locations and present results in Table 2. As shown, the larger the work function gradient, the weaker the interface.
Metal-ceramic interfaces show similar phenomenon. Figure 2 illustrates interfaces between (Fe 3 Cr 4)C 3 and ferrous matrix in a high-Cr cast iron. As illustrated, a larger dφ/dx results in a larger drop in modulus at location 2 (see Fig. 2(d and f)), corresponding to a lower mechanical stability of this interfacial zone. Similar situation is also observed in other metal-ceramic systems, e.g., TiC/Co interfaces as shown in Fig. 3, for which corresponding EWF gradients and interfacial moduli are given in Table 3.
(a) a MFM map (magnetic) and (b) corresponding EWF map of a TiC in a Co matrix; (c) linear profiles of EWF across three TiC/Co interfaces; EWF slopes and corresponding modulus values are given in Table 3.
To further look into the correlation between interfacial strength and EWF, we conducted first-principles analysis to look into variations in EWF across α/γ interfaces. Since we are interested in how the interfacial bonding strength is related to the work function rather than investigating specific interfaces, two interfaces consisting of low-index planes, (001)γ //(001)α and (001)γ //(021)α, were used for the analysis. The low-index surfaces, when joined, have relatively simple structures and low interfacial mismatches and stresses, which facilitate the analyses. Other pairs could also be used for the analysis. The interfacial strength is evaluated based on Griffith energy to destroy the interface. Figure 4 illustrates variations in EWF and electron density across two α/γ interfaces. Curves in blue represent the electrostatic potentials and red curves are work functions obtained by averaging the potentials. The sub-figures under the curves show variations in the electron density long [010] direction. Regions in blue are deficient in electrons while those in red are rich in electrons. The grey balls represent Fe ions.
Electrostatic potential, EWF and electron configuration in the interfacial regions of (a) (001) γ //(001) α interface with its binding energy = 7.758 eV/atom, and (b) (001) γ //(021) α interface with its binding energy = 5.475 eV/atom. The scale of the electron density ranges from −0.03 electron/Å3(blue) to 0.03 electron/Å3(red).
EWF is the energy required to move electrons at Fermi level from inside a metal to its surface without kinetic energy. We calculated the potentials (negative values) along [001] direction. Deep potential-wells correspond to large energies for electrons to be pulled out to the vacuum, while smaller energies are needed for electrons escape from lower potentials-wells. The average absolute value of potential along [001] represents the corresponding electron work function. In Fig. 4, average values of absolute potentials along [001] direction marked by red-lines are EWFs in our interface model. Thus, EWF gradient values, e.g., dφ/dx = 0.31 eV/Å, shown in Fig. 4(a) equals the difference in EWF (Δφ = 4.84–3.70 eV) between the two sides of the interface divided by the length of the interfacial region (Δx = 3.68 Å).
As shown in Fig. 4, the (001) γ //(001) α interface having a smaller EWF gradient (dφ/dx = 0.31 eV/Å) exhibits a stronger interface with its binding energy equal to 7.758 eV, while the (001) γ //(021) α interface with a larger work function gradient dφ/dx = 0.8 eV/Å is weaker with a binding energy of 5.475 eV. It should be noted that there is a drop of EWF at (001) γ //(021) α interface, which results from interfacial mismatch, leading to loose structure (see Fig. 4(b)). A loose structure is generally weaker with a lower electron density, corresponding to a lower EWF. This can be seen from the following analysis. As shown in Fig. 4(b), the trend of variations in EWF is similar to that for the electron density. This happens because the work function (φ) is correlated to the electron density (ρ e ) with a relationship20 as \(\phi \propto {\rho }_{e}^{1/6}\). A higher electron density corresponds to a higher work function. The electron density and its value and variation at interface affect the interfacial bonding, which is related to the electron density gradient: \(d\phi /dx\propto d/dx({\rho }_{e}^{1/6})\propto (1/6{\rho }_{e}^{5/6})d{\rho }_{e}/dx\). The drop in EWF at interface comes from lattice mismatch between two adjacent phases38, which results in interfacial strain or defects such as dislocations and vacancies. A loose interfacial structure has a lower electron density, which further increases the work function gradient as the denominator in the above equation is smaller. As a result, the local EWF gradient rather than average one should be used. For instance, in Fig. 4(b), dφ/dx = 0.8 eV/Å rather than dφ/dx = 0.26 eV/Å should be used for evaluating the interface. Or in other words, for a poor interface with a large lattice mismatch and resultant defects, the work function drops in the interfacial zone, which could be treated as a layer having a different configuration. In this case, the interfacial bonding strength should be dominated by the weakest region, corresponding to the steepest change in local work function i.e. the largest local work function gradient.
For a strong interface, strong interaction or “communication” between two sides of the interface results in a gradual change in EWF across the interface. If the interaction is weak, change in EWF across the interface should be steep. Steep variations in EWF are observed for incoherent interfaces and grain boundaries27, 38. The first-principle analysis supports the theoretical analysis, though further studies are needed in order to establish quantitative relationship between values from the experimental measurement and computational analysis.
We also analyzed interfaces between (Fe 3 Cr 4)C 3 and Fe with two orientation relationships: Fe(001)//(Fe 3 Cr 4)C 3(101) and Fe(001)//(Fe 3 Cr 4)C 3(001). Figure 5 shows interfacial structures, potentials and EWFs, and corresponding binding energies. Compared to the former, the latter is stronger with a smaller \(d\phi /dx=0.48eV/\mathop{{\rm{A}}}\limits^{\circ }\) corresponding to a larger binding energy of 543.18 eV/cell.
In order to understand the correlation between interfacial bonding and EWF or the electronic origin of interfacial strength, Fig. 6 illustrates what may happen as two metallic phases are in contact. As shown in Fig. 6(a and b), when two different metals are brought into contact, their Fermi levels must become equal39, 40. Thus, electrons will move from the metal with a lower work function (φ A ) to that having a high one (φ B ), driven by a potential difference, ΔV = (φ B − φ A )/e 0, where e 0 is the unit charge. As a result, a dipole layer will form at the A/B interface. If A and B are two pieces of identical metals, there is no a dipole layer and electrons can move freely across the interface, thus establishing metallic interaction or bonding, forming an integrated system as Fig. 6(c) shows. However, when two dissimilar metals are in contact, free electrons tend to locally redistribute, moving from the metal with a higher electron density to the one with a low electron density. However, on the other hand, the difference in EWF drives electrons to move from the metal having a low EWF to that having a high EWF. As a result, the dipole layer would act as a barrier to the electron migration, thus negatively affecting the development of interfacial bonding (Fig. 6(d)). Therefore, for a pair of dissimilar metals, the larger the difference in their EWF, the larger the barrier to the electron redistribution. Using the pair of identical metals with zero interfacial EWF (dφ/dx|int = 0) as a reference, a larger dφ/dx|int implies weaker “communication” between the two pieces of metals having a larger degree of dissimilarity. If there is no interaction, dφ/dx|int = ∞. \(\frac{d\varphi }{dx}{|}_{\mathrm{int}}\to \infty \) is an extreme case. Very dissimilar materials may still have strong interactions. For instance, carbides in cast irons show good bonding with the ferrous matrix, since the carbides have metallic bond components41, 42, leading to interactions with the metallic matrix. Van deer Waals interaction may also contribute to the interfacial bonding. For completely non-conductive materials, if there is no charge redistribution, interfacial bonding is hard to be established.
(a) Metals A and B are brought into contact, electrons migrate from A to B due to φ A < φ B ; (b) When A and B in contact, an interfacial dipole layer is established, driven by the potential difference, ΔV; (c) If A and B are identical, there is no a dipole layer and electrons can move freely across the interface; (d) If A and B are dissimilar, electrons tend to move from metal B with a higher electron density to metal A. On the other hand, the difference in EWF drives electrons to move from metal A to B. As a result, the formed dipole layer would act as a barrier to electron migration, thus negatively affecting the development of interfacial bonding.
The interfacial work function gradient is determinable. As Fig. 6(b) illustrates, there are charge depletion zones with opposite signs at two sides of the interface. The depletion width, x d , is proportional to the square root of the difference in EWF between the metals43, 44 i.e. \({x}_{d}^{2} \sim {\rm{\Delta }}\phi ={\phi }_{B}-{\phi }_{A}\). Thus, one may represent the EWF gradient at the interface as \({d\phi /dx|}_{\mathrm{int}}\approx {\rm{\Delta }}\phi /2{x}_{d}={\rm{\Delta }}\phi /2\sqrt{{\rm{\Delta }}\phi }=\sqrt{\Delta \phi }/2\). Such a relationship indicates that when two metals having a larger difference in EWF, a larger interfacial EWF gradient is generated, corresponding to weaker interfacial bonding. If one of the materials is non-conductive, no charge transfer is possible, leading to an infinite EWF gradient without forming interfacial bonding. For an interface with large lattice mismatch, one may treat the interfacial region as a layer of different material with high disordering. The above discussion or theoretical consideration is still applicable.
It should be pointed out that the formation of the diploe layer causes local charge redistribution, which is related to local atomic displacement or local oscillations of interplanar distances45, 46 and thus generates interfacial strain. From the view-point of thermodynamics, if the two dissimilar materials have little interaction, no or little local charge redistribution would occur at the interface, corresponding to a large interfacial EWF gradient, dφ/dx|int and a high interfacial energy (γ AB ). If the dissimilar materials chemically interact but no sufficient local lattice relaxation occurs (corresponding to high dφ/dx|int), the large interfacial misfit strain helps increase the interfacial energy (γ AB ). As a result, the work of adhesion, W AB = γ A + γ B − γ AB (γ A and γ B are surface energies of materials A and B), would be low, corresponding to weak interfacial bonding. If the interfacial structure can be relaxed with minimized interfacial strain towards equilibrium, stronger bonding with a lowered interfacial EWF gradient is expected. We would like to indicate that though the local charge redistribution is complicated, depending on the specific material pair and bond type45,46,47, the proposed mechanism for the interfacial bonding should be a general view related to electronic process for the development of interfacial bonding.
In conclusion, we demonstrate a novel method to diagnose local interphase boundary based on interfacial electron work function (EWF) and its gradient across the interface (\(\frac{d\phi }{dx}{|}_{\mathrm{int}}\)), which can be analyzed using a nano-Kelvin probe with atomic force microscope. It is shown that that a strong interface has its electron work function gradually changed across the interface, while a weaker one shows a steeper change in EWF across the interface. Besides, EWF may drop at a poor interface, e.g., an incoherent interface where interfacial defects lead to lowered electron density, since EWF is related the electron density. In this case, the drop of EWF caused by the interfacial defects enlarges the local \(\frac{d\phi }{dx}{|}_{\mathrm{int}}\), thus further weakening the interface. Both experimental and theoretical studies confirm that the interfacial work function gradient is a measure of the interaction between two sides of the interface. The effectiveness of this method is demonstrated by analyzing sample metal-metal and metal-ceramic interfaces. Underlying mechanism is elucidated.
References
Du, J. L. et al. What determines the interfacial configuration of Nb/Al2O3 and Nb/MgO interface. Scientific Reports 6, 33931 (2016).
Torazawa, N., Arai, S., Takase, Y., Sasaki, K. & Saka, H. Transmission Electron Microscopy of Interfaces in Joints between Pb-Free Solders and Electroless Ni–P. Materials Transactions 44, 1438–1447 (2003).
Lv, C. et al. Effect of Chemisorption on the Interfacial Bonding Characteristics of Graphene−Polymer Composites. J. Phys. Chem. C 114, 6588–6594 (2010).
Cao, R. et al. Interfacial bonding and electronic structure of GaN/GaAs interface: A first-principles study. J. Appl. Phys. 117, 135302 (2015).
Shieu, F. S. & Shiao, M. H. Measurement of the interfacial mechanical properties of a thin ceramic coating on ductile substrates. Thin Solid Film 306, 124–129 (1997).
Laua, D., Broderick, K., Buehlera, M. J. & Oral, B. A robust nanoscale experimental quantification of fracture energy in a bilayer material system. PNAS 111, 11990–11995 (2014).
Xie, M. & Vistasp, K. Peel test for characterization of polymer composite/concrete interface. J Compos Mater. 32, 1894–1913 (1998).
Molina-Aldareguia, J. M., Rodriguez, M., González, C. & Llorca, J. An experimental and numerical study of the influence of local effects on the application of the fibre push-in test. Phil. Mag. A 91, 1293–1307 (2011).
Kong, D., Fu, G. & Wang, J. Interfacial bonding mechanism and bonding strength of AlTiCrN coating by cathodic arc ion plating. Surf. Interface Anal. 47, 198–205 (2015).
Liu, C. Q., Li, M. S., Jin, Z. J. & Wu, W. T. Tensile and adhesive strengths of fine TiN film on Ti substrate. Acta Metqllurfica Sinica, Series B: Process metallurgy and Miscellaneous 6B, 126–129 (1993).
Burnett, P. J. & Rickerby, D. S. The scratch adhesion Test: an elastic-plastic indentation analysis. Thin Solid Film 157, 233–254 (1988).
Dai, Y. & Kim, J. K. Numerical study of the single fibre push-out test: Part I. Mechanics of the test. Composite Interfaces 5, 323–343 (1998).
Chen, J. J. & Bull, S. J. Approaches to investigate delamination and interfacial toughness in coated systems: an overview. Journal of Physics D: Applied Physics 44, 034001 (2010).
Hainsworth, S. V., McGurk, M. R. & Page, T. F. The effect of coating cracking on the indentation response of thin hard-coated systems. Surface coatings and technology 102, 97–107 (1998).
Lu, Y. & Shinozaki, D. M. Microindentation induced debonding of polymer thin films from rigid substrates. Journal of Materials Science 37, 1283–1293 (2002).
Demarecaus, P. H., Chicot, D. & Lesage, J. Interface indentation test for the determination of adhesive properties of thermal sprayed coatings. Journal of materials science letters 15, 1377–1380 (1996).
Xiong, K. et al. Interfacial bonding and electronic structure of HfO2/GaSb interfaces: A first principles study. Appl. Phys. Lett. 102, 022901 (2013).
Magri, R. & Zunger, A. Effects of interfacial atomic segregation and intermixing on the electronic properties of InAs/GaSb superlattices. Phys. Rev. B 65, 165302 (2002).
Aouadi, S. M., Shreeman, P. K., Ge, Q., Xu, J. & Mishra, S. R. Correlation Between Interfacial Electronic Structure and Mechanical Properties of ZrN–Me (Me=Ag, Au, or Pd) Nanocomposite Films. Applied Physics Letters 87, 041902 (2005).
Hua, G. & Li, D. Y. Generic Relation between the Electron Work Function and Young’s Modulus of Metals. Appl. Phys. Lett. 99, 041907 (2011).
Lu, H. et al. Electron work function – a promising guiding parameter for material design. Scientific Report - Nature, Sci Rep. 6, 243662016 (2016).
Hua, G. & Li, D. Y. Electron Work Function: A Novel Probe for Toughness. PCCP 18, 4753–4759 (2016).
Wang, X. F. et al. An electronic criterion for assessing intrinsic brittleness of metallic glasses. The Journal of Chemical Physics 141, 024503 (2014).
Lang, N. D. & Kohn, W. Theory of Metal Surfaces: Work Function. Phys. Rev. B3, 1215–1223 (1971).
Li, W. & Li, D. Y. Variations of work function and corrosion behaviour of deformed copper surfaces. Appl. Surf. Sci. 240, 388–395 (2005).
Li, W. & Li, D. Y. Characterization of interfacial bonding using a scanning Kelvin probe. J. of Appl. Phys. 97, 014909 (2005).
Li, W. & Li, D. Y. Effect of grain size on the electron work function of Cu and Al. Surf. Rev. and Lett. 11, 173–178 (2004).
Wadsworth, J., Ruano, O. A. & Sherby, O. D. Denuded Zones, Diffusional Creep, and Grain Boundary Sliding. Metall. and Mater. Trans. 33A, 2002–219 (2002).
Mosleh-Shirazi, S, Hua, G., Akhlaghi, F, Yan, X. G., Li, D. Y. Interfacial valence electron localization and the corrosion resistance of Al-SiC nanocomposite. Scientific Report - Nature 18154 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B 54, 11169 (1996).
Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. Journal of computational chemistry 29, 2044–2078 (2008).
Vočadlo, L., Alfè, D. & Gillan, M. J. et al. Possible thermal and chemical stabilization of body-centred-cubic iron in the Earth’s core. Nature 424, 536–539 (2003).
Alfe, D., Gillan, M. J. & Price, G. D. Constraints on the composition of the Earth’s core from ab initio calculations. Nature 405, 172–175 (2000).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Physical Review B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Physical Review Letters 77, 3865 (1996).
Le, E A., Nairn, John A. Measuring Interfacial Stiffness of Adhesively-Bonded Wood, Wood Science & Technology, doi: 10.1007/ s00226-014-0661-0 (2014).
Cantrell, J. H. Hydrogen bonds, interfacial stiffness moduli, and the interlaminar shear strength of carbon fiber-epoxy matrix composites. AIP Advances 5, 037125 (2015).
Yang, Z. R., Lu, H., Liu, Z. R., Yan, X. G. & Li, D. Y. Effect of particle size on the surface activity of TiC-Ni composite coating via the interfacial valence electron localization. RSC Advances 6, 18793–18799 (2016).
Peljo, P., Manzanares, Jose, A., Girault & Hubert, H. Contact Potentials, Fermi Level Equilibration, and Surface Charging. Langmuir 32, 5765–5775 (2016).
Marder, M P. Condensed Matter Physics, John Wiley & Sons, Inc., New York (2000).
Cuppari, M. G. D. V. Santos, Sydney Ferreira, Physical Properties of the NbC Carbide. Metals 6, 250, doi:10.3390/met6100250 (2016).
Gubanov, V. A., Ivanovsky, A. L., Zhukov, V. P. Electronic Structure of Refractory Carbides and Nitrides; Cambridge University Press: Cambridge, UK, (2005).
Wallis, R. H. Chapter 6 - Key Electrical Devices, In Electronic Materials from silicon to organics, edited by L. S. Miller & J. B. Mullin, Plenum Press, New York, (1991).
Ibach, Harald, Luth, Hans, Solid-State Physics – An introduction to principles of materials science, 4th ed., Springer, New York, 2009).
Zhang, Z. et al. Superlattice-induced oscillations of interplanar distances and strain effects in the CrN/AlN system. Physical Review B 95, 155305 (2017).
Zhang, R. F., Argon, A. S. & Veprek, S. Friedel Oscillations are Limiting the Strength of Superhard Nanocomposites and Heterostructures. Physical Review Letts. 102, 015503 (2009).
Zhang, R. F., Argon, A. S. & Veprek, S. Understanding why the thinnest SiNx interface in transition-metal nitrides is stronger than the ideal bulk crystal. Physical Review B 81, 245418 (2010).
Acknowledgements
The authors are grateful for financial support from the Natural Science and Engineering Research Council of Canada, Camber Technology Corp., Suncor Energy, Shell Canada Ltd., Magna International Inc. and Volant Products Inc. The authors would also like to thank V. Kumar for relevant discussions.
Author information
Authors and Affiliations
Contributions
D.Y. Li conceived the original idea and planned the study, conducted the theoretical analysis, and wrote the manuscript; Liqiu Guo carried out AFM mapping for duplex stainless steel and cast iron as well as prepared a portion of initial draft, including experimental methods, observations and relevant discussions; Lei Li conducted the first-principle calculations and provided the description of calculation methods; Hao Lu conducted AFM mapping for the TiC/Co sample.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, D.Y., Guo, L., Li, L. et al. Electron work function – a probe for interfacial diagnosis. Sci Rep 7, 9673 (2017). https://doi.org/10.1038/s41598-017-08841-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-08841-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.